30 Winkelfunktionen im rechtwinkligen Dreieck

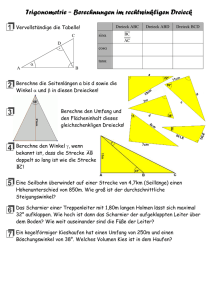
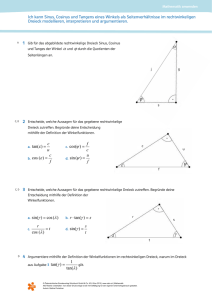
30 Winkelfunktionen im rechtwinkligen Dreieck
B
1
P
cos a
b
1 = ____
__
⇔ cos a = __
c
c
b
Ankathete von a
_____________
cos a = Hypotenuse
c
1
Ankathete von a
tan a
a
tan a
a
1 = ____
__
__
a ⇔ tan a = b
b
Gegenkathete von a
tan a = ________________
Das rechtwinklige
Dreieck mit dem weiteren Winkel a kann so
auf den Einheitskreis
gelegt werden, dass eine
„Strahlensatzfigur“
entsteht.
1. Ergänze die fehlende Seite.
a)
w
s
sin a = __
p
1
y
x
b
a
c
a
a
a
y
b
b
____
cos a = __
y ⇔ y = cos a
sin a = __ax ⇔ x = a · sin a
w
tan a = __
m
m
cos a = __
r
m
tan d = __
w
w
cos d = __
r
m
sin d = __
r
b
b
x+y
tan a = ____
a
b
cos g = __
c
a
cos a = __
x+y
sin a = ____
g
h
g
«
f
t
h
tan g = __
d
f
3. Berechne die fehlenden Seiten des Dreiecks.
y
9,5 cm
cos 41° = _____
tan 41° = _____
x
9,5 cm
c) eine Kathete gegeben und
die andere Kathete gesucht.
w
sin a = __
r
g
a
Neben dem rechten Winkel ist ein weiterer Winkel a gegeben, außerdem sei:
b) eine Kathete gegeben und
die Hypotenuse gesucht.
b)
c
a
Berechnung von Seiten im rechtwinkligen Dreieck
x
tan b = _st
d
C
d
t
a
cos a
b
r
a
d
a) die Hypotenuse gegeben
und eine Kathete gesucht.
a
p
s
x
A
2. Schreibe das Seitenverhältnis auf.
m
a)
b
b)
sin a
sin a
a
1 = ____
__
__
c
a ⇔ sin a = c
Gegenkathete von a
sin a = ________________
Hypotenuse
9,5 cm
x = ______
cos 41°
y = 9,5 cm · tan 41°
x ≈ 12,6 cm
y ≈ 8,3 cm
9,5 cm
Sinus, Kosinus und Tangens als Seitenverhältnisse
t
cos « = __
g
h
sin « = __
g
x
41º
y
4. Ein startendes Flugzeug hebt an der Stelle F ab und steigt mit 6° an.
Wie hoch überfliegt es das 25 km von F entfernte Dorf Schulzenheim?
z
c
tan a = _cz ⇔ z = ____
tan a
x
F
x
tan 6° = _____
25 km
Berechnung eines Winkels im rechtwinkligen Dreieck
gegeben: a und m; gesucht: a
m
a
a
a
a
__
cos a = __
m ⇔ a = inv cos ( m )
5. Berechne den Winkel a.
gegeben: p und q; gesucht: b
Statt „invers cosinus“
sagt man auch
„arcus cosinus“,
im Zeichen: „arc cos“.
p
q
b
p
( p)
__
tan b = __
q ⇔ b = arc tan q
x ≈ 2,63 km ⇒ Es überfliegt Schulzenheim in ca. 2,63 km Höhe.
a
9,
6c
7,2 cm
m
7,2 cm
sin a = _____
9,6 cm
sin a = 0,75
a ≈ 48,6°
sin a = 0,75
Zur Berechnung von a
muss ich die Tastenfolge
2nd sin bzw. INV sin
drücken.