Teil 3

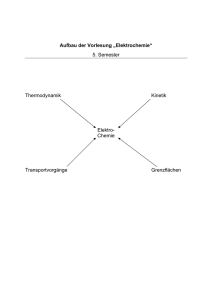
Elektrochemie
Transportphänomene
Diffusion, elektrische
Leitfähigkeit
GS
23.05.2007
Vorlesung Elektrochemie
65
Elektrochemie
Transportphänomene, Diffusion, elektrische Leitfähigkeit
• Fluss J von Teilchen i in einem homogenen
Medium durch eine (beliebig kleine) Fläche A
• Nur der zu A senkrechte Anteil des Flusses
wird berücksichtigt
J
• Volumen V bleibt konstant
G 1 ∂ ni rGi
G
G
,
Ji =
=
c
r
t
⋅
v
(
)
G
i
i
i
A ∂ t ri
A
G
• vi lokale Geschwindigkeit der lokalen Konzentration ci(r, t)
G G
G
vi = viint + viext
• erzwungene (externe) Geschwindigkeit durch Rühren o.a.
• Interne Geschwindigkeit durch Felder (elektrisch, Gravitation)
und durch Konzentrationsgradienten
GS
23.05.2007
Vorlesung Elektrochemie
G
viext
G
viint
66
Elektrochemie
Transportphänomene, Diffusion, elektrische Leitfähigkeit
Materiefluss in homogenen dichten Medien
→
G
D ⋅z ⋅F G
G
J i = − Di ⋅ gradci + ci i i
E + ci ⋅ viext
RT
• Erster Term: Diffusion in einem Konzentrationsgradienten
• Zweiter Term: Migration im äußeren Feld
(elektrisch, magnetisch, Gravitation)
• Dritter Term: Konvektion durch eine von
außen erzwungene Geschwindigkeit der
Lösung.
GS
23.05.2007
Nernst-Planck-Gleichung
1. Diffusion
2. Migration
3. Konvektion
Vorlesung Elektrochemie
⎫G
⎛ Di ci ⎞ → ⎬ Ji = − ⎜
⎟ grad μi
RT
⎝
⎠
⎭
G
G
J i = ci v ext
67
Elektrochemie
Transportphänomene, Diffusion, elektrische Leitfähigkeit
Elektrochemisches Potential einer Ionensorte i :
→
c
G
μ i = μi + ne− Fϕ = μiØ + RT ln Øi + ne− Fϕ
E = − gradϕ
c
Chemisches Potential geladener Komponenten in einem äußeren elektrischen Feld
Hier keine Berücksichtigung des Aktivitätskoeffizienten
Kraft auf die Komponente i durch elektrochemisches Potential
→
Gμ
K i = − grad μ i
μ i elektrochemisches Potential der
Komponente i
Gegenkraft durch innere Reibung der
Teilchen
Gω
G
K i = −viint N A Ri
Ri
Reibungskoeffizient des Teilchens i
Ri = 1 ωi ωi : Generalisierte Geschwindigkeit
G μ Gω
Stationärer Zustand: K i + K i = 0
G
Konstante interne Geschwindigkeit: viint = const
→
G
− grad μ i = viint N A Ri
GS
23.05.2007
Vorlesung Elektrochemie
68
Elektrochemie
Transportphänomene, Diffusion, elektrische Leitfähigkeit
Das elektrochemische Potential
Gradient des elektrochemischen Potentials
→
→
→
→
RT →
gradμ i = RT grad ln ( ci ) + zi ⋅ F ⋅ gradϕ =
gradci + zi ⋅ F ⋅ gradϕ
ci
Interne Geschwindigkeit
→
ωi RT →
ωi
G int
vi = −
zi ⋅ F ⋅ gradϕ
gradci −
N Aci
NA
→
G
Di ⋅ zi ⋅ F →
G
J i = − Di ⋅ gradci − ci
gradϕ + ci ⋅ viext
RT
→
G
Di ⋅ zi ⋅ F G
G
J i = − Di ⋅ gradci + ci
E + ci ⋅ viext
RT
23.05.2007
ωi RT
NA
= k BT ωi
Di : Diffusionskoeffizient
Materiefluss
GS
Di =
G
E : elektrisches Feld
Vorlesung Elektrochemie
69
Elektrochemie
Transportphänomene, Diffusion, elektrische Leitfähigkeit
Modell 1
G
• Keine erzwungene Strömung viext = 0
G
• Kein elektrisches Feld
E=0
• Nur Diffusion
→
G
J i = − Di ⋅ gradci
1. Ficksches Gesetz
• Keine Kraft durch irgendein Feld notwendig
Diffusion als molekularer Prozess
• Bewegung von Teilchen auch in homogenen Medien durch lokale Dichtegradienten
• Wechsel des Ortes eine Teilchens zu einem anderen über eine charakteristische Strecke l
innerhalb einer Zeit τ
• Bewegungsrichtung ist zufällig
GS
23.05.2007
Vorlesung Elektrochemie
70
Elektrochemie
Transportphänomene, Diffusion, elektrische Leitfähigkeit
Diffusion als molekularer Prozess
Schrittweise ungerichtete Bewegung
x22 = 2l 2 − 2l 2 cosθ 2
x32 = l 2 + x22 − 2lx2 cosθ3
= 3l 2 − 2l 2 cosθ 2 − 2l 2 2 − 2cosθ 2 cosθ 3
n
xn2 = nl 2 − ∑ ai cosθi
θ3
θ2
i=2
Mittelwertbildung
π
Integration über alle Winkel von 0 bis π
2
n
x
= nl
2
∫ cosθ dθ = sin θ
π
0
=0
0
Mittleres Abstandsquadrat proportional der Anzahl n Sprünge
Gesamtdauer t der Bewegung: t = n·τ
GS
23.05.2007
x
Vorlesung Elektrochemie
2
n
=t
l2
τ
71
Elektrochemie
Transportphänomene, Diffusion, elektrische Leitfähigkeit
Diffusion
Mittlere Stecke eines Teilchens innerhalb t
x2
Menge von Teilchen in linkem Kompartiment,
die sich durch Fläche T in der Zeit t von links
nach rechts bewegen
n
1
nL = 1 2 cL A x 2
J L = L = cL x 2
At 2t
Menge von Teilchen rechts nach links
nR = 1 2 cR A
JR =
x2
nR
1
= cR
At 2t
L
JL
cL
JR
T
cR
R
2
x2
√<x >
Resultierender Fluss
J = JL − JR =
GS
1
2t
23.05.2007
x2
( cL − cR )
Vorlesung Elektrochemie
72
Elektrochemie
Transportphänomene, Diffusion, elektrische Leitfähigkeit
Diffusion
Konzentrationsgradient
dc cR − cL
c −c
≈
=− L R
dx
x2
x2
Einsetzen in Flussgleichung
cL − cR = −
x2
dc
dx
Ficksches Gesetz
1 2 dc
dc
x
J = −D
2t
dx
dx
Gleichung von Einstein-Smoluchowski
J =−
Diffusionskoeffizient
x2
D=
2t
x 2 = 2tD
Reduktion auf einen einzigen Platzwechsel mit mittlerer Sprunglänge l
l 2 = 2 Dτ
D ≈ 10-5 - 10-4 cm2s-1
k = τ −1: Mittlere Sprungfrequenz eines Diffusionsschrittes l ≈ 10-8 - 10-7 cm
τ ≈ 10-9 - 10-8 s
Diffusion über makroskopische Strecken : sehr langsamer Prozess
GS
23.05.2007
Vorlesung Elektrochemie
73
Elektrochemie
Transportphänomene, Diffusion, elektrische Leitfähigkeit
Diffusion
Nicht-stationäre Bedingungen für Fluss, wenn c ortsabhängig
links
G
dc
J in = − D
dx
Jin
Δx
c
G
G
d 2c
J out − J in = D 2 Δx
dx
Wenn
(
rechts
G
d ⎛
dc ⎞
J out = − D ⎜ c − Δx ⎟
dx ⎝
dx ⎠
Jout
A
dc
d 2c
= − D + D 2 Δx
dx
dx
c - (dc/dx)Δx
G
G
J out − J in
dJ
dJ ⋅ A
dn
dc
⇒ x = x
=
=−
Δx
dx
A ⋅ dx dt ⋅V
dt
G
G
J out − J in > 0, ist Konzentrationsänderung in Volumen V negativ
)
Erweiterung auf 3 Koordinaten x, y, z
G
dJ y dJ z ⎞
⎛ dJ
dc
div
J
= −⎜ x +
+
=
−
⎟
dt
dy
dz ⎠
⎝ dx
Netto-Änderung der Menge im Volumen dV = Ergiebigkeit = Divergenz des Flusses J
GS
23.05.2007
Vorlesung Elektrochemie
74
Elektrochemie
Transportphänomene, Diffusion, elektrische Leitfähigkeit
Diffusion
Verallgemeinerung auf beliebiges 3-dimensionales Koordinatensystem
Lokale Konzentration als Funktion von Ort und Zeit
2. Ficksches Gesetz
G
→
→
G
∂ ci ( r , t )
G
G
G
= −div J i = div Di grad ci (r , t ) = Di div grad ci ( r , t ) = Di Δci (r , t )
∂t
→
div grad = Δ ; Δ = Laplace-Operator
Gerichteter Materiefluss ändert die Konzentrationen ⇒
2. Ficksches Gesetz Grundlage aller Modelle, bei denen in homogener Lösung Komponenten
verbraucht oder gebildet werden
∂ ci
G
= Di Δci (r , t )
∂t
Wird später bei Untersuchung von Prozessen an Elektroden gebraucht
GS
23.05.2007
Vorlesung Elektrochemie
75
Elektrochemie
Transportphänomene, Diffusion, elektrische Leitfähigkeit
Geometrie
Laplace-Operator
Geometrie
Zylinderkoordinaten: ρ, φ, z
Kartesische Koordinaten: x, y, z
∂2 2 ∂
∂2
1 ∂2
Δ= 2 +
+
+
∂ρ
ρ ∂ρ ∂ z 2 ρ 2 ∂φ 2
z
x
y
Δ=
∂
∂
∂
+
+
∂ x2 ∂ y2 ∂ z 2
2
Laplace-Operator
2
2
Kartesische Koordinaten, 1 Richtung: x
∂2
Δ= 2
∂x
Kugelkoordinaten: r, θ, φ
θ
r
φ
Kugelkoordinaten, keine Winkelabhängigkeit,
nur Abhängigkeit in r
Δ=
∂2 2 ∂
Δ= 2 +
∂r
r ∂r
GS
23.05.2007
Vorlesung Elektrochemie
1 ∂ ⎛ 2 ∂ ⎞
1
∂ ⎛
∂ ⎞
r
sin
θ
+
⎜
⎟
⎜
r 2 ∂ r ⎝ ∂ r ⎠ r 2 sin θ ∂θ ⎝
∂θ ⎟⎠
1
∂2
+ 2
r (sin θ ) 2 ∂φ 2
76
Elektrochemie
Transportphänomene, Diffusion, elektrische Leitfähigkeit
Diffusion
Diffusion:
• Selbst-Diffusion oder Tracer Diffusion
Mikroskopischer Prozess, Diffusion eines markierten Teilchens in einer Lösung konstanter
Konzentration
Radioaktive Markierung
• Chemische Diffusion
Phaseneigenschaft einer Lösung; Erzeugung eines Konzentrationsgradienten
Freie Diffusion bei Konzentrationsgradient in räumlich unbeschränkten Volumen
Beschränkte Diffusion mit definierten Konzentrations-Bedingungen an
Volumengrenzen
Steady-State Diffusion durch Diaphragma
Diffusion durch Konzentrationsfluktuationen δci in der Lösung (i = + oder -)
→
G
G
e0 zi G
∂
⎡
⎤
c
J
J
D
c
D
c
E
δ
div
δ
;
grad
=
−
=
−
+
[ i]
i⎦
i
i
i
i i
⎣
kT
∂t
B
GS
23.05.2007
Vorlesung Elektrochemie
77
Elektrochemie
Transportphänomene, Diffusion, elektrische Leitfähigkeit
Diffusion
Diffusion:
G
ε 0ε div E = e0 N A ∑ zi ( cieq − δ ci )
Poisson-Gleichung
i
Lösung des Gleichungssystems liefert
(
)
−1
τ D = q D+ + q D−
• Debye-Relaxationszeit τD:
Zeit zur Einstellung der lokalen Elektroneutralität: τD ≈ 1 bis 10 ns
2
+
• Diffusionskoeffizient D des Elektrolyten (Nernst-Hartley)
exakt nur für unendlich kleine Konzentration
• Gekoppelte Diffusion
2
−
D=
e02 zi2
; q =
N Acieq
ε 0ε kT
2
i
D+ D− ( q+2 + q−2 )
q+2 D+ + q−2 D−
∞
= DNH
Kopplung beider Prozesse
• Kopplung von Diffusion mit chemischer Reaktion
Erzeugung von Konzentrationsquellen und Senken durch chemische Reaktionen
GS
23.05.2007
Vorlesung Elektrochemie
78
Elektrochemie
Laplace-Transformation (Zusatz)
Lösung der partiellen Differentialgleichung
∂ ci
G
Ableitungen nach Zeit und Ort
= Di Δci (r , t )
∂t
Laplace-Transformation dann, wenn Zeitabhängigkeit zwischen 0 und +∞
∞
L { f (t )} = f ( s ) = ∫ f (t )e − st dt
0
Beispiele:
∞
∞
a
f (t ) = a : L { f (t )} = ∫ a ⋅ e dt =
s
0
f (t ) = t : L { f (t )} = ∫ t ⋅ e − st dt =
− st
∞
0
n!
f (t ) = t : L { f (t )} = ∫ t ⋅ e dt = n +1
s
0
n
n
∞
f ( x) :
L { f ( x )} = ∫ f ( x ) ⋅ e − st dt =
0
GS
− st
23.05.2007
f (t ) = a ⋅ e
− b( t −τ )
∞
1
s2
: L { f (t )} = ∫ a ⋅ e
0
b( t −τ )
e − bτ
⋅ e dt = a
s−b
− st
f ( x)
s
Vorlesung Elektrochemie
79
Elektrochemie
Laplace-Transformation (Zusatz)
f (t )
L { f ( x )} = f ( s )
1
1s
λ
λ s
1 πt
1
eω t
1 (s − ω)
1
1 ( s2 + ω 2 )
ω
sin (ωt )
cos (ωt )
⎡ k2 ⎤
exp ⎢ − ⎥
πt
⎣ 4t ⎦
1
⎡ k2 ⎤
⎛ k ⎞
2
exp ⎢ − ⎥ − k erfc ⎜
⎟
π
⎝2 t ⎠
⎣ 4t ⎦
t
GS
23.05.2007
s
s ( s2 + ω 2 )
1
exp ⎡⎣ − k s ⎤⎦ ; ( k > 0 )
s
s −3 2 exp ⎡⎣ − k s ⎤⎦ ; ( k > 0 )
Vorlesung Elektrochemie
80
Elektrochemie
Laplace-Transformation (Zusatz)
Laplace-Transformation der Zeit-Ableitung
∂ f (t )
∂t
∞
L { f ′(t )} = ∫ f ′(t ) ⋅ e dt = f (t ) ⋅ e
− st
− st ∞
0
0
∞
+ s ∫ f (t ) ⋅ e − st dt = − f (0) + s ⋅ f ( s )
0
Partielle Integration ⇒ Umwandlung der Differentialgleichung in analytische Gleichung, aber
Einbezug der Anfangsbedingung!
Linke Seite der Diffusionsgleichung mit 1 Translationskoordinate:
∂ c( x, t )
⇒ s ⋅ c ( x, s ) − c( x,0) = s ⋅ c ( x, s ) − c 0
∂t
c0 = globale Konzentration vor
Diffusionsprozess
Rechte Seite der Diffusionsgleichung:
L {D ⋅ Δc( x, t )} = D ⋅ Δc ( x, t )
2. Ficksche Gleichung im Laplace-Raum
∂ 2 c ( x, s )
s ⋅ c ( x, s ) − c = D
∂ x2
0
GS
23.05.2007
Totale DGL in einer Ortskoordinate
Vorlesung Elektrochemie
81
Elektrochemie
Laplace-Transformation (Zusatz)
Transformation auf Störung gegenüber der globalen Konzentration c0 ≠ f(x,t)
∂c( x, t ) ∂c1 ( x, t ) ∂ 2 c( x, t ) ∂ 2 c1 ( x, t ) 0
c( x, t ) = c1 ( x, t ) + c ⇒
;
; c1 = 0
=
=
∂t
∂t
∂x 2
∂x 2
0
∂ 2 c1 ( x, s ) s
= ⋅ c1 ( x, s )
2
D
∂x
Allgemeine Lösung
⎡
⎡ s ⎤
s ⎤
c1 ( x, s ) = A( s ) exp ⎢ −
x ⎥ + B ( s ) exp ⎢
x⎥
D
D
⎣
⎦
⎣
⎦
Laplace-Transformation der Randbedingungen:
1.2.1
c1 ( x, s ) bleibt endlich für große x
⎡
s ⎤
c1 ( x, s ) = A( s ) exp ⎢ −
x⎥
D
⎣
⎦
GS
23.05.2007
Vorlesung Elektrochemie
82
Elektrochemie
Laplace-Transformation (Zusatz)
1.2.2 Bei x = 0 werde ein konstanter Teilchenfluss J0 erzeugt
J0
⎛ ∂ c ( x, t ) ⎞
⎛ ∂ c1 ( x, t ) ⎞
⇒
=
−
J0 = −D ⎜ 1
⎟
⎜
⎟
D
⎝ ∂ x ⎠ x =0
⎝ ∂ x ⎠ x =0
⎧⎛ ∂ c ( x, t ) ⎞ ⎫ ⎛ ∂ c1 ( x, t ) ⎞
1
1 J0
L ⎨⎜ 1
L
J
=
=
−
=
−
{ 0}
⎟ ⎬ ⎜
⎟
∂
x
∂
x
D
D s
⎝
⎠
⎝
⎠
⎩
x =0 ⎭
x =0
J0
0
Es gilt aber auch:
t
⎛ s
⎡
s ⎤⎞
s
⎛ ∂ c1 ( x, t ) ⎞
A
exp
x
A
=
−
−
=
−
⎜
⎟
⎢
⎥
⎜
⎟
⎜ D
⎟
D
⎝ ∂ x ⎠ x =0
⎣ D ⎦ ⎠ x =0
⎝
Für A gilt dann:
−A
GS
J
J
s
= − 0 ⇒ A= 32 0 12
D
s⋅D
s ⋅D
23.05.2007
Vorlesung Elektrochemie
83
Elektrochemie
Laplace-Transformation (Zusatz)
Damit gilt:
c1 ( x, s ) =
⎡
⎡
J0
s ⎤
1
s ⎤ −
=
−
exp
x
exp
x⎥ ⋅ J 0
⎢
⎥
⎢
12
12
⋅
s 3 2 ⋅ D1 2
D
s
D
D
⎣
⎦
⎣
⎦
Lösung der Differentialgleichung im Zeit-Raum
Rücktransformation
{
}
L−1 f ( s ) = f (t )
im komplexen Laplace-Raum oder mit Tabelle
Damit muss gelten mit k = x
D:
⎡ x2 ⎤
J0 ⎡ t
x
⎛ x ⎞⎤
c1 ( x, t ) = ⎢ 2
exp ⎢ −
erfc
−
⎜
⎟⎥
⎥
D⎣ π
D
⎝ 2 Dt ⎠ ⎦
⎣ 4 Dt ⎦
⎡ x2 ⎤
J0 ⎡ t
x
⎛ x ⎞⎤
c ( x, t ) = c0 − c1 ( x, t ) = c0 − ⎢ 2
exp ⎢ −
⎥ − D erfc ⎜ 2 Dt ⎟ ⎥
D⎣ π
Dt
4
⎝
⎠⎦
⎣
⎦
GS
23.05.2007
Vorlesung Elektrochemie
84
Elektrochemie
Laplace-Transformation (Zusatz)
Allgemein kann man schreiben:
c ( x, s ) = y ( s ) ⋅ J
y(s) = nicht-lineare Übertragungsfunktion
1
⎡
1
s ⎤
y ( s ) = 1 2 1 2 exp ⎢ −
x⎥
s ⋅D
D
⎣
⎦
Puls eines Konzentrationsflusses
im Laplace-Raum
J Puls ( x ) =
dJ Step
J0
dt
⎧∂ J ⎫
J
L {J Puls } = J Puls = L ⎨ Step ⎬ = sJ Step = s 0 = J 0
s
⎩ ∂t ⎭
c1 ( x, s ) = y ( s ) ⋅ J puls =
⎡
1
s ⎤
exp
x⎥ ⋅ J 0
−
⎢
12
12
s ⋅D
⎣ D ⎦
0
c1 ( x, t ) = J 0
t
⎡ x2 ⎤
exp ⎢ −
⎥
πt
⎣ 4 Dt ⎦
1
Verschmieren der Konzentration mit Gausskurve
Absinken des Maximums und Verbreiterung mit wachsender Zeit.
GS
23.05.2007
Vorlesung Elektrochemie
85
Elektrochemie
Transportphänomene, Diffusion, elektrische Leitfähigkeit
Leitfähigkeit
Modell 2: Ionen-Migration in elektrischem Feld
(Diffusion von geringerer Bedeutung)
v+
• Kugelförmige Ionen in einem homogenen Medium
G
• Elektrisches Feld E (positive und negative Elektrode)
G
erzeugt Kraft K el auf die Ionen
G
G
K el = zi e0 E
• Reibungskraft in viskosem Medium
G
G 1
K R = −vi
ωi
wirkt der Kraft des elektrischen Feldes entgegen
GS
23.05.2007
+
v-
+
+
+
+
A
+
ε
• Medium (Lösungsmittel) hat die DK ε und die
Viskosität η
E
η
+
ωi : generalisierte Geschwindigkeit
G
vi : Wanderungsgeschwindigkeit des Ions i
Vorlesung Elektrochemie
86
Elektrochemie
Transportphänomene, Diffusion, elektrische Leitfähigkeit
Leitfähigkeit
Stationäre Bewegung mit konstanter Geschwindigkeit
G
G
G G
K R + K el = 0 ⇒ zi e0 E = vi ⋅ 1 ωi
Stokessches Gesetz: Reibung bedingt durch Viskosität der Lösung
ωi =
1
6πη Ri
Ri : Radius des Ions i
η : Viskosität der Lösung
Laminare Strömung der inkompressiblen Flüssigkeit um starre Kugeln
Zusammenhang zwischen Diffusionskoeffizient und Viskosität
Stokes-Einstein-Beziehung
ωi =
GS
Di
1
kT
=
⇒ Di = B
k BT 6πη Ri
6πη Ri
23.05.2007
Vorlesung Elektrochemie
87
Elektrochemie
Transportphänomene, Diffusion, elektrische Leitfähigkeit
Leitfähigkeit
G
konstante Wanderungsgeschwindigkeit vi der Ionen in elektrischem Feld
G
ze G
G
vi = zi e0ωi ⋅ E = i 0 E
6πη Ri
• Konstante Migrationsgeschwindigkeit führt zu einem elektrischen Strom durch Lösung
• Sowohl Kationen (N+) als auch Anionen (N-) tragen zu Strom bei. j = Stromdichte
G G
G
G
j = I A = e0 ( N + z+ v+ + N − z− v− ) Ni : Teilchendichte
Ni = cYν i N A
• Stromdichte ist proportional zu elektrischem Feld
G
G
j = κE
• Spezifische Leitfähigkeit κ , spezifischer Widerstand ρ = 1/κ
Ohmsches Gesetz
G
G
E
G A E
G
U
=
I = j A=
A= E l
l=
ρ
ρl R
R
GS
23.05.2007
R=ρ
l
A
Vorlesung Elektrochemie
88
Elektrochemie
Transportphänomene, Diffusion, elektrische Leitfähigkeit
Leitfähigkeit
G
G
G
κ E A = e0 AN AcY (ν + z+ v+ + ν − z− v−
Kopplung mit Stromdichte
⎛
κ = FcY ⎜ν + z+
⎜
⎝
G
v+
G + ν − z−
E
G
v− ⎞
G ⎟
E ⎟
⎠
Elektrochemische Wertigkeit
ne = ν + z+ = ν − z−
Ionen-Beweglichkeit ui
G
v+
u+ = G ;
E
Ionen-Leitfähigkeit λi
λi = F ui
Äquivalentleitfähigkeit des Elektrolyten Λ
Λ = λ+ + λ−
κ = Fne cY ( u+ + u− )
= cY ne ( λ+ + λ− ) = cY ne Λ
GS
23.05.2007
)
G
v−
u− = G
E
Ionen tragen unabhängig voneinander zur
Leitfähigkeit bei
Vorlesung Elektrochemie
89
Elektrochemie
Transportphänomene, Diffusion, elektrische Leitfähigkeit
Leitfähigkeit
Einzelionen-Leitfähigkeit
Waldensche Regel
zi e0
zi e0 2
λi = F
= NA
6πη Ri
6πη Ri
zi e0 2
λη
≡ konstant
i = NA
6π Ri
Probleme:
• Produkt λη
sollte für selben Elektrolyt bei konstanter Temperatur konstant sein:
i
Aber!
NaCl bei 298 K
Lösungsmittel
Wasser
Λ
η
Λη
126.4
0.00895
1.131
Methanol
96.9
0.00546
0.529
Ethanol
42.5
0.01096
0.466
• Äquivalentleitfähigkeit sollte unabhängig von Konzentration sein
Aber: Kohlrausch fand empirische Abhängigkeit für kleine Konzentrationen
Λ = Λ0 − A ⋅ c
GS
23.05.2007
Vorlesung Elektrochemie
90
Elektrochemie
Transportphänomene, Diffusion, elektrische Leitfähigkeit
Leitfähigkeit
Bisherige Ableitungen gelten nur für verschwindende Konzentration
• Λ0 als Grenzwert verschwindender Konzentration: lim Λ = Λ 0 (bzw. Λ ∞ )
c →0
• Keine Ion-Ion-Wechselwirkungen
Endliche Konzentrationen (c > 0)
• feldfreier Zustand:
• Ionenwolke kugelsymmetrisch, positives und
negatives Ladungszentrum fallen zusammen
• Elektrisches Feld:
• Verzerrung der Ladungsverteilung
• Ladungszentren fallen nicht mehr zusammen
• Abstand d zwischen beiden Zentren
• Bewegung des Zentralions und der
Ionenwolke in entgegengesetzte Richtung
• Internes Feld ΔE dem äußeren E entgegengesetzt
GS
23.05.2007
Vorlesung Elektrochemie
E
δ+ δ-
+
ΔE
91
Elektrochemie
Transportphänomene, Diffusion, elektrische Leitfähigkeit
Leitfähigkeit
2 Effekte beeinflussen die Leitfähigkeit
Relaxation
• Ionenwolke muss sich bei Verzerrung der
Ladungsverteilung neu aufbauen
• Relaxationszeit der Ionenwolke =
Zeit zur Bildung oder zum Zerfall der
Ionenwolke
Elektrophorese
• Ionenwolke bewegt sich gegen Richtung des
Zentralions
• ⇒ Bewegung eines Teilchens mit dem
Radius κ-1 in dichtem Medium mit Viskosität
η
• Stationäre Geschwindigkeit eines Teilchens
mit Radius κ-1
• Modifikation des elektrischen Feldes am Ort des Ions
• Beide Effekte verringern die Leitfähigkeit
G eff G ⎛
ΔE ⎞
E = E ⎜1 −
E ⎟⎠
⎝
• Modifikation der Leitfähigkeit
λi = λi0 − Δλirelax − Δλielpho
GS
23.05.2007
Λ = Λ 0 − Δ Λ relax − Δ Λ elpho
Vorlesung Elektrochemie
92
Elektrochemie
Transportphänomene, Diffusion, elektrische Leitfähigkeit
Leitfähigkeit
Relaxation (Onsager)
Δλirelax = λi0
Elektrophorese (Debye-Hückel)
ΔE
E
Elektrophoretische Geschwindigkeit
Relaxationszeit:
Zeit für die Bewegung von Teilchen über
den Abstand κ-1
κ )
(
=
−1
τ
relax
i
2
2 Di
(κ )
−1
=
2
Elektrophoretischer Leitfähigkeitsanteil
2ωi k BT
Verzerrung der Ladungsverteilung um
Abstand d in gleicher Zeit
(κ )
−1 2
d =τ
GS
relax
i
⋅v =
0
i
2ωi k BT
23.05.2007
G elpho zi e0κ G ⎛
ΔE ⎞
vi
E ⎜1 −
bzw.
=
⎟
6πη ⎝
E ⎠
ΔE ⎞
G elpho zi e0 κ G ⎛
vi
E ⎜1 −
=
6πη 1 + κ R ⎝
E ⎟⎠
mit κR → 0
Δλ
elpho
i
zi e0 2 ⎛
ΔE ⎞
κ ⎜1 −
=
6πη ⎝
E ⎟⎠
vi0
Vorlesung Elektrochemie
93
Elektrochemie
Transportphänomene, Diffusion, elektrische Leitfähigkeit
Leitfähigkeit
Relaxation
Ladungstrennung erzeugt Kraft zwischen Ladungszentren: Proportional der Ladungstrennung
Anteil d/κ-1 der maximalen Kraft bei r = κ-1
G
G relax
zi2e02
zi2e02κ vi0
d
Ki =
=
2
−1
−1
κ
8πεε 0 k BT ωi
4πεε 0 (κ )
G
G0
vi = zi eoωi E
G −1
G relax
vi = zi eoωi ΔE ⋅ f corr
G
zi2e02vi0κ
G relax
vi =
8πεε 0 k BT
G
virelax
ΔE
= G 0 ⋅ f corr
E
vi
Elektrophorese von
Relaxation abhängig
Korrekturterm von Onsager:
• Bewegung der Ionen zum Wiederaufbau der Ionenwolke ist teilweise zufällig
• Beweglichkeit aller Ionen maßgebend: Vielteilchen-Wechselwirkung
f corr =
GS
z+ z−
2p
zi2 3 1 + p
(
23.05.2007
)
mit p =
z+ z−
λ+ + λ−
z+ + z− z+ λ+ + z− λ−
Vorlesung Elektrochemie
p = 0.5 für symmetrische
Elektrolyte
94
Elektrochemie
Transportphänomene, Diffusion, elektrische Leitfähigkeit
Leitfähigkeit
Relaxationsanteil des elektrischen Feldes
z+ z− e02κ
ΔE
p
=
4πεε 0 k BT 3 1 + p
E
Leitfähigkeitsgleichung
2
ΔE ⎞ ⎡ 0 zi e0 ⎤ ⎛
ΔE ⎞
zi e02 ⎛
0
0 ΔE
−
=
−
−
λi = λi − λi
κ ⎜1 −
λ
κ
1
⎢ i
⎥
6πη ⎝
6πη ⎦ ⎜⎝
E
E ⎟⎠ ⎣
E ⎟⎠
(
)
⎞
⎡ 0 zi e02 ⎤ ⎛
z+ z− e02κ
p
⎟
= ⎢λi −
κ ⎥ ⎜1 −
6πη ⎦ ⎜ 4πεε 0k BT 3 1 + p ⎟
⎣
⎝
⎠
Ausmultiplizieren
(
)
⎛ z z e2
zi e02 ⎞
zi e02 2
z+ z− e02
p
p
0
+ − 0
⎟κ +
λi = λ − ⎜
λi +
κ
k
T
k
T
πεε
πη
πεε
πη
4
6
4
6
⎜
⎟
3 1+ p
3 1+ p
0 B
0 B
⎝
⎠
0
i
(
)
(
)
Vernachlässigung des dritten Terms (bei kleinen Konzentrationen)
⎛ z z e2
zi e02 ⎞
p
0
+ − 0
⎟κ
λi = λ − ⎜
λi +
6πη ⎟
⎜ 4πεε 0k BT 3 1 + p
⎝
⎠
0
i
GS
(
23.05.2007
)
Vorlesung Elektrochemie
95
Elektrochemie
Transportphänomene, Diffusion, elektrische Leitfähigkeit
Leitfähigkeit
Äquivalentleitfähigkeit Λ
⎛ z z e2
2
e
p
0
0
0
+
−
0
Λ = Λ −⎜
Λ +
( z+ + z−
⎜ 4πεε 0 k BT 3 1 + p
6πη
⎝
(
)
⎞
) ⎟⎟ κ
⎠
Symmetrische Elektrolyte: z = z+ = |z-|
⎛
2 2
2 ⎞
z
e
ze
2
0
0
0
0
⎟κ
Λ = Λ −⎜
Λ +
⎜ 8πεε 0 k BT 3 1 + 2
3πη ⎟
⎝
⎠
(
)
Grenzgleichung der Äquivalentleitfähigkeit von Onsager
Λ = Λ 0 − ( S1Λ 0 + S 2 ) c = Λ 0 − S c
Entspricht dem Gesetz von Kohlrausch
z 2e02
2
S1 =
8πεε 0 k BT 3 1 + 2
ze02
S2 =
3πη
(
)
2 z 2 N Ae02
εε 0 k B T
2 z 2 N Ae02
εε 0 k B T
Gilt für punktförmige Ionen bei sehr kleinen Konzentrationen
GS
23.05.2007
Vorlesung Elektrochemie
96
Elektrochemie
Transportphänomene, Diffusion, elektrische Leitfähigkeit
Leitfähigkeit
Onsager-Grenzgesetz
Erweiterte Leitfähigkeitsgleichung aus
verbesserten Modellen bis hohe Konzentrationen
Berücksichtigung der Ionengröße und detaillierter
hydrodynamischer Effekte
Λ = Λ 0 − S c + Ec ln c + J1 ( R )c + J 2 ( R)c 3 2
J1 und J2 enthalten Anpassungsparameter !
Äquivalentleitfähigkeit
von Pr4NI in EtOH von
-45°C bis 25°C
GS
23.05.2007
Vorlesung Elektrochemie
97
Elektrochemie
Transportphänomene, Diffusion, elektrische Leitfähigkeit
Leitfähigkeit
Unvollständige Dissoziation oder Assoziation
⎯⎯
→ H+ + AHA ←⎯
⎯
c A = α ⋅ c ; cM = α ⋅ c cMA = (1 − α ) ⋅ c
⎯⎯
→ MA
M + + A - ←⎯
⎯
a
(1 − α )c ⋅ yMA (1 − α )
K A = K D−1 = MA =
= 2
2
2 2
a A ⋅ aM
α ⋅ c y±
α c ⋅ y±2
Nur Ionen tragen zur Leitfähigkeit bei, Aktivitätskoeffizient des Moleküls/Ionenpaars = 1
Messung von κ bei der Elektrolytkonzentration c
κ = Λ ⋅c
Aber: Nur freie Ionen leiten Strom
κ = Λ′ ⋅ α ⋅ c ⇒ Λ = α ⋅ Λ′
Λ′ = Λ 0 − S α c + E (α c ) ln (α c ) + J1 ( R )α c + J 2 ( R) (α c )
(
32
Λ = α Λ 0 − S α c + E (α c ) ln (α c ) + J1 ( R)α c + J 2 ( R) (α c )
Leitfähigkeit der freien Ionen
32
)
Bestimmung von Assoziations-/Dissoziationsgraden aus Leitfähigkeitsmessungen
GS
23.05.2007
Vorlesung Elektrochemie
98
Elektrochemie
Transportphänomene, Diffusion, elektrische Leitfähigkeit
Leitfähigkeit
Bestimmung von Assoziations-/Dissoziationsgraden aus Leitfähigkeitsmessungen
Sehr kleine Konzentrationen: Λ´= Λ0 und y± = 1
Λ
κ = Λ ⋅ c = Λ0 ⋅ α ⋅ c ⇒ Λ = α ⋅ Λ0 ; α = 0
Λ
(Λ Λ0 )
2
Λ2
KD =
c= 0
c
0
0
(1 − Λ Λ ) (Λ − Λ)Λ
Sehr hohe Konzentrationen:
Bildung von Ionenpaaren, Ionentripeln und höheren Assoziaten:
Anstieg und Abfall der Äquivalentleitfähigkeit
Äquivalentleitfähigkeit von LiBF4 in 1,2-Dimethoxyethan bei -45°C und 25°C
GS
23.05.2007
Vorlesung Elektrochemie
99
Elektrochemie
Transportphänomene, Diffusion, elektrische Leitfähigkeit
Leitfähigkeit
Messung der elektrischen Leitfähigkeit: Kohlrauschbrücke
Wechselspannung zwischen 50 und 50000 Hz, Extrapolation auf 1/f → 0
U~
U~
C
Z3
I
Z3
Z4
Z1 = Z 2
Z1
Z2
Z3
Z4
A
I
Z4
D
Z1
Z2
B
E
Z5
Z6
Stromdurchgang im Galvanometer = 0
Wagner-Hilfszweig (Z5 und Z6) um Punkt C auf
Kapazitiver Abgleich notwendig, da
Erdpotential zu bringen
Elektrolytlösungen keine reinen Ohmschen
Widerstände
Hochpräzise Messungen möglich: Fehler < 0.1%
GS
23.05.2007
Vorlesung Elektrochemie
100
Elektrochemie
Transportphänomene, Diffusion, elektrische Leitfähigkeit
Leitfähigkeit
Messzelle für Leitfähigkeitsmessungen
• Platinierte Platinelektroden
• Verminderung der Polarisation
• Dreielektroden-Anordnung
• kein Streufeld außerhalb der Elektroden
• Effektive Durchmischung
• Messung unter Schutzgas
• Großes Temperaturintervall
• Genaue Thermostatisierung nötig
• Beginn der Messung mit reinem Lösungsmittel
• Diskrete Zugaben genau bekannter Elektrolytmengen
• Berücksichtigung der Frequenzabhängigkeit der
Impedanzen
• Bestimmung der Zellkonstante mit KCl-Lösung
• Leitfähigkeit von KCl-Wasser sehr genau in
Abhängigkeit von c und T bekannt
GS
23.05.2007
Vorlesung Elektrochemie
101