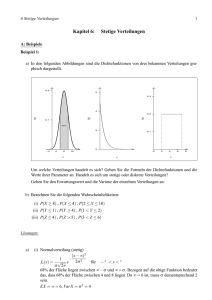
Statistik
Werbung

Statistik R. Frühwirth Statistik R. Frühwirth [email protected] VO 142.090 http://tinyurl.com/TU142090 Februar 2010 R. Frühwirth Statistik 1/319 Übersicht über die Vorlesung Statistik R. Frühwirth Teil 1: Deskriptive Statistik Teil 2: Wahrscheinlichkeitsrechnung Teil 3: Zufallsvariable Teil 4: Parameterschätzung R. Frühwirth Statistik 2/319 Übersicht über die Vorlesung Statistik R. Frühwirth Teil 5: Testen von Hypothesen Teil 6: Regressionsanalyse Teil 7: Simulation von Experimenten R. Frühwirth Statistik 3/319 Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Teil 3 Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Zufallsvariable Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 165/319 Übersicht Teil 3 Statistik R. Frühwirth Eindimensionale Zufallsvariable 8 Eindimensionale Zufallsvariable 9 Mehrdimensionale Zufallsvariable 10 Wichtige Verteilungen 11 Momente 12 Rechnen mit Verteilungen Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 166/319 Abschnitt 8: Eindimensionale Zufallsvariable Statistik R. Frühwirth Eindimensionale Zufallsvariable 8 Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable 9 Mehrdimensionale Zufallsvariable 10 Wichtige Verteilungen 11 Momente 12 Rechnen mit Verteilungen Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 167/319 Unterabschnitt: Grundbegriffe Statistik R. Frühwirth Eindimensionale Zufallsvariable 8 Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable 9 Mehrdimensionale Zufallsvariable 10 Wichtige Verteilungen 11 Momente 12 Rechnen mit Verteilungen Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 168/319 Grundbegriffe Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Definition (Zufallsvariable) Eine Abbildung X: ω ∈ Ω 7→ x = X(ω) ∈ R die jedem Element ω des Ereignisraums Ω eine reelle Zahl zuordnet, heißt eine (eindimensionale) Zufallsvariable. Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze Ist Ω endlich oder abzählbar unendlich, ist jede beliebige Abbildung X zugelassen. Ist Ω überabzählbar unendlich, muss X eine messbare Abbildung sein. Da der Wert einer Zufallsvariablen vom Ausgang des Experiments abhängt, kann man den möglichen Werten Wahrscheinlichkeiten zuschreiben. R. Frühwirth Statistik 169/319 Grundbegriffe Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Nimmt die Zufallsvariable X nur endlich oder abzählbar unendlich viele Werte an, heißt sie diskret. Nimmt die Zufallsvariable X ein Kontinuum von Werte an, heißt sie kontinuierlich. Beispiel Die Abbildung, die beim Würfeln dem Elementarereignis ei die Augenzahl i zuordnet, ist eine diskrete Zufallsvariable. Natürlich wäre auch die Abbildung ei :−→ 7 − i eine diskrete Zufallsvariable. Beispiel Momente Erwartung Varianz Schiefe Die Abbildung, die dem Zerfall eines Teilchens die Lebensdauer x zuordnet, ist eine kontinuierliche Zufallsvariable. Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 170/319 Unterabschnitt: Diskrete Zufallsvariable Statistik R. Frühwirth Eindimensionale Zufallsvariable 8 Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable 9 Mehrdimensionale Zufallsvariable 10 Wichtige Verteilungen 11 Momente 12 Rechnen mit Verteilungen Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 171/319 Diskrete Zufallsvariable Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze Diskrete Zufallsvariable sind oft das Resultat von Zählvorgängen. In der physikalischen Praxis kommen diskrete Zufallsvariable häufig vor: man denke an das Zählen von Ereignissen in einem festen Zeitintervall (Poissonverteilung), an das Abzählen von Alternativversuchen (Binomialverteilung), oder auch an die Besetzungshäufigkeit der diskreten Energieniveaus des Wasserstoffatoms. Im folgenden nehmen wir an, dass die Werte einer diskreten Zufallsvariablen nichtnegative ganze Zahlen sind. Dies ist keine Einschränkung, weil jede abzählbare Menge von reellen Zahlen bijektiv auf (eine Teilmenge von) N0 abgebildet werden kann. Die Ereignisalgebra ist die Potenzmenge (Menge aller Teilmengen) P von N0 . R. Frühwirth Statistik 172/319 Diskrete Zufallsvariable Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Ist auf der Ereignisalgebra Σ(Ω) ein Wahrscheinlichkeitsmaß W definiert, so kann man mit Hilfe der Zufallsvariablen X auf der Potenzmenge P von N0 ebenfalls ein Wahrscheinlichkeitsmaß definieren. Definition (Verteilung einer diskreten Zufallsvariablen) Es sei Σ(Ω) eine diskrete Ereignisalgebra. Die diskrete Zufallsvariable X : Ω 7→ N0 induziert ein Wahrscheinlichkeitsmaß auf N0 mittels X WX ({k}) = W (X −1 (k)) = W ({ω}) Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze X(ω)=k WX wird als die Verteilung von X bezeichnet, und zwar als diskrete oder Spektralverteilung. R. Frühwirth Statistik 173/319 Diskrete Zufallsvariable Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Beispiel Wir ordnen den geraden Augenzahlen des Würfels die Zahl 0 zu, den ungeraden die Zahl 1: X : ω 7→ mod (ω, 2) Die Verteilung von X ist dann gegeben durch 1 2 1 WX (1) = W (X −1 (1)) = W ({1, 3, 5}) = 2 WX (0) = W (X −1 (0)) = W ({2, 4, 6}) = Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 174/319 Diskrete Zufallsvariable Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Beispiel Wir ordnen dem Ausgang eines Doppelwurfs die Summe der Augenzahlen zu: X : (i, j) 7→ i + j Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Die Werte von X sind die natürlichen Zahlen von 2 bis 12. Die Verteilung von X ist dann gegeben durch k−1 , k≤7 X −1 36 WX (k) = W (X (k)) = W ({(i, j)}) = i+j=k 13 − k , k ≥ 7 36 Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 175/319 Diskrete Zufallsvariable Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Die Zahlen WX (k) können als Funktionswerte einer Spektralfunktion fX angesehen werden: ( WX (k), wenn x = k fX (x) = 0, sonst Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Definition (Diskrete Dichtefunktion) Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Die Funktion fX (k) wird als Wahrscheinlichkeitsdichtefunktion oder kurz Dichte der Zufallsvariablen X bezeichnet. Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 176/319 Diskrete Zufallsvariable Statistik R. Frühwirth Die Dichte der Zufallsvariablen X = i + j: Eindimensionale Zufallsvariable Dichtefunktion 0.18 Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable 0.16 Mehrdimensionale Zufallsvariable 0.14 0.12 Wichtige Verteilungen 0.1 Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen f(x) Grundbegriffe Randverteilungen und bedingte Verteilungen 0.08 0.06 Momente Erwartung Varianz Schiefe 0.04 0.02 Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze 0 2 3 R. Frühwirth 4 5 6 Statistik 7 x 8 9 10 11 12 177/319 Diskrete Zufallsvariable Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Die Wahrscheinlichkeit WX (E) eines Ereignisses E lässt sich bequem mit Hilfe der Dichte von X berechnen: X WX (E) = fX (k) k∈E Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Definition (Diskrete Verteilungsfunktion) Ist X eine diskrete Zufallsvariable, so ist die Verteilungsfunktion FX von X definiert durch: FX (x) = W (X ≤ x) Momente Erwartung Varianz Schiefe Es gilt offenbar: Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze FX (x) = X fX (k) = k≤x R. Frühwirth Statistik X WX ({k}) k≤x 178/319 Diskrete Zufallsvariable Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Eigenschaften einer diskreten Verteilungsfunktion F 1 F hat eine Sprungstelle in allen Punkten des Wertebereichs 2 Die Sprunghöhe im Punkt k ist gleich fX (k) 3 0 ≤ F (x) ≤ 1 ∀x ∈ R 4 x ≤ y =⇒ F (x) ≤ F (y) ∀x, y ∈ R 5 limx→−∞ F (x) = 0; limx→∞ F (x) = 1 6 Die Wahrscheinlichkeit, dass r in das Intervall (a, b] fällt, ist F (b) − F (a): W (r ≤ a) + W (a < r ≤ b) = W (r ≤ b) =⇒ W (a < r ≤ b) = F (b) − F (a) Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 179/319 Diskrete Zufallsvariable Statistik R. Frühwirth Die Verteilungsfunktion der Zufallsvariablen X = i + j: Eindimensionale Zufallsvariable Verteilungsfunktion 1 Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable 0.9 0.8 Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen 0.7 0.6 Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe F(x) Wichtige Verteilungen 0.5 0.4 0.3 0.2 0.1 Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze 0 2 3 4 R. Frühwirth 5 6 Statistik 7 x 8 9 10 11 12 180/319 Unterabschnitt: Stetige Zufallsvariable Statistik R. Frühwirth Eindimensionale Zufallsvariable 8 Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable 9 Mehrdimensionale Zufallsvariable 10 Wichtige Verteilungen 11 Momente 12 Rechnen mit Verteilungen Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 181/319 Stetige Zufallsvariable Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Bisher wurden nur solche Zufallsvariable behandelt, die auf diskreten Ereignisalgebren definiert waren. Diese Beschränkung soll nun fallengelassen werden, d.h es werden jetzt überabzählbar viele Elementarereignisse zugelassen. Das ist notwendig, wenn nicht nur Zählvorgänge, sondern beliebige Messvorgänge zugelassen werden. Eine Funktion X, die auf einer solchen überabzählbaren Menge von Elementarereignissen definiert ist, kann beliebige reelle Werte annehmen. Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 182/319 Stetige Zufallsvariable Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Definition (Stetige Verteilungsfunktion) Es sei (Σ, W ) ein Wahrscheinlichkeitsraum über einer überabzählbaren Ergebnismenge Ω. X sei eine Zufallsvariable, also eine (messbare) Funktion von Ω in R. Die Funktion FX , definiert durch: FX (x) = W (X ≤ x) Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe heißt die Verteilungsfunktion von X. Die Wahrscheinlichkeit, dass X in ein Intervall (x, x + ∆x] fällt, ist dann: W (x < X ≤ x + ∆x) = FX (x + ∆x) − FX (x) = ∆FX . Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 183/319 Stetige Zufallsvariable Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze Eigenschaften einer stetigen Verteilungsfunktion 1 0 ≤ F (x) ≤ 1 ∀x ∈ R 2 x1 ≤ x2 =⇒ F (x1 ) ≤ F (x2 ) ∀x1 , x2 ∈ R 3 limx→−∞ F (x) = 0; limx→∞ F (x) = 1 Definition (Quantil) Es sei FX (x) eine stetige Verteilungsfunktion. Der Wert xα , für den FX (xα ) = α, 0 < α < 1 gilt, heißt das α-Quantil der Verteilung von X. Die Funktion −1 x = FX (α), 0<α<1 heißt die Quantilsfunktion der Verteilung von X. R. Frühwirth Statistik 184/319 Stetige Zufallsvariable Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Definition (Quartil) Die Quantile zu den Werten α = 0.25, 0.5, 0.75 heißen Quartile. Das Quantil zum Wert α = 0.5 heißt Median der Verteilung. Quantile können auch für diskrete Verteilungen definiert werden, jedoch sind sie dann nicht immer eindeutig. Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 185/319 Stetige Zufallsvariable Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Definition (Stetige Dichtefunktion) Ist FX differenzierbar, heißt X eine stetige Zufallsvariable. Für die Verteilung von X gilt nach dem Hauptsatz der Integralrechnung: Z x2 WX (x1 < X ≤ x2 ) = FX (x2 ) − FX (x1 ) = fX (x) dx x1 Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen 0 wobei fX (x) = FX (x) ist. Die Ableitung der Verteilungsfunktion, die Funktion fX , wird als Wahrscheinlichkeitsdichtefunktion oder wieder kurz Dichte von X bezeichnet. Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 186/319 Stetige Zufallsvariable Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze Das Wahrscheinlichkeitsmaß WX heißt die Verteilung von X. Es ist auf einer Ereignisalgebra Σ definiert, die aus Mengen reeller Zahlen besteht und zumindest alle Intervalle und deren Vereinigungen als Elemente enthält. Ähnlich wie bei diskreten Zufallsvariablen lässt sich die Wahrscheinlichkeit WX einer Menge M ∈ Σ leicht mit Hilfe der Dichte angeben: Z WX (M ) = fX (x) dx M Die Wahrscheinlichkeit eines einzelnen Punktes ist immer gleich 0: Z x WX ({x}) = fX (x) dx = 0 x R. Frühwirth Statistik 187/319 Stetige Zufallsvariable Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Daher ist auch WX ((x1 , x2 ]) = WX ((x1 , x2 )) = WX ([x1 , x2 ]). Ganz allgemein erhält man eine Aussage über stetige Zufallsvariable dadurch, dass man in einer Aussage über diskrete Zufallsvariable die Summation durch eine Integration ersetzt. Gilt zum Beispiel für eine diskrete Dichte f : X f (k) = 1 k∈N0 Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze so gilt für eine stetige Dichte f : Z ∞ f (x) dx = 1 −∞ R. Frühwirth Statistik 188/319 Stetige Zufallsvariable Statistik R. Frühwirth Dichtefunktion Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze f(x) Mehrdimensionale Zufallsvariable Verteilungsfunktion 0.2 1 0.18 0.9 0.16 0.8 0.14 0.7 0.12 0.6 F(x) Eindimensionale Zufallsvariable 0.1 0.5 0.08 0.4 0.06 0.3 0.04 0.2 0.02 0.1 0 0 5 10 x R. Frühwirth 15 20 Statistik 0 0 5 10 x 15 20 189/319 Abschnitt 9: Mehrdimensionale Zufallsvariable Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable 8 Eindimensionale Zufallsvariable 9 Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen 10 Wichtige Verteilungen 11 Momente 12 Rechnen mit Verteilungen Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 190/319 Unterabschnitt: Grundbegriffe Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable 8 Eindimensionale Zufallsvariable 9 Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen 10 Wichtige Verteilungen 11 Momente 12 Rechnen mit Verteilungen Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 191/319 Grundbegriffe Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Definition (Zufallsvariable) Eine Abbildung X: ω ∈ Ω 7→ x = X(ω) ∈ Rd die jedem Element ω des Ereignisraums Ω einen reellen Vektor x ∈ Rd zuordnet, heißt eine d-dimensionale Zufallsvariable. Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Mehrdimensionale Zufallsvariablen können diskret oder stetig sein. Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 192/319 Grundbegriffe Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Definition (Verteilungsfunktion) Ist X = (X1 , . . . , Xd ) eine d-dimensionale Zufallsvariable, so ist die Verteilungsfunktion FX durch FX (x1 , . . . , xd ) = W (X1 ≤ x1 ∩ . . . ∩ Xd ≤ xd ) definiert. Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Definition (Dichtefunktion) Ist X = (X1 , . . . , Xd ) eine d-dimensionale diskrete Zufallsvariable, so ist die Dichtefunktion fX durch fX (x1 , . . . , xd ) = W (X1 = x1 ∩ . . . ∩ Xd = xd ) Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze definiert. R. Frühwirth Statistik 193/319 Grundbegriffe Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Beispiel Die zweidimensionale Zufallsvariable X = (X1 , X2 ) ordnet dem Ergebnis des Wurfs mit zwei Würfeln die Augenzahlen (i, j) zu. Sind alle Ausgänge gleichwahrscheinlich, so ist WX gegeben durch: Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen 1 WX {(i, j)} = 36 Die Dichte fX lautet: ( fX (x1 , x2 ) = 1 , 36 0, x1 ∈ {1, . . . , 6} ∩ x2 ∈ {1, . . . , 6} sonst Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 194/319 Grundbegriffe Statistik R. Frühwirth Eindimensionale Zufallsvariable 0.03 Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen 0.02 w(x1,x2) Mehrdimensionale Zufallsvariable 0.025 0.015 0.01 Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe 0.005 0 1 2 3 5 4 5 Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze 6 4 3 6 x2 R. Frühwirth 2 1 x1 Statistik 195/319 Grundbegriffe Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Beispiel (Fortsetzung) Die Verteilungsfunktion F ist daher: F (x1 , x2 ) = W (X1 ≤ x1 ∩ X2 ≤ x2 ) = Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze f (i, j) i≤x1 ∩j≤x2 Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen X Beispielsweise ist F (3, 4) = 1 i≤3∩j≤4 36 P = 12 36 = 13 . Wegen der Abzählbarkeit der Elementarereignisse können diese auch durch eine eindimensionale Zufallsvariable Y eindeutig in R abgebildet werden, z. B.: Y : (ei , ej ) −→ 6i + j − 6 Der Wertevorrat von Y sind die natürlichen Zahlen zwischen 1 und 36, und Ws ist gegeben durch: 1 Ws {k} = , 1 ≤ k ≤ 36 36 R. Frühwirth Statistik 196/319 Grundbegriffe Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Definition (Dichtefunktion) Ist X = (X1 , . . . , Xd ) eine d-dimensionale stetige Zufallsvariable, so ist die Dichtefunktion fX durch Mehrdimensionale Zufallsvariable fX (x1 , . . . , xd ) = Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen ∂ d FX ∂x1 . . . ∂xd definiert. Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 197/319 Unterabschnitt: Randverteilungen und bedingte Verteilungen Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable 8 Eindimensionale Zufallsvariable 9 Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen 10 Wichtige Verteilungen 11 Momente 12 Rechnen mit Verteilungen Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 198/319 Randverteilungen und bedingte Verteilungen Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Sind X1 und X2 zwei (diskrete oder stetige) 1-dimensionale Zufallsvariable, so ist X = (X1 , X2 ) eine zweidimensionale Zufallsvariable. Die Verteilung (Verteilungsfunktion, Dichte) von X heißt auch die gemeinsame Verteilung (Verteilungsfunktion, Dichte) von X1 und X2 . Es stellt sich nun das folgende Problem: Kann man die Verteilung von X1 bzw. X2 aus der gemeinsamen Verteilung berechnen? Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 199/319 Randverteilungen und bedingte Verteilungen Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Es sei F die Verteilungsfunktion und f die Dichte der stetigen Zufallsvariablen X = (X1 , X2 ). Dann ist die Verteilungsfunktion F1 von X1 gegeben durch: F1 (x1 ) = W (X1 ≤ x1 ) = W (X1 ≤ x1 ∩ −∞ < X2 < ∞) = Z x1 Z ∞ = f (x1 , x2 ) dx2 dx1 −∞ −∞ Daraus folgt: Z f (x1 , x2 ) dx2 −∞ Momente Erwartung Varianz Schiefe ∞ f1 (x1 ) = ist die Dichte von X1 . Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 200/319 Randverteilungen und bedingte Verteilungen Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Definition (Randverteilung) Es sei X = (X1 , X2 ) eine zweidimensionale stetige Zufallsvariable mit der Verteilungsfunktion F und der Dichte f . Die Verteilung von X1 heißt die Randverteilung von X1 bezüglich X. Ihre Dichte f1 lautet: Z ∞ f1 (x1 ) = f (x1 , x2 ) dx2 . −∞ Ist X = (X1 , X2 ) diskret mit der Dichte f , so ist analog die Dichte f1 der Randverteilung von X1 bezüglich X gegeben durch: X f1 (k1 ) = f (k1 , k2 ) Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze k2 R. Frühwirth Statistik 201/319 Randverteilungen und bedingte Verteilungen Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Die Verteilungen von X1 und X2 lassen sich also aus der gemeinsamen Verteilung von X1 und X2 berechnen. Der umgekehrte Vorgang ist im allgemeinen nicht möglich, da die gemeinsame Verteilung auch Information über mögliche Zusammenhänge (Kopplung) zwischen X1 und X2 enthält. Es seien X1 und X2 zwei diskrete Zufallsvariable mit der gemeinsamen Dichte f (k1 , k2 ) und den Randverteilungsdichten f1 (k1 ) und f2 (k2 ). Dann ist die bedingte Wahrscheinlichkeit des Ereignisses X1 = k1 unter der Bedingung X2 = k2 gegeben durch: W (X1 = k1 |X2 = k2 ) = Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth W (X1 = k1 ∩ X2 = k2 ) f (k1 , k2 ) = W (X2 = k2 ) f2 (k2 ) Statistik 202/319 Randverteilungen und bedingte Verteilungen Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Definition (Bedingte Dichte) Es sei X = (X1 , X2 ) eine 2-dimensionale diskrete Zufallsvariable mit der Dichte f (k1 , k2 ) und den Randverteilungsdichten f1 (k1 ) bzw. f2 (k2 ). Die Funktion f (k1 |k2 ), definiert durch: Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen f (k1 |k2 ) = f (k1 , k2 ) f2 (k2 ) Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe heißt die durch X2 bedingte Dichte von X1 . Die bedingte Dichte ist für festes k2 die Dichte eine Verteilung, der durch X2 = k2 bedingten Verteilung von X1 . Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 203/319 Randverteilungen und bedingte Verteilungen Statistik R. Frühwirth Ist X = (X1 , X2 ) stetig, so ist analog f (x1 |x2 ) definiert durch: Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen f (x1 |x2 ) = f (x1 , x2 ) (f2 (x2 ) 6= 0) f2 (x2 ) f (x1 |x2 ) ist für festes x2 die Dichte einer Verteilung, der durch X2 = x2 bedingten Verteilung von X1 . Dass f (x1 |x2 ) tatsächlich eine Dichte ist, läßt sich leicht nachprüfen: Z ∞ Z ∞ f (x1 , x2 ) f2 (x2 ) f (x1 |x2 ) dx1 = dx1 = =1 f (x ) f2 (x2 ) 2 2 −∞ −∞ und analog für diskretes X. Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 204/319 Randverteilungen und bedingte Verteilungen Statistik R. Frühwirth Es gilt: Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze f (x1 , x2 ) = f (x1 |x2 ) · f2 (x2 ) Z ∞ f1 (x1 ) = f (x1 |x2 ) · f2 (x2 ) dx2 −∞ und analog für diskrete Dichten. Definition (Unabhängigkeit von Zufallsvariablen) Ist die (unbedingte) Dichte der Randverteilung von X1 gleich der durch X2 bedingten Dichte, so heißen X1 und X2 unabhängig. X1 und X2 unabhängig ⇐⇒ f (x1 |x2 ) = f1 (x1 ) R. Frühwirth Statistik 205/319 Randverteilungen und bedingte Verteilungen Statistik R. Frühwirth Eindimensionale Zufallsvariable Für unabhängige Zufallsvariablen X1 und X2 gilt: f (x1 |x2 ) = f1 (x1 ) ⇐⇒ f (x2 |x1 ) = f2 (x1 ) Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe ⇐⇒ f (x1 , x2 ) = f1 (x1 ) · f2 (x2 ) und analog für diskretes X. Für unabhängige Zufallsvariable X1 ,X2 ist also die Dichte der gemeinsamen Verteilung gleich dem Produkt der einzelnen Dichten. Ist X = (X1 , . . . , Xd ), d > 2, so müssen die Definitionen der Randverteilung, der bedingten Dichten und der Unabhängigkeit entsprechend verallgemeinert werden. Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 206/319 Randverteilungen und bedingte Verteilungen Statistik R. Frühwirth Die Dichte der Randverteilung von Xi1 , . . . , Xim ist gegeben durch: Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen fi1 ,...,im (xi1 , . . . , xim ) Z ∞ Z ∞ = ... f (x1 , . . . , xn ) dxim+1 . . . dxin −∞ −∞ Die durch Xj bedingte Dichte von Xi ist gegeben durch: Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen f (xi |xj ) = Momente Erwartung Varianz Schiefe fi,j (xi , xj ) fj (xj ) wobei fi,j (xi , xj ) die Randverteilungsdichte von Xi , Xj ist. Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 207/319 Randverteilungen und bedingte Verteilungen Statistik R. Frühwirth Eindimensionale Zufallsvariable Xi1 , . . . , Xik heißen unabhängig, wenn die Dichte der Randverteilung von Xi1 , . . . , Xik das Produkt der Dichten der Randverteilungen der einzelnen Xij ist. Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 208/319 Randverteilungen und bedingte Verteilungen Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Beispiel (Die Akzeptanz oder Nachweiswahrscheinlichkeit) X sei eine Zufallsvariable mit der Dichte f (x). Nimmt X den Wert x an, so gibt es eine Wahrscheinlichkeit a(x) dafür, dass x auch tatsächlich beobachtet wird. Man definiert nun eine Zufallsvariable I, die 1 ist, wenn x beobachtet wird, und 0 sonst. Dann ist I unter der Bedingung X = x alternativ nach Aa(x) verteilt: W (I = 1|X = x) = a(x) Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe W (I = 0|X = x) = 1 − a(x) Die gemeinsame Dichte von X und I ist daher: f (x, 1) = a(x)f (x) f (x, 0) = [1 − a(x)]f (x) Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 209/319 Randverteilungen und bedingte Verteilungen Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Beispiel (Fortsetzung) Da der Experimentator nur mit beobachteten Größen arbeiten kann, schränkt er seine Grundgesamtheit auf die nachgewiesenen Ereignisse ein, d.h. er braucht die Dichte von X unter der Bedingung, dass X beobachtet wird: fA (x) = f (x|I = 1) = f (x, 1) a(x)f (x) = R f2 (1) a(x)f (x) dx Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze Als konkretes Beispiel diene die Messung einer Lebensdauer. Die Messung möge bei tmin beginnen und bei tmax enden. Dann hat a(t) die folgende Gestalt: 0, für t ≤ tmin a(t) = 1, für tmin < t ≤ tmax 0, für t > tmax R. Frühwirth Statistik 210/319 Randverteilungen und bedingte Verteilungen Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Beispiel (Fortsetzung) Für die gemessene Wahrscheinlichkeitsdichte gilt: 0, t ≤ tmin 1 exp(−t/τ ) τ fA (t) = , tmin ≤ t < tmax exp(−t /τ ) − exp(−tmax /τ ) min 0, t > t max Der Faktor 1/[exp(−tmin /τ ) − exp(−tmax /τ )] korrigiert für jene Teilchen, die vor tmin oder nach tmax zerfallen. Die Nachweiswahrscheinlichkeit a(t) kann auch von der Geometrie des Detektors oder deren Ansprechwahrscheinlichkeit bestimmt werden und eine komplizierte Abhängigkeit von t haben. So kann es etwa von der Konfiguration der Zerfallsprodukte abhängen, ob ein Zerfall bei t beobachtet werden kann oder nicht. Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 211/319 Abschnitt 10: Wichtige Verteilungen Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable 8 Eindimensionale Zufallsvariable 9 Mehrdimensionale Zufallsvariable 10 Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen 11 Momente 12 Rechnen mit Verteilungen Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 212/319 Unterabschnitt: Diskrete Verteilungen Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable 8 Eindimensionale Zufallsvariable 9 Mehrdimensionale Zufallsvariable 10 Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen 11 Momente 12 Rechnen mit Verteilungen Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 213/319 Diskrete Verteilungen Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Die diskrete Gleichverteilung auf n Punkten, Gl(n) Die Verteilung einer Zufallsvariablen X, die die Werte 1, . . . , n mit gleicher Wahrscheinlichkeit annimmt.. Die Dichte fX lautet: ( fX = Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente 1 n, 0, x ∈ {1, . . . , n} sonst Die Verteilungsfunktion FX ist eine Stufenfunktion mit Sprüngen der Größe n1 in den Punkten 1, . . . , n. Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 214/319 Diskrete Verteilungen Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Die Alternativ- oder Bernoulliverteilung Al(p) Die Verteilung einer Zufallsvariablen, die den Ausgängen eines Alternativversuchs die Werte 1 (Erfolg) bzw. 0 (Misserfolg) zuordnet. Die Dichte fX lautet: fX (0) = 1 − p, fX (1) = p oder fX (x) = px (1 − p)1−x , Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 215/319 Diskrete Verteilungen Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Die Binomialverteilung Bi(n, p) Wird der Alternativversuch n mal unabhängig durchgeführt, so gibt es 2n Elementarereignisse, nämlich die Folgen der Form e = (ei1 , . . . , ein ), ij = 0 oder 1. Die diskrete Zufallsvariable X bildet die Folge e auf die Häufigkeit von e1 ab: Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze r(e) = n X ij j=1 Der Wertebereich von X ist die Menge {0, 1, . . . , n}. Auf die Zahl k (0 ≤ k ≤ n) werden alle Folgen abgebildet, bei denen e1 genau k-mal eintritt. Es gibt Ckn solche Folgen, und jede hat die Wahrscheinlichkeit pk (1 − p)n−k . R. Frühwirth Statistik 216/319 Diskrete Verteilungen Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Die Dichte f ist daher: ! n k f (k) = p (1 − p)n−k , 0 ≤ k ≤ n k Die Verteilung von X wird als Binomialverteilung Bi(n, p) mit den Parametern n und p bezeichnet. Es gilt ! n X n k p (1 − p)n−k = 1 f (k) = k k=0 k=0 n X Das ist gerade der binomische Lehrsatz. Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 217/319 Diskrete Verteilungen Statistik R. Frühwirth 0.4 0.4 Bi(10,0.3) Eindimensionale Zufallsvariable 0.3 P(k) P(k) Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Bi(10,0.5) 0.3 0.2 0.1 Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen 0 0.2 0.1 0 1 2 3 4 5 k 6 7 8 9 0 10 0 1 2 3 4 5 k 6 7 8 9 10 2 3 4 5 k 6 7 8 9 10 Wichtige Verteilungen Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze 0.4 Bi(10,0.7) Bi(10,0.9) 0.3 0.3 P(k) Momente 0.4 P(k) Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen 0.2 0.1 0 0.2 0.1 0 1 2 3 4 5 k 6 7 R. Frühwirth 8 9 10 Statistik 0 0 1 218/319 Diskrete Verteilungen Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Die Multinomialverteilung Mu(n, p1 , . . . , pd ) Der Alternativversuch kann dahingehend verallgemeinert werden, dass man nicht nur zwei, sondern d Elementarereignisse e1 , . . . , ed zulässt, denen die Wahrscheinlichkeiten p1 , . . . , pd zugeordnet werden, die nur Grundbegriffe Randverteilungen und bedingte Verteilungen d X Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze pi = 1 i=1 erfüllen müssen. Führt man den verallgemeinerten Alternativversuch n-mal durch, so sind die Elementarereignisse die Folgen der Form: (ei1 , . . . , ein ), 1 ≤ ij ≤ d R. Frühwirth Statistik 219/319 Diskrete Verteilungen Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Sind die n Teilversuche unabhängig, gilt: W (ei1 , . . . , ein ) = n Y W (eij ) = j=1 n Y j=1 pij = d Y pni i i=1 wobei ni die Anzahl des Eintretens von ei ist. Die Summe der ni ist daher n. Die d-dimensionale Zufallsvariable X = (X1 , . . . , Xd ) bildet die Folge (ei1 , . . . , ein ) auf den Vektor (n1 , . . . , nd ) ab. Dabei werden n!/(n1 !· · ·nd !) Folgen auf den gleichen Vektor abgebildet. Momente Erwartung Varianz Schiefe Die Dichte von X lautet daher: Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze f (n1 , . . . , nd ) = d d d Y X X n! pni i , ni = n, pi = 1 n1 ! . . . nd ! i=1 i=1 i=1 R. Frühwirth Statistik 220/319 Diskrete Verteilungen Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze Die Verteilung von X wird als Multinomialverteilung mit den Parametern n und p1 , . . . , pd bezeichnet: WX = Mu(n, p1 , . . . , pd ) Das klassische Beispiel einer multinomialverteilten Zufallsvariablen ist das Histogramm (gruppierte Häufigkeitsverteilung), das zur graphischen Darstellung der (absoluten) experimentellen Häufigkeit verwendet wird. Xi ist die Anzahl der Fälle, in denen die Zufallsvariable R, das experimentelle Ergebnis, in Gruppe i fällt. Die Wahrscheinlichkeit, dass R in Gruppe i fällt, sei gleich pi . Werden in das Histogramm n Ergebnisse eingefüllt, so sind die Gruppeninhalte (X1 , . . . , Xd ) multinomial nach Mu(n, p1 , . . . , pd ) verteilt. R. Frühwirth Statistik 221/319 Diskrete Verteilungen Statistik R. Frühwirth Ein Histogramm Eindimensionale Zufallsvariable 25 Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable 20 Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze 15 ni Wichtige Verteilungen 10 5 0 0 1 2 R. Frühwirth 3 4 Statistik 5 x 6 7 8 9 10 222/319 Diskrete Verteilungen Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Die Poissonverteilung Po(λ) Die Poissonverteilung entsteht aus der Binomialverteilung durch den Grenzübergang n → ∞ unter der Bedingung n · p = λ. Das klassische Beispiel einer Poissonverteilten Zufallsvariablen ist die Anzahl der Zerfälle pro Zeiteinheit in einer radioaktiven Quelle. Allgemein gilt: Ist die Wartezeit zwischen zwei Ereignissen eines Zufallsprozesses exponentialverteilt, so ist die Anzahl der Ereignisse pro Zeiteinheit Poissonverteilt. Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 223/319 Diskrete Verteilungen Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Die Dichte der Poissonverteilung folgt aus der Berechnung des Grenzwertes: Pλ (k) = lim Bn; λ (k) n→∞ = lim n→∞ n! k!(n − k)! k n−k λ λ 1− = n n n(n − 1) . . . (n − k + 1) λk n→∞ nk k! " k # i−1 λk Y 1 − n · 1− = lim λ n→∞ k! 1− n i=1 = lim Momente Erwartung Varianz Schiefe n = 1− λ n n λ k n = 1− n λ = n λk −λ ·e k! Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 224/319 Diskrete Verteilungen Statistik R. Frühwirth 0.4 Eindimensionale Zufallsvariable 0.2 0.1 Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Po(2) 0.3 w(k) 0.3 w(k) Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable 0.4 Po(1) 0.2 0.1 0 0 1 2 3 4 5 6 7 8 9 0 10 0 1 2 3 4 k 5 6 7 8 9 10 k Wichtige Verteilungen Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze 0.2 Po(5) 0.15 0.1 0.05 0 Po(10) 0.15 w(k) Momente 0.2 w(k) Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen 0.1 0.05 0 5 10 15 k R. Frühwirth 0 0 5 10 15 20 25 k Statistik 225/319 Diskrete Verteilungen Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze Die hypergeometrische Verteilung Hy(N, M, n) Grundgesamtheit von N Objekten, davon haben M eine bestimmte Eigenschaft E. Es werden n Objekte gezogen, wobei jedes Objekt die gleiche Wahrscheinlickeit hat, gezogen zu werden. Einmal gezogene Objekte werden nicht zurückgelegt. Die Anzahl der gezogenen Objekte mit der Eigenschaft E ist eine Zufallsvariable X. Die Verteilung von X wird hypergeometrische Verteilung Hy(N, M, n) genannt. Ihre Dichte lautet: M N −M m n−m , 0 ≤ m ≤ min(n, M ) f (m) = N n R. Frühwirth Statistik 226/319 Diskrete Verteilungen Statistik 0.5 R. Frühwirth Mehrdimensionale Zufallsvariable 0.3 0.2 0.2 0.1 0.1 0 1 2 3 4 5 k 6 7 8 9 0 10 0.4 Wichtige Verteilungen 0 1 2 3 4 5 k 6 7 8 9 10 2 3 4 5 k 6 7 8 9 10 0.4 Hy(100,40,10) Bi(10,0.4) 0.3 P(k) 0.3 P(k) Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen 0.3 0 Grundbegriffe Randverteilungen und bedingte Verteilungen Bi(10,0.6) 0.4 P(k) P(k) Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable 0.5 Hy(20,12,10) 0.4 0.2 0.2 Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze 0.1 0 0.1 0 1 2 3 4 5 k 6 7 8 9 10 0 0 1 Zwei Hypergeometrische Verteilungen und die entsprechenden Binomialverteilungen R. Frühwirth Statistik 227/319 Diskrete Verteilungen Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Beispiel (Wiederholung eines Alternativversuchs.) Die Ereignisalgebra hat 2n Elementarereignisse, nämlich die Folgen der Form f = (ei1 , . . . , ein ), ij = 0 oder 1. Die diskrete Zufallsvariable X bildet die Folge f auf die Häufigkeit von e1 ab: r(f ) = Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe n X ij j=1 Der Wertebereich von X ist die Menge {0, 1, . . . , n}. Auf die Zahl k, 0 ≤ k ≤ n werden alle Folgen abgebildet, bei denen e1 genau k-mal eintritt. Es gibt Ckn solche Folgen, und jede hat die Wahrscheinlichkeit pk (1 − p)n−k . Es gilt daher ! n WX (k) = f (k) = pk (1 − p)n−k , 0 ≤ k ≤ n k Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 228/319 Diskrete Verteilungen Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Beispiel (Wiederholung eines Alternativversuchs) Die Wahrscheinlichkeit, dass e1 höchstens einmal eintritt, ist gleich WX (k ≤ 1) = f (0) + f (1) = (1 − p)n + np(1 − p)n−1 Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 229/319 Unterabschnitt: Stetige Verteilungen Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable 8 Eindimensionale Zufallsvariable 9 Mehrdimensionale Zufallsvariable 10 Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen 11 Momente 12 Rechnen mit Verteilungen Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 230/319 Stetige Verteilungen Statistik Die stetige Gleichverteilung Un(a, b) Eindimensionale Zufallsvariable Die stetige Gleichverteilung auf dem Intervall [a, b] hat die Dichte: 0, x < a 1 f (x|a, b) = I[a,b] = 1/(b − a), a ≤ x ≤ b b−a 0, b < x Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Dichtefunktion der Gleichverteilung Un(0,1) Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze f(x) Momente Erwartung Varianz Schiefe Verteilungsfunktion der Gleichverteilung Un(0,1) 1.2 1.2 1 1 0.8 0.8 F(x) R. Frühwirth 0.6 0.4 0.4 0.2 0 −0.5 0.6 0.2 0 0.5 x R. Frühwirth 1 1.5 Statistik 0 −0.5 0 0.5 x 1 1.5 231/319 Stetige Verteilungen Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Die Gauß- oder Normalverteilung No(µ, σ 2 ) Die Normalverteilung ist eine der wichtigsten Verteilungen in Wissenschaft und Technik. Ihre Dichte lautet: f (x|µ, σ 2 ) = √ Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe (x−µ)2 1 e− 2σ2 2πσ Im Fall von µ = 0, σ = 1 heißt sie Standardnormalverteilung. Die Verteilungsfunktion Φ(x) ist nicht durch elementare Funktionen darstellbar. Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 232/319 Stetige Verteilungen Statistik R. Frühwirth Dichtefunktion der Standardnormalverteilung Verteilungsfunktion der Standardnormalverteilung 0.5 Eindimensionale Zufallsvariable 0.45 1 Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable 0.4 0.35 Mehrdimensionale Zufallsvariable F(x) f(x) Grundbegriffe Randverteilungen und bedingte Verteilungen 0.8 0.3 0.25 0.6 0.2 Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen 0.4 0.15 0.1 0.2 0.05 Momente Erwartung Varianz Schiefe 0 −5 0 x 5 0 −5 0 x 5 Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 233/319 Stetige Verteilungen Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Die Exponentialverteilung Ex(τ ) Die Exponentialverteilung ist die Wartezeitverteilung des radioaktiven Zerfalls von Atomen und allgemein des Zerfalls von Elementarteilchen. Ihre Dichte lautet: f (x|τ ) = 1 −x/τ e · I[0,∞) (x) τ Ihre Verteilungsfunktion lautet: F (x|τ ) = 1 − e−x/τ · I[0,∞) (x) Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 234/319 Stetige Verteilungen Statistik R. Frühwirth Dichtefunktion der Exponentialverteilung Ex(2) Verteilungsfunktion der Exponentialverteilung Ex(2) Eindimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen f(x) Mehrdimensionale Zufallsvariable 0.5 1 0.4 0.8 F(x) Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable 0.3 0.6 0.2 0.4 0.1 0.2 Momente Erwartung Varianz Schiefe 0 0 2 4 6 8 10 x 0 0 2 4 6 8 10 x Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 235/319 Stetige Verteilungen Statistik R. Frühwirth Der Poissonprozess Eindimensionale Zufallsvariable Wir beobachten einen Prozess, bei dem gewisse Ereignisse zu zufälligen Zeitpunkten eintreten. Ist die Anzahl der Ereignisse pro Zeiteinheit unabhängig und Poisson-verteilt gemäß Po(λ), sprechen wir von einem Poissonprozess mit Intensität λ. Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Eigenschaften eines Poissonprozesses 1 Die Anzahl der Ereignisse in einem Zeitintervall der Länge T ist Poisson-verteilt gemäß Po(λT ). 2 Die Wartezeit zwischen zwei aufeinanderfolgenden Ereignissen ist exponentialverteilt gemäß Ex(1/λ). 3 Sind die Wartezeiten eines Prozesses unabhängig und exponentialverteilt gemäß Ex(τ ), so ist der Prozess ein Poissonprozess mit Intensität λ = 1/τ . Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 236/319 Stetige Verteilungen Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze Die Gammaverteilung Ga(a, b) Die Exponentialverteilung ist eine Spezialfall einer allgemeineren Familie von Verteilungen, der Gammaverteilung. Die Dichte der Gammaverteilung lautet: f (x|a, b) = xa−1 e−x/b · I[0,∞) (x) ba Γ(a) Ihre Verteilungsfunktion ist die regularisierte unvollständige Gammafunktion: Z x a−1 −x/b x e γ(a, x/b F (x|a, b) = dx = a b Γ(a) Γ(a) 0 R. Frühwirth Statistik 237/319 Stetige Verteilungen Statistik R. Frühwirth 0.4 0.35 0.3 Eindimensionale Zufallsvariable 0.2 0.2 0.15 0.1 0.1 Mehrdimensionale Zufallsvariable Ga(3,1) 0.25 f(x) f(x) Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Ga(2,1) 0.3 0.05 Grundbegriffe Randverteilungen und bedingte Verteilungen 0 0 5 10 x 15 0 20 0 5 10 x 15 20 Wichtige Verteilungen 0.2 Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze 0.12 Ga(5,1) Ga(10,1) 0.1 f(x) 0.15 f(x) Momente 0.14 0.1 0.08 0.06 0.04 0.05 0.02 0 0 5 10 x R. Frühwirth 15 20 Statistik 0 0 5 10 x 15 20 238/319 Unterabschnitt: Die Normalverteilung und verwandte Verteilungen Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable 8 Eindimensionale Zufallsvariable 9 Mehrdimensionale Zufallsvariable 10 Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen 11 Momente 12 Rechnen mit Verteilungen Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 239/319 Die Normalverteilung und verwandte Verteilungen Statistik R. Frühwirth Eindimensionale Zufallsvariable Die eindimensionale Normalverteilung Ihre Dichte ist die bekannte Glockenkurve: Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable f (x) = Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen (x−µ)2 1 √ e− 2σ2 σ 2π Das Maximum ist bei x = µ, die Wendepunkte bei x = µ ± σ. Die √ halbe Breite auf halber Höhe (HWHM) ist gleich σ 2 ln 2 ≈ 1, 177σ. Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 240/319 Die Normalverteilung und verwandte Verteilungen Statistik R. Frühwirth 0.5 Eindimensionale Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente fmax=0.39894 0.4 f((x−µ)/σ) Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable 0.3 HWHM 0.2 0.1 0 −4 −3 −2 −1 0 (x−µ)/σ 1 2 3 4 Eindimensionale Normalverteilung, gelber Bereich = 68.2% Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 241/319 Die Normalverteilung und verwandte Verteilungen Statistik Es gilt: R. Frühwirth W (|r − µ| ≥ σ) W (|r − µ| ≥ 2σ) W (|r − µ| ≥ 3σ) Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable = 31.8% = 4.6% = 0.2% Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Eigenschaften der Normalverteilung 1 Die Faltung zweier Normalverteilungen ist wieder eine Normalverteilung. 2 Ist die Faltung von zwei Verteilungen eine Normalverteilung, so sind auch die beiden Summanden Normalverteilungen. Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 242/319 Die Normalverteilung und verwandte Verteilungen Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze Die d-dimensionale Normalverteilung No(µ, V) Ihre Dichte lautet: 1 1 T −1 exp − (x − µ) V (x − µ) f (x) = dp 2 (2π) 2 |V| V und V−1 sind symmetrische positiv definite d × d-Matrizen. Ist X normalverteilt gemäß No(µ, V) und H eine m × d Matrix, so ist Y = HX normalverteilt gemäß No(Hµ, HVHT ). Jede Randverteilung einer Normalverteilung ist wieder eine Normalverteilung. Mittelwert und Matrix der Randverteilung entstehen durch Streichen der Spalten und Zeilen der restlichen Variablen. R. Frühwirth Statistik 243/319 Die Normalverteilung und verwandte Verteilungen Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Jede bedingte Verteilung einer Normalverteilung ist wieder eine Normalverteilung. Ist X normalverteilt gemäß No(µ, V), so kann V als positiv definite symmetrische Matrix mittels einer orthogonalen Transformation auf Diagonalform gebracht werden: UVUT = D2 Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Alle Digonalelemente von D2 sind positiv. Die Zufallsvariable Y = DU(X − µ) ist dann standardnormalverteilt. Die Drehung U heißt Hauptachsentransformation. Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 244/319 Die Normalverteilung und verwandte Verteilungen Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze Die zweidimensionale Normalverteilung Für d = 2 und µ = 0 kann die Dichte folgendermaßen angeschrieben werden: 2 h x1 1√ 1 f (x1 , x2 ) = exp − 2(1−ρ − 2 σρ 1xσ1 2x2 + 2) σ2 2 2πσ1 σ2 1−ρ 1 x22 σ22 i ρ = σ12 /(σ1 σ2 ) ist der Korrelationskoeffizient. Sind X1 und X2 unkorreliert, also ρ = 0, folgt: 1 x21 x22 1 f (x1 , x2 ) = exp − + 2 = f1 (x1 ) · f2 (x2 ) 2πσ1 σ2 2 σ12 σ2 Zwei unkorrelierte normalverteilte Zufallsvariable mit gemeinsamer Normalverteilung sind daher unabhängig. R. Frühwirth Statistik 245/319 Die Normalverteilung und verwandte Verteilungen Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen σ1=1, σ2=1, ρ=0.6 3 0.2 2 0.15 1 0.1 0 0.05 −1 Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente 0 −2 2 2 0 0 −2 −3 −3 −2 −1 0 1 2 3 −2 Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 246/319 Die Normalverteilung und verwandte Verteilungen Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Die bedingte Dichte f (x1 |x2 ) ist gegeben durch f (x1 |x2 ) = f (x1 , x2 ) = f (x2 ) " 1 1 p exp − =√ 2 σ12 (1 − ρ2 ) 2πσ1 1 − ρ2 2 # ρ x2 σ1 x1 − σ2 X1 |X2 = x2 ist also eine normalverteilte Zufallsvariable mit der Erwartung E[X1 |X2 ] = ρx2 σ1 /σ2 Momente Erwartung Varianz Schiefe E[X1 |X2 ] heißt die bedingte Erwartung. Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 247/319 Die Normalverteilung und verwandte Verteilungen Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Je nach Vorzeichen von ρ fällt oder wächst die bedingte Erwartung von X1 , wenn X2 wächst. Ist ρ = 1, sind X1 und X2 proportional: X1 = X2 σ1 /σ2 . Die Höhenschichtlinien der Dichtefunktion sind Ellipsen. Die Hauptachsentransformation ist jene Drehung, die die Ellipsen in achsenparallele Lage bringt. Sie hängt im Fall d = 2 nur von ρ ab. Ist ρ = 0, sind X1 und X2 bereits unabhängig, und der Drehwinkel ist gleich 0. Ist ρ 6= 0, ist die Drehmatrix U gleich ! cos ϕ − sin ϕ 1 σ 2 − σ12 U= mit ϕ = − arccot 2 2 2ρσ1 σ2 sin ϕ cos ϕ Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 248/319 Die Normalverteilung und verwandte Verteilungen Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze Die t-Verteilung t(n) Die Dichte der t-Verteilung mit n Freiheitsgraden lautet: −(n+1)/2 Γ( n+1 ) x2 f (x|n) = √ 2 n 1+ n nπ Γ( 2 ) Die χ2 -Verteilung χ2 (n) Die Dichte der χ2 -Verteilung mit n Freiheitsgraden lautet: f (x|n) = 1 2n/2 Γ( n2 ) xn/2−1 e−x/2 · I[0,∞) (x) Sie ist die Gammaverteilung Ga(n/2, 2). Ist X standardnormalverteilt, so ist Y = X 2 χ2 -verteilt mit einem Freiheitsgrad. R. Frühwirth Statistik 249/319 Die Normalverteilung und verwandte Verteilungen Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Die F-Verteilung F(n, m) Die Dichte der F-Verteilung (Fisher-Snedecor-Verteilung) mit n bzw. m Freiheitsgraden lautet: f (x|n, m) = n/2 m/2 Γ( n+m m xn/2−1 2 )n · I[0,∞) (x) n m Γ( 2 )Γ( 2 ) (m + nx)(n+m)/2 Sind X und Y unabhängig und χ2 -verteilt mit n bzw. n Freiheitsgraden, so ist F = Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen X/n Y /m verteilt gemäß F(n, m). Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 250/319 Abschnitt 11: Momente Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable 8 Eindimensionale Zufallsvariable 9 Mehrdimensionale Zufallsvariable 10 Wichtige Verteilungen 11 Momente Erwartung Varianz Schiefe 12 Rechnen mit Verteilungen Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 251/319 Unterabschnitt: Erwartung Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable 8 Eindimensionale Zufallsvariable 9 Mehrdimensionale Zufallsvariable 10 Wichtige Verteilungen 11 Momente Erwartung Varianz Schiefe 12 Rechnen mit Verteilungen Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 252/319 Erwartung Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Definition (Erwartung) Es sei X eine (diskrete oder stetige) Zufallsvariable mit der Dichte f (x). Ferner sei g eine beliebige stetige reelle oder komplexe Funktion. Man definiert EX [g] = E[g(X)] durch: Z ∞ X g(x)f (x) dx g(k)f (k) bzw. E[g(X)] = E[g(X)] = −∞ k∈N0 EX [g] = E[g(X)] heißt die Erwartung von g(X). Ist g ein k-dimensionaler Vektor von Funktionen, dann ist auch E[g(X)] ein k-dimensionaler Vektor. Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 253/319 Erwartung Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Definition (Erwartung einer Zufallsvariablen) Ist g(x) = x, so heißt E[g(X)] = E[X] die Erwartung oder der Mittelwert von X. Z ∞ X E[X] = xf (x) dx bzw. E[X] = k f (k) −∞ Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe k∈N0 Ist X = (X1 , . . . , Xd ), wird die Erwartung entsprechend verallgemeinert: Z ∞ Z ∞ ... g(x1 , . . . , xd ) f (x1 , . . . , xd ) dx1 . . . dxd EX [g] = −∞ −∞ Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 254/319 Erwartung Statistik Die Erwartung ist ein Lageparameter. R. Frühwirth Die Erwartung braucht nicht zu existieren. Ein Beispiel ist die Cauchy-Verteilung (t-Verteilung mit einem Freiheitsgrad) mit der Dichte Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable f (x) = Grundbegriffe Randverteilungen und bedingte Verteilungen 1 , x∈R π(1 + x2 ) Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Eigenschaften der Erwartung 1 E[c] = c, c ∈ R 2 E[aX + b] = aE[X] + b 3 E[X1 + X2 ] = E[X1 ] + E[X2 ] 4 X1 und X2 unabhängig =⇒ E[X1 X2 ] = E[X1 ] · E[X2 ] Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 255/319 Erwartung Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze Beispiel (Die Erwartung der Alternativverteilung) Es sei X alternativverteilt nach Al(p). Dann gilt E[X] = 1 · p + 0 · (1 − p) = p Beispiel (Die Erwartung der Binomialverteilung) Es sei X binomialverteilt nach Bi(n, p). ! n n X X n E[X] = k pk (1 − p)n−k = k k k=1 k=0 ! n pk (1 − p)n−k k Mit k0 = k − 1 und n0 = n − 1 folgt ! n0 X 0 0 0 n E[X] = np pk (1 − p)n −k = np k k0 =0 R. Frühwirth Statistik 256/319 Erwartung Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Beispiel (Fortsetzung) Da X die Anzahl des Eintretens von e1 in n unabhängigen Alternativversuchen angibt, kann X auch als die Summe von n alternativverteilten Zufallsvariablen X1 , . . . , Xn betrachtet werden: Mehrdimensionale Zufallsvariable r= Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen n X Xi . i=1 Dann folgt E[X] = np aus der Additivität der Ewartung. Beispiel (Die Erwartung der Poissonverteilung) Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze Es sei X nach Po(λ) poissonverteilt: E[X] = ∞ X k=0 k· 0 ∞ ∞ X λk −λ X λk λk −λ e = e−λ = λ e =λ k! (k − 1)! k0 ! 0 k=1 R. Frühwirth Statistik k =0 257/319 Erwartung Statistik R. Frühwirth Eindimensionale Zufallsvariable Beispiel (Die Erwartung der hypergeometrischen Verteilung) Es sei X hypergeometrisch verteilt nach Hy(N, M, n). Dann gilt Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable E[X] = Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze nM N Beispiel (Die Erwartung der Binomialverteilung) Es sei X binomialverteilt nach Bi(n, p). ! n n X X n E[X] = k pk (1 − p)n−k = k k k=0 k=1 ! n pk (1 − p)n−k k Mit k0 = k − 1 und n0 = n − 1 folgt ! n0 X 0 0 0 n np pk (1 − p)n −k = np E[X] = k k0 =0 R. Frühwirth Statistik 258/319 Erwartung Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Beispiel (Die Erwartung der stetigen Gleichverteilung) Es sei X gleichverteilt auf dem Intervall [a, b]: Z b x a+b E[X] = dx = 2 a b−a Beispiel (Die Erwartung der Exponentialverteilung) Es sei X exponentialverteilt gemäß Eτ : Z ∞ ∞ t −t/τ E[X] = e dt = −te−t/τ − τ e−t/τ = τ τ 0 0 Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze Beispiel (Die Erwartung der Normalverteilung) Es sei X normalverteilt gemäß No(µ, σ 2 ): E[X − µ] = 0 =⇒ E[X] − µ = 0 =⇒ E[X] = µ R. Frühwirth Statistik 259/319 Erwartung Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Beispiel (Die Erwartung der Gammaverteilung) Es sei X gammaverteilt gemäß Ga(a, b): 0 Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen ∞ Z E[X] = xa e−x/b dx = ab ba Γ(a) Beispiel (Die Erwartung der χ2 -Verteilung) Es sei X χ2 -verteilt mit n Freiheitsgraden: E[X] = n Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 260/319 Erwartung Statistik R. Frühwirth Eindimensionale Zufallsvariable Beispiel (Die Erwartung der t-Verteilung) Es sei X t-verteilt mit n Freiheitsgraden: Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen E[X] = 0, n > 1 Für n = 1 (Cauchy- oder Breit-Wigner-Verteilung) existiert die Erwartung nicht. Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Beispiel (Die Erwartung der F-Verteilung) Es sei X F-verteilt mit n bzw. m Freiheitsgraden: E[X] = m ,m > 2 m−2 Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 261/319 Erwartung Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Definition (Momente) Sei X eine Zufallsvariable. Die Erwartung von g(x) = (x − a)k , sofern sie existiert, heißt k-tes Moment von X um a. Das k-te Moment um 0 wird mit µ0k bezeichnet. Das k-te Moment um den Erwartungswert E[X] wird als zentrales Moment µk bezeichnet. Die zentralen Momente µ1 , . . . , µk können aus den Momenten um 0 µ01 , . . . , µ0k berechnet werden, und umgekehrt. Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 262/319 Erwartung Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Beispiel (Umrechnung von zentralen Momenten und Momenten um 0) µ2 = µ02 − µ01 2 µ3 = µ03 − 3µ01 µ02 + 2µ01 3 2 µ4 = µ04 − 4µ01 µ03 + 6µ01 µ02 − 3µ01 4 Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe µ02 = µ2 + µ01 2 µ03 = µ3 + 3µ01 µ2 + µ01 3 2 µ04 = µ4 + 4µ01 µ3 + 6µ01 µ2 + µ01 4 Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 263/319 Unterabschnitt: Varianz Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable 8 Eindimensionale Zufallsvariable 9 Mehrdimensionale Zufallsvariable 10 Wichtige Verteilungen 11 Momente Erwartung Varianz Schiefe 12 Rechnen mit Verteilungen Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 264/319 Varianz Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Definition (Varianz) Das zweite zentrale Moment µ2 heißt die Varianz von X, bezeichnet mit var[X]. Die Wurzel aus der Varianz heißt die Standardabweichung von X, bezeichnet mit σ[X]. Die Standardabweichung ist ein Skalenparameter, der die Breite der Verteilung beschreiben. Die Standardabweichung hat die gleiche Dimension wie die Zufallsvariable. Varianz und Standardabweichung sind (wie alle zentralen Momente) invariant gegen Translationen. Die Varianz braucht nicht zu existieren. Ein Beispiel ist die t-Verteilung mit zwei Freiheitsgraden mit der Dichte Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze f (x) = R. Frühwirth 1 , x∈R (2 + x2 )3/2 Statistik 265/319 Varianz Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Die Tschebyscheff’sche Ungleichung Es sei X eine Zufallsvariable mit der Erwartung E[X] = µ und der Varianz var[X] = σ 2 . Für g > 0 gilt: W (|X − µ| > gσ) ≤ Grundbegriffe Randverteilungen und bedingte Verteilungen 1 g2 Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 266/319 Varianz Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Definition (Kovarianz) Sei X = (X1 , . . . , Xn ) eine n-dimensionale Zufallsvariable und E[Xi ] = µ0i . cov[Xi , Xj ] = E[(Xi − µ0i )(Xj − µ0j )] = Z = (xi − µ0i )(xj − µ0j ) f (x1 , . . . xn ) dx1 . . . dxn = n ZR∞ Z ∞ (xi − µ0i )(xj − µ0j ) fij (xi , xj ) dxi dxj = −∞ −∞ heißt die Kovarianz von Xi und Xj , auch σij geschrieben. Die Matrix V mit Vij = cov[Xi , Xj ] heißt die Kovarianzmatrix von X, bezeichnet mit Cov[X]. Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 267/319 Varianz Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Eigenschaften der Varianz bzw. der Kovarianz 1 var[X] = E[r2 ] − (E[X])2 2 cov[X1 , X2 ] = E[X1 X2 ] − E[X1 ] · E[X2 ] 3 var[aX + b] = a2 var[X] 4 Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe 5 var[a1 X1 + a2 X2 ] = a21 var[X1 ] + a22 var[X2 ] + 2a1 a2 cov[X1 , X2 ] " n # n X n X X var Xi = cov[Xi , Xj ] = i=1 n X i=1 i=1 j=1 var[Xi ] + 2 n n X X cov[Xi , Xj ] i=1 j=i+1 Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 268/319 Varianz Statistik Für unabhängige Zufallsgrößen gilt: R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen 1 X1 , X2 unabhängig =⇒ cov[X1 , X2 ] = 0 2 X1 , . . . , Xn unabhängig: " n # n X X var Xi = var[Xi ] i=1 i=1 Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 269/319 Varianz Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Definition (Korrelationskoeffizient) σij heißt der Korrelationskoeffizient von Xi Die Größe ρij = σi σj und Xj . Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Eigenschaften des Korrelationskoeffizienten 1 Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen 2 −1 ≤ ρij ≤ 1 Ist |ρij | = 1, so sind Xi und Xj linear abhängig. Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 270/319 Varianz Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Beispiel (Die Varianz der Alternativverteilung) Es sei X alternativverteilt nach Al(p). var[X] = E[X 2 ] − p2 = 12 · p + 02 · (1 − p) − p2 = p(1 − p) Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Beispiel (Die Varianz der Binomialverteilung) Ist X nach Bi(n, p) verteilt, so ist X die Summe von n unabhängigen alternativverteilten Zufallsvariablen. Es gilt daher: var[X] = np(1 − p) Ist Y = X/n die relative Häufigkeit des Eintretens von e1 , so gilt E[Y ] = p, var[Y ] = p(1 − p)/n Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 271/319 Varianz Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Beispiel (Die Varianz der hypergeometrischen Verteilung) Es sei X hypergeometrisch verteilt nach Hy(N, M, n). Dann gilt var[X] = Mehrdimensionale Zufallsvariable nM (N − n)(N − M ) N 2 (N − 1) Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 272/319 Varianz Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Beispiel (Die Kovarianzmatrix der Multinomialverteilung) Sei X = (X1 , . . . , Xd ) nach Mu(n; p1 , . . . , pd ) verteilt (d ≥ 2). Da Xi binomialverteilt ist, gilt var[Xi ] = npi (1 − pi ) Für ein Histogramm ist also die Varianz des Gruppeninhaltes gleich npi (1 − pi ). Für pi 1 (viele Gruppen) ist das ungefähr gleich npi , der Erwartung des Gruppeninhaltes. cov[Xi , Xj ] =E[Xi Xj ] − E[Xi ] · E[Xj ] = =n(n − 1)pi pj − npi npj = Momente = − npi pj Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 273/319 Varianz Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Beispiel (Die Varianz der Poissonverteilung) E[X 2 ] = = Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen = = Rechnen mit Verteilungen k=0 ∞ X k=0 ∞ X k2 λk −λ e = k! k·λ· λk−1 e−λ = (k − 1)! 0 (k0 + 1) · λ · k0 =0 ∞ X λk −λ e = k0 ! 00 λ2 k00 =0 2 Momente Erwartung Varianz Schiefe ∞ X λk −λ e +λ= k00 ! =λ + λ var[X] =E[X 2 ] − λ2 = λ Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 274/319 Varianz Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Beispiel (Die Varianz der stetigen Gleichverteilung) b b3 − a3 3(b − a) a 2 3 3 (b − a)2 b −a b+a − = var[X] = 3(b − a) 2 12 E[X 2 ] = 1 b−a Z x2 dx = Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Beispiel (Die Varianz der Exponentialverteilung) E[X 2 ] = 1 τ Z ∞ t2 e−t/τ dt = 2τ 2 0 2 var[X] = E[X ] − τ 2 = τ 2 Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 275/319 Varianz Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Beispiel (Die Varianz der Normalverteilung) Es gilt: √ 1 2π σ Z 1 (x − µ)2 exp − dx = 1 für alle µ. 2 σ2 Nach zweimaligem Differenzieren nach µ, wobei Differentiation und Integration vertauscht werden dürfen, erhält man: Z (x − µ)2 1 1 1 (x − µ)2 √ − 2 + exp − dx = 0 σ σ2 2 σ2 2π σ Z 1 (x − µ)2 1 √ (x − µ)2 exp − dx = σ 2 2 σ2 2π σ var[X] = σ 2 Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 276/319 Varianz Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Beispiel (Die Varianz der Gammaverteilung) Es sei X gammaverteilt gemäß Ga(a, b): E[X 2 ] = ∞ Z 0 xa+1 e−x/b dx = a(a + 1)b2 ba Γ(a) var[X] = ab2 Beispiel (Die Varianz der χ2 -Verteilung) Es sei X χ2 -verteilt mit n Freiheitsgraden: Momente var[X] = 2 n Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 277/319 Varianz Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Beispiel (Die Varianz der t-Verteilung) Es sei X t-verteilt mit n Freiheitsgraden: var[X] = n ,n > 2 n−2 Für n ≤ 2 existiert die Varianz nicht. Beispiel (Die Varianz der F-Verteilung) Es sei X F-verteilt mit n bzw. m Freiheitsgraden: var[X] = Erwartung Varianz Schiefe 2m2 (n + m − 2) ,m > 4 n(m − 2)2 (m − 4) Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 278/319 Unterabschnitt: Schiefe Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable 8 Eindimensionale Zufallsvariable 9 Mehrdimensionale Zufallsvariable 10 Wichtige Verteilungen 11 Momente Erwartung Varianz Schiefe 12 Rechnen mit Verteilungen Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 279/319 Schiefe Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Definition (Schiefe) Das reduzierte dritte zentrale Moment γ = µ3 /σ 3 heißt die Schiefe. Die Schiefe misst die Asymmetrie einer Verteilung. Ist die Schiefe positiv (negativ), heißt die Verteilung rechtsschief (linksschief). Für symmetrische Verteilungen ist sie 0. Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Beispiel (Die Schiefe der Exponentialverteilung) Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze µ3 = E[(X − E[X])3 ] = ∞ Z 0 (t − τ )3 −t/τ e dt = 2τ 3 τ Die Schiefe ist daher gleich γ = 2. R. Frühwirth Statistik 280/319 Schiefe Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Beispiel (Die Schiefe der Gammaverteilung) ∞ (x − ab)3 a−1 −x/b x e dx = 2ab3 ba Γ(a) 0 √ Die Schiefe ist daher gleich γ = 2/ a und strebt für a → ∞ gegen 0. µ3 = E[(X − E[X])3 ] = Z Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Selbst wenn alle Momente einer Verteilung existieren, ist sie dadurch nicht eindeutig bestimmt. Zum Beispiel haben die Verteilungen mit den Dichten 1 f (x) = √ x− ln x [1 − λ sin(4π ln x)], 0 ≤ x ≤ ∞, 0 ≤ λ ≤ 1 4 π2 e dieselben Momente µ0k = ek(k+2)/4 , unabhängig von λ. Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 281/319 Abschnitt 12: Rechnen mit Verteilungen Statistik R. Frühwirth 8 Eindimensionale Zufallsvariable 9 Mehrdimensionale Zufallsvariable 10 Wichtige Verteilungen 11 Momente 12 Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 282/319 Unterabschnitt: Faltung und Messfehler Statistik R. Frühwirth 8 Eindimensionale Zufallsvariable 9 Mehrdimensionale Zufallsvariable 10 Wichtige Verteilungen 11 Momente 12 Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 283/319 Faltung und Messfehler Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Definition (Faltung) Es seien X1 und X2 zwei unabhängige Zufallsvariablen. Die Summe X = X1 + X2 heißt die Faltung von X1 und X2 . Satz Sind X1 und X2 zwei unabhängige Zufallsvariable mit der gemeinsamen Dichte f (x1 , x2 ) = f1 (x1 ) · f2 (x2 ), so hat ihre Summe X = X1 + X2 die Dichte Z ∞ f1 (x − x2 ) · f2 (x2 ) dx2 = g(x) = −∞ Z ∞ = f1 (x1 ) · f2 (x − x1 ) dx1 −∞ Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 284/319 Faltung und Messfehler Statistik R. Frühwirth Die Dichte g wird als Faltungsprodukt von f1 und f2 bezeichnet: g = f1 ∗ f2 . Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Beispiel (Faltung von zwei Exponentialverteilungen) Es seien X1 und X2 exponentialverteilt gemäß Eτ . Die Summe X = X1 + X2 hat die folgende Dichte: Z ∞ g(t) = f1 (t − t2 )f2 (t2 ) dt2 = Z −∞ t = 0 = 1 (t2 −t)/τ −t2 /τ e e dt2 = τ2 1 −t/τ te τ2 Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 285/319 Faltung und Messfehler Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze Beispiel (Faltung von zwei Gleichverteilungen) Es seien X1 und X2 gleichverteilt im Intervall [0, 1]. Die Summe X = X1 + X2 hat die folgende Dichte: Z ∞ g(x) = f1 (x − x2 )f2 (x2 ) dx2 −∞ Das Produkt der Dichten ist nur ungleich 0, wenn 0 ≤ x − x2 ≤ 1 und 0 ≤ x2 ≤ 1 gilt. Die effektiven Integrationsgrenzen sind daher xmin = max(0, x − 1) und xmax = min(x, 1). Ist 0 ≤ x ≤ 1, ist xmin = 0 und xmax = x; ist 1 ≤ x ≤ 2, ist xmin = x − 1 und xmax = 1. Die Dichte g(x) lautet daher: wenn 0 ≤ x ≤ 1 x, g(x) = 2 − x, wenn 1 ≤ x ≤ 2 0, sonst Die Summenverteilung heißt Dreiecksverteilung. R. Frühwirth Statistik 286/319 Faltung und Messfehler Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Beispiel (Der Messfehler) Es wird eine Zufallsgröße X beobachtet. Der Messfehler wird durch eine bedingte Dichte b(x0 |x) beschrieben, die die Wahrscheinlichkeit angibt, dass x0 bei der Messung registriert wird, wenn X den Wert x annimmt. Für die gemessene Verteilung gilt dann: Z ∞ Z ∞ f (x0 , x) dx b(x0 |x)f (x) dx = fM (x0 ) = −∞ −∞ Im günstigsten Fall hängt b nur von der Differenz x0 − x ab, oder eine weitere explizite Abhängigkeit von x ist vernachlässigbar. Dann wird aus dem Integral ein Faltungsintegral. Dies ist genau dann der Fall, wenn der Messfehler und die Messung unabhängig sind. Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 287/319 Faltung und Messfehler Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Die Faltung von zwei Zufallsvariablen X1 und X2 kann auch mit Hilfe ihrer charakteristischen Funktionen berechnet werden. Definition (Charakteristische Funktion) Es sei X eine Zufallsvariable. Die charakteristische Funktion von X ist definiert durch: ϕX (t) = E[ exp(itX) ], t ∈ R Satz Ist X = X1 + X2 die Faltung von X1 und X2 , so gilt: Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze ϕX (t) = ϕX1 (t) · ϕX2 (t) R. Frühwirth Statistik 288/319 Faltung und Messfehler Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Beispiel (Faltung von zwei Poissonverteilungen) Es seien X1 und X2 Poisson-verteilt gemäß Po(λ1 ) bzw. Po(λ2 ). Die charakteristische Funktion von Xi lautet: ϕXi (t) = ∞ X eikt λki e−λi = exp[λi (eit − 1)] k! k=0 Die charakteristische Funktion von X = X1 + X2 ist daher gleich ϕX (t) = exp[λ1 (eit − 1)] exp[λ2 (eit − 1)] = exp[(λ1 + λ2 )(eit − 1)] X ist also Poisson-verteilt gemäß Po(λ) mit λ = λ1 + λ2 . Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 289/319 Faltung und Messfehler Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Beispiel (Faltung von zwei χ2 -Verteilungen) Es seien X1 und X2 χ2 -verteilt mit n1 bzw. n2 Freiheitsgraden. Die charakteristische Funktion von Xi lautet: ϕXi (t) = Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Die charakteristische Funktion von X = X1 + X2 ist daher gleich Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente 1 (1 − 2it)ni /2 ϕX (t) = 1 1 = (1 − 2it)n1 /2 (1 − 2it)n2 /2 (1 − 2it)(n1 +n2 )/2 X ist also χ2 -verteilt mit n = n1 + n2 Freiheitsgraden. Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 290/319 Unterabschnitt: Fehlerfortpflanzung, Transformation von Dichten Statistik R. Frühwirth 8 Eindimensionale Zufallsvariable 9 Mehrdimensionale Zufallsvariable 10 Wichtige Verteilungen 11 Momente 12 Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 291/319 Fehlerfortpflanzung, Transformation von Dichten Statistik Im folgenden Abschnitt sollen Linearkombinationen von — nicht notwendig unabhängigen — Zufallsvariablen betrachtet werden. R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Es sei X = (X1 , . . . , Xn ) eine n-dimensionale Zufallsvariable und H eine m × n - Matrix. Dann ist Y = (Y1 , . . . Ym ) = HX — wie jede deterministische Funktion einer Zufallsvariablen — wieder eine Zufallsvariable. Wie ist Y verteilt? Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Es gilt exakt: Lineare Transformation von Erwartung und Varianz 1 E[Y ] = H · E[X] 2 Cov[Y ] = H · Cov[X] · HT Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 292/319 Fehlerfortpflanzung, Transformation von Dichten Statistik Es soll nun statt der linearen Abbildung H eine allgemeine Funktion h = (h1 , . . . , hm ) betrachtet werden. R. Frühwirth Eindimensionale Zufallsvariable Es wird angenommen, dass h in jenem Bereich, in dem die Dichte von X signifikant von 0 verschieden ist, genügend gut durch eine lineare Funktion angenähert werden kann. Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Entwickelt man h an der Stelle E[X], so gilt in 1. Näherung: Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Lineare Fehlerfortpflanzung 1 2 E[Y ] = h(E[X]) T ∂h ∂h Cov[Y ] = · Cov[X] · ∂x ∂x Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 293/319 Fehlerfortpflanzung, Transformation von Dichten Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Ist h = (h1 , . . . , hn ) eine umkehrbar eindeutige Abbildung h : Rn → Rn , so läßt sich die Dichte von Y = (Y1 , . . . , Yn ) = h(X1 , . . . , Xn ) berechnen. Es sei X = (X1 , . . . , Xd ) eine d-dimensionale Zufallsvariable mit der Dichte fX (x1 , . . . , xd ), h eine umkehrbare Abbildung h : Rd → Rd , g die Umkehrfunktion von h, Y = h(X) und fY (y1 , . . . , yd ) die Dichte von Y . Dann gilt: Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze Transformation der Dichte ∂g fY (y1 , . . . , yd ) = fX (g(y1 , . . . , yd )) · ∂y ∂g wobei der Betrag der Funktionaldeterminante ist. ∂y R. Frühwirth Statistik 294/319 Fehlerfortpflanzung, Transformation von Dichten Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Beispiel (Transformation unter einer affinen Abbildung) Es sei X eine d-dimensionale Zufallsvariable mit Dichte fX (x) und Y = AX + b. Ist A regulär, ist die Dichte von Y gegeben durch: fY (y) = fX (A−1 (y − b)) · Mehrdimensionale Zufallsvariable 1 |A| Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze Beispiel (Transformation mit der Verteilungsfunktion) Es sei X eine stetige Zufallsvariable mit der Dichte f (x) und der Verteilungsfunktion F (x), und Y = F (X). Dann ist die Dichte von Y gegeben durch: dF −1 = f (x)/f (x) = 1 g(y) = f (x) · dy Y ist also gleichverteilt im Intervall [0, 1]. Y wird als p-Wert (probability transform) von X bezeichnet. R. Frühwirth Statistik 295/319 Fehlerfortpflanzung, Transformation von Dichten Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze Beispiel (Transformation mit der inversen Verteilungsfunktion) Es sei U gleichverteilt im Intervall [0, 1], F (x) (f (x)) die Verteilungsfunktion (Dichtefunktion) einer stetigen Verteilung, und X = F −1 (U ). Dann ist die Dichte von X gegeben durch: dF = f (x) g(x) = 1 · dx X ist also verteilt mit der Verteilungsfunktion F und der Dichte f . Beispiel Es sei X gleichverteilt im Intervall [0, 1] und Y = − ln(X). Dann ist g(y) = exp(−y) und dg = e−y fY (y) = fX (exp(−y)) · dy Y ist daher exponentialverteilt mit τ = 1. R. Frühwirth Statistik 296/319 Fehlerfortpflanzung, Transformation von Dichten Statistik Beispiel (Transformation auf Polarkoordinaten) R. Frühwirth Eindimensionale Zufallsvariable Es seien (X, Y ) unabhängig und standardnormalverteilt. Wir suchen die Verteilung der Polarkoordinaten (R, Φ), definiert durch: Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe X = R cos(Φ), Y = R sin(Φ) Die Funktionaldeterminante lautet: ∂(x, y) ∂(r, ϕ) = r Die Dichte ist daher f (r, ϕ) = 2 1 re−r /2 2π R und Φ sind unabhängig mit den Randdichten Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze f1 (r) = re−r R. Frühwirth 2 Statistik /2 , f2 (ϕ) = 1 2π 297/319 Fehlerfortpflanzung, Transformation von Dichten Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Beispiel (Transformation auf Kugelkoordinaten) Es seien (X, Y, Z) unabhängig und standardnormalverteilt. Wir suchen die Verteilung der Kugelkoordinaten (R, Θ, Φ), definiert durch: X = R sin(Θ) cos(Φ), Y = R sin(Θ) sin(Φ), z = R cos(Θ) Die Funktionaldeterminante lautet: ∂(x, y, z) 2 ∂(r, θ, ϕ) = r sin(θ) Die Dichte ist daher Momente Erwartung Varianz Schiefe f (r, θ, ϕ) = 1 (2π) 3/2 e−r 2 /2 2 r sin(θ) Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 298/319 Fehlerfortpflanzung, Transformation von Dichten Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Beispiel (Fortsetzung) R, θ und ϕ sind unabhängig mit den Randdichten √ 2 2 1 1 f1 (r) = √ r2 e−r /2 , f2 (θ) = sin(θ), f3 (ϕ) = 2 2π π Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Beispiel (Geschwindigkeitsverteilung im idealen Gas) Im idealen Gas sind die Komponenten (Vx , Vy , Vz ) der Molekülgeschwindigkeit in guter Näherung normalverteilt, mit Mittelwert 0 und Varianz σ 2 = kT /m, wobei m die Molekülmasse, k die Boltzmannkonstante und T die Temperatur ist. Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 299/319 Fehlerfortpflanzung, Transformation von Dichten Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Beispiel (Fortsetzung) Der Betrag V der Geschwindigkeit hat dann die Dichte √ 3/2 2 2m f (v) = √ v 2 e−mv /2kT π(kT )3/2 Die Verteilung wird Maxwell-Verteilung genannt. Mittelwert und Standardabweichung sind r r 8 kT 3 kT , σ[V ] = E[V ] = πm m Die häufigste Geschwindigkeit (das Maximum der Dichte) ist bei r 2 kT Vmax = m Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 300/319 Fehlerfortpflanzung, Transformation von Dichten Statistik R. Frühwirth 0.7 Eindimensionale Zufallsvariable vmax 0.6 Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Maxwell−Verteilung mit kT=m E[v] 0.5 Mehrdimensionale Zufallsvariable Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe 0.4 f(v) Grundbegriffe Randverteilungen und bedingte Verteilungen 0.3 0.2 0.1 0 0 0.5 1 1.5 2 Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze 2.5 v 3 3.5 4 4.5 5 Maxwell-Verteilung, kT = m R. Frühwirth Statistik 301/319 Unterabschnitt: Systematische Fehler Statistik R. Frühwirth 8 Eindimensionale Zufallsvariable 9 Mehrdimensionale Zufallsvariable 10 Wichtige Verteilungen 11 Momente 12 Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 302/319 Systematische Fehler Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze Kann der Messfehler durch eine Zufallsvariable mit Mittel 0 beschrieben werden, hat die Messung nur einen statistischen Fehler. Die Messung kann jedoch durch eine falsche Kalibration (z.B. Skalenfehler oder Nullpunktfehler) des Messgeräts verfälscht sein. Solche Fehler werden systematische Fehler genannt. Systematische Fehler werden durch Vergrößerung der Stichprobe nicht kleiner! Die Korrektur von systematischen Fehlern erfordert solgfältige Kalibaration der Messaparatur, Überprüfung von theoretischen Annahmen, etc. Das Gesetz der Fehlerfortpflanzung gilt nicht für systematische Fehler! R. Frühwirth Statistik 303/319 Systematische Fehler Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Beispiel Wir messen zwei Spannungen U1 , U2 mit dem gleichen Messgerät. Durch fehlerhafte Kalibration misst das Gerät statt der wahren Spannung U die Spannung Um = aU + b + ε, mit a = 0.99, b = 0.05, σ[ε] = 0.03 V. Der Mittelwert Ū der beiden Spannungen hat dann einen statistischen Fehler von 0.02 V. Der systematische Fehler des Mittelwerts wird beschrieben durch Ūm = aŪ + b, ist also der der Einzelmessung. Der systematische Fehler der Differenz ∆U wird beschrieben durch ∆Um = a∆U . Der Nullpunktfehler ist verschwunden. Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 304/319 Unterabschnitt: Grenzverteilungssätze Statistik R. Frühwirth 8 Eindimensionale Zufallsvariable 9 Mehrdimensionale Zufallsvariable 10 Wichtige Verteilungen 11 Momente 12 Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 305/319 Grenzverteilungssätze Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Zentraler Grenzwertsatz für identisch verteilte Folgen von Zufallsvariablen Sei (Xi )i∈N eine Folge von unabhängigen Zufallsvariablen, die die gleiche Verteilung besitzen, mit endlicher Erwartung µ und endlicher Varianz σ 2 . Definiert man Sn und Un durch: Sn = n X Xi , Un = i=1 Sn − E[Sn ] Sn − nµ = √ σ[Sn ] n·σ so ist U = limn→∞ Un standardnormalverteilt. Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 306/319 Grenzverteilungssätze Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze Zentraler Grenzwertsatz für beliebig verteilte Folgen von Zufallsvariablen Sei (Xi )i∈N eine Folge von unabhängigen Zufallsvariablen mit beliebigen Verteilungen. µi = E[Xi ] und σi2 = var[Xi ] seien endlich für alle i ∈ N. Definiert man für jedes n ∈ N Ui und Yn durch: n X Xi − µi , Yn = Ui Ui = √ nσi i=1 so ist Y = limn→∞ Yn standardnormalverteilt. Der zentrale Grenzwertsatz erklärt, warum die Normalverteilung in der Natur eine so bedeutende Rolle spielt, etwa bei der Verteilung der Impulskomponenten von Gasmolekülen, die das Ergebnis von zahlreichen Stößen ist. R. Frühwirth Statistik 307/319 Grenzverteilungssätze Statistik R. Frühwirth Auch bei relativ kleinem n ist die Normalverteilung of eine gute Näherung für die Summe von Zufallsvariablen. Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Beispiel (Binomialverteilung für großes n) Da eine gemäß Bi(n, p) verteilte Zufallsvariable als Summe von n alternativverteilten Zufallsvariablen dargestellt werden kann, muss die Binomialverteilung für n → ∞ gegen eine Normalverteilung streben. Die Abbildung zeigt die Verteilungsfunktion der Binomialverteilung Bi(n, p) mit n = 200 und p = 0.1, sowie die Verteilungsfunktion der Normalverteilung No(µ, σ 2 ) mit µ = np = 20 und σ 2 = np(1 − p) = 18. Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 308/319 Grenzverteilungssätze Statistik R. Frühwirth 1 Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable 0.8 0.7 Mehrdimensionale Zufallsvariable 0.6 F(x) Grundbegriffe Randverteilungen und bedingte Verteilungen Bi(200,0.1) No(20,18) 0.9 0.5 Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen 0.4 0.3 0.2 0.1 0 0 5 10 15 Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 20 x 25 30 35 40 309/319 Grenzverteilungssätze Statistik R. Frühwirth Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable Mehrdimensionale Zufallsvariable Grundbegriffe Randverteilungen und bedingte Verteilungen Beispiel (Poissonverteilung für großes n) Da eine gemäß Po(λ) verteilte Zufallsvariable als Summe von λ P (1)-verteilten Zufallsvariablen dargestellt werden kann, muss die Poissonverteilung für λ → ∞ gegen eine Normalverteilung streben. Die Abbildung zeigt die Verteilungsfunktion der Poissonverteilung Po(λ) mit λ = 25, sowie die Verteilungsfunktion der Normalverteilung No(µ, σ 2 ) mit µ = λ = 25 und σ 2 = λ = 25. Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 310/319 Grenzverteilungssätze Statistik R. Frühwirth 1 Eindimensionale Zufallsvariable Grundbegriffe Diskrete Zufallsvariable Stetige Zufallsvariable 0.8 0.7 Mehrdimensionale Zufallsvariable 0.6 F(x) Grundbegriffe Randverteilungen und bedingte Verteilungen Po(25) N(25,25) 0.9 0.5 Wichtige Verteilungen Diskrete Verteilungen Stetige Verteilungen Die Normalverteilung und verwandte Verteilungen Momente Erwartung Varianz Schiefe Rechnen mit Verteilungen 0.4 0.3 0.2 0.1 0 0 5 10 15 20 Faltung und Messfehler Fehlerfortpflanzung, Transformation von Dichten Systematische Fehler Grenzverteilungssätze R. Frühwirth Statistik 25 x 30 35 40 45 50 311/319