Trigonometrie

Einführung in die Trigonometrie
Das Wort Trigonometrie stammt aus dem Griechischen und enthält die beiden Wörter Dreieck
(Trigon) und Messen (metrein). Wie der Name also sagt, versteht man unter Trigonometrie
das Messen und Berechnen von Dreiecken.
Viele Probleme aus den verschiedensten Bereichen wie
 Landvermessung
 Astronomie
 Seefahrt etc.
lassen sich mit Hilfe trigonometrischer Berechnungen lösen.
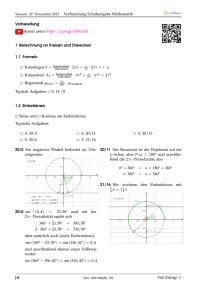
Beispiel
1) Höhenbestimmung eines Baumes

Distanz
2) Höhenbestimmung eines Berges


Standlinie
3) Kurs eines Schiffes
1
4) Entfernungsmessung über einen See hinweg
B
A
Offenbar ist allen Beispielen gemeinsam, daß Dreiecke mit ihren
-
Seitenlängen und
Winkeln
eine wesentliche Rolle spielen. Trigonometrie bedeutet somit, die Beziehungen in einem
Dreieck zu studieren.
Betrachten wir zunächst das folgende Dreieck etwas genauer.

Erinnern wir uns an den Strahlensatz, so wissen wir, daß die Verhältnisse aus
Höhenzuwachs
:
zurückgelegtem Weg
der beiden Dreiecke gleich sind. Oder anders formuliert: In ähnlichen Dreiecken sind die
Seitenverhältnisse der einander entsprechenden Seiten gleich.
Demnach liegt es nahe, das obige Seitenverhältnis mit dem Winkel  zu identifizieren. Man
sagt auch, daß das Verhältnis eine Funktion des Winkels ist. Diese Funktion nennt man den
Sinus des Winkels  und definiert:
Gegenkathe te
sin  
Hypotenuse
2
Weitere wichtige Definitionen für Seitenverhältnisse im Dreieck sind:
cos  
Ankathete
Hypotenuse
tan  
Gegenkathe te
Ankathete
Nun kommen wir zur Definition der trigonometrischen Funktionen am Kreis mit Radius 1 –
man spricht dann vom Einheitskreis.
P
tan 
1
sin 

cos 
Zur Motivation
sollten wir uns jedoch noch einmal klar machen, warum es genügt, diese Definitionen am
Einheitskreis zu formulieren. Dazu betrachten wir erneut Beispiel 1, wo die Höhe eines
Baumes bestimmt werden soll.
Wir messen zuerst die Distanz zwischen unserem Beobachtungsstandpunkt und dem
Baumstamm und dann den Winkel , mit dem wir die Spitze des Baumes anvisieren. Nehmen
wir folgende Messergebnisse an:  = 30° und Distanz = 25 m.
Am Einheitskreis verschieben wir Punkt P so, daß wir gerade einen Winkel von  = 30°
erhalten, und messen die Strecke tan , die ja das Verhältnis aus Gegenkathete zu Ankathete
darstellt. Wir erhalten ungefähr 0,58. Jetzt fassen wir unsere Ergebnisse in folgender
Zeichnung zusammen:
3
h
0,58
30°
1m
25 m
Da das graue Dreieck aus dem Einheitskreis dem großen Dreieck ähnlich ist, wissen wir, daß
deren Seitenverhältnisse gleich sind. Somit können wir die unbekannte Höhe h des Baumes
mit der folgenden Gleichung bestimmen:
0,58 h

 h  14,5
1
25
Halten wir also fest: Wir können die Höhe des Baumes bestimmen, da uns mit Kenntnis des
Winkels  das Seitenverhältnis
Gegenkathe te
tan  
Ankathete
am Einheitskreis bekannt ist und damit ist aus Ähnlichkeitsgründen auch das Seitenverhältnis
des großen Dreiecks.
Natürlich müssen wir nicht jedes Mal am Einheitskreis die Seitenverhältnisse messen, um
solche Aufgaben zu rechnen. Vielmehr ist es angebracht, zunächst einmal die Sinus-,
Kosinus- und Tangenswerte bestimmter Winkel mit Hilfe des Einheitskreises zu ermitteln und
in einer Tabelle zusammen zu fassen.
Oder man stellt sich mit Hilfe eines Taschenrechners eine solche Tabelle her; denn die dort
vorzufindenden Werte beziehen sich auf den Einheitskreis.
Gebräuchliche Werte trigonometrischer Funktionen
0°
30°
45°
60°
90°

1
1
1
sin 
0
1
2
2 2
2 3
cos 
1
1
2
3
tan 
0
1
3
3
1
2
2
1
1
2
3
0
nicht definiert
Für die Höhenbestimmung des Baumes formulieren wir also die Gleichung wie folgt um:
tan 30 
h Taschenrechner
h
 0,58 
 h  14,5
25
25
Wir haben damit ein Beispiel gesehen, wo die Kenntnis der Werte trigonometrischer
Funktionen am Einheitskreis zur Problemlösung führte.
4
Im folgenden betrachten wir die Winkelfunktionen sin, cos und tan, die alle aus dem
Einheitskreis hervorgehen. Eine schöne Veranschaulichung dieses Sachverhaltes findet man
im Netz auf der Seite www.mathe-online.at/galerie/wfun/wfun.html#winkelf
Die Winkelfunktion 
sin 
Jeder Gradzahl  wird die Strecke sin  aus dem Einheitskreis zugeordnet. Man kann direkt
die nachfolgend aufgeführten Werte ablesen.
0  sin 0  0
90  sin 90  1
180  sin 180  0
270  sin 270  1
360  sin 360  0
1,5
1
0,5
0
-0,5
0
90
180
270
360
450
540
630
720
-1
-1,5
Gradzahl 
Wie am Einheitskreis schon zu vermuten war, wiederholen sich die Werte sin  stets nach
360°. Die Sinusfunktion hat damit die Periode 360° und nimmt zudem nur Werte im Intervall
[-1, 1] an.
Allerdings besitzt diese Funktion einen Nachteil. Ihr Definitionsbereich besteht nicht aus
reellen Zahlen, sondern aus Gradzahlen. Dieser Umstand läßt sich jedoch leicht beheben,
wenn man die Gradzahl 360° mit dem Umfang des Einheitskreises, der gerade 2 ist,
identifiziert. Unter Verwendung des Dreisatzes hat man damit etwa folgende Tabelle:
0  0
90 

2
180  
270 
3
2
360  2
Allgemein wandelt man wie folgt um:



180
Ersetzt man Gradmaß durch Bogenmaß, so erhält man die Sinusfunktion mit reellem Definitionsbereich.
5
Die Winkelfunktion 
cos 
Jeder Gradzahl  wird die Strecke cos  aus dem Einheitskreis zugeordnet. Man kann direkt
die nachfolgend aufgeführten Werte ablesen.
0  cos 0  1
90  cos 90  0
180  cos180  1
270  cos 270  0
360  cos 360  1
1,5
1
0,5
0
-0,5
0
90
180
270
360
450
540
630
720
-1
-1,5
Gradzahl 
Wie am Einheitskreis schon zu vermuten war, wiederholen sich auch die Werte cos  stets
nach 360°. Die Kosinusfunktion hat damit ebenso die Periode 360° und nimmt zudem nur
Werte im Intervall [-1, 1] an.
Selbstverständlich kann auch die Kosinusfunktion mit einem reellen Definitionsbereich
formuliert werden, indem Gradmaß in Bogenmaß umgewandelt wird.
Die Winkelfunktion 
tan 
Jeder Gradzahl  wird die Strecke tan  aus dem Einheitskreis zugeordnet. Man kann direkt
die nachfolgend aufgeführten Werte ablesen.
0  tan 0  0
45  tan 45  1
90  nicht definiert
135  tan 135  1
180  tan 180  0
Im Gegensatz zur Sinus- und Kosinusfunktion hat die Tangensfunktion die Periode 180°. Ihre
Werte nimmt sie in ganz IR an und ist für 90° und 270° nicht definiert.
Anmerkung: Strebt  von „links“ gegen 90°, so wird tan  immer größer. Strebt  von
„rechts“ gegen 90°, so wird tan  immer kleiner. Was dies genau bedeutet,
wird später bei der Betrachtung von Grenzwerten klar werden.
6
10
8
6
4
2
0
-2 0
30
60
90
120
150
180
210
240
270
300
330
360
-4
-6
-8
-10
Gradzahl 
Bemerkung Zwischen den Winkelfunktionen kann man viele nützliche Beziehungen
herstellen, die das Rechnen in der Trigonometrie unter Umständen sehr
vereinfachen können.
Wir betrachten zunächst folgende Beispiele:
1)
Die Koordinaten des Punktes P am Einheitskreis sind offenbar P = (cos  / sin ). Mit
der Anwendung des Satzes von Pythagoras gilt:
(sin )2 + (cos )2 = 1
2)
Für eine reelle Zahl r gilt unter Berücksichtigung der Periode 2
sin(r + 2) = sin(r)
3)
Die Sinusfunktion ist symmetrisch zum Ursprung. Daher gilt für eine reelle Zahl r:
sin(-r) = -sin(r)
4)
Verschiebt man die Kosinuskurve um /2 nach rechts, so geht sie in die Sinuskurve
über. Es gilt demnach für eine reelle Zahl r:
cos(r - /2) = sin(r)
7
Umkehrfunktionen trigonometrischer Funktionen
Das nachfolgende Rechteck ist eindeutig bestimmt durch die beiden Seiten a = 3 und b = 5.
b
a

Wie läßt sich nun mit den bekannten Angaben der Winkel  bestimmen?
-
Man kann das Dreieck mit Zirkel und Lineal konstruieren (Wie lautet eigentlich
die Konstruktionsbeschreibung dieses Dreieckes?) und dann  messen.
Man weiß allerdings auch, daß das Verhältnis
Gegenkathe te a 3
   0,6
Hypotenuse
b 5
eine Funktion des Winkels ist und damit sin  = 0,6 sein muß.
Eine Umkehrfunktion, die bestimmten reellen Zahlen Gradzahl oder Bogenzahl zuordnete,
könnte also einen entscheidenden Beitrag zur Lösung des oben aufgeführten Problems leisten.
Wir fragen uns daher, ob die Sinusfunktion eine Umkehrfunktion besitzt.
Wir erinnern uns, daß aber nur streng monotone Funktionen eine Umkehrfunktion besitzen.
Die periodische Sinusfunktion ist aber – wie wir gesehen haben – nicht streng monoton.
Zum Glück läßt sich jedoch auch dieses Problem ganz leicht beheben; denn schließlich kennt
man die Sinuskurve bereits auf ganz IR, wenn man sie nur auf einem Intervall I kennt. Warum
wohl??
Betrachten wir die Sinuskurve auf dem Intervall I =  2 , 2 , so können wir feststellen, daß die
Sinusfunktion dort streng monoton wächst und somit eine Umkehrfunktion besitzt – nämlich
sin-1 : [-1, 1]   2 , 2 
Da auf den meisten Taschenrechnern die Umkehrfunktionen der trigonometrischen
Funktionen zu finden sind, können wir das einführende Beispiel sofort lösen. Wir verwenden
Gradzahlen und erhalten
sin   0,6    sin 1 (0,6)
Taschenrechner

36,86 .
So weit, so gut. Dennoch müssen wir uns mit einem weiteren Problem herum schlagen.
Betrachten wir nämlich für 0    360 und 1  a  1 die Gleichung
sin  = a,
so zeigt uns die Sinuskurve, daß mitunter mehrerer Lösungen auf dem Intervall [0°, 360°]
möglich sind. Der Taschenrechner liefert uns für jede Gleichung jedoch stets nur einen Wert
T. (Der Index T steht für Taschenrechner!)
8
Zur Lösung des Problems
betrachten wir die Gleichung für zwei Fälle.
0  a 1
1. Fall
1,5
a
1
0,5
0
0
90
180
270
360
450
540
630
720
-0,5
-1
-1,5
Gradzahl 
aT
eine weitere Lösung
Da sin auf [0°, 180°] symmetrisch zur Geraden durch 90° ist, erhält man als zweite
Lösung 180° - T und damit als Lösungsmenge der Gleichung
IL = {T, 180° - T}
1  a  0
2. Fall
die beiden Lösungen
1,5
-a
1
0,5
0
0
90
180
270
360
450
540
630
720
-0,5
a
-1
-1,5
aT
Gradzahl 
Ist a negativ, so ist –a positiv. Der Taschenrechner liefert für –a den Wert T. Da die
Sinuskurve symmetrisch zum Punkt (180°, 0) und periodisch mit 360° ist, lautet die
Lösungsmenge:
IL = {T + 180, 360 - T}
9
Aufgabe
Für cos und tan geht man analog vor. Ermittle auf der Grundlage des Beispiels der Sinuskurve
die Lösungsmengen der Gleichungen
cos  = a
und
tan  = a
und benutze dafür die Schaubilder der Funktionen.
10