Fernunterricht Mathematik Vorkurs VK

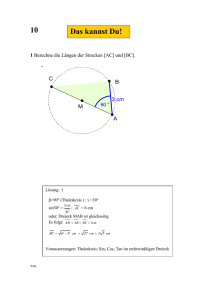
579909739
FERNUNTERRICHT
ZUR VORBEREITUNG AUF DEN
UNMITTELBAREN EINTRITT IN EINEN
FACHHOCHSCHULREIFE - LEHRGANG
DER
BUNDESWEHRFACHSCHULE
M A T H E M A T I K
LEHREINHEIT 08
INHALT: Trigonometrie
1 / 13
Stand: 28.09.2006
579909739
INHALTSVERZEICHNIS ZUR LEHREINHEIT 08
Seite
8
Trigonometrie
3 - 12
8.1
Ein Problem und dessen Lösung
3 - 4
8.2
Sinus und Kosinus im rechtwinkligen Dreieck
4 - 6
8.3
Sinussatz und Kosinussatz
7 - 10
8.4
Der Tangens
10 - 11
Aufgaben zur Lehreinheit 08
11
Lösungen der Übungen und Aufgaben
11
Einsendeaufgaben zur Lehreinheit 08
12
2 / 13
Stand: 28.09.2006
579909739
8 TRIGONOMETRIE
8.1 Ein Problem und dessen Lösung
Der Bau einer Brücke:
Abb. 8.1
Über ein Tal soll eine waagerechte Brücke
mit 6 Pfeilern gebaut werden (siehe Abb. 8.1).
Dazu müssen vor dem Bau der Brückenpfeiler
deren Höhen bestimmt werden.
Die Höhe der beiden linken Brückenpfeiler in Abb. 8.1 soll nun ermittelt werden, wobei zur
Vereinfachung angenommen werden soll, dass der Hang gleichmäßig fällt.
Im Gelände werden folgende Größen gemessen:
Der Talhang fällt in einem Winkel von  = 30°, die Hanglänge c1 = AB1 beträgt 83,70m,
die Hanglänge c2 = AB2 beträgt 167,40m.
Fertigen Sie dazu eine möglichst genaue Zeichnung im Maßstab 1 : 2000 an (1cm = 20m).
Lesen Sie in Ihrer Zeichnung die Höhen h1 und h2 ab: Bei einer guten Zeichnung können Sie
ablesen: h1 liegt in der Zeichnung zwischen 2,05cm und 2,1cm, d.h. der 1. Pfeiler muss 41m bis 42m
hoch werden. h2 liegt zwischen 4,15cm und 4,2cm, d.h. der 2. Pfeiler muss 83m bis 84m hoch werden.
1m Höhendifferenz! Das ist zu ungenau!
Eine größere Zeichnung im Maßstab 1: 1000 würde keine wesentliche Verbesserung bringen, da der
kleinste Fehler beim Zeichnen oder beim Ablesen in der Realität 1000 mal größer wird!
Die Pfeilerhöhen müssen exakt berechnet werden.
Abb. 8.2
Nun ist in diesem Fall "glücklicherweise"  = 30°,
d.h.  ist jeweils 60° (siehe Abb. 8.2).
Das Dreieck AB1C1 ist daher ein halbes
gleichseitiges Dreieck, d.h. für die tatsächliche
Höhe h1 gilt: h1 = 0,5 ∙ c1 = 0,5 ∙ 83,70m = 41,85m.
Ebenso gilt: h2 = 0,5 ∙ c2 = 0,5 ∙167,40m = 83,70m.
Der Idealfall  = 30° ist leider nur äußerst selten anzutreffen. Wie berechnet man die Höhen, wenn z.B.
 = 35,8° gilt?
Beachten Sie dazu folgende'Überlegungen:
Nach dem 2. Strahlensatz (LE 07 / 7.4.2) gilt, und zwar unabhängig vom Winkel  , folgendes
h1 h2
Verhältnis:

c1 c 2
In dem speziellen Fall  = 30° kann das Verhältnis genau angegeben werden; Pfeilerhöhe und
entsprechende Hanglänge stehen immer im Verhältnis 1 : 2 , d.h.
h1 1  41,85m 1 
h2 1  83,70m 1 
und
 , 
 
 , 
 
c1 2  83,70m 2 
c 2 2  167,40m 2 
Das bedeutet: Zu dem Winkel  = 30° gehört die Verhältniszahl 0,5.
Überlegen Sie: Für den Winkel  = 35,8° muss es ebenfalls eine entsprechende Verhältniszahl
geben! Für jeden Winkel zwischen 0° und 90° muss es eine bestimmte Verhältniszahl geben!
Es gibt jeweils eine! Wo?
Sie finden alle beispielsweise im Taschenrechner mit Hilfe der Taste sin (von Sinus). Prüfen Sie:
Eingabe 30 sin , es erscheint 0.5 . Eingabe 35,8 sin , es erscheint 0.584957675
3 / 13
Stand: 28.09.2006
579909739
Definition: Unter dem Sinus eines Winkels  im rechtwinkligen Dreieck versteht man das
Streckenverhältnis von Gegenkathete und Hypotenuse.
sin  
Gegenkathe te des Winkels 
Hypotenuse
( 0° <  < 90° )
Bezogen auf die Zeichnung bedeutet dies: sin  
a
c
Mit Hilfe des Sinus kann nun zu jedem beliebigen Winkel  bei einem gemessenen Hangabschnitt c
die jeweilige Pfeilerhöhe h berechnet werden.
Die Berechnung der Pfeilerhöhen beim Brückenbau für  = 35,8°:
Mit  = 35,8° und c1 = 83,70m erhält man
h1
 sin 35,8  h1
 83,70m ∙ sin 35,8° = h1  h1 = 48,9609574m,
sin  
83,70m
c1
das ist sehr genau! Eine bezüglich der Aufgabenstellung sinnvolle Rundung ist h1  48,96m.
Mit  = 35,8° und c2 = 167,40m erhält man h2  97,92m.
Beachten Sie bei einer Eingabe von sin 35,8° in den Taschenrechner, dass im Unterschied zur
mathematischen Schreibweise oft zuerst die Gradzahl eingegeben und dann die Sinustaste gedrückt
wird.
Die möglichen Verhältniszahlen von sin  sind meistens irrationale Zahlen, von denen im
Taschenrechner nur ein Teil der Stellen hinter dem Komma angezeigt wird. Man kann damit aber in
Berechnungen jede gewünschte Genauigkeit erhalten.
8.2 Sinus und Kosinus im rechtwinkligen Dreieck
Der Sinus
In 8.1 haben Sie den Sinus kennen gelernt. Bevor Sie erfahren, was ein Kosinus ist, sollen Sie
zunächst mit dem Sinus vertrauter werden. Es folgen Beispiele zur Berechnung von Seiten und
Winkeln in rechtwinkligen Dreiecken.
Dabei lautet der Ansatz immer:
sin( Winkel ) 
Gegenkathete des Winkels
Hypotenuse
Beachten Sie die Einschränkung "in rechtwinkligen Dreiecken". Es bleibt nicht dabei!
Am Ende dieses Teilkapitels und vor allem in 8.3 werden Sie erfahren, wie man Seiten und Winkel in
beliebigen Dreiecken berechnen kann. Dazu müssen vorweg einige Grundlagen behandelt werden.
Beispiel zur Berechnung von Seiten in einem rechtwinkligen Dreieck:
Abb. 8.3
Neben dem rechten Winkel sind ein weiterer Winkel und eine
Seite gegeben.
In Abb. 8.3 ist ein rechtwinkliges Dreieck
dargestellt, von dem folgende Größen bekannt
sind:  = 42°, a = 2,0cm.
Gesucht sind die Seitenlängen b und c.
Berechnung von c:
a
Ansatz: sin   . Da  und a gegeben sind und c gesucht ist, muss die Formel zunächst nach c
c
umgestellt werden. Man erhält nach der Multiplikation mit c:
a
2cm
2cm
 3,0cm
c ∙ sin  = a I : sin   c 
. Einsetzen: c 

sin 42  0,699
sin 
4 / 13
Stand: 28.09.2006
579909739
2cm
kann verzichtet werden. Man kann im Taschenrechner direkt
0,699
eingeben: 2 : 42 sin = , es erscheint 2.9889... (bei manchen Taschenrechnern 2 : sin 42)
Berechnung von b:
b liegt gegenüber von ß, d.h. b ist Gegenkathete von ß. Mit ß = 90° -  = 48° erhält man:
b
Ansatz:
I ∙ c  c ∙ sin ß = b . Einsetzen: b  3,0cm ∙ sin 48°  b  2,2cm .
sin  
c
Auf das Zwischenergebnis
Bemerkung: Nach der Berechnung von c kann b auch mit dem Satz des Pythagoras berechnet
werden. Berechnen Sie b auch auf diesem Weg!
Beispiel zur Berechnung von Winkeln in einem rechtwinkligen Dreieck:
Abb. 8.4
Neben dem rechten Winkel sind zwei Seiten gegeben.
In Abb. 8.4 ist ein rechtwinkliges Dreieck dargestellt,
von dem folgende Größen bekannt sind: a = 3cm, b = 4cm.
Gesucht sind  und .
Berechnung von  :
b ist Hypotenuse, a ist Gegenkathete von 
3
a
Ansatz: sin   . Einsetzen: sin  = = 0,75. Wie findet man jetzt umgekehrt a, wenn sin 
4
b
bekannt ist? Wieder mit Hilfe des Taschenrechners.
"Umgekehrt." bedeutet: Die „Umkehrtaste“ (z.B. inv , invers) muss benutzt werden .
Geben Sie ein: 0.75 inv sin , Sie erhalten  48,59    48,59° .
Berechnung von y:  = 90° -  
  41,41°
Zur Übung sollten Sie  so berechnen: Berechnen zunächst c und anschließend  mit sin  = ... .
Lösungswege in der Trigonometrie sollten immer folgende Struktur haben:
1. Ansatz mit einer Formel.
2. Die Formel wird eventuell umgestellt.
3. Gegebene Größen werden eingesetzt und die gesuchte Größe wird berechnet. Falls nicht anders
gefordert, genügt eine Rundung auf zwei gültige Stellen hinter dem Komma.
Übungen:
1. In einem rechtwinkligen Dreieck sind gegeben:  = 90°; ß = 25°; a = 5,0cm.
Zeichnen Sie das Dreieck, berechnen Sie b, , c und überprüfen Sie die Ergebnisse an der
Zeichnung. Die Lösungen lauten b  2,1cm,  = 65°, c  4,5cm.
2. In einem rechtwinkligen Dreieck sind gegeben:  = 90°, c = 4,0cm; b = 2,0cm.
Zeichnen Sie das Dreieck, berechnen Sie , , a und überprüfen Sie die Ergebnisse an der
Zeichnung. Die Lösungen lauten: ß = 30°,  = 60°, a  3,5cm.
Nun zum Kosinus
Definition: Unter dein Kosinus eines Winkels  im rechtwinkligen Dreieck versteht man das
Streckenverhältnis von Ankathete zur Hypotenuse.
cos  
Ankathete des Winkels 
Hypotenuse
( 0° <  < 90° )
Bezogen auf die Zeichnung bedeutet dies: cos  
b
.
c
Die entsprechenden Verhältniszahlen finden Sie im
Taschenrechner mit Hilfe der Taste cos .
5 / 13
Stand: 28.09.2006
579909739
Ein Zusammenhang zwischen Sinus und Kosinus:
Die Gegenkathete von  ist die Ankathete von ß, d.h. cos  
b
b
, sin  
,
c
c
 cos  = sin ß .
a
= sin  .
c
Da ß = 90° -  ist, folgt: Im rechtwinkligen Dreieck ist cos  = sin (90° -  ) .
Für Berechnungen im rechtwinkligen Dreieck hat demzufolge der Kosinus keine größere Bedeutung,
da er durch den Sinus leicht ersetzt werden kann. Große Bedeutung erlangt er jedoch für
Berechnungen in beliebigen Dreiecken (siehe 8.3: Kosinussatz).
Ebenso gilt:
cos  
Berechnungen in beliebigen Dreiecken mit Hilfe einer Höhe
Beispiel:
Von dem nicht-rechtwinkligen Dreieck in Abb. 8.5 sind folgende
Größen bekannt :  = 30°, b = 3,0cm, ß = 40° .
Gesucht sind a und c.
Abb. 8.5
Berechnung von a:
Mit Hilfe der Höhe hc wird das Dreieck ABC in zwei
rechtwinklige Dreiecke geteilt! Diese Höhe kann berechnet werden:
h
sin   c  b ∙ sin α = hc  hc = 1,5cm.
b
h
hc
Jetzt lässt sich a berechnen: sin   c  a =
 a ≈ 2,3cm.
a
sin 
Berechnung von c:
Dazu müssen die Teilstücke c1 und c2 berechnet werden. Dies ist entweder mit dem Satz des
Pythagoras möglich (z.B. c1² = b² - hc²) oder mit Hilfe des Kosinus oder Sinus.
Mit Hilfe des Kosinus gilt:
c
cos   1 │∙ b  b ∙ cos α = c1  c1 ≈ 2,6cm;
b
c
cos   2 │∙ a  a ∙ cos β = c2  c2 ≈ 1,8cm. Weil c = c1 + c2 ist  c = 4,4cm .
a
Für eine Berechnung mit dem Sinus müssen zunächst die Winkel  1 = 90°- α und  2 = 90°- β
bestimmt werden.
Übungen zu 8.2
1. Eine Leiter von 4m Länge steht an einer senkrechten Wand und ist im Winkel  = 70° geneigt.
a) Fertigen Sie dazu eine Zeichnung an.
b) Wie hoch reicht die Leiter?
c) Wie weit ist das untere Leiterende von der Wand entfernt?
2. In einem Dreieck sind folgende Größen gegeben: a = 4m, c = 6cm, ß = 60°.
Fertigen Sie eine Zeichnung an und berechnen Sie b und  .
Anleitung für die Berechnung von b: Berechnen Sie zunächst hc .
Ein Hinweis für Neugierige
Sinus und Kosinus sind auch für Winkel zwischen 90° und 180° erkläbar, auch für Winkel von 180° bis
360°. Dies geschieht mit Hilfe des Einheitskreises. Es ist sogar sinnvoll, die Definitionen von Sinus
und Kosinus auf Winkel von über 360° und 0° oder unter 0° auszudehnen (ein Rad, welches sich
zweimal dreht, hat einen „Winkel von 720° zurück gelegt“). Probieren Sie mit dem Taschenrechner!
Man erhält Sinus- und Kosinusfunktionen für beliebige reelle Zahlen α . Im Rahmen dieser
Erweiterung kann man Sinus und Kosinus auch in Abhängigkeit von Längen erklären, man erhält das
Bogenmaß (achten Sie darauf, dass Sie für Berechnungen mit Winkeln im Taschenrechner die
Einstellung DRG gewählt haben und nicht RAD für das Bogenmaß). Die Behandlung dieser Inhalte
würde hier zu weit führen, sie werden in einigen Lehrgängen der Bundeswehrfachschulen behandelt.
6 / 13
Stand: 28.09.2006
579909739
8.3 Sinussatz und Kosinussatz
Bald können Sie Winkel und Seiten in beliebigen Dreiecken „ohne Umwege“ berechnen!!!
Der Sinussatz
Beispiel: Eine Seite wird gesucht.
Betrachten Sie zu den folgenden Überlegungen nochmals Abb. 8.5. Im Dreieck sind gegeben:
α = 30°, b = 3,0cm ,  = 40° . Die Seitenlänge a soll direkt mit Hilfe der gegebenen Größen berechnet
werden. Diese Aufgaben wurde am Ende von 8.2 mit Hilfe der Berechnungen von hc gelöst.
h
Es gilt: sin   c  a , : sin   I. a  hc . hc ist nicht bekannt, hc lässt sich aber durch die
a
sin 
gegebenen Größen b und  folgendermaßen angeben: sin  
hc
 II. hc = b ∙ sin α.
b
b  sin  wird für hc in Gleichung I eingesetzt
b  sin 
3cm  sin 30 
 a
 a
 a ≈ 2,3cm.
sin 
sin 40 
Sie sehen hc muss nicht berechnet werden! Für den folgenden Sinussatz ist es vorteilhaft,
b  sin 
a sin 
in 
umzuformen.
a
sin 
b sin 
a sin  b sin 
Bei entsprechend gegebenen Größen kann man ebenso finden:
;
.


c sin 
c sin 
Sinussatz:
In jedem Dreieck verhalten sich die Längen zweier Seiten wie
die Sinuswerte der Gegenwinkel dieser Seiten.
Bezogen auf die Bezeichnungen des abgebildeten Dreiecks gilt:
a sin  a sin  b sin 
; 
;


c sin 
b sin  c sin 
Zu dem obigen Beispiel lässt sich auch c mit dem Sinussatz
berechnen. Beachten Sie dazu noch folgenden Tipp: Bei einer Anwendung des Sinussatzes ist es
rechentechnisch günstig, die gesuchte Größe in den ersten Zähler zu schreiben!
sin 110   3cm
c sin 
sin   b
. Mit  = 180° -  -  = 110° folgt c 
, c ≈ 4,4cm.

 c
sin 40 
b sin 
sin 
Beispiel: Ein Winkel ist gesucht
Gegeben ist ein Dreieck mit c = 5,0 cm ;  = 60° ; a = 3,0 cm. Zeichnen Sie das Dreieck. Gesucht ist .
a  sin 
sin  a
3cm  sin 60 
inv sin  α ≈ 31,31° .
Lösung:

 sin   sin  
 sin  
5cm
c
sin  c
Berechnen Sie zur Übung die Länge der Seite b. Das Ergebnis lautet: b ≈ 5,8cm.
Der Sinussatz gilt speziell auch für rechtwinklige Dreiecke:
Beispiel:  = 90° .
sin  a
a
sin  a

bzw. sin α = !
 . Da sin  = sin 90° = 1 ist folgt:
1
c
c
sin  c
Man erhält als Sonderfall die Definition des Sinus im rechtwinkligen Dreieck (siehe 8.1).
7 / 13
Stand: 28.09.2006
579909739
Aufgabe: Eine Seite ist gesucht
In einem Dreieck ist gegeben: c = 3,0cm,  = 60° , b = 2,0cm. Zeichnen Sie das Dreieck.
Gesucht ist a.
Bevor Sie weiter lesen: Überlegen Sie sich einen Lösungsweg!
Mit dem Sinussatz geht es nicht! Statt b müsste  bekannt sein, oder statt c der Winkel .
Es bleibt der Lösungsweg mit Hilfe von hc übrig. Wenn Sie möchten, probieren Sie. Wenn nicht,
schauen Sie sich den Kosinussatz an.
Der Kosinussatz
Mit Hilfe der obigen Aufgabe wird der Kosinussatz hergeleitet:
I
a² = hc² + c2² , hc und c2 sind unbekannt, a soll durch die
bekannten Größen b, c und  ausgedrückt werden.
Es gilt: II hc² = b² - c1² . Eingesetzt in I :
I1 a² = b² - c1² + c2² , c1 und c2 sind unbekannt , b ist bekannt.
Es gilt: c = c1 + c2  III c2 = c - c1 . Eingesetzt in I1 :
I2 a² = b² - c1² + ( c – c1)²  a² = b² - c1² + c² - 2cc1 + c1²
 a² = b² + c² - 2cc1 , c1 ist unbekannt, b und c sind bekannt.
Es gilt: cos  
c1
b
 IV c1 = b ∙ cos α. Eingesetzt in I2 :
I3 a² = b² +c² - 2c  b  cos  , alle Größen der rechten Seite sind bekannt.
Lösung der Aufgabe:
a² = 2² + 3² - 2  3  2  cos 60°  a² = 4 + 9 – 12  cos 60°  a² = 7 
 a  2,7cm.
Auf ähnliche Weise kann man finden: b² = a² + c² - 2ac  cos  , c² = a² + b² - 2ab  cos 
.
Kosinussatz:
In jedem Dreieck gilt (bezogen auf die Bezeichnungen des abgebildeten Dreiecks) :
a² = b² + c² - 2bc  cos  ; b² = a² + c² - 2ac  cos  ; c² = a² + b² - 2ab  cos 
Der Kosinussatz in Worten:
„In jedem Dreieck ist das Quadrat einer Seitenlänge
gleich der Summe der Quadrate der beiden anderen
Seitenlängen, vermindert um das doppelte Produkt
der Längen dieser Seiten und dem Kosinuswert des
von ihnen eingeschlossenen Winkels“.
(Das ist doch beeindruckend!)
So gilt z.B. in dem hier abgebildeten Dreieck :
x² = y² + z² - 2yz  cos 
Schreiben Sie ebenso auf : y² =... ; z² = ...
Der Kosinussatz gilt speziell auch für rechtwinklige Dreiecke:
Beispiel:  = 90° .
c² = a² + b² - 2ab  cos  . Da  = 90° ist, ist cos  = cos 90° = 0  c² = a² + b² - 2ab  0
 c² = a² + b² ! Der Kosinussatz heißt auch „verallgemeinerter Satz des Pythagoras“!
8 / 13
Stand: 28.09.2006
579909739
Beispiel: Ein Winkel ist gesucht
Gegeben ist ein Dreieck mit a= 4,0 cm ; b = 3,0 cm; c = 3,5 cm . Zeichnen Sie das Dreieck.
Gesucht ist .
Lösung:
a² = b² + c² -2bc  cos  . Diese Formel lässt sich nach cos  umstellen:
a² = b² + c² -2bc  cos   +2bc  cos  - a²  2bc  cos  = b² + c² - a²  : 2bc
b²  c ²  a²
9  12,25  16 5,25

 cos  
 cos  
 α ≈ 75,52° .
2bc
2  3  3,5
21
Berechnen Sie zur Übung  auf 2 Arten: a) mit Hilfe des Kosinussatzes, b) mit Hilfe des Sinussatzes
und des berechneten Wertes für . Das Ergebnis lautet:   46,57° .
Sinussatz oder Kosinussatz?
Beachten Sie die Kongruenzsätze (LE 07 / 7.3.2)
Gegeben sind
1. Drei Seiten (SSS)
2. Zwei Seiten und der
eingeschlossene Winkel
3. Eine Seite und zwei Winkel
(SWW) (der dritte Winkel lässt
sich direkt bestimmen)
Direkt berechnet werden kann
ein Winkel
eine Seite
Lösungsweg mit dem
Kosinussatz
Kosinussatz
eine Seite
Sinussatz
4. Zwei Seiten und der Winkel
gegenüber der größeren Seite
(SSWg)
der Winkel gegenüber der
kleineren Seite
Sinussatz
Vorsicht:
In dem abgebildeten stumpfwinkligen Dreieck ist
c = 3,0 cm; a = 1,5 cm; und  = 28 °, d.h. gegeben
sind zwei Seiten und der Winkel gegenüber der
kleineren gegebenen Seite ( SSWk). Gesucht ist .
Der Sinussatz liefert:
c
sin  c
3

 sin 28° ≈ 0,94 | inv sin    69,87° .
 sin    sin  =
sin  a
a
1,5
Dieses Ergebnis kann nicht stimmen (siehe Zeichnung). Das richtige Ergebnis lautet   110,13°, d.h.
 = 180° - 69,87°. Mit der Tastenfolge inv sin kann man nur Winkel zwischen -90° und + 90° erhalten,
der Grund liegt im Verlauf der hier nicht behandelten Sinusfunktion.
Vorsicht also wenn Sie den Sinussatz in stumpfwinkligen Dreiecken zur Berechnung des stumpfen
Winkels benutzen. Der im Taschenrechner ausgegebene Winkel muss von 180° abgezogen werden.
Die Breite eines Sees wird ermittelt:
Am Ende dieses Teilkapitels soll noch einmal das Problem
des Landvermesserlehrlings aus LE 07 / 7.3.2 aufgegriffen werden.
Die Messvorgänge sollten so durchgeführt werden, dass sie nicht
zu aufwendig sind und das AB mit ihrer Hilfe direkt berechnet
werden kann. Dazu eignen sich folgende zwei Möglichkeiten (von A aus):
a) Gemessen wird AC ,  und CB , AB wird mit dem Kosinussatz
berechnet.
Ansatz: AB ² = AC ² + CB ² - 2 AC  CB  cos  .
Mit AC = 39m; CB = 44m und  = 100,24° erhält man AB  63,77m.
b) Gemessen wird , AC und , AB wird mit dem Sinussatz berechnet.
Ansatz: = 180° -  - ,
AB
AC

sin 
sin 
 AC
Mit AC = 39 m,  = 42,76° und  = 100,24° erhält man ebenfalls: AB  63,77m.
9 / 13
Stand: 28.09.2006
579909739
Übungen zu 8.5
1. Fertigen Sie zu den folgenden Dreiecken jeweils eine Zeichnung an, berechnen Sie die fehlenden
Seiten und Winkel und überprüfen Sie die Ergebnisse anhand der Zeichnung.
a) c = 3cm,  = 70°,  = 48° ;
b) a = 4cm, b = 5 cm,  = 60° ;
c) a = 4cm, b = 5cm, c = 4cm , d) b = 3cm, a = 4cm,  = 50° .
2. Die Breite DC eines Flusses soll berechnet werden.
Gemessen wird: AB = 20m,  = 59°,  = 47°.
Anleitung zur Berechnung von DC :
Berechnen Sie zunächst AC mit Hilfe von AB ,  und .
8.6 Der Tangens
Das Thema „Trigonometrie“ könnte hier abgeschlossen sein, denn mit dem Sinussatz und dem
Kosinussatz sind Sie für Berechnungen in Dreiecken bestens ausgerüstet.
Wozu benötigt man den Tangens? Was versteht man unter dem Tangens?
Definition: Unter dem Tangens eines Winkels  im rechtwinkligen Dreieck versteht man
das Streckenverhältnis von Gegenkathete zur Ankathete
tan  
Gegenkathe te
Ankathete
a
b
Die Tangenswerte finden Sie im Taschenrechner mit der Taste tan
Bezogen auf die Zeichnung bedeutet dies: tan  
1.Beispiel:
Sie möchten die Höhe h eines Turmes berechnen (siehe Skizze), dieses mal scheint die Sonne nicht
(vgl. LE 07 / 7.4.2), dafür haben Sie neben dem Zollstock einen Theodolithen zur Verfügung.
Sie können  und AB messen. Annahme:  = 70°, AB = 8m.
Die Berechnung von h mit Hilfe des Sinussatzes (SWW!)
h
sin 
mit  = 90° -  = 20°

AB sin 
sin 70 
sin 
 8m  h ≈ 22m ..
 AB 
 h
sin 20 
sin 
Die Berechnung von h mit dem Tangens:
h
tan  
 AB  h  AB  tan   h = 8m ∙ tan 70°  h ≈ 22m .
AB
2.Beispiel:
Die Steigung einer Straße beträgt 16%.
In welchem Winkel steigt die Straße an ?
Die Berechnung von  mit einer der bisher
behandelten Möglichkeiten ist umständlich,
da in jedem Fall zuerst die Straßenlänge l
berechnet werden muss.
Die Berechnung von  mit dem Tangens ist erstaunlich einfach: tan   16
100
inv tan  α ≈ 9,09°.
Das überzeugt doch! 12% Steigung bedeutet: tan  = 12% = 0,12    6,84°.
Umgekehrt: steigt ein Gelände um 15% an, dann beträgt die Steigung tan 15°  0,268 = 28,8%.
45° Anstieg bedeuten eine Steigung von tan 45° = 1 = 100% Tangens = Steigung !
10 / 13
Stand: 28.09.2006
579909739
Höhenunter schied
“ in LE 06 / 6.3.1).
Waagerecht enuntersch ied
Diese Beziehung hat Bedeutung für das Thema „Analysis“ in den Fachhochschulreifelehrgängen.
Mehr dazu erfahren Sie in LE 12.
(Vergleichen Sie mit den Begriff „Steigung =
Übung zu 8.6
Von der Spitze S eines 30m hohen Turmes wird der Randpunkt einer Autobahn mit einem
Tiefenwinkel von  = 17° anvisiert (von einer gedachten waagerechten Linie aus werden 17° „nach
unten“ gemessen). Der Fußpunkt F des Turmes und die Autobahn liegen auf gleicher Höhe. Wie weit
ist der Punkt A vom Fußpunkt F des Turmes entfernt?
Anleitung : Beachten Sie, dass der Winkel mit dem Scheitel A ebenfalls 17° beträgt (Wechselwinkel an
Parallelen ).
AUFGABEN ZUR LEHREINHEIT 08
1. In einem Dreieck sind gegeben: hc = 3,0cm ; c1 = 1,5cm ; c2 = 2,0cm .
Berechnen Sie b, a, , , .
2. Die Höhe eines am gegenüberliegenden Ufer eines Flusses stehenden Turmes soll bestimmt
werden. Es wird eine Standlinie AB  20m gemessen, die auf den Fußpunkt des Turmes zuläuft.
Von den Punkten A und B aus wird die Spitze S des Turmes, unter den Höhenwinkeln  = 35°
und  = 55° aus einer Augenhöhe von 1,5 m anvisiert. Der Fußpunkt F des Turmes und die
Standlinie des Beobachters befinden sich in gleicher Höhe. Wie hoch ist der Turm ?
3. In einem Parallelogramm sind folgenden Größen gegeben: a = 3 cm; b = 2cm;  = 120°.
Zeichnen Sie das Parallelogramm. Berechnen Sie die Längen der Diagonalen e und f und den
Flächeninhalt.
4. Gegeben ist eine gerade Pyramide, deren Grundfläche ein Quadrat ist, mit a = 4cm und h = 7cm.
Fertigen Sie eine Skizze an. Berechnen Sie AS und den Winkel, den AS mit AM bildet (S ist die
Spitze, M ist der Mittelpunkt der Grundfläche).
5. Auf einer Straße von 15 % Steigung wird ein Weg von 620m zurückgelegt (gleichmäßig
ansteigend, ohne Kurven).
a) In welchem Winkel steigt die Straße an?
b) Welcher Höhenunterschied wird dabei überwunden?
c) Das oben genannte Stück der Straße soll in einer Karte von Maßstab 1:25000 eingezeichnet
werden. Wie lang muss die entsprechende Strecke werden?
LÖSUNGEN DER ÜBUNGEN UND AUFGABEN
Übungen zu 8.2: 1. a) h  3,76cm ; b) 1,37cm .
2. hc ≈ 3,46cm ; c2 = 2cm ; b ≈ 5,3cm ; α ≈ 40,8° .
Übungen zu 8.5: 1. a)  = 62° ; b  3,8cm (Sinussatz) ; a  3,6cm (Sinussatz)
b) c  4,6cm (Kosinussatz) ;   49° (Sinussatz) ;   71°
c)   51,3° (Kosinussatz) ;   51,3° (gleichschenkliges Dreieck!) ;   77,4°
d)   35,1° (Sinussatz) ;   94,9° ; c  5,2cm
2. AC  15,22m (Sinussatz) ; DC  13,05m
Übung zu 8.6:
AF  98,13m
Aufgabe 1: b  3,35cm ; a  3,61cm ;   63,4° ;   56,3° ;   60,3°
Aufgabe 2: Im Dreieck A’B’S sind alle Winkel bekannt (in diesem Dreieck liegt der Nebenwinkel ß’
von ß mit ß’ = 125°!). B' S  33,54m ; h  28,97m
Aufgabe3: e  4,36cm (Kosinussatz); ha ≈ 1,73cm ; A  5,20cm²; f ≈ 2,65cm (Kosinussatz)
Aufgabe4: AM  2,83cm ; AS  7,55cm ; der gesuchte Winkel ist ≈ 68,7°
Aufgabe5: a)   8,53°; b) h  92m; c) w  613m, das sind  2,45cm in der Karte
11 / 13
Stand: 28.09.2006
579909739
FERNUNTERRICHT DER BUNDESWEHRFACHSCHULE
Einsendeaufgaben zur Lehreinheit 08
Dienstgrad, Name,
Einheit,
Vorname
Standort,
Privatanschrift
DZF
Datum
Email
1. In einem Dreieck sind folgende Größen gegeben: a = 5,8cm; b = 4,0cm;  = 55°
a) Zeichnen Sie das Dreieck.
b) Berechnen Sie , , c und den Flächeninhalt.
c) Berechnen Sie wα (Winkelhalbierende von ).
2. Berechnen Sie in der abgebildeten Figur BC , BD , und .
3. Auf der Karte (Maßstab 1 : 10000) wird die Strecke AB = 1,3 cm zwischen zwei
Höhenlinien gemessen (siehe Skizze; der Anstieg von A nach B ist gleichmäßig).
a) Wie groß ist die Steigung (in %) von A nach B?
b) In welchen Winkel steigt das Gelände von A nach B an ?
c) Wie groß ist die Entfernung im Gelände zwischen A und
B?
Senden Sie die Lösungen auf dem beigefügten DIN A4 Blatt an
die für Sie zuständige Bundeswehrfachschule (Name, Adresse und
Email nicht vergessen!)
12 / 13
Stand: 28.09.2006
579909739
DStG
Name
Vorname
Blatt:
Lösungen zu den Einsendeaufgaben LE 08
13 / 13
Stand: 28.09.2006