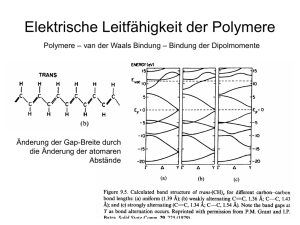
5.4 Optische und elektrische Eigenschaften

410
5.4 Optische und elektrische Eigenschaften
5.4 Optische und elektrische Eigenschaften
5.4.1 Optische Eigenschaften
Technische Artikel und Gebrauchsgegenstände aus Kunststoffen werden oft ganz wesentlich von
den optischen Eigenschaften geprägt. Bei den im folgenden näher erklärten optischen Eigenschaften
handelt es sich einmal um physikalische Phänomene wie Lichtbrechung, Doppelbrechung, Reflexion, Absorption, Streuung und nichtlineare optische Eigenschaften und zum anderen um mehr technische Eigenschaften wie Glanz, Trübung, Irideszenz, Opazität und Farbe.
5.4.1.1 Brechung, Reflexion, Absorption, Transparenz und Streuung
Abbildung 5.60 stellt den Weg eines Lichtstrahls von einem optisch dünneren in ein optisch dichteres und wieder in ein optisch dünneres Medium dar. Der Brechungsindex eines Materials ist durch
das Snelliussche Brechungsgesetz definiert
n = sinβ 1 sinβ 2
(5.175)
wobei β 1 der Einfallswinkel und β 2 der Brechungswinkel beim Übergang vom Vakuum in das
Material ist. Für den Übergang eines Lichtstrahls von einem Medium in ein anderes mit
unterschiedlichen Brechungsindizes lautet das Brechungsgesetz:
n2 n1 = sinβ 1 sinβ 2
(5.176)
Abbildung 5.60:
Zur Definition von Brechungsindex, Reflexion,
Absorption, Streuung und Transparenz
Der Brechungsindex eines Materials hängt von der Polarisierbarkeit α der Moleküle ab (siehe
Kapitel 4.3.3.1). Lorentz und Lorenz formulierten mit Hilfe der Maxwell-Gleichungen die theoretisch begründete Beziehung
(
) (n
 n2 − 1

2
)
+ 2  ( M ρ ) = ( 4 π 3) N A α ≡ RLL

(5.177)
wobei M die Molmasse, ρ die Dichte, α die Polarisierbarkeit und RLL die Molrefraktion sind. Eine
ebenfalls häufig verwendete, aber theoretisch nicht begründete Beziehung zwischen Brechungsindex und Dichte eines Materials ist die Gleichung von Gladstone und Dale:
( n − 1) ( M ρ ) = RGD
(5.178)
Beim Auftreffen eines Lichtstrahls mit der Intensität I0 auf ein Material mit der Dicke d wird ein
Teil des einfallenden Lichts an der Vorderseite des Materials reflektiert; die Intensität des reflektierten Strahls wird mit IR bezeichnet (siehe Abbildung 5.60). Beim Durchgang des Lichts durch das
Material wird ein Teil des Lichts von den anwesenden Molekülen absorbiert (IA) und ein anderer
Teil gestreut (IS). Der verbleibende transparente Anteil des Lichts verläßt dann das Material mit der
Intensität IT. Die soeben erwähnten Größen hängen miteinander zusammen. Es gilt:
I 0 = I R + I A + IS + I T
(5.179)
5 Das Makromolekül als Festkörper und als Schmelze
411
Die Größe I R / I 0 = R wird als Reflexion, I A / I 0 = A als Absorption, I S / I 0 = S als Streuung und
I T / I 0 = T als Transparenz bezeichnet. Gleichung (5.179a) geht damit über in
R+ A+S+T =1
(5.180)
Brechung, Reflexion und Absorption werden im wesentlichen von den durchschnittlichen optischen
Eigenschaften des Materials beeinflußt während die Lichtstreuung auf lokalen Schwankungen der
optischen Eigenschaften des Mediums basiert. In einer Reihe von Fällen kann man die Reflexion
und die Streuung gegenüber der Absorption vernachlässigen. Die Gleichungen (5.179) und (5.180)
gehen dann über in
I0 = IA + IT ;
A = 1− T
Der Intensitätsverlauf eines Lichtstrahls durch ein Medium wird bezüglich der Absorption und der
Streuung durch das Lambertsche Gesetz beschrieben:
A = lg ( I 0 I ) = E d
(5.181)
wobei E der Schwächungsmodul und d die Dicke des Materials ist. Der Schwächungsmodul setzt
sich dabei additiv aus dem Streumodul τ (auch Turbidität oder Trübungsmodul genannt) und dem
Absorptionsmodul K zusammen
E =τ +K
(5.182)
Die Größe A wurde früher im deutschen Sprachgebrauch mit Extinktion bezeichnet. Nach der neueren Nomenklatur ist A = lg ( I 0 I ) die Absorbanz.
Bisher wurden nur optisch isotrope homogene Materialien behandelt. Optisch anisotrope Makromoleküle haben richtungsabhängige Polarisierbarkeiten und damit auch Brechungsindizes. Diese
Erscheinung kann durch Kristallbildung, Orientierung und Deformation der Kettenmoleküle hervorgerufen werden. Bezeichnen wir die Brechungsindizes entlang der drei Hauptachsen mit nx , ny und
nz, so sind bei isotropen Stoffen alle drei Größen gleich groß und bei anisotropen Materialien
mindestens zwei Brechungsindizes verschieden groß. Bei anisotropen Materialien wird die Differenz von je zwei der Brechungsindizes nx , ny und nz als Doppelbrechung ∆n bezeichnet.
5.4.1.2 Totalreflexion, Wellenleitung, optische Speicher
Trifft ein Lichtstrahl in einem optisch dichteren Medium 2 auf die Grenzfläche zu einem optisch
dünneren Medium 1 unter einem Winkel β ′ , dessen Sinus größer als das Verhältnis der Brechungsindizes der Medien n2/n1 ist, so wird das Licht in das optisch dichtere Medium zurückgespiegelt
(siehe Abbildung 5.61).
(5.183)
sinβ ′ > n2 n1
Abbildung 5.61:
Totalreflexion in
einem Lichtleiter
Diesen Vorgang nennt man Totalreflexion; er wird ausgenutzt bei der Konstruktion von Lichtleitern
und Wellenleitern zur optischen Nachrichtenübermittlung und zur nichtgeradlinigen Weiterleitung
von Licht für technische und medizinische Anwendungen. Für kurze Strecken und starke Krümmungen werden vorzugsweise Makromoleküle (z.B. Polymethylmethacrylat) verwendet, da diese
nicht so spröde wie Glasfasern sind.
Bei der Herstellung von Komponenten für die integrierte Optik (Entwicklung von optischen
Computern) macht man sich die Tatsache zunutze, daß die Dichten und nach Gleichung (5.177)
412
5.4 Optische und elektrische Eigenschaften
damit auch die Brechungsindizes der Polymeren größer als diejenigen der entsprechenden Monomere sind. Durch Bestrahlung von Polymeren, die einen gewissen Anteil Monomere (10 − 20%)
enthalten, mit einem Lichtmuster wird durch Polymerisation an den belichteten Stellen ein dreidimensionales Brechungsindexmuster erzeugt. Diesen Vorgang macht man sich z.B. bei der Entwicklung von optischen Speichern und Gitterkopplern als Prismenersatz zum Einkoppeln von Licht
in Wellenleiter zunutze.
5.4.1.3 Glanz, Trübung, Farbe
Bei diesen Begriffen handelt es sich um technische Eigenschaften. Als Glanz wird das Verhältnis
der Reflexion R der Probe zur Reflexion Rst eines Standards definiert. Der Glanz ist abhängig vom
Einfallswinkel des Lichts, den Brechungsindizes der Probe und des Standards und von den
Inhomogenitäten der Probenoberfläche.
Die Trübung als Folge der Lichtstreuung wurde bereits in Kapitel 5.4.1.1 behandelt. Die exakte Behandlung der Trübung in einem Polymermaterial ist ziemlich kompliziert, da sich Streuung,
Reflexion und Absorption überlagern. Hierzu wird auf weiterführende Literatur verwiesen.
Die Farbe eines Materials ist eine physiologische Größe, die nur in Gegenwart von Licht auftritt. Zur Quantifizierung werden zwei verschiedene Verfahren angewendet. Beim ersten Verfahren
wird die zu prüfende Farbe mit einer genormten Sammlung von Farbproben verglichen. Zusätzlich
zum Farbton wird noch die Helligkeit und die Sättigung angegeben.
Das zweite Verfahren, das ohne Vergleichsproben auskommt, basiert auf der Annahme, daß
sich eine Farbe F additiv aus Einzelfarben x1, x2, x3 , ... zusammensetzt
,
(5.184)
F = a1 x1 + a2 x2 + a3 x3 +.....
wobei a1, a2, a3 , ... die zugehörigen Farbwertanteile sind. Es hat sich gezeigt, daß zur vollständigen
Beschreibung einer Farbe drei monochromatische Einzelfarben ausreichen. In der Praxis werden
hierzu die Einzelfarben Magenta (700,0 nm), Cyan (546,1 nm) und Blau (435,8 nm) verwendet.
Durch Mischen dieser drei Grundfarben ist die zu untersuchende Farbe nachstellbar. Dies geschieht
in der Weise, daß die Farbe mit einem Spektralphotometer im sichtbaren Wellenlängenbereich gemessen und anschließend mit Hilfe von Gleichung (5.184) mathematisch und experimentell nachgestellt wird; auf diese Weise erhält man das Mischungsverhältnis der drei Einzelfarben. Mit den
oben angeführten Problemen befaßt sich die Farbmetrik.
5.4.1.4 Nichtlineare optische Eigenschaften
Wird ein Polymermaterial elektromagnetischer Strahlung ausgesetzt, so sind für niedrige Strahlungsintensitäten das induzierte Dipolmoment p und die induzierte Polarisation P proportional der
elektrischen Feldstärke E
p=α E ;
P=χE
(5.185)
wobei α die Polarisierbarkeit des Moleküls und χ die elektrische Suszeptibilität sind. Bei größeren
Strahlungsintensitäten, wie sie z.B. bei Lasern auftreten, ergeben sich zusätzlich zur linearen Abhängigkeit quadratische und kubische Abhängigkeiten,
p = α ( ) E + α ( ) E E + α ( ) E E E + ...
1
2
3
(5.186)
P = χ ( ) E + χ ( ) E E + χ ( ) E E E + ...
1
(2)
2
(3)
3
(5.187)
(i)
wobei α und α die erste und zweite Hyperpolarisierbarkeit und χ die elektrischen Suszeptibilitäten erster, zweiter und dritter Ordnung sind.
Die möglichen Anwendungen dieses Effekts für die Elektrooptik sind bedeutend und in ihrer
Tragweite noch nicht ganz abzuschätzen. Beispiele hierfür sind Flüssigkristallanzeigen, Frequenz-
5 Das Makromolekül als Festkörper und als Schmelze
413
verdoppler, Frequenz-Mixing, elektro-optische Modulatoren, optische Schalter und optische Speicher.
5.4.2 Elektrische Eigenschaften
Da Polymere in nahezu allen Fällen aus nichtmetallischen Molekülgruppen aufgebaut sind, besitzen
sie dielektrische Eigenschaften und sind elektrische Isolatoren. Zunächst sollen daher die dielektrischen Eigenschaften der Polymere besprochen werden. Unter bestimmten Voraussetzungen ist es
allerdings möglich, Makromoleküle so zu modifizieren, daß sie zu elektrischen Leitern oder Halbleitern werden; im zweiten Abschnitt dieses Kapitels wollen wir uns deshalb mit der elektrischen
Leitfähigkeit beschäftigen.
5.4.2.1 Dielektrische Eigenschaften
Polarisierbarkeit und Polarisation  Wie in den Kapiteln 4.3.3 und 5.4.1 bereits ausgeführt, erzeugt ein elektrisches Feld E in einem Nichtleiter (Dielektrikum) ein elektrisches Dipolmoment p
p = α Eeff
(5.188)
wobei α die Polarisierbarkeit ist. Es werden durch das elektrische Feld molekulare Dipole induziert
oder vorhandene permanente Dipole orientiert. Im ersten Fall handelt es sich um eine Verschiebungspolarisierbarkeit αV und im zweiten Fall um eine Orientierungspolarisierbarkeit αO. Bei der
Verschiebungspolarisierbarkeit kann man unterscheiden in eine Verschiebung der Elektronen (Elektronenpolarisierbarkeit αVe) und in eine Deformation des Moleküls (Atompolarisierbarkeit αVa).
In Kapitel 4.3.3 wurde gezeigt, daß der Zusammenhang zwischen der Orientierungspolarisierbarkeit
und dem permanenten elektrischen Dipolmoment durch die Gleichung α O = p
2
( 3 kB T )
gegeben
ist.
Die Polarisation eines Dielektrikums P ist das elektrische Gesamtdipolmoment pro Volumeneinheit:
N
a f ∑q
P= 1V
i =1
i
ri
a f
Ptotal = PVe + PVa + PO = α total N V Eeff = α Ve + α Va + p
2
b3 k T g a N V f E
B
(5.189)
eff
wobei ri der Ortsvektor der Ladung qi ist, die Indizes Ve, Va und O sich auf die Elektronenpolarisation, die Atompolarisation und die Orientierungspolarisation beziehen und N/V die Ladungsdichte
bedeutet.
Während für die optischen Eigenschaften eines Polymers im wesentlichen die Elektronenpolarisation verantwortlich ist, werden die elektrischen Eigenschaften von den permanenten Dipolmomenten und damit von der Orientierungspolarisation beeinflußt. Abbildung 5.62 stellt die elektrischen Verhältnisse in einem Kondensator ohne Materie und in einem solchen mit Dielektrikum
dar.
414
5.4 Optische und elektrische Eigenschaften
Abbildung 5.62:
Kondensator ohne
und mit Dielektrikum
Es gilt allgemein:
E = U d ; ϕ = E A ; Q = ε0 ϕ = ε0 E A ; D = Q A = ε0 E ; C = Q U
(5.190)
wobei U die elektrische Spannung, d und A der Plattenabstand und die Fläche des Kondensators, ϕ
der elektrische Fluß, Q die Ladung auf dem Kondensator, ε0 die elektrische Feldkonstante, D die
Verschiebungsdichte (Flächenladungsdichte) und C die Kapazität sind.
Befindet sich zwischen den Kondensatorplatten ein Dielektrikum, so erzeugt eine Spannung
U zwischen den Platten eine höhere Feldstärke als beim leeren Kondensator
(5.191)
E = E0 + P ,
wobei E0 die Feldstärke beim leeren Kondensator und P die eben besprochene dielektrische Polarisation der Materie zwischen den Kondensatorplatten ist. Mit der Erhöhung der Feldstärke werden
auch der elektrische Fluß, die Ladung, die Verschiebungsdichte und die Kapazität des Kondensators
erhöht. Für den Kondensator mit Dielektrikum gilt deshalb:
c
c
h
h
ϕ m = E0 + P A ; Qm = ε 0 ϕ m = ε 0 E0 + P A
c
(5.192)
c
h
h
Dm = Qm A = ε 0 E0 + P = D0 + ε 0 P ; Cm = Qm U = ε 0 E0 + P A U
(5.193)
wobei die Indizes 0 und m sich auf die Größen beim leeren Kondensator und beim Kondensator mit
Dielektrikum beziehen.
Die relative Permittivität ε und dielektrische Verluste  Die relative Permittivität ε (früher Dielektrizitätskonstante genannt) ist definiert als Verhältnis der Kapazitäten, der Ladungen, der elektrischen Flüsse und der Verschiebungsdichten des leeren Kondensators und des Kondensators mit
Dielektrikum
ε = Cm C0 = Qm Q0 = ϕ m ϕ 0 = Dm D0 = ( E0 + P ) E0
(5.194)
Aus praktischen Gründen wird häufig noch die dielektrische Suszeptibilität χ mit P = χ E0 definiert. Gleichung (5.194) liefert den Zusammenhang von χ und ε : ε = 1 + χ .
Der Zusammenhang zwischen der Polarisierbarkeit oder der Polarisation und der relativen
Permittivität wird durch verschiedene theoretisch begründete und empirische Beziehungen beschrieben. Neben der Kirkwood-Onsager-Gleichung (4.338) wird häufig die Clausius-MosottiGleichung (4.337) verwendet:
M ρ ε − 1 ε + 2 = 4 π 3 N V α total
(5.195)
a fa f a
f a
fa f
wobei M die Molmasse und ρ die Dichte des dielektrischen Materials sind.
Für Polymere kann die relative Permittivität Werte von 1 bis etwa 200 erreichen; in einzelnen
Fällen werden auch sehr viel höhere Werte erzielt. Tabelle 5.27 gibt einen Überblick über die relativen Permittivitäten von ausgewählten Polymeren; sie zeigt, daß man die höchsten Permittivitäten
bei Thermoplasten und Elastomeren erhält, die mit Mineralstoffen oder Metallpulvern gefüllt sind.
5 Das Makromolekül als Festkörper und als Schmelze
415
Tabelle 5.27: Relative Permittivitäten ε von einigen Kunststoffen
ε
Material
Luft
Wasser
Polytetrafluorethylen
1,0006
81
2,0
Material
Polyethylen
Polycaprolactam
Polyisopren
ε
2,25
4,3
13
Material
ε
gefüllte Thermoplaste
gefüllte Elastomere
3 − 170
3 − 18000
Polarisationsvorgänge laufen innerhalb relativ kurzer Zeiträume ab. Die Grenzfrequenzen für die
einzelnen Polarisationen betragen für die Elektronenpolarisation 1016 Hz, für die Atompolarisation
1012 Hz und für die Orientierungspolarisation 1010 Hz. Wegen dieser hohen Frequenzen kann die
Polarisation schnellen elektrischen Wechselfeldern folgen, was zu Phasenverschiebungen zwischen
Spannung und Strom führt. Die Polarisation setzt sich daher aus den folgenden Anteilen zusammen:
1) Die Polarisation folgt dem elektrischen Wechselfeld in Phase und ist proportional der elektrischen Suszeptibilität χ ′ = ε ′ − 1 .
2) Die Polarisation hinkt dem elektrischen Wechselfeld mit einer Phasenverschiebung nach und ist
proportional zu χ ′′ = ε ′′ − 1. Dieser Anteil führt zu dielektrischen Energieverlusten. χ und ε können daher als komplexe Größen aufgefaßt werden:
χ ω = χ ′ ω − i χ ′′ ω ; ε ω = ε ′ ω − i ε ′′ ω
(5.196)
af
af
af
af af
af
Die Realteile χ′ und ε′ werden als eigentliche Suszeptibilität und Permittivität und der Imaginärteil
ε′′ als dielektrische Verlustzahl bezeichnet. Die Größen χ′, χ′′, ε′ und ε′′ sind abhängig von der
Kreisfrequenz ω = 2 π / T des elektrischen Feldes und von der Temperatur.
Je mehr die Polarisation dem elektrischen Wechselfeld nachhinkt, desto größer ist die verbrauchte elektrische Energie; diese ist für eine elektrische Arbeit nicht mehr verfügbar, da sie in
Wärme umgesetzt wird. Damit kann die Gleichung (5.196) anschaulich gedeutet werden: die Realteile χ′ und ε′ bestimmen die im Dielektrikum gespeicherte Energie, und die Imaginärteile χ′′ und
ε′′ geben an, wieviel Energie in Wärme umgewandelt wird:
W = E2 ω ε
(5.197)
Die dielektrischen Verluste können bei Polymeren beträchtliche Werte erreichen; dies muß z.B. bei
der Auswahl von Kunststoffen für die Isolierung von Hochfrequenzkabeln berücksichtigt werden.
Von technischer Bedeutung ist hierbei der dielektrische Verlustfaktor tg δ = ε ′′ / ε ′ .
Elektrischer Durchschlag, Kriechstrom, Aufladung  Für technische Anwendungen gibt es eine
Reihe von Kenngrößen, die mehr von technischem als von wissenschaftlichem Interesse sind. Als
Durchschlagfestigkeit Ed hat man den Quotienten aus der Durchschlagspannung Ud und der Dicke d
des Materials festgelegt, wobei die Durchschlagspannung der Effektivwert der Wechselspannung
einer bestimmten Frequenz (meist 50 Hz) ist, die den Durchschlag verursacht, d.h. bei der das dielektrische Material elektrisch versagt und die Spannung zwischen den Elektroden unter Zerstörung
des Dielekrikums zusammenbricht:
Ed = U d d
(5.198)
Als Gründe für den Durchschlag kommen in Frage:
1) Dielektrische Verluste führen bei Polymeren beim Anlegen eines Feldes zur Erwärmung. Falls
die Wärme nicht schnell genug abgeführt werden kann, kommt es zu Temperaturerhöhungen und
damit zu irreversiblen Zerstörungen des Materials. Dieser Effekt wird Wärmedurchschlag genannt.
2) Durch ein elektrisches Feld können die Ladungsträger aus dem Festkörper herausgelöst und beschleunigt werden. Die Folge ist eine Zunahme des Stromes und bei Überschreiten einer kritischen
Spannung der Durchschlag. Man bezeichnet diesen Effekt als elektrischen Durchschlag.
416
5.4 Optische und elektrische Eigenschaften
3) Beim Durchschlag durch Entladung führen durch das Feld verursachte lokale Entladungen zur
Zerstörung des Dielektrikums; dabei bilden sich unter Gasentwicklung Entladungskanäle (Treeing),
die schließlich zum Durchschlag führen.
Die beschriebenen Effekte überlagern sich weitgehend. Es ist auch ohne weiteres einleuchtend, daß
die Durchschlagfestigkeit von der Temperatur, der Morphologie, den mechanischen Spannungen
und der Feuchtigkeit des Materials abhängt.
Der Kriechstrom ist der Oberflächenstrom eines Dielektrikums, der sich aufgrund von Normalverunreinigungen auf der Oberfläche bildet. Zur Bestimmung des Kriechstroms werden häufig
wässrige Salzlösungen verwendet, die tropfenweise solange auf die Oberfläche des Materials gegeben werden, bis ein Kurzschluß entsteht. Die Zahl der zugeführten Tropfen bis zum Kurzschluß ist
dann ein Maß für die Kriechstromfestigkeit. Außer faserverstärkten Polymeren, Polystyrol und
Polystyrol-Copolymerisaten besitzen die meisten Polymere eine gute Kriechstromfestigkeit.
Da die meisten Kunststoffe gute Isolatoren sind, neigen sie zu elektrostatischer Aufladung.
Diese entsteht durch Über- oder Unterschuß von Elektronen auf der Oberfläche des Materials und
kann durch Kontakt der Oberfläche mit Ionen oder durch Reiben zweier Oberflächen gegeneinander
erzeugt werden. Die elektrostatische Aufladung läuft umso einfacher ab, je niedriger die elektrische
Leitfähigkeit des Materials und die relative Luftfeuchtigkeit sind. Die elektrostatische Aufladung
von Polymeren macht sich oft sehr störend bemerkbar und bringt eine Reihe ungünstiger und gefährlicher Effekte mit sich. Zur Verhinderung dieses Effekts werden Substanzen eingesetzt, die die
Leitfähigkeit auf der Oberfläche des Polymers (Antistatika) oder des gesamten Polymers (Ruß- oder
Metallpulvergefüllte Polymere) erhöhen.
Elektrete, Pyroelektrika, Piezoelektrika  Elektrete sind dielektrische Materialien, bei denen die
durch ein elektrisches Feld induzierten oder orientierten Dipole über einen längeren Zeitraum erhalten bleiben. Zur Herstellung von polymeren Elektreten werden die Polymere auf Temperaturen
oberhalb der Glastemperatur gebracht, ein starkes elektrisches Feld angelegt und anschließend das
Polymer unter der Wirkung des elektrischen Feldes abgekühlt. Damit werden die induzierten und
orientierten Dipole eingefroren. Die Abklingkonstante (d.h. die Zeit, bei der die Ladung auf den
1/e-ten Teil abgeklungen ist) beträgt bis zu 50 Jahre. Beispiele für polymere Elektrete sind Poly(ethylen-co-propylen), Polycarbonat, Polytetrafluorethylen und Polypropylen. Sie werden in steigendem Maße für Luftfilter, Strahlungsmeßgeräte und elektroakustische Wandler verwendet.
Pyroelektrika und Piezoelektrika sind dielektrische Materialien, bei denen eine Ladungserzeugung durch Temperaturerhöhung und durch mechanischen Druck erzeugt wird. Die Ladungserzeugung erfolgt dabei durch Ladungsverschiebung oder -orientierung. Bei piezoelektrischen Polymeren ist die erzeugte Ladung häufig proportional dem angelegten Druck. Ein pyro- und piezoelektrisches Polymer ist z.B. Poly(vinylidenfluorid). Der entgegengesetzte Effekt zum piezoelektrischen Effekt, nämlich die Kontraktion eines Materials durch Anlegen eines elektrischen Feldes
heißt Elektrostriktion.
Für pyro- und piezoelektrische Polymere bieten sich zahlreiche Anwendungsmöglichkeiten
an, z.B. Wärmedetektoren, Schallwellensender und -empfänger, elektroakustische und
elektromechanische Wandler und Elemente, elektronische Bauelemente.
5.4.2.2 Elektrische Leitfähigkeit
Befinden sich in einem Material bewegliche Ladungsträger, so werden diese bei Anlegen eines
elektrischen Feldes verschoben. Für den Strom I = Q / t ergibt sich
I = (N V ) w e A
(5.199)
wobei N/V die Zahl der Ladungsträger pro Volumeneinheit (Ladungsdichte), w die Wanderungsgeschwindigkeit der Ladungsträger, e die Elementarladung und A die stromdurchflossene Fläche sind.
5 Das Makromolekül als Festkörper und als Schmelze
417
Definiert man als Beweglichkeit µ die Wanderungsgeschwindigkeit bei der Feldstärke eins und als
Stromdichte J den Strom pro Flächeneinheit
(5.200)
µ=w E ; J=I A
so ergibt sich
J = (N V ) µ e E =σ E
wobei σ = ( N V ) µ e = J
,
(5.201)
E als spezifische elektrische Leitfähigkeit bezeichnet wird.
Als Ladungsträger können Elektronen und bewegliche Ionen auftreten. Während für Metalle
und viele Halbleiter die Leitfähigkeit mit Hilfe des Bändermodells der Elektronen- und Löcherleitfähigkeit erklärt werden kann (siehe Lehrbücher der Physik oder der Physikalischen Chemie), sind
die Verhältnisse bei Polymeren komplizierter.
Fast alle reinen Polymere weisen bei nicht zu hohen Temperaturen eine geringe elektrische
Leitfähigkeit auf und sind daher Isolatoren. Sie werden für zahlreiche Anwendungen in der Elektrotechnik und in der Elektronik eingesetzt. Tabelle 5.28 zeigt die spezifischen Leitfähigkeiten einiger
typischer Polymere.
Tabelle 5.28: Spezifische elektrische Leitfähigkeiten σ in 1/(Ω cm) von reinen, gefüllten [...] und dotierten {...} Polymeren bei T = 25 °C. Konzentrationsangaben in Massen %
Polymer
Polyethylen
Polycarbonat
Polymethylmethacrylat
Polyoximethylen
Polypropylen
Polyvinylchlorid, weich
Polyvinylchlorid, hart
Polystyrol
Polyurethan
cis-Polyacetylen
Poly(p-phenylen)
Polypyrrol
Polyanilin
Polythiophen
Polyazasulfen
Graphit
Quecksilber
Kupfer
Silber
Leitfähigkeit σ in Ω−1 cm−1
10−18
10−17
10−15 − 10−17
10−15 − 10−16
10−18
10−12 − 10−13
10−16
10−14 − 10−17
10−9 − 10−12
10−9
10−15
10−8
10−14
10−11
4 ⋅ 103
104
1,04 ⋅ 104
6,45 ⋅ 105
6,71 ⋅ 105
10−8 [70 % Ni] ; 104 [85 % Ag]
10−8 − 10−1 [5 − 20 % Ruß]
10−2 [15 % Ruß]
10−2 [25 % Ruß]
6 ⋅ 102 {AsF5} ; 102 {J2}
5 ⋅ 102 {AsF5} ; 103 {Na}
102 {J2} ; 2 ⋅ 102 {ClO4−}
10 {H2SO4}
20 {(C6H5)4N+}
4 ⋅ 104 {J2}
418
5.4 Optische und elektrische Eigenschaften
Abbildung 5.63: Leitfähigkeiten anorganischer
und organischer Stoffe
Trotz der prinzipiellen Isolatoreigenschaften der Polymere wurden große Anstrengungen unternommen, um elektrisch leitfähige
Polymere mit dem Ziel zu entwickeln, metallische Eigenschaften mit den verarbeitungstechnischen Merkmalen und den mechanischen
Eigenschaften von Polymeren zu koppeln.
Prinzipiell kann man elektrisch leitfähige Polymere nach der Art der für den Ladungstransport verantwortlichen Ladungsträger in ionisch
und elektronisch leitende Polymere unterscheiden. Elektronisch leitende Polymere können weiter in gefüllte leitfähige Polymere und
intrinsisch leitfähige Polymere (ICP, „intrinsically conducting polymers“) unterteilt werden.
Ionisch leitende Polymere  Ionisch leitende
Polymere können alle Polyelektrolyte oder
salzhaltige Polymere sein. Als Ladungsträger
wirken bewegliche Ionen, wobei der elektrische Strom mit einer Diffusion der Ionen verbunden ist. Als Beispiel für einen ionisch leitenden Festelektrolyten sei LiClO4-haltiges
Polyethylenoxid erwähnt, das in Batterien
Verwendung findet.
Gefüllte leitfähige Polymere  Eine prinzipiell
einfache Möglichkeit zur Erhöhung der elektrischen Leitfähigkeit von Polymeren ist das Einarbeiten von leitfähigen Materialien in Form
feinverteilter Partikel in die Polymermatrix.
Als leitfähige Materialien werden eingesetzt:
• Metalle (Gold, Silber, Aluminium, Eisen, Kupfer, Nickel)
• Kohlenstoff in Form von Ruß oder Graphit
• Organische Leiter und Charge-Transfer-Komplexe (Tetrathiafulvalen, Tetracyanochinondimethan, Hexamethylentetraselenfulvalen, Tetraselenotetracenchlorid)
Abbildung 5.64
Typischer Verlauf der Leitfähigkeit eines
Polymers, das mit Leitpartikeln (z.B. mit Ruß)
gefüllt ist
Tabelle 5.28 zeigt die Leitfähigkeiten einiger mit Metallpulver und mit Ruß gefüllter Polymere im
Vergleich zu den reinen Polymeren. In Abbildung 5.64 ist der typische Verlauf der elektrischen Leitfähigkeit σ eines gefüllten Polymers als Funktion der Leitpartikelkonzentration dargestellt. Bei
niedriger Konzentration sind die einzelnen Leitpartikel noch voneinander getrennt und berühren
sich noch nicht, so daß das Produkt das Isolationsverhalten der Polymermatrix besitzt. Innerhalb
5 Das Makromolekül als Festkörper und als Schmelze
419
eines engen Konzentrationsbereichs bilden sich durchgehende „Leitpartikelpfade“ in Form eines
Perkolations-Netzwerks aus. Die Leitfähigkeit steigt sehr rasch um viele Größenordnungen an. Eine
weitere Zugabe von Leitpartikeln jenseits dieser „Perkolationsschwelle“ erhöht die Leitfähigkeit
nur noch geringfügig; es wird ein Plateau erreicht.
Durch den Tunneleffekt kann ein Strom zwischen zwei Teilchen fließen, wenn sich diese nicht
berühren und noch einige Nanometer voneinander entfernt sind. Trotzdem wurde experimentell
festgestellt, daß die höchste Leitfähigkeit, die man bei gefüllten leitfähigen Polymeren gemessen
hat, (Plateauleitfähigkeit) immer um ein bis zwei Größenordnungen unter der Leitfähigkeit des reinen Füllmaterials liegt.
Die Leitpartikel kann man in Form von Kugeln, Plättchen, Nadeln, Fäden oder Gewebe in das
Polymer einarbeiten. Die Perkolationsschwelle folgt aus rein geometrischen Betrachtungen. Für
eine Zufallsverteilung von kugelförmigen Leitpartikeln liegt sie bei 15 Vol% und von nadel- oder
fadenförmigen Leitpartikeln sogar unter 1 Vol%. Weit unter 15 Vol% liegt die Perkolationsschwelle,
wenn die Leitpartikel in der Polymermatrix nicht zufallsverteilt sind, sondern sich kettenartig anordnen. Wird die gleiche Menge, z.B. des Russes nach demselben Verfahren in verschiedene Thermoplaste eingearbeitet, so zeigen diese Mischungen erhebliche Unterschiede in der Leitfähigkeit.
Die Leitfähigkeitsdifferenzen sind durch unterschiedliches rheologisches Verhalten bei der Verarbeitung, unterschiedliche Benetzbarkeit des Polymers für die Leitpartikel, unterschiedliche Kristallinität und die Leitfähigkeit des Polymeren selbst verursacht.
Bei teilkristallinen Polymeren wird der Ruß im Zuge der Kristallisation aus den sphärulitisch
kristallisierenden Bereichen verdrängt und reichert sich zwischen den Sphärulithen an. Um die gleiche Leitfähigkeit zu erreichen, braucht man deswegen bei teilkristallinen Polymeren geringere
Mengen an Ruß einzuarbeiten, als es bei amorphen Polymeren nötig ist.
Die wichtigsten Anwendungen gefüllter elektrisch leitfähiger Polymere sind: anti-statische
Verpackungen, elektromagnetische Abschirmung von elektronischen Baugruppen und elektrischen
Geräten, selbstregelnde Heizungen, Klebstoffe für die Elektronikfertigung, Energiekabelummantelung sowie Herstellung von Kontaktelementen und Kontaktmatten für Rechner und elektronische
Geräte.
Intrinsisch leitfähige Polymere (ICP)  Zu den intrinsisch leitenden Polymeren gehören die Polymere, deren elektronische Leitfähigkeit nicht aus dem Zusatz leitfähiger Additive sondern aus der
Molekülstruktur resultiert. Gemeinsames und für die Leitfähigkeit verantwortliches Strukturmerkmal der ICP sind ausgedehnte konjugierte Doppelbindungen. Chemische Strukturen der wichtigsten
Polymeren mit konjugierten Doppelbindungen sind in Tabelle 5.29 gezeigt. Im Gegensatz zu früheren Vorstellungen sind Polymere mit konjugierten Doppelbindungen in reinem Zustand elektrische
Isolatoren (siehe Tabelle 5.28).
Tabelle 5.29: Polymere mit konjugierten Doppelbindungen
trans-Polyacetylen
Polypyrrol
Polyanilin
Poly(p-phenylen)
H
N
N
H
N
H
N
H
N
H
Polythiophen
S
S
S
420
5.4 Optische und elektrische Eigenschaften
Dies liegt daran, daß bei den genannten Polymeren die π-Orbitale nicht überlappen, sondern aus
energetischen Gründen instabil sind; erst bei Temperaturen oberhalb T = 104 K überlappen die
π-Orbitale. Unterhalb dieser Temperatur überlappen die π-Orbitale nicht, so daß diese Polymere im
reinen Zustand keine Leiter, sondern Isolatoren sind. Polymere mit konjugierten Doppelbindungen
werden Peierls-Isolatoren genannt. Die beschriebene Behauptung heißt Peierls-Theorem.
C
C
C
C
C
C
C
C
C
C
C
C
C
T > 104 K
C
C
C
C
T < 104 K
C
Abbildung 5.65: Polymer mit konjugierten Doppelbindungen
Intrinsisch leitfähige Polymere (Halbleiter und Leiter) werden durch die Behandlung von
Polymeren mit konjugierten Doppelbindungen mit Oxidations- oder Reduktionsmitteln erreicht.
Diese Behandlung wird in Anlehnung an die Halbleiterphysik Dotierung genannt. Als Dotierungsmittel wurden bisher Jod (J2), Arsenpentafluorid (AsF5), Bortrifluorid (BF3), Brom (Br2), Natrium
(Na) u. a. verwendet. Tabelle 5.28 zeigt, daß die Leitfähigkeit von mit geeigneten Fremdmolekülen
dotierten Polymeren mit konjugierten Doppelbindungen sprunghaft um viele Zehnerpotenzen ansteigt und damit echte halbleitende oder leitende Polymere entstehen.
Bei der Oxidation von Polymeren mit konjugierten Doppelbindungen mit einem Dotierungsmittel werden Elektronen aus dem vollen Valenzband des Polymers entfernt und bei der Reduktion
in ein leeres Leitungsband eingeführt. Aus Gründen der Ladungsneutralität erfolgt die Einlagerung
des dabei entstehenden Anions oder Kations in das Polymer; man kann sagen, daß durch die Dotierung polymere Salze entstehen. Bei den oxidierenden Dotierungsmitteln (AsF5, J2. BF3) werden
Carbokationen entlang der Polymerkette gebildet; diese ermöglichen eine Ladungsverschiebung
längs der Kette. Der Ladungstransport zwischen den Polymerketten und über die nichtleitenden
Polymerkettenstücke erfolgt durch Tunneln oder Hüpfen („variable range hopping“).
Die Herstellung der ICP verläuft in zwei Stufen: 1) Synthese von Polymeren mit konjugierten
Doppelbindungssystemen und 2) Dotierung. Die Syntheseprinzipien sind vielfältig. Die konjugierten polymeren Doppelbindungssysteme kann man durch oxidative Polymerisation, Eliminierungsreaktionen, Wittig-Reaktionen, Grignard-Kupplung von dihalogenierten Monomeren und ZieglerNatta-Katalysatoren herstellen.
Die oxidative Polymerisation hat besondere Bedeutung. Sie wird bevorzugt bei fünfgliedrigen
heterozyklischen Monomeren, wie Pyrrol, Thiophen oder Furan angewandt, aber auch bei Aromaten
wie Benzol, Phenylensulfid oder Anilin. Die Oxidation kann chemisch oder elektrochemisch durchgeführt werden. Für die oxidative Polymerisation des Pyrrols, das stellvertretend für die Vielzahl
von polymerisierbaren 5-Ring-Heterocyclen ist, wurde unabhängig davon, ob die Oxidation chemisch oder elektrochemisch abläuft, folgendes Reaktionsschema vorgeschlagen:
− e−
N
H
N
H
+
2
N
H
+
+
N
H H
H H
N
+
− 2 H+
N
H
H
N
Abbildung 5.66: Mechanismus der oxidativen Polymerisation des Pyrrols



N
H


n
5 Das Makromolekül als Festkörper und als Schmelze
421
Die Polymerisation des Pyrrols wird wie bei anderen heterocyclischen oder aromatischen
Monomeren durch primär gebildete Radikal-Kationen ausgelöst. Die entstehenden RadikalKationen werden im Idealfall ausschließlich über die α-C-Atome des Pyrrols zu Polymeren verknüpft.
Um einen Anstieg der elektrischen Leitfähigkeit zu realisieren, muß man im Anschluß an die
Ausbildung des konjugierten polymeren Doppelbindungssystems die positiven oder negativen
Überschußladungen durch chemische oder elektrochemische Oxidation bzw. Reduktion synthetisierter Polymere erzeugen (Dotierung). Beim Dotieren entstehen positive oder negative Ladungen
in der Polymerkette, die innerhalb eines bestimmten Bereichs der π-Konjugation delokalisieren.
Zum Ladungsausgleich werden Gegenionen, die sich aus dem Dotierungsmittel bilden, in das Polymer eingelagert. Als Oxidationsmittel werden J2, AsF5, SbF5, Br2, FeCl3, AgClO4, S2O8−, NOPF6
und als Reduktionsmittel Na/K-Legierungen, Na in flüssigem Ammoniak, Li2OC(C6H5)2 benutzt.
Das Dotieren gelingt auch mit nichtoxidierenden Protonensäuren (HF, HCl) z.B. bei Polyanilin.
Im Idealfall kann man die chemisch oxidative Polymerisation des Pyrrols (Py) und die gleichzeitige chemische Dotierung des Polypyrrols mit K3Fe(CN)6 als Oxidationsmittel durch folgende
Brutto-Reaktionsgleichung darstellen:
n Py + n(2 + y) K3Fe(CN)6 → {Pyy+[Fe(CN)63–]y/3}n + 2 n H+ +
+ 2 n(1 + y/3)Fe(CN)64– + 3 n(2 + y)K+
(5.202)
wobei y der Dotierungsgrad ist. Der Gehalt an eingebauten Anionen hängt von den Reaktionsbedingungen ab. Im allgemeinen kommen auf ein Anion 3 bis 4 Pyrrol Einheiten (y = 0,0 bis 0,3).
Bei der elektrochemischen Dotierung wird statt durch einen chemischen Reaktionspartner das
Polymer durch das Anlegen eines elektrochemischen Potentials oxidiert oder reduziert. Während
des Stromflusses wird das Polypyrrol, z.B. als Anode, oxidativ unter Einlagerung der Ionen des
Leitsalzes (LiClO4) dotiert:
Oxidation
(C4H3N)y − y x e− + y x ClO4− ←→ [(C4H3N) x+y (ClO4−)x]
Reduktion
(5.203)
Wenn man als Gegenelektrode (Kathode) Lithium wählt, scheidet sich aus dem Leitsalz metallisches Lithium aus:
+
y x Li + y x e
−
Reduktion
←→ y x Li
Oxidation
(5.204)
Beide Reaktionen (Gleichungen (5.203) und (5.204)) sind reversibel, d.h. Polypyrrol besitzt das
Potential eines Elektrodenmaterials und kann, wie auch andere ICP, für wiederaufladbare elektrochemische Zellen verwendet werden.
Zur Erklärung des Leitfähigkeitsverhaltens des Ladungstransports entlang einer Polyenkette
wurde ein Solitonenmodell vorgeschlagen. Solitonen sind freie Radikale, die sich eindimensional
über das konjugierte π-Bindungssystem einer Kette bewegen können.
Die schrittweise Dotierung von z.B. Polypyrrol, Polyphenylenvinylen und Polyanilin durch
die Oxidation bzw. Abspaltung eines Elektrons aus dem Valenzband führt anfangs zur Bildung von
Polaronen (Radikalkationische Zustände, die stark an den Gitterverzerrungen lokalisiert sind) und
dann durch die Abspaltung eines zweiten Elektrons vorwiegend zu spinlosen Bipolaronen in der
Bandlücke. Abbildung 5.67 zeigt Polaron und Bipolaron am Beispiel des Polypyrrols. Die gebildeten Polaronen und Bipolaronen sind für den Anstieg der Leitfähigkeit während der Dotierung verantwortlich. Die Leitfähigkeit des Polypyrrols steigt mit der Zahl gebildeten Polaronen und Bipolaronen solange an, bis ein Plateau erreicht ist. Eine weitere Dotierung des Polypyrrols erhöht die
Leitfähigkeit nur noch geringfügig.
422
5.4 Optische und elektrische Eigenschaften
Polaron (S = 1/2)
Bipolaron (S = 0)
Abbildung 5.67: Dotierung von Polypyrrol
H
N
N
H




H
N
N
H




H
N
N
H
H
N
N
H




H
N
N
H




H
N
N
H
Solitonen, Polaronen und Bipolaronen können sich nur innerhalb einer Kette bewegen. Quer
zur Kette gibt es zumindest im undotierten Zustand kaum bindende Wechselwirkungen, und es bilden sich damit auch keine Energiebänder. Zwischen den Ketten müssen „konventionelle“ Ladungsträger fliessen, hüpfen oder tunneln. Obwohl die Leitfähigkeit quer zu den Ketten gestört ist, wurde
gezeigt, daß im hochdotierten Zustand die Leitfähigkeit immer noch metallisch ist. Das bedeutet,
daß sich die Polymerketten im dotierten Zustand zu einer Struktur ordnen, bei der auch quer zu den
Ketten eine metallische Leitfähigkeit möglich ist. Anisotrope Leitfähigkeit wurde an gestreckten
(orientierten) Polymeren beobachtet. Obwohl die leitfähigen Polymere nur in beschränktem Umfang orientierbar sind, weil sie hauptsächlich nicht löslich und nicht schmelzbar sind, wurden mittels Messungen an gestrecktem Polyacetylen (Streckungsgrad 3) gezeigt, daß das Verhältnis der
Leitfähigkeiten parallel (σ║) und senkrecht (σ⊥) zur Verstreckungsrichtung ungefähr 20 beträgt.
Obwohl die Zusammenhänge zwischen Dotierung und übermolekularer Struktur noch nicht vollständig geklärt sind, kann man schließen, daß die hohe Kristallinität der Ausgangspolymeren die
Dotierungs-Reaktion begünstigt und damit die makroskopische Leitfähigkeit erhöht.
Die Grundidee bei der Entwicklung der ICP, nämlich die Vereinigung von metallischer Leitfähigkeit mit verarbeitungstechnischen Merkmalen der Kunststoffe, wurde noch nicht realisiert. ICP
sind als Reinsubstanzen in dotierter Form fast ausnahmslos spröde, unlöslich, unschmelzbar und
nicht thermoplastisch verarbeitbar (Ausnahme: Poly(para-phenylensulfid) und Polythiophen im
undotierten Zustand). Die mangelnde Stabilität der ICP unter Umgebungsbedingungen stellt ein
besonderes Problem für die Anwendung dar, insbesondere bei erhöhten Temperaturen. Dies bedeutet im allgemeinen eine Abnahme der Leitfähigkeit und eine Verschlechterung der mechanischen
Eigenschaften bei zunehmender Lager- oder Nutzungsdauer. Lagert man z.B. Polyacetylen bei
Zimmertemperatur an Luft, nimmt die Leitfähigkeit so schnell ab, daß die Anwendung des
Polyacetylens praktisch unmöglich wird, obwohl es für die Grundlagenforschung hochinteressant
ist. Eine höhere Stabilität zeigen Polypyrrol, Polyanilin, Polyphenylenvinylen und Polythiophen.
Unter gleichen Bedingungen nimmt z.B. die Leitfähigkeit des Polypyrrols in 200 Tagen um nur 10
% ab. Durch die Wahl der Herstellungsbedingungen (Reagenzien, Lösemittel, Leitsalz, Konzentrationen, Temperatur, Stromdichte usw.) aber auch durch Mischen mit nicht leitfähigen Polymeren läßt
sich die Stabilität der elektrischen und mechanischen Eigenschaften wesentlich beeinflussen. Durch
geeignete Wahl des Leitsalzes, z.B. n-Dodecylsulfat, aromatischer Sulfonsäuren oder Camphersulfonsäure, statt LiClO4, kann man bei elektrochemischer Polymerisation des Pyrrols flexible, elastische und glatte Polypyrrolfilme herstellen.
ICP kann man dort einsetzen, wo man auch gefüllte elektrisch leitfähige Polymere benutzt,
aber auch für die Herstellung von Elektrolytkondensatoren, Polymerbatterien und -akkumulatoren
hoher Energiedichte, Bauteile für integrierte Schaltungen und Solarzellen, Leuchtdioden auf Polymerbasis, elektrochrome Verglasungen, analytische Sensoren, Elektroden, flexible elektrische Leiter, Leiterplatten, transparente leitfähige Schichten, Elektrolyse-Membranen, Korrosionsschutz usw.