Mikroökonomik 3.5 Konsumentenrente Wir gehen zunächst davon

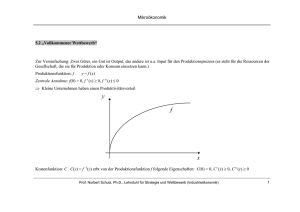
Mikroökonomik
3.5 Konsumentenrente
Wir gehen zunächst davon aus, dass das erste Gut nur in den Mengen 0,1,2,... konsumiert werden kann. Das zweite Gut ist weiterhin
beliebig teilbar.
Präferenzen:
u ( x1, x2 ) = v (x1) + x2
v (x1) + m - px1
Zur Vereinfachung setzen wir v ( 0 ) = 0 voraus. Wie viel x1 maximiert diesen Nutzen?
Zunächst wird der Konsument zumindest eine Einheit kaufen, wenn
r ( 1 ) := v ( 1 ) - v ( 0 ) > p
Reservationspreis oder maximale Zahlungsbereitschaft für die erste Einheit des ersten Gutes. Gegeben er kauft eine Einheit, wird er
auch eine zweite Einheit kaufen, wenn
r ( 2 ) := v ( 2 ) - v ( 1 ) > p
Wir nehmen an, dass die Reservationspreise in der Menge fallen:
Prof. Norbert Schulz, Ph.D., Lehrstuhl für Strategie und Wettbewerb (Industrieökonomik)
1
Mikroökonomik
r ( 1 ) > r ( 2 ) > r ( 3 ) > ...
Reservationspreis
r(1)
r(2)
r(3)
r(4)
r(5)
1 2 3 4
x1
Der Konsument wird nach der obigen Überlegung soviel vom ersten Gut, x1, nachfragen, dass gilt:
Prof. Norbert Schulz, Ph.D., Lehrstuhl für Strategie und Wettbewerb (Industrieökonomik)
2
Mikroökonomik
r ( x1 ) ≥ p > r ( x1 + 1 )
Daher gibt die obige Kurve auch die Nachfragekurve für das erste Gut wieder.
Menge des ersten Gutes
4
3
2
1
r(4) r(3)
p
r(2) r(1)
Preis
Prof. Norbert Schulz, Ph.D., Lehrstuhl für Strategie und Wettbewerb (Industrieökonomik)
3
Mikroökonomik
Der Nutzen aus dem ersten Gut ergibt sich nun für die Menge x1 ( im Beispiel x1 = 2 ) als
v (2) = v (2) - v (1) + v (1) - v (0) = r (2) + r (1)
= Fläche unter der r (.)-Kurve in der ersten Graphik bis einschließlich x1 = 2
Der Nutzen aus beiden Gütern zusammen ist dann v (x1) + m - px1, im Beispiel der Graphik:
v (2) + m - p2 = m + v (2) - p2.
v (2) - p2= "Nutzenüberschuss" = Konsumentenrente aus dem Konsum von (in diesem Fall) 2 Einheiten vom ersten Gut.
Sie gibt also an, um wie viel der Nutzen aus dem Kauf, v (2), die dazu notwendigen Ausgaben, p2, übersteigt.
Prof. Norbert Schulz, Ph.D., Lehrstuhl für Strategie und Wettbewerb (Industrieökonomik)
4
Mikroökonomik
Menge des ersten Gutes
4
3
2
1
r(4)
r(3)
p
r(2) r(1)
Preis
Graphisch ist dies gerade die Fläche unter der Nachfragekurve zwischen p und dem höchsten Reservationspreis r (1).
für teilbare Güter analog: Gehen wir weiter von quasilinearen Präferenzen aus.
Maximierung des Nutzens unter der Budgetrestriktion ergibt:
Prof. Norbert Schulz, Ph.D., Lehrstuhl für Strategie und Wettbewerb (Industrieökonomik)
5
Mikroökonomik
v' ( x1 ) = p
v' = Grenznutzen = Reservationspreis (= marginale Zahlungsbereitschaft!)
Der Nutzen aus dem Konsum von x1 Einheiten vom ersten Gut lässt sich dann schreiben als
x1
v ( x1 ) = ∫ v' ( x)dx
0
= Fläche unter der Grenznutzenkurve zwischen 0 und x1 (farbige Fläche)
Prof. Norbert Schulz, Ph.D., Lehrstuhl für Strategie und Wettbewerb (Industrieökonomik)
6
Mikroökonomik
Grenznutzen
p
x1
Menge des Gutes 1
Konsumentenrente = Fläche unter der Nachfragekurve oberhalb von p(x1) (blaue Fläche).
Prof. Norbert Schulz, Ph.D., Lehrstuhl für Strategie und Wettbewerb (Industrieökonomik)
7
Mikroökonomik
Konsumentenrente = Maß für den Nutzenanstieg, der mit der Bereitstellung von x1 (Projekt) gegenüber dem status quo x2 = m
verbunden ist,
u(x1, x2) - u(0, m) = v ( x1 ) - p(x1) x1,
Diese lässt sich bei Kenntnis der Nachfragefunktion berechnen.
Projektwirkung: Preis von einem Niveau p0 auf ein Niveau p1 fällt.
In diesem Fall ist die damit verbundene Konsumentenrente gleich der Fläche unter der Nachfragefunktion zwischen den Preisen p1 und
p0 .
Annahme quasilinearer Präferenzen kritisch! Es ergibt sich daher auch die Frage, wie groß der Fehler ist, den man macht, wenn man das
Maß der Konsumentenrente trotzdem benutzt.
Prof. Norbert Schulz, Ph.D., Lehrstuhl für Strategie und Wettbewerb (Industrieökonomik)
8