Mikroökonomik 5.2 „Vollkommener Wettbewerb“ Zur Vereinfachung

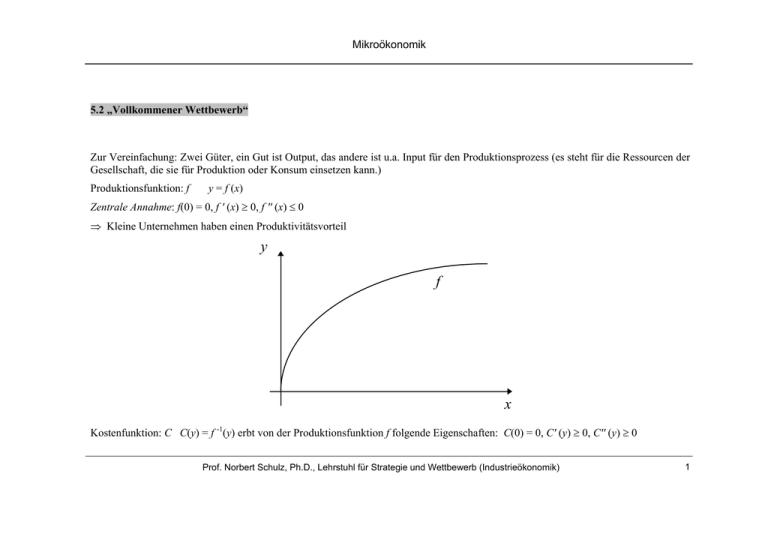
Mikroökonomik
5.2 „Vollkommener Wettbewerb“
Zur Vereinfachung: Zwei Güter, ein Gut ist Output, das andere ist u.a. Input für den Produktionsprozess (es steht für die Ressourcen der
Gesellschaft, die sie für Produktion oder Konsum einsetzen kann.)
Produktionsfunktion: f
y = f (x)
Zentrale Annahme: f(0) = 0, f ' (x) ≥ 0, f '' (x) ≤ 0
⇒ Kleine Unternehmen haben einen Produktivitätsvorteil
y
f
x
Kostenfunktion: C C(y) = f -1(y) erbt von der Produktionsfunktion f folgende Eigenschaften: C(0) = 0, C' (y) ≥ 0, C'' (y) ≥ 0
Prof. Norbert Schulz, Ph.D., Lehrstuhl für Strategie und Wettbewerb (Industrieökonomik)
1
Mikroökonomik
⇒ Kleine Unternehmen haben Kostenvorteil
x
C
y
Positive Theorie: Welches Marktergebnis ist in einem solchen Markt zu erwarten?
Strukturannahme: Es gibt viele Nachfrager, potentiell viele Anbieter, keine Markteintrittsbarrieren, keine Produktdifferenzierung,
Kostenstruktur wie oben
Verhaltensannahme: Gewinnmotiv und als Hilfsannahme: Preisnehmer-verhalten
Prof. Norbert Schulz, Ph.D., Lehrstuhl für Strategie und Wettbewerb (Industrieökonomik)
2
Mikroökonomik
Dies impliziert die Grenzkosten-Preisregel:
p = C ′( y )
und determiniert gleichzeitig das Angebotsverhalten eines Unternehmens.
Solange p > C' (0) positiver Gewinn:
⎛
C ( y) ⎞
⎟ > y ( p − MC ( y )) = 0
py − C ( y ) = y⎜⎜ p −
y ⎟⎠
⎝
⇒ Eintritt neuer Unternehmen
Aggregierte Angebotsfunktion:
p
Angebotsfunktion von
1 Unternehmen
Angebotsfunktion
von 2 Untern.
Nachfrage
y
Prof. Norbert Schulz, Ph.D., Lehrstuhl für Strategie und Wettbewerb (Industrieökonomik)
3
Mikroökonomik
Marktergebnis:
• Preis = Grenzkosten bei 0 = niedrigster Kosten-deckender Preis und
• sehr viele kleine Unternehmen im Markt
Normative Theorie: Welches Ergebnis ist aus Effizienzsicht anzustreben?
Der einfachste Fall: 1 repräsentativer Konsument. Vor Produktion hat der Konsument m Einheiten des Inputgutes und nichts vom
produzierten Gut. Seine Präferenzen sind quasilinear:
u ( y, z ) = v( y ) + z
y = Menge des produzierten Gutes, z = Menge des für Konsum zur Verfügung stehenden Inputgutes.
Paretoeffizienz bedeutet hier: Ergebnis maximiert den Nutzen des Konsumenten.
Umformulierung des Konsumentennutzens:
Wenn nichts produziert wird:
u (0, m) = v(0) + m = m
Wenn y produziert wird bleibt für Konsum nur z = m – C° (y) vom Inputgut übrig: Der Nutzen ist dann
u ( y, m − C °( y )) = v( y ) + m − C °( y )
Prof. Norbert Schulz, Ph.D., Lehrstuhl für Strategie und Wettbewerb (Industrieökonomik)
4
Mikroökonomik
Sozialer Überschuss (Gesamtrente, Wohlfahrt) durch Produktion von y :
u ( y, m − C °( y )) − u (0, m) = v( y ) − C °( y )
Maximierung des Nutzen des Konsumenten ist hier äquivalent zur Maximierung des sozialen Überschusses.
y
y
0
0
Sozialer Überschuss lässt sich auch schreiben als: ∫ v′( s )ds − ∫ C °′( s )ds
Vorteil: graphische Darstellbarkeit:
v'
C°'
y
s
Prof. Norbert Schulz, Ph.D., Lehrstuhl für Strategie und Wettbewerb (Industrieökonomik)
5
Mikroökonomik
Der soziale Überschuss ist maximal, wenn:
v′( y ) = C °′( y )
Außerdem: sozialer Überschuss = Konsumentenrente + Produzentenrente
y
y
y
0
0
0
∫ v′( s)ds − ∫ C °′( s)ds = ∫ p( s)ds − C °( y) =
∞
y
p( y ) y − C °( y ) = ∫ y (q)dq + p( y ) y − C °( y )
∫ p( s)ds − p( y ) y + 1
44244
3
0 44
1
42444
3 Produzentenrente p ( y )
Konsumentenrente
Die Kosten C°(y, n) der Bereitstellung von y hängt von der Anzahl der Unternehmen ab:
Bei n Unternehmen kostet dies
⎛ y⎞
C °( y, n) = nC ⎜ ⎟
⎝n⎠
Ableitung nach n:
⎡ ⎛ y⎞
C⎜ ⎟
y⎞ y
y⎢ ⎝n⎠
⎛ y⎞
⎛
C ⎜ ⎟ − nC ′⎜ ⎟
= ⎢
y
⎝n⎠
⎝ n ⎠ n2 n ⎢
n
⎣⎢
⎤
⎛ y ⎞⎥
− C ′⎜ ⎟⎥ < 0
⎝ n ⎠⎥
⎦⎥
⇒ Verteilung der Produktion auf mehr Unternehmen senkt die Kosten
⇒ effiziente Produktion erfordert sehr viele kleine Unternehmen mit sehr kleiner Produktionsmenge; Gewünscht: n → ∞.
Prof. Norbert Schulz, Ph.D., Lehrstuhl für Strategie und Wettbewerb (Industrieökonomik)
6
Mikroökonomik
Grenzkosten bei n Unternehmen (Ableitung der Kosten nach y)
⎛ y⎞
C °′( y, n) = C ′⎜ ⎟
⎝n⎠
⇒ für sehr viele Unternehmen C°´(y, ∞) = C' (0)
Zusammenfassung für effiziente Produktion:
• Grenznutzen = Grenzkosten bei 0 (determiniert bereitzustellende Menge)
• Gleichmäßige Verteilung auf unendlich viele kleine Unternehmen
• Bei quasilinearen Präferenzen: Grenznutzen = Preisabsatzfunktion
Das Ergebnis dieser normativen Analyse ist eindeutig und identisch mit dem Ergebnis der positiven Analyse. In diesem Sinn liefert der
Wettbewerb ein vollkommenes Resultat.
⇒ Das Marktergebnis im vollkommenem Wettbewerb ist (Pareto-) effizient!
Hauptsatz der Wohlfahrtsökonomik
Problem der Fixkosten: C ( y ) = F + cy + dy 2 ; AC ( y ) =
C ( y) F
= + c + dy
y
y
Prof. Norbert Schulz, Ph.D., Lehrstuhl für Strategie und Wettbewerb (Industrieökonomik)
7
Mikroökonomik
AC
MC
y
⇒ Unternehmen braucht Mindestgröße! ⇒ Die Theorie des vollkommenen Wettbewerbs hat Probleme bei dem Phänomen der
Größenvorteile!
Prof. Norbert Schulz, Ph.D., Lehrstuhl für Strategie und Wettbewerb (Industrieökonomik)
8