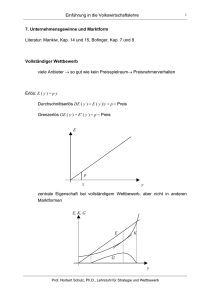
6.1 Duopol à la Cournot

Mikroökonomik
Kapitel 6: „Statische Oligopoltheorie“
6.1 Duopol à la Cournot
6.2 Allgemeines Cournot-Oligopol
6.3 Kostendifferenzen
6.4 Cournot ohne homogene Güter
6.5 Preis als strategische Variable
6.1 Duopol à la Cournot
Marktstruktur: Viele kleine Nachfrager, wenige Anbieter, möglicherweise mit Größenvorteilen, ein vollkommen homogenes Gut
Marktverhalten: Gewinnmaximierung (zunächst durch Entscheidung über Outputmenge)
Marktergebnis?
Das Besondere der oligopolistischen Situation: Entscheidungen eines Unternehmens haben fühlbare Auswirkungen auf die
Gewinnsituation der anderen Unternehmen (bei Duopol: des anderen Unternehmens).
Prof. Norbert Schulz, Ph.D., Lehrstuhl für Strategie und Wettbewerb (Industrieökonomik)
1
Mikroökonomik
Eine einfache (beispielhafte) formale Darstellung:
Wir betrachten 2 Unternehmen
•
Output des Unternehmens i
yi , i = 1, 2
•
Preisabsatzfunktion
P (y1, y2) = a - b (y1 + y2)
•
Kostenfunktion
C (yi) = F + c yi , i = 1, 2
Der Gewinn des Unternehmens 1: (a - b (y1 + y2)) y1 - F - c y1
hängt offenbar von y2 ab.
Eine Möglichkeit, mit dieser wechselseitigen Abhängigkeit umzugehen, besteht in der Nutzung rationaler Erwartungen und
Entscheidungen: Sie sind charakterisiert durch die Forderungen:
•
gegeben die Erwartung an die Entscheidung des anderen, wähle die Gewinn maximierende Alternative
•
Übereinstimmung der Entscheidung mit der Erwartung an diese Entscheidung durch den jeweils anderen (sich erfüllende
Erwartungen)
Prof. Norbert Schulz, Ph.D., Lehrstuhl für Strategie und Wettbewerb (Industrieökonomik)
2
Mikroökonomik
Im Rahmen unseres formalen Beispiels:
Kalkül des Unternehmens 1: Erwartung von 1 über y2: ye2
Erwarteter Gewinn des Unternehmens 1: (a - b (y1 + ye2)) q1 - F - c y1
Gewinnmaximierung bei
y1 =
a−c 1 e
− y 2 =: y1 y 2e
2b
2
y2 =
a−c 1 e
− y1 =: y 2 y1e
2b
2
( )
Analog: Kalkül des Unternehmens 2:
( )
Erfüllte Erwartungen: y1 = y1e ; y 2 = y 2e
Dies ergibt 4 Gleichungen für die 4 Unbekannten y1 , y1e , y 2 , y 2e
Das Ergebnis (Lösung dieses Gleichungssystems) und - damit das Marktergebnis - ist
⇒ y1c =
( )
a−c
2(a − c)
= y 2c , Y c = y1c + y 2c =
3b
3b
Anmerkung: y 2 y1e heißt „Beste Antwort Funktion“ oder „Reaktionsfunktion“ von 2.
Prof. Norbert Schulz, Ph.D., Lehrstuhl für Strategie und Wettbewerb (Industrieökonomik)
3
Mikroökonomik
Für spätere Analysen ist folgende Notation nützlich: Marktgröße = Nachgefragte Menge bei p = c: S = (a – c)/b
Damit lässt sich das Marktergebnis schreiben als
y1c =
2S
S
= y 2c , Y c = y1c + y 2c =
3
3
2
⎛S⎞
⇒ π 1c = π 2c = b⎜ ⎟ − F
⎝3⎠
Man beachte: Obwohl die Kostenfunktion subadditiv ist, können mehrere Unternehmen profitabel tätig sein.
Exkurs Spieltheorie: Nash Gleichgewicht
hier vereinfacht für n = 2 Spieler
Beschreibung des "Spiels" durch
•
Ai
: Strategiemenge des Spielers i, i = 1, 2
•
πi
Auszahlungsfunktion des Spielers i
Definition eines Nash Gleichgewichts:
Prof. Norbert Schulz, Ph.D., Lehrstuhl für Strategie und Wettbewerb (Industrieökonomik)
4
Mikroökonomik
(a , a )∈ A × A heißt Nash Gleichgewicht
<=> π (a , a ) ≥ π (a , a ) für alle a ∈ A und
π (a , a ) ≥ π (a , a ) für alle a ∈ A
*
1
*
2
1
1
2
(
*
1
*
1
2
*
2
*
2
1
2
1
*
2
1
*
1
2
2
1
2
)
Das Cournot Gleichgewicht y1c , y 2c ist ein Nash-Gleichgewicht des folgenden Spiels:
•
A1 = A2 = [0, ∞) , yi entspricht ai
•
π i (a1 , a 2 ) = π i ( y1 , y 2 ) = (a − b( y1 + y 2 )) y i − F − cyi
Bedingung für Nash Gleichgewicht für Spieler 1:
π 1 (a1* , a2* ) ≥ π 1 (a1 , a2* ) für alle a1 ∈ A1
<=> a1* maximiert π 1 bei gegebenem a2*
Im Cournot Modell:
( )
y1* = y1 y 2* =
S y 2*
−
2 2
Bedingung für Nash Gleichgewicht für Spieler 2 analog
Prof. Norbert Schulz, Ph.D., Lehrstuhl für Strategie und Wettbewerb (Industrieökonomik)
5
Mikroökonomik
Im Cournot Modell:
( )
S y1*
y = y2 y = −
2 2
*
2
*
1
Im Nash Gleichgewicht müssen beide Bedingungen
gleichzeitig erfüllt sein.
y 2* =
S y1*
−
2 2
y1* =
S y 2*
−
2 2
Lösung:
y1* = y 2* =
S
= y1c = y 2c
3
Ende Exkurs Spieltheorie.
Kritik des Cournot-Modells:
•
hyperrational
•
Wer bestimmt den Preis?
Beide Kritikpunkte überzeugen nicht!
Prof. Norbert Schulz, Ph.D., Lehrstuhl für Strategie und Wettbewerb (Industrieökonomik)
6
Mikroökonomik
Zur Frage des Preises: Man interpretiere die Mengen als Produktionskapazitäten, über die vor der Produktion entschieden werden muss.
Gegeben diese Kapazitäten können dann die Unternehmen über die Preise entscheiden. Formalisiert man diese Situation
(Kreps/Scheinkman), so resultiert (unter gewissen Annahmen) dasselbe Resultat für die Kapazitäten wie im Cournotmodell für die
Mengen.
Hyperrationalität: Die Rationalitätsannahme ist nicht unbedingt notwendig:
y2
y1( )
y2c
y2( )
y1c
y1
Prof. Norbert Schulz, Ph.D., Lehrstuhl für Strategie und Wettbewerb (Industrieökonomik)
7