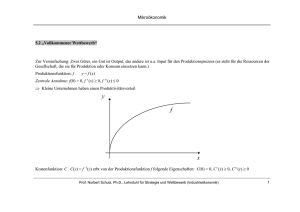
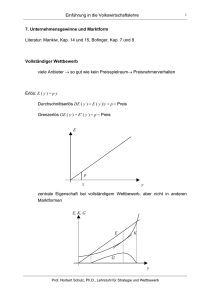
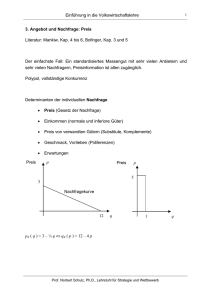
α λ λ

Mikroökonomik
4.4 Güterangebot und Faktornachfrage bei „Preisnehmerverhalten“
Verhaltensannahme: Unternehmen versuchen, möglichst hohe Gewinne zu erwirtschaften.
Formale Modellierung:
max py − w1x1 − w2 x2 u.d.N. f ( x1, x2 ) ≥ y
x, y
wobei neben den Inputpreisen w1 und w2 in diesem Abschnitt der Outputpreis p als exogen gegeben angenommen wird (Die
Unternehmen haben keinen Einfluss auf den Preis, Preisnehmerverhalten).
Die Wahl von Absatzniveau y und Inputniveau x1, bzw. x2, hängt von den Preisen ab und wird beschrieben durch
•
die Angebotsfunktion: y ( p, w1, w2 )
•
die Faktornachfragefunktionen: xi ( p, w1, w2 )
Beispiel für eine Cobb-Douglas Produktionsfunktion: f ( x1, x2 ) = x1α x2β mit α + β < 1
Lagrangeansatz: L( y, x1, x2 , λ ) = py − w1x1 − w2 x2 + λ ( f ( x1, x2 ) − y )
Prof. Norbert Schulz, Ph.D., Lehrstuhl für Strategie und Wettbewerb (Industrieökonomik)
1
Mikroökonomik
∂L
= p−λ =0⇔ λ = p
∂y
(1)
f ( x1, x2 )
∂L
∂f
= − w1 + λ
= 0 ⇔ w1 = λα x1α −1x2β = λα
x1
∂x1
∂x1
(2)
f ( x1, x2 )
∂L
∂f
= − w2 + λ
= 0 ⇔ w2 = λβ x1α x2β −1 = λβ
x2
∂x2
∂x2
(3)
f ( x1, x2 ) = y ⇔ x1α x2β = y
(4)
Aus (2) und (3) folgt:
∂f
∂x1 w1
α x2 w1
=
⇔
=
(5)
∂f
w2
β x1 w2
∂x2
Dies entspricht zusammen mit (4) der Bedingung für Kostenminimierung! Löst man (5) nach x2 auf und setzt dies in (2) ein, so erhält
man nach Berücksichtigung von (1):
Prof. Norbert Schulz, Ph.D., Lehrstuhl für Strategie und Wettbewerb (Industrieökonomik)
2
Mikroökonomik
x1 ( p, w1, w2 ) = A1 p
1
1−α − β
β −1
1−α − β
w1
−β
w21−α − β
Setzt man dies wieder in die Auflösung von (5) nach x2 ein, so erhält man
x2 ( p, w1, w2 ) = A2 p
1
1−α − β
−α
α −1
1−α − β 1−α − β
w1
w2
Setzt man dies in (4) ein, so erhält man:
−α
−β
α +β
y ( p, w1, w2 ) = A3 p 1−α − β w11−α − β w21−α − β
Dabei sind Ai jeweils Abkürzungen für positive Konstanten, die von α und β abhängen und daher für die Abhängigkeit von den Preisen
keine weitere Bedeutung haben.
•
Die Angebotsfunktion steigt im Produktpreis
•
Die Faktornachfragefunktion fällt im eigenen Faktorpreis
Diese beiden Eigenschaften haben alle Angebots- und Faktornachfragefunktionen bei Preisnehmerverhalten.
Prof. Norbert Schulz, Ph.D., Lehrstuhl für Strategie und Wettbewerb (Industrieökonomik)
3
Mikroökonomik
In einem Zwischenschritt ist bei dem Beispiel das Resultat erreicht worden, dass Gewinnmaximierung Kostenminimierung automatisch
erfüllt sein muss. Wir können daher auch so vorgehen, dass zunächst für jede Absatzmenge y die Kostenfunktion, C ( y ), bestimmt
wird, und dann das Optimierungsproblem:
max py − C ( y )
y
Daraus ergibt sich:
p=
∂C
= MC ( y )
∂y
Das Gewinn maximierende Angebot bestimmt sich demnach bei dem Absatzniveau, bei dem der (vorgegebene) Preis den Grenzkosten
entspricht. Dies ist die berühmte „Preis gleich Grenzkostenregel“, die allerdings nur bei Preisnehmerverhalten gilt.
Man beachte, dass die Bedingung zweiter Ordnung für ein Maximum auch erfüllt sein muss. Dies impliziert, dass die Kostenfunktion
konvex in y sein muss. Wäre sie strikt konkav (dies ist der Fall für α + β > 1 im Cobb Douglas Beispiel), so würden wir mit der obigen
Bedingung erster Ordnung ein Gewinnminimum bestimmen. Für den Rest dieses Abschnitts gehen wir davon aus, dass eine konvexe
Kostenfunktion vorliegt.
Wenn wir demnach die Grenzkostenkurve kennen, so entspricht diese der Angebotskurve eines Gewinn maximierenden
Unternehmens.
Prof. Norbert Schulz, Ph.D., Lehrstuhl für Strategie und Wettbewerb (Industrieökonomik)
4
Mikroökonomik
p
MC
y
Diese Aussage ist jedoch ungenau. Die Bedingung erster Ordnung garantiert hier nur, dass wir ein Maximum des Gewinns bestimmt
haben, aber nicht ob dieser Gewinn positiv ist. Bei negativem Gewinn ist es besser, nichts anzubieten.
Wann ist der Gewinn nicht negativ?
py − C ( y ) = y ( p − AC ( y ))
Der Gewinn ist positiv bei einem Absatzniveau y, wenn der Preis über den Durchschnittskosten bei diesem Absatzniveau liegt.
Prof. Norbert Schulz, Ph.D., Lehrstuhl für Strategie und Wettbewerb (Industrieökonomik)
5
Mikroökonomik
p
MC
AC
y
Gewinn maximierendes Verhalten muss daher zwei Bedingungen erfüllen:
•
Der Preis muss bei dem Gewinn maximierenden Absatzniveau den Grenzkosten entsprechen und
•
der Preis muss bei diesem Absatzniveau über den Durchschnittskosten liegen.
Folglich ist nur der Teil der Grenzkostenkurve gleich der Angebotskurve, der nicht unterhalb der Durchschnittskostenkurve liegt.
Es gibt zwei gern genutzte Möglichkeiten, in Graphiken wie der letzten auch den Gewinn zu veranschaulichen.
Die erste basiert genau auf der Darstellung des Gewinns durch
py − C ( y ) = y ( p − AC ( y ))
Prof. Norbert Schulz, Ph.D., Lehrstuhl für Strategie und Wettbewerb (Industrieökonomik)
6
Mikroökonomik
p
MC
AC
p*
y*
y
Der Fall einer zunächst fallenden Durchschnittskostenkurve ist mit der Annahme einer konvexen Kostenfunktion nur konsistent, wenn
es Fixkosten gibt. In diesem Fall hat die Kostenfunktion die Form:
C ( y ) = F + VC ( y ) = Fixkosten plus variable Kosten
In unserem Cobb-Douglas Beispiel traten keine Fixkosten auf. Deshalb können die Durchschnittskosten in diesem Beispiel nie oberhalb
der Grenzkosten liegen. Dies gilt allgemeiner. Wenn keine Fixkosten vorliegen, dann können die Durchschnittskosten nicht über den
Grenzkosten liegen.
Wenn keine Fixkosten vorliegen, können wir uns den Gewinn auch anderes veranschaulichen, indem wir die Darstellung aus dem
letzten Kapitel nutzen.
Bei dieser Darstellung wird der Gewinn auch oft „Produzentenrente“ genannt. Wir werden davon in der Vorlesung jedoch keinen
Gebrauch machen. Der Begriff der Produzentenrente wird darüber hinaus sehr unterschiedlich in verschiedenen Kontexten genutzt (z.B.
im Skript von Prof. Fehr).
Prof. Norbert Schulz, Ph.D., Lehrstuhl für Strategie und Wettbewerb (Industrieökonomik)
7
Mikroökonomik
p
MC
p*
y*
y
Prof. Norbert Schulz, Ph.D., Lehrstuhl für Strategie und Wettbewerb (Industrieökonomik)
8