Erwartungswert – Varianz – Standardabweichung P

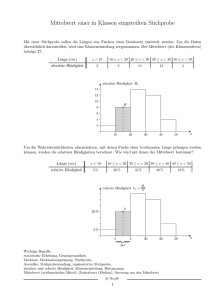
Veranstaltung: Statistik für das Lehramt
Dozent: Martin Tautenhahn
Referenten: Belinda Höher, Thomas Holub, Maria Böhm
16.12.2016
Erwartungswert – Varianz – Standardabweichung
Die Wahrscheinlichkeitsverteilung einer Zufallsfunktion lässt sich vollständig beschreiben
mit:
 Verteilfunktion
F(x)
 Wahrscheinlichkeitsfunktion / Dichtefunktion
f(x)  diskret
f(x) = P(X=x)
 stetig
Eine komplette Beschreibung der Verteilung ist oft gar nicht nötig. Um einen Überblick über
die Verteilung zu gewinnen sehen wir uns charakteristische “Maßzahlen“ an.
Lageparameter
Erwartungswert E(X)
Streuungsparameter
Varianz Var(X) = σ2
Standardabweichung σ
Erwartungswert
(Einsatz 3,- €)
Bsp.: Glücksrad
diskrete Dichtefunktion
P(X=xi)
Grün
4,- € Gewinn
Weiß
3,- € Gewinn
Rot
1,- € Gewinn
xi
f(x)
x
stetige Dichtefunktion
f(x)
Erwartungswert E(X)
3 4 5
x
1
Nützliche Regeln für die Berechnung bzw. den Vergleich von Erwartungswerten
verschiedener Zufallsvariablen
1) Ist die Wahrscheinlichkeits- bzw. Dichtefunktion f von X symmetrisch bzgl. eines
Punktes x=a (d.h. ist f(a-x) = f(a+x) für alle x) so gilt: E(X) = a ( Anwendung bei
besonderen Verteilungen)
Bsp.: Normalverteilung
Bsp.: Gleichverteilung
2) Häufig ist nicht der Erwartungswert von X gesucht, sondern der Erwartungswert einer
Zufallsvariablen Y, die eine Funktion von X darstellt: Y = g(X), z.B. Y = X². Statt für
alle Werte von Y die Wahrscheinlichkeit P (Y=y) bzw. die Dichtefunktion fY(y)
herzuleiten, kann mit dem folgenden Satz die Wahrscheinlichkeitsfunktion bzw. die
Dichtefunktion von X verwendet werden (ohne die Verteilung von Y explizit zu
kennen):
Transformationsregel für Erwartungswerte:
Gegeben ist eine reelle Funktion g(x). Dann gilt für den Erwartungswert der
transformierten Zufallsvariablen Y = g(X):
Dabei bezeichnet f(x) die Wahrscheinlichkeitsfunktion (diskreter Fall) bzw. die
Dichtefunktion (stetiger Fall).
3) Unmittelbare Folgerung aus Regel 2 mit g(x) = a + bx:
4) Für die Summe von n Zufallsvariablen X1, …, Xn gilt stets
5) Sind X und Y unabhängige Zufallsvariablen, so ist E(X·Y) = E(X) · E(Y).
6) Ist für zwei Zufallsvariablen X und Y das Ereignis X≤Y sicher, d.h. gilt für jedes
Elementarereignis ѡ des zu Grunde liegenden Zufallsvorgangs die Ungleichung X(ѡ)
≤ Y(ѡ), so folgt auch E(X) ≤ E(Y); in diesem Sinne stellt E(X) eine monotone
Operation dar.
2
Varianz und Standardabweichung
Die Varianz Var(X) dient als Streuungsmaß für die Verteilung einer Zufallsvariablen X. Sie
entspricht der mittleren quadratischen Abweichung einer Häufigkeitsverteilung. Anstelle von
Var(X) schreibt man oft kürzer σ2.
Idee: Wie weit liegt der erzielte Wert X (also die Zufallsgröße) vom Erwartungswert weg?
x
a) diskrete Zufallsvariable
heißt die Varianz einer diskreten Zufallsvariable X mit den Werten x1, x2,…, dem Erwartungswert E (X) und der
Wahrscheinlichkeitsfunktion f(x) = P(X=x)
b) stetige Zufallsvariable
heißt die Varianz einer stetigen Zufallsvariable X mit E(X) = μ und der Dichtefunktion f(x).
Die positive Wurzel der Varianz heißt Standardabweichung und ist gegeben durch:
3
Weitere Aussagen über Erwartungswert und Varianz
Ist X eine Zufallsvariable mit E(X ) = μ und Var(X) = σ2, so besitzt die
standardisierte Zufallsvariable Y =
den Erwartungswert 0 und die Varianz 1.
Sind X1, …, Xn unabhängige Zufallsvariablen mit E(Xi) = μ und Var(Xi) = σ2 für alle i = 1,…,n,
so besitzt die Zufallsvariable
den Erwartungswert μ und die Varianz
Insbesondere gilt dies, wenn die Zufallsvariablen X1,…, Xn unabhängige Wiederholungen
derselben Zufallsvariablen darstellen; Xn wird dann als Stichprobenmittel bezeichnet.
Ungleichungvon Tschebyscheff
Mithilfe der Varianz die Wahrscheinlichkeit abschätzen, dass eine Zufallsvariable X um
mindestens den Wert c von ihrem Erwartungswert abweicht. (Ohne Kenntnis der Verteilung
von X.)
Analogien zwischen Häufigkeitsverteilungen und Wahrscheinlichkeitsverteilungen
4
Wichtige Verteilungen im Überblick
Wahrschein
-lichkeitsverteilunge
n
Binomialverteilung
B (n,p)
Normalverteilung
N (μ, σ)
Gleichverteilung
in [a;b] mit a<b
Exponentialverteilung
mit dem Parameter λ
Dichtefunktion
Bild Dichtefunktion
E(X)
Var(X)
Beispiel
5
6