1 Sinus und Kosinus
Werbung
Ingo Blechschmidt, 10C
1 SINUS UND KOSINUS
1
y
1
P(x; y)
y
1
−1
x
1 x
−1
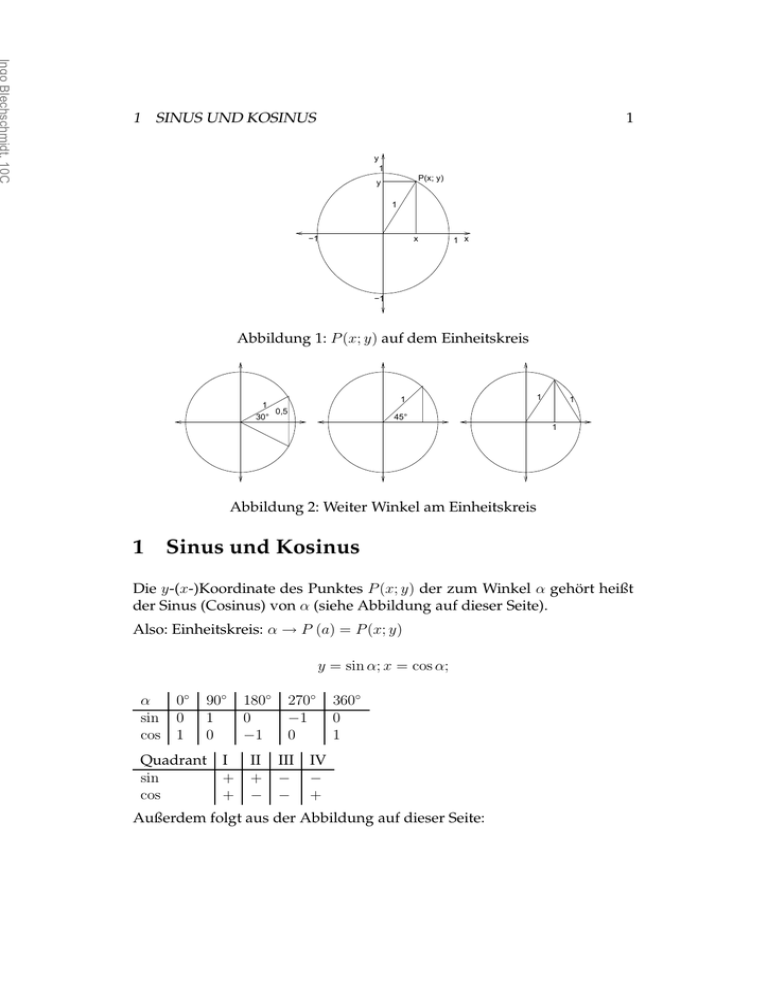
Abbildung 1: P (x; y) auf dem Einheitskreis
1
30°
1
0,5
1
1
45°
1
Abbildung 2: Weiter Winkel am Einheitskreis
1 Sinus und Kosinus
Die y-(x-)Koordinate des Punktes P (x; y) der zum Winkel α gehört heißt
der Sinus (Cosinus) von α (siehe Abbildung auf dieser Seite).
Also: Einheitskreis: α → P (a) = P (x; y)
y = sin α; x = cos α;
α
sin
cos
0◦
0
1
90◦
1
0
Quadrant
sin
cos
I
+
+
180◦
0
−1
II
+
−
270◦
−1
0
III
−
−
360◦
0
1
IV
−
+
Außerdem folgt aus der Abbildung auf dieser Seite:
Ingo Blechschmidt, 10C
1 SINUS UND KOSINUS
α
sin
cos
30◦
45◦
1
2√
1
3
2
√1
2
√1
2
2
60√◦
1
3
2
1
2
1.1 Winkel größer als 90◦
• II. Quadrant: sin(180◦ − α) = sin(α); cos(180◦ − α) = − cos(α);
• III. Quadrant: sin(180◦ + α) = − sin(α); cos(180◦ + α) = − cos(α);
• IV. Quadrant: sin(360◦ − α) = − sin(α); cos(360◦ − α) = cos(α);
(Private Ergänzung:
• II: α → 180◦ − α (+/-)
• III: α → α − 180◦ (-/-)
• IV: α → 360◦ − α (-/+)
)
1.2 Negative Winkel
sin(−α) = − sin(α); cos(−α) = cos(α);
1.3 Winkel größer als 360◦
sin(α + k · 360◦ ) = sin(α); cos(α + k · 360◦ ) = cos(α);
Sinus und Kosinus haben die Periode 360◦ .
1.4 Zusammenhang zwischen dem Sinus und dem Kosinus gleicher Winkel
sin2 α + cos2 α = 1
Ingo Blechschmidt, 10C
1 SINUS UND KOSINUS
3
Beispiel: α ∈ [180◦ ; 360◦ ] und sin α = −0, 6 Berechne cos α (ohne α auszurechnen).
sin2 α + cos2 α
(−0, 6)2 + cos2 α
cos2 α
cos α
=⇒
=
=
=
=
1
1
0, 84
±0, 8
= {−0, 8; 0, 8}
1.5 Komplementärwinkel
sin (90◦ − α) = cos α; cos (90◦ − α) = sin α; 0◦ ≤ α ≤ 90◦
1.6 Berechnungen im rechtwinkligen Dreieck
Im rechtwinkligen Dreieck gilt:
sin α =
a
b
=
Gegenkathete
;
Hypothenuse
cos α =
c
b
=
Ankathete
;
Hypothenuse











