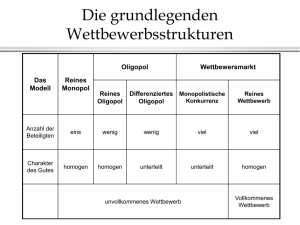
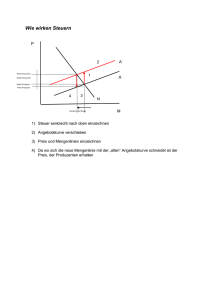
Handout Uebung 13

Übung zu Mikro III (SS 04)
Tri Vi Dang
Handout zu Übung 13
Vorbemerkung:
Hinweise auf Fehler sind willkommen.
Keine Gewähr für die vollständige Richtigkeit der Ausführungen.
Thema: Preisdifferenzierung
Aufgabe 4.4
Spieler
1 Firma bietet ein Produkt an
2 Typen von Konsumenten
10 Konsument P
10 Konsument S
Spielstruktur und Strategien
Stufe 1 :
Stufe 2 :
Firma wählt Preise
Æ
Tarifstruktur (Gi, pi), um Gewinn zu maximieren
Æ
Verschiedene Restriktionen von (Gi, pi) in den Teilaufgaben
Konsumenten treffen Kaufentscheidung
Æ
Kein Kauf, Kauf
Æ
Falls Kauf, dann Kaufmenge
Nutzenfunktion
Firmen :
Æ
Gewinnmaximierung bei MC=0 und keine Fixkosten
1
Konsument
Zahlungsbereitschaft (Inverse Nachfrage) von Konsument P
p P = 100 − q P
Zahlungsbereitschaft (inverse Nachfrage) von Konsument S
p S = 80 − q S
Frage 1
Wie hängt diese Aufgabe mit den Aufgaben 4.1 bis 4.3 zusammen?
Antwort 1
Gemeinsamkeit:
Konsumenten haben verschiedene Zahlungsbereitschaften
Unterschiede
Vorher
Konsument kauft eine Einheit.
Firma verlangt einen einheitlichen Preis für alle unabhängig von den Typen der
Konsumenten
Wettbewerb zwischen 2 Firmen
Hier :
Konsumenten können beliebig viele Einheiten kaufen
Firma kann verschiedene Preise von verschiedenen Kunden (bzw. Kundengruppen)
verlagen.
Firma ist Monopolist
2
Frage 2
Welche Möglichkeiten hat die Firma, um die Konsumentenrente abzuschöpfen?
Antwort 2
Preisdifferenzierung (Preisdiskriminierung)
Verschiedene Kunden müssen für gleiche / ähnliche Produkte unterschiedliche Preise
bezahlen.
PD 1. Grades
-
Jeder Kunde bezahlt einen Preis in Höhe seines Reservationsnutzens (maximaler
Zahlungsbereitschaft)
Konsumentenrente wird vollständig abgeschöpft
PD 2. Grades
-
Berechnung unterschiedlicher Preise für verschiedene Mengen
Z.B. Mengenrabatt
PD 3. Grades
-
Berechnung unterschiedlicher Preise für unterschiedliche Nachfragegruppen.
Gruppen haben verschiedene Nachfragefunktionen.
Aufgabe 4.4 a
Frage 3
Was für Preise setzt die Firma, wenn sie Preisdiskriminierung 1. Grades betreibt und
Konsument P und S unterscheiden kann?
Antwort 3
3
Schritt 1
Preis=MC=0
Æ
pP=pS=0
Schritt 2
q P = 100 − p P = 100
q S = 80 − p S = 80
Schritt 3
100
qP
1 

CS P = ∫ (100 −q ) − p P dq = (100 − p P )q − q 2 
2 0

0
1
= 100 ⋅ 100 − 100 2 = 5000
2
qS
80
1 

CS S = ∫ (80 −q) − p S dq = 80q − q 2 
2 0

0
1
= 80 ⋅ 80 − 80 2 = 3200
2
Bemerkung: Graphische Bestimmung kann durchaus schneller gehen.
Schritt 4
G P = CS P = 5000
G S = CS S = 3200
Firma bietet zwei Angebote an.
4
Frage 4
Wie hoch ist die Konsumentenrente und die Wohlfahrt?
Antwort 4
CSP=5000−GP=0,
(pro Konsument P)
CSS=3200−GS=0,
(pro Konsument S)
PS=10⋅GP+10⋅GS=10⋅5000+10⋅3200=82000
10
10
i =1
i =1
W = ∑ CS Pi + ∑ CSSi + PS = 82000
Graphische Darstellung
Konsument P
Konsument S
p
100
80
100
q
80
Frage 5
Gibt es noch eine andere Preisstrategie?
Antwort 5
Preise in Abhängigkeit von
Konsumentengruppen UND
bereits konsumierter Menge
5
Für Konsument P
Preis für die erste Einheit
1
1
1 

p P (1) = ∫ (100 −q P )dq P = (100q P − q 2 
2 0

0
1
= 100 − = 99.5
2
D.h. Konsument P zahlt für die erste Einheit einen Preis von pP(1)=99.5.
Preis für die zweite Einheit
2
2
1 

p P (2) = ∫ (100 −q P )dq P = (100q P − q 2 
2 1

1
= (200 − 2) − (100 − 0.5) = 98.5
usw.
Æ
Durch diese Strategie kann man auch die gesamte Konsumentenrente abschöpfen.
Aufgabe 4.4 b
Frage 6
Die Firma kann die Konsumententypen unterscheiden und betreibt Preisdiskriminierung 3.
Grades. Welchen Preis müssen Konsument P und S bezahlen und wie viel wird nachgefragt?
Antwort 6
6
(Schritt 1)
Konsument P
Æ
Konsument S
q P1 = 100 − p P1
q S1 = 100 − p S1
q P2 = 100 − p P2
q S2 = 100 − p S2
M
q P10 = 100 − p P10
_______________
M
q S10 = 100 − p S10
_______________
Q P = 1000 − 10p P
Q S = 800 − 10p S
p P = 100 −
1
QP
10
p S = 80 −
1
QS
10
Schritt 2
π S = p S (Q S ) ⋅ Q S
π P = p P (Q P ) ⋅ Q P
mit
p P = 100 −


1
QP
10
π P = 100 −
p S = 80 −


1

QP  ⋅ QP
10

1
QS
10
π S =  80 −
1

QS  ⋅ QS
10

dπ P
1
= 100 − Q P − 0{ = 0
dp P 142543 MC
dπ S
1
= 80 − Q P = 400
5
dp S
Æ
Q P = 500
Æ
Q S = 400
Æ
p P = 50
Æ
p S = 40
MR P
7
Alternative 2
Schritt 2
π P = Q P (p P ) ⋅ p P
π S = Q S (p S ) ⋅ p S
π P = (1000 − 10p P ) ⋅ p P
π S = (800 − 10p S ) ⋅ p S
dπ P
= 1000 − 20p P = 0
dp P
dπ S
= 800 − 20p P = 0
dp S
Æ
p P = 50
Æ
p S = 40
Æ
Q P = 500
Æ
Q S = 400
Bemerkung: Wenn es positive Kosten (MC) gibt, dann muss man bei der Maximierung
über Preise die Kostenfunktion als Funktion von p darstellen, d.h. K(Q(p)).
Frage 7
Wie hoch sind Konsumentenrenten und Wohlfahrt?
Antwort 7
Konsument P kauft q P = 100 − p P = 50 Einheiten
Jeder Konsument P
50
qP
1 

CS P = ∫ (100 −q) − p P dq = (100 − 50)q − q 2 
2 0

0
1
= 50 ⋅ 50 − 50 2 = 1250
2
∑ CS
P
= 10 ⋅ 1250 = 12500
Alternative Rechnung
Aus Q P = 1000 − 10p P folgt p P (Q P ) = 100 −
QP
∑ CS P = ∫ (100 −
0
= 50 ⋅ 500 −
1
QP
10
500
1
1 

Q) − p P dQ = (100 − 50)Q − Q 2 
10
5 0

1
⋅ 500 2 = 12500
5
8
Jeder Konsument S kauft 40 Einheiten
40
qS
1 

CS S = ∫ (80 −q) − p S dq = 40q − q 2 
2 0

0
1
= 40 ⋅ 40 − 40 2 = 800
2
∑ CS
S
= 10 ⋅ 800 = 8000
Gewinn / Produzentenrente
PS=500⋅pP+400⋅pS=500⋅50+400⋅40=41000
Wohlfahrt
W = ∑ CS P + ∑ CS S + PS = 61500
Graphische Darstellung
Konsument P
Konsument S
p
100
80
50
40
MR
MB
50
100
q
40
9
80
Frage 8
Warum ist die Wohlfahrt bei Preisdiskriminierung 3. Grades niedriger als die Wohlfahrt bei
Preisdiskriminierung 1. Grades?
Antwort 8
Preisdiskriminierung 3. Grades
Standard-Monopol-Problem
Preisdiskriminierung 1. Grades
Preis=MC
(wie beim vollkommenen Wettberwerb)
Aufgabe 4.4 c
Frage 9
Preisdiskriminierung ist nicht möglich, weil die Firma die Konsumententypen nicht
unterscheiden kann. Welchen (einheitlichen) Preis wählt der Monopolist?
Antwort 9
10
Schritt 1
Q P = 1000 − 10p P
Q S = 800 − 10p S
_____________
Q = 1800 − 20p
1800 − 20p
Q=
1000 − 10p
1

90 − 20 Q
p=
100 − 1 p

10
für p ≤ 80
für p > 80
für Q ≥ 800
für Q < 800
Schritt 2
1

90 − 10 Q
MR = 
100 − 1 p

5
für Q ≥ 800
für Q < 800
MR=MC
1
Q=0
10
⇔
90 −
⇔
Q=900
Gewinnmaximum ist im zulässigen Bereich.
Ansonsten Gewinnmaximierung nur über die Gruppe mit höherer Zahlungsbereitschaft.
Alternative 2
π = Q( p) ⋅ p
π = (1800 − 20p ) ⋅ p
dπ
= 1800 − 40p P = 0
dp
Æ
p = 45
Optimaler Preis ist im zulässigen Bereich.
11
Schritt 3
Gewinnmaximaler Preis :
p = 90 −
1
Q = 45
20
Nachfrage von P
Jeder Konsument P kauft q P = 100 − p = 55
Nachfrage von S
Jeder Konsument P kauft q S = 80 − p = 35
Frage 10
Wie hoch sind Konsumentenrenten und Wohlfahrt?
Antwort 10
Konsumentenrente von P-Typen
55
qP
1 

CS P = ∫ (100 −q ) − pdq = 100q − 45q − q 2 
2 0

0
1
= 55 ⋅ 55 − 55 2 = 1512.5
2
Æ
∑ CS
P
= 10 ⋅151.25 = 15125
Konsumentenrente von S-Typen
35
q
S
1 

CSS = ∫ (80 −q ) − pdq = 35q − q 2 
2 0

0
1
= 35 ⋅ 35 − 35 2 = 612.5
2
Æ
∑ CS
S
= 10 ⋅ 612.5 = 6125
Gewinn / Produzentenrente
PS=(550+350)⋅p=900⋅45=40500
Wohlfahrt
W = ∑ CS P + ∑ CSS + PS = 61750
12
Graphische Darstellung
1 P-Typ und 1 S-Typ
Preis
100
80
MBGesamt
60
20
90
180
Menge
Bemerkung: Bei jeweils 10 Konsumenten pro Typ q-Werte mit 10 multiplizieren.
Bemerkung: Wenn es steigende MC gibt, dann löst man ein Gleichungssystem.
Aufgabe 4.4 d
Frage 11
Wie hoch sind Konsumentenrenten und Wohlfahrt, wenn der Monopolist einen Preis verlangt,
der sich auf einem Markt mit vollkommenen Wettbewerb etablieren würde?
Antwort 11
Vollkommener Wettbewerb
Preis = MC=0
Implikationen für Konsumentenrente und Wohlfahrt siehe Antworten zu Aufgabe (a) mit dem
einzigen Unterschied, dass es hier keine fixe Gebühr gibt.
13
Frage 12
Was kann man zusammenfassend sagen?
Antwort 12
(a)
(b)
(c)
(d)
pP
0
50
45
0
pS
0
40
45
0
GP
5000
-
GS
3200
-
∑q
P
∑q
1000
500
550
1000
S
800
400
350
800
∑ CS ∑ CS
P
S
0
12500
15125
50000
0
8000
6125
32000
PS
82000
41000
40500
0
W
82000
61500
61750
82000
Vergleich von (b) und (c)
Gewinn der Firma mit Preisdiskriminierung (b) ist größer als in (c)
In (c) Falls es keine Preisdiskriminierung gibt, ist die aggregierte Nachfrage der zwei Typen
relevant.
Abwägung zwischen hohem Preis mit niedriger Menge (verlieren Kunden mit
niedriger Zahlungsbereitschaft) und niedrigem Preis (kann höhere
Zahlungsbereitschaft einiger Kunden nicht abschöpfen) und größerer
Gesamtnachfrage.
In (b) Dieser Trade-off wird abgeschwächt durch Preisdiskriminierung.
CS der P-Typen ohne Preisdiskriminierung ist höher.
Sie zahlen weniger UND konsumieren mehr.
CS der S-Typen ohne Preisdiskriminierung ist niedriger.
Sie zahlen mehr UND konsumieren weniger.
Wohlfahrt in (c) ist höher als in (b)
In dem Beispiel: Zunahme von
∑ CS
P
ist stärker als die Abnahme von
14
∑ CS
S
und PS.