amwen_3 - Strahlensatz

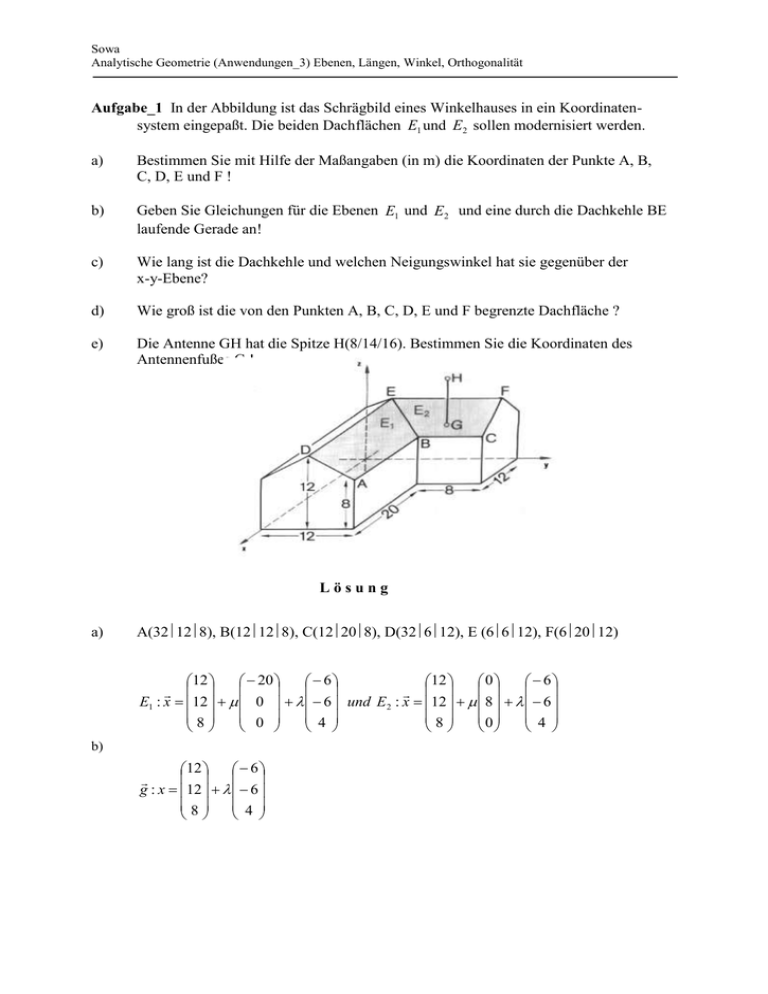
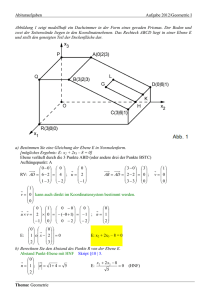
Sowa
Analytische Geometrie (Anwendungen_3) Ebenen, Längen, Winkel, Orthogonalität
Aufgabe_1 In der Abbildung ist das Schrägbild eines Winkelhauses in ein Koordinatensystem eingepaßt. Die beiden Dachflächen E1 und E2 sollen modernisiert werden.
a)
Bestimmen Sie mit Hilfe der Maßangaben (in m) die Koordinaten der Punkte A, B,
C, D, E und F !
b)
Geben Sie Gleichungen für die Ebenen E1 und E2 und eine durch die Dachkehle BE
laufende Gerade an!
c)
Wie lang ist die Dachkehle und welchen Neigungswinkel hat sie gegenüber der
x-y-Ebene?
d)
Wie groß ist die von den Punkten A, B, C, D, E und F begrenzte Dachfläche ?
e)
Die Antenne GH hat die Spitze H(8/14/16). Bestimmen Sie die Koordinaten des
Antennenfußes G !
Lösung
a)
A(32128), B(12128), C(12208), D(32612), E (6612), F(62012)
12 
  20 
  6
12 
 0
  6


 
 
 
  
  
E1 : x  12     0      6  und E2 : x  12     8      6 
8
 0 
 4 
8
 0
 4 
 


 
 
 
 
b)
12    6 
   

g : x  12      6 
8  4 
   
Sowa
Analytische Geometrie (Anwendungen_3) Ebenen, Längen, Winkel, Orthogonalität
c)
EB 
(6) 2  (6) 2  4 2  88  9,38 m
und
cos(  ) =
  12    6 

  
  12  *   6 
 0   4 

  
= 0,9
288 * 88
 = 25,23°
d)
Elementar aus der Zeichnung lösbar: 144,2 m² +21,6 m² + 21,6 m² + 57,6 m² = 245 m²
e)
Über Schnittpunkt Ebene/Gerade oder elementar mit Strahlensatz lösbar. Die erste und zweite
Koordinate von G sind aus H(8/14/16) übertragbar, also G(8/14/?). Es muss nur noch die
z-Koordinate berechnet werden. Lösung: G(8/14/10,66)