Division komplexer Zahlen

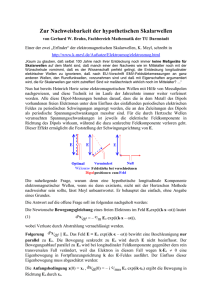
Division komplexer Zahlen
Der Quotient z1 /z2 zweier komplexer Zahlen
zk = xk + iyk = rk exp(iϕk )
ist
r1
x1 x2 + y1 y2 x2 y1 − x1 y2
+
i = exp(i(ϕ1 − ϕ2 )) .
2
2
2
2
r2
x2 + y2
x2 + y2
Speziell ist
1
1
1
x
y
= 2 z̄ = exp(−iϕ) = 2 − 2 i .
z
r
r
r
r
Division komplexer Zahlen
1-1
Division komplexer Zahlen
Der Quotient z1 /z2 zweier komplexer Zahlen
zk = xk + iyk = rk exp(iϕk )
ist
r1
x1 x2 + y1 y2 x2 y1 − x1 y2
+
i = exp(i(ϕ1 − ϕ2 )) .
2
2
2
2
r2
x2 + y2
x2 + y2
Speziell ist
1
1
1
x
y
= 2 z̄ = exp(−iϕ) = 2 − 2 i .
z
r
r
r
r
Der Kehrwert einer komplexen Zahl läßt sich durch Spiegelung am
Einheitskreis C konstruieren, wie in der Abbildung veranschaulicht ist.
Division komplexer Zahlen
1-2
1 v
z
w
z/2
0
1/z
Die komplex konjugierte Zahl w = 1/z̄ ist der Schnittpunkt der
Diagonalen des Vierecks aus den Tangenten an C durch den Punkt z und
den rechtwinklig schneidenden Radii. Die Zahl 1/z erhält man dann durch
Spiegelung an der reellen Achse.
Division komplexer Zahlen
1-3
Beweis:
(i) Quotient zweier komplexer Zahlen:
Division komplexer Zahlen
2-1
Beweis:
(i) Quotient zweier komplexer Zahlen:
zk = xk + iyk = rk exp(iϕk ),
k = 1, 2
Division komplexer Zahlen
2-2
Beweis:
(i) Quotient zweier komplexer Zahlen:
zk = xk + iyk = rk exp(iϕk ),
k = 1, 2
Standardform
z1
z2
=
=
x1 + iy1
(x1 + iy1 )(x2 − iy2 )
=
x2 + iy2
(x2 + iy2 )(x2 − iy2 )
(x1 x2 + y1 y2 ) + (x2 y1 − x1 y2 )i
x22 + y22
Division komplexer Zahlen
2-3
Beweis:
(i) Quotient zweier komplexer Zahlen:
zk = xk + iyk = rk exp(iϕk ),
k = 1, 2
Standardform
z1
z2
=
=
Polarform
x1 + iy1
(x1 + iy1 )(x2 − iy2 )
=
x2 + iy2
(x2 + iy2 )(x2 − iy2 )
(x1 x2 + y1 y2 ) + (x2 y1 − x1 y2 )i
x22 + y22
z1
r1 exp(iϕ1 )
r1
=
= exp(iϕ1 − iϕ2 )
z2
r2 exp(iϕ2 )
r2
Division komplexer Zahlen
2-4
(ii) Kehrwert:
Division komplexer Zahlen
2-5
(ii) Kehrwert:
1
z
=
=
1
x − iy
=
x + iy
(x + iy )(x − iy )
z̄
z̄
1
= 2 = exp(−iϕ)
2
2
x +y
r
r
Division komplexer Zahlen
2-6
(ii) Kehrwert:
1
z
=
=
1
x − iy
=
x + iy
(x + iy )(x − iy )
z̄
z̄
1
= 2 = exp(−iϕ)
2
2
x +y
r
r
(iii) Geometrische Konstruktion mit Hilfe des Satzes von Pythagoras:
|w | |z| = 12
(Quadrat einer Kathete = Produkt von Hypothenuse und entsprechendem
Hypothenusenabschnitt)
Division komplexer Zahlen
2-7
(ii) Kehrwert:
1
z
=
=
1
x − iy
=
x + iy
(x + iy )(x − iy )
z̄
z̄
1
= 2 = exp(−iϕ)
2
2
x +y
r
r
(iii) Geometrische Konstruktion mit Hilfe des Satzes von Pythagoras:
|w | |z| = 12
(Quadrat einer Kathete = Produkt von Hypothenuse und entsprechendem
Hypothenusenabschnitt)
korrekter Betrag von w = 1/z̄:
|w̄ | = |w | = 1/|z| = |1/z|
Division komplexer Zahlen
2-8
(ii) Kehrwert:
1
z
=
=
1
x − iy
=
x + iy
(x + iy )(x − iy )
z̄
z̄
1
= 2 = exp(−iϕ)
2
2
x +y
r
r
(iii) Geometrische Konstruktion mit Hilfe des Satzes von Pythagoras:
|w | |z| = 12
(Quadrat einer Kathete = Produkt von Hypothenuse und entsprechendem
Hypothenusenabschnitt)
korrekter Betrag von w = 1/z̄:
|w̄ | = |w | = 1/|z| = |1/z|
Spiegelung an der reellen Achse
Änderung des Vorzeichen des
Arguments:
arg w̄ = − arg w = − arg z = arg(1/z)
Division komplexer Zahlen
2-9
Beispiel:
(1 +
√
3i) + 2 exp(−iπ/6)
exp(iπ/2)(1 − i)
Division komplexer Zahlen
3-1
Beispiel:
√
3i) + 2 exp(−iπ/6)
exp(iπ/2)(1 − i)
Summe im Zähler in Standardform:
√
√
√
√
(1 + 3i) + 2
3/2 − i/2 = (1 + 3) + ( 3 − 1)i
(1 +
Division komplexer Zahlen
3-2
Beispiel:
√
3i) + 2 exp(−iπ/6)
exp(iπ/2)(1 − i)
Summe im Zähler in Standardform:
√
√
√
√
(1 + 3i) + 2
3/2 − i/2 = (1 + 3) + ( 3 − 1)i
(1 +
Produkt im Nenner in Polarform:
√
√
exp(iπ/2) · 2 exp(−iπ/4) = 2 exp(iπ/4) = 1 + i
Division komplexer Zahlen
3-3
Beispiel:
√
3i) + 2 exp(−iπ/6)
exp(iπ/2)(1 − i)
Summe im Zähler in Standardform:
√
√
√
√
(1 + 3i) + 2
3/2 − i/2 = (1 + 3) + ( 3 − 1)i
(1 +
Produkt im Nenner in Polarform:
√
√
exp(iπ/2) · 2 exp(−iπ/4) = 2 exp(iπ/4) = 1 + i
Quotient, erweitert mit (1 − i)
√
√
√
((1 + 3) + ( 3 − 1)i)(1 − i)
2 3 − 2i
=
= 2 exp(−iπ/6)
(1 + i)(1 − i)
2
bzw. in Standardform
2(cos(π/6) − i sin(π/6)) =
√
3−i
Division komplexer Zahlen
3-4
Beispiel:
Spannung und Stromstärke bei linearen Wechselstromnetzwerken
U(t) = U0 e i(ωt+ϕ) ,
I (t) = I0 e i(ωt+ψ)
Division komplexer Zahlen
4-1
Beispiel:
Spannung und Stromstärke bei linearen Wechselstromnetzwerken
U(t) = U0 e i(ωt+ϕ) ,
I (t) = I0 e i(ωt+ψ)
zeitunabhängiger komplexer Widerstand
Z = U(t)/I (t)
Division komplexer Zahlen
4-2
Beispiel:
Spannung und Stromstärke bei linearen Wechselstromnetzwerken
U(t) = U0 e i(ωt+ϕ) ,
I (t) = I0 e i(ωt+ψ)
zeitunabhängiger komplexer Widerstand
Z = U(t)/I (t)
Widerstand R
Spule L
Kondensator C
Z =R
Z = iωL
Z = (iωC )−1
Division komplexer Zahlen
4-3
Addition der komplexen Widerstände bei Serienschaltung:
Zgesamt = Z1 + Z2
Division komplexer Zahlen
4-4
Addition der komplexen Widerstände bei Serienschaltung:
Zgesamt = Z1 + Z2
Addition der Kehrwerte der komplexen Widerstände bei Parallelschaltung:
1
Zgesamt
=
1
1
+
Z1 Z2
⇒
Zgesamt =
Z1 Z2
Z1 + Z2
Division komplexer Zahlen
4-5
Addition der komplexen Widerstände bei Serienschaltung:
Zgesamt = Z1 + Z2
Addition der Kehrwerte der komplexen Widerstände bei Parallelschaltung:
1
Zgesamt
=
Re Z : Wirkwiderstand,
oder Impedanz
1
1
+
Z1 Z2
⇒
Zgesamt =
Im Z : Blindwiderstand,
Z1 Z2
Z1 + Z2
|Z |: Scheinwiderstand
Division komplexer Zahlen
4-6
Addition der komplexen Widerstände bei Serienschaltung:
Zgesamt = Z1 + Z2
Addition der Kehrwerte der komplexen Widerstände bei Parallelschaltung:
1
Zgesamt
=
Re Z : Wirkwiderstand,
oder Impedanz
1
1
+
Z1 Z2
⇒
Zgesamt =
Im Z : Blindwiderstand,
Z1 Z2
Z1 + Z2
|Z |: Scheinwiderstand
ωL = 100Ω
(ωC)−1 = 200Ω
R = 300Ω
Division komplexer Zahlen
4-7
Gesamtwiderstand
R(iωC )−1
300Ω(−200iΩ)
Zgesamt = iωL +
= 100iΩ +
R + (iωC )−1
300Ω − 200iΩ
1200 − 500i
6i
· 100Ω =
Ω ≈ (92.31 − 38.46i)Ω
=
i−
3 − 2i
13
Division komplexer Zahlen
4-8
Gesamtwiderstand
R(iωC )−1
300Ω(−200iΩ)
Zgesamt = iωL +
= 100iΩ +
R + (iωC )−1
300Ω − 200iΩ
1200 − 500i
6i
· 100Ω =
Ω ≈ (92.31 − 38.46i)Ω
=
i−
3 − 2i
13
Wechselspannung von Ueffektiv = 220V
Ieffektiv =
Effektivstrom
220V
Ueffektiv
=
= 2.2A
|Z |
100Ω
Division komplexer Zahlen
4-9