2. Potentialströmungen

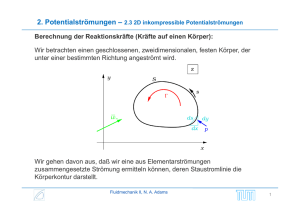
2. Potentialströmungen – 2.3 2D inkompressible Potentialströmungen
Zur Untersuchung zweidimensionaler Strömungen treffen wir folgende
Vereinbarungen:
1. Vereinfachung der Nomenklatur:
x1  x
x2  y
u1  u
u2  v
u
2
 u2  v2  q2
2. Einheitsbreite in x3
Zweidimensionale inkompressible Strömungen (nicht nur Potentialströmungen)
können vollständig durch die Stromfunktion  x, y beschrieben werden.


Die Stromfunktion wird definiert durch:


u,
 v
y
x
Fluidmechanik II, N. A. Adams
(2.4)
1
2. Potentialströmungen – 2.3 2D inkompressible Potentialströmungen
Mit der Stromfunktion wird die Kontinuitätsgleichung für inkompressible
Strömungen exakt erfüllt:
u v  2  2
u 



0
x y yx xy
Eigenschaften der Stromfunktion:
1. Linien
2.
  x, y   const
sind Stromlinien
dx dy


dx 
dy  0 
  x, y   const  d   0 

u
v
x
y
Die Differenz von  auf zwei Stromlinien S1 und S2 entspricht dem
Volumenfluß zwischen diesen Stromlinien.
Fluidmechanik II, N. A. Adams
2
2. Potentialströmungen – 2.3 2D inkompressible Potentialströmungen
Box 21: Stromfunktion
Fluidmechanik II, N. A. Adams
3
2. Potentialströmungen – 2.3 2D inkompressible Potentialströmungen
Linien mit konstanter Potentialfunktion
Potentiallinien.
  x, y 
bezeichnet man als
dx
dy


  x, y   const  d   0  dx  dy  0 

v
u
x
y
Potential- und Stromlinien bilden orthogonale Kurvenscharen:
  
   

 uv  uv  0
x x y y
Zwischen Potential und Stromfunktion
gelten die sogenannten Cauchy-RiemannDifferentialgleichungen:
 




u
, v
x y
y
x
(2.5)
Fluidmechanik II, N. A. Adams
4
2. Potentialströmungen – 2.3 2D inkompressible Potentialströmungen
Oft ist eine Darstellung zweidimensionaler Potentialströmungen in
Polarkoordinaten zweckmäßig.
Für die Transformation der Geschwindigkeit zwischen kartesischen und polaren
Koordinaten gilt folgende Vorschrift:
ur ,
 ur 
 cos  sin   u 
  
 v 
u



sin
cos
 
   r , 
Fluidmechanik II, N. A. Adams
(2.6)
5
2. Potentialströmungen – 2.3 2D inkompressible Potentialströmungen
Die Ableitungen der Potentialfunktion nach Polarkoordinaten lassen sich wie
folgt ermitteln:
Mi
x  r cos  und y  r sin  erhält man
  x  y


 u cos   v sin   ur
r x r y r
  x  y


 u r sin   v r cos   r u
 x  y 
Damit auch in Polarkoordinaten Strom- und Potentiallinien orthogonal sind, muß
man also fordern
  1  1 
  

0
r r r  r 

1 
 ur
 u
0
r
r 
Fluidmechanik II, N. A. Adams
6
2. Potentialströmungen – 2.3 2D inkompressible Potentialströmungen
In Polarkoordinaten gilt also folgender Zusammenhang zwischen
Geschwindigkeit, Potentialfunktion und Stromfunktion:
 1 

ur 
r r 

1 
u 

r 
r
Fluidmechanik II, N. A. Adams
(2.7)
7
2. Potentialströmungen – 2.3 2D inkompressible Potentialströmungen
Zusammenfassung einiger für das Weitere wichtigen Fakten aus der komplexen
Analysis (Funktionentheorie):
Komplexe Zahlen sind nichts anderes als eine spezielle Platzhalternotation für
eine zwei-komponentige Vektordarstellung.
Es zeigt sich, daß mit dieser Platzhalternotation viele Operation aus der reellen
Analysis direkt auf die komplexe Analysis übertragbar sind.
Darstellung von komplexen Zahlen  
x  iy x, y   , wobei
Fluidmechanik II, N. A. Adams
i  1
8
2. Potentialströmungen – 2.3 2D inkompressible Potentialströmungen
Darstellung in:
Kartesischen Koordinaten
x, y  
z  x  iy
Re  z   x
Im  z   y
Polarkoordinaten
r, 
z  r ei
r  z  x2  y2
y
  atan  arg  z 
x
Eulersche Relation:
ei  cos   i sin 
ei  1
Fluidmechanik II, N. A. Adams
9
2. Potentialströmungen – 2.3 2D inkompressible Potentialströmungen
Das konjugiert Komplexe z einer komplexen Zahl z erhält man durch
Spiegelung an der reellen Achse:
z  x  iy  r e-i
Damit gilt für den Betrag einer komplexen Zahl z z  z
und für das Inverse einer komplexen Zahl
2
 r2
1
1
1
z
z
 i  2 z  2 
z re
r
zz
z
Eine Funktion f  z   f R  x, y   if I  x, y  ist analytisch, wenn f R und f I stetig
differenzierbar sind und die Cauchy-Riemann-Differentialgleichungen erfüllen:
f R f I

x y
f R
f
 I
y
x
Fluidmechanik II, N. A. Adams
10
2. Potentialströmungen – 2.3 2D inkompressible Potentialströmungen
Eine Funktion f
z
ist konform, wenn sie analytisch ist und außerdem
f   z   0 ist. Die Abbildung z  z'  f  z  ist dann winkeltreu:
Wichtige Elementarfunktionen:
1. Exponentialfunktion
e z  e x iy  e x eiy
eiz  e-iz
2. Trigonometrische Funktionen cos z 
2
3. Logarithmus
eiz  e-iz
sin z 
2i
ln z  ln  rei   ln r  i  z  i arg  z   i2k
Hauptzweig: k
 0 , k-ter Nebenzweig k  0
Fluidmechanik II, N. A. Adams
11
2. Potentialströmungen – 2.3 2D inkompressible Potentialströmungen
Komplexe Differentiation:
f  z  f  z 
Eine komplexe Funktion ist differenzierbar, wenn f   z   lim
z  z
z  z

unabhängig vom Weg der Annäherung z  z existiert.
Verallgemeinerung der Taylorreihe:
Jede auf einem Kreisring konvergente Laurentreihe
eine analytische Funktion dar.
Fluidmechanik II, N. A. Adams
f z 

a z
n 
n
n
stellt dort
12
2. Potentialströmungen – 2.3 2D inkompressible Potentialströmungen
Komplexe Integration:
f  z  analytisch auf einem Gebiet A bis auf isolierte Singularitäten (Punkte
z , in denen f  z  nicht definiert ist) und trifft bzw. umläuft der Integrationsweg
S keine Singularität, dann ist das Integral wegunabhängig
Ist
b
 f  z  dz   f  z  dz   f  z  dz  ...   f  z  dz  F  b   F  a 
S
S1
S
2
dF
wobei F   z  
 f z
dz
a
Fluidmechanik II, N. A. Adams
13
2. Potentialströmungen – 2.3 2D inkompressible Potentialströmungen
Komplexe Integration:
Umläuft oder trifft ein geschlossener Integrationsweg
Singularitäten, dann ist
S , der ganz in A liegt,
 f  z  dz  2i   p  Res f  z 
s
S
p
p
Hierin ist:
p : Index der Singularität in A
 s  p  : Umlaufzahl dieser Singularität
Res f  z p  : Residuum von f in z p
Fluidmechanik II, N. A. Adams
14
2. Potentialströmungen – 2.3 2D inkompressible Potentialströmungen
Box 22: Integration
Fluidmechanik II, N. A. Adams
15
2. Potentialströmungen – 2.3 2D inkompressible Potentialströmungen
Box 23: Integration
Fluidmechanik II, N. A. Adams
16
2. Potentialströmungen
• Welche Beziehung wird durch den Ansatz einer Stromfunktion exakt
erfüllt ?
• Wie kann man für 2D Strömungen den Volumenstrom zwischen zwei
Stromlinien durch die Stromfunktion ausdrücken ?
• Welche Beziehung besteht zwischen Stromlinien und Potentiallinien ?
• Was versteht man unter einer analytischen Funktion und was unter
einer konformen Abbildung ?
Fluidmechanik II, N. A. Adams
17