7.1pdf

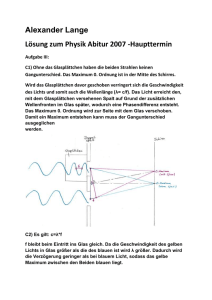
Kapitel 7
Einführung in der Quantenmechanik
7.1
Grenzen der klassischen Physik
In unserer bisherigen Betrachtung der Physik haben wir immer eine klare Abgrenzung zwischen Wellenphänomenen und Teilchenphänomenen ziehen können. Beispielsweise waren
wir in der Lage alle Eigenschaften von Licht im Rahmen einer Wellentheorie zu deuten.
Auf der anderen Seite konnten wir in der Mechanik und Thermodynamik die Eigenschaften von Atomen, Molekülen und anderen Körpern stets als Teilchenphänomene erklären.
Gegen Ende des 19. Jahrhunderts und auch am Anfang des 20. Jahrhunderts wurde in
der Physik eine Reihe wichtiger Experimente durchgeführt, die nicht im Einklang mit der
damals existierenden Theorie zu bringen waren. Zusammen mit der Entwicklung einiger
neuer theoretischer Konzepte stellen diese Experimente die Geburtsstunde der Quantenphysik dar.
Zielsetzung dieses Abschnitts ist sowohl die Vorstellung dieser historisch wichtigen Entwicklungen als auch die Betrachtung einiger späteren Experimente, die die Grenzen der
klassischen Physik klar darstellen. Insbesondere werden wir Experimente diskutiern, die
- die Teilchen Eigenschaften des Lichts,
- der Wellencharakter von Teilchen, und
- die Quantisierung physikalischer Größen darstellen.
7.1.1
Der Fotoeffekt
Der Fotoeffekt wurde von Heinrich Hertz 1887 im Rahmen seiner Untersuchungen zur
Ausbreitung elektromagnetischer Strahlung gefunden. Wenn metallische Platten mit Licht
bestrahlt werden, können Elektronen1 emittiert werden. Die Emission einer positiven Ladung wird dabei niemals beobachtet. Die Emission findet erst statt, wenn die Frequenz
ν der elektromagnetischen Strahlung eine kritische Frequenz νo überschreitet. Diese kritische Frequenz ist Metall spezifisch, z.B. für Lithium beträgt sie νo = 5.7 × 1014 Hz
entsprechend einer Wellenlänge von λ = 526 nm (grünes Licht). Der emittierte Strom ist
1
Der Beweis für die Emission von Elektronen kam natürlich erst später mit der Entdeckung des
Elektrons durch J.J. Thomson im Jahr 1897, der erstmals das Verhältnis e/m für die emittierte negative
Ladung bestimmt hat.
1
2
KAPITEL 7. EINFÜHRUNG IN DER QUANTENMECHANIK
Abbildung 7.1: Das Stopping Potential wird in Abhängigkeit der Frequenz qualitativ dargestellt (aus Gasiorowicz: Quantum Physics“).
”
direkt proportional zur Intensität des eingestrahlten Lichts. Andererseits ist die Energie
der emittierten Fotoelektronen nicht von der Intensität des Lichts abhängig, sondern von
der Frequenz des eingestrahlten Lichts.
Um dieses Phänomen zu eklären, führte Einstein 1905 den radikalen Vorschlag ein, dass
Licht aus einer Ansammlung von sogenannten Quanten besteht. Aus unserer heutigen
Sicht sind diese Quanten mit den Photonen des Lichts zu identifizieren, wobei jedes Photon die Energie hν besitzt. Hier ist die Konstante h = 6.63 × 10−34 Js die Planck’sche
Wirkungskonstante, die Planck zur Klärung der Schwarzkörperstrahlung zuvor eingeführt
hat. Die Energie der elektromagnetischen Welle wird durch die Absorption der Photonen
auf die Materie übertragen. Im Rahmen des Quantenbilds wird die Energie eines Elektrons
im Metall durch die Absorption eines Photons um ∆E = hν erhöht. Um die Bindungsenergie des Elektrons im Metall zu überwinden, muss die sogenannte Austrittsarbeit WA
vorhanden sein. Im Modell von Einstein steht der Rest der Energie in Form kinetischer
Energie des Elektrons zur Verfügung. Somit erhalten wir für die kinetische Energie:
1 2
mv = hν − WA .
2
(7.1)
Eine quantitative Bestimmung der kinetischen Energie erfolgt mittels der Bestimmung des
Stopping“-Potentials. Hierbei wird die notwendige Spannung zur Unterdrückung des Fo”
toeffekts in Abhängigkeit der Frequenz des eingestrahlten Lichts bestimmt, wie in Abb. 7.1
dargestellt. Es wird keine Fotoemission beobachtet, wenn die elektrostatische potentielle
Energie die kinetische Energie exakt kompensiert: eUsp + mv 2 /2 = 0. Erwartungsgemäß
erhalten wir für die Frequenzabhängigkeit des Stopping-Potentials eine mit der Frequenz
lineare Abhängigkeit:
−Usp =
mv 2
h
WA
= ν−
.
2e
e
e
(7.2)
Die Steigung dieser Linie bietet eine Möglichkeit zur direkten Bestimmung der Planck’schen
Wirkungskonstante, und der Schnittpunkt mit der Frequenzachse ohne angelegtes Stoppingpotential liefert die Austrittsarbeit.
7.1. GRENZEN DER KLASSISCHEN PHYSIK
7.1.2
3
Schwarzkörperstrahlung
Unter Schwarzkörperstrahlung verstehen wir den Energieaustausch zwischen einem Körper
und seiner Umgebung, der durch elektromagnetische Strahlung erfolgt. Am deutlichsten
sichtbar wird diese Strahlung bei Körpern mit einer im Vergleich mit ihrer Umgebung
erhöhten Temperatur. Erfahrungsgemäß wissen wir, dass die maximale Frequenz der
Strahlung mit der Temperatur zunimmt. Für die klassische Physik stellte die Berechnung
der Energiedichte für einen Schwarzkörper eine wichtige Frage dar.
Als Idealisierung für einen perfekten Schwarzkörper betrachten wir nun einen Hohlraum,
der Energie mit seiner Umgebung nur durch ein Loch, dessen Abmessung vernachlässigbar klein im Vergleich mit den Abmessungen des Hohlkörpers ist, austauschen kann. Die
aus dem Loch emittierte Strahlung stellt eine exzellente Näherung zur Schwarzkörperstrahlung dar. Im Rahmen einer thermodynamischen Betrachtung haben Rayleigh und
Jeans im Jahr 1900 eine Theorie aufgestellt, bei der die Energiedichte der Strahlung im
Frequenzbereich (ν, ν + δν) gegeben ist durch:
8πν 2
kB T.
(7.3)
c3
Dieses Ergebnis lässt sich am einfachsten verstehen im Rahmen des Gleichverteilungssatzes. Jede elektromagnetische Mode des Hohlraums besitzt zwei Freiheitsgrade2 , die
im Gleichgewicht jeweils die thermische Energie kB T /2 haben. Die Anzahl der Moden im
Hohlraum im Frequenzbereich (ν, ν +δν) kann unter Berücksichtigung der Randbedingungen an den Wänden des Hohlraums berechnet werden, und ist durch 8πν 2 /c3 gegeben3 .
Bei niedrigen Frequenzen ist das Ergebnis von Gleichung (7.3) in guter Übereinstimmung mit den empirischen Daten, allerdings werden bei höheren Frequenzen erhebliche
Abweichungen beobachtet. Die von Gleichung (7.3) vorhergesagte Divergenz bei hohen
Frequenzen findet nicht statt, sondern es wird eine Abnahme der Energiedichte mit der
Frequenz beobachtet.
u(ν, T ) =
Bereits im Jahr 1894 hatte Wien aus einer allgemeinen theoretischen Betrachtung heraus
eine alternative Beschreibung für die Energiedichte im Hohlraum gefunden:
u(ν, T ) ∝ ν 3 f (ν/T ).
(7.4)
Im Rahmen dieses Modells wurde eine Anpassung mit der Funktion (mit den zwei freien
Parametern C und β)f (ν/T ) = C exp (−βν/T ) durchgeführt, und eine exzellente Übereinstimmung bei hohen Frequenzen gefunden. (Bei tiefen Frequenzen liefert das Modell
von Wien allerdings eine kubische Frequenzabhängigkeit).
Im Jahr 1900 fand Planck mittels einer Interpolation zwischen den beiden obigen Modellen
eine Theorie, die die Energiedichte über dem ganzen Spektrum zuverlässig wiedergab
(siehe Abbildung (7.2):4
u(ν, T ) =
2
8πh
ν3
.
c3 exp (hν/kB T ) − 1
(7.5)
Die Moden des Hohlraums werden analog zu den Schwingungen eines harmonischen Oszillators betrachtet: sie besitzen sowohl potentielle als auch kinetische Energie.
3
Bei der Berechnung der Modendichte ist ein Faktor 2 für die zwei verschiedene Polarisationen bereits
berücksichtigt.
4
Für eine elegante Herleitung dieses Ergebnis wird auf Kapitel 4 des Buches Thermal Physics“, von
”
Kittel verwiesen.
4
KAPITEL 7. EINFÜHRUNG IN DER QUANTENMECHANIK
Abbildung 7.2: Die Energiedichte der Schwarzkörperstrahlung wird als Funktion
der normalisierten Frequenz dargestellt (aus Kittel: Thermal Physics“).
”
Um diese korrekte Formulierung zu bekommen, musste Planck annehmen, dass der Austausch der Energie zwischen Hohlraummoden und dem Schwarzkörper quantisiert ist, und
zwar in Einheiten hν. Später zeigte Einstein, dass diese Quantisierung nicht nur für den
Energieaustausch selbst gilt, sondern zwingenderweise auch für die Energie der Photonen
in den Moden des Hohlraums.
Für niedrige Frequenzen, hν kB T , kann der Exponent im Nenner von Gleichung (7.5)
entwickelt werden:
hν
1
exp (hν/kB T ) ≈ 1 +
+
kB T
2!
hν
kB T
2
+...
(7.6)
Unter Berücksichtigung nur der beiden ersten Glieder der Entwicklung wird das RayleighJeans Ergebnis von Gleichung (7.3) wiedergewonnen. Desweiteren können wir die Gesamtenergie der Schwarzkörperstrahlung berechnen:
U(T ) =
∞
dνu(ν, T ) =
0
8πh ∞
ν3
dν.
c3 0 exp (hν/kB T ) − 1
(7.7)
Durch die Substitution x = hν/kB T kann das obige Integral elegant umgeschrieben werden:
4 ∞
x3
8πh kB T
U(T ) = 3
dx.
(7.8)
c
h
exp (x) − 1
0
Wir sehen sofort, dass die Gesamtenergie der Schwarzkörperstrahlung zum einen endlich bleibt. Desweiteren erkennen wir die charakteristische Temperaturabhängigkeit der
Strahlung, die das bekannte Stefan-Boltzmann Gesetz liefert. Das Integral in der obigen
Gleichung kann auf einfacher Weise ausgerechnet werden (siehe z.B. Gasiorowicz, Kapitel 1) und liefert den Wert π 4 /15. Somit gewinnen wir als Endergebnis für die gesamte
Strahlungsenergie des Hohlraums:
U(T ) =
4
4
8π 5 kB
π 2 kB
4
4
4
T
=
3 3 T = σT .
3
3
15h c
15h̄ c
(7.9)
Das bekannte Stefan-Boltzmann Gesetz für die Energieflußdichte eines Schwarzkörpers
kann auch somit berechnet werden und liefert JU = σB T 4 mit σB = 5.67×10−8 Wm−2 K−4 .
7.1. GRENZEN DER KLASSISCHEN PHYSIK
5
Abbildung 7.3: Die Intensität des Streulichts wird als Funktion der Wellenlänge für
Streuung an einen dünnen Metallfilm dargestellt. Das Maximum bei kleiner Wellenlänge stellt das ursprüngliche Licht dar, das Maximum bei langen Wellenlänge ist
das Ergebnis der Compton-Streuung.(Aus GAsiorowicz: Quantum Physics“).
”
7.1.3
Compton Effekt
Der direkteste Nachweis des Teilchen-Charakters des Lichts wird durch die Streuung von
hochenergetischen Photonen an Atomen geliefert. Wenn Röntgenstrahlen durch dünne
Metallfilme geschickt werden, beobachtet man zwei spektrale Komponenten im gestreuten Licht. Eine Komponente hat die Wellenlänge des ursprünglichen Lichts, die zweite
Komponente dagegen wird zu größeren Wellenlängen verschoben, wobei die Verschiebung
mit dem Ablenkwinkel zunimmt. Dieser Effekt, der erstmals durch Compton 1928 beobachtet wurde, läßt sich als die elastische Streuung von Licht an Elektronen deuten.
Wie bereits bei unserer klassischen Betrachtung von Licht gefunden wurde, kann eine
elektromagnetische Welle einen Impuls, der proportional zur Energie p = E/c ist, übertragen. In Verbindung mit unserer Definition der Photonenenergie können wir auch den
übertragenen Impuls mit der Wellenlänge des Lichts verknüpfen: p = hν/c = h/λ.
Aus der relativistischen Mechanik kann die Energie eines Teilchens mit der Ruhemasse
und dem Impuls des Teilchens bestimmt werden:
E = (mo c2 )2 + (pc)2
1/2
.
(7.10)
Die Geschwindigkeit des Teilchens kann dann durch Ableitung der obigen Gleichung gewonnen werden:
dE
pc2
vg =
=
.
(7.11)
dp
[m2o c4 + p2 c2 ]1/2
Für kleine Impulse gewinnen wir durch Entwicklung des Nenners den üblichen Ausdruck
p/mo für die Teilchengeschwindigkeit. Aber für ein Teilchen, das sich mit Lichtgeschwindigkeit bewegt, fordern wir v = c. Diese Forderung kann nur für den Fall mo = 0 erfüllt
werden, und wir erkennen, dass Photonen keine Ruhemasse haben können.
Um das Phänomen der Compton-Streuung im Detail zu verstehen, wenden wir die klassischen Erhaltungssätze von Energie und Impuls direkt an. Das am Streuprozeß beteiligte
6
KAPITEL 7. EINFÜHRUNG IN DER QUANTENMECHANIK
Elektron befindet sich vor der Kollision in Ruhe und somit erhalten wir für die Impulserhaltung:
(7.12)
pi = pf + pe .
In dieser Gleichung sind pi und pf der Impuls des Photons vor und nach der Kollision,
und pe der nach der Kollision vorhandene Impuls des Elektrons. Daraus ergibt sich auch
folgende Beziehung für den Elektronenimpuls:
pe2 = (pi − pf )2 = pi2 + pf2 − 2pi · pf .
(7.13)
Aus Energieerhaltung bei der Kollision bekommen wir auch folgende Gleichung:
hν + mc2 = hν + (m2 c4 + p2e c2 )1/2 .
(7.14)
Hier ist m die Ruhemasse des Elektrons und pe = |pe | der Betrag des Elektronenimpulses,
ν und ν sind die Frequenzen des Lichts vor und nach der Kollision. Diese Gleichung läßt
sich folgendermaßen umschreiben:
m2 c4 + p2e c2
=
hν − hν + mc2
2
= (hν − hν ) + 2mc2 (nν − hν ) + m2 c4 .
2
(7.15)
Somit erhalten wir für das Produkt pe c den Ausdruck:
p2e c2 = (hν − hν ) + 2mc2 (hν − hν ) .
2
(7.16)
Dieser Ausdruck kann dann direkt mit dem Ergebnis aus der Impulserhaltung verglichen
werden:
2 2
hν hν hν
hν 2
+
−2
cos θ,
(7.17)
pe =
c
c
c c
das sich auch folgendermaßen umschreiben läßt:
p2e c2 = (hν − hν ) + 2hνhν [1 − cos θ] .
2
(7.18)
Hierbei ist θ der Ablenkwinkel, oder der Streuwinkel zwischen den einfallenden und auslaufenden Lichtstrahlen. Somit erhalten wir als Ergebnis eine Beziehung, die die Frequenzen
vor (ν) und nach (ν ) der Streuung mit dem Streuwinkel verbindet:
mc2 (hν − hν ) = hνhν [1 − cos θ] .
(7.19)
Für die Wellenlängenverschiebung erhalten wir als Endergebnis:
λ − λ =
c
c
h
− =
[1 − cos θ] .
ν
ν
mc
(7.20)
Der Vorfaktor h/mc = 2.4 × 10−12 ist die sogenannte Compton-Wellenlänge eines Elektrons. Dieses Ergebnis liefert eine exzellente Übereinstimmung für die Wellenlängenverschiebung des gestreuten Lichts als Funktion des Ablenkwinkels. Auch das nicht”
verschobene“ Licht wird um den Winkel θ gestreut und eine genaue Betrachtung dieses
Lichts zeigt, dass dieses Licht als vom Atom Compton-gestreutes Licht zu betrachten
ist. Aufgrund der deutlich schwereren Masse des Atoms ist die Wellenlängenverschiebung
allerdings entsprechend geringer.
7.1. GRENZEN DER KLASSISCHEN PHYSIK
7.1.4
7
Elektronenbeugung und Elektroneninterferenz
In Anlehnung an die Teilcheneigenschaften des Lichts hat de Broglie 1923 den Vorschlag
verbreitet, dass auch Materie eine Wellenlänge hat:
λdB =
h
.
p
(7.21)
Als Konsequenz dieser Betrachtung stellt sich die Frage, ob auch Materie Interferenz und
Beugungsphänomene zeigen kann.
Der Nachweis, dass dies in der Tat der Fall ist, wurde von Davisson und Germer mittels
Elektronenbeugung an Kristallen geliefert. In einem periodischen Kristall mit Gitterperiode a zwischen benachbarten Kristallebenen wurden Reflexionsmessungen mit Elektronen
durchgeführt. Bei bestimmten Einfallswinkel θ, mit θ = 0 für einen Strahl parallel zur
Kristalloberfläche, wurden Intensitätsmaxima des reflektierten Strahls gefunden. Die Bedingung für konstruktive Interferenz nλ = 2a sin θ mit ganzzahligem n kann aus einer
einfachen geometrischen Betrachtung heraus bestätigt werden und ist in Übereinstimmung mit den experimentellen Beobachtungen. Unter der Annahme, dass die Elektronen
als nichtrelativistische Teilchen behandelt werden können, können wir aus der Bedingung
λdB ∼ a die Energie der Elektronen bestimmen:
E=
p2
h2
=
.
2m
2mλ2dB
(7.22)
Für einen typischen Kristall ist a ≈ 10−10 m und die notwendige Elektronenenergie liegt
bei etwa 2 × 10−17 J oder 140 eV.
Aus Tübinger Sicht stellen allerdings die Experimente zur Elektroneninterferenz die Krönung der Welleneigenschaften der Materie dar. Ausschlaggebend für diese Experimente war
die Entwicklung des sogenannten Möllenstedt’schen Biprismas Anfang der 50er Jahren,
das die gleiche Rolle in der Elektronenoptik wie das Fresnel’sche Biprisma für die Lichtoptik spielt. Das Mollenstedt’sche Biprisma besteht aus einem dünnen leitenden Faden, der
parallel zwischen zwei geerdeten Platten aufgespannt wird. Durch Anlegen einer positiven
Spannung werden negativ geladene Teilchen, die die Anordnung passieren entsprechend
abgelenkt5 , und können anschliessend mit sich selbst interferieren. Somit ergibt sich für eine Punktquelle von Elektronen, wie beispielsweise in einem Elektronenmikroskop gegeben,
eine Biprisma-Anordnung wie bereits aus der Optik bekannt. Die erstmalige Beobachtung
der Elektroneninterferenz fand 1956 mittels einer solchen Anordnung in Tübingen statt.
Der Nachweis von Interferenz mit Licht in der Doppelspalt Anordnung von Thomas Young
galt als einschlägiger Nachweis der Wellennatur des Lichts. Auch dieses Experiment ist
erstmals mit Elektronen in Tübingen 1959 durchgeführt worden, und zwar in einem Experiment, das die Methoden der Nanostrukturierung eingesetzt hat!
Auch bei Elektronen ensteht ein Interferenzmuster mit periodischen Maxima, deren Abstand mit der de-Broglie Wellenlänge der Elektronen skaliert. In Abbildung (7.4) wird die
zeitliche Entwicklung eines solchen Interferenzmusters dargestellt. Bei dieser Messreihe
5
Für eine sehr schöne und didaktische Darstellung der Physik der Elektroneninterferenz mit einem
Biprisma sei an dieser Stelle auf folgende Webseite hingewiesen:
http://www.lamel.bo.cnr.it/educational/educational.html
8
KAPITEL 7. EINFÜHRUNG IN DER QUANTENMECHANIK
Abbildung 7.4: Die zeitliche Entwicklung eines Elektronen-Interferenzmusters wird
dargestellt. (Diese Aufnahme können Sie bei der Fussnote (5) nachschauen).
wurde der Strahlstrom der Elektronen so gewählt, dass die Ankunft der einzelnen Elektronen deutlich aufgelöst werden konnte. Obwohl bei langen Belichtungszeiten ein periodischer Intensitätsverlauf, der an den entsprechenden optischen Verlauf stark erinnert, klar
zu erkennen ist, sehen wir dass die Detektion auf kurzen Zeitskalen eine eher stochastische
Verteilung der Elektronen liefert. Bei der Deutung dieses Experiments müssen wir annehmen, dass das Interferenzmuster durch eine Selbstinterferenz der einzelnen Elektronen
entsteht, und dass die Verteilung der Elektronen am Detektor durch eine Wahrscheinlichkeitsverteilung gegeben ist, die die Phasendifferenz der Elektronenwellen berücksichtigt,
wie bei Lichtinterferenz. Desweiteren stellen wir fest, dass die Beobachtung des Vorgangs
eine entscheidende Rolle spielt: Wenn wir beispielsweise Blenden einführen, die den Weg
der Elektronen durch die Apparatur eindeutig bestimmen, ist das Interferenzmuster nicht
mehr sichtbar. Umgekehrt mussen wir schliessen, dass die Beobachtung eines Interferenzmusters nur zu erklären ist, wenn wir akzeptieren, dass die Elektronenwelle sich durch die
Gesamtanordnung ausbreitet - wir können nicht sagen, welchen Weg das Elektron genommen hat, oder - noch deutlicher - es ist nicht sinnvoll eine teilchenartige Trajektorie dem
Elektron zuzuordnen.