1 Biologische Thermodynamik (I) Wintersemester 2009/10

Biologische Thermodynamik (I)
Wintersemester 2009/10
Vorlesungen: Marvin Schuly
Übungen: Katarzyna Tyc & Susanne Gerber
Literatur:
G. Kluge & Neugebauer: Grundlagen der Thermodynamik, Spektrum Akadem. Verlag, 1994
R. Heinrich & S. Schuster, The Regulation of Cellular Systems, Chapman & Hall, New York,
1996
G. Nicolis & I. Prigogine, Self-Organization in Nonequilibrium, Systems; John Wiley &
Sons, New York, 1977
1. Einführung
Thermodynamik ist eine Theorie, in der, wie der Name sagt, die Begriffe „Temperatur“ und
„Wärme“ und „Bewegung“ eine zentrale Rolle spielen.
Grundgrößen der Mechanik:
Länge, Zeit, Masse
Elektrodynamik:
zusätzliche Ladung, gemessen in C (Coulomb, As)
Früher: (noch im 19. Jahrhundert) wurde die Wärme als ein besonderer Stoff, als eine
Flüssigkeit, angesehen. Wärmeübergang von einem Körper zum anderen wurde betrachtet als
ein Transport dieses Wärmestoffes.
Diese Betrachtungsweise ist längst überholt. Dennoch wurden verschiedene, immer noch
gültige, Grundgesetze der Thermodynamik auf der Grundlage dieser „Wärme-FlüssigkeitsHypothese“ abgeleitet. Grundlagen des II. Hauptsatzes durch Carnot (1824).
1
Heute: Kinetische Interpretation der Wärme
Thermische Phänomene werden zurückgeführt auf die ungeordnete Bewegung von Atomen
und Molekülen.
Prinzipiell ist also Thermodynamik als ein spezieller Zweig der Mechanik anzusehen, und
zwar der Mechanik von Systemen, die aus einer außerordentlich großen Zahl von Teilchen
bestehen.
In dieser Vorlesung: Gleichgewichts- und Nichtgleichgewichtsthermodynamik (Teil I),
später: Statistische Thermodynamik
Zahl der Teilchen:
1 Mol: N=6,022 x 1023 Teilchen (Avagadrosche Zahl,
Loschmidt’sche Zahl)
In der Mechanik wird ein System vollständig charakterisiert, durch Angabe der Positionen
und Geschwindigkeiten zu einem bestimmten Zeitpunkt, sowie der Kräfte, die zwischen den
Teilchen wirken.
3 Raumkoordinaten, 3 Geschwindigkeitskoordinaten ⇒ 6 N Variable
Demnach wird 1 Mol wird charakterisiert durch
6 ⋅ 6 ,022 ⋅ 10 23 ≈ 3,6 ⋅ 10 24 Variable
Vollständige Lösung der Bewegungsgleichungen
mi
r
d 2 ri
dt 2
r r r
r
= K i (r1 , r2 ,..., rN )
selbstverständlich unmöglich. Es können nur noch Wahrscheinlichkeitsaussagen über den
Zustand eines Systems getroffen werden ⇒ statistische Mechanik.
2
Obwohl die Thermodynamik heute eine statistische Begründung besitzt, ist das ursprüngliche
Herangehen von dem der Mechanik zunächst völlig verschieden. In der Thermodynamik wird
der Zustand eines Systems durch sehr wenige Zustandsvariablen beschrieben, Größen, die
unseren Sinneswahrnehmungen, oder präziser, unseren makroskopischen Meßgeräten
angepaßt sind. Was kann gemessen werden?
z. B. Temperatur, Volumen, Druck (bei einem Gas oder einer Flüssigkeit, das aus nur einer
Substanz besteht),
im anisotropen Festkörper (Kristall) z.B. zusätzlich: Druck in verschiedenen Richtungen,
in einer Flüssigkeit oder in einem Gas, das aus verschiedenen Stoffen besteht: zusätzlich
Konzentrationen der einzelnen Komponenten.
Typische Teilchenzahlen von Systemen, mit denen man sich in der Biophysik beschäftigt:
1m molar : 6 ,022 ⋅ 1020
Volumen einer Zelle:
Teilchen
Liter
V ≅ 100(µm )3
V = 100 ⋅ 10 −18 m 3 = 10 −16 m 3 = 10 −13 l
1m molar =$ 6, 022 ⋅ 1020 ⋅ 10−13 ≅ 6 x 10+7 Teilchen → z. B. ATP-Konzentration
Hb-Konzentration in Erythrozyten: 7 mM ≈ 4 ⋅108 Proteinmol eküle
Protonenkonzentration
 2+
Ca - Konzentration
0 ,1µM =$ 6 ⋅ 103 Teilchen,
Ca2+: spielt eine wichtige Rolle bei Signaltransduktion
mRNS-Moleküle einer Sorte pro Zelle =$ 100
Na/K-ATPasen pro Erythrozytenmembran =$ 300
3
DNS-Moleküle: 1
Die thermodynamischen Größen sind Mittelwerte.
Aus der Statistik weiß man, daß stets Fluktuationen um die Mittelwerte auftreten und daß
näherungsweise die folgende Beziehung gilt:
σ
1
≈
N
N
;
σ2 : mittlere quadratische Abweichung vom Mittelwert
für Teilchenzahl in einem bestimmten Volumen. Ähnliche Gesetze gelten für andere
physikalische Größen, z. B. Volumen, das von N Teilchen eingenommen wird:
σV
V
≈
1
N = 108 ;
N
1
= 10−4 << 1, d.h. geringe relative Abweichungen
N
Bei Größen wie der Protonen- oder Ca-Konzentration muss die Gültigkeit der
thermodynamischen (d. h. makroskopischen) Beschreibungsweise schon kritischer gesehen
werden..
1
=
N
1
6 ⋅ 103
≅
1
= 0 , 013 > 1%
77
Energie
Thermodynamik befaßt sich mit der Energie und ihrer Umwandlung von einer
Erscheinungsform in die andere. Oder noch genauer: mit den Einschränkungen, denen diese
Umwandlungen unterliegen.
Das System hat kann durch seine potentielle und kinetische Energie (s. Mechanik!)
charakterisiert werden. Diese hängen von Ort und Geschwindigkeit des Gesamtsystems ab
4
und werden auch als äußere Energie des Systems bezeichnet. In der Thermodynamik
interessiert aber besonders die innere Energie. Sie charakterisiert den inneren Zustand des
Systems, die im „Innern der Materie“ gespeicherte Energie. Diese ist wiederum ein Mittelwert
der Energien der mikroskopischen Teilchen aus denen unser System zusammengesetzt ist.
Beispiele:
Translationsenergie (Geschwindigkeit in drei Dimensionen von dem Gesamtmolekül)
Vibrationsenergie (Schwingungen der innerhalb der Moleküle Atomen),
Rotationsenergie (Drehung), Bindungsenergie, potentielle Energie von intermolekularen
Wechselwirkungen, Elektronenenergie, Kernenergie
System und Umgebung
Anwendung der Thermodynamik und ihrer Hauptsätze auf einen Teilbereich des Universums
verlangt die Definition eines Systems und seiner Umgebung. System kann jeder Körper,
Materiemenge, Teilgebiet eines Raumes sein, den man gedanklich vom Rest trennt. Der
„Rest“ ist die Umgebung. Die Beschaffenheit der Begrenzung zwischen System und
Umgebung bestimmt
die möglichen Arten der Wechselwirkungen (nämlich den
Energieaustausch) zwischen System und Umgebung und ist daher in der Thermodynamik sehr
wichtig (s.u.)
Zustandsgrößen
In der Thermodynamik interessiert man sich vorrangig für die makroskopischen
Eigenschaften, weniger für die mikroskopischen. Die detaillierte molekulare Struktur des
Systems bleibt unberücksichtigt. Als thermodynamische Koordinaten kommen nur „grobe“
Eigenschaften in Betracht, wie Temperatur und Druck, die in der Regel Mittelwerte darstellen
und unseren Sinnesempfindungen und Meßgeräten zugänglich sind.
5
Eine Größe, die ausschließlich durch den Zustand eines Systems bestimmt wird, nennen wir
Zustandsgröße. Beispiele sind: die innere Energie (U), die Masse (m), die Mol-Mengen jedes
chemischen Stoffes (n), sein Volumen (V), der Druck (p) und die absolute Temperatur (T).
Anhand der Zustandsfunktionen kann ein homogenes System beschrieben werden.
Der Zustand eines Systems ist die Gesamtheit aller Zustandsgrößen, die ein System besitzt.
Nicht alle in der Thermodynamik betrachteten Größen sind Zustandsgrößen. Beispiele für
Nicht-Zustandsgrößen sind die Arbeit, die Wärme (dazu später)
Man
unterscheidet
extensive
und
intensive
Zustandsfunktionen.
Extensive
Zustandsfunktionen sind abhängig von der Größe, der Extension des Systems. Intensive
Zustandsfunktionen sind das nicht. Verdoppeln wir z.B. ein System, dann verdoppelt sich
auch das Volumen, die Masse, die innere Energie. Die sind extensive Zustandsfunktionen.
Die intensiven Zustandsfunktionen wie Temperatur und Druck verdoppeln sich nicht, sondern
bleiben gleich.
Extensive Größen (Quantitätsgrößen) sind der Masse des Systems, dem sie zugeordnet sind,
proportional. Verdoppelung des Systems → Verdoppelung der Zustandsvariablen.
S1
+
S2
S1 S2
Beispiele: Masse, Volumen, Energie, Entropie, usw.
Extensive Größen bleiben in Systemen ohne Produktion / Abbau erhalten, können aber
ineinander umgewandelt werden
Intensive Größen (Qualitätsgrößen) sind unabhängig von der Masse des Systems, dem sie
zugeordnet sind.
6
Beispiele: Temperatur (T), Druck (p), Dichte ( ρ )
Jeder Quotient zweier extensiver Größen ist eine intensive Größe, z. B.
Dichte: ρ =
M
V
Außerdem können intensive Größen über Kontaktgleichgewichte beschrieben werden.
Zur Beschreibung von Nichtgleichgewichtsprozessen sind sie für Diskretisierungen besser
geeignet.
Intensive Größen können in unterschiedlicher Weise definiert werden. A sei irgendeine
extensive Größe
A
(Dichte)
V
A
a$ =
(Spezifische Größe)
M
A
a=
(Molare Größe)
n
a% =
Meistens werden extensive Größen durch große und intensive Größen durch kleine
Buchstaben bezeichnet (Ausnahme: T, Temperatur, intensiv; n, Molzahl, extensiv).
Gleichgewichtszustände
Erfahrungssatz: Jedes von der Umgebung isolierte makroskopische System geht nach
hinreichend langer Zeit in einen Zustand über, den es spontan nicht wieder verläßt.
Auch ein System, das mit seiner Umgebung Stoff oder Energie austauscht kann einen
statischen Endzustand erreichen. In der Regel ist das kein Gleichgewichtsszustand, sondern
z.B. ein Fließgleichgewicht.
7
Gleichgewichtszustände sind gegenüber Nichtgleichgewichtszuständen dadurch ausgezeichnet, daß sie durch eine kleinere Zahl von Zustandsvariablen beschrieben werden können.
(Turbulenz; räumliche Inhomogenität).
Beispiel
Wir betrachten zunächst ein ideales Gas, das in einem Behälter eingeschlossen ist.
Meßgrößen sind
p, V, T
Druck p, Temperatur T
Volumen V, Molzahl n: hier konstant
Die Erfahrung zeigt, daß diese Größen nicht völlig unabhängig voneinander sind:
*)
pV = nRT
pV =
; n:Molzahl
n=
M ← Masse
M Mol . ← Molmasse
Kraft
Volumen = Kraft x Weg =Energie
Fläche
R = 8,31441J ⋅ mol −1K −1
R: universelle Gaskonstante
1Joule = 1Ws
R = 1,986 kcal ⋅ kmol −1 ⋅ K −1
*) Ist eine Zustandsgleichung. Die in ihr auftretenden Größen beziehen sich auf ein
Gleichgewicht.
Alte Maßeinheit für Energie: Eine Kalorie ist diejenige Wärmemenge, die man 1g Wasser
zuführen
muß,
um
es
bei
Atmosphärendruck
erwärmen 1kcal = 4,1868kJ .
8
von
14,5oC
auf
15,5oC
zu
Es gibt einen kleinstmöglichen Satz von Zustandsvariablen, die anderen Größen können als
Funktionen dieser Zustandsvariablen beschrieben werden.
Ideales Gas:
p ,V ⇒ T ,
p ,T ⇒ V ,
V ,T ⇒ p
Man unterscheidet deshalb zwischen abhängigen und unabhängigen Zustandsgrößen. Welche
Größen als abhängige und welche als unabhängige Zustandsgrößen behandelt werden, ist
relativ willkürlich.
Zustandsvariable = unabhängige Zustandsgröße
Zahl f der unabhängigen Zustandsvariablen ist aber konstant, beim idealen Gas: f = 2,
f:
Anzahl der thermodynamischen Freiheitsgrade
Zustandsänderungen: Betrachtet man ein System zu zwei verschiedenen Zeitpunkten
t1 und t2 mit t2 > t1 und stellt man bei t2 einen anderen Zustand fest als bei t1 , hat eine
Zustandsänderung stattgefunden. Diese Zustandsänderungen sind Prozesse.
Zustandsänderungen können:
von selbst ablaufen, z. B. Temperaturausgleich oder können
von außen erzwungen werden (Wärmezufuhr, Volumenänderung, Arbeitsleistung an dem
System u. s. w.).
Besonders wichtig: Unterscheidung von reversiblen und irreversiblen Zustandsänderungen.
Kann der Ausgangszustand des Systems nicht ohne bleibende Änderung in der
Umgebung wiederhergestellt werden, heißt der Prozeß irreversibel.
9
Im Prinzip sind alle natürlichen Prozesse irreversibel (Stein, der nach unter fällt, usw.).
Reversible Zustandsänderung: Grenzfall; äußerst langsame, eigentlich unendlich langsame
Zustandsänderungen, bei denen stets Zeit genug ist, daß sich das System in
Gleichgewichtszuständen befindet.
langsames Herabdrücken des Stempels,
keine Strömungen, keine Turbulenzen
Quasi-statische Prozesse
Gas
Infinitesimale Änderung der äußeren
Bedingungen
Gleichgewichtsthermodynamik ist eine Theorie quasi-statischer Prozesse
Wie langsam der Prozeß sein muß hängt von der Relaxationszeit τ ab, die das System
benötigt, um nach einer Störung wieder das Gleichgewicht zu erreichen. Alle Veränderungen
müssen langsam im Vergleich zu τ sein.
Beispiel: Wenn das Gas in einem Kolben beim Zusammendrücken auf das halbe Volumen
nach τ = 10 −3 s das Gleichgewicht erreicht, dann ist dieser Prozeß bei Durchführung in 0,1s
in guter Näherung ein quasi-statischer Prozeß.
Klassifizierung von Prozessen:
isotherm: T = konst. ,
isobar:
p = konst. ,
isochor: V = konst.
+ weitere Möglichkeiten, die wir später kennenlernen.
Wechselwirkung eines thermodynamischen Systems mit seiner Umgebung
10
Arbeit
Stoff
S
Je nachdem, welche
Wärme
(termo4.cw2)
Wechselwirkungen existieren, ergibt
sich folgende Klassifikation:
Art der Wechselwirkung
Bezeichnung
Energie- und Stoffaustausch
offenes System
Energie- aber kein Stoffaustausch
geschlossenes System
kein Wärmeaustausch
adiabatisch isoliertes System
kein Energie- und kein Stoffaustausch
abgeschlossenes System
Arbeit
Arbeitsleistung (spezieller Fall des Energieaustausches)
∆ A = − K ⋅ ∆h = −( p + ∆ p )F ⋅ ∆h
∆h
p, V, T
Reversibler Prozess: infinitesimal kleine Änderungen:
(termo5.cw2)
dA = − p 1
F2
⋅3
dh = − pdV
dV
dV < 0 ⇒ dA > 0 „An dem System wird Arbeit geleistet.“
dV > 0 ⇒ dA < 0 „Das System leistet Arbeit.“ (hier Kompressionsarbeit)
Arbeitsleistung bei quasi-statischen Veränderungen zwischen Volumina V1 und V2
11
V2
∆ A = − ∫ pdV
; hier ist p eine Funktion von V.
V1
Unter Verwendung der Zustandsgleichung: pV = nRT
V2
∆A = − ∫
V1
nRT
dV
V
Bei isothermen Zustandsänderungen: T = konst .
V2
∆ A = −nRT
V
2
dV
nRT
V
=
−
ln
∫V
V
V
1
1
= −nRT ln
V2 < V1 ⇒ ∆ A > 0
p1V1 = p2V2
∆ A = nRT ln
V2
V1
Kompressionsarbeit. Wegen T = konst. gilt
V2 p1
=
V1 p2
;
p2
p1
;
p2 > p1 ⇒ ∆ A > 0
Zustandsdiagramm: Graphische Darstellung einer Zustandsgleichung
Ideales Gas: Es reicht ein 2-dimensionales Koordinatensystem, da nur f = 2 Freiheitsgrade
12
( p,V ) Diagramm
p
pV = nRT ; p =
T
Isothermen
nRT
V
T = konst ., Hyperbeln
V
(termo6)
Arbeitsleitung ∆ A (oben berechnet für ein ideales Gas) hat im (p,V)-Zustandsdiagrammen
eine einfache geometrische Interpretation.
V2
p
∆ A = − ∫ pdV
p=
V1
nRT
=p (V )
V
∆ A = Fläche unter der Kurve
V1
V2
Kreisprozeß:
p
Das System leistet Arbeit.
∆ A = − ∫ pdV
Fhin
V1
p
V2
V2
V1
V1
V2
V2
V2
V1
V1
= − ∫ pdV −
∫ pdV
V
An dem System wird Arbeit geleistet.
= − ∫ pdV +
Frück
V1
V2
= − Fhin
V
13
∫ pdV
+ Frück
p
∆F = + ∆A
Expansion bei niedrigem Druck;
Kompression bei hohem Druck.
V
(Vorzeichen der Arbeitsleistung hängt davon
ab, in welcher Richtung der Kreisprozeß
durchlaufen wird.)
Nach Abschluß des Kreisprozesses:
p ,V ,T : gehen wieder zu den ursprünglichen Werten zurück, ∆ p , ∆ V = 0 ; ∆ T = 0
A: hat nach Abschluß des Prozesses einen anderen Wert (in der Regel),
∆A≠0
p und V sind Zustandsgrößen, während A keine Zustandsgröße ist.
Genauere Definition von Zustandsgrößen:
Sind Größen, die entweder selbst Zustandsvariable sind oder eindeutig von den unabhängigen
Zustandsvariablen abhängen. Sind unabhäng vom Weg, auf dem ein bestimmter Zustand
erreicht wird.
a
p
2
Zustand 1: p1 ,V1 ⇒ T1 =
p1V1
nR
1
b
V
Zustand 2: p2 ,V2 ⇒ T2 =
p2V2
nR
Das heißt, neben p und V ist auch T eine Zustandsvariable.
A ist deshalb keine Zustandsvariable, weil ∆ A abhängig davon ist, ob man Zustand 2 auf dem
Weg a oder Weg b erreicht.
14
Für Zustandsgrößen Z gilt demnach:
2
2
1
(a )∫ dZ = (b )∫ dZ = −(b )∫ dZ
1
1
∫ dZ = 0
2
1
1
2
(a )∫ dZ + (b )∫ dZ = 0 ⇒
,
2
∫ dZ = 0
ist nur dann für beliebige geschlossene Integrationswege erfüllt, wenn dZ ein
vollständiges Differential darstellt. Beweis:
x und y seien zwei unabhängige Zustandsvariable, dann gilt allgemein für die Variation
irgendeiner anderen abhängigen Größe (Zustandsgröße oder nicht):
dZ = f (x , y )dx + g (x , y )dy
∫ dZ = ∫ [ f (c, y )dx + g (x, y )dy ]
Intergration:
Stokes‘scher Satz:
 ∂g
∂f 
∫ dZ = ∫∫  ∂x − ∂y dxdy = 0
Diese Bedingung ist nur dann immer erfüllt, wenn gilt
f =
∂Z
,
∂x
folgt
dZ =
wegen:
∫ dZ =0
∂g ∂ 2 Z
=
∂ x ∂ x∂ y
;
∂g ∂f
∂Z
, woraus folgt: g =
und
=
∂y
∂x ∂y
∂f ∂ 2 Z
=
∂ y ∂ x∂ y
*) integrale Bedingung für Zustandsvariable
∂Z
∂Z
dx +
dy : differentielle Bedingung
∂x
∂y
15
2. Hauptsätze der Thermodynamik
Bekannt sind vor allem der I. und II. Hauptsatz der Thermodynamik. Man spricht auch vom 0.
Hauptsatz und es gibt zusätzlich den III. Hauptsatz.
0. HS:
Einführung der Temperatur als Zustandsgröße
I. HS:
Energieerhaltungssatz
II. HS:
Einführung der Entropie als Zustandsgröße
(Aussagen über die Richtung von Prozeßabläufen)
III. HS:
Nernst‘scher Wärmesatz (Hauptkonsequenz: Unerreichbarkeit des
absoluten Nullpunktes der Temperatur)
2.1. 0. Hauptsatz
Es gibt eine Zustandsgröße, die Temperatur. Ihre Gleichheit ist Bedingung des thermischen
Gleichgewichtes zweier Systeme, S1 und S2, oder zweier Teile desselben Systems, S.
Zum 1. Mal so formuliert von Fowler (1931) bei Bemühungen, der Thermodynamik einen
axiomatischen Aufbau zu geben.
S1
S2
Vor dem Kontakt: S1 sei wärmer als S2
T (S1 ) > T (S 2 )
S1
nach dem Kontakt drei Möglichkeiten denkbar.
S2
a)
T (S1 ) > T (S 2 )
b)
T (S1 ) = T (S 2 )
c)
T (S1 ) < T (S 2 )
← nie beobachtet.
Ob a) oder b) realisiert, hängt von der Art der Kontaktfläche ab;
a) adiabatisch isolierende Wände
16
b)
thermisch leitende Wände
Fall a) kann nicht beliebig lange aufrecht erhalten werden.
2.2. I. Hauptsatz
Energieerhaltungssatz; Robert Mayer, H. Helmholtz (aber eigentlich bereits von W. Leibnitz)
Wir betrachten ein geschlossenes System (kein Stoffaustausch, aber Energieaustausch)
Neben mechanischer Arbeitsleistung wird Wärme als Energieform betrachtet.
I. Hauptsatz:
Jedes thermodynamische System besitzt eine extensive Zustandsgröße U, die sogenannte
innere Energie. Sie wächst durch Zufuhr von Wärme δQ und von Arbeit δA . Für
abgeschlossene Systeme ist die innere Energie eine Erhaltungsgröße (U = konst.).
dU = δQ + δA
δQ
dU
δ : wenn Variation einer Größe, die keine
Zustandsgröße, oder wenn wir noch nicht
δA
wissen, ob Zustandsgröße.
Für abgeschlossene Systeme gilt δA = δQ = 0 und damit
dU = 0 ; U = konst . Energieerhaltungssatz für die innere Energie.
δA : Arbeitsdifferential
δA = − pdV für Kompressionsarbeit (Spezialfall).
Andere Möglichkeiten für die thermodynamische Arbeit:
δA = σ dF ; Oberflächenvergrößerung oder –verkleinerung σ : Oberflächenspannung
dF : Flächenänderung
17
δA = ψ ⋅ de
Änderung der Ladung in einem elektrischen Feld
ψ Potential (s. Elektrolyte), e: Ladung (s. Membranpotential)
Integrale Formulierung des I. Hauptsatzes
Die innere Energie ist eine Zustandsgröße; Also gilt bei Kreisprozeß:
∫ dU = 0 ⇒ ∫ δ A + ∫ δ Q = 0
Zwei Fälle
1. wenn kein Wärmeaustausch stattfindet:
2. mit Wärmeaustausch:
∫ δQ = 0 ⇒ ∫ δA = 0 , keine Arbeit
geleistet
∫ δA < 0 ⇒ ∫ δQ > 0
Wenn Arbeit abgegeben werden soll; muß Wärme zugeführt werden.
Äquivalente Formulierung des I. Hauptsatzes: „Satz von der Unmöglichkeit eines
Perpetuum mobile“
Es ist unmöglich, ein perpetuum mobile 1. Art, d. h. eine periodisch arbeitende Maschine zu
bauen, die Arbeit abgibt, ohne Energie in irgendeiner anderen Form aufzunehmen.
Diese Aussage ist äquivalent zur Aussage, daß U eine Zustandsgröße ist.
Einige Folgerungen aus dem I. Hauptsatz
(für Systeme, die im ( p ,V , T )-Zustandsdiagramm beschrieben werden können; hier waren 2
Zustandsvariablen unabhängig.) U Zustandsgröße:
U = U ( p ,V ) , oder U = U ( p ,T ) ; U = U (V ,T )
Weil unterschiedliche funktionelle Abhängigkeiten möglich sind, ist es wichtig, klarzustellen,
welche Größe konstant bleibt, wenn eine andere variiert wird.
18
z. B.
 ∂U 


 ∂T V
bedeutet: es wird die Funktion U = U (T ,V ) differenziert
und nicht etwa U = U (T , p ) .
Welche Größen man als unabhängige Variable ansieht, ist z.B. wichtig bei Berechnung der
Wärmekapazität.
C=
δQ
∆Q
=
∆T ∆T →0 dT
Wärme, die bei Temperaturerhöhung von dem Körper absorbiert wird.
dU = δQ − pdV - I. Hauptsatz als Ausgangspunkt
δQ = dU + pdV
1) V, T als unabhängige Zustandsvariable
 ∂U 
 ∂U 
U = U (T ,V ) ⇒ dU = 
 dT + 
dV
 ∂T V
 ∂V 
 ∂U 

 ∂U 

 dT + 
 + p  dV = δQ
 ∂T V
 ∂V T

2) p, T als unabhängige Zustandsvariable
 ∂U 
 ∂U 
U = U (T , p ) ; dU = 
 dp ,
 dT + 
 ∂T  p
 ∂p  T
 ∂U 
 ∂U 
 dp +

 dT + 
 ∂T  p
 ∂p  T
 ∂V
 ∂V 
dV = 
 dT + 
 ∂T  p
 ∂p
 ∂V 

 ∂V 
 dp  = δQ
p 
 dT + 
 ∂T  p
 ∂p T 
19

 dp
T
 ∂U 
 ∂U 
 ∂V  
 ∂V  
 + p
  dp = δQ

 + p
  dT + 
 ∂T  p 
 ∂T  p
 ∂p T 
 ∂p T
C ist offenbar davon abhängig davon, wie der Prozeß der Temperaturerhöhung abläuft, z. B.
ob bei konstantem Volumen oder bei konstantem Druck.
aus 1)
aus 2)
dV = 0
dp = 0
;
;
V = konst .
p = konst .
,
,
δQ
dT
V = konst.
 ∂U 
= CV = 

 ∂T V
p = konst
 ∂U 
 ∂V 
=
 + p
 = Cp
 ∂T  p
 ∂T  p
δQ
dT
In der Regel ist C p ≠ CV . Unterschied in der Wärmekapazitäten resultiert aus der Tatsache,
daß bei p = konst . und variablem Volumen Arbeit geleistet wird.
Das Gewicht wird bei
Erwärmung ein Stück
nach oben geschoben.
V = konst.
p = konst.
(termo17.cw2)
Für ein ideales Gas gilt U = U (T ) , Theoretisches Argument: U nicht vom Volumen und nicht
vom Druck abhängig da keine Wechselwirkung der Teilchen.
20
Experiment: Gay-Lussac‘scher Überströmversuch (irreversible Gasexpansion).
isoliertes System:
δA = 0 , δQ = 0
(termo18.cw2)
dU = 0 , U = konst .
U 1 = U (V1 , T1 )
U 2 = U (V2 ,T2 ) = U 1
1: vor der Expansion, 2: nach der Expansion
U (V1, T1 ) = U (V2 , T2 )
Experimenteller Fakt: Keine (oder nahezu keine) Temperaturveränderung: T1 = T2 = T .
U (V1, T ) = U (V2 , T )
;
V1 ≠ V2
Schlußfolgerung: entweder V1 = V2 , was in der vorgegebenen Situation nicht gilt, oder U
unabhängig von V; Gutes experimentelles Beispiel für ein annähernd ideales Gas: Helium bei
Zimmertemperatur.
Also: U = U (T )
 ∂U
Daraus folgt (nur für ideales Gas): 
 ∂T

 ∂U 
 =
 = CV
V  ∂ T  p
V =
Unter Verwendung der Zustandsgleichung:
C p = CV + p
nR
p
,
C p − CV = nR
21
,
 ∂V 
C p = CV + p 

 ∂T  p
nRT
nR
 ∂V 
; 
 =
p
p
 ∂T  p
Cp
Cp
n
−
CV
=R
n
C
, V
n
n
, {{
/
/
Molwärme (Wärmekapazität/Mol)
c p − cV = R > 0 , wichtige Formel der Thermodynamik.
Aus der kinetischen Gastheorie folgt für ein einatomiges Gas: cV =
2
5
R ⇒ cp = R
3
2
Adiabatische Zustandsänderungen
Treten auf, wenn das System thermisch isoliert ist. (Kein Austausch von Stoff oder Wärme,
nur von Arbeit)
δQ = 0
z. B. Gas Expansion, δA < 0
(System leistet Arbeit)
⇒ δU < 0
U = U (T )
ideales Gas: ⇒ Temperaturerniedrigung
dU = δQ + δA ,
Ideales Gas: wegen
dU + pdV = 0
dU
= CV folgt
dT
22
nRT
dV = 0
V
dT nRdV
+
=0
T
CV V
CV dT +
ln T +
R
ln V = konst .
cV
das bedeutet: TV R / cV = konst .
verwendet man:
R c p − cV c p
=
=
− 1 , mit κ > 1 ,
cV
cV
cV
{
κ
gilt:
T=
konst .
V κ −1
(adiabatische Zustandsgleichung)
Andere Formen :
TV κ
= konst .
V
nRT = pV
T
p
=
V nR
pV κ
= konst .
nR
pV κ = konst .
p
T = konst.
p=
konst .
isotherm
V
p=
konst .
adiabatisch
Vκ
δQ=0
V
(termo19.cw2)
Adiabaten sind im p-V-Diagramm steiler als
Isothermen
23
2.3.
II. Hauptsatz
I. Hauptsatz: Energieerhaltungssatz; es gibt keine Maschine, die Energie produziert.
Aber: keine Limitationen, wie eine Energieform in die andere überführt werden kann.
Erfahrung:
(Mech.) Arbeit
Wärme
Stein, der nach unten fällt:
→ Wärme:
stets vollständig möglich
→ Arbeit:
nicht unbegrenzt möglich
Umwandlung mechanischer Arbeit in Wärme
Umgekehrter Prozeß spontan nicht möglich.
Natürlich kann Wärme in Arbeit umgewandelt werden, aber es gibt Limitationen.
Erfahrungssätze:
Postulat von Lord Kelvin:
Eine Zustandsänderung, deren einziges Endergebnis darin besteht, Wärme aus einem
einzigen Reservoir zu extrahieren und diese in Arbeit umzuwandeln, ist unmöglich.
Äquivalent dazu ist das Postulat von Clausius:
Eine Zustandsänderung, deren einziges Endergebnis darin besteht, Wärme von einem Körper
der Temperatur T1 zu einem anderen Körper T2 mit T2 > T1 zu transportieren, ist unmöglich.
2.3.1. Der Carnot‘sche Kreisprozeß und Entropie als neue Zustandsgröße
24
Wir betrachten den folgenden Kreisprozeß, durchgeführt mit einem idealen Gas.
Quasi-statisch, d. h. unendlich langsam.
Adiabaten
V
p
A
T 2 > T1
Arbeit wird
dem System
zugeführt.
T2
B
D
Isothermen
T1
p
C
V
V
Arbeit wird
von dem System
geleistet.
(termo21.cw2)
p
(termo22.cw2)
Isothermen (1 Mol): pV = RT2 ,
pV = RT1
Adiabaten: pV κ = konst .
∆A
∆U
∆Q
nach Ablauf des Kreisprozesses hat das System Arbeit geleistet und es wurde Wärme
zugeführt
da U eine Zustandsgröße:
∆ U = ∆ A + ∆ Q = 0 , ∆U = 0 ⇒ ∆ A < 0 , ∆ Q > 0
Q ist keine Zustandsgröße, aber wir werden im folgenden sehen, dass man eine neue
Zustandsgröße (Entropie) einführen kann, die direkt von Q abhängt.
∆ A + ∆ Q2 + ∆ Q1 = 0 *)
25
∆ A : die am System geleistete Arbeit, − ∆ A : die vom System geleistete Arbeit (hier positiv)
∆Q2 , ∆Q1 : die von dem System (bei isothermen Abschnitten) aufgenommene Wärme.
Isotherme Zustandsänderungen laufen bei idealen Gasen ohne Änderung der inneren Energie
ab. Daher
B
B
B
∫ dU = 0 = ∫ δQ − ∫ pdV = ∆Q2 + AAB
A
A
,
∆Q2 = − AAB
A
Analog: ∆Q1 = − ACD
Berechnung von ∆Q1 und ∆Q2 über Berechnung der einzelnen Arbeitsanteile möglich
Abschnitt A → B , isotherme Expansion
VB
VB
VA
VA
AAB = − ∫ pdV = − ∫
RT2
V
dV = − RT2 ln B
V
VA
,
VB > VA , AAB < 0 : das System leistet
Arbeit, ∆Q1 > 0 , es wird Wärme aufgenommen.
Abschnitt C → D , isotherme Kompression ist analog zur isothermen Expansion:
VD
VD
VC
VC
ACD = − ∫ pdV = −
∫
V
RT1
dV = − RT1ln D
VC
V
, VD < VC , ACD > 0 , ∆Q1 < 0
Es wird Wärme abgegeben.
Bei reversibler Prozeßführung: läßt sich das Verhältnis ∆Q1 ∆Q2 durch das Verhältnis der
Temperaturen T1 und T2 ausdrücken. Beweis:
26
Wir hatten abgeleitet: ∆ Q2 = RT2 ln
VB
> 0,
VA
∆ Q1 = RT1 ln
VD
<0
VC
Punkte A und D sowie B und C liegen auf adiabatischer Kurve TV κ −1 = konst
κ −1
κ −1
TV
1 D = T2VA
κ −1
TV
= T2VBκ −1
1 C
Division
VDκ −1 VAκ −1
=
VCκ −1 VBκ −1
oder
∆ Q2 = RT2 ln
VB
VA
∆ Q1 = RT1 ln
VD
VC
∆Q1
T1
+
∆Q2
T2
VD VA
=
VC VB


T
 ∆ Q1
=− 1

V ∆Q2
T2
= − RT1 ln B 
V A 
=0
infinitesimale Änderungen:
δ Q1 δ Q2
+
=0
T1
T2
Ein beliebiger Kreisprozeß läßt sich stets auffassen als zusammengesetzt aus Isothermen und
Adiabaten, deshalb allgemein:
27
∫
δQ
T
=0
für einen beliebigen Kreisprozeß.
Wir haben eine neue Zustandsgröße gefunden. Hier abgeleitet aus Zustandsgleichung des
idealen Gases.
dS =
δQ
T
Wärme Q keine Zustandsgröße, aber S: Entropie
Diese Beziehung gilt für reversible Zustandsänderung (unendlich langsam).
B
B
A
A
 δQrev 

T 
∫ dS =S B − S A = ∆S = ∫ 
Wirkungsgrad eines Carnot-Prozesses:
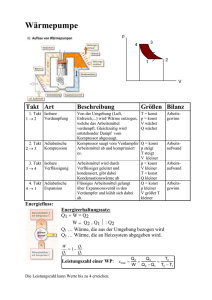
=7
− ∆4
A8
64
∆Q2 + ∆Q1
η=
∆Q2
η = 1+
, geleistete Arbeit im Verhältnis zu aufgewendeten Wärmemenge
T
T −T
∆Q1
= 1 − 1 = 2 1 , wegen T2 > T1 , 0 ≤ η ≤ 1
T2
T2
∆Q2
obige Formel gilt für reversible Zustandsänderungen. Wenn der Prozeß irreversibel ist oder
irreversible Anteile enthält, gilt
η=
T
∆Q2 + ∆Q1 T2 − T1
∆Q1
< − 1 , weil die gewonnene Arbeit geringer ist als
<
, also
∆Q2
T2
∆Q2
T2
∆Q2 + ∆Q1 (z.B. wird mehr Wärme abgegeben, Reibungsverluste o.ä.)
∆Q1
T1
+
∆Q2
T2
≤0
28
allgemeiner:
∫
δQ
T
≤ 0 bei irreversibler oder teilweise irreversiblen Prozessen.
Um die Entropieänderungen bei irrevbersiblen Prozessen zu berechnen, betrachtet man
reversible Ersatzprozesse, die den gleichen Ausgangs- und Endzustand haben:
A
reversibel, Ersatzprozeß
B
irreversibel
Wir betrachten obigen Prozess als Kreisprozess:
0≥∫
 B δQ 
 A δQ 



= ∫
+∫
 T 
 T 
T
A
 irr  B
 rev
δQ
A
 B δQ 
B

 + dS = δQ  + S − S
0 ≥ ∫
A
B
∫
∫
 T 
 T 
A
A
 irr B
 irr
 B δQ 
 .
⇒ SB − S A ≥  ∫
 T 
A
 irr
Erfolgt der irreversible Prozess in einem abgeschlossenen System, gilt δQirr = 0 ⇒
S B − S A = ∆S ≥ 0
In abgeschlossenen Systemen kann die Entropie nicht abfallen.
δS ges =
δQ
T
{
+ δSirr , mit δSirr > 0 : Entropieproduktion
dS rev
29
Formulierung des 2. Hauptsatzes nach Sommerfeld:
"Jedes thermodynamische System besitzt eine extensive Zustandsgröße S, die Entropie. Ihre
Zunahme bei reversiblen Zustandsänderungen berechnet man, indem man die zugeführte
Wärmemenge
durch
die
absolute
Temperatur
dividiert.
Bei
Zustandsänderungen wird im Inneren des Systems Entropie produziert."
Nachtrag: Arbeitsanteile bei adiabatischer Expansion und Kompression
B → C , adiabatische Expansion.
Hier gilt pV κ = konst . = k = p BV Bκ = pC VCκ
also:
VC
VC
k
ABC = − ∫ pdV = − ∫
VB V
VB
==
pC VCκ VC(1−κ )
1−κ
+
κ
dV = −
p BVBκ V B(1−κ )
1−κ
(
k
V (1−κ ) − V B(1−κ )
(1 − κ ) C
=
)
−1
(p V − p V )
(1 − κ ) C C B B
−R
(T − T ) = +CV (T1 − T2 )
(1 − κ ) 1 2
da T1 < T2 ist ABC < 0 , das System leistet Arbeit
D → A , adiabatische Kompression, umgekehrt analog zu 2.Schritt:
ADA = −CV (T1 − T2 ) = − ABC
ist also positiv, aufgenommene Arbeit
30
allen
irreversiblen
3. Direkte Folgerungen aus dem I. und II. Hauptsatz
3.1. Die Gibbs'sche Fundamentalgleichung
I. HS: dU = δQ + δA
δQ
II. HS: dS =
(bei reversibler Prozeßführung)
T
Durch Elimination von δQ erhält man
dS =
dU − δA dU δA
=
−
T
T
T
z. B. δA = − pdV
dS =
dU pdV
+
T
T
b.z.w.
TdS = dU + pdV
Für die Arbeitsterme kann man allgemein schreiben
δA = ∑ ai dAi
i
dU 1 n
dS =
− ∑ ai dAi
T T i =1
Die Gibbs’sche Fundamentalgleichung bildet die Grundlage der
Gleichgewichtsthermodynamik
Entropieänderung bei irreversibler Expansion eines idealen Gases
34
irreversibler Prozeß,
verläuft irgendwie
p
1
V2
V1
Gleichgewichtsprozeß
2
V1
(termo29.cw2)
V1 + V2
V
(termo27.cw2)
Wir wissen T = konst .
Wir müssen, um ∆S zu berechnen, einen "reversiblen Ersatzprozeß" finden, der ebenfalls
vom Zustand 1 in Zustand 2 führt.
dS =
δ Qrev
reversibler Ersatzprozeß: isotherme Expansion, Prozessführung
T
gegen äußeren Druck, damit langsam
nach I. Hauptsatz
dU = δQrev − pdV
U = U (T ) ; dT = 0 ⇒ dU = 0
innere Energie nur abhängig von Temparatur
keine Temp.änderung, keine Änderung von U
⇒ δQrev = pdV
pdV
;
T
dV
dS = nR
V
dS =
pV = nRT
;
p=
nRT
V
Integration:
35
∆ S = nR ln
 V 
V1 + V2
= nR ln 1 + 2  > 0
V1
 V1 
Konzept des reversiblen Ersatzprozesses ist sehr wichtig.
∆S ≈ n :
S ist eine extensive Zustandsgröße, weil proportional zur Größe des Systems
3.2. Thermische und kalorische Zustandsgleichung
dS =
dU + pdV
T
dS ist nur dann ein vollständiges Differential (also eine Zustandsgröße), wenn gilt
∂S 
∂S 
S = S (U ,V ) ⇒ dS = 
 dU + 
 dV
 ∂ U V
 ∂ V U
Aus Vergleich folgt
1
 ∂S 

 =
 ∂U V T
p
 ∂S 
; 
 =
 ∂V U T
S = S (U ,V )
T = T (U ,V )
p = p (T ,U ,V ) ; U = U (T ,V )
p = p (T ,V )
oder
U = U (T ,V )
p = p(T ,V )
kalorische
Zustandsgleichung
thermische Zustandsgleichung
36
nRT
V
nRT
A2
−
oder p =
V − B V2
z. B. p =
Die kalorische und die thermische Zustandsgröße sind nicht völlig unabhängig voneinander,
da sie aus ein- und derselben Funktion S = S (U ,V ) resultieren.
Wechsel der Variablen, U, V → T, V
 ∂U 
 ∂U 
TdS = dU + pdV ; U = U (T ,V ) ; dU = 
 dT + 
 dV
 ∂T V
 ∂V  T
 ∂U 

 ∂U 
TdS = 
 dT + 
 + p  dV
 ∂T V
 ∂V  T

In dieser Schreibweise sind T und V die unabhängigen Variablen (und nicht U und V).
Es gilt demzufolge:
 ∂S 
 ∂S 
dS = 
 dT + 
 dV
 ∂T V
 ∂V  T
durch Vergleich folgt:
1  ∂U 
 ∂S 

 = 

 ∂T V T  ∂T V

1  ∂U 
 ∂S 
; 
 = 
 + p
 ∂V  T T  ∂V  T

Gemischte Ableitungen müssen gleich sein:
1 ∂ 2U
∂  ∂S 
  =
∂V  ∂T  V T ∂T ∂V
 1 ∂ 2U 1  ∂p 
1  ∂U 
∂  ∂S 
+  

 = − 2 
 + p +
∂T  ∂V  T
T  ∂V  T
 T ∂V∂T T  ∂T V
37
1  ∂U 
1  ∂p 
p
= 
−



T 2  ∂V  T T  ∂T V T 2
 ∂U 
 ∂p 

 = T
 −p
 ∂V  T
 ∂T V
 ∂U 

 : kalorische Zustandsgleichung, Differentiation von U = U (V ,T )
 ∂V  T
 ∂p 
T
 : thermische Zustandsgleichung, Differentiation von p = p(T ,V )
 ∂T V
z. B. ist eine Konsequenz:
Ideales Gas: p =
nRT
: thermische Zustandsgleichung
V
nR p
 ∂p 
=
  =
 ∂T  V V T
p
 ∂U 

 =T − p =0 ;
T
 ∂V  T
 ∂U 

 =0
 ∂V  T
Das heißt, wenn die thermische Zustandsgröße für ideales Gas gültig, dann muß U, die innere
Energie, unabhängig vom Volumen sein. (Hatten wir vorher nur aus Gay-Lussac-Experiment
geschlossen).
3.3. Wärmekapazitäten und Enthalpie
Wir hatten bereits definiert:
C=
δQ
dT
Wärmekapazität
C
δQ / n δ q
=c=
=
: Molwärme
n
dT
dT
38
Mit dem I. HS: δQ = dU + pdV
C=
dU + pdV
dT
Mit kalorischer Zustandsgleichung: U = U (T ,V )
 ∂U 
 ∂U 
dU = 
 dT + 
 dV
 ∂T V
 ∂V  T
 ∂U 
 dV
 ∂U 
C =
 + 
 + p
 ∂T V  ∂V T
 dT
allgemein
 ∂U 
isochorer Prozeß dV = 0 : CV = 

 ∂T  V
isobarer Prozeß dp = 0
 ∂U
: Cp = 
 ∂T
 ∂ U

 + 
V  ∂ V
 ∂V

 + p 
T
 ∂T


p
Daß CV und C p verschieden sein müssen, davon hatten wir uns bereits überzeugt.
Asymmetrie in der Formulierung, die unschön und auch unpraktisch ist.
Zur Charakterisierung von Prozessen, die bei konstantem Druck ablaufen, ist es günstig, eine
neue Zustandsgröße, die Enthalpie, einzuführen.
dU = δQ − pdV , d.h. dU ist die bei konstantem Volumen zugeführte Wärmemenge
Definition:
H = U + pV
dH = dU + dpV + pdV = δQ + Vdp
H: Enthalpie,
Wärmekapazität:
dH ist die bei konstantem Druck zugeführte Wärmemenge
 δQ   dH − Vdp 
C =
=

dT
 dT  

39
 ∂H 
 ∂H 
 dp
dH = 
 dT + 
 ∂T  p
 ∂p  T
 dp
  ∂H 
 ∂H 
 − V 
C =
 +  
 dT
 ∂T  p   ∂p  T

 ∂H 
Cp = 

 ∂T  p
 ∂U 
CV = 

 ∂T  V
zum Vergleich:
U = U (T ,V ) Energie
H =U +pV


hat ebenfalls Maßeinheit  ⇒ thermodynamische Potentiale

einer Energie

Weitere thermodynamische Potentiale:
z.B. freie Energie und freie Enthalpie, lernen wir später kennen.
Berechnung der Entropie für ideales Gas
δ Q = dU + pdV
,
 ∂U 
 ∂U 
 dT + 
 dV + pdV
∂V T
 ∂T V
1
424
3
δQ = 
=0
δQ = TdS = CV dT + pdV
C
R
dS = V dT + dV
T
V
Integration für Übergang von Zustand 1 nach Zustand 2
∆S = CV ln
T2
V
+ R ln 2
T1
V1
Entropie steigt bei Temperaturerhöhung und Volumenvergrößerung.
40
4. Van-der-Waalsches Gas
als Beispiel für eine empirische Zustandsgleichung
Frage: In welcher Richtung muß die Zustandsgleichung eines idealen Gases pV = nRT
abgeändert werden, damit auch reale Gase beschreibbar sind? (obwohl einige Gase, z.B.
Helium, gut als ideale Gase beschrieben werden können)
1) Offenbar berücksichtigt ideale Gasgleichung nicht, daß Atome ein Eigenvolumen besitzen:
V=
nRT
p
Korrektur:
; p→∞ ; V →0
V=
nRT
+B ; p→∞ ; V → B
p
B: gemeinsames Eigenvolumen aller Moleküle der Substanz:
p=
nRT
V −B
2) Wechselwirkung (Anziehungskräfte) der Teilchen untereinander wurden nicht
berücksichtigt. Wie könnten die sich bemerkbar machen?
K
W and
M olek üle in der M itte:
A lle K räf te heben
sich auf .
W and
M olek üle am R and:
... (s39) A nziehungsk raf t
in R ichtung auf den
I nnenraum
ter m o28.c w 2
Der vom Gas ausgeübte Druck sollte deshalb geringer sein.
→
p' ~
Einführung einer Korrekturgröße, die proportional dem Quadrat der Teilchendichte ist.
N N A2
=
V V V2
41
Van-der-Waals Gleichung:
nRT
A2
p=
−
V − B V2
Gleichung 3. Grades für V:
pV 3 − V 2 ( pB + nRT ) + A 2V − A 2 B = 0
p als Funktion von V zeigt die folgende Abhängigkeit ( T = konst ., Isothermen):
p
2
T
1
V
B
(termo30.cw2)
Im Gebiet der Isotherme zwischen den Punkten 1 und 2 gilt
dp
>0
dV
Bei Verkleinerung des
Volumens würde der Druck
sinken.
Fluktuation dV < 0 ⇒ dp < 0 des Gases. Außendruck würde überwiegen ⇒ weitere
Verkleinerung des Volumens. Diese Situation ist instabil. Instabiler Bereich der Isotherme,
physikalisch nicht realisierbar.
p
instabiler Bereich der Isotherme
V
(termo31.cw2)
42
In Wirklichkeit tritt im instabilen Bereich der Isotherme etwas anderes auf: Die Substanz
spaltet sich in zwei Komponenten auf: gasförmige und flüssige Phase.
p
G as
Gas
f lüssi g
f l üssi g
V
Im horizontalen Teil der Isotherme wandelt sich das Gas allmählich in eine Flüssigkeit um.
p(T ) : Dampfdruck
p
Später zeigen wir, daß der horizontale
Bereich der Kurve so konstruiert werden
T
muß, daß die beiden Flächen F1 und F2 über
bzw. unter der Geraden gleich groß sind.
V
(termo34.cw2)
p
F1 = F2
F2
F1
(wird später bewiesen)
V
(termo35.cw2)
Für T > Tkrit keine Phasenumwandlung mehr.
43
p
Tkrit , V krit , pkrit
ungef. wie ideales Gas
5 Bereiche in der
(V, p)-Ebene
flüssig
Gas (Kondensation möglich)
V
nicht
erreichbar
2-Phasensystem
(termo36.cw2)
Kritische Isotherme besitzt keinen Extremwert, sondern Wendepunkt.
p=
RT
A2
− 2 = p (V ) ;
V −B V
dp
=0 ;
dV
dp 2
dV 2
=0
Aus diesen drei Gleichungen folgen die Koordinaten des kritischen Punktes in Abhängigkeit
von den Parametern A und B (Hausaufgabe).
Vkrit = 3B
;
B=
Vkrit
3
R=
8 A2
27 ⋅ B ⋅ Tkrit
;
pkrit =
pkrit =
A2
27 B 2
A2 ⋅ 9
2
27 ⋅Vkrit
,
Tkrit =
;
⇒
R=
8 A2
27 B ⋅ R
2
A2 = 3 pkrit Vkrit
2
8 ⋅ 3 pkrit Vkrit
⋅ 3 8 pkrit ⋅Vkrit
=
27 ⋅Vkrit ⋅ Tkrit
3 Tkrit
Die Van-der-Waals-Gleichung läßt sich unter Verwendung der kritischen Werte
folgendermaßen umschreiben ( n = 1) :

A2 
 p + 2  (V − B ) = RT
V 

2

 p + 3 p krit ⋅ Vkrit

V2


V − Vkrit  = T ⋅ 8 p krit Vkrit

3 
3 Tkrit

44
Einführung von Relativwerten: Tr =
2
 p
3Vkrit

+
 p krit
V2

V
p
T
, pr =
, Vr =
Vkrit
p krit
Tkrit
 V
1 8 T

− =
 Vkrit 3  3 Tkrit



 p r + 3 Vr − 1  = 8 Tr

3 3
Vr2 

In dieser Schreibweise besitzt die Van-der-Waals-Gleichung eine große Allgemeingültigkeit
unabhängig von der Art der Substanz und mit experimentell messbaren Parametern.
45
5. Die Thermodynamischen Potentiale
5.1. Einführung der Potentiale
Gibbs'sche Fundamentalgleichung.
TdS = dU + pdV
dS =
,
dU + pdV δ Q
=
T
T
Ist die Entropie als Funktion von U und V bekannt,
S = S (U ,V )
dann lassen sich durch Differentiation die Zustandsgleichungen ableiten,
dS =
∂S (U ,V )
∂S (U ,V )
dV
dU +
∂U
∂V
und es gilt nach Vergleich mit obiger Gleichung
∂S (U ,V ) 1
=
∂U
T
T = T (U ,V )
;
∂S (U ,V ) p
=
∂V
T
p = p(T ,V )
p = p(T ,U ,V )
kalorische ZG
thermische ZG
Die Entropie S ist ein thermodynamisches Potential in den Variablen U und V; Unter Verwendung der
Gibbs-Gleichung lassen sich bei Kenntnis der Funktion S = S (U ,V ) die Zustandsgrößen des
thermodynamischen Systems berechnen.
Analogie zur Mechanik
Potential: V = V (x , y , z )
 Kx 
 ∂V ∂ x 
r


K = − grad V ⇒  K y  = −  ∂ V ∂ y 
∂V ∂ z 
K 


 z
,
m
r
d 2r
dt 2
x
 &&
∂V ∂ x 
 && 


= m y  = − ∂V ∂ y 
 &&

∂V ∂ z 
z


Durch Differentiation des mechanischen Potentials erhält man die Bewegungsgleichungen.
47
Thermodynamik:
Durch Differentiation des thermodynamischen Potentials erhält man die
Zustandsgleichungen.
Außer der Entropie S lassen sich noch andere Potentiale angeben, die sich je nach den
thermodynamischen Bedingungen für unterschiedliche Situationen besonders gut eignen.
a) Innere Energie als Potential
(Auflösen der Gibbs-Fundgl. nach dU)
dU = TdS − pdV
U als Funktion von S und V:
U = U ( S ,V )
U als Zustandsgröße:
 ∂U 
 ∂U 
dU = 
 dS + 
 dV
 ∂S V
 ∂V  S
 ∂U 
 =T
Vergleich liefert die Zustandsgleichungen: 
 ∂S V
 ∂U 
; 
 = −p
 ∂V  S
b) Enthalpie als Potential
H = U + pV
;
dH = dU + Vdp + pdV
dH = TdS − pdV + Vdp + pdV
dH = TdS + Vdp
∂H 
∂H 
H = H ( S , p ) ; dH = 
 dp
 dS + 
 ∂ S p
 ∂ p S
Zustandsgleichungen:
 ∂H 

 =T
 ∂S  p
 ∂H 
 = V
; 
 ∂p  S
c) Freie Energie als Potential
Definition:
F = U − TS
;
dF = dU − S ⋅ dT − T ⋅ dS
dF = TdS − pdV − S ⋅ dT − T ⋅ dS
48
dF = − SdT − pdV
F = F (T ,V )
 ∂F 
 ∂F 

 = −S ; 
 = −p
 ∂T V
 ∂V  T
d) Die freie Enthalpie als Potential
G = U − TS + pV = H − TS
dG = dH − S ⋅ dT − T ⋅ dS
= TdS + Vdp − S ⋅ dT − T ⋅ dS
dG = − S ⋅ dT + Vdp ; G = G ( p ,T )
 ∂G 
 ∂G 
 dp + 
dG = 
 dT
 ∂T  p
 ∂p  T
 ∂G 
 = V

 ∂p  T
 ∂G 
; 
 = −S
 ∂T  p
Die freie Enthalpie G (T , p ) (auch genannt Freie Gibbs-Energie) ist für praktische
Anwendungen, z. B. in der Chemie, besonders gut geeignet, weil Prozesse häufig bei
konstantem Druck und Temperatur ablaufen.
Besonders wichtig: Sonderrolle von G:
G hängt nur von den intensiven Variablen p und T ab. In einem zusammengesetzten
System stimmen p und T im Gleichgewicht in allen Komponenten überein.
Alle anderen thermodynamischen Potentiale hängen auch (oder ausschließlich) von
extensiven Größen ab.
Das Potential F(T,V) wurde von Helmholtz eingeführt. Der Name Freie Energie beruht auf der
Tatsache, daß bei isothermen Prozessen ein thermodynamisches System Arbeit nicht auf
49
Kosten seiner inneren Energie leistet, sondern auf Kosten der Freien Energie, da wegen
dF = − SdT − pdV für dT = 0 gilt: dF = − pdV .
Die einzelnen Potentiale lassen sich umkehrbar eindeutig ineinander umrechnen. Sie enthalten
deshalb genau wie die Entropie S(U,V) alle Informationen über das thermodynamische
System.
Zusammenfassung
Thermodyn.
Vollständiges
Potential
Differential
(weil 2. gemischte
dU = TdS − pdV
Abl. gleich)
 ∂T 
 ∂p 

 = − 
 ∂V  S
 ∂S V
U = U (S ,V )
H = H (S , p )
H = U + pV
F = F (T ,V )
F = U − TS
G (T , p )
G = U − TS + pV
dH = TdS + Vdp
dF = − SdT − pdV
dG = − SdT − Vdp
Partielle Ableitung
 ∂U

 ∂S
 ∂U

 ∂V

 =T
V
Maxwell-Beziehung

 = −p
S
 ∂H 

 =T
 ∂S  p
 ∂T 
 ∂V 
 = 


 ∂p  S  ∂S  p
 ∂H 
 = V

 ∂p  S
 ∂F 

 = −S
 ∂T V
 ∂S 
 ∂p 

 =

 ∂V T  ∂T V
 ∂F 

 = −p
 ∂V  T
 ∂G 

 = −S
 ∂T  p
 ∂S 
 ∂V 
  = −

 ∂T  p
 ∂p T
 ∂G 
 = V

 ∂p  T
5.2. Die thermodynamischen Potentiale des idealen Gases
Ziel: Berechnung der thermodynamischen Potentiale U, H, F, G für ein ideales Gas
 ∂U
Ausgangspunkte: CV = 
 ∂T

 = const. und thermische Zgl. pV = nRT
V
50
Innere Energie: dU = CV dT ,
U = CV (T − T0 ) + U 0
Integration: ∫ CV dT = ∫ dU
: kalorische Zustandgleichung U = U ( T ,V )
(1)
mit Gibbs’scher Fundamentalgleichung: TdS = dU + pdV
dS =
CV
nR
dT +
dV
T
V
S − S 0 = CV ln
V
T
+ nRln
V0
T0
(2)
Ableitung der Potentiale in den Abhängigkeiten:
U = U ( S ,V ) , H = H ( S , p ) , F = F (T ,V ) , G = G ( p,T )
Innere Energie:
Auflösen von (2) nach T liefert:
1−κ
V 
T = T0  
 V0 
e
S − S0
CV
, mit κ =
Cp
CV
und C p − CV = nR
Einsetzen von T in kalorischen Zgl. (1) liefert das thermodynamische Potential U(S,V)
1−κ S − S0



 V 
CV
− 1 + U 0
U = CV T0   e

 V0 


(3)
(hier kann man sehen, dass (∂U ∂S )V wirklich T und zwar in obiger Form ergibt)
Freie Energie:
Einsetzen von U aus (1) und S aus (2) in F = U − TS :
51


V
T
F = CV (T − T0 ) − T CV ln + nRln + S 0  + U 0
V0
T0


(4)
Enthalpie (entsprechende Herleitung):
κ −1 S − S0


 p  κ

Cp
H ( S , p ) = C pT0 
e
− 1 + H 0

 p0 



(5)
Freie Enthalpie:


p
T
+ S0  + H 0
G (T , p ) = C p (T − T0 ) − T C p ln − nRln
p0
T0


Hier wurden der Nullpunkt für Entropie und innere Energie willkürlich gewählt.
52
6. Gleichgewichts- und Stabilitätsbedingungen
II. Hauptsatz: dS =
δQ
T
{
+ di S
,
δQ
T
{
- Austausch von Entropie mit der Umgebung (durch
da S
da S
Wärmeaustausch) , d i S - Entropieproduktion im Inneren des Systems bei spontanen
Prozessen
Solange in einem System irreversible Prozesse ablaufen, wird Entropie produziert. Wenn das
System abgeschlossen ist, kann seine Entropie nur anwachsen.
Im Gleichgewicht: Es laufen makroskopisch keine Prozesse mehr ab.
d i S = 0 und die Entropie erreicht ein Maximum.
Gleichgewicht
S
t
Damit Entropie im Gleichgewicht ein Maximum annimmt, muß neben dS = 0
δ 2 S < 0 gelten.
äquivalent:
∂S
=0
∂x
,
∂ 2S
< 0 , wobei x einen Systemparameter bezeichnet, dessen
∂x 2
Variation mit den Nebenbedingungen vereinbar ist.
Ähnliche Extremalbedingungen lassen sich auch für die anderen thermodynamischen
Potentiale angeben (s.u.)
Beispiel: Maximum der Entropie im Gleichgewicht
Ideales Gas im Gleichgewicht, im Gesamtvolumen V.
53
V
Entropie sei S0 , Gesamtzahl der Mole n.
Die Auslenkung aus dem Gleichgewicht ist in vielerlei Weise möglich.
Wir betrachten eine Aufteilung von V in 2 Volumen, V1 + V2 , z.B. durch Einschieben einer
Trennwand.
V1
V2
Es gilt im Gleichgewicht:
S10 =
V1
S0 ,
V1 + V2
S20 =
V2
S0
V1 + V2
weil Entropie eine extensive Größe ist, S10 + S20 = S0 .
n1 =
nV1
V1 + V2
;
n2 =
nV2
V1 + V2
Verschiebung der Wand
V1 → V1 + ∆ V ,
V2 → V2 − ∆ V
System befindet sich nicht mehr im Gleichgewicht.
für die Entropie eines idealen Gases in Abhängigkeit vom Volumen hatten wir hergeleitet:
S = S0 + nR ln
V
V0
,
V0 , S0 : Referenzzustand.
entsprechend:
54
∆S1 = S1 − S10 = n1 R ln
V1 + ∆V
V1
∆ S2 = S2 − S20 = n2 R ln
V2 − ∆V
V2
S1 + S 2 = S10 + S 20 + n1R ln
1
424
3
S0
V1 + ∆V
V − ∆V
+ n2 R ln 2
V1
V2
 V1
V + ∆V
V2
V − ∆V
+
S = S 0 + nR
ln 1
ln 2
V1
V1 + V2
V2
 V1 + V2



 V
dS
V1
1
V2
V2
= nR  1 ⋅
⋅ +
⋅
d (∆V ) ∆V = 0
V1 + V2 V1 + ∆V V1 V1 + V2 V2 − ∆V
=
d 2S
d (∆V )2
=
∂ (∆V )2
 V1
V2

−
 V1 + ∆V V2 − ∆V


=0 ,
 ∆V = 0

nR 
V1
V2

−
−
V1 + V2  (V1 + ∆V )2 (V2 − ∆V )2 
∆V = 0
=
∂ 2S
nR
V1 + V2
nR
V1 + V2
=−
 1
1 
nR
 − −
 = −
V1 + V2
 V1 V2 
nR
V1 + V2
1
1 
 +
 < 0
 V1 V2 
1
1 
 +

 V1 V2 
Maximum
55
,
⇒ S = S (∆V )
 1 
 −  

 V2  
⇒ Extremwert
S
S0
V2
- V1
Extremfälle:
∆ V=V 2
∆ V= _V 1
S
S
_ oo
_ oo
∆V
(termo39.cw2)
Extremalbedingungen für die anderen thermodynamischen Potentiale:
Aus
dS ≥
δQ
bei spontanen Prozessen, δQ ≤ TdS , folgt:
T
1) δQ = dU + pdV ≤ TdS
 H = U + pV
2) δQ = dH − pdV − Vdp + pdV ← 
dU = dH − pdV − Vdp
δQ = dH − Vdp ≤ TdS
 F = U − TS
3) δQ = dF + dT ⋅ S + dS ⋅ T + pdV ≤ TdS ← 
dU = dF + dT ⋅ S + dS ⋅ T
δQ = dF + SdT + pdV ≤ 0
G = H − T ⋅ S
4) δQ = dG + dT ⋅ S + dS ⋅ T − Vdp ≤ TdS ← 
dH = dG + dT ⋅ S + dS ⋅ T
δQ = dG + dT ⋅ S − Vdp ≤ 0
Aus 1) – 4)
56
dU ≤ TdS − pdV
dH ≤ TdS + Vdp
dF ≤ − SdT − pdV
dG ≤ − SdT + Vdp
U,
H,
F,
G
nehmen Minimum an, wenn
(T, V)
(S, V)
konstant gehalten werden.
(T, p)
(S, p)
(termo38.cw2)
δ 2U > 0
H : δ 2H > 0
Minimum von U :
F:
δ F >0
G:
δ 2G > 0
Besonders wichtig:
Entropie im Gleichgewicht maximal.
Alle anderen thermodynamischen
2
Potentiale nehmen ein Minimum an
G → Minimum im Gleichgewicht, bei T = konst . ; p = konst .
Die Vorzeichenbedingungen für die 2. Ableitung in der Nähe von Gleichgewichtszuständen
haben wichtige Konsequenzen, z. B.:
+δV
-δV
Wir betrachten zwei Teilsysteme
eines Systems, V = konst. , T = const.
!
Fluktuation: ∆ F = (F (V + dV ) + F (V − dV )) − 2U (V ) > 0
Reihenentwicklung:


1 d 2F
1 d 2F
dF
dF


2
2
(
)
∆U =  F (V ) +
dV
+
−
+
dV
F
V
dV +
dV


 − 2 F (V )
2
2
2 dV
2 dV
dV
dV

T 
T
57
∆´F =
1  ∂ 2 F 
(dV )2
2  ∂V 2 
T
Konsequenz:
 ∂ 2F  !


 ∂V 2  > 0

T
 ∂F 
Es gilt aber: 
 = −p
 ∂V T
,
,
∂ 2F
 ∂p 
=
−

 >0
∂V 2
 ∂V T
,
 ∂p 
⇒ 
 <0
 ∂V T
Eine Vergrößerung des Volumens führt im Gleichgewicht stets zu einer Verringerung des
Druckes.
zur Erinnerung: Teil der Isotherme des Van-der-Waals-Gases, wo
∂p
<0
∂V
∂p
<0
∂V
∂p
>0
∂V
stabil,
instabil.
58
∂p
> 0 , war instabil.
∂V
7. Stofflich offene Systeme
Alle bisherigen Betrachtungen bezogen sich auf stofflich abgeschlossene Systeme. Diese Einschränkung soll jetzt fallengelassen werden, d. h. es wird zugelassen, dass sich die
Stoffmenge eines Systems durch Stoffzufuhr oder -abfuhr verändert.
7.1. Einkomponentensysteme
Nur eine Stoffsorte.
Zunächst: Der I. Hauptsatz kann nicht mehr in der einfachen Form dU = δQ + δA verwendet
werden.
Zusammenführung zweier identischer Systeme
p, T , V + p, T , V
Es wird weder Arbeit geleistet noch Wärme zugeführt.
δQ = 0 ; δA = 0 , trotzdem verdoppelt sich U.
Um dieses Dilemma zu umgehen, schreiben wir den I. Hauptsatz in der Form:
du = δq + δa ; d. h. mit intensiven Größen (hier: molare Größen)
Das oben genannte Problem tritt hier nicht auf, da sich durch Addition von Systemen u, q, a
nicht ändern.
U = n ⋅u ; Q = n ⋅ q ; A = n ⋅ a
δq = Tds
du = Tds − pdv
Multiplikation mit n:
ndu = Tnds − p ⋅ ndv
d (nu ) = n ⋅ du + u ⋅ dn = dU
d (ns ) = n ⋅ ds + s ⋅ dn = dS
d (nv ) = n ⋅ dv + v ⋅ dn = dV
59
d1(nu
) − dn3
⋅ u = Td
(ns
) − Tsdn
− pd (nv ) + pdn ⋅ v
4
4244
14
4244
3 1442443
dU = TdS − pdV + (u + pv − Ts ) ⋅ dn
entspricht: dU = TdS − pdV + gdn
mit g = u + pv − Ts : freie Enthalpie/Mol
Mit
 ∂U 
 ∂U 
 ∂U 
dU = 
 dS + 
 dV + 
 dn
 ∂S V ,n
 ∂V  S ,n
 ∂n  S ,V
gilt
 ∂U 
=g


 ∂n  S ,V
und nach wie vor:
 ∂U 
 ∂U 

 =T ; 
 = −p .
 ∂S V ,n
 ∂V  S , n
Das ist die Gibbs'sche Fundamentalgleichung für stofflich offene Systeme. Der Term gdn
berücksichtigt die Änderung der inneren Energie infolge Stoffzufuhr. Hier können die
Molzahlen als zusätzliche unabhängige Variable betrachtet werden, d.h. es gilt jetzt:
U = U (V , S , n ) .
Auch die anderen thermodynamischen Potentiale hängen jetzt von n ab, z.B.
dh = Tds + vdp
ndh = Tnds + nvdp
d (n ⋅ h ) − h ⋅ dn = Td (n ⋅ s ) − Tdn ⋅ s + nvdp
dH = TdS + Vdp + (h − Ts ) dn
123
u + pv −Ts = g
dH = TdS + Vdp + g ⋅ dn
7.2. Mehrkomponentensysteme
60
Wir betrachten ein homogenes System, das sich aus K verschiedenen Stoffen zusammensetzt
(z. B. Gasgemisch). Zu jedem Stoff gehört eine Molzahl ni . Das thermodynamische Potential
hängt jetzt nicht nur von n, sondern von den ni ab.
U = U (S ,V , ni )
Das vollständige Differential lautet:
K
 ∂U 
 ∂U 
 ∂U 

dU = 
dni
 dS + 
 dV + ∑ 
 ∂S V ,n j
 ∂V  S , n j
i =1  ∂ni  S ,V ,n
j ≠i
↑
µi =
−p
T
Die Größen µi = (∂U ∂ni )S ,V , n
j ≠i
∂U
∂ni
n j ≠ ni
bezeichnet man als chemische Potentiale der Stoffsorten i.
U = U (S , V , n j ) ⇒ µ i = µi (S , V , n j )
Da
Für Systeme, die nur aus einer Stoffkomponente bestehen, ist das chemische Potential gleich
der molaren freien Enthalpie:
 ∂U 
=g

 ∂n  S ,V
µ =
dU = TdS − pdV + ∑ µi dni
Änderung der inneren Energie schreibbar:
i
Analog für die anderen thermodynamischen Potentiale:
dH = TdS + Vdp + ∑ µ i dni ⇒ µ i (S , p, n j ) =
i
∂H
∂ni
dF = − SdT − pdV + ∑ µ i dni ⇒ µ i (T , V , n j ) =
i
n j ≠ ni
∂F
∂ni
61
n j ≠ ni
dG = − SdT + Vdp + ∑ µ i dni ⇒ µi (T , p, n j ) =
i
∂G
∂ni n ≠n
j
i
Die Vertauschbarkeit der zweiten partiellen Ableitungen führt zu Gleichungen der Form
 ∂V 
 ∂µ 


=  i 
 ∂ni T , p ,n j  ∂p T ,n j
Gibbs-Duhem'sche Gleichung
mathemat. Einschub: eine homogene Funktion
f ( x1 ,.., x n ) vom Grad k hat folgende
Eigenschaften
f (λx1 ,.., λxn ) = λk f ( x1 ,.., xn )
Differentiation nach λ :
n
∂f
∑ ∂(λxi )xi = kλk −1 f ,
und speziell für λ = 1
i =1
kf =
n
∂f
∑ xi ∂xi
i =1
Andere Schreibweise: k =
n
∑
i =1
xi ∂f
=
f ∂xi
n
∂lnf
∑ ∂lnxi
i =1
Die extensiven Größen der Thermodynamik sind homogene Funktionen vom Grade k = 1
bezüglich ihrer unabhängigen extensiven Zustandsvariablen.
Beispiel:
λF (T ,V , ni ) = F (T , λV , λni ) , Verdopplung von Volumen und Molzahl bei konst.
Temperatur führt zur Verdopplung der freien Energie
Wir gehen von der freien Enthalpie aus. G ist eine extensive Größe. Vergrößerung der
Molzahlen um Faktor λ bei konstanten T und p.
62
G (T , p , λni ) = λG (T , p , ni )
14444244443
Mathematisch: G ist eine homogene Funktion vom Grade 1 in den Variablen ni .
∂G (T , p , λni )
= G (T , p , ni )
∂λ
∂G (T , p , λni ) ∂ (λni )
⋅
=G
∂
(
λ
)
λ
∂
n
i
1
2
3
i =1
K
∑
ni
λ beliebig, z. B. = 1
∑ µ i ni = G(T , p , n j )
∂G
∑ ∂n ni = G oder
i
i =1
K
K
Gibbs-Duhem-Beziehung
i =1
K
G = U − TS + pV = ∑ µi ni
Wegen:
i =1
folgt:
U − TS + pV − ∑ µi ni = 0
(andere Form der Gibbs-Duhem-Gl.)
i
oder( in differentieller Form): dU − dT ⋅ S − TdS + dpV + pdV − ∑ µ i dni − ∑ ni dµ i = 0
i
i
und unter Verwendung der Gibbs’schen Fundamentalglg:. dU = TdS − pdV + ∑ µi dni
i
folgt
TdS − pdV + ∑ µ i dni − dT ⋅ S − TdS + dpV + pdV − ∑ µ i dni − ∑ ni dµ i = 0
i
SdT − Vdp + ∑ ni dµ i = 0
i
i
Differentielle Form der Gibbs-Duhem-Beziehung.
i
Generell: Die intensiven thermodyn. Größen sind bzgl. ihrer unabh. extensiven
Zustandsvariablen
homogene
Funktionen
vom
Grade
k = 0.
So
gilt
z.B.
p(T ,V , n ) = p(T , λV , λn ) , d.h. Verdopplung von V, n bei konst. T führt nicht zur Änderung
von p.
63
Chemische Potentiale sind intensive Variable (Differentialquotient zweier extensiver Größen).
Sie ändern sich nicht, wenn alle Molzahlen ni um den gleichen Faktor vergrößert werden.
daraus folgt z.B.:
 ∂µ 
∑ nl  ∂nk 
l

Als
l
T , p ,ni
= 0 ⋅ µk = 0
intensive
Duhem-Margulesche Beziehung
Größen
hängen
die
chemischen
µ l = µ l ( p ,T , ni ) = µ l ( p ,T , n1 ,..., n k ) von den ni nur in der Form
xi =
ni
n
= i :
∑ nj n
Potentiale
Molenbrüche
j
ab, d.h. µ l = µ l ( p ,T , xi ) . Offensichtlich gilt:
K
∑ xi = 1
i =1
Besteht ein System aus k Stoffen, ist die Zahl der unabhängigen Molenbrüche gleich k − 1.
Gleichgewichtsbedingung für ein Mehrkomponentensystem
Im Gleichgewicht nimmt G ein Minimum an. Wir betrachten wieder eine Fluktuation, wobei
bei p = konst . , T = konst . und n = ∑ ni = konst . einige Moleküle aus einer Hälfte des Systems in die andere übergehen:
+δni
-δni
System, bestehend aus zwei gleichen Teilen
!
∆G = (G (ni + δni )) + (G (ni − δni )) − 2G (ni ) > 0
Taylorreihenentwicklung:
64
K
K


1
∂G
∂ 2G


δni +
∆G = G +
δniδn j ...
∂ni
2 i , j =1∂ni∂n j


i =1
K
K


!
1
∂G
∂ 2G


δni +
+ G −
δniδn j  − 2G > 0
∂ni
2 i , j =1∂ni∂n j


i =1
2
δ G=
K
∑
i, j
Es gilt:
∑
∑
∑
∑
!
∂ 2G
δniδn j > 0
∂ni∂n j
,
bei Änderung aller K Molzahlen
positiv definite quadratische Form
∂µ i ∂µ j
∂ 2G
∂ 2G
=
und deshalb:
=
∂ni∂n j ∂n j ∂ni
∂n j ∂ni
Etwas über quadratische Formen:
F=
K
∑ aij xi x j
i, j =1
K = 2:
{ }
mit aij = a ji , Elemente einer symmetrischen Matrix A = aij
F = a11 x12 + a12 x1 x2 + a21 x1 x2 + a22 x22 ,
F = a11 x12 + 2a12 x1 x2 + a22 x22
Wann ist F, unabhängig von den Werten x1, x2 , immer >0 und nur =0 für x1 = x2 = 0 ?
F
x2
x1
(termo40.cw2)
Wir fordern, daß F = 0 keine nichttrivialen reellen Nullstellen hat.
!
 2a

a
x12 +  12 x 2  x1 + 22 x 22 = 0
a11
 a11

65
a
x1 = − 12 x2 ±
a11
2
 a12 x2   a22  2

 − 
 x2
 a11   a11 
Zunächst muß gelten a11 > 0 und a22 > 0 .
Denn wäre a11 < 0 , dann F < 0 für x2 = 0 , für alle x1 ≠ 0 ; F = a11x12
oder wäre a22 < 0 , dann F < 0 für x1 = 0 , für alle x2 ≠ 0 ; F = a22 x22
Weiterhin: Damit keine reelle Nullstelle
2
 a12  a22

 −
<0
a
a
 11 
11
2
× a{
11
>0
a122 − a11a22 < 0 ; a11a22 − a12 a21 > 0
a11 =$
In unserem Fall ist:
∂2G ∂µ1
=
∂n12 ∂n1
∂ 2G ∂µ 2
a12 =
=
∂n1∂n2 ∂n1
;
a22 =$
∂2G ∂µ 2
=
∂n22 ∂n2
∂ 2G ∂µ1
; a21 =
=
∂n2∂n1 ∂n2
Bedingung dafür, daß die quadratische Form positiv definit ist.
∂ 2G ∂ 2G  ∂ 2G  ∂ 2G 
>0
−
∂n12 ∂n22  ∂n1∂n2  ∂n2∂n1 
sowie
∂ 2G
>0 ;
∂n12
oder:
∂2 G
>0
∂n22
∂µ1
>0 ;
∂n1
∂µ 2
>0 ;
∂n2
∂µ1 ∂µ 2 ∂µ1 ∂µ 2
−
⋅
>0
∂n1 ∂n2 ∂n2 ∂n1
66
Allgemein:
 ∂µ1

 ∂n1
 ∂µ 2

 ∂n1
 M
 ∂µ k
 ∂n
 1
∂µ1
∂n 2
∂µ 2
∂n1
∂µ k
∂n 2
∂µ1
∂µ1 
L

∂n 3
∂n k 




∂µ k 
L
∂nk 
; Bedingung:
∂µi
>0
∂ni
Alle Hauptdeterminanten > 0. Für K = 2 erhält man obiges Resultat.
7.3. Mischung idealer Gase
K verschiedene ideale Gase werden durchmischt.
Keine chemische Reaktionen, keine anderen Wechselwirkungen.
Eigenschaften im gemischten Zustand
piV = ni RT
o
x
ox o x
V
o
x x o
o
Gültigkeit der Zst.gl., für jedes Gas
K
K
p = ∑ pi
pi : Partialdrücke
i =1
K
K
i =1
i =1
n = ∑ ni
i =1
V ∑ pi = RT ∑ ni = nRT
pV = nRT
Gültigkeit der Zustandsgleichung, allgemein
Daltonsches Gesetz: Die Partialdrücke pi eines Gemisches idealer Gase sind durch die
Temperatur T und das Gesamtvolumen V über die Zustandsgleichung piV = ni RT bestimmt
und der Gesamtdruck setzt sich additiv aus den Partialdrücken zusammen.
67
Ungemischter Zustand
p, T
p, T
p, T
p, T
V1
V2
V3
Vk
n1
n2
n3
nk
pVi = ni RT für jede Komponente
p ∑ Vi = RT ∑ ni = nRT
K
∑ Vi = V
i =1
Vi : Teilvolumina
Beweglich, aber undurchlässige Trennwände.
Übergang vom ungemischten in den gemischten Zustand (nach Herausziehen der
Trennwände): spontaner Prozeß
Entropieänderung bei Mischung
Entropie erhöht sich. Gesucht:
∆S = nR ln
Vende
Vanfang
(bereits bekanntes Resultat)
In unserem Fall:
∆Si = ni R ln
V
Vi
∆Si = ni R ln
n
ni
; mit
K
K
i =1
i =1
∆S = ∑ ∆Si =R ∑ ni ln
wegen
ni
<1
n
pVi = ni RT  V
n
 =
pV = nRT  Vi ni
K
n
n
= − R ∑ ni ln i
ni
n
i =1
folgt ∆S > 0
**)
∆S - „Mischungsentropie“
Entropieänderung bei Durchmischung ist stets positiv, d.h. Mischung ist ein spontaner Prozeß.
{Anmerkung: in der statistischen Thermodynamik kann man den folgenden Ausdruck für die
Entropie herleiten:
S = −k
∑ piln pi
i
68
Steht in enger Beziehung zu **): Umformung ∆S = − Rn
K
n
n
∑ ni ln ni
. Mit Definition:
i =1
pi = ni n (Wahrscheinlichkeit dafür, ein Teilchen der Sorte i anzutreffen). n = 1 : Entropie
pro Mol:
∆S
n
= −R
K
∑
i =1
ni ni
ln = − R
n
n
K
∑ pi ln pi
i =1
Entropie pro Teilchen:
∆S
R
=−
nL
L
K
K
i =1
i =1
∑ pi ln pi = −k ∑ pi ln pi
mit der Avogradroschen Zahl L, und der Boltzmann-Konstante: k =
R
L
Freie Enthalpie:
G = H − TS = U + pV − TS
∆Gi = ∆U i + ∆ ( pV )i − T∆S i
0
da vorher pVi = ni RT nachher piV = ni RT
0
∆Gi nur aufgrund Entropieänderung
Gi (nachher) = Gi (vorher) − T∆Si
, Gi (vorher) = Gi ( p, T )
Gi ( p ,T , ni ) = Gi ( p ,T ) − T∆S i
Gi ( p , T , ni ) = Gi ( p , T ) + RTni ln
ni
n
K
n
G ( p ,T , ni ) = ∑ g i ni + RT ∑ ni ln i
n
i
i =1
K
Unter Verwendung der Gibbs-Duhem-Beziehung: G = ∑ niµi folgt
i =1
µ i = g i ( p ,T ) + RT ln
ni
= g i ( p , T ) + RT ln xi
n
µ i : chemisches Potential
69
p: Gesamtdruck (= Druck jeder einzelnen Komponente vor der Durchmischung)
Darstellung von µ mittels Konzentrationen:
i = 1,..., K
xi =
ni
=
n
gelöste Stoffe ,
ni
ci =
xi =
K
∑ ni + n0 ∑ ni
i =1
Lösungsmittel
ni V
=
K
i = 0:
i =1
V + n0 V
ni
: Konzentration
V
ci
K
∑ ci + c0
≈
ci
für i > 0 falls c0 >> ci ,
c0
i =1
d. h. wenn Lösungsmittel in großem Überschuß vorliegt.
µi ≅
c
g i (T , p ) + RT ln i
c0
14442444
3
für i > 0
Unabhängig von der Maßeinheit, in
der Konzentrationen gemessen werden.
µ i = g i (T , p ) − RT ln c0 + RT ln ci
14442444
3
µi0 ( p ,T )
µ i0 : Abhängig von Konzentrationsmaßeinheit,
µi0 ( p, T ) :
Konzentration c gemessen in Mol/l (molar)
chemisches Standardpotential, (chemisches Potential, wenn gelöster Stoff in
Konzentration 1 molar vorliegt).
µ i = µ i0 ( p ,T ) + RT ln ci
7.4. Chemische Reaktionen
Wir interessieren uns hier zunächst nur für das chemische Gleichgewicht.
70
Allgemein können wir eine chemische Reaktion folgendermaßen schreiben:
K
M
∑ (− ν i )Bi
∑ νi Bi
i =1
i = M +1
mit den Eingangsstoffen:
B1,..., BM
und den Endstoffen:
BM +1,..., BK
ν i stöchiometrische Koeffizienten
ν i < 0 für i = 1,..., M
ν i > 0 für i = M + 1,...K
z. B. monomolekulare Reaktion, M = 1, K = 2
B1
B2 ,
ein Mol B1 geht über in ein Mol B2 (oder 5 Mol in 5 Mol)
ν1 = −1 ; ν2 = 1
Biomolekulare Reaktion z. B. H2 + Cl2
2 HCl
( M = 2, K = 3 )
B1 = H2 ; B2 = Cl2 ; B3 = HCl
B1 + B2
2 B3
ν1 = −1 ; ν2 = −1 ; ν3 = 2
Wir nehmen an, daß die chemische Reaktion bei konstantem Druck und konstanter
Temperatur abläuft.
Gleichgewicht gekennzeichnet durch: G → min.
Fluktuationen von ni möglich.
71
(δG )T , p = ∑  ∂G 
K


i =1
 ∂ni  p ,T ,nl
K
δni = ∑ µ iδni = 0
!
i =1
Bei chemischen Reaktionen sind die δni nicht unabhängig voneinander wählbar.
z. B. im Fall: B1
oder für:
δni = νiδξ .
B2 ,
B1 + B2
n1 + n2 = n = const
2 B3
,
⇒
− δn1 = + δn2
⇒ − δn1 = − δn2 = 2 δn3
oder: ni = ni0 + νiξ
ξ - Reaktionslaufzahl,
ξ = 1: ein Formelumsatz
Beim Fortschreiten der Reaktion ändern sich die Molzahlen entsprechend den
stöchiometrischen Koeffizienten.
K
Mit
∑ µiδni = 0
i =1
K
folgt
∑ µ ν δξ = 0
i =1
i i
; δξ ≠ 0 frei wählbar, also kürzbar
K
∑ µi νi = 0
im chemischen Gleichgewicht, allgemeinste Form der GG-Bedingung für
i =1
eine (einzelne) chem. Reaktion bei T, p=konst.
K
Die Größe A = −∑ µ iν i wird Affinität der Reaktion genannt (Vorzeichenkonvention nicht
i =1
eindeutig in Literatur). Hier so gewählt, dass A > 0 eine positive Reaktionsgeschwindigkeit
bedingt, v > 0 , Spontane Reaktion: A > 0 .
chemisches Gleichgewicht: A = 0, Affinität verschwindet.
Monomolekulare Reaktion: ν1 = −1 ; ν2 = 1 ,
72
A = + µ1 − µ 2
µ1 = µ10 ( p ,T ) + RT ln c1
µ 2 = µ 20 ( p , T ) + RT ln c 2
A = + µ10 − µ 02 + RT ln c1 − RT ln c2
Daraus folgt:
Chemisches Gleichgewicht A = 0:
RT ln
c 2eq
c1eq
c2eq
Andererseits
c1eq
= µ10 − µ 20
= K eq : Gleichgewichtskonstante
Verhältnis von Produkt- zu Substratkonzentrationen im Gleichgewicht
RT ln K eq =
µ10
− µ 20
,
K eq = e
µ10 − µ 20
RT
somit Affinität darstellbar in der Form: A = + RT ln K eq + RT ln c1 − RT ln c 2
A = RT ln K eq
c1
c2
Reaktion spontan, wenn A > 0 :
K eq
c1
>1 ,
c2
c2
k
<K= 1
c1
k−1
ν 1 = k1c1 − k−1c2 > 0
Allgemein:
µ i = µ i0 ( p ,T ) + RT ln ci
K
Im Gleichgewicht:
∑ νiµi = 0
i =1
73
∑ν (µ ( p, T ) + RT ln c ) = 0
0
i
i
eq
i
i
K
∑ν i ln cieq = −
i =1
1
RT
K
∑ν i µi0 ( p ,T ) = ln K eq ( p ,T )
i =1
Gleichgewichtskonstante nur von p, T abhängig (sowie deren numerischer Wert, wegen der
Definition von µi0 , von der gewählten Konzentrationseinheit)
K
e
e
∑ν i ln ci
eq
i =1
= K eq ( p ,T )
(ν lnc
1
eq
+ν 2lnceq + ...ν K lnceq
1
2
K
) = K ( p ,T )
eq
c1ν,1eq cν2 2,eq ...cνKK,eq = K eq ( p ,T )
K
∏ cνi ,eq = K eq ( p ,T )
i
Massenwirkungsgesetz
i =1
Wegen νi < 0 für Ausgangsstoffe. Konzentration der Eingangsstoffe im Nenner.
z. B.
A+ B
Ceq ⋅ Deq
Aeq ⋅ Beq
C + D;
νC = ν D = 1 , ν A = ν B = −1
= K eq , hier Aeq usw, Konzentrationen der jeweiligen Stoffe
Massenwirkungsgesetz (MWG) wurde eingeführt von GULDBERG und WAAGE, 1867.
Es gestattet bei vorgegebenen Anfangsmolzahlen die Berechnung der Molzahlen nach Ablauf
der chemischen Reaktion im Gleichgewicht.
Charakterisierung von chemischen Reaktionen durch ∆G -Werte:
74
K 
K
∂G 
 δni = ∑ µ i δni
dG = ∑ 
i =1  ∂ni  p ,T
i =1
δni gekoppelt über stöchiometrische Koeffizienten.
δni = νiδξ
Reaktionslaufzahl
wenn δξ = 1 dann
∆ni = νi
(ein Formelumsatz in Mol)
Wenn Reaktionsgefäß sehr groß, bleibt Konzentration und deshalb das chemische Potential
konstant.
K
∆G = ∑ µi νi = − A
;
$ ∆G = 0
A=0⇒
i =1
hier ist ∆G die Änderung der freien Enthalpie pro Formelumsatz.
Wenn
∆G < 0 dann ist A > 0 : spontane Reaktion.
Van't Hoffsche Gleichung
Ausgangspunkt wieder:
dG = − SdT + Vdp + ∑ µ i dni
i
 ∂G 


=V
 ∂p T ,ni
 ∂G 
; 
= −S

 ∂T  p ,ni
außerdem galt: ln K eq ( p, T ) = −
1
RT
K
∑ν µ ( p, T )
i =1
i
0
i
und: µ i0 = g i (T , p ) − RT ln c 0
75
 ∂lnK 
1

 = −
RT
 ∂p T
 ∂g i 
K
∑ν  ∂p 
i =1
i

T
=−
1
RT
∑ν v
i i
i
vi : Molares Volumen des Stoffes i.
z. B. Monomolekulare Reaktion:
ν1 = −1 ; ν2 = +1
 ∂lnK 
1
(− v1 + v2 ) = v1 − v2 = − ∆v

 = −
RT
RT
RT
 ∂p T
∆v = v2 − v1
∆v : Änderung des molaren Volumens
wenn ∆v < 0 ⇒ v2 < v1 :
Endstoffe haben ein kleines Volumen.
 ∂lnK 

 > 0
 ∂p T
Bei Druckerhöhung wird das Gleichgewicht zugunsten der Endstoffe verschoben (Erhöhung
der Gleichgewichtskonstante).
Allgemeiner: Druckerhöhung verschiebt das Gleichgewicht zugunsten des Zustandes mit
kleinerem Volumen; ist wichtig bei Steuerung von Prozessen, z.B. wenn Gase in andere
Aggregatzustände umgewandelt werden.
Ist
∆v = 0
sind
die
Gleichgewichtsmolenbrüche
(oder
–konzentrationen)
Druckänderung nicht zu beeinflussen.
∆h
 ∂lnK 
Ähnlich läßt sich herleiten: 
 =
2
 ∂T  p RT
∆h : Änderung der molaren Enthalpien bei einem Formelumsatz ( ξ = 1 )
( ∆h = q ) – also die bei der Reaktion freiwerdende oder zuzuführende Wärme (isobar!)
76
durch
exotherme Reaktion: ∆h < 0 : Die Endstoffe haben einen kleineren Wärmeinhalt als die
Eingangsstoffe
 ∂lnK 

 <0⇒
 ∂T  p
Bei Temperaturerhöhung wird das Gleichgewicht zugunsten der Ausgangsstoffe verschoben.
endotherme Reaktion:
∆h = q > 0
Temp.erhöhung verschiebt sich das Gleichggewicht zugunsten der Produkte.
 ∂lnK 
∆v
 = −

RT
 ∂p  T
∆h
 ∂lnK 
; 
 =
 ∂T  p RT 2
:
Van't Hoffsche Gleichungen
77
8. Der osmotische Druck
Ihnen bereits bekanntes Phänomen, hier dargestellt als spezieller Fall der Anwendung von
Gleichgewichtsbeziehungen.
Wir betrachten folgende Anordnung:
(B)
(A)
A
n0
V = V (1) + V (2 ) = konst .
nB0
n1A
semipermeable Wand (durchlässig für Lösungsmittel)
Lösungsmittel (0) kommt in beiden Kammern vor: n0A ; n0B
gelöste Substanz (1): nur in der linken Kammer: n1A
Wir wollen für dieses System die Gleichgewichtsbedingung betrachten.
Wegen T = konst . , V = konst . ist im Gleichgewicht die Freie Energie F minimal.
dF = − SdT − pdV + ∑ µ i dni
,
F = F (T ,V , n1 ,..., n K )
i
Die Gleichgewichtsbedingung lautet: (δF )T ,V ,M = 0
, M: konstante Gesamtmenge; δF
bezieht sich auf "erlaubte" Fluktuationen.
hier: Fluktuation des Lösungsmittels von einer Teilkammer in die andere.
(
)
( )
F = F A + F B ; F A = F A n0A , n1A ; F B = F B n0B
 ∂F A  A  ∂F A  A  ∂F B  B
δn + 
δn
δn + 
 ∂n A  0  ∂n A  1  ∂n B  0
 1 
 0 
 0 
δF = δF A + δF B = 
Erlaubte Fluktuation:
78
n0A + n0B = konst . ⇒ δn0A = −δn0B

A
 ⇒ δn1 = 0
n1A = konst .
 ∂F A   ∂F B 
δn A = 0
−
0
A  
B 

 ∂n0   ∂n0 
δF = 
↓
↓
µ0A
µ 0B
µ 0A = µ 0B
daraus folgt:
Im Gleichgewicht müssen die chemischen Potentiale des Lösungsmittels gleich sein.
Nach unserer Ableitung gilt:
µ 0A = µ 0A (V A ,T ; n0A , n1A ) ,
µ 0B = µ 0B (V B , T , n0B )
Wir ersetzen V A und V B durch die thermische Zustandsgleichung:
(
)
V A = V A p A ,T ,
(
V B = V B p B ,T
)
und erhalten
µ 0A = µ 0A ( p A , T , n0A , n1A ) ,
µ 0A = g 0 ( p A ,T ) − RT ln
µ 0B = µ 0B ( p B , T , n0B )
n0A + n1A ! B
= µ 0 = g 0 p B ,T
A
n0
(
)
Wir entwickeln den Logarithmus (nur bis linearen Term):
ln
 n1A  n1A
n0A + n1A
1 + A  ≅ A
=
ln
n0A
 n0  n0
und erhalten
79
(
)
g 0 p A , T − RT
(
n1A
= g 0 p B ,T
n0A
)
Wir definieren: π = p A − p B , Druckdifferenz
pB = p A −π
(
)
(
)
∂g
nA
g 0 p A , T − RT 1 = g 0 p A − π = g 0 ( p A , T ) − 0
π
A
∂p p = p A
n0
π klein, verdünnte Lösung
− RT
 ∂g 
n1A
= − 0 
π
A
n0
 ∂p  p = p A
,
 ∂G 

 = V
 ∂p T
∂g 0
= v0 molares Volumen des Lösungsmittels
∂p
RTn1A = n0A ⋅ v0 ⋅ π
In guter Näherung kann man für verdünnte Lösungen schreiben
n0A v0 = V A
RTn1A = V Aπ
Der osmotische Druck p A − p B = π von n Molen eines im Lösungsmittel mit dem
Volumen V gelösten Stoffes ist gleich dem Druck von n Molen eines idealen Gases im
Volumen V.
π hängt nicht ab von der Art des Lösungsmittels und dem gelösten Stoff.
πV = nRT .
80
9. Das elektrochemische Potential
Bisher wurden nur Systeme untersucht, deren Komponenten aus elektrisch neutralen Teilchen
bestanden. Betrachtet werden jetzt auch Ionen oder Elektronen, z. B. Elektrolyte.
Ausgangspunkt: Erneut Gibbs'sche Fundamentalgleichung:
dU = TdS − pdV + ∑ µ i dni
i
TdS = dU + pdV − ∑ µ i dni
i
dU: Änderung der inneren Energie infolge von Wärmezufuhr und mechanischer
Arbeit.Berücksichtigt bisher nicht die Änderung der inneren Energie infolge Änderung der
Zahl der geladenen Teilchen.
Gesamt innere Energie: U + = U + Q eϕ
Q eϕ : elektrostatische Energie
ϕ:
elektrisches Potential
Qe :
Ladung
z:
Ladungszahl
Qe = z ⋅ F ⋅ n , falls mehrere Komponenten: Qe = ∑ zi F ⋅ ni
i
Ladung
As ← Coulomb
;
Mol
Mol .
F:
Faraday-Konstante, F = 9,649 ⋅10 4
F:
Elementarladung x Loschmidt‘sche Zahl: F = 1,602 ⋅10−19 As ⋅ 6,025 ⋅10 23 / Mol .
( )


dU = dU + − d Q eϕ = dU + − d  ∑ z i Fniϕ 
 i

82


TdS = dU + − d  ∑ z i Fni ϕ  + pdV − ∑ µ i dni
i
 i





TdS = dU + −  ∑ z i Fni dϕ + pdV − ∑ µ i dni −  ∑ z i Fϕ dni
i

 i

 i
In vielen Fällen kann man annehmen, daß Gesamtladung = 0 (insbesondere in homogenen
Phasen). Bedingung der globalen Elektroneutralität. Wir erhalten so:
TdS = dU + + pdV − ∑ (µ i + z i Fϕ )dni
14243
i
η i = µ i + z i Fϕ ,
ηi
elektrochemisches Potential
dU + = TdS − pdV + ∑ ηi dni
i
Eine entsprechende Gleichung erhält man für die freie Enthalpie:
dG + = − SdT + Vdp + ∑ηi dni
i
,
 ∂G +

 ∂n
 i


= ηi

 p ,T
Wir betrachten als Beispiel ein Gleichgewicht, das sich in folgendem System einstellt:
Untersuchung des Phasengleichgewichts an einer festen, semipermeablen Wand, die nur
Ionen einer Art durchläßt. System ist z.B. wäßrige Lösungen von CuSO4 und ZnSO4, die
durch eine für SO4-Ionen durchlässige Membran getrennt sind. T, p sind in beiden Phasen
gleich->passendes Potential zur GG-Berechnung ist G+(p,T,ni)
(A)
(B)
Cu++
Zn++
SO4--
SO4--
semipermeable Wand,
permeabel für SO42− Ionen
83
( )
Im thermodynamischen Gleichgewicht muß gelten: δG +
n1: SO42 −
T , p ,M
=0
n1A + n1B = konst. ; δn1A + δn1B = 0
 ∂G A  A  ∂G B
0 =  A δn1 +  B
 ∂n1
 ∂n1 
 B
δn1 = 0 ,

 ∂G A   ∂G B
0 =  A  −  B
 ∂n1   ∂n1
 A
δn1

η1A = η1B
Im thermodynamischen Gleichgewicht sind hier die elektrochemischen Potentiale
derjenigen Atomsorte, die die semipermeable Wand passieren können, gleich. Es folgt:
µ1A + z1 Fϕ A = µ1B + z1 Fϕ B
ϕ A −ϕ B =
i. a.
µ1A ≠ µ1B
µ1B − µ1A
z1 F
Es entsteht eine elektrische Potentialdifferenz zwischen beiden Phasen
µ1A = µ1A, 0 + RT ln c1A
∆ϕ = ϕ A − ϕ B =
µ1B = µ1B , 0 + RT ln c1B
µ1B , 0 + RT ln c1B − µ1A, 0 − RT ln c1A
z1 F
µ1A, 0 = µ1B , 0 Standardpotentiale gleich.
Im einfachsten Fall:
∆ϕ = −
,
cA
1
ln 1
z1F c1B
,
Nernst'sche Gleichung
z. B.: c1A > c1B ⇒ ϕ A − ϕ B > 0
z1 < 0
84
10. Phasenumwandlungen
Stoffe existieren, abhängig von den äußeren Bedingungen in verschiedenen Phasen: fest,
flüssig, gasförmig. Die Zustände innerhalb der Existenzbedingungen einzelner Phasen sind
stabil. Phasenübergang findet statt, wenn man sich dem Rand des Stabilitätsbereiches nähert
und überschreitet.
An der Stabilitätsgrenze können die Zustände noch stabil oder schon instabil sein:
stabil – Phasenübergang 1. Art, 2 Phasen können nebeneinander existieren.
instabil – Phasenübergang 2. Art
Bei der Betrachtung des Van-der-Waals-Gases hatten wir gesehen
p
instabiles Gebiet
Es liegt in einem bestimmten Gebiet
ein 2-Phasensystem vor.
V
Isotherme muß ersetzt werden durch
p
p +δp
T + dTp
T
V
(hier dargestellt: zwei nah benachbarte Isothermen)
Im Phasenumwandlungsgebiet ist p nur abhängig von T, aber nicht von V. p = p(T ) ,
gasförmig
flüssig
85
n1 : Anzahl der Mole in der flüssigen Phase, n2 : in der gasförmigen Phase.
Vorgabe von p: T = T ( p ) : Umwandlungstemperatur; p = p(T ) : Dampfdruck.
Im folgenden werden die Bedingungen formuliert, unter denen zwei Phasen eines Stoffes im
Gleichgewicht nebeneinander existieren. können
Voraussetzung: thermisches und mechanisches GG zwischen beiden Phasen, d.h. p, T fest.
⇒ als Gleichgewichtsbedingung
(δG )p,T
= 0 weil Freie Enthalpie minimal.
Bei der Variation von G können nur die Molzahlen n1 und n2 der Phasen (1) und (2) geändert
werden und zwar unter der Nebendedingung n1 + n2 = n = konst.
G als extensive Größe (Additivität): G = n1 g1 ( p, T ) + n2 g 2 ( p, T )
Variation:
Mit:
(δG )T , p =  ∂G  δn1 +  ∂G  δn2 = 0



 ∂n2 T , p
 ∂n1 T , p
∂G
= g1 ( p, T ) ;
∂n1

∂G
= g 2 ( p, T ) und δn1 = −δn2
∂n2
erhält man als Gleichgewichtsbedingung:
g1 ( p, T ) = g 2 ( p, T ) .
Diese Beziehung definiert (implizit) eine Gleichung p = p(T ) . Allerdings sind die molaren
freien Enthalpien oft nicht bekannt. Um die Gleichgewichtsbedingung mit leicht meßbaren
Größen zu verbinden wird für die Beziehung von p = p(T ) im folgenden eine
Differenzialgleichung abgeleitet:
Differentielle Form: dg1 = dg 2
 ∂g 
wegen: 
 = − s;
 ∂T  p
!
 ∂g 
 ∂g 
 ∂g 
 ∂g 
⇒  1  dp +  1  dT =  2  dp +  2  dT
 ∂T  p
 ∂T  p
 ∂p T
 ∂p T
 ∂g 
  = v
 ∂ p T
(Potentialeigenschaften von g)
86
erhält man: v1dp − s1dT = v2 dp − s2 dT
dp(v1 − v2 ) = dT (s1 − s2 )
dp s2 − s1
=
dT v2 − v1
(Claperonsche Gleichung), s1, s2 und v1, v2 molare Entropien und Volumina
beider Phasen.
Aus der Beziehung δq = Tds ergibt sich der Ansatz: s2 − s1 =
q12
mit q12 als
T
Umwandlungswärme (Wärme, die erforderlich ist, um 1 Mol Flüssigkeit in 1 Mol Gas
umzuwandeln). Wegen
s2 > s1 gilt q12 > 0 .
dp
q12
=
dT T (v2 − v1 )
Diese Formel gilt allgemein für Phasenumwandlungen, bei denen Umwandlungswärmen und
Volumenveränderungen auftreten, z.B. fest - flüssig, fest – dampfförmig.
Wenn Phase 1) flüssig und Phase 2) gasförmig,gilt v2 >> v1 (Volumen des Gases sehr viel
größer als das Volumen der Flüssigkeit)
näherungsweise gilt deshalb:
dp q12 p
=
>0 :
dT RT 2
dp
q
RT
= 12 , andererseits: v2 =
p
dT T ⋅ v2
Dampfdruckkformel von Clausius-Clapeyron
Interpretation: Bei Erhöhung des Druckes nimmt Umwandlungstemperatur zu (vgl. Änderung
der Siedetemperatur des Wassers in Abhängigkeit von Höhe über dem Meeresspiegel).
Unter der Voraussetzung, daß q12 konstant läßt sich diese Differentialgleichung integrieren
und man erhält:
dp q12 dT
=
p
R T2
,
q 1 1 
lnp = − 12  −  + lnp0
R  T T0 
87
p = p0 e
Aus
−
q12  1 1
 −
R  T T0



, beschreibt, wie Dampfdruck steigt mit zunehmender Temperatur.
dp
q12
=
dT T (v2 − v1 )
Es gilt nicht nur
läßt sich weiterhin der folgende interessante Sachverhalt ableiten:
q flü . / gasf .
dp
=
sondern auch:
dT T (vgasf . − v flü . )
In der Regel gilt v fest < v flüssig ⇒
q fest / flü .
dp
=
dT T (v flü . − v fest )
dp
>0
dT
Bei Erhöhung des Drucks nimmt Umwandlungstemperatur zu ⇒ feste Phase wird bevorzugt.
Anomalie des Wassers: v fest > v flüssig (vgl. Eis schwimmt oben) bedeutet:
dp
<0
dT
Bei Erhöhung des Drucks nimmt Umwandlungstemperatur ab. Bei gegebener Temperatur
wird flüssige Phase bevorzugt. vgl. Schlittschuhlaufen
(niedriger Druck: Umwandlungstemperatur bei 0oC, Hoher Druck: Umwandlungstemperatur
<0oC. D.h. bei 0oC und hohem Druck besteht die Möglichkeit, dass Eis sich schon Wasser
umgewandelt hat)
Maxwell-Konstruktion:
Bei der Behandlung des Van-der-Waals-Gases war die Frage offen geblieben, wo die Gerade
p = p(T ) gelegt werden muß.
p
Gleichgewichtsbedingung
1
2
g1 ( p , T ) = g 2 ( p , T )
überall auf der Geraden.
n1 + n2 = n ,
1: flüssig,
Im Zustand 1: n1 = n ,
V
2: gasförmig
im Zustand 2: n2 = n
G1 = n ⋅ g1 ( p , T ) , G2 = ng 2 ( p , T )
88
Also G1 = G2 für die Zustände 1 und 2.
U1 + p1V1 − T1S1 = U 2 + p 2V2 − T2 S 2
T1 = T2 = T
(wegen Isotherme),
außerdem: p1 = p 2 = p ;
Gerade p = p(T )
U1 + pV1 − TS1 = U 2 + pV2 − TS 2
U 2 − U1 + p(V2 − V1 ) − T (S 2 − S1 ) = 0
∆U + p∆V − T∆S = 0
∆S =
, oder:
∆U + p∆V
T
S ist eine Zustandsgröße, wenn Integration von 1 nach 2 vorgenommen wird, ist S 2
unabhängig vom Integrationsweg.
Gibbs'sche Fundamentalgleichung
TdS = dU + pdV ,
dS =
dU + pdV
T
2
dU + pdV
T
1
∆S = S 2 − S1 = ∫
,
Integration entlang einer Van-der-Waals'schen Isotherme:
2
2
1
1
∆S = S 2 − S1 = ∫ dU + ∫ pdV
T1
T1
U ebenfalls Zustandsgröße:
∆U
2
1
+ ∫ pdV
S 2 − S1 =
T
T1
Vergleich:
89
p = p (V ) =
RT
A2
− 2
V −B V
∆U p∆V ! ∆U 1
+
=
+ ∫ pdV
T
T
T
T1
2
2
p∆V = ∫ pdV
1
p
p
F1
1
1
2
F2
2
V
Gerade muß so gelegt
werden, daß F1 = F2
V
2
∫ pdV
p∆V
1
Maxwellsche Regel: Wenn p der Sättigungsdampfdruck ist, der die Zustandsgleichung
erfüllt, besitzen die Flächen F1 und F2 den gleichen Flächeninhalt (und umgekehrt). Die
entsprechende Isobare bezeichnet man auch als Maxwellgerade.
90
11. Ansätze der irreversiblen Thermodynamik
Gleichgewichtsthermodynamik: räumlich homogene Systeme bzw. aus homogenen Phasen
zusammengesetzte Systeme.
Bei Prozessen betrachteten wir nur Anfangs- und Endzustände, die beide
Gleichgewichtszustände waren. Der Prozeßverlauf konnte im einzelnen nicht beschrieben
werden.
Irreversible Thermodynamik: Analyse von räumlich inhomogenen Systemen und von
zeitabhängigen Prozessen.
Wichtig: Bei Prozessen, die in räumlich inhomogenen Systemen auftreten, können wir die
Zustandsvariablen nicht mehr auf das System als Ganzes beziehen.
Beispiel: Temperaturausbreitung in einem Stab:
Wärmebad
Wärmebad
T1 für t < 0
T2 > T1 für t ≥ 0
T1
T
t
T2
T1
t=0
X
Die Temperatur ist abhängig von Ort und Zeit: T = T ( x , t )
91
allgemein: T = T (x, y , z , t )
,
r
T = T (r , t ) ,
"Temperaturfeld"
Besonderes Problem: Definition von extensiven Zustandsvariablen wie Energie,
Entropie u.s.w.
System
Y
Um der räumlichen Inhomogenität gerecht zu
werden, wird das System in viele kleine
Teilsysteme aufgeteilt. Diese Aufteilung kann
zunächst beliebig fein sein.
X
Teilsysteme können durch ihre Lage im Raum, also durch den Ortsvektor
r
r = ( x , y , z )T charakterisiert werden.
Volumen- bzw. Massenelemente sollen so klein sein, daß ihr Inneres als annähernd
homogen angesehen werden kann.
r
r
r
r
∆M (r ), ∆S (r ), ∆U (r ), ∆G (r ) seien die extensiven Größen dieser Subsysteme. Bei immer
stärkerer Verfeinerung bleiben die folgenden Grenzwerte endlich (während die extensiven
Größen selbst gegen Null gehen).
r
r
∆U
∆G
∆S (r )
; gˆ =
u.s.w.
sˆ (r ) =
r ; uˆ =
∆M (r )
∆M
∆M
∆M → 0 : ortsabhängige spezifische Größen, oder
r
r ∆S (r ) ~ ∆U
~
s (r ) =
; u=
∆V
∆V
u.s.w.
die Dichten der Größen S, U, G...
Außer dem Temperaturfeld lassen sich noch andere Zustandsfelder definieren:
r
r
~
s (r ) oder ~
s (r , t )
,
r
r
u~(r ) oder u~(r , t )
u.s.w.
92
Berücksichtigung makroskopischer mechanischer Bewegungen:
r r
Geschwindigkeitsfeld v(r , t )
 vx 
r  
r
v =  v y  als Funktion von r und t.
v 
 z
r
v
: Transport von Masse
Die Beziehungen der Gleichgewichtsthermodynamik sind für das folgende nur dann
von Nutzen, wenn wir voraussetzen können, dass zwar nicht das Gesamtsystem, aber
doch die infinitesimal kleinen Subsysteme als im Gleichgewicht befindlich angesehen
werden können: Konzept des "lokalen" Gleichgewichts
Die Definition des lokalen Gleichgewichtes birgt in sich eine gewisse Problematik.
Einerseits sollen die Volumenelemente "infinitesimal" klein sein, andererseits müssen sie sehr
viele Teilchen enthalten, damit überhaupt Thermodynamik betrieben werden kann.
⇒ Der Ansatz der irreversiblen Thermodynamik in dem hier beschriebenen Sinne verliert
seine Gültigkeit, wenn entweder die Prozesse sehr schnell ablaufen (die Voraussetzung des
lokalen Gleichgewichtes wird verletzt) oder die Inhomogenitäten sehr groß sind (es lassen
sich keine Volumenelemente mit thermodynamischen Eigenschaften definieren).
Rechnungen mit Hilfe der kinetischen Theorie von Transportprozessen ergeben etwa folgende
Aussage: Solange Temperaturveränderungen über die Größe der mittleren freien Weglänge
(Weg, der ins Mittel zwischen zwei Stößen zurückgelegt wird) klein gegenüber der Temperatur
selbst sind, kann man lokales Gleichgewicht voraussetzen.
Beispiel:
d M = 10 −5 ...10 −4 cm .
In makroskopischen Systemen ist diese Länge klein gegenüber den charakteristischen Größen
des Systems
93
(wenn Temperaturdifferenz ∆T = 1o K über 1 cm, relative Tempertaturdifferenz;
(∆T T )1cm≅ 1 300 . Dementsprechend über die Länge von 10−4 cm :
(∆T T )10− 4 cm≅ 0,3 ×10−6 << 1 ).
Bilanzgleichungen - Allgemeine Form
Wir betrachten ein bestimmtes Volumen V, in dem eine (beliebige) extensive Größe A
entweder entsteht oder vernichtet werden kann oder durch Transport von außen hereingetragen
(oder abtransportiert) wird.
V
df
df
A(t ) = a~ (x, y, z, t )dxdydz
123
∫
A
dV
,
∆A 

JA =

∆F∆t 

dA
dA d a A
=
+ i
dt
dt
dt
{
{
Es gilt allgemein:
Transport
Für den Transportterm gilt:
r r
J A df < 0
V
Erzeugung
oder
Vernichtun g
r
r r
da A
= − ∫ J A (r , t )df
dt
r
df
r
r
J A ⋅ df > 0
r
JA
r
JA
r
df
r
r
J A : Flussvektor, df : gerichtetes Flächenelement (zeigt nach außen)
r r
da A
Wenn sign J A df < 0 gilt
> 0 (Hineintransport)
dt
(
)
Für den Produktionsterm gilt:
94
di A
r
= ∫ q A (r , t )dV ; q A : Quellstärke
dt V
r r d
r
dA
= ∫ q A (r , t )dV − ∫ J A df = ∫ a~dV
dt V
dt V
Gauss'scher Satz:
r r
r
J
d
f
=
div
J
∫ A ∫ A dV
V
r
r
∂J A, x ∂J A, y ∂J A, z
∂J A
=
+
divJ A =
+
r
∂r
∂z
∂y
∂x
{
alternative
Schreibweise
r
∂a~
d ~
dV = − ∫ divJ A dV + ∫ q A dV
a
dV
=
∫
∫
∂t
dt V
V
V
V
(erstes Gleichheitszeichen: sofern Integralgrenzen konstant)
Integrale Darstellung muss für alle Volumina, auch infinitesimal, gültig sein:
r
∂a~
+ divJ A = q A ,
∂t
lokale Form der Bilanzgleichung
Wenn q A = 0 (A kann nicht vernichtet oder erzeugt werden), gilt:
r
∂a~
+ divJ A = 0 ,
∂t
Kontinuitätsgleichung
95
12. Spezielle Bilanzgleichungen
12.1 Massebilanz
A sei Masse. a~ = ρ : Massendichte, J M : Massenstromdichte
Explizite Darstellung von J M :
JM ,x =
∆m ∆m ∆x
=
≅ ρv x
F∆t {
F∆x ∆t
∆V
Vx
F
}
∆x = v x ∆t
Allgemein:
r
r
r
dr
JM = ρ
=ρv ,
dt
r
r
J M , i = ρ i v i , bei Mischungen
Falls keine chemischen Reaktionen stattfinden gilt für alle Komponenten i unabhängig
voneinander die Massenerhaltung.
∂ρ i
+ divJ M , i = 0 ,
∂t
∂ρ i
+ div(ρ i v i ) = 0 ,
∂t
Kontinuitätsgleichung
Beteiligung von chemischen Reaktionen:
96
∂ci
=
∂t
R
∑ν ir wr
wr : Reaktionsgeschwindigkeiten w, (w, damit keine Verwechslung
r =1
mit mechanischer Bewegung v), ν ir : stöchiometrische Koeffizienten der Stoffe i in den
Reaktionen r.
ci : Konzentrationen ; ci =
ρi =
∆ni
Mol
,
Volumen
∆V
∆mi ∆mi
∆n
1
=
∆ni ⋅
= M i i = M i ci
∆V
∆ni
∆V
∆V
∂ρ i
∂c
= Mi i =
∂t
∂t
,
M i : Molmasse
R
∑ M iν ir wr = qM ,i
,
q M : Quellterm
r =1
∂ρ i
+ div(ρ i vi ) =
∂t
R
∑ M iν ir wr
r =1
Addition:
K
∑
i =1
∂ρi
+ div
∂t
K R
∑∑
K
K R
i =1
i =1 r =1
∑ (ρi vi ) = ∑∑ M iν ir wr
M iν ir wr =
i =1 r =1
R K
∑∑ M iν ir wr =0
r =1 i =1
weil für jede chemische Reaktion getrennt die Massenerhaltung gilt.
Demzufolge:
∑
i
q M , i = 0 und
K
∑
i =1
∂ρi
+ div
∂t
K
∑ ( ρ i vi ) = 0
i =1
Darstellung der Bilanzgleichungen in Konzentrationen. Division durch M i : ci =
97
ρi
Mi
dci
+ div(ci v i ) =
123
dt
J ci
R
∑ν ir wr
r =1
Bei mechanischer Bewegung im System:
98
r
ρ i vi
Schwerpunktsgeschwindigkeit:
Ableitung für Gemisch aus 2 Stoffen:
r
r
r
∆m1r (t ) + ∆m2 r (t ) r
= r (t ) .
Schwerpunkt eines Volumenelements zum Zeitpunkt t: rS (t ) =
∆m1 + ∆m1
Im Zeitintervall ∆t bewegen sich die Sorten 1 und 2 in unterschiedliche Richtung und mit
unterschiedlichen Geschwindigkeiten:
r
r
r
∆m1(r (t ) + v1∆t ) + ∆m2 (r (t ) + v 2 ∆t )
rS (t + ∆t ) =
∆m1 + ∆m1
∆rS rS (t + ∆t ) − rS (t ) ∆m1v1 + ∆m2 v 2
=
=
∆t
∆t
∆m1 + ∆m1
r
vS =
r
r
∑ ρi vi
r
allgemein: v S = i
∑ ρi
r
i
r
1
vS =
ρ
K
∑ ρi vi
mit: ρ =
i =1
K
∑ ρi
i =1
r
Wenn v S ≠ 0 befindet sich das Gesamtsystem in Strömung.
Definition einer Diffusionsstromdichte
r r
Diff
JM
, i = ρ i (v i − v S ) ,
K
∑
i =1
K
Diff
JM
,i
=
∑
i =1
r r
ρi vi − v S
Geschwindigkeit relativ zum Schwerpunkt
K
∑ ρi = 0
i =1
99
Summe aller Diffusionsstromdichten = Null
r
Wenn v S = 0 : Diffusionsstromdichte identisch mit Massenstromdichte.
12.2 Entropiebilanz
Aus der allgemeinen Gleichung
r
∂a~
+ div J A = q A
∂t
folgt:
r
∂s
= − div J S + σ
∂t
r
s : Entropiedichte, J S : Entropiestromdichte,
σ : Entropieproduktionsdichte, von zentraler Bedeutung für irreversible
Thermodynamik
r
Wie hängen J S und σ von den anderen thermodynamischen Größen ab?
2 Ausgangspunkte:
K
1. Gibbs-Duhem-Gleichung: G = U + pV − TS =
∑ µi ni
i =1
Folgende Relationen gelten für ein kleines Volumenelement ∆V :
K
∆G = ∆U + p∆V − T∆S =
∑ µi ∆ni
i =1
Division durch ∆V :
K
g = u + p − Ts =
∆G ∆U
∆S
=
+ p −T
=
∆V ∆V
∆V
∑ µi ci
K
∆n
∑ µi ∆Vi
i =1
, kleine Buchstaben bezeichnen hier Dichten: g~ , ~
s , u~
i =1
100
2. Gibbs'sche Fundamentalgleichung
dU = T dS − p dV +
∑ µidni
,
i
Anwendung auf kleines Volumenelement:
Td (∆S ) = d(∆U ) + pd (∆V ) −
K
∑ µi d(∆ni )
i =1
Übergang zu intensiven Größen:
∆S = s∆V ; ∆U = u∆V ; ∆ni = ci ∆V
Td (s∆V ) = d(u∆V ) + pd (∆V ) −
K
∑ µi d(ci ∆V )
i =1
Produktenregel:
Tds ⋅ ∆V + Tsd (∆V ) = du ⋅ ∆V + u ⋅ d (∆V ) + pd(∆V ) −
K
K
i =1
i =1
∑ µi ci d(∆V ) − ∑ µi (∆V )dci
Sortieren:

∆V  T ds − du +


K




µ i dci = d(∆V )− T ⋅ s + u + p − µ i ci 



i =1
i =1

14444244
443
K
∑
∑
= 0, siehe oben
Tds − du +
K
∑ µi dci
i =1
Bei zeitlichen Veränderungen
101
T
∂s ∂u
−
+
∂t ∂t
K
∂c
∑ µi ∂ti = 0
i =1
Ziel: Überführung dieser Gleichung in eine Bilanzgleichung der Form:
r
∂s
= −divJ S + σ .
∂t
Das gelingt durch Berücksichtigung der Bilanzgleichungen für u sowie ci .
Bilanzgleichung für die Innere Energie:
Wir betrachten den Spezialfall: 1. keine äußere Arbeitsleistung an dem System; 2. keine
innere Wärmeproduktion aufgrund innerer Reibung.
dU = δ Q + δ A
mit δA = 0
,
Innere Energie ändert sich nur durch Wärmestrom
r
∂u
+ div J Q = 0
∂t
,
r
mit J Q : Wärmestromdichte
Bilanzgleichung für die Konzentrationen:
∂ci
+ divJ ci =
∂t
R
∑ vir wr
r =1
mit J ci = ci v i
Einsetzen in:
K
T
∂c
∂s ∂u
=
−
µi i
∂t ∂t i =1
∂t
∑
liefert:
T
K
R


r
r
∂s
µ i − divJ ci + ν ir wr  ,
= −divJ Q −
∂t


i =1
r =1
∑
∑
102
r
∂s
1
= − divJ Q +
T
∂t
K
µi
∑T
i =1
r
divJ ci −
K
R
∑∑
ν ir wr µ i
i =1 r =1
T
Umformung der beiden ersten Terme auf der rechten Seite nach den
Differentiationsregeln der Vektoranalysis:
r r
sei ψ = ψ (x, y , z ) ein skalares Feld, und a = a (x, y , z ) ein Vektorfeld. Dann gilt
r
div(ψa ) =
r
(1
gradψ )a
424
3
r
+ ψdiva )
Skalarprodukt
 ∂ψ ∂x 


∂a y ∂a z
r ∂a
mit gradψ =  ∂ψ ∂y  und diva = x +
+
∂x
∂z
∂y
 ∂ψ ∂z 


Dementsprechend:
1.Term:
r
 JQ
r
1
div J Q = div
 T
T

 r
 − J grad 1 
 Q
T 

r
r r
"Produktregel" div(φv ) = φdivv + vgradφ ,
mit gradφ =
∂φ
∂φ
∂φ
i+
j+
k
∂x
∂y
∂x
r
φ : skalares Feld, v : Vektorfeld
2. Term:
r
 µi J c
r
µi
i
div J ci = div
 T
T

 r
 − J grad µ i  :
 ci
T 

Man erhält:
r
 JQ  r
∂s
 + J grad 1  +
= −div
 T  Q
∂t
T 


r
 µi J c
i
div
 T
i =1

K
∑
K R
 K r
ν ir wr µ i
µ 
−
J ci grad i  −

 T  i =1 r =1 T
 i =1
K
mit Ar = −
∑
∑∑
∑ µiν ir (Affinität einer chem. Reaktion) erhält man daraus:
i =1
103
K
r
r
J −
µi J ci
Q

∂s
i =1
= −div
T
∂t



∑


K r
 r
µ
1
 + J Q grad  −
J ci grad i
 T  i =1

T


∑
R
wr Ar

+
 r =1 T
∑
r
∂s
= −div J S + σ liefert:
∂t
Vergleich mit:
K
r
r 
1  r
JS =
J Q − µi J ci 

T
i =1


∑
,
Entropiestromdichte
K r
r
µ
1
σ = J Qgrad   − J ci grad i
 T  i =1
T
∑
 R wr Ar
+

 r =1 T
∑
,
Entropieproduktionsdichte
σ : Summe von Produkten zweier Größen
Veranschaulichung, daß die einzelnen Terme von σ positiv sind:
r
1
1. Term: J Q grad  
T 
T
1
T
X
X
Wärmestrom in positive x- Richtung:
104
r
1
J Q > 0 wenn grad T < 0 bzw. grad   > 0
T 
Temperaturgradient verursacht Wärmestrom: Fouriersches Gesetz (1811)
r
µ 
2. Term: − J ci grad  i 
T 
Chem. Potential:
µ i = µ i 0 ( p , T ) + RT ln ci
µ 
grad  i  = Rgrad ( ln ci )
T 
=
R dci
ci dx
p, T konstant
(für eine Raumrichtung)
ci
x
r
dci
< 0 ⇒ J ci > 0
dx
Konzentrationsgradient verursacht Diffusionsstrom.
R
∑
wr Ar
T
r =1
3. Term:
k
+
→
S1 ← S 2
k−
Beispiel: monomolekulare Reaktion
k+
= K eq
k−
Wir hatten früher hergeleitet : A = RT ln
A = RT ln
K eq S1
S2
k + S1
k− S2
105
A > 0 für k + S1 > k − S 2 ,
d.h. k+ S1 − k− S2 = w > 0 .
Allgemein gilt für die einzelnen Terme der Entropieproduktionsdichte:
σ=
∑
r
Ji X i
i
=
∑ Flüsse × Kräfte
i
Beispiele für Kräfte:
Temperaturgradient verursacht Wärmestrom.
Konzentrationsgradient verursacht Diffusionsstrom.
Chemische Affinität ≠ 0 verursacht Reaktionsgeschwindigkeit.
Andere Schreibweise für Entropieproduktion
r
1
Ausgangspunkt: σ = J Q grad   −
T 
K
∑
i =1
r
µ 
J ci grad  i  +
T 
R
∑
wr Ar
T
r =1
Mit:
1 1
grad   = 2 grad (− T )
T  T
K
r
µ  1
J ci grad  i  = 2
T  T
i =1
∑
K
r
1
J ci µi grad (− T ) +
T
i =1
∑
K
r
∑ J c grad (µi )
i =1
i
erhält man
σ=
1 r
1
J grad (− T ) − 2
2 Q
T
T
K
r
1
J ci µi grad (− T ) −
T
i =1
∑
106
K
∑
i =1
r
J ci grad (µi ) +
R
∑
wr Ar
T
r =1
r
J −
 Q
σ ⋅T = Φ = 

r
J ci µi 

i =1
 grad (− T ) +
T
K
∑
r
σ ⋅ T = Φ = J S grad (− T ) +
K
∑
i =1
K
∑
i =1
r
J ci grad (− µi ) +
r
J ci grad (− µi ) +
R
∑ wr Ar
r =1
R
∑ wr Ar
r =1
Φ : Rayleigh'sche Dissipationsfunktion: Maß für die Wärmeproduktion infolge der im
System ablaufenden irreversiblen Prozesse.
σ ≥0 ⇒ Φ ≥0
12.3 Lineare phänomenologische Gleichungen
σ = ∑ Ji X i
i
Die in dem Ausdruck für die Entropieproduktionsdichte stehenden Größen J i und X i werden
als zueinander konjugierte Flüsse und Kräfte bezeichnet.
J i : generalisierte Flüsse, X i : Generalisierte Kräfte
Es ist empirisch bekannt, daß eine Kraft X i nicht nur den zu ihr konjugierten Fluß, sondern
auch andere irreversible Veränderungen hervorrufen kann.
Ji ↔ X i
konjugierte Flüsse & Kräfte waren
chemische Reaktion ↔ Affinität ≠ 0
Diffusionsstrom
↔ Gradient des chemischen Potentials/Temperatur
Wärmestrom
↔ Temperaturgradient
Andere Möglichkeiten
107
J Diff
JQ
↑
↑
grad c
grad T
J elektrisch
JQ
J Diff
konj.
J elektrisch
aber auch: Die chemische Affinität Ai > 0 einer Reaktion i kann eine andere chemische
Reaktion j mit A j < 0 antreiben (später ausführlicher).
Beispiel: Membrantransport
außen
A
0
B
A0
0
B0
aber wenn Kopplung
durch einen Carrier (Cotransport)
innen
Ai
Bi
Ai
Bi
Konzentrationsgradient ∆A = Ai − A0 > 0 kann bei stöchiometrischer Kopplung beider
Transportprozesse den Prozeß J B antreiben.
Es kann J B > 0 gelten, selbst wenn ∆B = B i − B 0 < 0 (Transport gegen
Konzentrationsgradient von B).
Allgemein gilt:
J i = J i ( X 1 ,...., X n ) Fluß als Funktion der Kräfte
Gleichgewicht:
J i = 0 wenn X j = 0 für alle j
Entwicklung in der Nähe des Gleichgewichtes
108
Ji = ∑
j
∂J i
∂2 Ji
1
X j + ∑∑
X j X k + .....
∂X j
2 j k ∂X j ∂X k
( X j , X k entspricht hier ∆X j , ∆X k , da im Gleichgewicht: X j = 0 )
Beschränkung auf kleine Auslenkungen
J i = ∑ Lij X j
mit
Lij =
j
∂J i
∂X j
Lij : phänomenologische Koeffizienten
lineare Fluß-Kraft-Beziehungen
σ=
∑ J i X i = ∑∑ Lij X i X j
i 24
1
4
3
j
1i 44
2443
gilt allgemein
gilt nur in der
Nähe des Gleichgew.
(Entropieproduktionsdichte)
Bedingungen für phänomenologische Koeffizienten
Spezialfall: es existiert nur eine Kraft X i ≠ 0 , d.h. X j = 0 für i ≠ j
σ = Lii X i2 ⇒ Lii > 0
Die Hauptdiagonalelemente der Matrix der phänomenologischen Koeffizienten müssen alle
positiv sein.
Lij für (i ≠ j ) ,
Kopplungskoeffizienten
Aus der Forderung der positiven Definitheit von σ ergeben sich auch Bedingungen für die
Kopplungskoeffizienten.
{ }
Zerlegung der Matrix Lij in einen symmetrischen und einen antisymmetrischen Anteil
109
Lij =
(
) (
1
1
Lij + L ji + Lij − L ji
2
2
)
Abkürzung:
Lsym (ij ) =
(
)
1
Lij + L ji ,
2
Lantisym [ij ] =
(
1
Lij − L ji
2
)
Lantisym [ij ] = − Lantisym [ ji ]
Lsym (ij ) = Lsym ( ji ) ;
Der antisymmetrische Anteil Lantisym trägt nichts zu σ bei:
[ij ]
∑ (Lij − L ji )X i X j = ∑ Lij X i X j − ∑ L ji X i X j
i, j
ij
=0
ij
1
4243
Vertauschung der
Indizes
Es gilt demnach: σ =
Xi X j
∑∑ Lsym
( )
ij
i
j
Algebra: Eine quadratische Form mit einer symmetrischen Matrix ist dann positiv definit,
wenn alle Eigenwerte der Matrix Lsym (ij ) positiv sind.
Beispiel: i , j = 1,2
L
Lij =  11
 L21
1


(
L11
L12 + L21 )

2

Lsym (ij ) = 
1

 (L + L )
L22
12
21

2
L12 

L22 
Berechnung der Eigenwerte:
(L11 − λ )(L22 − λ ) − 1 (L12 + L21 )2 = 0
4
λ2 − (L11 + L22 ) λ + L11 L22 −
1
(L12 + L21 )2 = 0
4
110
λ1 / 2 = +
λ1 / 2 =
2
1
L11 + L22
L +L 
±  11 22  − L11 L22 + (L12 + L21 )2
2
2
4


L11 + L22
(L11 − L22 )2 + (L12 + L21 )2
±
2
4 442444
4 43
144
>0
Eigenwerte reell, und λ1 > 0
Damit auch λ2 > 0 muß gelten:
(L11 + L22 )2 > (L11 − L22 )2 + (L12 + L21 )2
4
4
4
L112 L22 2 L11 L22 L112 L22 2 L11 L22 (L12 + L21 )2
+
+
>
+
−
+
4
4
2
4
4
2
4
4 L11L22 > (L12 + L21 )2
Die Matrix der phänomenologischen Koeffizienten ist symmetrisch (Theorem von Onsager,
1931)
Lij = L ji ,
Onsagersche Reziprozitätsbeziehung (folgt aus dem Prinzip der detaillierten
Balance, wird später behandelt).
Ist für die gesamte Theorie der irreversiblen Prozesse von grundlegender Bedeutung.
Wegen L12 = L21 folgt aus 4 L11L22 > (L12 + L21 )2 = 4 L12 2
L11L22 > L12 2 = L12 L21 ,
oder: L11L22 − L12 L21 > 0
( )
Det Lij > 0
111
Bedeutung der Onsagerschen Reziprozitäts-Bedingung: Lij = L ji
Reduktion der Anzahl der unabhängigen phänomenologischen Koeffizienten.
Aber noch wichtiger: Immer dann wenn eine Kraft X j einen Fluß J i hervorruft, gilt, daß auch
eine Kraft X i einen Fluß J j bewirkt. Entspricht experimenteller Erfahrung.
Satz von Curie-Prigogine:
r
wr Ar
µ 
1
J ci grad  i  +
T  i =1
4
 T  r =1 T
142
4 43
424
3
1442443 1
r
σ = J Q grad   −
K
R
∑
Vektoren
∑
Vektoren
Skalare
Es gibt vektorielle Prozesse (Diffusion, Wärmeleitung,....) und skalare Prozesse (chemische
Reaktionen)
Im Rahmen der linearen irreversiblen Thermodynamik gibt es in isotropen Medien keine
Kopplung zwischen vektoriellen und skalaren Prozessen.
skalare Ströme sind nur abhängig von skalaren Kräften
vektorielle Ströme sind nur abhängig von vektoriellen Kräften
Konsequenz: weitere Reduktion der Anzahl von phänomenologischen Koeffizienten
(Kopplungskoeff.= 0)
z.B. keine Kopplung zwischen chemischen Reaktionen und Wärmeleitung
1
T 
σ = J Q grad   +
w⋅ A
T
112
Betrachtung eines räumlich 1-dimensionalen Systems: zur Veranschaulichung der
Unmöglichkeit der Kopplung skalarer und vektorieller Flüsse und Kräfte
σ = J Q, x
J Q , x dT w ⋅ A
d  1  w⋅ A
=− 2
+
 +
T
T
dx  T 
T dx
hier ist J1 = J Q ,x , J 2 = w , Kraft X 1 = −
1 dT
T 2 dx
und Kraft X 2 =
A
T
Lineare phänomenologische Beziehungen hätten die Gestalt:
A
 1 dT 
J Q , x = L11  − 2
 + L12 ⋅
T
 T dx 
A
 1 dT 
w = L21  − 2
 + L22
T
 T dx 
Wir nehmen an, daß
dT
=0:
dx
J Q, x
{
= L12 ⋅
Teil einer
vektor . Größe
A
T
{
Skalar
Wenn L12 ≠ 0 : "skalare Ursache" bedingt gerichteten Fluß, das würde gegen
Symmetrieprinzip verstoßen
Also: Eine chemische Reaktion kann keinen gerichteten Fluß erzeugen.
L12 = 0
Gilt nur in isotropen Medien (alle Richtungen gleichberechtigt).
Katchalsky (1968): Betrachtung nichtisotroper Medien, wo chemische Reaktion gerichtete
Flüsse hervorrufen können.
Wichtig für aktiven Membrantransport: z.B. K/Na-Pumpe
113
Ko
Na o
Na i
A TP
Pi
AD P
Ki
Keine Symmetrie zwischen innen und außen.
114
13. Carriertransport als Beispiel für gekoppelte Prozesse
Wir betrachten den Carriervermittelten Memtrantransport von 2 Stoffen, S1 und S 2 ,
entsprechend dem folgenden Mechanismus.
i
(CS1)
e+1
e- 1
a
(CS1)
a
S1
Ci
k+
Ca
k-
i
S2
i
(CS2)
e+2
e-2
a
S2
a
(CS2)
J1 , J 2 : Transportraten von S1 , S 2 von innen nach außen.
C i , C a : unbeladene Carrierformen innen und außen
(CS1 )i , (CS1 )a , (CS 2 )i , (CS 2 )a :
beladene Carrierformen
Die Konzentrationen von S1 , S 2 (innen nach außen) werden als fixiert angesehen.
Annahme: k + = k − = k ; l+1 = l−1 = l1 ; l + 2 = l − 2 = l 2 (symmetrische Membran)
l1 , l 2 : kinetische Konstanten der Translokationsschritte, k: kinetische Konstante der
Translokation des ungeladenen Carriers
Kinetische Beschreibung
1. Schnelle Bindungsgleichgewichte
113
(CS )1i
C
i
⋅ S1i
=
K1i
;
(CS )i2
C
i
⋅ S 2i
=
(CS )ia
K 2i
C
a
⋅ S1a
=
K1a ;
(CS )a2
C
a
⋅ S 2a
= K 2a
"Symmetrische Membran" K1i = K1a = K1 ; K 2i = K 2a = K 2
2. Erhaltungsgleichung für Gesamtkonzentration des Carriers:
Ctot = C i + C a + (CS )1i + (CS )i2 + (CS )1a + (CS )a2
(
)
(
Ctot = C i 1 + K1 S1i + K 2 S 2i + C a 1 + K1 S1a + K 2 S 2a
Abkürzung: Ai = 1 + K1 S1i + K 2 S 2i
Ctot = C i ⋅ Ai + C a ⋅ A a
)
A a = 1 + K1 S1a + K 2 S 2a
(*)
3. Steady state Bedingung für den Carrier
kC i + l1 (CS )1i + l 2 (CS )i2 = kC a + l1 (CS )1a + l2 (CS )a2
(
)
(
C i k + l1 K1S1i + l 2 K 2 S 2i = C a k + l1 K1S1a + l 2 K 2 S 2a
Abkürzung: B i = k + l1 K1S 2i + l 2 K 2 S 2i
C i ⋅ Bi = C a ⋅ B a
)
B a = k + l1 K1S1a + l 2 K 2 S 2a
,
(**)
Aus den Gleichungen (*) und (**) lassen sich die Konzentrationen des unbeladenen Carriers
berechnen.
aus (**):
Ca =
einsetzen in (*):
C i ⋅ Bi
Ba
i
i
Ctot = C ⋅ A +
C i ⋅ Bi
B
a
⋅ Aa
114
Ci =
Ctot ⋅ B a
Ai B a + A a B
; Ca =
i
Ctot ⋅ B i
Ai B a + A a B i
Durch Berücksichtigung der Bindungsgleichgewichte ergeben sich die Konzentrationen der
beladenen Formen des Carriers.
z.B. (CS )1i = K1C i S1i =
K1Ctot B a S1i
Ai B a + A a B i
Betrachtung der zeitlichen Änderung der Stoffkonzentrationen auf beiden Seiten:
[
]
dS1i
dS a
= − J1 = −l1 (CS )1i − (CS )1a = − 1
dt
dt
[
]
dS 2i
dS a
= − J 2 = −l 2 (CS )i2 − (− CS )2a = − 2
dt
dt
Ergebnis:
(
)
C ⋅ l K B a ⋅ S1i − B i S1a
dS1a
dS1i
= − tot 1 i 1 a
=
−
dt
dt
A B + Aa B i
(
)
C l K B a S i − Bi S a
dS 2i
dS a
= − tot 2 i 2 a 2a i 2 = − 2
dt
dt
AB +A B
Am Gleichgewicht gilt:
J1 = 0 ;
J2 = 0
(d.h.
dS1i,,2a
dt
= 0)
Aus den Bedingungen: B a S1i − B i S1a = 0 und B a S 2i − B i S 2a = 0 folgt, dass ein
Gleichgewicht vorliegt, wenn: S1i = S1a ; S 2i = S 2a gilt.
Herleitung:
kS1i + l1K1S1a S1i + l 2 K 2 S 2a S1i = kS1a + l1 K1S1i S1a + l 2 K 2 S 2i S1a
115
kS 2i + l1 K1S1a S 2i + l 2 K 2 S 2a S 2i = kS 2a + l1 K1S 2i S 2a + l 2 K 2 S 2i S 2a
lineares Gleichungssystem für S1i und S 2i (als Funktion von S1a und S 2a )
(
)(
)
S1i k + l 2 K 2 S 2a − l 2 K 2 S 2a S 2i = kS1a
(
)
(
)
− l1K1S 2a S1i + S 2i k + l1 K1S1a = l0 S 2a
Auflösung liefert: S1i = S1a ; S 2i = S 2a
Charakterisierung der Abweichung vom Gleichgewicht:
S1i + S1a = S1
mit
S 2i + S 2a = S 2
S1i − S1a = n1
S 2i − S 2a = n2
S1i =
S1 + n1
2
,
S1a =
S1 − n1
2
S 2i =
S 2 + n2
2
,
S 2a =
S 2 − n2
2
Gleichgewichtswerte:
S1i = S1 2 = S1a ;
S 2i = S 2a = S 2 2
A i = A a = A = 1 + K1
S1
S
+ K2 2
2
2
B i = B a = B = k + l1K1
S1
S
+ l2 K 2 2
2
2
Thermodynamische Beschreibungsweise:
µ1i = µ10 + RT ln S1i ;
µ1a = µ10 + RT ln S1a
116
µ 2i = µ 20 + RT ln S 2i ;
µ 2a = µ 20 + RT ln S 2a
(Standartpotentiale wurden als gleich innen und außen angenommen; p = gleich , T = gleich )
 µ  1 ∂µ 1 ∆µ
Kräfte: grad   =
≈
 T  T ∂x T ∆x
X1 =
(
1
RT ln S1i − RT ln S1a
T ⋅d
)
(allg., weil T konst.; Weg in x – Richtung)
mit ∆x = d Membrandicke.
R S1i
R S 2i
X 1 = ln a ; X 2 = ln a
d S1
d S2
kleine Konzentrationsdifferenzen n1 und n 2
X1 =
R S1 + n1
ln
d S1 − n1
X1 =
R  1 + n1 / S1 

ln 
d  1 − n1 / S1 
ni / S i << 1 :
X1 ≅
,
X2 =
,
R S 2 + n2
ln
d S 2 − n2
X2 =
R  1 + n2 / S 2 

ln 
d  1 − n2 / S 2 
R 2n1
⋅
d S1
J1 = L11 X 1 + L12 X 2 =
J 2 = L21 X 1 + L22 X 2 =
X2 ≅
R 2 n2
⋅
d S2
n1
n2 
2R 
 L11 + L12

d 
S1
S2 
n1
n2 
2R 

 L21 + L22
d 
S1
S2 
Diese aus der Thermodynamik folgenden Gleichungen lassen sich mit den kinetischen nur
vergleichen, wenn letztere ebenfalls in der Nähe des Gleichgewichts betrachtet werden.
Linearisierung von:
J1 =
(
Ctot l1 K1 B a S1i − B i S1a
i
a
a
AB +A B
i
117
)
J2 =
(
Ctot l 2 K 2 B a S 2i − B i S 2a
)
Ai B a + A a B i
Reiohenentwicklung: Zähler beginnt mit Termen proportional zu ~ n1 bzw. n2
Im Nenner gibt es Terme 0. Ordnung und die allein sind relevant, da lineare Terme zu
quadratischen Termen im Zähler werden.
Ai B a + A a B i = 2 AB
Linearisierung des Zählers: B a S1i und B i S1a liefern gleiche Beiträge
J1 ≅
2Ctot l1 K1  i ∂B a
∂S i 
∂B a
S1
n1 + S1i
n2 + B a 1 n1 
2 AB 
∂n1 
∂n1
∂n2
J2 ≅
2 Ctot l 2 K 2
2 AB
 i ∂B a

∂S i
∂B a
 S2
n2 + B a 2 n2 
n1 + S 2i

∂n2
∂n1
∂n2 

∂S1i ∂S 2i 1
=
= ;
∂n1 ∂n2 2
∂S1a
lK
∂B a
= l1 K1
also
=− 1 1
2
∂n1
∂n1
∂S 2a
l K
∂B a
= l2 K 2
und
=− 2 2
∂n2
2
∂n2
J1 =
Ctot l1 K1  S1 l1 K1
S l K
Bn 
n1 − 2 2 2 n2 + 1 
−
A⋅ B  2 2
2 2
2 
J2 =
Ctot l 2 K 2  S 2 l1 K1
S l K
Bn 
n1 − 2 2 2 n2 + 2 
−
2 2
2 
A⋅ B  2 2
Koeffizientenvergleich mit thermodynamischer Flux-Kraft-Gleichung
L12 = L21 = −
Ctot S1S 2 (l1 K1 )(l 2 K 2 ) d
8⋅ R ⋅ A⋅ B
118
L11 =
Ctot S1 (l1 K1 ) d Ctot S12 (l1 K1 ) d
−
4R⋅ A
8R ⋅ A⋅ B
L22 =
Ctot S 2 (l 2 K 2 ) d Ctot S 22 (l 2 K 2 ) d
−
4R⋅ A
8R ⋅ A⋅ B
2
2
Schlußfolgerungen:
1. Alle Lij ~ Ctot
2. Onsagersche Reziprozitätsbeziehungen sind erfüllt
3. Kreuzkopplungskoeffizientn sind negativ (Antiport, kompetitive Bindung)
4.
Die "Diagonalterme" enthalten auch "Selbstkopplungen", die formal eine den
Kreuzkopplungen entsprechende Struktur haben. (je die zweiten Terme)
5. Entkopplung: Der Faktor "B" tritt nur im Nenner der Kreuz- und Selbstkopplungen auf.
Z.B. k sehr groß → B sehr groß; k → ∞ , L12 , L21 → 0 : Entkopplung. Die beiden
Zyklen arbeiten unabhängig. Es bleiben nur positive L11 und L22 übrig
 2 Rn1  Ctot S/ 1 (l1 K1 ) d 2 R n1
 =
J1 = L11 
⋅
4R⋅ A
S/ 1 ⋅ d
 S1 ⋅ d 
 2 R n2  Ctot S 2 (l 2 K 2 ) d 2 R n2
 =
J 2 = L22 
⋅
4R⋅ A
S2 ⋅ d
 S2 d 
J1 =
Ctot l1 K1
n1 ,
2A
J2 =
Ctot l2 K 2
n2
2A
6. A berücksichtigt Sättigung. Bei hoher Sättigung wird Fluß bei vorgegebener Abweichung
n1 bzw. n 2 gering.
119
14. Spezielle lineare phänomenologische Gleichungen
Ji =
∑ Lik X k
, J =LX,
k
Lik : "Leitfähigkeitskoeffizienten", resultiert aus Terminologie bei Beschreibung elektrischer
Phänomene. L Matrix der phänomenologischen Koeffizienten.
Fall: n = 2 :
 J1   L11
  = 
 J 2   L21
L12   X 1 


L22   X 2 
L−1 J = X , mit L−1 = R
X = RJ ,
Vgl. Ohmschen Gesetz: U = R ⋅ I
R: Reibungskoeffizienten, Widerstände:
R
R =  11
 R21
R12 

R22 
14.1 Wärmeleitungsgleichung
Bilanzgleichung für innere Energie (ohne mechanische Arbeit)
r
∂u
+ div J Q = 0 ,
∂t
r
u : Dichte der inneren Energie
1
T 
σ = J Q grad  
r
1
Ansatz: J Q = L ⋅ grad  
T 

∂u
 1 
+ div  L grad   = 0
∂t
 T 

mit L = konst. folgt:
120
∂u
1
+ L div grad  = 0
∂t
T 
div grad = ∆ : Laplace operator =
∂2
∂x 2
+
∂2
∂y 2
+
∂2
∂z 2
(anzuwenden auf Skalar)
∂u
1
L ∆  = −
∂t
T 
im linearen 1-dimensionalen Fall:
2
∂ 2  1  ∂  1 ∂T 
2  ∂T 
1 ∂ 2T
−
=
−
=






2
2
∂x 
∂x 2  T  ∂x  T 2 ∂x 
T 342
1
43 T ∂x
vernachlässigbar
bei hohen T
−
∂ 2 
∂2
1  ∂ 2
1
1 ∂u
T
T
+
=
−
∆
≈
−
+
L ∂t
T 2  ∂x 2 ∂y 2 ∂z 2 
T2
Das thermodynamische Potential U ist eine Funktion von T und V :
V = konst.
∂u  ∂u  ∂T
∂T
= cV
=
 ⋅
∂t
∂t  ∂T V ∂t
zeitliche Änderung von u
damit:
1
T
2
∆T ≈
bzw.:
∂T
1
cV
L
∂t
∂T
L
= 2 ∆T
∂t T cV
,
Wärmeleitungsgleichung
 ∂2
∂T
∂2
∂2 
− λ 2 + 2 + 2  T = 0 ,
 ∂x
∂t
∂y
∂z 

partielle Differentialgleichung.
121
U = U (T ,V ) ,
T > 0 , L > 0 , cV > 0 ⇒ λ > 0
Lösung der Wärmeleitungsgleichung für den 1-dimensionalen Fall
∂T
∂ 2T
−λ 2 = 0
∂t
∂x
λ : Temperaturleitfähigkeit, [λ ] =
0
m2
min
x
Anfangsbedingung: T ( x,0) = Θ( x )
Randbedingungen: zwei Möglichkeiten
(1) Vorgabe der Temperatur an den Rändern, z.B. T (0, t ) = T0
(2) Vorgabe des Wärmeflusses an den Rändern, z.B.
∂T
∂x
= ψ 0 (t )
x =0
Stationäre Lösungen: lassen sich leicht ausrechnen
z.B. für langen Stab mit festen Temperaturen an den Enden
∂ 2T
= 0 , T (0) = T0 , T ( L) = TL (L Länge des Stabes)
∂x 2
x
Lösung: T ( x) = T0 + (TL − T0 ) , linearer Temperaturabfall
L
Temperaturverteilungen zwischen zwei Kugelschalen, bei r = r1 und r = r2 gelegen, mit
T (r1 ) = T1 und T (r2 ) = T2
ebenfalls eindimensionales Problem, da Kugelsymmetrie
1 ∂  ∂
Laplace-Operator ∆ = 2  r 2  , also
r ∂r  ∂r 
∂  2 ∂
r
=0
∂r  ∂r 
C
T −T
r T − rT
Lösung: T (r ) = C1 + 2 , Einsetzen in Randbedingungen liefert C1 = 2 2 1 1 , C2 = 2 1
1 1
r
r2 − r1
−
r2 r1
Hyperbolischer Temperaturabfall
122
Zeitabhängige Lösung
"unendlich langer" und sehr dünner Stab
Temperatur als Funktion von Ort und Zeit :
(x )
T = T (x, t )
mit T
T = T + T * ( x, t )
mit T * (x, t ) → 0 (Abweichung)
x → ±∞
=T
x → ±∞
Θ(x)
x
0
Anfangsbedingung: T ∗ ( x,0 ) = Θ( x )
Randbedingungen: T * (x, t ) = 0 für alle Zeiten t.
x → ±∞
Lösung der eindimensionalen Wärmeleitungsgleichung für beliebige Anfangsverteilung
der Temperatur (mittels Separationsansatz, siehe Anhang, Hier: T * = T )
T (x, t ) =
1
4πλt
∞
∫ Θ (x')e
−
( x'− x )2
4 λt
dx'
−∞
δ(x')
Spezialfall:
Θ (x' ) = T0 δ (x' ) Dirac'sche Delta-Funktion
x'
0
Es gilt: ∫ δ ( x' ) f ( x' )dx' = f (0 ) ,
woraus folgt:
f(x')
δ(x')
x'
0
123
T (x, t ) =
1
4πλt
x2
T0e 4λt
−
T(x)
x
ergibt sich
0
∆x
 x
−
1
4λ t
T ( x, t ) =
e 
4πλt



2
Gauss-Funktion
2
Vergleich: T (x ) =
1
2πσ
1 x − x 
− 

2  σ 
=
e
1
2π
1 x − x 
− 

1
2  σ 
e
2λt
2
σ 2 = 2λt
σ = 2λt ;
14.2. Diffusion und Elektrodiffusion
Zugehöriger Term bei der Entropieproduktion
K
r
 µi 

 T 
σ = ∑ J ci grad −
i =1
Wir betrachten nur eine bewegliche Komponente k
r
r
J ck = J k = Lkk X k
 µ 
wobei X k = grad − k 
 T 
Existieren elektrische Felder und ist die Komponente k geladen, gilt:
124
 η 
X k = grad − k 
 T 
η k : elektrochemisches Potential mit
η k = g k ( p ,T ) + RTln
nk
K
∑nj
+ z k Fϕ
j =1
oder in verdünnten Lösungen:
η k = µ ko + RTlnc k + z k F ⋅ ϕ
Dementsprechend können Diffusionsströme hervorgerufen werden durch
Konzentrationsgradienten, Gradienten des elektrischen Potentials, Druckgradienten und
durch Temperaturgradienten
Wir nehmen zunächst an, dass in unserem System keine Druck- und Temperaturgradienten
auftreten. Außerdem: Eindimensionaler Fall. Es treten nur Gradienten in x-Richtung auf.
Linearer Ansatz
η 
J = L X = − L grad 
T 
da T = konst . vorausgesetzt: J = −
L dη
T dx
Wir hatten bereits abgeleitet: J c = cv . Demnach: cv = −
v=−
L dη
T ⋅ c dx
v = −u
dη
,
dx
u: Beweglichkeit
125
L dη
T dx
Proportionalität zwischen Geschindigkeit und Gradient des elektrochemischen Potentials
dη
Man erkennt: v > 0 für
<0
dx
Elektrodiffusion erfolgt aus Gebieten höheren elektrochemischen Potentials in Gebiete
niedrigen elektrochemischen Potentials.
J = −uc
dη
¸
dx
daher:
dϕ 
dlnc

+ zF
J = −uc RT

dx 
dx

Wegen
η = µ 0 ( p ,T ) + RTlnc + zFϕ
dlnc 1 dc
=
dx
c dx
J k = −uk RT
, erhält man für die Komponente k:
dck
dϕ
− uk zk Fck
dx
dx
(dabei ist E x = −
dϕ
dx
:
Nernst-Planck-Gleichung
die x-Komponente der elektrischen Feldstärke)
Nernst-Planck-Gleichung:
Fluß J k ~ Konzentrationsgradient
~ Feldstärke
Diffusion ungeladener Stoffe
( z k = 0 oder
dϕ
= 0)
dx
von der Nernst-Planck-Gleichung bleibt:
J k = −u k RT
dck
dc
= − Dk k
dx
dx
Der Zusammenhang Dk = u k RT
(#)
zwischen Beweglichkeit u k und Diffusionskoeffizient
Dk wird als Einstein-Relation bezeichnet.
126
In Abwesenheit chemischer Reaktionen gilt die Massenbilanzgleichung
∂ck ∂J k
=0
+
∂x
∂t
(oder divJ k statt
∂c
∂c k ∂ 
+  − Dk k
∂x
∂t ∂x 
mit (#) folgt:
∂J k
)
∂x

=0

Für Dk = konst.
∂ck
∂ 2ck
= Dk
∂t
∂x 2
, oder:
∂ck
= Dk ∆ck ,
∂t
2. Ficksches Gesetz (Diffusionsgleichung), hat die gleiche mathematische Gestalt wie die
∂T
∂ 2T
Wärmeleitungsgleichung
−λ 2 = 0.
∂t
∂x
Permeabilitätskoeffizient
Spezialfall: Transport durch eine Membran:
innen
i
ck
Membran
außen
a
ck
x
-d
J = −D
∂c
∂x
0
Nernst-Planck-Gleichung für ungeladene Stoffe
Integration über die Membran
0
0
∫ J dx = − Dk ∫ dx dx = − D(c
−d
dc
a
− ci
)
(*)
−d
127
Transport stationär, wenn
∂c
∂t
=0 ⇒
∂J
∂x
= 0 (keine Konzentrationsveränderungen),
also J k = konst. (unabhängig von x)
0
0
−d
−d
∫ Jdx = J ∫ dx = Jd
(
)
Einsetzen in (*) gibt Jd = − D c a − c i , bzw.
J =−
D
d
(c
a
) (
− ci = P c i − c a
)
Permeabilitätskoeff.= Diffusions. koeff. durch Dicke der Membran)
J = P∆c
Maßeinheiten:
 ∂c   Mol 
   l ⋅ s  cm 2
[D] =  ∂2t  =  Mol
=
s
∂ c 
 2  l ⋅ cm 2
 ∂x 
D
cm
P = ⇒ [P ] =
("Geschwindigkeit")
d
s
128
15. Gleichgewichtszustände an biologischen Membranen
innen
Membran
außen
(i)
(m)
(a)
x=0
x=-d
x
Innen und außen: wässrige Lösung von geladenen oder ungeladenen Stoffen, für die die
Membran in unterschiedlichem Maße permeabel ist.
Betrachtung der Ortsabhängigkeit nur in x-Richtung: Hinreichend gute Näherung, wenn die
Membran nicht zu stark gekrümmt ist.
Gleichgewichtszustände: Wichtiger Grenzfall, lebende Zelle allerdings stets im
Nichtgleichgewicht; einige Prozesse, i. a. die sehr schnellen Prozesse, können aber als sich im
Gleichgewicht befindend angesehen werden.
Annahme: Keine chemischen Reaktionen, keine Temperaturgradienten.
η 
X k = −grad k  : bleibt nur der Gradient des elektrochem Potentials (dividiert durch T) als
T 
Kraft, mit
η k = g k ( p ,T ) + RTln
nk
+ z k Fϕ ,
n
oder:
η k = µ k0 + RTlnck + z k Fϕ
15.1 Nernst'sches Gleichgewicht
Zu beiden Seiten der Membran befindet sich die wässrige Lösung eines Salzes, das
vollständig in Ionen zerfallen ist. Die Membran sei für die eine Ionensorte k permeabel.
129
Im Gleichgewicht: keine Gradienten der elektrochemischen Potentiale
grad (η k ) = 0 , d.h. η k i = η k a , ∆ηk = ηki − ηka = 0
∆η k = ∆µ k0 + z k F∆ϕ + RT∆lnc k
mit: ∆lnc k = lncki − lnc ka = ln
cki
cka
folgt: 0 = ∆µ k0 + z k F∆ϕ + RT ⋅ ln
RTln
cki
cka
c ki
c ka
= − ∆µ k0 − z k F∆ϕ
 ∆µ k0 + z k F∆ϕ 


=
exp


RT
cki


cka
Sind die Eigenschaften des Lösungsmittels in beiden Teilsystemen identisch gilt:
(µ ) = (µ ) ;
0 a
k
0 i
k
∆µ k0 = 0
und demzufolge:
(
 zk F ϕ i − ϕ a
= exp

RT
cki

cka
)


Nernst-Gleichung
andere Schreibweise: ∆ϕ = ϕ i − ϕ a =
ca
RT
ln ki
z k F ck
∆ϕ : Nernst-Potential.
Maßeinheiten:
130
RT
= ϕ 0 = 26 ,7 mV bei T = 310 K
F
(
 zk ϕ i − ϕ a

exp
=

ϕ0
cki

cka
) kann entwickelt werden für ∆ϕ << 1


ϕ0
15.2. Donnan-Gleichgewicht
außen
innen
i
cp ;(c - )
(c + )
a
(c- )
a
i
(c +)
x=0
x=-d
x
c p : Konzentration impermeabler geladener Stubstanzen P, z. B. Proteine (negativ oder
positiv). P nur nur innen
c + , c − : Ionenkonzentrationen, jeweils innen und außen
Die Membran sei sowohl für Anionen als auch Kationen permeabel.
Die Anwendung der Gleichgewichtsbedingung führt auf
∆ϕ = ϕ i − ϕ a = −
RT c + ,i RT c − ,i
ln + ,a =
ln − ,a
F
F
c
c
Daraus folgt
c + ,i c − ,a
=
= r , Donnan-Quotient
c + ,a c − ,i
In beiden Kompartimenten muß Elektroneutralität herrschen.
innen:
c + ,i − c − ,i + z p c p = 0
außen:
c + ,a = c − ,a = c 0
z p : Ladungszahl der Proteine
131
r=
c + ,i
c0
=
c0
d.h.
c − ,i
c
+ ,i
= rc0 und
c
−,i
c0
=
r
Einsetzen in Elektroneutralitätsbedingung für Innenraum:
c + ,i − c − ,i + z p c p = 0
r2 = +
r=−
z pc p
c0
2c 0
rc 0 −

 +1


,
c0
+ z pc p = 0
r
⋅ r −1 = 0
 z pc p
±  0
 2c
z pc p
,
2
"Minus-Lösung" ohne physikalische Bedeutung, weil
r > 0 (Konzentrationsverhältnis)

 z pc p
RT  z p c p
RT
lnr = −
ln −
∆ϕ = −
+ 
0
F  2c
F
 2c 0

∆ϕ
2


 + 1




Donnan-Potential (1911)
Diskussion:
zp = 0:
r = 1 , c +,i = c +, a
c − ,a = c − ,i , c + ,i = c − ,i , c + ,i = c 0 , c − ,i = c 0
zp > 0 :
r <1 , r2 <1 , r2 =
c + ,i
c
0
⋅
c0
c
− ,i
=
c + ,i
c
− ,i
<1 ,
c + ,i < c − ,i
Positive Ladungen des beweglichen Ions
+
+
+ +
werden abgestoßen
⊕ = cp
Ähnlich: z p < 0 : r > 1 , c + , i > c -,i
Positive Ladungen des beweglichen Ions werden angezogen.
132
+
+
+
+
+
+
+
+
+
+
Koionen:
Haben Ladungsvorzeichen wie Proteine
Gegenionen:
Haben entgegengesetzte Vorzeichen
Im Innenraum wird die Konzentration der Gegenionen wird erhöht, im Außenraum verringert.
15.3 Elektrische Doppelschichten an der Membranoberfläche
Bisher wurde vorausgesetzt, dass innerhalb der Kompartimente keine
Konzentrationsgradienten auftreten. Das ist streng genommen nicht erfüllt. Besonders dann
nicht, wenn Membran selbst elektrisch geladene Komponenten enthält (z.B. ist PhosphatidylSerin negativ geladen).
äußere-Membran
Em
x=0
---
εm
geladene Membrankomponenten: Fixladungen
x
(im Gegensatz zu beweglichen Ladungen)
E
ε
Ausbildung einer Doppelschicht: Schicht der Fixladungen + diffundierende Schicht der
Elektrolytionen.
elektrochemisches Potential: η k = µ k0 + RTlnck + z k F ⋅ ϕ
grad(η k ) = 0 = RT
dlnck
dϕ
+ zk F
=0
dx
dx
(bei Vernachlässigung von Druckgradienten)
im folgenden ist nur eine Raumrichtung (x)interessant
Integration: RTlnck ( x ) + z k Fϕ ( x ) = C = konst .
133
lnck ( x ) =
z F
C
− k ϕ (x ) ,
RT RT
c k (x ) = e ⋅ e
~
c
−
zk F
ϕ (x )
RT
= ck ⋅ e
Abkürzung:
−
zk F
ϕ (x)
RT
C
= c~
RT
(*)
ck = c k bei ϕ = 0
Da nur Potentialdifferenzen definiert sind, wählt man den Nullpunkt von ϕ so, daß gilt:
ϕ = 0 für x → ∞ ⇒ ck = ck∞
Aus (*) läßt sich der Konzentrationsverlauf berechnen wenn ϕ ( x ) bekannt ist
Aus den Gesetzen der Elektrostatik folgt:
d 2ϕ
dx
2
=−
ρ (x )
εε o
Poisson-Gleichung
ρ (x ) - Ladungsdichte am Ort x, beinhaltet
Fixladungen + bewegliche Ladungen der
Elekrolyten
d 2ϕ
dx
2
=−
1
εε o
(ρ fix (x ) + ρ bew (x ))
Voraussetzung: Fixladungen nur an der Außenseite der Membran.
ρ fix = σδ (x ) , δ -Funktion
∞
Wegen
∫ δ (x )dx = 1
δ(x)
x=0
δ ( x ) hat die Maßeinheit 1 cm
−∞
σ ist die Flächenladungsdichte
134
x
Regeln der Elektrostatik in Substanzen:
An geladenen Grenzflächen zwischen Medien mit unterschiedlichen Dielektrizitätskonstanten
gibt es eine Unstetigkeit der elektrischen Feldstärke E = − dϕ dx
Es muß gelten:
εm
dϕ
dx
=ε
x→−0
dϕ
dx
+
x→+0
σ
ε0
bei x = 0
Wegen ε m ≈ 5 , ε ≈ 80 erhält man näherungsweise
dϕ
σ
=−
dx
εε 0
für x → +0
Für x > 0 tragen nur die beweglichen Ladungen des Elektrolyten zur Ladungsdichte bei:
ρ bew = F ∑ z k c k (x ) = F ∑
k
z F
− k ϕ (x )
∞
z k c k e RT
k
also folgt:
d 2ϕ
dx 2
=−

z k ck∞ exp ∑
εε 0

F
k
z k Fϕ ( x ) 
 ,
RT 
Für kleine Potentiale ϕ ( x ) <<
Poisson-Boltzmann-Gleichung
RT
, d.h. ϕ << 26mV
zk F
erhält man durch Reihenentwicklung der e-Funktion
d 2ϕ
dx
2
=−
F
εε 0

∑ z k ck∞ 1 k
z k Fϕ ( x ) 

RT 
135
d 2ϕ
dx 2
=−
 z k2 F 2 ck∞
∞
z
Fc
+
∑ k k ∑  εε RT
εε 0 k
14243 k  0
=0
1

ϕ ( x )


1. Term verschwindet, da in großer Entfernung von der Membran Elektroneutralität vorliegen
muss
mit der Abkürzung:
erhält man:
d 2ϕ
= κ 2ϕ
2
dx
z k2 F 2 c k∞
κ =∑
k εε 0 RT
2
(#)
κ trägt die Maßeinheit Länge-1
λD =
1
κ
: Debye-Hückel-Länge.
Bei einem 1:1-wertigen Elektrolyten findet man wegen c+∞ = c−∞ = c ∞ : λ D =
1
F
εε 0 RT
2c ∞
Mit zunehmender Elektrolytkonzentration c ∞ nimmt die Debye-Hückel-Länge ab.
Die Differentialgleichung (#) hat die Lösung:
ϕ (x ) = ϕ (0)e −κx
ϕ (0) : Oberflächenpotential
(Lösung ϕ ( x ) = ϕ (0)e +κx scheidet aus, da sie divergiert)
ϕ(x)
ϕ(0)>0
x
ϕ(0)<0
unter Berücksichtigung der Randbedingung:
136
σ
dϕ
=−
= −ϕ (0)κe −κx
εε 0
dx
σ
= ϕ (0 )
εε 0κ
,
x =0
σ - Flächenladungsdichte, folgt
,
ϕ (0) hat das gleiche Vorzeichen wie σ .
Für das Potential folgt als Lösung:
ϕ (x ) =
σ −κx
e
εε 0κ
wegen
ck+
(x ) =
F
− ϕ (x )
∞ RT
ck e
falls σ < 0 : ϕ ( x ) < 0 : Anhäufung positiver Ladungen an der Oberfläche
Berechnung des Potentialverlaufes auf der Grundlage der nichtlinearen PoissonBoltzmann-Gleichung
Wir beschränken uns auf den Fall ein-wertiger Ionen:
Fϕ
 Fϕ

d 2ϕ
Fc ∞  − RT

RT
e
e
=
−
−

2
εε 0  (↑ z =+1) (↑ z =−1) 
dx


=
2 Fc ∞
εε 0
 Fϕ 
sinh 

 RT 
Einschub:
ρ = F ∑ z k ck
ck =
ck∞ e
−
z k Fϕ
RT
k
e x − e−x
sinhx =
,
2
e x + e−x
coshx =
2
das ist eine nichtlineare Differentialgleichung, die etwas schwieriger zu integrieren ist.
137
Multiplikation beider Seiten mit
dϕ
:
dx
dϕ  d 2ϕ  2 Fc ∞
 Fϕ  dϕ
=
sinh

⋅
dx  dx 2 
εε 0
 RT  dx
2
d  2 RTc ∞
1 d  dϕ 
 Fϕ  
cosh


 = 
dx  εε 0
2 dx  dx 
 RT  
das läßt sich direkt integrieren:
1  dϕ 
2 RTc ∞
 Fϕ 
cosh 

 =
+C
εε 0
2  dx 
 RT 
2
dϕ
→ 0 und wegen cosh(0) = 1 folgt:
dx
weil für x → ∞ gilt ϕ → 0 und
1  dϕ 
2 RTc ∞

 =
εε 0
2  dx 
2

 Fϕ  
 cosh
 − 1
 RT  


 α 
weiterhin gilt coshα - 1 = 2 sinh   
 2 

1  dϕ 
4 RTc ∞

 =
εε 0
2  dx 
2
Mit κ 2 = ∑
k

 Fϕ  
 sinh 
 
 2 RT  

z k2 F 2 ck∞
εε 0 RT
=
zk2 =1
2
und damit:
2
2F 2c ∞
folgt
εε 0 RT
4c ∞ RT
εε 0
und damit
2
4κ 2 R 2T 2
 dϕ 

 =
 dx 
F2

 Fϕ  
 sinh 
 
 2 RT  

2
138
=
2κ 2 R 2T 2
F2
dϕ
2κRT
 Fϕ 
=−
sinh 

dx
F
 2 RT 
,
Lösung mit +-Vorzeichen würde divergieren
Um den Potentialverlauf zu berechnen ist noch eine Integration erforderlich.
Das Oberflächenpotential läßt sich aber bereits jetzt ausrechnen:
Randbedingung:
damit:
dϕ
dx
=−
x =0
σ
εε 0
σ
2κRT
 Fϕ 
sinh
=

εε 0
F
 2 RT 
σF
 Fϕ 
sinh
=
 2 RT  2κRTεε 0
Bildung der Umkehrfunktion:
ϕ (0) =
 σF 
2 RT

arsinh
F
 2κRTεε 0 
bei Betrachtung kleiner Oberflächenladungen: Reihenentwicklung der arsinh-Funktion:
arsinhx ≅ x
ϕ (0) ≅
σF
σ
2 RT
=
F 2κRTεε 0 εε 0κ
(entspricht der oben angegeben Lösung für den linearen Fall)
Den vollständigen Potentialverlauf erhält man durch eine weitere Integration:
2κRT
dϕ
 Fϕ 
=−
sinh 

dx
F
 2 RT 
ϕ
x
dϕ
2κRT
=− ∫
dx
∫
F
 Fϕ 
x
=
ϕ (0 ) sinh 
0

 2 RT 
139
Integraltafeln:

dα
α 
∫ sinhα = ln tanh 2  
mit tanhα =
sinhα eα − e − a
=
coshα eα + e −α
es folgt:
  Fϕ ( x )  Fϕ (0 )  

  2 RT
+ 1 e 2 RT − 1 
 e





κ ⋅ x = ln 
ϕ
(
)
ϕ
(
)
F
x
F
0



  2 RT



− 1 e 2 RT + 1 
  e





Das läßt sich nach ϕ ( x ) auflösen, obige Gleichung reicht aber zur Darstellung des
Potentialverlaufes:
ϕ(x)
lineare Näherung
nichtlin., exakte
x
140
16. Nichtgleichgewichtsprozesse an biologischen Membranen
Nernst-Planck-Gleichung:
J k = −u k RT
dck
dϕ
− u k z k Fc k
dx
dx
oder mit Ersetzen der Beweglichkeit u k = Dk RT durch Diffusionskoeffizient
J k = − Dk
dck Dk
dϕ
z k Fck
−
dx RT
dx
 η 
das war die Folgerung aus der linearen Beziehung J ck = J k = Lkk X k = Lkk grad − k 
 RT 
mit Lkk = ck u k T und u k = Dk RT
Membran
innen
Geometrie:
außen
x
x=0
x=-d
d
Diffusion ungeladener Stoffe:
aus der Kontinuitätsgleichung
J k = − Dk
0
und
dck
dx
∫ J k dx = − Dk
−d
∂ck ∂J k
+
= 0 folgt
∂t
∂x
0
(
)
(
)
dck
dx = − Dk cka − cki
dx
−d
∫
und im stationären Fall: J k = −
(
Dk a
c k − cki = − Pk cka − cki
d
141
)
wobei sich aus cka > cki ´ J k < 0 ergibt
16.1. Diffusion von Ionen
es war J k = − Dk
dck Dk
dϕ
−
und wird jetzt mit Trick integriert
z k Fck
dx RT
dx
Multiplizieren beider Seiten mit
Jk
zk Fϕ
e RT
Jk
zk Fϕ
e RT
zk Fϕ
e RT
z Fc dϕ 
 dc
= − Dk  k + k k
e
RT dx 
 dx
d 
= − Dk
ck e
dx 

z k Fϕ
RT
zk Fϕ
RT




Annahme stationärer Fluß: J k = konst . (unabhängig von x) → Integration
0
Jk
∫
z k Fϕ
e RT dx
−d

z Fϕ a
zk Fϕ i
 a k
= − Dk  c k e RT − c ki e RT







(*)
Auf der linken Seite kann die Integration vorerst nicht ausgeführt werden, da ϕ ( x ) innerhalb
der Membran nicht bekannt ist.
Bestimmte Schlüsse lassen sich aber doch ziehen:
Ussing’sche Gleichung
Aus (*) folgt, dass sich der Nettofluß J k aus der Differenz zweier Elementarflüsse ergibt:
J k = J ki→a − J ka→i
142
0
Benutzt man für das Integral die Abkürzung I =
∫
zk Fϕ
e RT dx
−d
erhält man:
z k Fϕ i
zk Fϕ a
D
D
J k = k cki e RT − k c ka e RT
I4
I 44244
1
4244
3 1
3
J i →a
J a →i
für cka = 0 gilt dann: J k = J ki→a
(plausibel)
für cki = 0 gilt dann: J k = − J ka→i
Für das Verhältnis der Elementarflüsse findet man
J ki→a
J ka→i
=
c ki
cka
(
)
zk F ϕ i −ϕ a
zk F∆ϕ
cki
RT
=
e RT
e
cka
Das ist die Ussingsche Gleichung (Ussing 1949). Das Verhältnis der Elementarflüsse ist
unabhängig vom Integral I und damit vom speziellen Potentialverlauf durch die Membran.
Die Elementarflüsse sind meßbar mittels radioaktiver Isotope.
Spezialfall: J k = 0 folgt:
cki
cka
z F∆ϕ
− k
= e RT
, Nernst’sche Gleichung
Goldman-Gleichung
Goldman integrierte die Elektrodiffusionsgleichung (*) unter der Annahme, dass die
Feldstärke innerhalb der Membran konstant ist
Membran
dϕ
E=−
= konst .
dx
ρ
d 2ϕ
bzw.
=
−
= 0 , also ρ = 0
εε 0
dx 2
ϕa
ϕi
x
-d
143
0
also gilt:
(
ϕ = ϕ a − ϕi −ϕ a
) dx = ϕ
a
− ∆ϕ
x
d
für − d ≤ x ≤ 0
( x = 0 → ϕ = ϕ a ; x = −d → ϕ = ϕ i )
Damit läßt sich das Integral berechnen:
0
I=
∫e
zk Fϕ
RT
0
dx =
−d
I =e


zk F  ϕ a − ∆ϕ
∫e
x

d
RT
dx
−d
z F∆ϕ x
zk Fϕ a 0
− k
RT
∫e
RT
d
dx
−d
I = −e
I = −e
zk Fϕ a
RT
zk Fϕ a
RT
0
 − zk F∆ϕ x 
RTd
e RT d 


z k F∆ϕ

 −d
∫e
,
−λx
=−
1
λ
e −λx
zk F∆ϕ 

1 − e RT  RTd

 z k F∆ϕ


D
Berücksichtigt man dieses Ergebnis in der Gleichung J k = k
I
z k Fϕ a
z k Fϕ i

 i RT
− cka e RT
 ck e


ergibt sich:
zk Fϕ a
zk Fϕ i

Dk z k F∆ϕ  i RT
Jk = −
ck e
− c ka e RT

RTd 

 − z k Fϕ

RT
e


a
zk F∆ϕ


RT
1 − e







mit Dk d = Pk und Zusammenfassung der e-Terme ergibt sich:
144
−1





z k F∆ϕ

Pk zk F∆ϕ  a
i
Jk =
ck − ck e RT
RT 

z k F∆ϕ 


RT 
1 − e





−1
(#)
Diese Gleichung beschreibt die Ionenflußdichte
Jk
in Abhängigkeit von den
Ionenkonzentrationen cka und cki und vom Membranpotential ∆ϕ . Sie kann auch dazu
verwendet werden, den Permeabilitätskoeffizienten unter beliebigen Bedingungen ( ∆ϕ ≠ 0 )
mit Hilfe von Isotopenflußmessungen zu bestimmen.
Für ∆ϕ → 0 wird der Nenner in der Gleichung für die Ionenflußdichte singulär, aber mit der
Näherung e x ≅ 1 + x folgt
zk F∆ϕ

Pk z k F∆ϕ  a
i
RT
Jk ≅
 ck − ck e
RT


−1

z k F∆ϕ 

i
a
1 − 1 − RT  ∆ϕ==0 Pk ck − ck



(
(wie gefordert für ungeladene Stoffe)
Mit der Abkürzung u =
F∆ϕ
erhält man:
RT
 c a − c i e zk u 
k
k

J k = Pk z k u 
1 − e zk u 


.
Verlauf der Funktion J k (∆ϕ ) für zk > 0 :
145
)
Da im Ruhezustand kein Strom durch die Membran fließt, muß der Ladungstransport durch
Kationen und Anionen ausgeglichen sein und es gilt:
∑ JK
∑JA
=
Kationen
I = F ∑ zk J k = 0
bzw.
Anionen
k
wobei I hier die Stromdichte ist. Diese Summation ist über alle permeablen Ionensorten zu
erstrecken. Angenommen, wir haben eine Membran, durch die nur K+, Na+ und Cl- fließen,
dann gilt:
J K + J Na − J Cl = 0
und damit
(c
P u
K
a
K
− c Ki e u
(1 − e )
u
) + P u (c
Na
(1 − e )
Multiplikation mit
a
Na
− c iNa e u
(1 − e )
u
) + P u (c
Cl
a
Cl
i −u
e
− cCl
(1 − e )
−u
)=0
u
u
(
)
(
liefert unter Berücksichtigung von
)
(
1 − eu
1− e
−u
= −e u
)
a
a u
i
PK c Ka − c Ki e u + PNa c Na
− c iNa e u − PCl cCl
e − cCl
=0
Auflösen nach eu :
u
e =
F∆ϕ
e RT
∆ϕ =
=
a
i
PK cKa + PNa c Na
+ PCl cCl
a
PK cKi + PNa c iNa + PCl cCl
a
i
RT PK cKa + PNa cNa
+ PCl cCl
ln
a
F
PK cKi + PNa ciNa + PCl cCl
,
Goldman-Gleichung
Diese Gleichung geht auf Arbeiten von D.E. Goldman (1943) sowie von A.L. Hodgkin und B.
Katz (1949) zurück. Die Goldman-Gleichung stellt gewissermaßen eine verallgemeinerte
146
Nernst-Gleichung dar, wobei die Beiträge einzelner Ionensorten nach dem Permeabilitätskoeffizienten Pk gewichtet sind.
Im Grenzfall PK >> PNa , PCl (Membran überwiegend K+-permeabel) geht die GoldmanGleichung in die Nernst-Gleichung über:
∆ϕ =
RT c Ka
ln i
F
cK
Die Goldman-Gleichung ist trotz der bei der Ableitung benutzten Einschränkungen von
großer Bedeutung. Ihre näherungsweise Gültigkeit ist durch unabhängige Meßungen der
Permeabilitäten in Isotopenfluß-messungen nachweisbar.
Die allgemeine Form der Goldman-Gleichung für beliebig viele Kationen und Anionen
lautet:
∆ϕ =
a
i
RT ∑ PKation c Kation + ∑ PAnion c Anion
ln
i
F
+ ∑ PAnion c aAnion
∑ PKation c Kation
Berechnung des Konzentrationsprofils innerhalb der Membran
Ausgangspunkt: J k = − Dk
dck Dk
dϕ
z k Fck
−
dx RT
dx
wir nehmen wieder an, dass Feldstärke innerhalb der Membran konstant ist:
(
ϕ = ϕ a − ϕi −ϕ a
) dx = ϕ
a
− ∆ϕ
x
d
damit:
dϕ
∆ϕ
=−
dx
d
z F ∆ϕ 
 dc
also ist: J k = − Dk  k − ck k

RT d 
 dx
147
dc k
= dx
 z k F∆ϕ  J k
ck 
−
 RTd  Dk
Bei Intergration erhält man auf der linken Seite ein Integral vom Typ:
dy
1
∫ ay − b = a ln(ay − b )
unter Berücksichtigung der Randbedingungen c k (0 ) = c ka , c k (− d ) = cki , ∆c k = c ki − c ka folgt

 z F∆ϕ ( x + d )  
 exp k
 −1
RTd


 
i
ck (x ) = ck − ∆ck 

 z F∆ϕ 
 exp k
 − 1 
 RT 


für ϕ i > ϕ a ist cki < c ka
für ∆ϕ ≠ 0 erhält man ein
Membran
Anionen
ca
∆ϕ=0
ci
ϕ i > ϕa
Kationen
x
-d
nichtlineares Konzentrationsprofil
0
also keine Elektroneutralität innerhalb der Membran.
Grenzfall ∆ϕ = 0 : mit e λ ≅ 1 + λ folgt c k ( x ) = c ki − ∆c k
x+d
lineare Fkt. von x
d
16.2. Transport durch elektroneutrale Membranen
Es gibt noch eine andere, erstmals von Planck (1890) angegebene Integration der
Elektrodiffusionsgleichung.
J k = − Dk
dck Dk
dϕ
z k Fck
−
dx RT
dx
Es wird wieder eine spezielle Annahme gemacht: Nicht nur in den homogenen
Kompartimenten, sondern auch innerhalb der Membran besteht Elektroneutralität
148
Anionen: z k = −1 , Kationen: z k = +1 (also z.B. Salz, dass in 2 einwertige Ionen zerfällt)
Es gelte:
innen: c+i = c −i = c i ,
außen: c+a = c−a = c a
in Membran: c+ ( x ) = c − ( x ) = c( x ) für − d ≤ x ≤ 0
J+
dc
c F dϕ
=− + − +
D+
dx
RT dx
J−
dc
c F dϕ
=− − + −
D−
dx
RT dx
mit obigen Annahmen ergibt die Addition bzw. Subtraktion der beiden Zeilen
J+ J−
dc
+
= −2
D+ D−
dx
(1)
J+ J−
cF dϕ
−
= −2
D+ D−
RT dx
(2)
unter stationären Bedingungen gilt: J + = konst . und J − = konst .
daraus folgt mit Gl.(1)
dc
= konst .
dx
damit ist c darstellbar als c( x ) = c a − ∆c
für Gl. (1) gilt dann:
1  J+ J−

+
2  D+ D−
(konstanter Konzentrationsgradient)
x
dc
∆c
, ∆c = c i − c a ;
=−
d
dx
d
 ∆c
 =
 d
(1*)
und Gl. (2) ergibt durch Umstellen
J
J
dϕ
= − + − −
dx
 D+ D−

RT

 2 F  c a − ∆c x 
d

Durch Integration folgt
149
J
J  RT d
ci
ln a
∆ϕ = ϕ i − ϕ a =  + − − 
 D+ D−  2 F ∆c c
(2*)
Mit den Gleichungen (1*) und (2*) hat man zwei Gleichungen zur Bestimmung von
J + und J − .
Man erhält:




∆c 
F∆ϕ 
1+
J + = D+
d 
ci 
 RTln a 
c 



∆c 
F∆ϕ
1−
J − = D−
d 
ci
 RTln a
c

Für ∆ϕ → 0 ⇒ J + = D+
∆ϕ = ϕ i − ϕ a






∆c
= D+ ∆c
d
∆c
= D− ∆c
J − = D−
d
falls ∆ϕ > 0;ϕ i > ϕ positive Ionen werden nach außen gedrückt
16.3 Diffusionspotentiale (aus Planck'scher Integration)
Im stationären Fall (Flüsse nicht unabhängig)
J + = J − = J da Elektroneutralität gewahrt bleiben muß

∆c 
F∆ϕ
1+
D+

d  RT ln c i
ca

D+ +
D+ F∆ϕ
i
RTln c
ca






∆c 
F∆ϕ 
 = D− d 1 −
ci 

ln
RT



ca 

= D− −
D− F∆ϕ
i
RTln c
ca
150
Auflösen nach ∆ϕ liefert
∆ϕ = −
RT
F
 D+ − D−  c i

 ln a
+
D
D
 +
− c
,
Diffusionspotential
korrespondiert mit der Gleichung
∆ϕ =
RT P+ c+a + P−c−i
ln
F
P+ c+i + P−c−a
aus dem Goldman'schen Ansatz
mit P = D d
In beiden Ansätzen entsteht ein Diffusionspotential nur dann, wenn sowohl D+ ≠ D− als
auch ci ≠ c a . Außerdem geht für sehr hohe Permabilität von einer Ionensorte, dass
Diffusionsprotential in das Nernst-Ptwntial dieser Ionensorte über.
Einsetzen von ∆ϕ in






∆c 
∆c 
F∆ϕ 
F∆ϕ
1+
1−
= J − = D−
J + = D+
i



d
d
c
ci
 RTln a 
 RTln a
c 
c




=J



liefert
J + = D+
J − = D−
J=
∆c 
D − D− 
∆c  2 D− 
 = D+

= J
1 − +
d  D+ + D− 
d  D+ + D− 
∆c 
∆c  2 D+ 
D − D− 
1 + +
 = D−

= J
d  D+ + D− 
d  D+ − D− 
∆c  2 D+ D− 
∆c

 = Deff
d  D+ + D− 
d
Für den gemeinsamen Transport von Anionen und Kationen ergibt sich ein effektiver
Diffusionskoeffizient.
151
1
1 
D + D− 1  1

= +
= 
+
2 D+ D−
2  D+ D− 
Deff
D+ > D−
Annahme
1
1
<
D+ D−
1
1
1
1
2
+
<
+
=
D+ D− D− D− D−
1
1 1
1  1
<
= 
+
2  D+ D−  D−
Deff
D− < Deff
,
⇒
ähnlich folgt: D+ > Deff
Richtung der Transmembranpotentials so, dass langsam diffundierende Teilchen bescheunigt
und schnelle gebremst werden.
16.4 Membranwiderstand
Da Diffusion von Ionen mit Ladungstransport verbunden ⇒ elektrische Stromdichte I k
I k = zk FJ k
Es gilt:
c z F dϕ 
 dc
J k = − Dk  k + k k

RT dx 
 dx
I k = − Dk zk F
dck
c z 2 F 2 dϕ
− Dk k k
dx
RT
dx

RT
Ik 
 D z 2 F 2c
 k k
k

 = − RT dck ⋅ 1 − dϕ

ck dx zk F dx

=−
RT d ln ck dϕ
−
zk F dx
dx
Durch Integration folgt:
0
Ik
∫
−d
RT dx
Dk zk 2 F 2c(x )
=
c i
RT
ln k + ∆ϕ
zk F ck a
0
Mit den Abkürzungen:
Rk =
RT dx
∫ Dk zk 2 F 2ck (x )
−d
152
Ek =
I k Rk = Ek + ∆ϕ
c i
RT
ln k
z k F ck a
Gleichgewicht: I k = 0
*)
RT
ck i
= − ∆ϕ
ln
zk F ck a
Ek = − ∆ϕ
Versteht man unter Rk den Membranwiderstand, entspricht *) dem Ohmschen Gesetz.
U k = Ek + ∆ϕ
I k Rk = U k
Strom wird durch zwei Spannungsdifferenzen hervorgerufen.
1) Membranpotential ∆ϕ
2) Spannungsdifferenz Ek , die durch Konzentrationsgrad hervorgerufen wird
Ek : Elektromotorische Kraft, entspricht dem Nernst-Potential der Ionen
Zur expliziten Berechnung des Widerstandes muß c(x ) bekannt sein. Verwendet man den
Ausdruck, der aus der „constant field“ Näherung folgt, ergibt sich:
 rc i 
R T (1 − r )ln k 
c a 
 k 
2 2
Rk =
(
Pk zk3 F 3∆ϕ cka − r cki
)
 z F∆ ϕ 
mit r = exp k

 RT 
Ohne Konzentrationsgrad. cki = cka = ck folgt:
RT
Rk =
Pk zk 2 F 2ck
Mit Gk =
Gk =
d
U k zk2 F 2ck
1
erhält man die Leitfähigkeit.
Rk
Pk zk2 F 2
ck
RT
I⋅
Rk =
Dk = uk RT
Pk =
uk RT
d
RT
= ∆ϕ
Pk zk2 F 2ck
153
154
17. Stationäre Nichtgleichgewichtszustände – Das Prinzip der minimalen
Entropieproduktion
(Abgehandelt an einem einfachen Beispiel)
Zeitunabhängige Zustände
d
(makroskopische Variable) = 0
4244444
3
dt 14444
V
dV
=0
dt
2 unterschiedliche Möglichkeiten: Gleichgewicht oder Fließgleichgewicht (steady state)
Die Einstellung eines Gleichgewichts in offenen Systemen kann durch Randbedingungen
verhindert werden.
Beispiel: (Bio)chemische Reaktionskette
P1 →
← S n −1 →
← P2
← S1 →
← S2 →
← S3 ⋅ ⋅ ⋅ →
Wenn abgeschlossenes System, dann Massenerhaltung
P1 + P2 +
n −1
∑ Si = konst
i =1
und das System geht für t → ∞ ins Gleichgewicht über ( wi : chemische
Reaktionsgeschwindigkeiten)
Offenes System, kann mittel "äußerer Zwänge" aufrechterhalten
z.B. P2 = konst; P2 = konst
Man erhält für t → ∞ ein Fließgleichgewicht (steady state) wi ≠ 0, alle wi gleich
w = J : "steady state flux"
156
Im Fließgleichgewicht wird Entropie produziert.
∫
P = σ ⋅ dV ≠ 0
σ ≠0 ,
V
P: Gesamte Entropieproduktion im System.
Berechnung von σ für lineare chemische Reaktionskette.
σ=
∑
i
A=−
wi Ai
A
; X i = i : Kräfte
T
T
∑ν i ⋅ µi
, ν i : stöchiometrische Koeffizienten, µ i : chem. Potentiale
S

Ai = RT ln i −1 ⋅ K i 
 Si

Wir hatten hergeleitet:
Ai > 0 ⇒ wi > 0 ,
K i Si −1
>1 ;
Si
Si
< Ki
Si −1
K i : Gleichgewichtskonstante.
Mit wi = J
1
σ = J⋅
T
n
∑
i =1
n
S

1
Ai = J ⋅ RT
ln i −1 Ki 
T
S

i =1  i
∑
 n S

i −1 ⋅ K 
σ = R ⋅ J ln 
i
 i =1 Si

∏
 S0 S1 S n −1

⋅ K1 K 2 L K n 
L
Sn
 S1 S2

σ = R ⋅ J ln 
157
mit
S0 = P1
,
S n = P2
P n

σ = R ⋅ J ln 1
Ki 
 P2

i =1
142
43
∏
Über − Alles
Affinität
Im steady state gilt σ ≠ 0 , aber man kann weitergehende allgemeine Aussagen darüber
treffen, wodurch sich stationäre Zustände gegenüber anderen Zuständen auszeichnen.
Wir betrachten das etwas einfachere System: P1 ≡ S ≡ P2 , mit P1 = konst , P2 = konst
Wie verhält sich σ gegenüber Fluktuationen?
beliebiger Zustand (nicht unbedingt stationärer Zustand), charakterisiert durch Raten w1 und
w2 sowie Konzentration S.
w1 = L11 A1 + L12 A2
w2 = L21 A1 + L22 A2
T=konst. inkorporiert in L's
σ = w1 A1 + w2 A2
(σ = ∑ J i X i )
Wir beweisen, dass σ im stationären Zustnd ein Minimum hat, bezüglich Fluktuationen von
Stoffkonzentrationen S.
dσ
=0 ,
dS
d 2σ
>0
dS 2
σ = (L11 A1 + L12 A2 )A1 + (L21 A1 + L22 A2 )A2
σ = L11 A12 + L12 A1 A2 + L21 A1 A2 + L22 A22
158
Onsager-Relation L12 = L21
σ = L11 A12 + 2 L12 A1 A2 + L22 A22
wobei:
A1 = µ P1 − µ S
und µ S = µ 0 + RT lnS
A2 = µ S − µ P2
∂A
∂σ
∂A
∂A 
 ∂A
= 2 L11 A1 1 + 2 L12  A1 2 + A2 1  + 2 L22 A2 2
∂S
∂S
∂S
∂S 
 ∂S
∂σ
∂A
∂A
= 2 (L11 A1 + L12 A2 ) 1 + 2(L12 A1 + L22 A2 ) 2
∂S
∂S
∂S
∂A1 ∂A1 ∂µ S
=
∂S ∂µ S ∂S
{
,
−1
;
∂A2 ∂A2 ∂µ S
=
∂S ∂µ S ∂S
{
+1
∂σ
dµ
= 2[− w1 + w2 ] S
∂S
dS
∂σ
∂µ
= 2(w2 − w1 ) S
∂S
∂S
Im stationären Zustand gilt w1 = w2 und deshalb:
2. Ableitung.
1 ∂ 2σ ∂w2 ∂µ S
∂ 2 µ S ∂w1 ∂µ S
∂2µS
w
w
=
−
+
−
2
1
2 ∂S 2
∂S ∂S
∂S ∂S
∂S 2
∂S 2
159
∂σ
=0
∂S
∂ 2µS
1 ∂ 2σ  ∂w2 ∂w1  ∂µ S
(
)
=
w
w
−
+
−


2
1
2
2 ∂S 2  ∂S
∂S  ∂S 14424∂4
S3
= 0 im stat. Zustand
1 ∂ 2σ  ∂w2 ∂w1  ∂µ S
=
−

2 ∂S 2  ∂S
∂S  ∂S
∂w2
>0 ,
∂S
∂w1
<0 ,
∂s
∂µ S
> 0 und deshalb
∂S
∂ 2σ
=0
∂S 2
Prinzip der minimalen Entropieproduktion von Prigogine:
σ hat im stationären Zustand ein Minimum (gegenüber Fluktuationen der Variablen).
Zu entprechender Schlussfolgerung gelangt man, wenn man das Zeitverhalten der
Entropieproduktion nach Auslenkung aus einem stationären Zustand berechnet.
σ = L11 A12 + 2 L12 A1 A2 + L22 A22
∂A
∂σ
∂A
∂A 
 ∂A
= 2 L11 A2 1 + 2 L12  A1 2 + A2 1  + 2 L12 A2 2
∂t
∂t
∂t
∂t
∂t 

∂σ
∂A
∂A 

= 2(L11 A1 + L12 A2 ) 1 + (L12 A1 + L22 A2 ) 2 
∂t
∂t
∂t 

∂σ
∂A 
 ∂A
= 2w1 1 + w2 2 
∂t
∂t 
 ∂t
A1 , A2 : Funktionen von µ S und damit von S, d.h. S (t )
160


 ∂A1 dµ S
∂σ
∂A2 ∂µ S 
= 2w1
+ w2

∂t
∂µ S dt
∂µ S dt 
 {
{


−1
+1
∂σ
dµ 

= 2(w2 − w1 ) S 
∂t
dt 

∂σ
∂µ dS 

= 2(w2 − w1 ) S
>0
∂t
∂s dt 

∂S
= w1 − w2
∂t
∂σ
∂µ
= −2(w2 − w1 )2
>0
∂t
∂S
∂σ
<0
∂t
∂σ
=0
∂t
im stationären Zustand
ρ
s
s
(stat. Zustand)
161
ρ
s2
s1
Verallgemeinerung: Im Bereich linearer Ansätze gilt
∫
1) σ (auch P = σdV ) nimmt beim Übergang in den stationären Zustand monoton ab.
( dσ dt ≤ 0 )
2) Im stationären Zustand nimmt σ (oder P) ein Minimum an.
3) Stationäre Zustände sind im Gültigkeitsbereich der linearen irreversiblen TD stabil. d.h.
nach Fluktuation um stat. Zustand gilt δσ > 0 ⇒ Im weiteren Verlauf dσ dt < 0 System,
das System kehrt in diesen stationären Zustand zurück.
σ (bzw. P) stellt eine „Ljapunov-Funktion“ dar.
(Vgl. Vorlesung über Systemtheorie, kinetische Stabilitätsanalyse)
162
18. Ein allgemeines Evolutionskriterium für den nichtlinearen Bereich
(ebenfalls am Beispiel chemischer Reaktionen)
Erfahrung: Diffusion und Wärmeleitung lassen sich in weiten Bereichen gut mit dem linearen
Ansatz beschreiben. Bei chemischen Reaktionen ist das nicht mehr der Fall.
Anmerkung: selbst die „lineare“ Kinetik w = k+ S − k− P fällt in der Regel nicht in den
Gültigkeitsbereich der linearen irreversiblen Thermodynamik.
k S

w = k− P + − 1
 k− P 
k
S 
A = kT ln K  ; K = +
k−
P 
(
)
w = k− P e A / kT − 1
w kann gar nicht ausschließlich als Funktion von A ausgedrückt werden.
nur in der Nähe des Gleichgewichtes:
P = P + δP
A


w ≅ k− (P = P + δP )1 +
− 1

 RT
w≅
k− P ⋅ A
A
+ k−δP
RT
1
42RT
4
3
2.Ordnung
w ≅ L⋅ A
Allgemein gilt σ =
∑ J i X i (linearer oder auch nichtlinearer Bereich)
164
dσ
=
dt
∂J
∂X i
∂t
i424
i 424
1
3 1
3
∑ ∂ti X i + ∑ J i
d Jσ
dt
dXσ
dt
J i = ∑ Lij X j
Im linearen Bereich:
j
∂X j
d Jσ
=
dt
∑∑
d Xσ
=
dt
∑∑ Lij X j
i
Lij
j
i
j
∂t
Xi
∂X i
=
∂t
∑∑ L ji X i
i
j
∂X j
∂t
Im linearen Bereich gilt
d Jσ d X σ
dσ
d σ
=
; oder
=2 X
dt
dt
dt
dt
dσ
d σ
=2 J
dt
dt
Im nichtlinearen Bereich gilt zwar nach wie vor
σ=
∑ Ji X i
i
aber nicht mehr: J i = ∑ Lij X j
i
d Xσ
=
dt
Wir betrachten
∑ wi
i
dAi
dt
, wobei: Ai = −
∑ µ jν ji
j
ν ji : stöchiometrischer Koeffizient des Stoffes j in der Reaktion i.
µ j : chemischesd Potential, abhängig von Stoffkonzentrationen
allgemein:
dAi
=−
dt
µ j = µ j (Sk )
∂µ dS k
ν ji
dt
∑ ∂Skj
j,k
165
∂µ j dSk
dXσ
wi
=−
ν ji = −
dt
∂
S
dt
k
i, j,k
∑
Einsetzen:
∂µ dS k
dt
∑ ∂Skj
jk
∑ν ji wi
i 24
1
4
3
dS j
dt
dXσ
=−
dt
∂µ ∂S j dS k
dt dt
∑ ∂Skj
j
(*)
Wir hatten weiter vorn hergeleitet, dass ∂µ j ∂S k die Elemente einer positiv definierten
Matrix sind. ⇒ Die quadratische Form (*) ist deshalb negativ definit.
dXσ
≤0
dt
Das ist das sogenannte allgemeine Entwicklungskriterium von Glansdorff & Prigogine.
Es spielt eine wichtige Rolle in der sogenannten thermodynamischen Stabilitätsanalyse, mit
(siehe Vorlesung "Systemtheorie")
166