Aufgabe 4-12

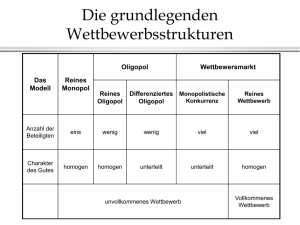
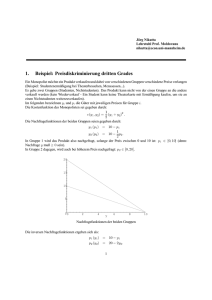
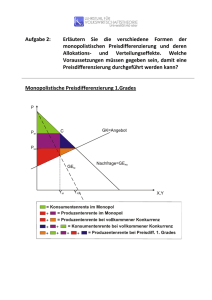
Aufgabensammlung Industrieökonomik FS 2009
Prof. Dr. Klaus Conrad
Aufgabe 4 (Preisdifferenzierung)
Sie sind Betreiber einer internetbasierten Datenbank für Artikel mikroökonomischer
Fachzeitschriften. Ihre Nachfrager lassen sich in zwei Gruppen einteilen, Professoren
und Studenten. Die inverse Nachfrage eines einzelnen Professors und eines
einzelnen Studenten ist gegeben mit: pP = 100 − qP
pS = 80 − qS
Die Preise werden in Cent gemessen. Die Mengen q stehen für die Anzahl von
Artikeln, auf die ein Nachfrager in der Datenbank zugreift. Die variablen Kosten, die
ein zusätzlicher Nutzer verursacht, sind 0. Es gebe 10 Professoren und 10
Studenten.
a) Sie kennen die Nachfrage jedes Konsumenten. Wie können Sie Preisdiskriminierung 1. Grades durchführen? Wie groß sind Renten und Wohlfahrt?
b) Sie können Professoren und Studenten unterscheiden und führen Preisdiskriminierung 3. Grades durch. Ermitteln Sie Preise und Mengen. Wie groß sind
Renten und Wohlfahrt?
c) Nehmen Sie nun an, dass Sie nicht zwischen beiden Gruppen unterscheiden
können und einen einheitlichen Preis setzen. Vergleichen Sie die Ergebnisse mit
den Resultaten aus b).
d) Wie hoch ist die Wohlfahrt, wenn Sie sich entscheiden, auf Ihre Monopolmacht zu
verzichten und sich zu verhalten wie bei vollkommener Konkurrenz?
1
Aufgabensammlung Industrieökonomik FS 2009
Prof. Dr. Klaus Conrad
Aufgabe 5 (Preisdifferenzierung dritten Grades)
Ein Monopolist bietet sein Produkt sowohl im Inland (I) als auch im Ausland (A) an.
Die Nachfragen für dieses Produkt auf den beiden Märkten sind in nachfolgender
Grafik dargestellt:
p
Inland
Ausland
p
100
DI
50
DA
xI
xA
100
50
Welche Mengen werden im Inland ( xI ) und im Ausland ( x A ) abgesetzt, wenn der
Monopolist Preisdiskriminierung 3. Grades betreibt und seine Kostenfunktion
C ( x) =
1 2
x lautet?
4
2
Aufgabensammlung Industrieökonomik FS 2009
Prof. Dr. Klaus Conrad
Aufgabe 6 (Preisdifferenzierung dritten Grades)
Ein monopolistisches Kino wird von Kindern und Erwachsenen besucht, die jeweils
homogene Konsumentengruppen darstellen. Da beim Kauf der Kinokarte der
Personalausweis vorgelegt werden muss, kann das Kino Preisdiskriminierung
betreiben.
a) Leiten Sie aus einer allgemeinen Gewinnmaximierung die Elastizitätenregel für
Preisdiskriminierung 3. Grades ab.
Gehen Sie von den folgenden Daten aus: Die betragsmäßige Preiselastizität der
Nachfrage nach Filmen ist 2 für Erwachsene und 6 für Kinder.
b) Wie hoch ist der Preis in € für Erwachsene, wenn der Preis für Kinder optimal
gewählt ist und 6€ beträgt?
c) Wie hoch sind die Grenzkosten des Monopolisten?
Die Steigung beider Nachfragefunktionen sei konstant und –1. Wie viele
Eintrittskarten werden an Kinder und Erwachsene verkauft?
Aufgabe 7 (Preisdifferenzierung dritten Grades)
Das Fitnessstudio Sports bedient zwei jeweils gleich große Nachfragergruppen,
Studenten
(S)
und
Nicht-Studenten
(N).
Die
(jeweils
aggregierten)
Nachfragefunktionen dieser Gruppen nach Monatsabonnements lauten:
pS = 50 − 0, 25 xS
und
pN = 80 − 0,5 xN
Die Kostenfunktion des Fitnessstudios in Abhängigkeit der insgesamt bereitgestellten
Monatsabonnements hat die Form C ( x) =
1 2
x + 50 .
3
Berechnen Sie die gewinnmaximalen Preise für ein Monatsabonnement pS und pN
sowie die im Optimum abgesetzte Menge an Monatsabonnements!
3
Aufgabensammlung Industrieökonomik FS 2009
Prof. Dr. Klaus Conrad
Aufgabe 8 (Preisdifferenzierung)
Eine Telefongesellschaft bietet einen Basistarif zu pB = 6 Cent pro Einheit an und
einen Diskonttarif. Dieser besteht aus einer Pauschale von 18 Cent bei 6
„Freieinheiten“ und für jede Einheit ab der siebenten ist pD = 3 Cent.
Betrachten Sie zur Beantwortung dieser Aufgabe die nachfolgende Grafik!
p
Haushalte
p
Firmen
12
6
DH
D
x
x
6
12
Welche der folgenden Aussagen trifft zu?
(a)
Die Haushalte sind indifferent zwischen den beiden Tarifen und die Firmen
bevorzugen den Diskonttarif.
(b)
Die Haushalte wählen den Diskonttarif und die Firmen den Basistarif.
(c)
Die Haushalte wählen den Basistarif und die Firmen den Diskonttarif.
(d)
Beide Gruppen sind indifferent zwischen den beiden Tarifen.
(e)
Beide Gruppen wählen den Diskonttarif.
4
Aufgabensammlung Industrieökonomik FS 2009
Prof. Dr. Klaus Conrad
Aufgabe 9 (Spitzenlastpreisbildung)
Die Lufthansa bediene als einzige Fluggesellschaft die Strecke Frankfurt-Kairo. Sie
kann Flugzeuge mit beliebiger Größe, d.h. mit beliebiger Anzahl von Sitzen für ein
Jahr leasen. Die Leasinggebühr pro Sitz und Jahr beträgt r . Die Nachfrage nach
Flügen schwankt saisonal ganz erheblich, da um die Weihnachtszeit und zu
Ramadan viele Gastarbeiter zu ihren Familien heimkehren. Im Winter lautet die
inverse Nachfrage pw = 10 − qw , im Sommer dagegen ps = 5 − qs . Wir nehmen
vereinfachend an, dass im Sommer und im Winter nur je ein Flug stattfindet. Es fallen
variable Kosten von Cv = cq (q=qW+qS) an. Hinzu kommen die Leasingkosten
(Kapazitätskosten).
a) Stellen Sie die Gewinnfunktion der Lufthansa auf und ermitteln Sie die
Optimalitätsbedingungen.
b) Es sei r=c=1. Welche Flugzeuggröße wählt die Lufthansa? Wie viele Tickets
werden jeweils im Sommer und im Winter angeboten? Wie hoch ist der
Gewinn der Lufthansa? Wie ändern sich die Ergebnisse für r=3?
c) Das Kartellamt wird auf das Monopol aufmerksam. Da aufgrund von
Flughafenkapazitäten aber kein Wettbewerber in den Markt eintreten kann,
muss der Preis reguliert werden. Welche Preise wird die Behörde festsetzen?
Ändert sich dann die Kapazitätsentscheidung der Lufthansa? Ändern sich die
Mengen der nachgefragten Tickets? Argumentieren Sie anhand einer
Zeichnung.
d) Was passiert, wenn das Kartellamt einen einheitlichen Preis von pW = pS =c+
für Sommer und Winter setzt? Würden die Konsumenten dadurch besser
gestellt?
e) Vergleichen Sie die Wohlfahrt, die sich unter b) bis d) jeweils ergibt.
Unterstellen Sie jeweils r = c = 1.
5
r
2
Aufgabensammlung Industrieökonomik FS 2009
Prof. Dr. Klaus Conrad
Aufgabe 10 (Spitzenlastpreisbildung)
Eine Brauerei kann ein einzigartiges Hefeweizen mit der Brauanlage „Hefemeister“
produzieren. Die Anschaffungskosten dieser Brauanlage betragen in Abhängigkeit
von der Kapazität κ pro Saison K HM = κ pκ mit pκ = 1. Ein Hefemeister hält genau ein
Jahr. Die Grenzkosten der Produktion einer Mengeneinheit x betragen für den
Hefemeister c = 1.
Für das Hefeweizen gibt es keine konkurrierenden Anbieter. Sein Absatz im
Sommerhalbjahr beträgt in Abhängigkeit vom Wetter, das mit dem Parameter H
beschrieben wird, x = 10H - p. Ein mieser Sommer wird mit H = 1 bewertet, ein
durchschnittlicher Sommer mit H = 5 und ein Spitzensommer mit H = 9. Im
Winterhalbjahr entspricht die Nachfrage derjenigen während eines miesen Sommers.
Die Brauerei setzt einen Preis für das Sommerhalbjahr und einen Preis für das
Winterhalbjahr.
Um einen Absatz von x realisieren zu können, benötigt sie eine Kapazität κ ≥ x.
Welche der folgenden Aussagen trifft zu?
a) Wird für das kommende Jahr ein mieser Sommer prognostiziert, wird die
Brauerei keinen Hefemeister anschaffen.
b) Wird kein mieser Sommer prognostiziert, bestimmt sich die Größe der zu
beschaffenden Anlage aus der aggregierten Nachfrage in Sommer und
Winter.
c) In einem Jahr mit einem Spitzensommer beträgt der Absatz an Hefeweizen
x = 48.5.
d) In einem durchschnittlichen Sommer beträgt der Absatz an Hefeweizen
x = 37.
e) Keine der Aussagen trifft zu.
6
Aufgabensammlung Industrieökonomik FS 2009
Prof. Dr. Klaus Conrad
Aufgabe 11 (Zweiteilige Tarife)
In einer wohlhabenden Gemeinde wird der erste Tennisklub gegründet. Der Klubmanager weiß, dass in dieser Gemeinde 100 Freizeitspieler und 100 ambitionierte
Tennisspieler wohnen und kennt deren Nachfragen nach Platzstunden q
Inverse Nachfrage eines Freizeitspielers:
pF = 6 − 2qF
Inverse Nachfrage eines ambitionierten Spielers:
pA = 6 − qA
Jedoch kann er einzelne Spieler nicht ihren Gruppen zuordnen und muss deshalb ein
einheitliches Preisschema für beide Gruppen festlegen..
Welchen zweiteiligen Tarif (bestehend aus einer Clubgebühr G und einem
Platzstundenpreis p) wählt er optimalerweise, wenn seine Grenzkosten 0 sind und
wenn er sicherstellen möchte, dass alle Tennisspieler Klubmitglied werden.
Aufgabe 12 (Preisstrategien)
Seit zwei Jahren können Studenten auf den Plätzen der Universität im Mannheimer
Schlossgarten Tennis spielen. Für die Universität, die als Monopolist agiert, fallen
keine Kosten an, da diese von der Heinrich-Vetter-Stiftung übernommen werden. Die
Universität weiß, dass es innerhalb der Studentenschaft drei gleich große Gruppen
von Tennisspielern gibt: Profis (P), Freizeitspieler (F) und Tennisinteressierte (I).
Ihre Nachfragefunktionen nach Platzstunden x in einem Jahr lauten:
xP = 10 − p
xF = 8 − p
xI = 6 − p
Die Universität kennt zwar die Nachfragefunktionen der Gruppen, kann jedoch nicht
einzelne Studenten diesen zuordnen.
Mit welcher Preisstrategie kann die Universität ihren Gewinn maximieren?
(a) Jahresgebühr, die zu unbegrenzter Nutzung berechtigt, in einer Höhe, so dass
alle Tennisspieler diese entrichten.
(b) Jahresgebühr, die zu unbegrenzter Nutzung berechtigt, in einer Höhe, so dass
alle Profis und Freizeitspieler diese entrichten.
(c) Platzstundengebühr von p = 3 .
(d) Platzstundengebühr von p = 4 .
7