2.6 Drehbewegung eines starren Körpers

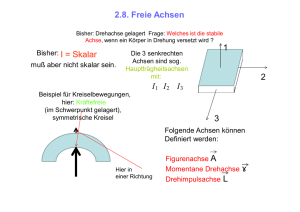
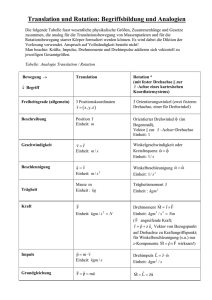
2.6 Drehbewegung eines starren Körpers
27
2.6 Drehbewegung
eines starren Körpers
2.6.1 Winkelbeschleunigung, Trägheitsmoment. Am einfachen Fall einer starren, um
eine feste Achse drehbaren Scheibe wollen
wir die wichtigsten Begriffe für Drehbewegungen kennenlernen. Dreht sie sich, so haben die verschiedenen Punkte der Scheibe
zwar dieselbe Winkelgeschwindigkeit w
(Abschn. 2.2.2), aber verschiedene Bahngeschwindigkeiten Vi= wri, wenn ri der Abstand des betreffenden Punktes von der
Drehachse ist. Auch die Winkelgeschwindigkeit ist ein Vektor, ein sog. achsialer Vektor,
der in der Drehachse liegt, die Richtung des
Pfeiles gibt den Drehsinn in Form einer
Rechtsschraube an, s. Abb. 2.34.
Wird die Scheibe aus der Ruhe in Drehung
versetzt, so ändert sich ihre Winkelgeschwindigkeit. Wir führen daher den Begriff der
Winkelbeschleunigung a ein und verstehen
darunter die Änderung der Winkelgeschwindigkeit LI w dividiert durch den dazu benötigten Zeitabschnitt LI t, also
. Llw
dw
d 2q;
a= h m - - = - = - -2 .
(2.39a)
,11-.0 LI t
dt
dt
Ihre Einheit ist s - 2. Bei konstanter Winkelbeschleunigung a ist der aus der Ruhe heraus
in der Zeitspanne t überstrichene Winkel
(fl
'f'
= 1...2 at 2
'
(2.39b)
und die Winkelgeschwindigkeit beträgt danach:
w = at ,
(2.39c)
vgl. Abschn.2.2.2 Fallgesetze. Nach dem
Winkel-Zeit-Gesetz kann man auch praktisch die Winkelbeschleunigung bestimmen.
- Jeder Massepunkt auf der Scheibe erleidet
eine Beschleunigung ai = ria in tangentialer
Richtung, nicht zu verwechseln mit der Zentripetalbeschleunigung w 2 ri in radialer Richtung, die außerdem auftritt.
Nach dieser Kinematik der Drehbewegung
fragen wir danach, wie eine Winkelbeschleunigung verursacht werden kann. Im Experiment verwenden wir dazu am einfachsten einen Schnurzug, der über eine Rolle läuft und
an dem ein Gewichtsstück hängt, s. Abb.
2.34. Es kommt nämlich nicht auf die einwir-
kende Kraft Fallein - eine z. B. im Drehpunkt 0 angreifende Kraft wäre unwirksam
-, sondern auf ihr "Drehmoment" M = rF
in bezug auf die Drehachse AA an. Die Drehung verläuft von unten gesehen im Uhrzeigersinne. Wie schon in Abschn. 2.5.2 ausgeführt, beschreiben wir das Drehmoment
durch einen Vektor M, der auf der Ebene r F
senkrecht steht; für seine Orientierung gilt
dasselbe wie für den Vektor der Winkelgeschwindigkeit w. Quantitative Experimente
beweisen, daß die aus dem Winkel-Zeit-Gesetz bestimmte Winkelbeschleunigung eines
drehbaren Körpers nur vom wirkenden
Drehmoment M = rF abhängt, gleichgültig
wie groß Fund r im einzelnen sind. Außerdem ergibt sich, daß die Winkelbeschleunigung a dem Drehmoment proportional, aber
natürlich von Körper zu Körper verschieden
ist, vgl. die geradlinige Beschleunigung
durch Kräfte (Abschn. 2.3.1).
Die Winkelbeschleunigung durch ein bestimmtes Drehmoment hängt nicht nur von
der Masse des Drehkörpers sondern auch
von deren Verteilung in bezug auf die Drehachse ab. Je weiter außen ein herausgegriffenes Massestück m auf der Scheibe liegt, um
so größer ist bei konstanter Winkelgeschwindigkeit seine Bahngeschwindigkeit und damit
auch seine kinetische Energie (Rotationsenergie) (m / 2)vr = (m/2)w 2rr. Die zum Erreichen einer bestimmten Winkelgeschwindigkeit erforderliche Beschleunigungsarbeit
wächst also nicht mit m, sondern mit mr;'
Wir nennen das Produkt aus der Masse und
dem Quadrat ihres Abstandes von der Drehachse das Trägheitsmoment I der Masse m in
bezug auf die betreffende Achse.
Ist ein Körper aus vielen Massen zusammengesetzt, so ist das Gesamtträgheitsmoment gleich der Summe der Trägheitsmomente der einzelnen Massen, oder
1= mld+ m2d+ ... = Emir;.
(2.40)
Das Trägheitsmoment eines Körpers ändert sich mit der Lage der Achse im Körper.
Betrachten wir nur die durch den Schwerpunkt gehenden Achsen, so gibt es eine bestimmte Achse A, s. Abb. 2.35, für die das
Trägheitsmoment am größten ist und dazu
senkrecht eine weitere Achse C, für die es am
A
I
I
I
I
I
I
I
Abb. 2.34. Drehsinn und Vektoren
von Drehmoment, Winkelgeschwindigkeit und Drehimpuls bei einer rotierenden Scheibe. Die Drehachse
steht au f der durch die Kraft und den
Fahrstra hl r definierten Ebene senkrecht
Abb.2.35.
Hauptträgheitsachsen einer Kiste
2. Allgemeine Mechanik
28
kleinsten wird. In bezug auf die zu diesen
bei den Achsen senkrechte Achse B hat das
Trägheitsmoment einen mittleren Wert. Diese drei Achsen nennen wir die Hauptträgheitsachsen des Körpers, die dazugehörigen
Momente seine Hauptträgheitsmomente.
Eine dünne kreisförmige Scheibe hat den Schwerpunkt im Kreismittelpunkt. Für eine Drehachse senkrecht zur Kreisfläche durch den Schwerpunkt ist das
Trägheitsmoment mR 2/2, für eine parallel zur Kreisfläche mR 2 / 4 (m Gesamunasse der Scheibe, R ihr Radius).
Für eine Kugel gilt 1= 2mR 2 / 5.
Das Trägheitsmoment I bei Rotation um eine beliebige Achse ist gleich dem Trägheitsmoment um die parallel verschobene Achse durch den Schwerpunkt vermehrt
um m/ 2 , wobei m die Masse des Körpers und I der Abstand zwischen Schwerpunkt und Drehachse ist (Steinerscher Satz).
ersetzen, vgl. die folgende Gegenüberstellung:
Einander entsprechende Größen und Gleichungen für
Translationsbewegung
Drehbewegung
Wegs
Geschwindigkeit v
Beschleunigung a
Massem
d
KraftF= ma = - (mv)
dt
Richtgröße 12 D = _F
x
Schwingungsdauer 13
T=2n
~
Kinetische Energie
2.6.2 Dynamisches Grundgesetz der Drehbewegung. Alle Beobachtungen an sich drehenden Körpern lassen sich durch das
Grundgesetz für Drehbewegungen beschreiben. Wirkt ein Drehmoment M auf einen
drehbaren Körper, so erteilt es ihm eine Winkelbeschleunigung, die sich aus der Gleichung
dw
dt
M = Ia = 1 -
(2.41)
bestimmt, wobei I das Trägheitsmoment in
bezug auf die Drehachse ist. Dieses Gesetz
läßt sich aus dem dynamischen Grundgesetz
F = ma ableiten, stellt also keine neue, unabhängige Erfahrung dar.
Wir betrachten dazu einen Massepunkt in der Entfernung r von der Drehachse, der durch die Kraft F die Beschleunigung a erfährt. Nun gilt F = Mi r und a = ar, in
das dynamische Grundgesetz der Kraft eingesetzt
(Abschn. 2.3.1) und umgeformt folgt daraus
M = m?a.
Zwischen der fortschreitenden oder Translationsbewegung und der Drehbewegung besteht außerdem eine weitgehende formale
Analogie. Die für die Translationsbewegung
bekannten Beziehungen lassen sich ohne weiteres auf die Drehbewegung übertragen,
wenn wir nur die Größen Weg, Kraft, Masse
usw. durch die entsprechenden Größen Winkel, Drehmoment, Trägheitsmoment usw.
E k . =~v2
In
2
Impulsp
=
mv
Winkel rp
Winkelgeschwindigkeit (j)
Winkelbeschleunigung a
Trägheitsmoment I
Drehmoment 12
dw
dL
M = la = I - = dt
dt
M
Rich tmoment 13 D . = -
rp
Schwingungsdauer 13
T = 2n
V
I
D·
Rotationsenergie
1
2
E rOl = - lw
2
Drehimpuls 12 L
=
I (J)
In der folgenden schematischen Übersicht
verfolgen wir die Analogie zwischen Translations- und Drehbewegung weiter. Man findet
dort dargestellt, wie die Bewegungsänderung
eines Körpers unter dem Einfluß einer Kraft
F bzw. eines Drehmomentes Mvon der Wirkungsrichtung bei der abhängt.
Richtung Wirkung
von Kraft
bzw.
Drehmoment
Beispiel
F ll v
Erhöhung der Bahngeschwindigkeit (Bahnbeschleunigung)
Freier Fall
Mllw
Erhöhung der Winkelgeschwindigkeit
Scheibe in
Abb.2.34
FJ..v
Richtungsänderung der
Geschwindigkeit (konstante
Radialbeschleunigung)
Kreisbahn
MJ..w
Richtungsänderung der
Kreisel in
Winkelgeschwindigkeit, also
Abb . 2.37
der Drehachse, falls diese frei ist
(Abschn. 2.6.4, 2.6.5)
12
13
Abschn. 2.6.3.
Abschn. 4.1.1.
2.6 Drehbewegung eines starren Körpers
2.6.3 Satz von der Erhaltung des Drehimpulses. Bei der fortschreitenden Bewegung haben wir den Satz von der Erhaltung des Impulses mv kennengelernt. Ihm entspricht bei
der Drehbewegung der Satz von der Erhaltung des Drehimpulses, wobei wir unter dem
Drehimpuls L das Produkt aus Trägheitsmoment und Winkelgeschwindigkeit verstehen,
also L = I w. Der Drehimpuls ist eine Vektorgröße. Seine Richtung, aus der wir den
Drehsinn ersehen, ist dieselbe wie die des
Vektors der Winkelgeschwindigkeit, vgl.
Abb.2.34.
Wirkt ein äußeres Drehmoment M während der Zeit L1 t ein, so ergibt dieser Drehstoß nach der Grundgleichung der Drehbewegung M = Ia = I L1 w/ L1 t eine Änderung
des Drehimpulses von der Größe
29
Arme ihre Drehgeschwindigkeit herabsetzen
und sie durch Hochziehen des Körpers in die
Nähe der Drehachse wieder steigern.
2.6.4 Freie Drehachsen. Bei unseren bisherigen Betrachtungen war die Drehachse des
Körpers festgelegt. Diese Beschränkung lassen wir jetzt fallen und fragen, welche Drehachsen ein Körper, durch einen Drehstoß in
Rotation versetzt, stabil beibehält. Von
vornherein werden wir sagen, daß sie durch
seinen Schwerpunkt gehen müssen. Bei einem sich selbst überlassenen Körper kann
der Schwerpunkt zwar eine unbeschleunigte,
geradlinige Bewegung ausführen, aber keine
Kreisbewegung. Die dazu notwendigen Zentripetalkräfte können nicht von einer freien
Drehachse ausgeübt werden.
Aber nicht um jede Achse durch seinen
(2.42) Schwerpunkt rotiert ein Körper frei und staL1L = I L1 w = M L1 t .
bil. Die bei der Drehung auftretenden ZentriDaraus folgt der Erhaltungssatz: In einem fugalkräfte ergeben nämlich im allgemeinen
System, in dem nur innere Kräfte wirksam ein Drehmoment, das den Körper zu kippen
sind, also ein äußeres Drehmoment fehlt, . versucht, so daß die Drehachse im Körper
bleibt der Drehimpuls konstant. Befindet ihre Richtung ändert. Bringen wir z. B. einen
man sich auf einer Drehscheibe und läuft am Ende aufgehängten zylindrischen Stab
man an ihrem Rande in einer Richtung, so mit Hilfe eines Motors um eine vertikale
gerät die Scheibe im entgegengesetzten Um- Achse in Drehung, so halten sich die Zen trilaufsinn in Drehung. Man sieht an diesem fugalkräfte im Gleichgewicht, s. Abb. 2.36a.
Fall, daß auch der Satz von der Erhaltung Bei der geringsten Abweichung von der vertides Drehimpulses eine Folge des Prinzips kalen Lage üben jedoch die bei den resultievon Kraft und Gegenkraft ist. - Bekannt- renden Zentrifugalkräfte F ein Drehmoment
lich fällt die Katze, wie man sie auch fallen aus, das den Stab in die horizontale Lage zu
läßt, immer wieder auf die Beine. Das ist nur drehen sucht, s. Abb. 2.36b. Man kann auch
dadurch möglich, daß der Schwanz eine der sagen, die Zentrifugalkräfte treiben die Masgewünschten Körperdrehung gegenläufige sen möglichst weit von der Drehachse weg.
Es wird also als Drehachse diejenige Achse
Drehbewegung macht.
Anders als beim Impuls, wo die Masse eine angestrebt, für die das Trägheitsmoment am
Konstante ist, kann man durch innere Kräfte größten ist, s. Abb. 2.36c. Um die Achse des
aber das Trägheitsmoment ändern, so daß größten Trägheitsmomentes vermag ein Körder Drehimpuls zwar konstant bleibt, die per ohne Lager stabil zu rotieren, da bei jeWinkelgeschwindigkeit sich aber ändert. Ein der Störung sofort ein rücktreibendes DrehDrehschemel z. B. rotiert langsamer, wenn moment auftritt. Wir bezeichnen daher diese
die darauf sitzende Versuchsperson in beiden Hauptträgheitsachse als eine freie Drehachse
Händen schwere Hanteln hält und die Arme des Körpers. Die Achse des kleinsten Trägplötzlich nach außen streckt (größeres Träg- heitsmomentes kann ebenfalls eine freie
heitsmoment). Zieht sie die Arme wieder an, Achse sein. Die Achse des mittleren Hauptso stellt sich die ursprüngliche Winkelge- trägheitsmomentes ist dagegen labil, die
schwindigkeit ein. - Ebenso kann die Eis- kleinste Störung verursacht Drehmomente,
kunstläuferin bei der Pirouette durch In-die- die die Drehachse verschieben. Versetzt man
Knie-Gehen oder seitliches Ausstrecken der einen Körper um diese Achse in Drehung,
I
I
I
~
F
S
;r
I
I
I
S
I
a
b
c
Abb. 2.36a - c. Zentrifugalkräfte
und freie Achsen bei einem rotierenden Kö rper
2. Allgemeine Mechanik
30
z. B. die in Abb. 2.34 gezeichnete Kiste um
die Achse B, so gerät sie ins Torkeln, während sie um die AchseA und bei einiger Vorsicht auch um C weiterrotiert.
2.6.5 Der Kreisel. Jeder freie oder höchstens
in einem Punkte festgehaltene rotierende
Körper wird als Kreisel bezeichnet. Die charakteristischen Erscheinungen zeigt schon
der rotationssymmetrische Kreisel, der uns
als Kinderkreisel bekannt ist. Seine Symmetrieachse, auch Figurenachse genannt, enthält den Schwerpunkt und ist die Achse des
größten Trägheitsmomentes, sie ist also eine
stabile freie Drehachse, s. Abb. 2.37.
A
Präzessionskegeli
1
<lJ1
",I
\
-SI
Cli
13 '
\
\\
,~l
,,> I
~:
\\
\
:t:JI
'-I
\
0...,
\
1
\0 1
\ \
1
\\1' I
o
1
:\
1 0
iLlL 1. Zeichenebene
i1 noch hinten gerichtet
1
A
Abb. 2.37. Präzession eines Kreisels. Er rotiert um seine
Figurenachse, Drehimpulsachse L. Diese läuft auf einem raumfesten Kegelmantel mitAA als Achse (M .Lw)
Unterstützen wir einen Kreisel im Schwerpunkt, so ist er den äußeren Schwerkräften
entzogen und behält, wenn er einmal um seine Figurenachse in Drehung versetzt worden
ist und sich dann selbst überlassen bleibt, die
Drehachse raumfest bei. In ihr liegt der Vektor des Drehimpulses, der nach Größe und
Richtung ohne äußere Kraftwirkung erhalten
bleibt (Satz von der Erhaltung des Drehimpulses). So bleibt bei der in Drehung versetzten abgeschleuderten Diskusscheibe die Figurenachse raumfest, s. Abb . 2.38. Der Diskus
2t::M:;~~~::;~
w,
Abb.2.38.
Flugbahn einer Diskusscheibe (aus Pohl: Mechanik)
erfährt daher im absteigenden Ast der Bahn
wie eine Tragfläche mit dem Anstellwinkel a
einen Auftrieb und erreicht daher eine größere Flugweite.
Beim Kinderkreisel befindet sich der
Schwerpunkt oberhalb des Unterstützungspunktes. Sobald die Figurenachse des Kreisels in Abb. 2.37 nicht genau senkrecht steht,
übt die Schwerkraft ein Drehmoment aus,
das den ruhenden Kreisel umkippen würde.
Der rotierende Kreisel fällt jedoch nicht um,
sondern weicht senkrecht zur einwirkenden
Kraft aus und beschreibt eine sog. Präzessionsbewegung. Seine Figurenachse läuft auf
einem Kegelmantel mit AA als Achse und
mit 0 als Spitze um. Diese überraschende Erscheinung erklärt sich folgendermaßen: Das
im Schwerpunkt S des Kreisels angreifende
Gewicht G erzeugt ein Drehmoment M um
die horizontale, zur Zeichenebene senkrechte
Achse aa. Dieses während der kurzen Zeit L1t
wirksame Moment gibt ihm einen zusätzlichen Drehimpuls L1L. Dieser ist dem Drehmoment gleichgerichtet, also horizontal, und
addiert sich geometrisch zum ursprünglichen
Drehimpuls L des Kreisels, so daß nach der
Zeit L1 t der neue Drehimpuls L I = L + L1L
ist. Die Figurenachse folgt dem Drehimpuls
und nimmt jetzt die neue Richtung L I ein, sie
hat sich also etwas nach hinten gedreht.
Wirkt die Kraft G dauernd ein, so weicht die
Kreiselachse ihr immer weiter stets senkrecht
aus und beschreibt die Präzessionsbewegung. Die Kreiselbewegung setzt sich hier aus
zwei Drehungen zusammen, der Drehung um
die Figurenachse und der Drehung der Figurenachse um die Präzessionsachse AA.
Die Präzession ist um so langsamer, je
größer der Drehimpuls des Kreisels ist. Der
Kreisel reagiert um so weniger auf äußere
Kräfte, je schneller er rotiert. Die Kreiselachse wird durch den Drehimpuls also im Raum
besser stabilisiert. Das ist die Folge der mit
der Drehgeschwindigkeit ansteigenden Trägheitswirkung.
Die Figurenachse sei um den Winkel '19 gegen das Lot
geneigt. Dann hat der Drehimpuls Leine raumfeste,
senkrecht stehende Komponente und eine horizontale
4, =L sin '19, die mit der Winkelgeschwindigkeit 11r.p/l1t
um AA als Achse rotiert: I1L/ l1t = Lh l1 r.p/l1t . Nach dem
Grundgesetz der Drehbewegung gilt I1L = Ml1t
2.7 Allgemeine Gravitation
(Abschn. 2.6.3). Die Präzessionsgeschwindigkeit ist also
tJcp/tJt = M/ Lh; sie wird um so kleiner, je größer der
Drehimpuls L = Iw des Krei sels ist.
Diese auf der Trägheit beruhenden Kreiselkräfte treten überall dort in Erscheinung,
wo den Drehachsen schnell rotierender Körper eine Richtungsänderung aufgezwungen
wird. Bei einem in die Kurve gehenden Fahrzeug wird jeder Radsatz mit den beiden rasch
umlaufenden Rädern um die Vertikalachse
gedreht. Die dabei auftretenden Kreiselkräfte rufen einen Zusatzdruck auf das äußere
Rad und eine Entlastung des inneren hervor,
wodurch das von den Zentrifugalkräften
herrührende Kipprnoment, vgl. Abb. 2.19,
noch verstärkt wird.
Eine einseitige Unebenheit der Fahrbahn,
die die Radachse plötzlich kippt, kann bei
großer Geschwindigkeit das Fahrzeug aus
der geradlinigen Fahrtrichtung herausschleudern. - Die Möglichkeit des freihändigen
Fahrens mit dem Fahrrad beruht gerade auf
den beim Kippen des Rades auftretenden
Kreiselkräften. Sie drehen das Vorderrad so,
daß eine Kurve es durch die Zentrifugalkraft
wieder aufrichtet.
Beim Kreise/kompaß steht die Rotationsachse stets horizontal, kann sich aber in der
Horizontalebene frei drehen. Sie stellt sich
dann der Erdachse möglichst weitgehend
parallel, schwenkt also in die Nord-SüdRichtung ein. In Ost-West-Einstellung sucht
die Erddrehung die Kreiselachse zu kippen.
Das dadurch entstehende Zusatzdrehrnoment zeigt nach Norden und läßt die Drehachse mehr in Nord-Süd-Richtung schwenken. Anders als bei der Präzessions bewegung
des Kinderkreisels nimmt das Drehmoment
dabei aber ab, so daß die Drehachse in NSRiChtung zur Ruhe kommt.
Von der Präzession eines Kreisels ist die Nutation zu
unterscheiden. Diese setzt ein, wenn wir gegen seine Figurenachse, um die er zunächst als freie Drehachse rotiert, einen kurzzeitigen, kräftigen Drehstoß ausüben.
Dabei liegt der Hebelarm in der Figurenachse. Damit geben wir dem Kreisel eine zusätzliche, erhebliche Drehimpulskomponente senkrecht zu seiner Figurenachse, so
daß sein Gesamtdrehimpuls schräg zu ihr steht. Bei
kräftefreiem Kreisel bleibt die Richtung des Drehimpulsvektors im Raume fest (Abschn. 2.6.3), und die Figurenachse läuft auf einem Kegel dem Nutationskegel,
um d'
,
lese Richtung als raumfeste Achse herum. Außerdem ist die momentane Drehachse des Kreisels auch
31
nicht mehr seine Figurenachse, sie liegt überhaupt nicht
fest weder im Kreisel noch im Raume. Figurenachse,
Drehimpulsachse und momentane Drehachse bilden in
jedem Zeitpunkt eine Ebene.
Aufgaben
2.6.1 Eine zunächst ruhende Drehscheibe wird durch
ein konstantes Drehmoment beschleunigt. Für die ersten
5 Umdrehungen benötigt sie 20 s. Wie groß ist die Winkelbeschleunigung a?
2.6.2 Eine Kugel von Radius 20 cm hat die Masse
200 kg und ist homogen mit Materie gefüllt. Sie wird um
eine Achse gedreht, die tangential zu ihrer Oberfläche
verläuft. Wie groß ist das Trägheitsmoment?
2.6.3 Ein Drehschemel mit Versuchsperson hat das
Trägheitsmoment 25 kg m2 und rotiert mit einer Winkelgeschwindigkeit von 5 S- I. Die Versuchsperson hält dabei zwei Hanteln von je 15 kg praktisch in der Drehachse. Beim Armstrecken werden sie um 0,9 m nach außen
verschoben. Wie groß ist jetzt die Winkelgeschwindigkeit?
2.6.4 Die Versuchsperson von Aufg. 2.6.3 zieht die
Arme wieder an. Um wieviel ändert sich dabei die Rotationsenergie? Auf welche Weise wird die dafür nötige
Arbeit geleistet?
2.6.5 Wie hängt die Präzessionsgeschwindigkeit in
Abb. 2.37 vom Winkel & zwischen Präzessionsachse und
Figurenachse ab?
2.7 AUgemeine Gravitation
2.7.1 Gravitationsgesetz. Aus der Tatsache,
daß alle Körper gleich schnell fallen, schließen wir auf eine nach dem Erdmittelpunkt
gerichtete Anziehungskraft, die Schwerkraft, die der Masse der Körper proportional
ist (Abschn. 2.3.2). Newton hat erkannt, daß
nicht nur die Erde alle in ihrer Nähe befindlichen Körper anzieht, sondern daß alle Massen, wo sie sich auch im Weltraum befinden
mögen, sich gegenseitig anziehen. Die irdische Schwerkraft ist also nur ein Sonderfall
der al/gemeinen Massenanziehung oder Gravitation. Das von Newton aus den Keplersehen Gesetzen der Planeten bewegung
(Abschn. 2.7.2) abgeleitete Gravitationsgesetz lautet: