Auf experimentell-heuristischem Weg zur Normalverteilung

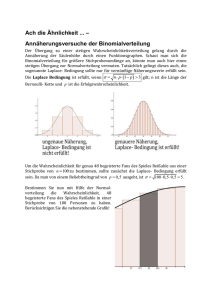
Auf experimentell-heuristischem Weg zur Normalverteilung
P ETRA H AUER -T YPPELT
Zusammenfassung: Die Motivation für diesen Unterrichtsvorschlag ist, die Lernenden im Sinne des
entdeckenden Lernens zunächst auf visueller Ebene an die Normalverteilung heran zu führen. Der
Zufallszahlengenerator des Microsoft Office Paketes
wird zur Simulation von empirischem Datenmaterial genutzt. Als Ergebnis interaktiver Tätigkeit der
Schüler1 soll das Verständnis für die Normalverteilung quantitativ erfassbarer Größen auf der ikonischen Ebene aufgebaut werden. Im Anschluss wird
durch Verbalisieren und Formalisieren von der BildEbene zur Symbolsprache der Mathematik übergegangen, um schließlich die Funktionsgleichung der
Gaußschen Glockenkurve als Ergebnis zu erhalten.
1 Visualisieren
1.1 Wie wird visualisiert - was leistet das
Programm?
Der Statistiker Quételet2 führte in der ersten Hälfte des 19. Jahrhunderts eine Erhebung durch, um
seine Vermutungen hinsichtlich der Normalverteilung gewisser empirischer Daten zu bestätigen. Seine
berühmt gewordene Messung des Brustumfangs von
über 5000 schottischen Soldaten stärkte seine Vermutung, dass zufällig gewählte, messbare Größen,
die von vielen Einflussfaktoren bestimmt werden,
normalverteilt sind. Die Bestätigung und auch Erklärung für diese Tatsache liefert der Zentrale Grenzwertsatz.
Auf den Ergebnissen einer Vielzahl von empirischen
Untersuchungen aufzubauen, deren graphische Darstellung jeweils annähernd eine Glockenkurve ergibt,
liefert einen günstigen Ansatz im Unterricht. Um den
Zeitaufwand der Datenerhebung zu sparen, verwenden wir den Computer zur Simulation von Datenmaterial.
Dabei geht es auch um Darstellen von Grafiken und
interaktives Lernen, das manifestiert die Entscheidung für den Computereinsatz. Ich greife auf das Tabellenkalkulationsprogramm EXCEL zurück, weil es
praktisch in allen Lehranstalten zur Verfügung steht
und damit ein unkomplizierter Einsatz garantiert ist.
Ein kurzes VBA3 –Programm bewerkstelligt das Er-
stellen einer Tabelle mit Zufallszahlen in Excel, die
graphisch dargestellt wird.
Unter Einsatz des Zufallszahlengenerators des
Office–Paketes werden ganzzahlige Zufallszahlen
von 1 bis 100 erzeugt. Dabei kann der Benutzer sowohl die Anzahl n der Stichproben als auch die Anzahl x der Zufallszahlen pro Stichprobe festlegen.
Wir dürfen davon ausgehen, dass jede der 100 Zufallszahlen mit gleicher Wahrscheinlichkeit vom Zufallszahlengenerator ausgewählt wird, also eine hinreichende Gleichverteilung vorliegt.
In Excel wird die Auswahl der Zahlen jeweils in einem Diagramm dargestellt. Jeder Zufallszahl wird eine Strecke zugeordnet, wobei die Streckenlänge die
relative Häufigkeit angibt, mit der eine Zufallszahl
ausgewählt wurde. Für n = 100 Stichproben mit jeweils einer Zufallszahl pro Stichprobe, also x = 1,
entsteht bei Gleichverteilung theoretisch ein Diagramm mit hundert gleich langen Strecken. In der
Praxis wirft das Programm eine solche Grafik allerdings praktisch nie aus, gerade weil eben der Zufall
bestimmend ist. Ein günstiger Anlass im Unterricht
die Begriffe “Zufall” und “Wahrscheinlichkeitsverteilung einer Größe”, hier am Beispiel der Gleichverteilung (wiederholend) zu thematisieren. Tietze et al.
gehen ausführlich auf Schwierigkeiten bei der Vermittlung von adäquaten Vorstellungen des “Konzepts
Zufall” ein, weil es sich eben nicht “durch rein verbale Erklärungen im Sinne einer Definition vermitteln
lässt” (Tietze, Klika & Wolpers, S. 146ff).
Abbildung 1 zeigt ein Ergebnis für n = 10000 Stichproben mit x = 1. Es ist keinerlei Struktur erkennbar,
die auf eine Bevorzugung bestimmter Zahlen schließen lässt. In der praktischen Durchführung ist es an
dieser Stelle natürlich notwendig eine Reihe von weiteren Diagrammen mit unterschiedlichen, auch sehr
großen n zu erstellen, um die Annahme der Gleichverteilung zumindest exemplarisch zu rechtfertigen.
Wir kommen im nächsten Abschnitt, wenn es darum
geht, konkrete Arbeitsaufträge für die Lernenden zu
erstellen, darauf zurück.
1 Die
Begriffe Schüler und Lehrer werden wegen der angenehmeren Lesbarkeit geschlechtsneutral verwendet.
Adolphe Jacques Quételet, belgischer Astronom und Statistiker, 1796-1874
3 Visual Basic for Applications. Auf Anfrage sende ich die entsprechende Excel-Datei gerne zu (e-mail-Adresse am Ende des Artikels).
2 Lambert
2
Stochastik in der Schule 26 (2006) 3 S. 2–10
Abb. 1: n = 10000 Stichproben; 1 Zufallszahl je
Stichprobe
Erhöht man n, am besten vorerst bei konstantem
x > 2, wird die Struktur der Grafik regelmäßiger.
Die Bevorzugung der Mitte und das umso seltenere Auftreten eines Wertes, je weiter er vom Mittelwert abweicht, werden offensichtlich. Außerdem
wird die Vermutung gestärkt, dass Abweichungen
nach oben bzw. nach unten gleich wahrscheinlich
sind. Je größer man n wählt, desto mehr nimmt der
obere Rand des Streckenschaubildes die Form einer
Glockenkurve an.
Mit genügend großem n erhält man eine nahezu perfekte Gauß-Glockenkurve, wie auch Abbildung 3
zeigt.
Der rote Faden hier muss sein, den Graph der Dichtefunktion der Normalverteilung schrittweise am Bildschirm entstehen zu lassen.
Dazu wird nun die Anzahl der Zufallszahlen pro
Stichprobe erhöht. Das Programm errechnet das
arithmetische Mittel dieser Zahlen, nimmt davon den
ganzzahligen Anteil und stellt die relative Häufigkeit dieses Werts wieder als Strecke dar. Die Skalierung der y-Achse wird jeweils den darzustellenden Werten angepasst. Als Beispiel zeigt Abbildung
2 ein Ergebnis für n = 1000 Stichproben und je 5 Zufallszahlen pro Stichprobe. Die grundsätzliche Struktur des Streckenschaubildes stellt sich bei wiederholter Durchführung der Stichprobe immer wieder ein:
Stichprobenmittelwerte im Bereich des Mittelwerts
50,5 der verwendeten Zufallszahlen treten gehäuft
auf4 .
Abb. 3: n = 500000 Stichproben; 5 Zufallszahlen je
Stichprobe
Zu klären bleibt noch, wie die Anzahl x der Zufallszahlen pro Stichprobe Einfluss nimmt.
Abb. 2: n = 1000 Stichproben; 5 Zufallszahlen je
Stichprobe
4 Der
Dazu zeigt Abbildung 4 vergleichend zwei Erhebungen mit gleichem n, aber unterschiedlichem x. Offensichtlich beeinflusst x die Breite der Glockenkurve. Das ist leicht einsichtig, denn klarerweise treten bei einer größeren Anzahl von Zufallszahlen pro
Stichprobe Ausreißer, d.h. Stichprobenmittelwerte
im Randbereich, noch seltener auf, als bei einer kleineren Anzahl von Zufallszahlen pro Stichprobe. Daher ist für ein kleineres x eine breitere Glockenkurve
als für ein großes x zu erwarten (siehe Abb. 4).
Mittelwert und die Varianz zu jeder Darstellung stehen im Tabellenteil der Ausgabe zu etwaigen Verwendung bereit.
3
Denn gerade das Ausprobieren und Sichten von vielen verschiedenen Histogrammen mit unterschiedlichen Werten für n und x ist eine tragende Säule dieses Unterrichtsvorschlages. Die Qualität des gesamten Unterrichtskonzeptes wird durch ein Streichen
dieses schülerzentrierten Teiles beeinträchtigt.
Ich selbst habe in meinem Unterricht beide Möglichkeiten durchgeführt, die zweite allerdings nur,
wenn zwingende zeitliche Rahmenbedingungen eine
selbstständige, interaktive Schülerarbeit nicht zuließen. Die Resultate der beiden Einsatzmöglichkeiten sind einfach zu unterschiedlich. Die interaktive Tätigkeit, die auch ein selbstständiges Dokumentieren von Ergebnissen einfordert, bringt erstens eine stärkere Identifikation mit der Materie und zweitens mehr eigenes nachhaltiges Wissen. HefendehlHebeker schreibt von der Herausbildung mathematischer Einsicht im Kopf des lernenden Individuums als empfindlicher Prozess (Hefendehl-Hebeker,
2003, S. 109). Dieser Prozess verläuft im vorliegenden Fall bei selbstständiger Schülerarbeit nicht zuletzt durch den größeren Zeitrahmen gewinnbringender als bei einem vergleichsweise kurzen Einsatz des
Programms zur Demonstration.
Abb. 4: Im Vergleich: n = 100000 Stichproben mit
unterschiedlichem x, oben x = 3, unten x = 7.
1.2 Hinweise zur praktischen Umsetzung Erfahrungsbericht
Grundsätzlich sind zwei Einsatzmöglichkeiten des
Programms denkbar.
Der eigentlichen Intention dieses Unterrichtsvorschlages folgend steht die Empfehlung zur Umsetzung in einem schüleraktiven Unterricht an erster Stelle. Die Lernenden verwenden dabei das
Programm selbstständig. Ziel ist Erkenntnisgewinn
durch konkretes, eigenständiges Handeln.
Selbstverständlich ist es auch möglich, das Programm rein zur Demonstration einzusetzen. Im Rahmen eines Lehrervortrages oder Lehrer-Schülergespräches werden die Diagramme zentral erstellt und
besprochen bzw. erklärt. Auf geradlinigem Weg kann
das Ziel, die Entstehung der Glockenkurve als oberer Rand des Histogramms, angepeilt werden. Freilich ist es eine Frage der Sichtweise, ob die Geradlinigkeit in diesem Fall tatsächlich ein Vorteil ist.
5 Klarerweise
Vorschläge für Arbeitsaufträge in einem
schülerzentrierten Unterricht:
Jeder durch Arbeitsaufträge motivierte schüleraktive Unterricht muss in besonderem Maße das Vorwissen und die Fähigkeit zur eigenständigen Arbeit der Schüler berücksichtigen. Davon abhängig
können Aufgabenstellungen sehr offen oder sehr zielorientiert formuliert werden. Die Risken einerseits
und Chancen andererseits beider Möglichkeiten sind
jedem Mathematik-Lehrenden bekannt.
Die nachstehende kleine Auswahl von Vorschlägen
für Arbeitsaufträge variiert in der Intensität der Hilfestellung, die durch die Formulierung des Arbeitsauftrages gegeben ist.
Fragen zur Gleichverteilung des Zufallszahlengenerators:
• Überprüfe den Zufallszahlengenerator exemplarisch: Liegt tatsächlich Gleichverteilung
vor, d.h., liegt keine Bevorzugung bestimmter
Zahlen vor?5 .
Deutlich stärkere inhaltliche und strategische Orientierung für die Lernenden bieten folgende Formulie-
ist durch eine “Überprüfung” dieser Art die Qualität des Zufallszahlengenerators keineswegs abgesichert. Ist entsprechend Zeit vorhanden, bietet sich hier die Möglichkeit genauer auf Zufallszahlengeneratoren und mögliche Fehlfunktionen einzugehen
4
rungen:
• Wähle x = 1 für die Anzahl der Zufallszahlen pro Stichprobe und lass für unterschiedliche n Diagramme erstellen. Welche n eignen
sich, um eine eventuelle Bevorzugung einzelner Zahlen zu erkennen?
• Wie viele Diagramme sind nötig, um zumindest exemplarisch die Annahme der Gleichverteilung zu rechtfertigen?
• Fallen zufällige Abweichungen von der
Gleichverteilung eher für große oder eher für
kleine n ins Gewicht?
Wir kommen nun zu Fragen, die sich auf das Erfassen der besonderen Merkmale der Histogramme beziehen.
Zunächst Beispiele für zielgerichtete Fragestellungen, jede Frage legt den Fokus auf ein bestimmtes
Merkmal:
• Wähle eine feste Anzahl x von Zufallszahlen je
Stichprobe und variiere n. Wie verändern sich
die Histogramme?
• Lass für ein festes n > 1000 und ein festes
x > 2 mehrere Diagramme erstellen. Treten
Werte > 70 oder Werte < 30 häufiger auf? Wie
lautet die Antwort für den Vergleich von Werten > 90 mit Werten < 10?
• Variiere nun bei fester Stichprobenanzahl n
die Anzahl x der Zufallszahlen pro Stichprobe. Wie beeinflusst die Wahl von x die Gestalt
der Histogramme?
Offen formuliert und daher hohe Anforderung an die
Eigenständigkeit des experimentellen Arbeitens der
Lernenden stellend ist:
• Erhöhe kontinuierlich die Anzahl x der Zufallszahlen pro Stichprobe bzw. die Stichprobenanzahl n. Wie verändern sich die Histogramme?
In der Sekundarstufe II habe ich mit zielgerichteten
Arbeitsaufträgen im Allgemeinen bessere Erfahrungen gemacht als mit offenen. Sie geben das “Was?”
und “Wie?” vor und bringen naturgemäß auch strukturiertere Ergebnisse als offene Fragestellungen und
damit eine gute Basis für das weitere Vorgehen.
In der Sekundarstufe II arbeite ich daher mittlerweile nur mit zielorientierten Fragen. Denn offene Formulierungen bewirkten in der Vergangenheit letztlich
immer, dass ich während der Stunde Hilfestellungen
gab, welche die Frage nach dem “Wie?” ebenso richtungsweisend beantworteten wie entsprechende Arbeitsaufträge. Solche Informationen verbreiten sich
bekanntlich wie ein Lauffeuer, können daher auch
kaum als individuelle Hilfestellungen betrachtet werden, und sind von der eigenständigen, konzentrierten
(Team-)Arbeit ablenkend.
Bei meiner Tätigkeit an der Pädagogischen Akademie in der Ausbildung von Mathematiklehrern für
Hauptschulen hat sich der Einsatz von offenen Fragestellungen eher bewährt. Auch in diesen Unterrichtssituationen waren teilweise strategische Hilfestellungen notwendig, aber entsprechend den Lernenden
(angehende Mathematiklehrer) in geringerem Ausmaß.
Jedenfalls geht es bei den Fragestellungen immer
darum, die besonderen Merkmale der Diagramme
zu erfassen. Dabei ist die Entscheidung, welche und
wie viele Graphiken dazu mit dem Programm erstellt
werden, als wesentliche Aufgabe zu sehen und daher
den Lernenden zu überlassen. In diesem Sinn ergibt
sich interaktives Handeln, denn die Wahl der Anzahl
der Stichproben bzw. die Anzahl der Zufallszahlen
pro Stichprobe für das erste Histogramm beeinflusst
die Auswahl für das zweite Histogramm usw. Somit werden die Grundlagen für die anschauliche Erkenntnis von den Lernenden innerhalb des Rahmens,
den das Programm bietet, selbst ausgewählt. Dies ist
ein bewusst betontes übergeordnetes Lernziel dieses
Unterrichtsvorschlages. Die selbstständige Auswahl
von Entscheidungsgrundlagen, sowohl in quantitativer als auch in qualitativer Hinsicht, ist eine Fähigkeit die weit über die Stochastik hinaus eine Rolle spielt. Hanisch schreibt in diesem Zusammenhang
von “latenten Lehrzielen”, die es im Auge zu halten
gilt (Hanisch, 1995, S. 112), in Übereinstimmung mit
Christmann, der das Ansteuern von Nahzielen stets
im Einklang mit langfristigen Zielsetzungen aufgebaut sehen will (Christmann, 1980, S. 215).
Ebenso verhält es sich mit dem Anspruch an die
Schüler, ihre auf der anschaulichen Ebene gewonnenen Erkenntnisse in die sprachliche Ebene zu übertragen. Die Überlegungen und Ergebnisse müssen so
festgehalten werden, dass ein sinnvolles Besprechen
und Vergleichen möglich ist. Dieser Anspruch kann,
wenn es notwendig erscheint und es für die Lernenden auf Grund vorangegangener Unterrichtseinheiten
nicht ohnehin selbstverständlich ist, in einem weiteren Arbeitsauftrag formuliert werden.
5
Wie die Schüler ihre Ergebnisse festhalten, bleibt ihnen an sich selbst überlassen. Nach meiner Erfahrung ist es allerdings unumgänglich, hier mit strategischen Hilfestellungen zur Seite zu stehen. Das
beeinflusst die Eigenständigkeit zwar deutlich, viele
Schüler neigen aber dazu ihre (oft sehr umfassenden)
Erkenntnisse zu oberflächlich zu dokumentieren. Das
erweist sich im weiteren Unterrichtsverlauf, der gerade auf diesen Erkenntnissen aufbaut, als Mangel.
Überdies ist es mir an dieser Stelle wichtig, die Bedeutung des sinnvollen Dokumentierens von Ergebnissen, sei es in verbaler oder graphischer Form, herauszustreichen. Es handelt sich dabei um eine wichtige Kompetenz, die wohl für viele Lebensbereiche
grundlegende Bedeutung hat.
2 Ein Weg zur Gleichung der
Dichtefunktion
Wir gehen nun vom Ergebnis eines Experiments aus,
bei dem die Werte einer Zufallsvariablen gemessen
wurden. Dieses Ergebnis sei graphisch durch eine
Kurve oder einen Polygonzug mit annähernd glockenförmigem Aussehen erfasst. In unserem konkreten Fall wird also der obere Rand der Streifenschaubilder durch einen Polygonzug dargestellt.
Die Ausprägung der “Knicke” im Polygonzug ist
durch die Anzahl der Stichproben begründet und ist
umso weniger stark, je größer die Anzahl der Stichproben und je feiner die Unterteilung der Skala für
die möglichen Ergebnisse ist. Außerdem ist zu bedenken, dass viele im Prinzip stetige Zufallsvariable
mittels Klasseneinteilung als diskrete Zufallsvariable
aufgefasst werden, um in einem Experiment messbare Ergebnisse erhalten zu können. Das gilt auch für
den Durchschnittswert von Zufallszahlen, der eine
kontinuierliche Größe ist, wenn man bei den Zufallszahlen alle Werte aus dem Intervall [1, 100] zulässt.
Erst durch die Einschränkung auf ganzzahlige Werte
bewegen wir uns im diskreten Bereich.
Das rechtfertigt den Grenzübergang n → ∞ und somit die Frage nach einer glatten Glockenkurve, um
die Verteilung der Zufallsvariablen idealisiert darzustellen.
Die durch empirische Befunde ausgewiesene Gemeinsamkeit der Verteilungen von verschiedensten
Zufallsvariablen bezieht sich natürlich nur auf eine
qualitative Gleichartigkeit der Kurve, niemals auf absolute Werte von Wahrscheinlichkeiten oder Häufigkeiten.
6 Durch
6
Z=
Wir suchen also nach einer Funktion, die als Dichtefunktion für Zufallsvariablen fungieren kann, deren Häufigkeitspolygone, basierend auf den Ergebnissen eines Experiments, annähernd eine Glockenkurve darstellen. Die Diagramme in 1.1 liefern Mittelwerte um 50,5 und unterschiedliche Varianzen, die
durch die unterschiedliche Anzahl der Zufallszahlen
je Stichprobe und unterschiedliche Anzahl an Stichproben bedingt sind. Es ist leicht plausibel zu machen, dass eine andere Wahl der Zufallszahlen (z.B.
von 1 bis 50) den Mittelwert verändert. Da es um die
qualitative Gleichartigkeit der Glockenkurven geht,
soll die Suche unabhängig vom jeweiligen Mittelwert
und von der jeweiligen Varianz sein. Daher wenden
wir eine spezielle lineare Transformation, die Standardisierung, an.
Durch Standardisieren kann man von jeder Zufallsvariable X mit beliebigem Erwartungswert µ und beliebiger Varianz σ2 zu einer Zufallsvariable mit µ = 0
und σ2 = 1 übergehen6 . Damit können wir unsere Suche auf eine spezielle Kurve einschränken.
Fassen wir nun die Eigenschaften zusammen, die wir
von der gesuchten Dichtefunktion ϕ aufgrund unserer experimentellen Ergebnisse und Vorüberlegungen
fordern:
1. Da nach den Ergebnissen der Experimente Abweichungen vom Mittelwert nach oben und
nach unten gleich wahrscheinlich sind, soll
die Funktion symmetrisch zum Erwartungswert sein. Entsprechend der Standardisierung
erhält µ den Wert 0, an dieser Stelle befindet
sich der einzige Extremwert (Maximum) der
Funktion. Die Kurve ist eingipfelig und im Intervall ] − ∞, 0[ monoton wachsend bzw. im Intervall [0, ∞[ monoton fallend. Die Zufallsvariable soll überdies die Varianz 1 besitzen.
2. Der glatte, glockenförmige Graph der Dichtefunktion soll ohne “Knicke” sein, was bedeutet, dass wir nach einer überall differenzierbaren Funktion ϕ fragen, die nirgends verschwindet.
3. Darüber hinaus muss wie für jede Wahrscheinlichkeitsdichte gelten ϕ(z) ≥ 0 ∀z ∈ R und
da die Gesamtfläche zwischen Dichtefunktion
und x-Achse den Wert 1 haben muss
Z ∞
−∞
ϕ(z)dz = 1.
X −µ
erhält man die zu X standardisierte Zufallsvariable Z mit Erwartungswert 0 und Varianz 1.
σ
Daraus folgt ϕ(z) → 0 für |z| → ∞, was auch
der Forderung, dass die Wahrscheinlichkeit extrem großer Abweichungen vom Mittelwert
(nach oben und nach unten) sehr klein wird,
entspricht.
divergiert.
Wir haben nun eine Funktion zu finden, die diesen
drei Forderungen genügt.
Als Ausgangspunkt sind verschiedenste elementare
Funktionen denkbar, die schrittweise, entsprechend
dem Forderungskatalog adaptiert werden. Je nachdem von welchem der drei Punkte man ausgeht, wird
die eine oder andere Funktion als “Startfunktion”
Verwendung finden.
So knüpft beispielsweise Strehl seine Überlegungen an die Funktion f (x) = 1x an (Strehl, 1984, S.
143). Ebbmeyer und Stamm setzen im ersten Versuch
mit einer abschnittsweisen Festlegung der gesuchten
Funktion an (Ebbmeyer & Stamm, 1985, S. 405).
Wir beginnen beim ersten Punkt mit der Forderung nach einer zum Erwartungswert symmetrischen
Funktion. Dieses Kriterium erfüllen z.B. Funktionen
mit den Funktionsgleichungen y = |x| bzw. y = x2n .
Aufgrund der Forderung nach einer überall differenzierbaren Funktion scheiden Betragsfunktionen aus,
um eine möglichst einfache Funktion zu erhalten,
wählen wir als Funktionsterm x2 .
Die Funktion widerspricht aber natürlich sowohl dem
Anspruch auf ein Maximum an der Stelle 0 als auch
dem Punkt (3). Daher ist der Übergang zur Funkti1
on f (x) = 2 nahe liegend, womit die asymptotische
x
Annäherung an die x-Achse für |x| → ∞ erfüllt ist.
Diese Funktion ist jedoch an der Stelle x = 0 nicht
definiert. Wir vermeiden das durch eine Änderung
im Nenner, beispielsweise durch Addition einer Konstanten a2
⇒
f (x) =
1
a2 + x2
,
a 6= 0
oder durch Anwendung der Exponentialfunktion
⇒
f (x) =
1
−x2
,
2 = a
x
a
σ =
7 siehe
Z ∞
−∞
x2
1
dx
a2 + x2
1
a2 + x2
.
1
2 haben wir als Funktiax
onsgraph ebenfalls bereits den Typ der Glockenkurve
vorliegen.
Mit der Funktion f (x) =
Die Wahl der Basis a ist beliebig, denn durch einen
Korrekturfaktor im Exponenten kann man jederzeit
von einer Basis a zu einer anderen Basis b übergehen.
Um die Handhabung der Funktion einfach zu machen, wählen wir daher als Basis die Euler’sche Zahl
2
2
e. Als “Korrekturfaktor” ist wegen a−x = e−x lna der
natürliche Logarithmus der Basis a anzuwenden.
Um als Dichte verwendet werden zu können, muss
für eine Funktion die Normierungsbedingung
(3)
Z
∞
erfüllt sein. Es gilt daher das Integral
−∞
2
e−x dx
zu berechnen. Die Berechnung dieses uneigentlichen
Integrals kann zum Beispiel durch den Übergang zu
einem Doppelintegral und Verwendung von Polarkoordinaten bewerkstelligt werden7 . Egal für welchen
Berechnungsweg man sich entscheidet, die notwendigen Vorkenntnisse sind auf Schulniveau im Normalfall nicht gegeben. Daher schlage ich an dieser
Stelle vor, das Integral von einem Computeralgebraprogramm (z.B. Derive) auswerten zu lassen, was sofort zum Ergebnis
a > 0.
Die erst genannte Möglichkeit, die anschaulich gut
passt (vgl. Abbildung 5), scheitert an der Forderung
für die Varianz σ2 = 1. Denn das für die Berechnung
der Varianz relevante Integral
2
Abb. 5: Graph der Funktion y =
Z ∞
−∞
2
e−x dx =
√
π
führt.
√
Wir verwenden somit π als Normierungsfaktor und
erhalten mit
2
1
f (x) = √ e−x
π
z.B. Barth & Haller (1988), S. 288f. oder Meyer (2004), S. 96f.
7
eine Funktion, die den Forderungen (2) und (3)
genügt, jedoch die in (1) genannte Bedingung nach
σ2 = 1 nicht erfüllt, sondern für die Varianz den Wert
1
2 aufweist.
Auch hier ist gemäß der Definition der Varianz die
Berechnung eines uneigentlichen Integrals, nämlich
σ2 =
Z ∞
−∞
Damit ergibt sich als Dichte ϕ der Zufallsvariable Z
z2
1
ϕ(z) = √ e− 2 ,
2π
und diese Funktion erfüllt nun alle drei gestellten
Forderungen!
x2 f (x)dx
erforderlich. Da man dieses Integral zumindest zu einem Teil mittels Grenzwertüberlegungen auswerten
kann, ist die Berechnung für manche Leistungskurse
auch auf schulischer Ebene machbar. In Österreich
wäre das beispielsweise im Wahlpflichtfach Mathematik, das an Allgemeinbildenden Höheren Schulen
angeboten wird, möglich.
Durch Einsetzen erhält man
Z ∞
1
2
1
x √ e−x dx = √
σ =
π
π
−∞
2
2
Z ∞
−∞
2
(−x)(−xe−x )dx.
Das Produkt wird partiell integriert. Durch Anwendung der Regel von de l’Hospital und dem Wissen
Z
∞
√
2
1
e−x dx = π von oben ergibt sich der Wert .8
2
−∞
1
Für unsere vorliegende Funktion gilt also σ2 = , der
2
Erwartungswert beträgt wegen der Symmetrie 09 .
Daher standardisieren wir die Zufallsvariable X , die
durch diese Dichtefunktion beschrieben wird:
X −µ X √
Z=
= = 2X
σ
σ
und berechnen die Dichtefunktion ϕ(z) der Zufallsvariablen Z mit dem Mittelwert 0 und der Varianz 1.
Für die Verteilungsfunktion der Zufallsvariablen X
gilt
Z x
2
1
Φ(x) = √
e−u du
π −∞
und damit für
z
1
Φ(z) = P(Z ≤ z) = P(X ≤ √ ) = √
π
2
Z
√z
2
−∞
2
e−u du.
Wir substituieren
1
Φ(z) = √
π
8 Ausführlicher
Z z
− 21 v2
e
−∞
1
1
√ dv = √
2
2π
Es bietet sich hier an, die eben durchgeführte Standardisierung anschaulich
√ zu reflektieren. Durch die
Transformation Z = 2X erfährt die Kurve
√ eine horizontale Streckung um den Faktor 2. Um den
Flächeninhalt zwischen Kurve und x-Achse konstant
auf dem Wert 1 zu halten, muss daher eine vertikale
1
Stauchung um den Faktor √ erfolgen (vgl. Abbil2
dung 6).
Spätestens jetzt erfolgt im Unterricht die Namensgebung der Normalverteilung.
1
u= √ v
2
und erhalten
1
2
Abb. 6: Vergleich der Graphen für f (x) = √ e−x
π
1 −x2
(oben) und ϕ(x) = √ e 2 .
2π
Z z
−∞
v2
e− 2 dv.
Unsere Vorgangsweise sagt natürlich nichts darüber
aus, ob es noch andere Funktionen gibt, die ebenso den Forderungskatalog erfüllen und somit als gesuchte Dichtefunktion fungieren könnten.
siehe Hauer-Typpelt, 1998, S. 65f.
9 Dieser Wert lässt sich über die Definition E(X) = R ∞ x · f (x)dx nachrechnen
−∞
8
Aufbauend auf den Ausgangspunkten unserer Überlegungen, den (simulierten) empirischen Befunden,
haben wir die Ansprüche an die Funktion formuliert
und diese für eine Funktion abgesichert.
Viele in der Natur auftretende Merkmale sind normalverteilt bzw. es hat sich gezeigt, dass viele
Häufigkeitsverteilungen gut durch die Normalverteilung approximiert werden können. Ob dies im Einzelfall zulässig ist, muss durch statistische Testverfahren abgesichert werden.
Im vorliegenden Zugang zur Normalverteilung sind
wir von gleichverteilten Größen, den Zufallszahlen,
ausgegangen. Das ist eine willkürliche Wahl, denn
diese ursprüngliche Verteilung der Größen spielt, in
dem Rahmen, den der zentrale Grenzwertsatz vorgibt, keine Rolle. Das gerade bewirkt ja die Bedeutung der Normalverteilung. Insofern ist der Zugang
ausbaufähig, indem man Experimente am Computer simulieren lässt, die von anders als gleichverteilten Größen ausgehen. Der Vergleich der Ergebnisse
von Experimenten, die letztlich alle zu Normalverteilung führen, ist sicher lehrreich und führt direkt
zur Grundaussage des zentralen Grenzwertsatzes. Im
Schulbereich wird der Zeitrahmen dafür allerdings
nur in Ausnahmefällen gegeben sein.
Praktische Umsetzung - didaktische
Bemerkungen
Aufbauend auf die Ergebnisse aus der Arbeit mit
dem Programm wird gemeinsam ein Forderungskatalog für die gesuchte Dichtefunktion erstellt. Die
selbstständige Schülertätigkeit, wie sie beim Arbeiten mit dem Programm erreicht werden kann,
darf nicht erwartet werden. Meiner Erfahrung nach
erweist sich hier das klassische Lehrer-SchülerGespräch als nützlich, indem sich sowohl eher lehrerzentrierte als auch eher schülerzentrierte Phasen einstellen. Eine detaillierte Aufschlüsselung dazu kann
an dieser Stelle nicht gegeben werden, da gruppenspezifische Einflussfaktoren eine zu große Rolle
spielen. Immer wieder ist es notwendig, dass konkrete Anstöße von der Lehrperson kommen. Zum Beispiel bei der Forderung nach Mittelwert 0 und Varianz 1, da sie sich aus den Diagrammen nicht zwingend ergibt, sondern aus oben genannten Gründen
(qualitative Gleichartigkeit der Glockenkurven) festgelegt wird. Der Vorgang der Standardisierung wird
als bekannt vorausgesetzt. In der konkreten Unterrichtssituation kann es natürlich hilfreich (manchmal
unerlässlich) sein, diese Transformation anschaulich
unterstützt zu erläutern. Eine der, oben zur Reflexion benutzten, Abbildung 6 ähnliche Darstellung, die
auch die Schiebung um µ enthält, eignet sich dazu.
Da das Programm Mittelwert und Varianz zu jedem
erstellten Histogramm liefert, kann auch anhand eines konkreten Schülerergebnisses die Standardisierung besprochen werden.
Wir knüpfen die ersten Überlegungen an die Funktion y = |x| bzw. y = x2n . An dieser willkürlichen
Auswahl muss natürlich nicht festgehalten werden.
Führen Schülerideen zu anderen Ausgangsfunktionen, so sollte man das unbedingt zulassen. Freilich
erfordert die Anpassung der vorgeschlagenen Funktionen an die gestellten Forderungen im Normalfall
Anleitungen von Seiten des Lehrers, so dass das Ganze auf ein angeleitetes Probieren, Annehmen und
Verwerfen von Ideen hinausläuft, bei dem die problemlösende Komponente betont wird. Dabei wird
eine möglichst hohe Schüleraktivität angestrebt was
das Einbringen von Ideen betrifft. Eine selbstständige Erarbeitung durch die Lernenden ist ein zu hoher
Anspruch. Die Befürchtung, dass Schüler kaum eigene Vorschläge bringen, weil das Thema zu schwierig ist, bestätigen sich in der Praxis nicht. Mitbestimmend für die Intensität der Schüleraktivität ist
natürlich das Vorwissen. Den wirklichen Ausschlag
gibt aber die intensive, interaktive Auseinandersetzung mit dem Thema auf der ikonischen Ebene, die
als Voraussetzung gegeben sein muss.
Tietze et al. betonen, dass gerade nach der interaktiven Arbeit mit Computerprogrammen “die gemeinsame Reflexion und Diskussion über die einzelnen Schritte des Mathematisierungsprozesses wichtig sind” (Tietze, Klika & Wolpers, S. 170) .
Vorschläge von Schülern sollten unbedingt aufgenommen und dürfen keinesfalls ohne zufrieden stellende Erklärung verworfen werden. Auch Humenberger und Reichel fordern “There must be time for
mistrials as well, and these must not simply be considered as wrong; there has to be an explanation” (Humenberger & Reichel, 1996, S. 201). Selbst wenn
manchmal regelrecht skurrile Vorschläge ins Rennen geschickt werden und man sich schnell in einem Wiederholungskurs “Funktionen und ihre Eigenschaften” wiederfindet. Ich sehe das aber als etwas Positives. Denn letztlich lässt sich an vielen,
auch ursprünglich nicht zielführenden Überlegungen
Sinnvolles anknüpfen. Außerdem ist auch das Einsehen mit einer Idee in einer Sackgasse gelandet zu sein
und die daraus gewonnen Erkenntnisse möglichst
gewinnbringend weiter zu verwenden eine wichtige Lernerfahrung. Immer wenn Schüler entdeckend
tätig werden “sind Irrwege, Querfeldeinpfade und
9
Sackgassen ganz natürliche und lehrreiche Erfahrungen.” (Krainer, 1993, S. 267). In diesem Sinn ist die
1
Besprechung der Funktion f (x) = 2
, a 6= 0
a + x2
zu sehen. Scheint der Graph anschaulich gut zu den
gewünschten Forderungen zu passen, so erfüllt die
Funktion letztlich doch nicht alle Ansprüche.
Dabei steht die genannte Funktion natürlich stellvertretend für alle jene, die argumentativ ähnlich zu behandeln sind. Denn je nach Ansatzpunkt und Unterrichtsverlauf wird man bei unterschiedlichen, zu besprechenden, Funktionstermen landen.
Eine grundsätzliche Überlegung fordert die Auswertung der in der Herleitung auftretenden Integrale. Auf Schulniveau Rist der Einsatz eines CAS bei
∞ −x2
der Berechnung von −∞
e dx , außer in Ausnahmefällen, unerlässlich. Daher ist auch die Entscheidung, alle weiteren Integrale mittels CAS auszuwerten, naheliegend. Ob man den - oben bewusst - “gemischt” gewählten Weg geht, der eine nähere Konfrontation mit den Integralen notwendig macht, oder
die Auswertung der Integrale mittels CAS aus dem
Zentrum der Überlegungen heraushält, hängt wesentlich vom Vorwissen der Schüler und der gewünschten Akzentuierung des Lehrers ab. Jedenfalls verträgt sich der Einsatz eines CAS meines Erachtens
sehr gut mit dem Charakter der Herleitung, die ja
auf Computereinsatz basiert. Überlegungen und Ideen der Lernenden zu fördern und einzubinden und
gleichzeitig den roten Faden nicht zu verlieren, ist die
zentrale Aufgabe des Lehrers bei der Herleitung des
Funktionsterms - zugegeben streckenweise ein Balanceakt. Zentral ist, dass die Lernenden an der Entwicklung der Funktionsgleichung aktiv beteiligt sind
und mathematischer Inhalt im genetischen Sinn entsteht.
Literatur
Barth F. und R. Haller (1988): Stochastik Leistungskurs. München: Ehrenwirt Verlag
Christmann N. (1980): Einführung in die Mathematik - Didaktik. Paderborn: Schöningh Verlag
Ebbmeyer B. und K. Stamm (1985): Die Approximation der Binomialverteilung durch
10
Schulfunktionen.
In:
Der
MathematischNaturwissenschaftliche Unterricht 38/7, S.
402 - 407
Hanisch G. (1995): Wozu ist der Mathematikunterricht gut? In: Grosser S. (Hrsg.): Didaktik-Reihe
der ÖMG, Heft 23, S. 106 - 127
Hauer-Typpelt P. (1998): Zugänge zur Normalverteilung und ihre fachdidaktische Analyse. Dissertation. Universität Wien
Hefendehl-Hebeker L. (2003): Erkenntnisgewinn in
der Mathematik. In: Leuders T. (Hrsg.): Mathematik Didaktik. Berlin: Cornelsen Verlag Scriptor, S.
107 - 118
Humenberger H. und H.-C. Reichel (1996): Problem
Solving as a Continuous Principle for Teaching:
Suggestions and Examples. In: Posamentier S. und
W. Schulz (Hrsg.): The Art of Problam Solving
Thousand Oaks, California: Corwin Press, S. 199
- 232
Krainer K. (1993): “Gesichertheit” versus “Ungesichertheit” - ein zentrales Dilemma im Mathematikunterricht. In: Schuhmann H. (Hrsg.): Beiträge zum Mathematikunterricht. Hildesheim: Verlag Franzbecker, S. 267 - 270
Meyer J. (2004): Schulnahe Beweise zum zentralen
Grenzwertsatz. Hildesheim, Berlin: Verlag Franzbecker
Strehl R. (1976): Wahrscheinlichkeitsrechnung. Freiburg i. Br.: Verlag Herder
Tietze, U.; Klika, M. und H. Wolpers (2002): Didaktik der Stochastik. Mathematikunterricht in der Sekundarstufe II, Band 3. Braunschweig/Wiesbaden:
Vieweg Verlag
Anschrift des Verfassers
Dr. Petra Hauer-Typpelt
Fakultät für Mathematik Universität Wien
Nordbergstraße 15
1090 Wien
Österreich
und
Landstraßer Gymnasium
Kundmanngasse 20-22
1030 Wien
Österreich
[email protected]