Rechtwinklige Dreiecke

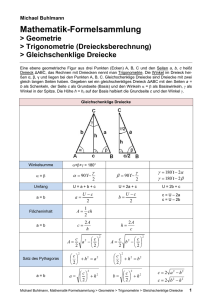
Michael Buhlmann
Mathematik-Formelsammlung
> Geometrie
> Trigonometrie (Dreiecksberechnung)
> Rechtwinklige Dreiecke
Eine ebene geometrische Figur aus drei Punkten (Ecken) A, B, C und den Seiten a, b, c heißt
Dreieck ∆ABC, das Rechnen mit Dreiecken nennt man Trigonometrie. Die Winkel im Dreieck heißen α, β, γ und liegen bei den Punkten A, B, C. Rechtwinklige Dreiecke sind Dreiecke, die einen
rechten Winkel enthalten. Gegeben sei ein rechtwinkliges Dreieck ∆ABC mit den Seiten a, b, c und
den Winkeln α, β, γ mit γ = 90°: a und b heißen Katheten, c heißt Hypotenuse, p und q heißen Hypotenusenabschnitte, h = hc heißt Höhe des Dreiecks.
Rechtwinklige Dreiecke
Winkelsumme
α+β+γ = 180°
γ = 90°
α+β = 90°
Umfang
U=a+b+c
a=U–b–c
Flächeninhalt
Satz des Pythagoras
A=
1
ab
2
a=
2A
b
α = 90° – β
β = 90° – α
b=U–a–c
c=U–a–b
b=
2A
a
A=
1
ch
2
c=
2A
h
a2 + b2 = c2
c2 = a2 + b2
a2 = c2 – b2
b2 = c2 – a2
c = a 2 + b2
a = c2 − b2
b = c2 − a2
Michael Buhlmann, Mathematik-Formelsammlung > Geometrie > Trigonometrie > Rechtwinklige Dreiecke
1
Kathetensatz
a2 = c·p
a = cp
a2
c=
p
a2
p=
c
b2
c=
q
b2
q=
c
h2
p=
q
h2
q=
p
b2 = c·q
b = cq
Höhensatz
h2 = p·q
h=
Trigonometrische
Funktionen
pq
h=
ab
c
h=
2A
c
a=
hc
b
b=
hc
a
sin α =
a Gegenkathete
=
c
Hypotenuse
a = c sin α
c=
b = c cos α
tan α =
c=
sin β =
b=
cos β =
a = c cos β
tan β =
c=
(Tangens)
(Sinus)
b
sin β
a
Ankathete
=
c Hypotenuse
c=
(Cosinus)
a
tan α
b Gegenkathete
=
c
Hypotenuse
b = c sin β
(Sinus)
b
cos α
sin α a Gegenkathe te
= =
cos α b
Ankathete
a = b tan α
ab
h
a
sin α
b
Ankathete
=
c Hypotenuse
cos α =
c=
(Cosinus)
a
cos β
sin β b Gegenkathete
= =
cos β a
Ankathete
(Tangens)
Michael Buhlmann, Mathematik-Formelsammlung > Geometrie > Trigonometrie > Rechtwinklige Dreiecke
2
b = a tan β
sin α = cos β
tan α =
1
tan β
a=
b
tan β
cos α = sin β
tan β =
1
tan α
Rechtwinklige Dreiecke
Michael Buhlmann, Mathematik-Formelsammlung > Geometrie > Trigonometrie > Rechtwinklige Dreiecke
3