Indizes (Indexzahlen)

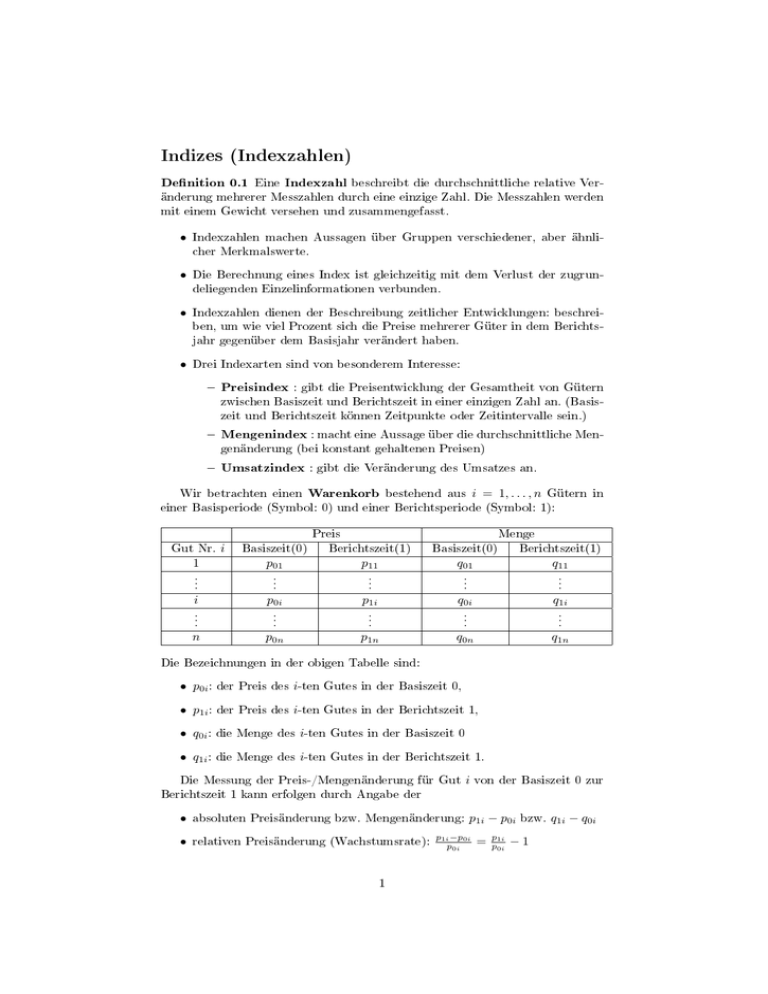
Indizes (Indexzahlen)
Denition 0.1
Eine
Indexzahl
beschreibt die durchschnittliche relative Ver-
änderung mehrerer Messzahlen durch eine einzige Zahl. Die Messzahlen werden
mit einem Gewicht versehen und zusammengefasst.
•
Indexzahlen machen Aussagen über Gruppen verschiedener, aber ähnlicher Merkmalswerte.
•
Die Berechnung eines Index ist gleichzeitig mit dem Verlust der zugrundeliegenden Einzelinformationen verbunden.
•
Indexzahlen dienen der Beschreibung zeitlicher Entwicklungen: beschreiben, um wie viel Prozent sich die Preise mehrerer Güter in dem Berichtsjahr gegenüber dem Basisjahr verändert haben.
•
Drei Indexarten sind von besonderem Interesse:
Preisindex
: gibt die Preisentwicklung der Gesamtheit von Gütern
zwischen Basiszeit und Berichtszeit in einer einzigen Zahl an. (Basiszeit und Berichtszeit können Zeitpunkte oder Zeitintervalle sein.)
Mengenindex : macht eine Aussage über die durchschnittliche Mengenänderung (bei konstant gehaltenen Preisen)
Umsatzindex : gibt die Veränderung des Umsatzes an.
Wir betrachten einen
Warenkorb
i = 1, . . . , n
bestehend aus
Gütern in
einer Basisperiode (Symbol: 0) und einer Berichtsperiode (Symbol: 1):
Preis
Gut Nr.
i
Menge
Basiszeit(0)
Berichtszeit(1)
Basiszeit(0)
Berichtszeit(1)
1
p01
p11
q01
q11
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
i
p0i
p1i
q0i
q1i
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
n
p0n
p1n
q0n
q1n
Die Bezeichnungen in der obigen Tabelle sind:
• p0i :
der Preis des
i-ten
Gutes in der Basiszeit 0,
• p1i :
der Preis des
i-ten
Gutes in der Berichtszeit 1,
• q0i :
die Menge des
i-ten
Gutes in der Basiszeit 0
• q1i :
die Menge des
i-ten
Gutes in der Berichtszeit 1.
Die Messung der Preis-/Mengenänderung für Gut
i
von der Basiszeit 0 zur
Berichtszeit 1 kann erfolgen durch Angabe der
•
absoluten Preisänderung bzw. Mengenänderung:
•
p1i −p0i
relativen Preisänderung (Wachstumsrate):
p0i
1
p1i − p0i
=
p1i
p0i
bzw.
−1
q1i − q0i
• Preismeÿzahl
(Wachstumsfaktor):
ipi =
p1i
p0i
• Mengenmeÿzahl
(Wachstumsfaktor):
iqi =
q1i
q0i
• Umsatzmeÿzahl
(Wachstumsfaktor):
ivi =
p1i q1i
p0i q0i
= ipi · iqi
Der Weg zur Bestimmung eines Preis- bzw. Mengenindex für die Berichtszeit
1 bezogen auf die Basiszeit 0 ist die Berechnung des gewogenen arithmetischen
Mittels der einzelnen Preis- bzw. Mengenmeÿzahlen:
Pn
p1i
wi
i=1
Pn p0i (·100%) bzw.
i=1 wi
Pn
q1i
i=1 q0i wi
Pn
i=1
wi
(·100%),
wi (i = 1, . . . , n) die Gewichte sind.
Wahl geeigneter Gewichte ist das zentrale
wo die Zahlen
Die
Problem der Indexkon-
struktion.
0.1
Preisindizes
Bei Bestimmung der Preisindizes werden die Mengen für Basis- und Berichtszeit
konstant gehalten, um die reine Preisentwicklung zu erfassen.
0.1.1
Die
Preisindex nach Laspeyres
Gewichte orientieren sich am Warenkorb (Mengen) der Basiszeit
(historisierender Index):
wi = p0i q0i
Basiszeit)
(die Ausgabensumme für das Gut
Pn
Ip0
=
p1i
p0i q0i
i=1
Pn p0i
i=1 p0i q0i
i
zur
P p1
p p0 q 0
= P0
,
p0 q 0
wo in der zweiten Formel die Additionsvariable
i
weggelassen wurde, um die
Formel einfacher zu haben.
Der Preisindex nach Laspeyres kann auch als ein gewogenes arithmetisches
Mittel der einzelnen Preismeÿzahlen
ip =
p1
p0 mit den Gewichten
p0 q 0
(das Ag-
gregat zur Basiszeit) gebildet werden:
Ip0 =
P
p q ·i
P0 0 p .
p0 q 0
Ordent man die Denition anderswie um, so kann der Preisindex nach Laspeyresals ein gewogenes harmonisches Mittel der einzelnen Preismeÿzahlen
mit den Gewichten
p1 q 0
ip
(ktives Aggregat) gebildet werden:
P p1
Ip0
P
P
p q
p1 q 0
p p0 q 0
P p11 q00 .
=
= P0
=P
p0 q 0
p1 q0 pp01
ip
Nach Kürzen bekommt man die
peyres:
Aggregatform
Pn
P
p1i q0i
p1 q 0
Ip0 = Pni=1
=P
,
p0 q 0
p
q
0i
0i
i=1
2
des Preisindex nach Las-
wo der Ausdruck
Pn
i=1
p0i q0i
im Nenner die Ausgabensumme für sämtliche Gü-
ter zur Basiszeit ist. Man schreibt in kurzer Form
P
(p̄1 , q̄0 )
p1 q 0
=
Ip0 = P
,
p0 q 0
(p̄0 , q̄0 )
wo die Preise (d.h.
p̄0 ; p̄1 )
und Mengen (d.h.
q̄0 ; q̄1 )
der einzelnen Güter jeweils
in Vektoren zusammengefaÿt worden sind, und(·, ·) das Skalarprodukt zweier
Vektoren bedeutet.
0.1.2
Die
zeit
Preisindex nach Paasche
Gewichte orientieren sich am Warenkorb (Mengen) der Berichts(aktueller Index): wi = p0i q1i (die ktive Ausgabensumme für das Gut i
berechnet als Menge der Berichtszeit zum Preis der Basiszeit)
Pn
Ip1
=
p1i
p0i q1i
i=1
Pn p0i
i=1 p0i q1i
P p1
p p0 q 1
= P0
.
p0 q 1
Der Preisindex nach Paasche als das gewogene arithmetische Mittel der einzelnen Preismeÿzahlen
ip
wird hier mit den Gewichten
p0 q 1
(ktives Aggregat)
gebildet:
P
p0 q1 · ip
1
Ip = P
.
p0 q 1
Anderswie geordnet bekommt man den Preisindex nach Paasche als gewogenes
harmonisches Mittel der einzelnen Preismeÿzahlen mit den Gewichten
p1 q 1
(die
Ausgabensumme für das jeweilige Gut zur Berichtszeit):
P p1
Ip1
P
P
p q
p1 q 1
p p0 q 1
P p11 q11 .
= P0
=
=P
p0 q 1
p1 q1 pp01
ip
Nach Kürzen bekommt man ähnlich wie oben die Aggregatform des Preisindex nach Paasche:
0.2
P
(p̄1 , q̄1 )
p1 q 1
=
Ip1 = P
p0 q 1
(p̄0 , q̄1 )
Mengenindizes
Bei Bestimmung der Mengenindizes werden die Preise für Basis- und Berichtszeit
konstant gehalten, um die durchschnittliche Mengenänderung zu erfassen.
0.2.1
Mengenindex nach Laspeyres
Berechnung erfolgt mit Preisen der Basiszeit:
Pn
Iq0
=
q1i
i=1 q0i p0i q0i
Pn
i=1
p0i q0i
Nach Umformung dieser Denition bekommt man den Mengenindex als gewogenes arithmetisches bzw. harmonisches Mittel der einzelnen Mengenmeÿzahlen:
Iq0 =
P
P
p q ·i
p q
P0 0 q = P p00 q11 ,
p0 q 0
iq
3
oder in der Aggregatform:
Iq0
0.2.2
P
(p̄0 , q̄1 )
p0 q 1
=
=P
.
p0 q 0
(p̄0 , q̄0 )
Mengenindex nach Paasche
Berechnung erfolgt mit Preisen der Berichtszeit:
Pn
Iq1
=
q1i
i=1 q0i p1i q0i
Pn
i=1
p1i q0i
=
Nach Umformung dieser Denition bekommt man den Mengenindex als gewogenes arithmetisches bzw. harmonisches Mittel der einzelnen Mengenmeÿzahlen:
Iq1
P
P
p1 q 1
p1 q0 · iq
= P p1 q1 ,
= P
p1 q 0
iq
oder in der Aggregatform:
Iq1
0.3
P
p1 q 1
(p̄1 , q̄1 )
=P
=
.
p1 q 0
(p̄1 , q̄0 )
Umsatzindizes (Wertindizes)
Erfaÿt die Veränderung des Umsatzes (des Wertes) von Basiszeit zur Berichtszeit:
Pn
P
p1i q1i
p1 q 1
(p̄1 , q̄1 )
i=1
Iv = Pn
=
=P
p
q
(p̄0 , q̄0 )
p
q
0 0
i=1 0i 0i
Der Umsatzindex kann auch in Form eines gewogenen Mittels geschrieben werden:
P
P
p1 q 1
p0 q0 · iv
= P p1 q1
Iv = P
p0 q 0
iv
Es bestehen zwischen den Indizes folgende Zusammenhänge:
iv
Iv
= ip · iq ,
= Iq0 · Ip1 = Iq1 · Ip0 .
Spezialfälle:
•
Iq0
•
p̄0 = p̄1
=
= Iv ,
Wenn
Wenn q̄0 = q̄1
Ip0 = Ip1 = Iv .
Eine
(keine Preisveränderung), dann sind
Iq1
n
i=1
und
Iq0 = Iq1 = 1
und
(keine Mengenveränderung), dann sind
preisbereinigte
(deationierte)
P
Umsatzgröÿe (
Ip0 = Ip1 = 1
p1i q1i )
Gröÿe erhält man, indem man die
durch den Preisindex nach Paasche dividiert:
Pn
p1i q1i
.
Ip1
i=1
Die Wertsteigerung wird preisbereinigt, indem man den Wertindex durch einen
Preisindex teilt. Dies gibt die reale Mengen-Veränderung wieder, sie gleicht einem Mengenindex.
4
0.4
Kreuzung der Indizes
Aus der
geometrischen Kreuzung der Indizes von Laspeyres und Paasche
ergeben sich die Idealindizes von Fischer:
IpF =
q
Ip0 · Ip1
und
IqF =
q
Iq0 · Iq1 .
Die obige Zusammenhänge zwischen Umsatz-, Preis- und Mengenindizes kann
man weiterführen:
Iv = Iq0 · Ip1 = Iq1 · Ip0 = IpF · IqF .
0.5
Zusammenhänge zwischen Aggregatformen
Die Indizes werden mit Hilfe der Quotienten der Aggregate gebildet. Die Dierenzen der Aggregate können auch gebildet werden. Man kann eine Maÿzahl für
die Messung der absoluten Umsatzveränderung (Kv ) bilden, und man kann auch
untersuchen, wie die Preisveränderungen (Kp ) bzw. die Mengenveränderungen
(Kq ) die Umsatzveränderung beeinussen. Man bildet
P
P
=
p1 q 1 − p0 q 0
P
P
=
p0 q 1 − p0 q 0
P
P
=
p1 q 1 − p0 q 1
Kv
(0)
Kq
(1)
Kp
P
P
=
p1 q 1 − p0 q 0
P
P
=
p1 q 1 − p1 q 0
P
P
=
p1 q 0 − p 0 q 0
Kv
(1)
Kq
(0)
Kp
oder
Die Zusammenhänge sind
Kv = Kq(0) + Kp(1) ,
Kv = Kq(1) + Kp(0) .
und
(Kq zeigt die Umsatzveränderung, die wegen der Mengenveränderung passiert
ist;
Kp
zeigt die Umsatzveränderung, die wegen der Preisveränderung passiert
ist.)
Zu den eigentlichen Berechnungen benutzt man üblicherweise die Arbeitstabelle, die mit Spalten erweitert wird, worin sich die Aggregate benden:
Preis
Menge
Aggregate
Gut Nr.i
Basisz.(0)
Berichtsz.(1)
Basisz.(0)
Berichtsz.(1)
Basisz.
Berichtsz.
ktiv
ktiv
1
p01
p11
q01
q11
p01 q01
p11 q11
p01 q11
p11 q01
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
n
P
p0n
−
p1n
−
q0n
−
q1n
−
p0n q0n
P
p0 q 0
p1n q1n
P
p1 q 1
p0n q1n
P
p0 q 1
p1n q0n
P
p1 q 0
Die Tabelle kann man vereinfacht betrachten:
Gut Nr.
Preis
Menge
Aggregate
i
p0
p1
q0
q1
p0 q 0
p1 q 1
p0 q 1
p1 q 0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
P
−
−
−
−
Beispiel 0.1
P
p0 q 0
P
p1 q 1
P
p0 q 1
P
p1 q 0
Ein Unternehmen handelt mit den Rohstoen A, B und C. Die
Entwicklung der Verkaufspreise und Absatzmengen geht aus folgender Tabelle
5
hervor:
Rohsto
A
B
C
Preis (DM/t)
Menge(1000 t)
1986
60
80
90
1986
100
150
80
1991
70
90
120
1991
120
120
75
(a) Berechnen Sie die Preisentwicklung im Berichtszeitraum anhand der Preisindices von Laspeyres und Paasche!
(b) Berechnen Sie die Mengenentwicklung im Berichtszeitraum anhand der
Mengenindices von Laspeyres und Paasche!
(c) Berechnen Sie die Preis- und Mengenentwicklung anhand der Indizes von
Fischer!
(d) Berechnen Sie den Umsatzindex!
(e) Berechnen Sie die durchschnittliche jährliche Preissteigerungsrate nach
Laspeyres, Paasche und Fischer!
(f ) Berechnen Sie die durchschnittliche jährliche Umsatzsteigerungsrate!
Lösung: Man erstellt die folgende Arbeitstabelle (Basisjahr=1986; Berichtsjahr=1991):
Preis
Rohsto
A
B
C
P
Menge
Aggregate
p0 p1
q0
q1
p0 q 0
p1 q 1
p0 q 1
p1 q 0
60 70 100 120 6000 8400 7200 7000
80 90 150 120 12000 10800 9600 13500
90 120 80 75 7200 9000 6750 9600
− −
−
− 25200 28200 23550 30100
(a) Die Preisentwicklung im Berichtszeitraum anhand der Preisindices von
Laspeyres:
Paasche:
Ip0 =
P
P pp qq
P
Ip1 = P pp qq
1 0
0 0
1 1
=
0 1
=
30100
25200
28200
23550
= 1, 1944
= 1, 1975
(b) Die Mengenentwicklung im Berichtszeitraum anhand der Preisindices von
Laspeyres:
Paasche:
Iq0 =
P
P pp qq
P
Iq1 = P pp qq
0 1
0 0
1 1
=
1 0
=
23550
25200
28200
30100
= 0, 9345
= 0, 9369
(c) Die Preis- und Mengenentwicklung anhand der Indizes von Fischer
Preisentwicklung:
Mengenentwicklung:
(d) Der Umsatzindex ist:
q
√
Ip0 · Ip1 = 1, 1944 · 1, 1975 = 1, 1959
q
√
IqF = Iq0 · Iq1 = 0, 9345 · 0, 9369 = 0, 9357
IpF =
Iv =
PP p q
p q
1 1
0 0
=
28200
25200
= 1, 1190
(e) Die durchschnittliche jährliche Preissteigerungsrate ist nach
6
√
6
1, 1944 = 1, 0300
√
6
1, 1975 = 1, 0305
Paasche: 3,05%, denn
√
6
Fischer: 3,03%, denn
1, 1959 = 1, 0303
Laspeyres: 3%, denn
(f ) Die durchschnittliche jährliche Umsatzsteigerungsrate ist 1,89%, denn
√
6
1, 1190 =
1, 0189
Beispiel 0.2
Die Verwertungsdaten eines Textiliengeschäfts in 1999 sind
Produkt-
Umsatz
gruppe
(EFt)
Herrensocken
2244
1530
3190
6964
Kindersocken
Strumpfhosen
Insgesamt
Mengen-
Preis-
änderung in % (Basis=1998)
2
0
10
−
10
2
16
−
(a) Berechnen Sie die Umsatzveränderung der einzelnen Produktgruppen!
(b) Berechnen Sie die gesamte Umsatzveränderung!
(c) Berechnen Sie die gesamte Preisveränderung der Waren!
(d) Berechnen Sie gesamte Mengenveränderung der Waren!
(e) Um wieviel Forint wurde der Umsatz des Geschäftes wegen der Preisveränderung erhöht?
Lösung: Die Tabelle kann mit den benutzten Bezeichnungen ergänzt werden
(Basisjahr(0)=1998, Berichtsjahr(1)=1999):
Produktgruppe
Herrensocken
Kindersocken
Strumpfhosen
P
p1 q 1
iq
ip
iv = ip · iq
2244 1, 02 1, 10
1, 122
1530 1, 00 1, 02
1, 020
3190 1, 10 1, 16
1, 276
6964
−
−
−
p0 q0 = p1ivq1
2000
1500
2500
6000
p1 q1
ip
= p0 q0 · iq
2040
1500
2750
6290
(a) Die Umsätze der einzelnen Produktgruppen stiegen jeweils um 12,2%, 2%
und 27,6%.
(b)
Iv =
P
P pp qq
1 1
0 0
=
6964
6000
= 1, 161.
Der gesamte Umsatz stieg also um 16,1%.
(c) Die Preisindizes sind:
Ip1
P
6964
p1 q 1
= 1, 107
= P p1 q1 =
6290
ip
0
und Ip
P
p0 q0 · ip
6630
= P
=
= 1, 105
p0 q 0
6000
(d) Die Mengenindizes sind:
Iq0
P
p0 q0 · iq
6290
= P
=
= 1, 048
p0 q 0
6000
7
1
und Iq
P
p1 q 1
6964
= P p1 q1 =
= 1, 050
6630
iq
p0 q0 · ip =
2200
1530
2900
6630
p1 q1
iq
(e) Man berechnet von den Aggregatformen:
Kp(0)
Kp(1)
X
X
p0 q0 · ip −
p0 q0 = 6630 − 6000 = 630
X
X
X
X
=
p1 q 1 −
p0 q 1 =
p1 q 1 −
p0 q0 · iq = 6964 − 6290 = 674
=
Aufgabe 0.1
p1 q 0 −
X
p0 q 0 =
X
(EFt)
(EFt)
Über das Konsumverhalten eines Haushalts zu vier Gütern (A,B,C,D)
liegen folgende Informationen vor:
Jahr
Preis des Gutes
A B
1970 5 2
1971 5 5
1972 5 8
C
5
6
10
D
4
5
10
Menge des Gutes
A B
4 5
8 6
8 5
C
6
5
5
D
8
10
7
(a) Berechnen Sie die Preisindices von Laspeyres und Paasche für 1971 und
1972 jeweils zur Basis 1970!
(b) Berechnen Sie die Mengenindices von Laspeyres und Paasche für 1971 und
1972 jeweils zur Basis 1970!
(c) Berechnen Sie die Preis- und Mengenindices anhand der Indizes von Fischer für 1971 und 1972 jeweils zur Basis 1970!
(d) Berechnen Sie den Umsatzindex für 1971 und 1972 jeweils zur Basis 1970!
Aufgabe 0.2
Für einen Zoo-Markt erweisen sich die hergestellten Hundehüt-
ten, Kaninchenställe und Vogelbauer als Renner. Mengen und Preise dieser
Produkte sind für die Jahre 1985 und 1990 in der folgenden Tabelle festgehalten:
1985
Produkte
Hundehütten
Kaninchenställe
Vogelbauer
1990
Menge (Stück)
Preis (DM/Stück)
Menge (Stück)
Preis (DM/Stück)
50
100
100
60
20
30
100
120
250
80
20
50
(a) Das Unternehmen berechnet zunächst einen Umsatz- oder Wertindex zur
Basis 1985, um einen Überblick über die Umsatzentwicklung zwischen 1985
und 1990 zu gewinnen. Welcher Indexwert wird berechnet?
(b) In einem zweiten Schritt wird die reine Mengenentwicklung bestimmt. Dazu wird der Umsatzindex mittels eines Paasche-Preisindex preisbereinigt.
Führen Sie diese Preisbereinigung durch; welche Mengenentwicklung ergibt sich?
(c) Zeigen Sie, daÿ Sie mit der Berechnung eines Laspeyres-Mengenindex zum
gleichen Ergebnis gekommen wären.
8