1 Beispiel 1.1 (Einige Aufgaben zum Preisindex nach Laspeyres

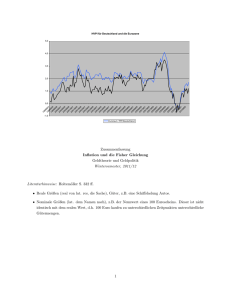
1
Beispiel 1.1 (Einige Aufgaben zum Preisindex nach Laspeyres, Paasche u.a.)
Aufgabe 1
Einem Konsumenten stehen drei Güter A, B, und C zur Verfügung. Die Preise der Güter
und die vom Konsumenten verbrauchten Mengen waren
Preise pro Mengeneinheit
Mengeneinheiten
1980
1982
1984
1980
1982
1984
A
4
5
8
2
2
1
B
3
2
1
4
5
7
C
5
7
5
2
1
3
a) Ermitteln Sie für das Jahr 1984 den Preisindex nach Laspeyres für die drei
Güter mit 1980 als Basisjahr.
b) Ermitteln Sie für das Jahr 1984 den Preisindex nach Paasche für die drei Güter
mit 1982 als Basisjahr.
Lösung zu a)
Indices nach Toernquist, Laspeyres, Paasche, Fisher
Die Werte von p und q mit 3 Beobachtungen:
erst die Basis, dann die Vergleichswerte
1
2
3
p (Basis)
4.00
3.00
5.00
q (Basis)
2.00
4.00
2.00
p (Vergleich)
8.00
1.00
5.00
q (Vergleich)
1.00
7.00
3.00
s0 (Basis)
.2667
.4000
.3333
s1 (Vergleich)
.2667
.2333
.5000
Toernquist-Index (Preis)=
Preis-Index (Laspeyres) =
(Fisher
) =
Mengen-Index (Laspeyres)=
(Fisher
)=
.84954 (Menge)
1.00000 (Paasche)
.86603
1.33333 (Paasche)
1.15470
=
=
1.17506
.75000
=
1.00000
Lösung zu b)
Indices nach Toernquist, Laspeyres, Paasche, Fisher
Die Werte von p und q mit 3 Beobachtungen:
erst die Basis, dann die Vergleichswerte
1
2
3
p (Basis)
5.00
2.00
7.00
q (Basis)
2.00
5.00
1.00
p (Vergleich)
8.00
1.00
5.00
q (Vergleich)
1.00
7.00
3.00
s0 (Basis)
.3704
.3704
.2593
s1 (Vergleich)
.2667
.2333
.5000
Toernquist-Index (Preis)=
.82923 (Menge)
= 1.34696
Preis-Index (Laspeyres) =
.96296 (Paasche)
=
.75000
(Fisher
) =
.84984
Mengen-Index (Laspeyres)= 1.48148 (Paasche)
= 1.15385
(Fisher
)= 1.30744
2
Aufgabe 2
Das Lieblingsgericht des Studenten U besteht aus Currywurst (C) mit Pommes Frites (P)
und einer extra Portion Ketchup (K), manchmal auch mit einer doppelten Portion.
In den Mensen der von U besuchten Institute ergab sich für eine Woche folgender Verzehr
zu folgenden Mengen (in Mengeneinheiten, ME) und Preisen (in DM):
C (ME)
PC (DM)
P (ME)
PP (DM)
K (ME)
PK (DM)
Mensa 1
3
2.50
2
1.00
3
0.50
Mensa 2
1
2.80
1
0.50
1
0.60
Mensa 3
2
3.00
2
0.75
2
0.40
Vergleichen Sie die Mensen, indem Sie jeweils einen Preisindex Ihrer Wahl (Laspeyres oder
Paasche) -d.h. also insgesamt zwei- mit der Basis Mensa 1 berechnen. (Diese alte
Klausuraufgabe ist nicht idiotisch, wie ein Prüfling in seiner Klausur vermerkte.)
3
Aufgabe 3
Der Warenkorb eines Durchschnittsdeutschen bestehe fiktiv aus Nahrungsmitteln, Miete
und Kleidung. Die 1980 erworbenen Mengen und Preise 1980 und 1988 lauteten:
1980
1988
Kategorie
Menge
Preis
Preis
Nahrungsmittel
200 kg
3 DM/kg
3,20 DM/kg
Miete
12 Monate
900 DM/Monat
980,-- DM/Monat
Kleidung
4 Stück
150 DM/Stück
180,-- DM/Stück
Stellen Sie einen Preisindex der Lebenshaltung für 1988 auf der Basis 1980 auf und
interpretieren Sie die Indexzahl.
Lösung:
Indices nach Toernquist, Laspeyres, Paasche, Fisher
Die Werte von p und q mit 3 Beobachtungen:
erst die Basis, dann die Vergleichswerte
1
2
3
p (Basis)
3.00 900.00 150.00
q (Basis)
200.00
12.00
4.00
p (Vergleich)
3.20 980.00 180.00
q (Vergleich)
200.00
12.00
4.00
s0 (Basis)
.0500
.9000
.0500
s1 (Vergleich)
.0488
.8963
.0549
Toernquist-Index (Preis)= 1.09334 (Menge)
= 1.00000
Preis-Index (Laspeyres) = 1.09333 (Paasche)
= 1.09333
(Fisher
) = 1.09333
Mengen-Index (Laspeyres)= 1.00000 (Paasche)
= 1.00000
(Fisher
)= 1.00000
NB:
Da
nur
eine
Menge
zur
Verfügung
steht,stimmen
Laspeyres
Mengenindex (formal) überein
und
Paasche
Eine Variante ist die folgende Aufgabe 3’:
Der Warenkorb eines Bewohners aus Land LLL bestehe aus Nahrung, Wohnung und
Kleidung. Die 1995 und 1996 erworbenen Mengen und Preise lauten:
Kategorie
Menge 1995
Preis 1995
Menge 1996
Preis 1996
Nahrung
200 kg
3 DM/kg
300 kg
2 DM/kg
Wohnung
1 Jahr
1000 DM/Monat
1 Jahr
1200 DM/Monat
Kleidung
5 Garnituren
200 DM/Garnitur
4 Garnituren
300 DM/Garnitur
Berechnen Sie einen Preisindex der Lebenshaltung Ihrer Wahl für 1996 auf der Basis von
1995 und interpretieren Sie die sich ergebende Indexzahl.
4
Aufgabe 4
In den Jahren 1970 bis 1973 seien von den folgenden Gütern jeweils die Menge q zum Preis
p abgesetzt worden:
1970 1971 1972 1973
Zement
Stahlbleche
Stahlträger
Bauholz
Ziegelsteine
q
10
11
12
13
p
1
2
3
4
q
1
2
4
8
p
3
3
3
3
q
5
5
5
5
p
2
4
8
16
q
10
10
12
15
p
25
20
15
10
q
3
7
12
18
p
40
20
10
5
Nehmen Sie an, der Index für Baustoffe setze sich aus den genannten Gütern zusammen.
a) Bestimmen Sie den Preisindex nach Laspeyres für Baustoffe für das Jahr 1972 zur
Basis 1970.
b) Bestimmen Sie den Mengenindex nach Paasche für Baustoffe für das Jahr 1973 zur
Basis 1971.
Geben Sie die Ergebnisse als Dezimalzahl an.
Aufgabe 5
Der Warenkorb eines Bewohners aus Land LLL bestehe aus Nahrung, Wohnung und
Kleidung. Die 1995 und 1996 erworbenen Mengen und Preise lauten:
Kategorie
Menge 1995
Preis 1995
Menge 1996
Preis 1996
Nahrung
200 kg
3 DM/kg
300 kg
2 DM/kg
Wohnung
1 Jahr
1000 DM/Monat
1 Jahr
1200 DM/Monat
Kleidung
5 Garnituren
200 DM/Garnitur
4 Garnituren
300 DM/Garnitur
Berechnen Sie einen Preisindex der Lebenshaltung Ihrer Wahl für 1996 auf der Basis von
1995 und interpretieren Sie die sich ergebende Indexzahl.
5
Aufgabe 6
Die jährlichen Ausgaben eines Mannes für Bekleidung sind in folgender Tabelle festgehalten:
1982
1985
1992
Menge
Preis
Menge
Preis
Menge
Preis
Schuhe
2
190
2
180
3
270
Anzüge
0.5
600
1
550
2
750
Hemden
12
80
10
90
15
150
Krawatten
5
55
3
50
15
95
a) Berechnen Sie die Preisindizes nach Laspeyres und nach Paasche für die Zeiträume von
1982 bis 1985 sowie 1982 bis 1992.
b) Berechnen Sie die Umsatzindizes für die Zeiträume von 1982 bis 1985 sowie 1982 bis
1992 und führen Sie eine Preisbereinigung dieser Umsatzentwicklungen mit Hilfe der
zugehörigen Paasche Preisindizes durch. Welche Mengenindizes erhalten Sie?
c) Bestimmen Sie die durchschnittlichen Preissteigerungsraten pro Jahr für die Zeit von
1982 bis 1992.
Aufgabe 7
Die Stadtwerke K versandten an den Haushalt H (so nach M. Missong, Aufgabensammlung zur deskriptiven Statistik, Aufgabe 7.4) folgende Abrechnungen:
Preis/m3, bzw /kwh
1991
1992
1993
Gas
1.50
1.55
1.60
Strom
0.18
0.21
0.25
Menge(m 3, bzw kwh)
1991
1992
1993
DM
55
57
60
m3
DM
800
1000
1200
kwh
a) Errechnen Sie für das Berichtsjahr 1993 die beiden Preis- und Mengen-Indizes
nach Paasche und Laspeyres mit 1991 als Basisjahr.
b) Welche Energieart ist vergleichsweise billiger geworden?
Aufgabe 8
Über Preise und Absatz von Milch, Butter und Käse (in kg) seien folgende Zahlen bekannt:
Preise
Mengen
1982
1983
1984
1982
1983
1984
Milch
0.98
1.02
1.10
9675
9717
10436
Butter
9.80
10.20
10.20
117
120
122
Käse
16.50
17.20
17.90
78
75
83
Errechnen Sie für das Jahr 1984 die beiden Preisindices nach Paasche und Laspeyres mit
1982 als Basisjahr.
6
Aufgabe 9
Für einen Zoo-Markt erweisen sich die hergestellten Hundehütten, Kaninchenställe und
Vogelbauer als "Renner". Mengen und Preise dieser Produkte sind für die Jahre 1985 und
1990 in der folgenden Tabelle festgehalten:
Produkte
1985
1990
Menge
Preis
Menge
Preis
(in Stück)
(in DM/Stück)
(in Stück)
(in DM/Stück)
Hundehütten
50
60.-
100
80.-
Kaninchenställe
100
20.-
120
20.-
Vogelbauer
100
30.-
250
50.-
a) Das Unternehmen berechnet zunächst einen Umsatz- oder Wertindex zur Basis
1985, um einen Überblick über die Umsatzentwicklung zwischen 1985 und 1990 zu
gewinnen. Welcher Indexwert wird berechnet?
b) In einem zweiten Schritt wird die reine Mengenentwicklung bestimmt. Dazu wird
der Umsatzindex mittels eines Paasche-Preisindex preisbereinigt. Führen Sie diese
Preisbereinigung durch; welche Mengenentwicklung ergibt sich?
c) Zeigen Sie, daß Sie mit der Berechnung eines Laspeyres-Mengenindex zum gleichen
Ergebnis gekommen wären.
Aufgabe 10
Ein Unternehmen handelt mit den Rohstoffen A, B, C und D. Die Entwicklung der
Verkaufspreise und Absatzmengen geht aus folgender Tabelle hervor:
Preis (DM/t)
Absatzmenge
(1000 t)
Rohstoff
1986
1991
1986
1991
A
60
70
100
120
B
80
90
150
120
C
90
120
80
75
D
400
500
20
20
a) Berechnen Sie die Mengenentwicklung im Berichtszeitraum anhand der Mengen
indices von Laspeyres und Paasche.
b) Erläutern Sie den Unterschied.
c) Berechnen Sie den Umsatzindex.
d) Berechnen Sie die Preisentwicklung im Berichtszeitraum anhand der Preisindices
von Laspeyres und Paasche.
e) Berechnen Sie die durchschnittliche jährliche Preissteigerungsrate nach Laspeyres.
7
Aufgabe 11
Zu den Warengruppen Nahrungsmittel (N), Getränke (G) und Tabakwaren(T) seien
folgende Preise (pro Mengeneinheit) und Mengen (in entsprechenden Einheiten) bekannt:
Preis
Menge
1987
1988
1989
1987
1988
1989
N
2.20
2.30
2.35
290
300
295
G
4.10
4.30
4.30
360
380
400
T
5.00
5.30
5.70
80
80
100
a) Bestimmen Sie die Preisindizes nach Laspeyres und Paasche von 1989 bezüglich des
Basisjahres 1987 bzw. 1988.
b) Welcher Laspeyres-Index P(L,t) ergäbe sich (unabhängig von den obigen Zahlen),
wenn der Tabakwarenpreis um 5% steigt, alle übrigen Preise unverändert bleiben
und das relative Gewicht von Tabakwaren im Warenkorb 0.1 ist?
c) Angenommen, P(L,t) zeige folgendes Verhalten:
Sinkt der Tabakwarenpreis gegenüber dem Basiszeitpunkt um 5% und bleiben alle
restlichen Preise unverändert, so ergibt sich P(L,t) = 0.996
Mit welchem relativen Gewicht ist dann das Gut 'Tabakwaren' im Warenkorb
vertreten?
Lösung zu a)
Indices nach Toernquist, Laspeyres, Paasche, Fisher
1
2
3
p (Basis)
2.20
4.10
5.00
q (Basis)
290.00 360.00
80.00
p (Vergleich)
2.35
4.30
5.70
q (Vergleich)
295.00 400.00 100.00
s0 (Basis)
.2538
.5871
.1591
s1 (Vergleich)
.2324
.5766
.1911
Toernquist-Index (Preis)= 1.06896 (Menge)
= 1.11019
Preis-Index (Laspeyres) = 1.06822 (Paasche)
= 1.06965
(Fisher
) = 1.06893
Mengen-Index (Laspeyres)= 1.10939 (Paasche)
= 1.11087
(Fisher
)= 1.11013
Indices nach Toernquist, Laspeyres, Paasche, Fisher
1
2
3
p (Basis)
2.30
4.30
5.30
q (Basis)
300.00 380.00
80.00
p (Vergleich)
2.35
4.30
5.70
q (Vergleich)
295.00 400.00 100.00
s0 (Basis)
.2511
.5946
.1543
s1 (Vergleich)
.2324
.5766
.1911
Toernquist-Index (Preis)= 1.01792 (Menge)
= 1.06663
Preis-Index (Laspeyres) = 1.01710 (Paasche)
= 1.01870
(Fisher
) = 1.01790
Mengen-Index (Laspeyres)= 1.06568 (Paasche)
= 1.06735
(Fisher
)= 1.06652
Lösung zu b) Sei pT1 = pT0 (1.05), dann 1.005, d.h. 5%o = 1/2%
Lösung zu c) 0.08
8
Aufgabe 12
Für die folgenden 3 Güter sei für 3 verschiedene Jahre jeweils die abgesetzte Menge q und
der Preis p gegeben:
1970
1973
1975
p
q
p
q
p
q
Feinzement
2
16
3
15
2
15
Kies
1
9
2
10
2
14
Kiefernholz
4
9
5
14
6
15
Berechnen Sie die Umsatzindices UL:= P L ⋅ Q P für die Jahre 1973 und 1975 zum Basisjahr
1970.
Aufgabe 12’
Auf die folgenden 4 Güter sei für 3 aufeinanderfolgende Jahre jeweils der Preis p und die
abgesetzte Menge q gegeben.
Jahr
1
2
3
Gut
p
q
p
q
p
q
Aluminium
1
9
2
10
2
13
Kupfer
2
16
3
15
2
15
Zinn
6
2
8
20
8
21
Zink
4
9
5
14
6
15
Wie groß ist der Preisindex für die Jahre 2 und 3 zum Basisjahr 1
a) nach Laspeyres
b) nach Paasche ?
9
Aufgabe 13
Von folgenden Getränkearten wurden in den angegebenen Zeitperioden die Mengen qk
(in 1000 Liter) zum Preis pk (in 1000 DM) abgesetzt; k = 1, 2, 3, 4:
Whiskey
Rotwein
Bier
Weinbrand
q1
p1
q2
p2
q3
p3
q4
p4
Jan. 1976
2
15
10
4
20
0.8
2
10
Dez. 1976
2
16
11
5
20
0.9
2
11
Jan. 1977
0.5
20
12
5
25
1.0
1
15
a) Berechen Sie mit Hilfe von Laspeyres-Indices die Preissteigerungsrate dieser Getränke,
und zwar:
aa)
für Januar 1977 gegenüber dem Vormonat,
ab)
für Januar 1977 gegenüber Januar 1976.
b) Berechnen Sie auch den Paasche-Index für Januar 1977 auf der Basis des Vormonats,
c) Welchen der beiden in aa) und b) berechneten Indices halten Sie als Index der
Konsumentenpreise für aussagekräftiger und warum?
Aufgabe 14
Für die Jahre 1970 bis 1973 werden der Preisindex der Lebenshaltungskosten und der
Preisindex für Agrarprodukte im Land D ermittelt:
1970
1971
1972
1973
Preisindex der Lebenshaltung
100
95
105
170
Preisindex für Agrarprodukte
140
100
120
180
a) Welche Indexreihe zeigt den größten relativen Preisanstieg?
b) Sie sollen die Interessen der Lanswirtschaft nun gegenüber der Regierung des
Landes D vertreten. Wie würden Sie die Daten verändern, um Subventionen
besonders notwendig für die Landwirtschaft erscheinen zu lassen?
10
Aufgabe 15
Über das Konsumverhalten eines Haushalts zu vier Gütern (A,B,C,D) liegen folgende
Informationen vor:
Jahr
Preis des Gutes
A
B
gekaufte Menge des Gutes
C
D
A
B
C
D
1970
5
2
5
4
4
5
6
8
1971
5
5
6
5
8
6
5
10
1972
5
8
10
10
8
5
5
7
Berechnen Sie folgende Indices für t = 1971 und t =1972 (jeweils zur Basis 1970):
a) die Preisindices PtL von Laspeyres und PtP von Paasche,
b) den Preisindex PtF :=
p tL .p tP von Fisher.
Aufgabe 15’ (eine Teil-Aufgabe zu der vorherigen)
Für den Warenkorb eines Einwohners der Stadt S kommen nur drei wichtige Güter, nämlich
A, B und C in Betracht, und es liegen folgende Informationen vor:
Jahr
1990
1991
1992
Preis des Gutes
A
B
C
5
2
5
5
5
6
5
8
10
gekaufte Menge des Gutes
A
B
C
4
5
6
8
6
5
8
5
5
a) Bestimmen Sie den Laspeyres-Preisindex des Warenkorbs für 1992 auf der Basis von
1990.
b) Wie ändert sich Ihr Ergebnis, wenn Gut C statt 10 Geldeinheiten in 1992 sich auf 20
Geldeinheiten verdoppelt?
c) Wie ändert sich Ihr Ergebnis, wenn alle Güter in 1992 sich im Preis verdoppeln;
d.h. auf 10, 16 und 20?
d) Wie ändert sich Ihr Ergebnis, falls statt der Basis 1990 die Basis 1991 gewählt wird?
Lösung:
a) P = 2, b) P = 3 (Ein steigender (sinkender) Preis läßt den Index steigen (sinken).),
c) P = 4 (Bei allseits verdoppelten Preisen ist der Index gleichfalls doppelt so hoch.)
11
Aufgabe 16
Für einen Vergleich der Lebenshaltungskosten in Deutschland (D) und Belgien (B) benutzen
Sie bitte die beiden folgenden typischen Hauhaltsausgabeübersichten. Die belgischen
Ausgaben sind bereits über den Wechselkurs in DM umgerechnet.
Brot
Fleisch
Butter
Obst &
Wein
Milch
Gemüse
Preise D
3.20
12.00
8.00
4.00
6.00
1.10
Menge D
400
130
60
400
80
250
Preise B
2.60
16.50
7.20
3.60
9.30
1.05
Menge B
600
80
50
550
20
300
a) Bestimmen Sie für beide Länder den Preisindex nach Laspeyres und Paasche, in dem Sie
den Warenkorb des jeweilig anderen Landes als Basis nehmen.
b) Beantworten Sie, ob es finanziell besser ist, bei einem Umzug den eigenen Warenkorb
beizubehalten oder sich den landesüblichen Eßgewohnheiten anzupassen.
c) Können Sie mit entsprechenden Überlegungen dem Bonner Beamten, der nach Berlin
umziehen “muß”, einen geeigneten Ratschlag für die Umstellung von der rheinischen zur
Berliner Küche erteilen?
Lösung zu 3:
a) Es gibt zwei Indexberechnungen, eine mit Basis D und eine mit Basis B:
Basis D: Preis-Index (Laspeyres)
= 1.06846 ←
Preis-Index (Paasche)
= 0.96476
Preis-Index (Fisher )
= 1.01528
∴ für einen deutschen Haushalt ist das Haushalten nach deutschem Schema etwas
ungünstiger in Belgien; d.h. 7% (der deutsche Warenkorb nach belgischen Preisen)
Basis B: Preis-Index (Laspeyres)
= 1.03653 ←
Preis-Index (Paasche)
= .93593
Preis-Index (Fisher )
= .98495
∴ für einen belgischen Haushalt ist das Haushalten nach belgischem Schema in Deutschland
teuerer als in Belgien, nämlich um 4% (der belgische Warenkorb nach deutschen Preisen)
b) folgt aus a)
c) Hier ist i.R. kein Ratschlag möglich, denn das Statistische Bundesamt differenziert den
Lebenhaltungskostenindex nicht nach Bundesländern. Möglicherweise gibt es aber Überlegungen in den Statistischen Landesämtern, d.h. es kommt also darauf an. Daß auch kleine
Regionen eigene Indices haben, dazu siehe Luxemburg im Vergleich zu Deutschland.
Aufgabe 17
Im Land El Paradiso besteht der Warenkorb eines Einwohners nur aus zwei Gütern Milch
und Honig. Trotz des schönen Landesnamens gibt es beide nicht umsonst, sondern sind mit
der Landeswährung £ zu bezahlen. Die 1985 und 1990 erworbenen Mengen und Preise sind
wie folgt:
1985
1990
Gut
Menge Preis
Menge
Preis
Milch
100 l
2 £/l
80 l
3 £/l
Honig
20 kg
5 £/kg
30 kg
4 £/kg
Bestimmen Sie einen Laspeyres-Preisindex für die Lebenshaltung für 1990 auf der Basis von
1985 und erklären Sie die Bedeutung der errechneten Indexzahl.
12
Aufgabe 18
Bewerten und vergleichen Sie über eine Preisindexberechnung die Kostensituation einer
Firma, die in den zwei vergangenen Jahren im wesentlichen von den folgenden fünf Grundstoffen abhing:
Grundstoff 1
Grundstoff 2
Grundstoff 3
Grundstoff 4
Grundstoff 5
Preise Jahr 1
12
27
4
40
16
Menge Jahr 1
85
40
18
8
22
Preise Jahr 2
17
26
3
58
18
Menge Jahr 2
95
45
20
10
22
Lösung zu 18:
Indices nach Laspeyres, Paasche, Fisher
Die Werte von p und q mit 5 Beobachtungen: erst die Basis, dann die Vergleichswerte
1
2
3
4
5
p (Basis)
12.00
27.00
4.00
40.00
16.00
q (Basis)
85.00
40.00
18.00
8.00
22.00
p (Vergleich)
17.00
26.00
3.00
58.00
18.00
q (Vergleich)
95.00
45.00
20.00
10.00
22.00
Preis-Index (Laspeyres)
Mengen-Index (Laspeyres)
= 1.19515; (Paasche) = 1.19893; (Fisher)= 1.19704
= 1.12060; (Paasche) = 1.12415; (Fisher)= 1.12238
Indices nach Laspeyres, Paasche, Fisher
Die Werte von p und q mit 5 Beobachtungen: erst die Basis, dann die Vergleichswerte
1
2
3
4
5
p (Basis)
17.00
26.00
3.00
58.00
18.00
q (Basis)
95.00
45.00
20.00
10.00
22.00
p (Vergleich)
12.00
27.00
4.00
40.00
16.00
q (Vergleich)
85.00
40.00
18.00
8.00
22.00
Preis-Index (Laspeyres)
Mengen-Index (Laspeyres)
= 0.83407; (Paasche) = 0.83672; (Fisher) = 0.83539
= 0.88956; (Paasche) = 0.89238; (Fisher)= 0.89097
13
Aufgabe 19
Im unruhegeschüttelten Reformstaat Novo-Macedonia ändern sich, wie die folgende Tabelle
zweier aufeinander folgenden Monate zeigt, die Preise außerordentlich schnell:
Gut des
Warenkorbs
A
B
C
D
E
Preise pro Mengeneinheit
Januar Februar
1,50
1,20
2,00
3,00
10,00
8,00
1,50
2,00
4,50
5,00
Mengeneinheiten
Januar
Februar
800
900
500
400
50
60
150
100
80
100
Die Weltbank wird Novo-Macedonia nur dann einen zugesagten Kredit von $100 Mio.
auszahlen, wenn die Inflation unter 5% pro Monat ist. Um die Bank von der Erfüllung dieser
Kondition zu überzeugen, bittet der Vertraute des Ministerpräsidenten daher bei einem
Abendessen den Präsidenten des international als unabhängig geachteten Statistischen
Landesamt mit einem geeigneten Preisindex an die Öffentlichkeit zu treten.
a)
Welchen Preisindex wird das Amt publizieren?
b)
Gibt es überhaupt einen solchen Preisindex, der die Kondition erfüllt?
Lösung zu 19:
Gut des
Warenkorbs
A
B
C
D
E
∑
Menge Januar mit Preis
Januar Februar
1200
960
1000
1500
500
400
225
300
360
400
3285
3560
Menge Februar mit Preis
Januar
Februar
1350
1080
800
1200
600
480
150
200
450
500
3350
3460
Preisindex (Laspeyres): 3560 / 3285 ≈ 1,083
Preisindex (Paasche): 3460 / 3350 ≈ 1,033, dieser Index erfüllt die Bedingung
14
Aufgabe 20
In den Jahren 1970 bis 1972 seien von den folgenden Gütern jeweils die Menge q zum Preis p
abgesetzt worden:
Butter
Mehl
Eier
Brot
p
q
p
q
p
q
p
q
1970
5
2
10
5
7
4
11
2
1971
7
3
13
4
6
5
8
4
1972
10
2
15
7
5
7
10
5
a) Berechnen Sie für die angegebenen Güter den Preisindex
aa) nach Laspeyres für das Jahr 1972 zur Basis 1970
ab) nach Paasche für das Jahr 1972 zur Basis 1971
b) Der Mengenindex LQ0t nach Laspeyres und der Mengenindex PQ0t nach Paasche werden
wie folgt berechnet, wobei der Subskript i das Gut i bezeichnet (i=1,2,3,4=m) und t die Zeit:
m
Σ
LQ0t
=
m
Σ qt,i ⋅ pt,i
qt,i ⋅ p0,i
i=1
m
Σ q0,i ⋅ p 0,i
i=1
, PQ0t =
i=1
m
Σ q 0,i ⋅ p t,i
i=1
Berechnen Sie für die angegebenen Güter den Mengenindex
ba) nach Laspeyres für das Jahr 1971 zur Basis 1970
bb) nach Paasche für das Jahr 1972 zur Basis 1970
c) Der Umsatzindex U0,t berechnet sich nach
m
Σ p t,i ⋅ qt,i
U0,t =
i=1
m
Σ p0.i ⋅ q0,i
i=1
ca) Berechnen Sie den Umsatzindex U für das Jahr 1971 zur Basis 1970.
cb) Zeigen Sie, daß gilt: LU01 = LP01 . PQ01
d) Eine Verständisfrage:
Um festzustellen, ob eine Umsatzsteigerung ausschließlich durch Preissteigerungen
hervorgerufen wird oder ob auch Mengensteigerungen erfolgt sind, führt man die
sogenannte Preisbereinigung des Umsatzes durch. Dazu dividiert man den Umsatzindex
durch einen Preisindex.
Führen Sie eine solche Preisbereinigung des Umsatzes sowohl mit dem Laspeyres-Preisindex
als auch mit dem Paasche-Preisindex durch und vergleichen Sie die Ergebnisse mit dem
Paasche- bzw. dem Laspeyres-Mengenindex.
15
Aufgabe 21
Der Autonarr Ottokar Raser möchte wissen, wie sich die Unterhaltskosten für sein Auto seit
1992 entwickelt haben. Er hat folgende Daten festgestellt:
Produkte
Preis 1992
Preis 1993
Menge 1992
Menge 1993
Benzin
1.4
1.5
4500
4600
Wartungen
130
140
2
2
Reparaturen
140
250
1
3
Steuer, Vers.
800
820
1
1
a) Berechnen Sie Laspeyres- und Paasche Preisindex für das Jahr 1993 mit der Basis 1992.
b) Wie groß ist die Umsatzänderung von 1992 bis 1993?
c) Welcher Anteil der Umsatzänderung ist auf reine Mengenänderung zurückzuführen,
wenn Sie die Preise des Jahres 1993 als Gewichtung verwenden?