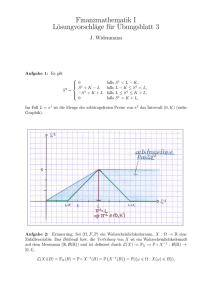
Wahrscheinlichkeitstheorie Fakultät für Mathematik Bergische

Wahrscheinlichkeitstheorie
Fakultät für Mathematik
Bergische Universität Wuppertal
Martin Friesen1
Letzte Version vom
7. Februar 2017
1
[email protected]
Inhaltsverzeichnis
1 Grundbegriffe der Wahrscheinlichkeitstheorie
1.1 Wahrscheinlichkeitsräume, Zufallsvariablen und Erwartungswerte
1.2 Konvergenzbegriffe . . . . . . . . . . . . . . . . . . . . . . . . . .
1.3 Beispiele von Wahrscheinlichkeitsräumen . . . . . . . . . . . . . .
1.4 Charakteristiken von Zufallsvariablen . . . . . . . . . . . . . . . .
.
.
.
.
1
1
5
9
16
2 Unabhängigkeit und bedingte Erwartungswerte
2.1 Unabhängigkeit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.2 Bedingte Erwartungswerte . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
22
22
28
3 Schwache Konvergenz
3.1 Konvergenz von Wahrscheinlichkeitsmaßen . . . . . . . . . . . . . . . . . . . . . .
3.2 Konvergenz von Zufallsvariablen . . . . . . . . . . . . . . . . . . . . . . . . . . .
33
35
45
4 Charakteristische Funktionen
4.1 Fouriertransformation von Funktionen . . . . . . . . . . . . . . . . . . . . . . . .
4.2 Charakteristische Funktion für Maße . . . . . . . . . . . . . . . . . . . . . . . . .
4.3 Charakteristische Funktion für Zufallsvariablen . . . . . . . . . . . . . . . . . . .
47
48
52
60
5 Grenzwertsätze
5.1 Gesetze der großen Zahlen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.2 Zentraler Grenzwertsatz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.3 Weitere Grenzwertsätze . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
63
63
68
73
6 Grundlagen stochastischer Prozesse
6.1 Konstruktion stochastischer Prozesse . . . . . . . . . . . . . . . . . . . . . . . . .
6.2 Eigenschaften stochastischer Prozesse . . . . . . . . . . . . . . . . . . . . . . . .
6.3 Stoppzeiten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
81
81
85
88
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
7 Martingale
91
7.1 Martingale in diskreter Zeit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 95
7.2 Martingale in stetiger Zeit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 103
8 Appendix
118
i
1
Grundbegriffe der Wahrscheinlichkeitstheorie
1.1
Wahrscheinlichkeitsräume, Zufallsvariablen und Erwartungswerte
Definition 1.1. Ein Wahrscheinlichkeitsraum ist ein Maßraum pΩ, F, Pq mit PpΩq “ 1.
Hier und im Folgenden bezeichnet pΩ, F, Pq einen Wahrscheinlichkeitsraum. Wir führen die
Folgende Notation ein:
• Ω – Ereignisraum
• ω P Ω – Elementarereignis
• A P F – Ereignis
• P – Wahrscheinlichkeitsmaß
• PpAq – Wahrscheinlichkeit von A.
• Ac – Ereignis A tritt nicht ein.
• A Y B – A oder B treten ein.
• A X B – A und B treten ein.
• A Ă B – A impliziert B.
Man beachte
0 ≤ PpAq ≤ PpAq ` PpAc q “ PpA Y Ac q “ 1
sowie
PpAc q “ PpΩzAq “ PpΩq ´ PpAq “ 1 ´ PpAq.
Für eine Folge von Mengen pAn qnPN Ă F gilt
˜
¸
8
ď
ÿ
P
An ≤
PpAn q.
n“1
nPN
Eine Menge N P F heißt Nullmenge, falls PpN q “ 0 gilt. Wir sagen, dass eine Eigenschaft fast
sicher gilt, falls es eine Menge Nullmenge N P F gibt und die Eigenschaft für alle ω R N erfüllt
ist.
Definition 1.2. Eine (reellwertige) Zufallsvariable, ist eine messbare Abbildung X : Ω ÝÑ R.
Für eine nicht-negative Zufallsvariable (d.h. X ≥ 0 fast sicher), ist der Erwartungswert definiert
über
ż
ż
EpXq :“ XdP :“ XpωqdPpωq.
Ω
Ω
Eine Zufallsvariable X heißt integrierbar, falls
ż
Ep|X|q “ |X|dP ă 8.
Ω
1
Es sei L1 “ L1 pΩ, Pq “ L1 pΩ, F, Pq die Menge aller reellwertigen, integrierbaren Zufallsvariablen. Für X P L1 ist der Erwartungswert definiert durch
ż
EpXq :“ XdP.
Ω
Man beachte, dass für X “ 1 gilt
Ep1q “ PpΩq “ 1.
Es ist nicht schwer zu zeigen, dass L1 ein Vektorraum ist und der Erwartungswert die folgenden
Eigenschaften hat (siehe Maßtheorie)
(a) Der Erwartungswert ist linear, d.h. sind X, Y P L1 und a, b P R, so gilt
EpaX ` bY q “ aEpXq ` bEpY q.
(b) Der Erwartungswert ist monoton, d.h. sind X, Y P L1 mit X ≤ Y fast sicher, so gilt
EpXq ≤ EpY q.
(c) Sei X P L1 und N P F eine Nullmenge, dann gilt
EpX 1N q “ 0.
Insbesondere: Ist Y eine weitere Zufallsvariable mit X “ Y fast sicher, so gilt
EpXq “ EpY q.
Analog definieren wir die Lp -Räume für p P p0, 8q. Genauer, sei Lp der Vektorraum aller Zufallsvariablen mit
1
}X}Lp :“ pEp|X|p qq p .
Für p “ 8 sei L8 der Raum der wesentlich beschränkten Zufallsvariablen. Eine Zufallsvariable
heißt wesentlich beschränkt falls
}X}L8 :“ ess sup |Xpωq| :“
ωPΩ
inf
sup |Xpωq| ă 8.
N PF , PpN q“0 ωPΩzN
Dann ist L8 ein Vektorraum.
Beispiel 1.3. Sei Ω “ r0, 1s, F “ Bpr0, 1sq, P “ m das Lebesgue Maß und für r P R sei
#
1
ω‰0
r,
Xpωq :“ ω
.
0,
ω“0
r “ 0: Dann ist X P Lp für alle p P r1, 8s.
r ‰ 0: Dann ist X R L8 . Für p ‰ 8 gilt
ż
p
ω ´rp mpdωq.
Ep|X| q “
p0,1s
Das rechte Integral ist endlich genau dann, wenn rp ă 1, d.h. X P Lp falls rp ă 1.
2
Lemma 1.4. Sei h : R ÝÑ R eine konvexe Funktion und X P L1 mit hpXq P L1 . Dann gilt
hpEpXqq ≤ EphpXqq.
Beweis. Da h konvex ist, gibt es eine affin lineare Funktion g mit g ≤ h und gpEpXqq “ hpEpXqq
(Stützgerade). Es folgt
hpEpXqq “ gpEpXqq “ EpgpXqq ≤ EphpXqq.
Korollar 1.5. Für alle 1 ≤ p ≤ q ≤ 8 gilt
}X}Lp ≤ }X}Lq
und somit ist Lq Ă Lp ein Teilvektorraum.
q
Beweis. Die Funktion hpxq :“ |x| p ist für 1 ≤ p ≤ q ă 8 konvex. Es folgt mit Y :“ |X|p
q
q
pEp|X|p qq p “ hpEpY qq ≤ EphpY qq “ Ep|Y | p q “ Ep|X|q q
und somit die Behauptung im Fall q ă 8. Für 1 ≤ p ă q “ 8 folgt aus der Monotonie des
Erwartungswertes
1
}X}Lp “ pEp|X|p qq p ≤ }X}L8 .
Satz 1.6. (Markovsche Ungleichung) Sei X eine Zufallsvariable und h ≥ 0 monoton steigend.
Dann gilt für alle c ą 0
hpcqPpX ≥ cq ≤ EphpXqq.
(1.1)
Insbesondere gilt die Markovsche Ungleichung
Pp|X| ≥ εq ≤
1
Ep|X|p q, ε ą 0.
εp
(1.2)
Weiterhin, sei X ≥ 0 fast sicher mit EpXq “ 0. Dann gilt X “ 0 fast sicher.
Beweis. Die Ungleichung (1.1) folgt aus
hpcqPpX ≥ cq ≤ hpcqPphpXq ≥ hpcqq “ Ephpcq1hpXq≥hpcq q ≤ EphpXqq.
Die Ungleichung (1.2) ist eine Folgerung für den Spezialfall hpxq “ |x|p . Wir zeigen die letzte
Behauptung. Aus (1.2) mit p “ 1 und ε “ n1 folgt für alle n ≥ 1 mit |X| “ X fast sicher
ˆ
˙
1
P X≥
≤ nEpXq “ 0.
n
Daraus folgt
*¸
ˆ
˙
8
ď"
ÿ
1
1
≤
P X≥
“0
PpX ą 0q “ P
X≥
n
n
n“1
n≥1
˜
und somit PpX “ 0q “ 1.
3
Lemma 1.7. Sei 1 ≤ p ≤ 8. Dann ist } ¨ }Lp eine Halbnorm, d.h. für X, Y P Lp und a P R gilt
(a) }aX}Lp “ |a|}X}Lp
(b) }X ` Y }Lp ≤ }X}Lp ` }Y }Lp .
(c) Ist }X}Lp “ 0 so ist X “ 0 fast sicher.
Beweis. Eigenschaft (a) folgt aus der Linearität des Erwartungswerts. Eigenschaft (b) ist die
Minkowski Ungleichung, siehe Maßtheorie oder Funktionalanalysis. Wir zeigen daher nur (c).
p ă 8: In diesem Fall folgt aus }X}Lp “ 0 auch
Ep|X|p q “ 0.
Damit folgt |X|p “ 0 fast sicher und somit X “ 0 fast sicher.
p “ 8: In diesem Fall gibt es zu jedem n P N ein Nn P F mit PpNn q “ 0 und
sup |Xpωq| ă
ωPΩzNn
Es sei N :“
Ť
1
.
n
Nn , dann ist N P F und es gilt
nPN
PpN q ≤
8
ÿ
PpNn q “ 0.
n“1
Ferner gilt für alle ω P ΩzN bereits
|Xpωq| ă
1
, @n ≥ 1
n
und damit X “ 0 fast sicher.
Es sei
N :“ tX Zufallsvariable mit X “ 0 fast sicher u .
Dann definiert
X „ Y ðñ X ´ Y P N
eine Äquivalenzrelation auf Lp für alle 1 ≤ p ≤ 8. Es sei Lp :“ Lp {N der Raum der Äquivalenzklassen
von Zufallsvariablen. Jedes rXs P Lp hat demnach einen Repräsentanten X P Lp . Der Erwartungswert ist definiert über
EprXsq :“ EpXq
und sei
}rXs}Lp :“ }X}Lp .
Da keine Verwechslung besteht, schreiben wir oft auch X anstelle von rXs, wo X ein Repräsentant von X ist. Man beachte, dass eine Äquivalenzklasse rXs nicht punktweise ausgewertet werden kann. D.h. rXspωq macht (im Allgemeinen) keinen Sinn. Wählen wir hingegen
einen Repräsentanten X von rXs, so ist Xpωq wohldefiniert.
Warnung: Ist X 1 ein weiterer Repräsentant, so ist X 1 pωq ‰ Xpωq möglich. Die Menge aller
solchen ω ist jedoch eine Nullmenge.
4
Satz 1.8. Sei 1 ≤ p ≤ 8. Dann ist pLp , } ¨ }Lp q ein Banachraum. Ist p “ 2, so ist L2 ein
Hilbertraum mit Skalarprodukt
xrXs, rY syL2 :“ EprX ¨ Y sq.
Satz 1.9. (Cauchy-Schwartz Ungleichung) Sind X, Y P L2 , so gilt X ¨ Y P L1 und
a
a
Ep|X ¨ Y |q ≤ Ep|X|2 q Ep|Y |2 q.
Diesselbe Aussage gilt für L2 und L1 anstelle von L2 und L1 .
Satz 1.10. (Hölder Ungleichung) Seien 1 ≤ p, q ≤ 8 mit
X P Lp , Y P Lq . Dann gilt X ¨ Y P L1 und
1
p
`
1
q
“ 1 ( wo
1
8
:“ 0 ) und
}X ¨ Y }L1 ≤ }X}Lp }Y }Lq .
Diesselbe Aussage gilt für Lp , Lq , L1 anstelle von Lp , Lq , L1 .
1.2
Konvergenzbegriffe
Wir wollen einige Resultate aus der Integrationstheorie wiederholen.
Definition 1.11. Seien pXn qnPN und X Zufallsvariablen.
(a) pXn qnPN konvergiert fast sicher gegen X, falls
´
¯
P lim Xn “ X “ 1.
nÑ8
(b) pXn qnPN konvergiert in Wahrscheinlichkeit gegen X, falls für alle ε ą 0
lim P p|Xn ´ X| ≥ εq “ 0.
nÑ8
(c) pXn qnPN konvergiert im p-ten Mittel (bzw. in Lp ) gegen X (wo p P p0, 8q), falls
Ep|Xn ´ X|p q ÝÑ 0, n Ñ 8.
Bemerkung 1.12. (a) Gilt Xn ÝÑ X in L1 , so konvergiert auch die Folge der Erwartungswerte pEpXn qqnPN gegen EpXq. Die Umkehrung ist im Allgemeinen falsch.
(b) Gilt Xn ÝÑ X in Lq , so gilt auch Xn ÝÑ X in Lp für alle 1 ≤ p ≤ q ≤ 8.
Der nächste Satz zeigt, dass unter der zusätzlichen Bedingung, dass die Folge pXn qnPN eine
Majorante besitzt, fast sichere Konvergenz die Konvergenz in L1 impliziert.
Satz 1.13. (Satz von Lebesgue, Satz der dominierten Konvergenz) Sei pXn qnPN Ă L1 eine Folge
von Zufallsvariablen und X P L1 . Es gebe Y P L1 mit
|Xn | ≤ Y, n ≥ 1
fast sicher
und Xn ÝÑ X fast sicher. Dann gilt Xn ÝÑ X in L1 .
5
Korollar 1.14. (Satz von Lebesgue für Lp ) Sei pXn qnPN eine Folge von Zufallsvariblen mit
Xn ÝÑ X fast sicher. Es gebe ein Y P Lp mit p P r1, 8q und |Xn | ≤ Y fast sicher. Dann gilt
Xn ÝÑ X in Lp .
Beweis. Es gilt |Xn ´ X|p ÝÑ 0 fast sicher. Folglich gibt es M P F mit PpM q “ 1 und n0 P N
mit
|Xpωq| ≤ |Xpωq ´ Xn pωq| ` |Xn pωq| ≤ 1 ` Y pωq, ω P M, n ≥ n0 .
Somit gilt für n ≥ n0 , ω P M mit pa ` bqp ≤ 2p´1 pap ` bp q
|Xn ´ X|p ≤ p|Xn | ` |X|qp ≤ p1 ` 2Y qp ≤ 2p´1 p1 ` 2p Y p q P L1 .
Die Behauptung folgt aus dem Satz von Lebesgue für p “ 1.
Satz 1.15. (Satz von Beppo-Levi, Satz der monotonen Konvergenz) Sei pXn qnPN eine Folge
nicht-negativer Zufallsvariablen mit Xn ≤ Xn`1 und Xn Õ X fast sicher, wo X eine weitere
Zufallsvariable ist. Dann gilt
EpXn q ÝÑ EpXq, n Ñ 8.
Korollar 1.16. Sei pXn qnPN eine Folge nicht-negativer Zufallsvariablen. Dann gilt
˜
¸
8
8
ÿ
ÿ
E
Xn “
EpXn q.
n“1
(1.3)
n“1
Hierbei ist 8 “ 8 zugelassen und die linke Seite ist endlich genau dann,
ř wenn die rechte Seite
endlich ist. Ist pXn qnPN eine Folge reellwertiger Zufallsvariablen mit 8
n“1 Ep|Xn |q ă 8 so gilt
(1.3) und beide Seiten sind endlich.
Beweis. Übung.
Lemma 1.17. (Lemma von Fatou) Sei pXn qnPN eine Folge nicht-negativer Zufallsvariablen.
Dann gilt
´
¯
E lim inf Xn ≤ lim inf EpXn q.
nÑ8
nÑ8
Satz 1.18. Seien pXn qnPN und X, Y Zufallsvariablen und p P p0, 8q. Dann gelten die folgenden
Aussagen:
(a) Angenommen Xn ÝÑ X fast sicher, dann gilt Xn ÝÑ X in Wahrscheinlichkeit.
(b) Angenommen Xn ÝÑ X in Lp , dann gilt Xn ÝÑ X in Wahrscheinlichkeit.
(c) Angenommen Xn ÝÑ X und Xn ÝÑ Y in Wahrscheinlichkeit. Dann gilt X “ Y fast
sicher.
Beweis. (a) Sei Yn :“ 1|Xn ´X|≥ε mit ε ą 0 fest. Dann gilt Yn ≤ 1 und Yn ÝÑ 0 fast sicher. Aus
dem Satz von Lebesgue folgt
Pp|Xn ´ X| ≥ εq “ EpYn q ÝÑ 0, n Ñ 8.
6
(b) Die Markovsche Ungleichung impliziert
Pp|Xn ´ X| ≥ εq ≤
1
Ep|Xn ´ X|p q ÝÑ 0, n Ñ 8.
εp
(c) Für alle ε ą 0 gilt
Pp|X ´ Y | ≥ εq ≤ Pp|Xn ´ X| ` |Xn ´ Y | ≥ εq
´!
ε )¯
ε) !
Y |Xn ´ Y | ≥
≤ P |Xn ´ X| ≥
2
2¯
´
´
ε¯
ε
≤ P |Xn ´ X| ≥
` P |Xn ´ X| ≥
ÝÑ 0, n Ñ 8.
2
2
Beispiel 1.19. Alle anderen Implikationen sind im Allgemeinen falsch. Sei hierzu pΩ, F, Pq “
pr0, 1s, Bpr0, 1sq, mpdxqq.
1
(a) Sei Xn “ n p 1r0, 1 s . Dann ist Xn P Lp mit Xn ÝÑ 0 fast sicher und damit auch in Wahrn
1
scheinlichkeit. Aber Ep|Xn |p q “ n1 pn p qp “ 1 zeigt, dass pXn qnPN nicht in Lp konvergiert.
(b) Sei
Xn :“ 1k2´m ,pk`1q2´m q , n “ 2m ` k, m P N0 , 0 ≤ k ă 2m .
Dann gilt
Pp|Xn | ≥ εq ≤ Pp|Xn | ą 0q “ 2´m ÝÑ 0, n Ñ 8
und
Ep|Xn |p q “ Pp|Xn | ą 0q “ 2´m .
Folglich gilt Xn ÝÑ 0 in Lp und in Wahrscheinlichkeit. Wir zeigen, dass pXn pωqqnPN für
kein ω P r0, 1q konvergiert. Sei ω P r0, 1q fixiert. Für jedes m P N finden wir genau ein
k “ kpω, mq mit ω P rk2´m , pk ` 1q2´m q. Also gilt Xkpω,mq`2m pωq “ 0. Für alle anderen
0 ≤ k 1 ă 2m ist Xk1 `2m pωq “ 0. Damit kann pXn pωqqnPN nicht konvergieren.
Im Folgenden betrachten wir die Konvergenz in Wahrscheinlihkeitstheorie und fast sichere
Konvergenz genauer.
8
ř
Lemma 1.20. (Erstes Borel-Cantelli Lemma) Sei pAn qnPN Ă F mit
PpAn q ă 8. Dann gilt
n“1
Pplim sup An q “ 0.
nÑ8
Hierbei ist lim sup An “
nÑ8
Ş Ť
Ak .
n≥1 k≥n
Ť
Beweis. Seien Bn :“
Ak . Dann ist Bn eine fallende Folge (d.h. Bn`1 Ă Bn für alle n ≥ 1)
k≥n
Ş
und es gilt
Bn “ lim sup An , d.h. Bn Œ lim sup An . Es folgt
n≥1
nÑ8
nÑ8
Pplim sup An q “ lim PpBn q ≤ lim
nÑ8
nÑ8
nÑ8
7
8
ÿ
k“n
PpAk q “ 0.
Satz 1.21. Sei pXn qnPN mit Xn ÝÑ X in Wahrscheinlichkeit. Dann gibt es eine Teilfolge
pnk qkPN mit Xnk ÝÑ X fast sicher.
Beweis. Da Xn ÝÑ X in Wahrscheinlichkeit, finden wir zu jedem k P N ein nk P N mit
ˆ
˙
1
1
P |Xnk ´ X| ≥
≤ 2.
k
k
Ohne Einschränkung der Allgemeinheit sei nk ă nk`1 für alle k. Setze M :“ lim sup Ak mit
kÑ8
(
1
´
X|
≥
AŤk :“
|X
.
Nach
dem
ersten
Borel-Cantelli
Lemma
folgt
PpM
q
“
0.
Für
ω P Mc “
n
k
k
Ş c
Ak , d.h. es gibt ein npωq ≥ 1 sodass für alle k ≥ npωq gilt: |Xnk pωq ´ Xpωq| ă k1 . Also
n≥1 k≥n
gilt
lim Xnk pωq “ Xpωq, ω P M c .
kÑ8
Satz 1.22. (Vollständigkeit bei fast sicherer Konvergenz) Sei pXn qnPN eine Folge von Zufallsvariablen mit
|Xn ´ Xm | ÝÑ 0, n, m Ñ 8
fast sicher.
(1.4)
Dann gibt es eine Zufallsvariable X mit Xn ÝÑ X fast sicher.
Beweis. Sei M P F mit PpM q “ 1 derart, dass (1.4) für jedes ω P M gilt. Da R vollständig ist,
gibt es für jedes ω P M einen Grenzwert Xpωq :“ lim Xn pωq. Für ω R M setze Xpωq :“ 0. Wir
nÑ8
zeigen, dass X messbar ist, dann folgt Xn ÝÑ X fast sicher und somit die Behauptung.
Sei X|M : M ÝÑ R, ω ÝÑ Xpωq “ lim Xn pωq. Dann ist X|M als Grenzwert messbarer
nÑ8
Abbildungen messbar bezüglich
F X M :“ tA X M | A P Fu.
Wegen M P F gilt F X M Ă F und damit ist X|M auch messbar bezüglich F. Die Darstellung
X “ 1M X|M ` 1M c ¨ 0
zeigt, dass X messbar ist.
Satz 1.23. (Vollständigkit bei Konvergenz in Wahrscheinlichkeit) Sei pXn qnPN mit
lim Pp|Xn ´ Xm | ≥ εq “ 0, @ε ą 0.
n,mÑ8
Dann gibt es eine Zufallsvariable X mit Xn ÝÑ X in Wahrscheinlichkeit.
Beweis. Sei pXnk qkPN eine Teilfolge mit
˙
ˆ
1
1
P |Xnk ´ Xnk`1 | ≥ 2 ≤ 2 .
k
k
8
Setze Ak “ t|Xnk ´ Xnk`1 | ≥
1
u
k2
und M :“ lim sup An . Nach dem ersten Borel-Cantelli Lemma
nÑ8
Ť Ş c
gilt PpM q “ 0, also PpM c q “ 1. Für jedes ω P M c “
Ak gibt es ein npωq ≥ 1 sodass für
n≥1 k≥n
alle k ≥ npωq
1
.
k2
eine Cauchy Folge in R. Sei Xpωq :“ lim Xnk pωq für alle ω P M c . Für
|Xnk pωq ´ Xnk`1 pωq| ă
Damit ist pXnk pωqqkPN
kÑ8
ω P M setze Xpωq :“ 0. Dann ist X eine Zufallsvariable mit Xnk ÝÑ X fast sicher. Es bleibt
zu zeigen, dass Xn ÝÑ X in Wahrscheinlichkeit konvergiert. Sei n P N und nk ≥ n, dann ist
Pp|Xn ´ X| ≥ εq ≤ Pp|Xn ´ Xnk | ` |Xnk ´ X| ≥ εq
´!
ε) !
ε )¯
≤ P |Xn ´ Xnk | ≥
Y |Xnk ´ X| ≥
2
2¯
´
´
ε¯
ε
≤ P |Xnk ´ X| ≥
` P |Xn ´ Xnk | ≥
.
2
2
Mit n, k Ñ 8 folgt die Behauptung.
1.3
Beispiele von Wahrscheinlichkeitsräumen
Diskreter Wahrscheinlichkeitsräume
Wir beginnen mit einem einfachen Beispiel mit einer ”diskreten” Wahrscheinlichkeitsverteilung.
Beispiel 1.24. (Punktmaß) Es sei ω P Ω fest. Dann defininiert
#
1, ω P A
δω pAq :“
0, ω R A
ein Wahrscheinlichkeitsmaß auf Ω. Die σ-Algebra F kann hierbei beliebig gewählt werden. Für
eine Zufallsvariable X auf Ω ist der Erwartungswert (für P “ δω ) gegeben durch
EpXq “ Xpωq.
Der folgende Satz erweitert obiges Beispiel auf abzählbar viele Punktmaße.
Satz 1.25. Sei pωn qnPN Ă Ω und ppn qnPN Ă r0, 1s. Dann definiert für jede σ-Algebra F auf Ω
8
ÿ
P“
pn δωn ,
n“1
ein Maß auf Ω. Dieses ist ein Wahrscheinlichkeitsmaß genau dann, wenn
1 “ PpΩq “
8
ÿ
n“1
9
pn .
(1.5)
Sei X eine Zufallsvariable. Dann ist X P L1 genau dann, wenn
8
ř
|Xpωn q|pn ă 8 gilt. In
n“1
diesem Fall ist das Integral bezüglich P gegeben durch
ż
8
ÿ
XdP “
Xpωn qpn .
(1.6)
n“1
Ω
Beweis. P ist eine positive Linearkombination von Maßen und damit wieder ein Maß. Die zweite
Behauptung ist offensichtlich. Für die letzte Behauptung zeigen wir zuerst (1.6) für alle nichtnegativen, messbaren Funktionen.
N
ř
ak 1A mit Ak P F und ak ≥ 0. Dann gilt
Fall 1: Sei X “
k“1
ż
XdP “
N
ÿ
ż
ak
k“1
Ω
N
ÿ
“
k“1
ak
1Ak dP “
N
ÿ
ak PpAk q
k“1
Ω
8
ÿ
pn δωn pAk q “
n“1
8
ÿ
n“1
pn
N
ÿ
ak 1Ak pωn q “
8
ÿ
Xpωn qpn .
n“1
k“1
Fall 2: Sei X ≥ 0 messbar, dann gibt es eine Folge von Zufallsvariablen pXn qnPN wie in Fall 1
mit Xn Õ X für n Ñ 8. Folglich gilt
8
ÿ
EpXn q “
Xn pωk qpk , n ≥ 1.
k“1
Beide Seiten sind monoton steigend in n. Aus dem Satz der monotonen Konvergenz folgt (1.6)
für alle Zufallsvariablen X ≥ 0. Insbesondere ist die linke Seite endlich genau dann, wenn die
rechte Seite endlich ist.
Fall 3: Es sei X eine beliebige Zufallsvariable. Wenden wir (1.6) für |X| an, so folgt X P L1
8
ř
genau dann wenn
|Xpωn q|pn ă 8. Zerlegen wir X “ X ` ´ X ´ mit X ˘ ≥ 0 in Positiv- und
n“1
Negativteil, so folgt
EpXq “ EpX ` q ´ EpX ´ q “
8
ÿ
X ` pωn qpn ´
n“1
8
ÿ
X ´ pωn qpn “
n“1
8
ÿ
Xpωn qpn .
n“1
Das folgende Beispiel ist ein Spezialfall von (1.5).
Beispiel 1.26. (diskrete Gleichverteilung) Sei Ω ist eine endliche Menge mit Potenz-σ-Algebra
F “ 2Ω . Die diskrete Gleichverteilung ist dadurch festgelegt, dass jedes Elementarereignis diesselbe Wahrscheinlichkeit hat, d.h. Pptωuq “ a für ein geeignetes a P r0, 1s und alle ω P Ω gilt.
1
, d.h.
Wegen PpΩq “ 1 folgt a “ |Ω|
Pptωuq “
1
, ω P Ω,
|Ω|
10
wo |Ω| :“
ř
1 die Anzahl der Elemente in Ω bezeichnet. Für eine Menge A Ă Ω gilt demnach
ωPΩ
ÿ
Pptωuq “
PpAq “
ωPA
|A|
.
|Ω|
Das so definierte Maß hat die Darstellung
1 ÿ
δω pAq.
|Ω| ωPΩ
PpAq “
Für eine Zufallsvariable X gilt demnach
ż
1 ÿ
XdP “
Xpωq.
|Ω| ωPΩ
Ω
Das Nachfolgende ist eine Verallgemeinerung und folgt aus Satz 1.25.
Korollar 1.27. Sei Ω eine höchstens abzählbare Menge und F die Potenz-σ-Algebra of Ω. Dann
gelten die folgenden Aussagen.
ř
ppωq “ 1. Dann definiert
(a) Sei p : Ω ÝÑ r0, 1s mit
ωPΩ
ÿ
ppωq, A Ă Ω
PpAq “
(1.7)
ωPA
ein Wahrscheinlichkeitsmaß auf Ω.
(b) Jedes Wahrscheinlichkeitsmaß P auf Ω ist von der Form (1.7) für eine geeignete Funktion
p : Ω ÝÑ r0, 1s.
ř
|Xpωq|ppωq ă 8 gilt
Für eine Zufallsvariable X mit
ωPΩ
ż
XdP “
ÿ
Xpωqppωq.
ωPΩ
Ω
Beweis. (a) P gegeben durch (1.7) hat die Darstellung
ÿ
PpAq “
ppηqδη pAq.
ηPΩ
Die Behauptung folgt aus Satz 1.25
(b) Sei P ein Wahrscheinlichkeitsmaß auf Ω und A Ă Ω. Dann gilt
˜
¸
ď
ÿ
PpAq “ P
tωu “
Pptωuq.
ωPA
ωPA
Also gilt (1.7) mit ppωq :“ Pptωuq. Die Identität (1.8) folgt aus Satz 1.25.
11
(1.8)
Beispiel 1.28. (Münzwurf ) Sei Ω “ t0, 1u mit F “ 2Ω . Hierbei steht 0 f ür Kopf und 1 für
Zahl. Unter der Annahme, dass die Münze fair ist (beide Ausgängesind gleich wahrscheinlich),
wählen wir P als diskrete Gleichverteilung auf Ω, d.h.
1
1
P “ δ0 ` δ1 .
2
2
Führen wir n ≥ 1 Münzwürfe mit derselben Münze aus, so wählen wir F “ 2Ω mit
Ω “ t0, 1un “ tω “ pω1 , . . . , ωn q | ωk P t0, 1u, k “ 1, . . . , nu.
Das Wahrscheinlichkeitsmaß ist demnach gegeben durch die Gleichverteilung auf Ω, d.h.
Pptωuq “
1
,
2n
siehe (1.7). Die Zufallsvariable
Xpωq “
n
ÿ
ωk
k“1
gibt demnach die absolute Häufigkeit von Zahl an. Um den Erwartungswert zu bestimmen betrachten wir die disjunkte Zerlegung
Ω“
n
ď
Ak , Ak “ tω P Ω | Xpωq “ ku.
k“0
Dann gilt |Ak | “
`n˘
k
und demnach
ˆ ˙
n
n
1 ÿ
1 ÿ ÿ
1 ÿ
n
n
EpXq “ n
Xpωq “ n
Xpωq “ n
k
“ .
2 ωPΩ
2 k“0 ωPA
2 k“0 k
2
k
Beispiel 1.29. (unfairer Münzwurf ) Führen wir n ≥ 1 Münzwürfe mit derselben Münze aus,
so wählen wir F “ 2Ω mit
Ω “ t0, 1un “ tω “ pω1 , . . . , ωn q | ωk P t0, 1u, k “ 1, . . . , nu.
Wir nehmen an, dass die Wahrscheinlichkeit Kopf (also 0) zu werfen gegeben ist durch p P r0, 1s.
Die Wahrscheinlichkeit Zahl (also 1) zu werfen, ist demnach 1 ´ p. Das Wahrscheinlichkeitsmaß
ist gegeben durch
n
ř
Pptωuq “ pk“1
Wir betrachten wir die Ereignisse
#
Ak “
ωPΩ|
p1´ωk q
n
ÿ
n
ř
p1 ´ pqk“1
ωk
, ω P Ω.
+
ωj “ k , k “ 1, . . . , n.
j“1
Dann gilt |Ak | “
`n˘
k
. Die Wahrscheinlichkeit k-mal Zahl zu werfen ist gegeben durch
n
ř
ÿ
PpAk q “
p
j“1
n
ř
p1´ωj q
p1 ´ pq
ωPAk
12
j“1
ωj
ˆ ˙
n n´k
“
p
p1 ´ pqk .
k
Beispiel 1.30. (Binomial Verteilung) Sei n ≥ 1 und p P r0, 1s. Wähle Ω “ t0, . . . , nu, F “ 2Ω
und
n ˆ ˙
ÿ
n n´k
P“
p
p1 ´ pqk δk
k
k“0
Dann heißt P Binomialverteilung auf t0, . . . , nu.
Beispiel 1.31. (Poisson Verteilung) Sei Ω “ R` mit F “ BpR` q. Die Poisson Verteilung mit
Parameter λ ą 0 ist gegeben durch
P “ e´λ
8
ÿ
λk
δk .
k!
k“0
Kontinuierliche Wahrscheinlichkeitsräume auf R
In diesem Abschnitt wollen wir Beispiele für Wahrscheinlichkeitsräume auf R betrachten. Hierfür
betrachten wir das Lebesgue Maß mpdxq auf R mit Borel-σ-Algebra BpRq erzeugt durch die
offenen Mengen im R.
Beispiel 1.32. (uniforme Verteilung) Es sei Ω Ă R messbar und
F “ tA P BpRq | A Ă Ωu
die Menge aller Borel messbaren Mengen in Ω. Die uniforme Verteilung auf Ω ist gegeben durch
ż
1
mpAq
PpAq :“
1A pxqmpdxq “
.
mpΩq
mpΩq
Ω
Obige Definition kürzen wir ab mit Ppdxq “
1
1
mpΩq Ω pxqmpdxq.
Beispiel 1.33. (Cauchy Verteilung) Es sei Ω “ R und Ppdxq “ ppxqmpdxq mit c ą 0, a P R
und
1
c
ppxq “
, x P R,
π c2 ` px ´ aq2
d.h.
ż
ppxqmpdxq, A P BpRq.
PpAq “
A
Dann ist P ein Wahrscheinlichkeitsmaß und es gilt
ż
|x|k ppxqmpdxq “ 8, k ≥ 1.
R
Beispiel 1.34. (Normalverteilung auf R) Es sei Ω “ R und Ppdxq “ ppxqmpdxq mit µ P R,
σ 2 ą 0 und
px´µq2
1
ppxq “ ?
e´ 2σ2 , x P R.
2πσ 2
13
Dann ist P ein Wahrscheinlichkeitsmaß mit
ż
xppxqmpdxq “ µ
R
und
ż
px ´ µq2 ppxqmpdxq “ σ 2 .
R
Obige Situation lässt sich abstrakt in folgender Definition zusammenfassen.
Definition 1.35. Seien P, Q zwei Wahrscheinlichkeitsmaße auf einem Maßraum pΩ, Fq. Q heißt
absolut stetig bezüglich P, falls für jedes A P F gilt
PpAq “ 0 ùñ QpAq “ 0.
Bemerkung 1.36. Obige Definition ist äquivalent zu: Für alle ε ą 0 gibt es ein δ ą 0 mit
PpAq ă ε ùñ QpAq ă δ,
@A P F.
Sei g : Ω ÝÑ R` integrierbar bezüglich P und sei
ż
QpAq :“ gpωqPpdωq, A P F.
A
Dann ist Q ein Maß und Q ist absolut stetig bezüglich P. Die Umkehrung ist im nachfolgenden
Satz formuliert.
Satz 1.37. (Satz von Radon-Nikodym) Seien P, Q zwei Wahrscheinlichkeitsmaße auf Ω. Die
folgenden Aussagen sind äquivalent:
(a) Q ist absolut stetig bezüglich P.
(b) Es gibt eine bezüglich P integrierbare Funktion
ż
QpAq “
dP
dQ
≥ 0 mit
dP
dP, A P F.
dQ
(1.9)
A
Ist g eine weitere bezüglich P integrierbare Funktion mit (1.9). Dann gilt
*˙
ˆ"
dP
pωq
“ 1.
P
ω P Ω | gpωq “
dQ
Die Funktion
dP
dQ
wird Radon-Nikodym Ableitung (bzw. Dichte) von P bezüglich Q genannt.
Definition 1.38. Ein Wahrscheinlichkeitsmaß P auf R hat eine Dichte, falls es absolut stetig
dP
bezüglich mpdxq ist. Die Dichte p ist definiert als die Radon-Nikodym Ableitung p “ dm
14
Satz 1.39. Sei g ≥ 0 messbar und
ż
gpωqdPpωq, A P F.
QpAq :“
A
Dann gilt für jede Zufallsvariable X
ż
1
X P L pΩ, F, Qq ðñ
|Xpωq|gpωqdPpωq ă 8.
Ω
In diesem Fall gilt
ż
EQ pXq :“
ż
XpωqdQpωq “
Ω
XpωqgpωqdPpωq.
Ω
Beweis. Übung.
Kontinuierliche Wahrscheinlichkeitsräume auf Rd
d
d
ř
Es sei |a| :“
a2k die euklidische Norm von a “ pa1 , . . . , ad q P Rd . Eine messbare Abbildung
k“1
d
R heißt
X : Ω ÝÑ
Rd -werige Zufallsvariable. Häufig lassen wir den Zusatz Rd -wertig weg,
sofern dieses aus dem Zusammenhang hervorgeht. Eine solche Abbildung hat eine Darstellung
in Komponenten über
Xpωq “ pX1 pωq, . . . , Xd pωqq,
wo Xj : Ω ÝÑ R Abbildungen sind.
Bemerkung 1.40. Sei X “ pX1 , . . . , Xd q : Ω ÝÑ Rd eine Abbildung. Dann sind äquivalent:
(a) X ist eine Rd -wertige Zufallsvariable.
(b) X1 , . . . , Xd sind Zufallsvariablen.
Lemma 1.41. Es sei X “ pX1 , . . . , Xd q eine Rd -wertige Zufallsvariable und p P r1, 8s. Dann
gilt
|X| P Lp ðñ Xk P Lp , k “ 1, . . . , d.
Beweis. Es reicht zu zeigen, dass
ż
ż
|X|p dP ă 8 ðñ |Xk |p dP ă 8, k “ 1, . . . , d.
Ω
ˆ
Es gilt
|X|p
“
d
ř
Ω
˙ p2
|Xk
|2
. Daraus folgt
k“1
˜
p
2
|Xk |p “ p|Xk |2 q ≤
d
ÿ
k“1
15
¸ p2
|Xk |2
“ |X|p .
Andererseits gilt auch
˜ ˆ
˙2 ¸ p2
ˆ
˙p
d
p
p ÿ
p
|X| ≤ d max |Xk |
“ d2
max |Xk | ≤ d 2
|Xk |p .
k“1,...,d
k“1,...,d
k“1
Für p P p0, 8q sei Lp pΩ, F, P; Rd q “ Lp pΩ; Rd q der Vektorraum der Rd -wertigen Zufallsvariablen mit
}X}Lp :“ Ep|X|p q ă 8.
Für p “ 8 sei L8 pΩ, F, P; Rd q “ L8 pΩ; Rd q der Vektorraum der Rd -wertigen Zufallsvariablen
mit
}X}L8 :“
inf
sup |Xpωq| ă 8.
N PF , PpN q“0 ωPΩzN
Analog zu dem eindimensionalen Fall lassen sich die Räume Lp pΩ; Rd q definieren. Diese sind
Banachräume.
Bemerkung 1.42. Es sei X P L2 pΩ; Rd q. Dann gilt
g
f d
2
2
ÿ
|Xk | ` |Xj |
1
1f
|Xk ¨ Xj | ≤
|Xk |2 “ |X|2 P L1 .
≤ e
2
2 k“1
2
Also gilt Xj ¨ Xk P L1 für alle j, k “ 1, . . . , d. Umgekehrt, gilt Xk ¨ Xj P L1 für alle j, k “ 1, . . . , d,
so ist offensichtlich X P L2 pΩ; Rd q.
Definition 1.43. Sei X “ pX1 , . . . Xd q eine Rd -wertige Zufallsvariable mit X P L1 pΩ; Rd q.
Dann ist der Erwartungswert definiert durch
EpXq :“ pEpX1 q, . . . , EpXd qq.
Zufallsvariablen mit Werten in messbaren Räumen
1.4
Charakteristiken von Zufallsvariablen
Definition 1.44. Sei pΩ, F, Pq ein Wahrscheinlichkeitsraum, pΩ1 , F 1 q ein messbarer Raum und
ϕ : Ω ÝÑ Ω1 messbar. Das Bildmaß P ˝ ϕ´1 auf pΩ1 , F 1 q ist definiert über
pP ˝ ϕ´1 qpAq “ Ppϕ´1 pAqq, A P F 1 .
(1.10)
Der nächste Satz folgt aus standard Argumenten der Maß und Integrationstheorie.
Satz 1.45. Sei pΩ, F, Pq ein Wahrscheinlichkeitsraum, pΩ1 , F 1 q ein messbarer Raum und ϕ :
Ω1 ÝÑ Ω messbar. Dann ist f : Ω1 ÝÑ R genau dann integrierbar bezüglich P ˝ ϕ´1 , wenn f ˝ ϕ
integrierbar ist bezüglich P. In diesem Fall gilt
ż
ż
f pϕpωqqPpdωq “ f pω 1 qpP ˝ ϕ´1 qpdω 1 q.
Ω
Ω1
16
Definition 1.46. (multivariate Normalverteilung)
(a) Die Standardnormalverteilung auf Rd ist gegeben durch ein WahrscheinlichkeitsmaßP auf
Rd mit Dichte
|x|2
d
ppxq :“ p2πq´ 2 e´ 2 , x P Rd .
(b) Es sei A eine reelle d ˆ d-Matrix und b P Rd . Sei T pxq :“ Ax ` b die dazugehörige affine
Abbildung. Dann heißt P ˝ T ´1 (multivariate) Normalverteilung, wo P gegeben ist wie in
(a).
Satz 1.47. Es gelten die folgenden Aussagen.
(a) Sei A invertierbar. Dann hat P ˝ T ´1 eine Dichte gegeben durch
1
1
d
dpP ˝ T ´1 q
t ´1
pxq “ p2πq´ 2 pdetpAAt qq´ 2 e´ 2 xpx´bq,pAA q px´bqy , x P Rd .
dm
Hierbei bezeichnet At die zu A transponierte Matrix und x¨, ¨y das Skalarprodukt im Rd .
(b) Ist A nicht invertierbar, so ist ImpT q eine Nullmenge bezüglich m und P ˝ T ´1 ist nicht
absolut stetig bezüglich m.
(c) Die Klasse der Normalverteilungen ist invariant unter affin linearen Transformationen
Rd ÝÑ Rd . Genauer, sei T pxq “ Ax ` b mit A eine d ˆ d-Matrix, b P Rd und sei ν eine
(multivariate) Normalverteilung. Dann ist ν ˝ T ´1 eine (multivariate) Normalverteilung
auf Rd .
Beweis. (a) Sei A invertierbar. Dann ist auch Σ :“ AAt invertierbar mit Σ´1 “ pAt q´1 A und
es gilt T ´1 pyq “ A´1 py ´ bq “ A´1 y ´ A´1 b. Aus der Translationsinvarianz von m und dem
Transformationssatz folgt für jedes Rechteck im Rd
pm ˝ T ´1 qpRq “ mpT ´1 pRqq “ detpA´1 qmpRq “ detpAq´1 mpRq.
Da Rechtecke einen X-stabilen Erzeuger der Borel-σ-Algebra bilden folgt
pm ˝ T ´1 qpBq “ detpAq´1 mpBq, B P BpRd q.
Also ist m ˝ T ´1 absolut stetig bezüglich m und es gilt mit dem Determinanten Produktsatz
1
dpm ˝ T ´1 q
“ detpA´1 q “ pdetpΣqq´ 2 .
dm
17
Die Behauptung folgt aus
ż
pP ˝ T
´1
ż
1B pxqpP ˝ T qpdxq “
´1
qpBq “
ż
1B pT pxqqp2πq´ 2 e´ 2 |T
d
“
1B pT pxqqPpdxq
Rd
Rd
1
´1 T x|2
mpdxq
Rd
ż
1B pyqp2πq´ 2 e´ 2 |T
d
“
1
´1 y|2
pm ˝ T ´1 qpdyq
Rd
ż
d
´1 py´bqy
p2πq´ 2 e´xy´b,Σ
“
1
pdetpΣqq´ 2 mpdyq.
B
Definition 1.48. Ein Polnischer Raum E ist ein topologischer Raum E derart dass eine Metrik
auf E existiert sodass
• Die Topologie auf E stimmt mit der durch die Metrik induzierte Topologie überein.
• E ist seperabel und vollständig bezüglich dieser Metrik.
Im folgenden Betrachten wir einige Beispiele für Polnische Räume.
Beispiel 1.49. Kontinuierliche Polnische Räume sind E “ R` und E “ Rd . Diskrete Polnische
Räume sind E “ Z` oder E “ Zd mit d ≥ 1. Die Metrik ist in allen Fällen gegeben durch
g
f d
fÿ
dpx, yq :“ e
|xk ´ yk |2 , x, y P E.
k“1
Beachte, dass im diskreten Fall jede Teilmenge A Ă E offen ist. Abzählbare Produkte von Polnischen Räumen sind wieder Polnisch, sofern diese mit der Produkttopologie versehen sind.
Insbesondere ist also
RZ` :“ tpxn qn≥0 | xn P Ru
ein Polnischer Raum.
Von besonderem Interesse sind hierbei Funktionenräume. Zufallsvariablen mit Werten in solchen Räumen können als stochastische Prozesse bzw. stochastische Felder interpretiert werden.
Man beachte, dass jeder seperable Banachraum ein Polnischer Raum ist.
Beispiel 1.50. Sei 1 ≤ p ă 8. Der Raum der Äquivalenzklassen Funktionen f mit
¨
˛1
p
ż
p
˝
‚
}f }Lp :“
|f pxq| mpdxq
Rd
wird mit Lp pRd , mpdxqq bezeichnet. Dieser ist Ein seperabler Banachraum und folglich ein Polnischer Raum, siehe [Wer00, Seite 33]. Insbesondere ist der Raum der quadratintegrierbaren
Funktionen E “ L2 pRd , mpdxqq ein Polnischer Raum.
18
Beispiel 1.51. Ist T ein kompakter metrischer Raum, so ist
CpT q :“ tf : T ÝÑ R | f ist stetig u
mit
}f }8 :“ sup |f ptq|
tPT
ein seperabler topologischer Raum, siehe [Wer00, Seite 33]. Man wähle zum Beispiel T “ r0, 1s.
Zufallsvariablen mit Werten in Cpr0, 1sq, d.h. X : Ω ÝÑ Cpr0, 1sq können somit als zufällige
Funktionen Xt : Ω ÝÑ R aufgefasst werden.
Beispiel 1.52. Der Raum Cpr0, 8qq mit der durch die Metrik
dpf, gq :“
8
ÿ
1 dk pf, gq
, dk pf, gq :“ sup |f pxq ´ gpxq|
2k 1 ` dk pf, gq
xPr0,ks
k“1
erzeugten Topologie ist ein Polnischer Raum.
Zufallsvariablen mit Werten in Räumen von Maßen treten in der Theorie der Punktprozesse
häufig auf. Genauer Betrachten wir Räume von Punktmaßen.
Beispiel 1.53. Der Raum der endlichen Punktmaße (bzw. der Raum aller endlichen Punktkonfigurationen) auf Rd ist definiert durch
: 0 :“ tη : BpRd q ÝÑ N0 | η ist endliches Maßu.
Γ
: 0 hat eine eindeutige Darstellung der Form
Behauptung: Jedes η P Γ
η“
N
ÿ
n k δ xk ,
k“1
wo N P N, n1 , . . . , nN P N und x1 , . . . , xN P Rd paarweise verschieden sind. Die Punkte
x1 , . . . , xN heissen Atome von η.
Beweis. Sei A :“ tx P Rd | ηptxuq ≥ 1u. Angenommen A enthält unendlich viele Elemente.
Dann gibt es eine Folge paarweise verschiedener Elemente pxn qnPN Ă A. Für diese Folge gilt
8
ÿ
8“
ηptxn uq “ ηttxn | n P Nuq ≤ ηpAq ≤ ηpRd q ă 8.
n“1
Also enthält A nur endlich viele Elemente. Sei A “ tx1 , . . . , xN u für paarweise verschiedene
x1 , . . . , xN P Rd und N P N0 . Definiere
µ :“ η ´
N
ÿ
k“1
19
nk δxk
mit nk :“ ηptxk uq. Dann fölgt für B P BpRd q aus ηpB X txk uq “ nk δxk pBq bereits
µpBq “ ηpBq ´
N
ÿ
nk δxk pBq ≥ ηpA X Bq ´
N
ÿ
ηpB X txk uq ´
k“1
nk δxk pBq
k“1
k“1
“
N
ÿ
N
ÿ
nk δxk pBq “ 0.
k“1
Damit ist µ ≥ 0 und folglich ein Maß mit Werten in N0 derart dass µptxuq “ 0 für alle x P Rd
gilt. Wir zeigen
µpBq “ 0, B P BpRd q
woraus die Behauptung folgt. Es gilt µpBq “ lim µpB X BR q, wo BR “ tx P Rd | |x| ≤ Ru.
RÑ8
Da µpB X BR q P N0 , gibt es ein R ą 0 derart dass µpBq “ µpB X BR q. Für jedes x P Rd
gilt µpBε pxqq Œ µptxuq “ 0 für ε Ñ 0. Wegen µpBε pxqq P N0 gibt es ein εpxq ą 0 derart,
dass µpBεpxq pxqq “ 0 gilt. Da B X BR beschränkt und abgeschlossen ist, ist diese Menge auch
kompakt. Wegen
ď
B X BR Ă
Uεpxq pxq
xPBXBR
mit Uεpxq pxq “ ty P
Rd
| |y ´ x| ă εpxqu gibt es endlich viele Punkte x1 , . . . , xm derart, dass
B X BR Ă
m
ď
m
ď
Uεpxj q pxj q Ă
Bεpxj q pxj q.
j“1
j“1
Daraus folgt
µpBq “ µpB X BR q ≤ µpB X BR q ≤
m
ÿ
µpBεpxj q pxj qq “ 0.
j“1
Der Raum der endlichen Teilmengen von Rd (bzw. der Raum der endlichen Konfigurationen)
ist gegeben durch
#
+
ÿ
d
Γ0 :“ η Ă R | |η| :“
1ă8 .
xPη
Jedes η P Γ0 kann vermöge
ř
: 0 identifiziert werden.
δx mit einem Element in Γ
xPη
Es sei Cc pRd q der Raum der stetigen Funktionen f : Rd ÝÑ R mit kompaktem Träger. Eine
Funktion f : Rd ÝÑ R hat kompakten Träger, falls es ein R ą 0 gibt mit f pxq “ 0 für alle
|x| ≥ R.
Beispiel 1.54. Der Raum aller lokal endlichen Teilmengen von Rd (bzw. lokal endlichen Konfigurationen) ist definiert durch
Γ :“ tγ Ă Rd | |γ X K| ă 8 K Ă Rd kompakt u.
20
Jedes γ P Γ kann vermöge
ř
xPγ
δx mit einem lokal endlichen Punktmaß auf Rd identifiziert werden.
Für jedes f P Cc pRd q sei
If pγq :“
ż
ÿ
f pxq “
xPγ
f pxqγpdxq
Γ
das Integral von f bezüglich des Punktmaßes γ. Die Topologie auf Γ ist definiert als die kleinste
Topologie derart, dass alle Abbildungen If stetig sind. Es lässt sich zeigen, dass Γ bezüglich
dieser Topologie ein Polnischer Raum ist, siehe [KK06].
Die Erweiterung auf alle lokal endlichen Punktmaße wird im nächsten Beispiel behandelt.
Beispiel 1.55. Der Raum aler lokal endlichen Punktmaße ist gegeben durch
: :“ tp
Γ
γ : BpRd q ÝÑ N0 Y t8u | γ
ppKq ă 8, K Ă Rd kompakt u.
: hat die Darstellung
Behauptung: Jedes γ
pPΓ
ÿ
p“
γ
nk δ x ,
xPγ
wo nx P N0 und γ P Γ.
Beweis. Sei BN :“ tx P Rd | |x| ≤ N u wo N P N. Dann ist
8
ď
d
R “
pBN `1 zBN q
N “0
eine disjunkte Zerlegung von Rd , wo B0 :“ H. Folglich gilt für jedes B P BpRd q
8
ÿ
ppBq “
γ
pppBN `1 zBN q X Bq.
γ
N “0
pN pBq :“ γ
pppBN `1 zBN q X Bq. Dann ist γ
p “
Sei γ
: 0 für alle N ≥ 0. Folglich gibt es
γ
pN P Γ
mit kpN q P N und N P N0 derart, dass
pN “
γ
8
ř
N “0
pN q
pN q
n1 , . . . , nkpN q
kpN
ÿq
pN q
nj
und es ist nicht schwer zu sehen, dass
δxpN q , N ≥ 0.
j
j“1
21
pN q
pN q
P N0 sowie x1 , . . . , xkpN q P BN `1 zBN
2
2.1
Unabhängigkeit und bedingte Erwartungswerte
Unabhängigkeit
Definition 2.1. Sei I eine beliebige Indexmenge.
(a) Eine Familie von Ereignissen tAi | i P Iu Ă F heißt unabhängig, wenn
¸
˜
ź
č
PpAj q
Aj “
P
jPJ
jPJ
für alle endlichen Teilmengen J Ă I gilt.
(b) Die Familie heißt paarweise unabhängig, wenn
PpAi X Aj q “ PpAi qPpAj q, @i, j P I, i ‰ j.
Bemerkung 2.2. Unabhängigkeit impliziert paarweise unabhängigkeit. Die Umkehrung ist im
Allgemeinen falsch.
Beispiel 2.3.
(a) Sei Ω “ t1, 2, 3, 4u mit F “ 2Ω und Gleichverteilung P auf Ω. Seien
A “ t1, 2u, B “ t2, 3u, C “ t1, 3u.
Dann gilt
PpAq “ PpBq “ PpCq “
1
2
und
1
PpA X Bq “ PpA X Cq “ PpB X Cq “ .
4
D.h. die Ereignisse sind paarweise unabhängig. Die Ereignisse sind nicht unabhängig, da
ˆ ˙3
1
PpA X B X Cq “ 0 ‰
“ PpAqPpBqPpCq.
2
(b) Sei I “ t1, 2u mit Mengen A1 , A2 . Dann ist Unabhängigkeit äquivalent zu
PpA1 X A2 q “ PpA1 qPpA2 q.
(c) Sei I “ t1, 2, 3u mit Mengen A1 , A2 , A3 . Dann ist Unabhängigkeit äquivalent zu PpA1 X
A2 q “ PpA1 qPpA2 q, PpA1 X A3 q “ PpA1 qPpA3 q, PpA2 X A3 q “ PpA2 qPpA3 q und
PpA1 X A2 X A3 q “ PpA1 qPpA2 qPpA3 q.
Definition 2.4. Sei I eine Indexmenge und für i P I seien Mengensysteme Ei Ă F gegeben. Die
Familie tEi | i P Iu heißt unabhängig, wenn für jede Wahl Ai P Ei die Familie tAi | i P Iu von
Ereignissen unabhängig ist.
Äquivalent: Für jede endliche Teilmenge J Ă I und jede Wahl Aj P Ej mit j P J gilt
˜
¸
č
ź
P
Aj “
PpAj q.
jPJ
jPJ
22
Bemerkung 2.5.
(a) Seien pΩi , Fi , Pi q mit i “ 1, . . . , n Wahrscheinlichkeitsräume. Setze Ω “ Ω1 ˆ ¨ ¨ ¨ ˆ Ωn mit
n
n
Â
Â
F“
Fi und P “
Pi . Seien Mengen Ai gegeben durch
i“1
i“1
A1 :“ B1 ˆ Ω2 ˆ ¨ ¨ ¨ ˆ Ωn , B1 P F1
¨¨¨
An :“ Ω1 ˆ ¨ ¨ ¨ ˆ Bn , Bn P Fn .
Dann ist die Familie tA1 , . . . , An u unabhängig unter P.
(b) tEi | i P Iu ist unabhängig genau dann, wenn tEi | i P Ju für alle endlichen Teilmengen
J Ă I unabhängig ist.
(c) Ist Ai Ă Ei für alle i P I, so gilt
tEi | i P Iu ist unabhängig ùñ tAi | i P Iu ist unabhängig.
Die Umkehrung ist im Allgemeinen falsch.
Satz 2.6. Sei tEi | i P Iu eine unabhängige Familie. Dann ist auch die Familie der erzeugten
Dynkin-Systeme tdpEi q | i P Iu unabhängig.
Beweis. Wegen Bemerkung 2.5 sei ohne Einschränkung I endlich mit I “ t1, . . . , nu. Für i0 P I
sei
Di0 :“ tA P F | tE1 , . . . , Ei0 ´1 , tAu, Ei0 `1 , . . . , En u ist unabhängige Familieu.
Wir zeigen, dass Di0 ein Dynkin-System ist. Hierfür sei ti1 , . . . , ik u Ă Izti0 u beliebig und wähle
Aiν P Eiν , wo ν “ 1, . . . , k.
1. Da die kleinere Auswahl von Mengen auch unabhängig ist, folgt
PpAi1 X ¨ ¨ ¨ X Aik X Ωq “ PpAi1 q ¨ ¨ ¨ PpAik q ¨ 1.
Also ist Ω P Di0 .
2. Sei A P Di0 . Dann ist
PpAi1 X ¨ ¨ ¨ X Aik X Ac q “ PpAi1 X ¨ ¨ ¨ X Aik X Ωq ´ PpAi1 X ¨ ¨ ¨ X Aik X Aq
“ PpAi1 q ¨ ¨ ¨ PpAik qp1 ´ PpAqq “ PpAi1 q ¨ ¨ ¨ PpAik qPpAc q
und folglich Ac P Di0 .
3. Seien Bl P Di0 mit l P N disjunkt. Dann ist
˜
¸
˜
¸
8
8
ď
ď
P Ai1 X ¨ ¨ ¨ X Aik X
Bl “ P
Ai1 X ¨ ¨ ¨ X Aik X Bl
l“1
8
ÿ
“
l“1
PpAi1 X ¨ ¨ ¨ X Aik X Bl q “
l“1
8
ÿ
PpAi1 q ¨ ¨ ¨ PpAik q ¨ PpBl q
l“1
˜
8
ď
“ PpAi1 q ¨ ¨ ¨ PpAik qP
¸
Bl
l“1
23
und folglich
8
Ť
Bl P Di0 .
l“1
Damit ist Di0 ein Dynkin System und tE1 , . . . , Ei0 ´1 , Di0 , Ei0 `1 , . . . , En u ist eine unabhängige
Familie. Es gilt Ei0 Ă Di0 und da Di0 ein Dynkin System ist, folgt Ei0 Ă dpEi0 q Ă Di0 . Nach Bemerkung 2.5 ist tE1 , . . . , Ei0 ´1 , dpEi0 q, Ei0 `1 , . . . , En u eine unabhängige Familie. Da i0 P I beliebig
war, folgt die Behauptung durch Induktion.
Korollar 2.7. Sei tEi | i P Iu eine unabhängige Familie von X-stabilen Mengensystemen mit
Ei Ă F. Dann ist tσpEi q | i P Iu eine unabhängige Familie von σ-Algebren.
Satz 2.8. Sei tAi | i P Iu unabhängig mit Ai P F. Für jedes i P I seien A˚i P tH, Ai , Aci , Ωu.
Dann ist tA˚i | i P Iu auch unabhängig.
Beweis. Sei Ei “ tAi u, dann ist nach Voraussetzung tEi | i P Iu eine unabhängige Familie
von X-stabilen Mengensystemen. Nach Korollar 2.7 ist auch tσpEi q | i P Iu unabhängig. Die
Behauptung folgt aus σpEi q “ tH, Ai , Aci , Ωu.
Ť
Ij
Lemma 2.9. (Gruppieren) Sei tEi | i P Iu unabhängig und X-stabil mit Ei Ă F. Sei I “
jPJ
˜
¸
Ť
Ej . Dann ist tAj | j P Ju eine unabhängige Familie.
eine disjunkte Zerlegung und Aj “ σ
iPIj
Beweis. Für k P J sei
Dk “ tAi1 X ¨ ¨ ¨ X Ain | Ail P Eil , i1 , . . . , in P Ik , n P Nu
Ť
Ei . Dann ist Dk per Definition X-stabil.
die Menge aller endlichen Schnitte von Mengen aus
iPIk
Weiterhin ist tDk | k P Ju unabhängig, da die Ei unabhängig sind. Wegen
˜
¸
ď
Ak “ σ
Ei “ σpDk q, k P J
iPIk
und Korollar 2.7 ist tAk | k P Ju unabhängig.
Satz 2.10. (Kolmogorovsches 0-1-Gesetz) Sei pFn qnPN eine Folge unabhängiger σ-Algebren mit
Fn Ă F. Sei
˜
¸
ł
ď
An :“
Fk :“ σ
Fk
k≥n
und T8 :“
Ş
k≥n
An die terminale σ-Algebra. Dann gilt
n≥1
A P T8 ùñ PpAq P t0, 1u.
Notation: E1 K E2 ðñ tE1 , E2 u unabhängige Familie.
24
Beweis. Idee: A P T8 , dann ist A unabhängig von A, d.h. PpAq2 “ PpAq.
Nach Korollar 2.7 und Lemma 2.9 gilt für n P N
An`1 K
n
ł
Fk .
k“1
Insbesondere also T8 “
Ş
Ak K
k≥n`1
n
Ž
Fk . Daraus folgt
k“1
T8 K
n
ďł
Fk ,
n≥1 k“1
da zu jeder Menge aus
n
Ť Ž
Fk es ein n P N gibt, sodasss diese in
n≥1 k“1
n
Ž
Fk liegt. Korollar 2.7
k“1
impliziert
T8 K
8
ł
˜
Fn “ σ
n“1
Es ist T8 Ă Ak Ă A1 “
8
Ž
n
ďł
¸
Fk
.
n≥1 k“1
Fk und somit T8 K T8 .
k“1
Satz 2.11. Sei T Ă F eine σ-Algebra mit PpAq P t0, 1u für alle A P T . Sei Z : Ω ÝÑ R Y t˘8u
eine T messbare Zufallsvariable. Dann gibt es ein c P R Y t˘8u mit PpZ “ cq “ 1.
Beweis. Nach Voraussetzung ist tZ ≤ tu P T für alle t P R. Also ist F ptq :“ PpZ ≤ tq monoton
wachsend mit F ptq P t0, 1u für alle t.
Fall 1. F ptq “ 0 für alle t P R. Dann ist PpZ ą nq “ 1 für alle n P N und somit
PpZ “ `8q “ lim PpZ ą nq “ 1.
nÑ8
Also c “ `8.
Fall 2. F ptq “ 1 für alle t P R. Dann ist
PpZ “ ´8q “ lim PpZ ≤ ´nq “ 1.
nÑ8
Also c “ ´8.
Fall 3. Es gibt ein t0 P R mit
#
F ptq “
0,
1,
t ă t0
.
t ≥ t0
Dann ist
ˆ
˙
ˆ
˙
ˆ
˙
1
1
1
1
1 “ F t0 `
´ F t0 ´
“ P t0 ´ ă Z ≤ t0 `
, n P N.
n
n
n
n
Also gilt
ˆ
˙
1
1
PpZ “ t0 q “ lim P t0 ´ ă Z ≤ t0 `
“ 1.
nÑ8
n
n
25
Definition 2.12. Sei I eine Indexmenge und Xi Zufallsvariablen mit Werten in einem Maßraum
pEi , Ei q für alle i P I. Die Familie tXi | i P Iu heißt unabhängig, falls die σ-Algebren
σpXi q :“ Xi´1 pEi q “ tXi´1 pAq | A P Ei u
eine unabhängige Familie tσpXi q | i P Iu bilden.
Bemerkung 2.13. (a) Falls Xi messbar bezüglich Di -Ei sind und tDi | i P Iu unabhängig
sind, so ist tXi | i P Iu unabhängig.
(b) tXi | i P Iu ist eine Familie von unabhängigen Zufallsvariablen genau dann, wenn für alle
n P N, i1 , . . . , in P I paarweise verschieden und Ai1 P Ei1 , . . . , Ain P Ein gilt
PpXi1 P Ai1 , . . . , Xin P Ain q “
n
ź
PpXij P Aij q.
(2.1)
j“1
Wegen PpXi1 P Ai1 , . . . , Xin P Ain q “ P ˝ pXin , . . . , Xin q´1 pAi1 ˆ ¨ ¨ ¨ ˆ Ain q ist folglich
tXi | i P Iu genau dann unabhängig, wenn alle endlich dimensionalen Verteilungen P ˝
pXin , . . . , Xin q´1 Produktmaße sind, d.h.
P ˝ pXin , . . . , Xin q´1 “ P ˝ Xi´1
b ¨ ¨ ¨ b P ˝ Xi´1
.
n
1
(c) Seien tXi | i P Iu unabhängig und ϕi : Ei ÝÑ Wi messbar. Dann ist tϕi ˝ Xi } i P Iu
unabhängig.
Lemma 2.14. Seien Xi Zufallsvariablen mit Werten in R. Genau dann ist tXi | i P Iu unabhängig, wenn für alle n P N, alle paarweise verschiedenen i1 , . . . , in P I und alle t1 , . . . , tn P R
PpXi1 ≤ t1 , . . . , Xin ≤ tn q “
n
ź
PpXij ≤ tj q.
(2.2)
j“1
Beweis. Ist tXi | i P Iu unabhängig, so folgt (2.2) direkt aus der Definition. Es gelte also (2.2).
Sei n P N, i1 , . . . , in P I paarweise verschieden. Es reicht (2.1) zu zeigen. Diese gilt wegen (2.2)
für alle Mengen der Form Aik “ p´8, tk s mit tk P R und k “ 1, . . . , n. Da Mengen dieser Form
ein X-stabiles Erzeugendensystem bilden, folgt die Behauptung.
Lemma 2.15. Seien X, Y unabhängige R-wertige Zufallsvariablen. Sei X “ X ` ´ X ´ und
Y “ Y ` ´ Y ´ die Zerlegung in Positiv und Negativteil. Dann sind unabhängig:
• X `, Y `.
• X ´, Y ´.
• X `, Y ´.
• X ´, Y `.
26
Beweis. Wegen X ` “ maxt0, Xu und X ´ “ maxt0, ´Xu sind X ˘ messbar ist bezüglich σpXq.
Also gilt σpX ˘ q Ă σpXq. Analog sehen wir σpY ˘ q Ă σpY q. Da σpXq K σpY q folgt die Behauptung.
Satz 2.16. Seien X, Y P L1 .
(a) Sind X, Y unabhängig, so gilt X ¨ Y P L1 und EpX ¨ Y q “ EpXq ¨ EpY q.
(b) Sind X, Y unabhängig mit X, Y P L2 , so gilt covpX, Y q “ 0 und
varpX ` Y q “ varpXq ` varpY q.
(c) X, Y sind genau dann unabhängig, wenn für alle messbaren, beschränkten Funktionen f, g :
R ÝÑ C gilt
Epf pXqgpY qq “ Epf pXqqEpgpY qq.
(2.3)
Beweis. Teil (b) folgt direkt aus (a). Wir zeigen zunächst (a). Wir zeigen die Behauptung für
X, Y ≥ 0. Der allgemeine Fall ist eine Konsequenz aus Lemma 2.15 und der Zerlegung in Positivund Negativteil.
Fall 1. X “ 1A und Y “ 1B . Dann gilt 0 ≤ X ¨ Y ≤ 1, also X ¨ Y P L1 . Ferner gilt
EpX ¨ Y q “ Ep1AXB q “ PpA X Bq “ PpAqPpBq “ EpXqEpY q.
Fall 2. X “
N
ř
n“1
an 1An und Y “
M
ř
m“1
bm 1Bm mit an , bm ≥ 0, N, M P N und An , Bm P F. Dann
gilt
X ¨Y “
N ÿ
M
ÿ
an bm 1An XBm P L1 .
n“1 m“1
Ferner gilt
EpX ¨ Y q “
N ÿ
M
ÿ
n“1 m“1
˜
N
ÿ
an bm PpAn X Bm q “
n“1
an bm PpAn qPpBm q
n“1 m“1
¸˜
an PpAn q
“
N ÿ
M
ÿ
M
ÿ
¸
bm PpBm q
“ EpXqEpY q.
m“1
Fall 3. Seien X, Y P L1 , Xn , Yn Folgen von Elementarfunktionen wie in Fall 2 mit Xn Õ X und
Yn Õ Y . Dann gilt Xn ¨ Yn P L1 , Xn ¨ Yn Õ X ¨ Y und EpXn ¨ Yn q “ EpXn qEpYn q. Aus dem Satz
der monotonen Konvergenz folgt
EpX ¨ Y q “ lim EpXn ¨ Yn q “ lim EpXn qEpYn q “ EpXqEpY q ă 8.
nÑ8
nÑ8
Es bleibt (c) zu zeigen. Sind X, Y unabhängig, so sind auch f pXq, gpY q unabhängig und folglich
gilt (2.3). Umgekehrt gelte (2.3). Seien A P σpXq und B P σpY q, dann gibt es A1 und B 1 mit
A “ X ´1 pA1 q und B “ X ´1 pB 1 q. Es gilt 1A1 pXq “ 1A und 1B 1 pY q “ 1B und folglich
PpA X Bq “ Ep1A1 pXq1B 1 pY qq “ Ep1A1 pXqqEp1B 1 pY qq “ PpAqPpBq.
27
2.2
Bedingte Erwartungswerte
Im folgenden betrachten wir stets R-wertige Zufallsvariablen. Für Rd -wertige Zufallsvariablen
lassen sich alle Resultate durch komponentenweise Anwendung übertragen.
Definition 2.17. Seien A, B P F und PpBq ą 0. Die bedingte Wahrscheinlichkeit von A gegeben
B ist definiert über
PpA X Bq
PpA|Bq :“
.
PpBq
Bemerkung 2.18. A ÞÝÑ PpA|Bq ist für festes B mit PpBq ą 0 ein Wahrscheinlichkeitsmaß.
Für eine Zufallsvariable X P L1 ist der bedingte Erwartungswert von X gegeben B definiert über
ż
EpX|Bq :“ XpωqPpdω|Bq.
Ω
Satz 2.19. (Formel
der totalen Wahrscheinlichkeit) Sei pBn qnPN Ă F eine Folge disjunkter
Ť
Bn “ Ω und PpBn q ą 0 für alle n ≥ 1. Dann gilt für alle A P F
Mengen mit
n≥1
8
ÿ
PpAq “
PpA|Bn qPpBn q.
n“1
Beweis. Es gilt
˜
¸
ď
PpAq “ P
n≥1
A X Bn
8
ÿ
PpA X Bn q “
“
n“1
8
ÿ
PpA|Bn qPpBn q.
n“1
Definition 2.20. Sei X eine Zufallsvariable mit höchstens abzählbar vielen Werten txk ukPN .
Definiere
# PpAXtX“x uq
k
PpX“xk q , PpX “ xk q ą 0
PpA|X “ xk q “
.
0,
sonst
Der bedingte Erwartungswert einer weiteren Zufallsvariable Y gegeben X “ xk ist in diesem Fall
definiert als
ż
EpY |X “ xk q “ Y pωqPpdω|X “ xk q,
Ω
sofern Y bezüglich Pp¨|X “ xk q integrierbar ist.
Wir wollen diese Definition auf Zufallsvariablen mit kontinuierlichem Bild erweitern. Ist
PpX P Bq ą 0, so ist
PpA X tX P Buq
PpA|X P Bq “
PpX P Bq
28
wohldefiniert. Für B “ txu mit x P Rd ist jedoch in vielen Fällen PpX “ xq “ 0. Die Idee ist
PpA X tX P px ´ h, x ` hquq
.
hÑ0
PpX P px ´ h, x ` hqq
PpA|X “ xq “ lim
Problem: Der Limes muss nicht existieren!
Lösung: Wir benutzen den Satz von Radon-Nikodym.
Definition 2.21. Sei A Ă F eine Teil-σ-Algebra und X P L1 . Der bedingte Erwartungswert von
X gegeben A wird mit EpX|Aq bezeichnet. Dieser ist definiert über die folgenden Eigenschaften
• EpX|Aq P L1 pΩ, A, Pq.
• Für alle A P A gilt
Ep1A ¨ Xq “ Ep1A EpX|Aqq
(2.4)
Kurz: Der bedingte Erwartungswert ist die bezüglich A messbare Zufallsvariable mit (2.4).
Satz 2.22. (Existenz und Eindeutigkeit vom bedingten Erwartungswert) Sei A Ă F eine Teil-σAlgebra und X P L1 . Dann gibt es den bedingten Erwartungswert EpX|Aq. Dieser ist eindeutig
in dem folgenden Sinn:
Ist g P L1 pΩ, A, Pq gegeben mit
Ep1A ¨ Xq “ Ep1A ¨ gq, A P A,
so gilt g “ EpX|Aq fast sicher.
Beweis. Wir zeigen zunächst die Existenz.
Fall 1: Sei X ≥ 0 fast sicher. Dann definiert
ż
A Q A ÞÝÑ XdP “ Ep1A ¨ Xq ≥ 0
A
ein Maß auf A. Ist A derart, dass PpAq “ 0. So gilt auch Ep1A ¨ Xq “ 0. Der Satz von RadonNikodym liefert die Existenz einer Zufallsvariable EpX|Aq P L1 pΩ, A, Pq mit
Ep1A ¨ Xq “ Ep1A ¨ gq, A P A.
Dieses zeigt die Existenz in diesem Fall.
Fall 2: Sei X P L1 beliebig. Betrachte die Zerlegung X “ X ` ´ X ´ in Positiv- und Negativteil.
Dann sind X ˘ P L1 nicht-negativ. Aus Fall 1 folgt die Existenz vom bedingten Erwartungswert
EpX ˘ |Aq P L1 pΩ, A, Pq. Setze EpX|Aq :“ EpX ` |Aq´EpX ´ |Aq. Dann gilt EpX|Aq P L1 pΩ, A, Pq
und für alle A P A
Ep1A ¨ Xq “ Ep1A ¨ X ` q ´ Ep1A ¨ X ´ q “ Ep1A EpX ` |Aqq ´ Ep1A ¨ EpX ´ |Aqq “ Ep1A EpX|Aqq.
29
Dieses zeigt die Existenz im allgemeinen Fall. Wir zeigen die Eindeutigkeit. Seien dazu g1 , g2 P
L1 pΩ, A, Pq gegeben mit
Ep1A ¨ g1 q “ Ep1A ¨ Xq “ Ep1A ¨ g2 q, A P A.
(2.5)
Dann ist A1 :“ tg1 ´ g2 ą 0u P A und A2 :“ tg2 ´ g1 ą 0u P A. Aus (2.5) folgt Ep1Aj ¨ g1 q “
Ep1Aj ¨ g2 q mit j “ 1, 2. Daraus folgt
Ep1A1 pg1 ´ g2 qq “ 0 “ Ep1A2 pg2 ´ g1 qq.
Da die Integranden nicht-negativ sind, sind diese fast sicher Null. Wegen der Wahl der Mengen
Aj ist 1A1 “ 0 “ 1A2 fast sicher, d.h. PpA1 q “ PpA2 q “ 0. Insbesondere ist
Ppg1 ‰ g2 q “ PpA1 Y A2 q “ PpA1 q ` PpA2 q “ 0.
Bemerkung 2.23. Die Eindeutigkeit folgt aus dem Satz von Radon-Nikodym und hätte daher
nicht gesondert gezeigt werden müssen.
Das nächste Lemma sammelt einige wichtige Eigenschaften des bedingten Erwartungswertes.
Lemma 2.24. Sei A Ă F eine Teil-σ-Algebra und X P L1 . Es gelten die folgenden Eigenschaften:
(a) Ist X messbar bezüglich A, so gilt EpX|Aq “ X.
(b) Ist X unabhängig von A, so gilt EpX|Aq “ EpXq.
(c) Es gilt EpX|tH, Ωuq “ EpXq.
(d) Für A P F mit PpAq P p0, 1q sei G “ tA, Ac , H, Ωu. Dann gilt
EpX|Gq “ EpX|Aq1A ` EpX|Ac q1Ac .
(e) Ist Y P L1 und a, b P R so gilt
EpaX ` bY |Aq “ aEpX|Aq ` bEpY |Aq.
(f ) Sei G Ă A eine weitere Teil-σ-Algebra. Dann gilt
EpEpX|Aq|Gq “ EpX|Gq.
(g) Es gilt EpEpX|Aqq “ EpXq.
(h) Sei Y P L1 mit Y ≤ X. Dann gilt EpY |Aq ≤ EpX|Aq.
(i) Es gilt |EpX|Aq| ≤ Ep|X||Aq.
Beweis. Übung.
30
Wir schreiben EpX|Y q für EpX|σpY qq für zwei Zufallsvariablen X, Y .
Satz 2.25. Sei A Ă F eine Teil-σ-Algebra. Dann gelten die folgenden Aussagen.
(a) Sei 0 ≤ Xn P L1 und 0 ≤ X P L1 . Es gelte Xn Õ X fast sicher für n Ñ 8. Dann gilt auch
EpXn |Aq Õ EpX|Aq, n Ñ 8
fast sicher.
(b) Sei Xn P L1 und X P L1 . Sei ϕ P L1 mit |Xn | ≤ ϕ für alle n ≥ 1 und es gelte Xn ÝÑ X
fast sicher. Dann gilt
EpXn |Aq ÝÑ EpX|Aq, n Ñ 8
fast sicher.
(c) Seien X, Y Zufallsvariablen mit X ¨ Y, Y P L1 . Ferner sei X messbar bezüglich A. Dann
gilt
EpX ¨ Y |Aq “ XEpY |Aq
fast sicher.
Beweis. (a) Aus der Monotonie des bedingten Erwartungswertes folgt 0 ≤ EpXn |Aq ≤ EpXn`1 |Aq.
Es sei Y :“ lim EpXn |Aq “ sup EpXn |Aq P R Y t˘8u. Dann ist Y messbar bezüglich A. Für
nÑ8
jedes A P A gilt
nPN
Ep1A ¨ Xn q “ Ep1A ¨ EpXn |Aqq, n ≥ 1.
Aus dem Satz der monotonen Konvergenz folgt
Ep1A ¨ Xq “ Ep1A ¨ Y q, A P A.
(b) Wir betrachten zuerst den Fall Xn ≥ 0 fast sicher. In diesem Fall ist auch X ≥ 0 fast
sicher. Angenommen Xn ist monoton. Wir betrachten den Fall, dass Xn monoton steigend ist.
Der Fall einer monoton fallenden Folge geht analog. Ist Xn monoton steigend, so folgt aus (a)
EpXn |Aq Õ EpX|Aq für n Ñ 8. Ist Xn nicht monoton, so betrachten wir Xn1 :“ inf Xm und
m≥n
Xn2 “ sup Xm . Dann gilt Xn1 , Xn2 ≤ ϕ. Diese Folgen sind monoton mit Xn1 Õ lim inf Xn “ X
nÑ8
m≥n
und Xn2 Œ lim sup Xn “ X fast sicher. Aus dem ersten Fall folgt
nÑ8
lim EpXn1 |Aq “ EpX|Aq “ lim EpXn2 |Aq.
nÑ8
nÑ8
Wegen Xn1 ≤ Xn ≤ Xn2 folgt in diesem Fall die Behauptung aus
EpXn1 |Aq ≤ EpXn |Aq ≤ EpXn2 |Aq, n ≥ 1.
Im allgemeinen Fall, sei Xn “ Xn` ´ Xn´ sowie X “ X ` ´ X ´ die Zerlegung in Positiv- und
Negativteil. Dann folgt
EpXn |Aq “ EpXn` |Aq ´ EpXn´ |Aq ÝÑ EpX ` |Aq ´ EpX ´ |Aq “ EpX|Aq
31
fast sicher.
(c) Fall 1. Sei X “ 1B mit B P A. Dann gilt für jede Menge A P A
Ep1A X ¨ Y q “ Ep1AXB Y q “ Ep1AXB EpY |Aqq “ Ep1A XEpY |Aqq.
Fall 2. Aufgrund der Linearität obiger Gleichung golt die Behauptung für alle ElementarfunkN
ř
tionen X “
an 1Bn mit an P R und Bn P A.
n“1
Fall 3. Seien X, Y ≥ 0. Dann gibt es eine Folge von Elementarfunktionen Xn mit Xn Õ X.
Dann gilt Xn ¨ Y Õ X ¨ Y und wir erhalten aus (a)
EpX ¨ Y |Aq “ lim EpXn ¨ Y |Aq “ lim Xn EpY |Aq “ XEpY |Aq.
nÑ8
nÑ8
Fall 4. Seien X, Y wie in der Behauptung. Durch Zerlegung in Positiv- und Negativteil erhalten
wir
EpX ¨ Y |Aq “ XEpY |Aq.
Satz 2.26. (Jensen Ungleichung für bedingte Erwartungswerte, [Bil99]) Sei ϕ : R ÝÑ R konvex
und X eine Zufallsvariable mit X, ϕ ˝ X P L1 . Sei A Ă F eine Teil-σ-Algebra. Dann gilt
ϕpEpX|Aqq ≤ Epϕ ˝ X|Aq.
Definition 2.27. Sei A Ă F eine Teil-σ-Algebra, pE, Eq ein Maßraum und X eine E-wertige
Zufallsvariable. Eine Abbildung Q : Ω ˆ E ÝÑ r0, 1s heißt regulärer bedingter Erwartungswert
von X gegeben A, wenn die folgenden Eigenschaften gelten:
(a) Für jedes ω P Ω ist Qpω, ¨q : E ÝÑ r0, 1s ein Wahrscheinlichkeitsmaß auf E.
(b) Für jedes B P E ist Qp¨, Bq : Ω ÝÑ r0, 1s messbar bezüglich A.
(c) Für jedes B P E gilt Ep1XPB |Aq “ Qp¨, Bq fast sicher.
Satz 2.28. [KS07] Sei E ein Polnischer Raum. Ferner sei A Ă F eine Teil-σ-Algebra. Für jede
E-wertige Zufallsvariable X gibt es einen regulären bedingten Erwartungswert von X gegeben A.
Dieser ist eindeutig in dem folgenden Sinn:
Gegeben zwei reguläre bedingte Erwartungswerte Q, Q1 . Dann ist gibt es eine Menge M P F
mit PpM q “ 1 derart, dass
Qpω, Bq “ Q1 pω, Bq, B P E, ω P M.
Satz 2.29. Sei E ein Polnischer Raum. Ferner sei A Ă F eine Teil-σ-Algebra. Sei X eine
E-wertige Zufallsvariable und Qpω, dxq der reguläre bedingte Erwartungswert. Sei ϕ : E ÝÑ R
messbar mit ϕ ˝ X P L1 . Dann gilt
ż
|ϕpxq|Qpω, dxq ă 8 fast sicher
E
32
und
ż
ϕpxqQpω, dxq
EpϕpXq|Aqpωq “
(2.6)
E
für fast alle ω.
Beweis. Fall 1. Sei ϕ “ 1B mit B P BpEq. Dann ist fast sicher
EpϕpXq|Aqpωq “ Ep1XPB |Aqpωq “ Qpω, Bq.
Fall 2. Da (2.6) linear in ϕ ist, gilt die Behauptung fdirur alle Elementarfunktionen.
Fall 3. Sei ϕ ≥ 0. Dann gibt es eine Folge von Elementarfunktionen ϕn mit ϕn Õ ϕ. Dann ist
ż
ϕn pxqQpω, dxq “ Epϕn pXq|Aq Õ EpϕpXq|Aq
E
fast sicher. Aus dem Sart der monotonen Konvergenz folgt
ż
ż
ϕn pxqQpω, dxq Õ ϕpxqQpω, dxq “ EpϕpXq|Aq ă 8.
E
E
Fall 4. Zerlege in Positiv- und Negativteil und benutze Fall 3.
Beispiel 2.30. Es sei E “ R und A Ă F eine Teil-σ-Algebra. Sei X P L1 und ϕpxq “ x. Sei
Qpω, dxq der reguläre bedingte Erwartungswert. Dann gilt für fast alle ω P Ω
ż
|x|Qpω, dxq ă 8
R
und
ż
xQpω, dxq.
EpX|Aqpωq “
R
3
Schwache Konvergenz
Sei pE, dq ein metrischer Raum und sei PpEq der Raum der Wahrscheinlichkeitsmaße auf E. Im
ersten Teil untersuchen wir die Konvergenz von Wahrscheinlichkeitsmaßen.
Idee: Mengenweise Konvergenz, d.h.
µn pAq ÝÑ µpAq, A P E, n Ñ 8.
(3.1)
Problem: Für viele praktische Anwendungen ist diese Art der Konvergenz zu stark. Dazu
betrachten wir die Folge µn pdxq “ n1r0, 1 s pxqmpdxq und A “ p0, 1s. Dann gilt µn pAq “ 1. Es
n
liegt nahe anzunehmen, dass µn ÝÑ δ0 konvergiert. Es gilt jedoch δ0 pAq “ 0. Eine mengenweise
Konvergenz liegt in diesem Beispiel nicht vor.
33
Wir brauchen daher eine abgeschwächte Form von (3.1). Die Idee ist es Konvergenz über
die Konvergenz der dazugehörigen Momente bzw. Erwartungswerte zu beschreiben. Genauer sei
M pEq eine geeignete Familie von messbaren Funktionen auf E. Die Konvergenz µn ÝÑ µ wird
daher definiert über
ż
ż
f pxqdµn pxq ÝÑ f pxqdµpxq, n Ñ 8
(3.2)
E
E
für alle f P M pEq.
Bemerkung 3.1. Es sei pµn qnPN Ă PpEq und µ P PpEq. Genau dann gilt (3.1), wenn (3.2) für
alle beschränkten messbaren Funktionen f : E ÝÑ R gilt.
Beweis. Gilt (3.2), so wählen wir f “ 1A für A P E. Umgekehrt gelte (3.1). Dann gilt (3.2) für
alle Indikatiorfunktionen f “ 1A und mittels Linearität auch für alle Elementarfunktionen. Es
reicht (3.2) für alle f ≥ 0 zu zeigen. Sei dazu f ≥ 0 beschränkt und messbar und ε ą 0 beliebig.
Dann gibt es eine Elementarfunktion g mit 0 ≤ g ≤ f und suppf pxq ´ gpxqq ă ε. Daraus folgt
xPE
ˇ
ˇ ˇ
ˇ
ˇż
ˇ ˇż
ˇ
ż
ż
ˇ
ˇ ˇ
ˇ
ˇ f pxqdµpxq ´ f pxqdµn pxqˇ ≤ ˇ f pxqdµpxq ´ gpxqdµpxqˇ
ˇ
ˇ ˇ
ˇ
ˇ
ˇ ˇ
ˇ
E
E
E
E
ˇ
ˇ ˇ
ˇ
ˇż
ˇ ˇż
ˇ
ż
ż
ˇ
ˇ ˇ
ˇ
ˇ
ˇ
ˇ
` ˇ gpxqdµpxq ´ gpxqdµn pxqˇ ` ˇ gpxqdµn pxq ´ f pxqdµn pxqˇˇ
ˇ
ˇ ˇ
ˇ
E
E
E
E
ˇ
ˇ
ˇż
ˇ
ż
ˇ
ˇ
ˇ
≤ 2 sup |f pxq ´ gpxq| ` ˇ gpxqdµpxq ´ gpxqdµn pxqˇˇ
xPE
ˇ
ˇ
E
ˇ
ˇ E
ˇż
ˇ
ż
ˇ
ˇ
ˇ
≤ 2ε ` ˇ gpxqdµpxq ´ gpxqdµn pxqˇˇ
ˇ
ˇ
E
E
welches mit n Ñ 8 die Behauptung zeigt.
Es liegt daher nahe die Menge M pEq geeignet einzuschränken. In diesem Kapitel betrachten
wir den Fall M pEq “ Cb pEq, wo Cb pEq der Raum der stetigen, beschränkten Funktionen f :
E ÝÑ R ist. Dieser ist ein Banachraum mit der Supremumsnorm
}f }8 :“ sup |f pxq|.
xPE
Der Zusammenhang zu Zufallsvariablen ist dann gegeben durch µn :“ P˝Xn´1 und µ :“ P˝X ´1 .
Dieses führt zu dem Begriff der Konvergenz in Verteilung.
34
3.1
Konvergenz von Wahrscheinlichkeitsmaßen
Sei im Folgenden pE, dq ein metrischer Raum.
Definition 3.2. Eine Folge pµn qnPN Ă PpEq konvergiert schwach gegen µ P PpEq, falls für alle
f P Cb pEq
ż
ż
f pxqdµn pxq ÝÑ f pxqdµpxq, n Ñ 8.
E
E
Das nächste Lemma zeigt, dass der Grenzwert bei schwacher Konvergenz eindeutig ist.
Lemma 3.3. Sei pµn qnPN Ă PpEq. Angenommen es gibt µ, ν P PpEq derart, dass µn schwach
gegen µ konvergiert. Dann ist µ “ ν.
Für den Beweis ist die folgende Funktion hilfreich. Sei A Ă E. Der Abstand von x P E zu A
ist definiert über
dpx, Aq :“ inftdpx, aq | a P Au.
Es gilt
|dpx, Aq ´ dpy, Aq| ≤ dpx, yq, x, y P E
und dpx, Aq “ 0 genau dann, wenn x P A. Hierbei bezeichnet A den Abschluss von A.
Beweis. Aus der schwachen Konvergenz folgt
ż
ż
f pxqdµpxq “ f pxqdνpxq, f P Cb pEq.
E
E
Es reicht zu zeigen, dass µpKq “ νpKq#für alle abgeschlossenen Mengen K Ă E gilt. Es sei
1 ´ t, t P r0, 1s
K Ă E abgeschlossen. Definiere ϕptq :“
und sei
0,
t≥1
fn pxq :“ ϕpndpx, Kqq, x P E.
Dann ist 0 ≤ fn ≤ 1 und fn ist stetig für jedes n ≥ 1. Ferner gilt fn pxq ÝÑ
und jedes x P E. Damit folgt
ż
ż
µpKq “ lim fn pxqdµpxq “ lim fn pxqdνpxq “ νpKq.
nÑ8
1K pxq für n Ñ 8
nÑ8
E
E
Beispiel 3.4. (a) Sei pxn qnPN Ă E und x P E. Falls dpxn , xq ÝÑ 0 für n Ñ 8 gilt, so
konvergiert δxn schwach gegen δx .
(b) Sei µn pdxq “ pn pxqmpdxq mit
c
pn pxq “
n ´ n x2
e 2 , x P R.
2π
Dann konvergiert µn schwach gegen δ0 .
35
(c) Sei µn pdxq “ n1r0, 1 s pxqmpdxq. Dann konvergiert µn schwach gegen δ0 .
n
Beweis. Übung.
Satz 3.5. (Portmanteau-Theorem) Sei pE, dq ein metrischer Raum mit Borel-σ-Algebra BpEq.
Sei pµn qnPN Ă PpEq und µ P PpEq. Dann sind die folgenden Aussagen äquivalent.
(a) µn ÝÑ µ schwach für n Ñ 8.
(b) Für alle gleichmässig stetigen Funktionen f P Cb pEq gilt
ż
ż
f pxqdµn pxq ÝÑ f pxqdµpxq, n Ñ 8.
E
E
(c) Für alle abgeschlossenen Mengen F Ă E gilt
lim sup µn pF q ≤ µpF q.
nÑ8
(d) Für alle offenen Mengen O Ă E gilt
lim inf µn pOq ≥ µpOq.
nÑ8
(e) Für alle Mengen A P BpEq mit µpBAq “ 0 gilt
lim µn pAq “ µpAq.
nÑ8
Bevor wir den Beweis führen brauchen wir das folgende Lemma.
Lemma 3.6. Sei g : E ÝÑ R eine stetige Funktion und a P R. Dann gilt
Btx P E | gpxq ≤ au Ă tx P E | gpxq “ au.
Beweis. Sei x P Btx P R | gpxq ≤ au. Dann gilt für alle ε ą 0
Uε pxq X ty P E | gpyq ą au ‰ H
sowie
Uε pxq X ty P E | gpyq ≤ au ‰ H.
Hierbei bezeichnet Uε pxq :“ ty P E | dpx, yq ă εu den offenen Ball mit Radius ε ą 0 und
Mittelpunkt x. Für ε “ n1 mit n P N erhalten wir zwei Folgen pxn qnPN und pyn qnPN mit dpx, xn q ă
1
1
n sowie dpx, yn q ă n derart, dass gpxn q ą a und gpyn q ≤ a. Weiterhin gilt xn , yn ÝÑ x und
somit
a ≤ lim gpxn q “ gpxq “ lim gpyn q ≤ a.
nÑ8
nÑ8
36
Wir kommen zum Beweis von Satz 3.5.
Beweis. pcq ðñ pdq: klar durch Komplementbildung.
paq ùñ pbq : trivial.
pbq ùñ pcq : Sei F Ă E abgeschlossen und setze
*
"
1
.
Gm :“ x P E | dpx, F q ă
m
Ş
Dann ist Gm offen, Gm`1 Ă Gm und F “
Gm . Folglich gilt µpGm q ÝÑ µpF q für m Ñ 8.
m≥1
Sei
#
ϕptq :“
1 ´ t, t P r0, 1s
0,
t≥1
und setze fm pxq :“ ϕpmdpx, F qq. Dann gilt 0 ≤ fm ≤ 1, fm |Gcm “ 0, fm |F “ 1 und fm ist
Lipschitz stetig. Insbesondere ist fm gleichmässig stetig mit 1F ≤ fm ≤ 1Gm . Daraus folgt
ż
ż
lim sup µn pF q ≤ lim sup fm dµn “ fm dµ ≤ µpGm q ÝÑ µpF q.
nÑ8
nÑ8
E
E
pcq ùñ peq : Sei A P BpEq mit µpBAq “ 0. Dann gilt
˝
˝
µpAq “ µpAq ≤ lim inf µn pAq ≤ lim inf µn pAq ≤ lim sup µn pAq
nÑ8
nÑ8
nÑ8
≤ lim sup µn pAq ≤ µpAq “ µpAq.
nÑ8
peq ùñ pcq : Sei F Ă E abgeschlossen. Auf Lemma 3.6 folgt für alle δ ą 0
Btx P E | dpx, F q ≤ δu Ă tx P E | dpx, F q “ δu.
(3.3)
Da tx P E | dpx, F q “ δu für alle δ ą 0 eine abgeschlossene Menge ist, liegt sie in BpEq. Weiterhin
gilt
tx P E | dpx, F q “ δu X tx P E | dpx, F q “ δ 1 u “ H, δ ‰ δ 1 .
Für n P N sei
(3.4)
"
ˆ"
*˙*
1
x P E | dpx, F q ≥
Dn :“ δ ą 0 | µ
.
n
Behauptung: Dn enthält für jedes n P N nur endlich viele Elemente.
Beweis. Angenommen nicht. Dann gibt es ein n P N und eine Folge paarweise verschiedener
Elemente pδk qkPN Ă Dn . Dann folgt aus (3.4)
˜
¸
8
8
ď
ÿ
ÿ
1
1≥µ
tx P E | dpx, F q “ δk u “
µptx P E | dpx, F q “ δk uq ≥
“ 8.
n
k≥1
k“1
k“1
37
Also ist D “
Ť
Dn abzählbar. Folglich gibt es eine Nullfolge pδk qkPN Ă r0, 8qzD. Aus (3.3)
n≥1
folgt
µpBFk q ≤ µptx P E | dpx, F q “ δk uq “ 0
für Fk :“ tx P E | dpx, F q ≤ δk u und alle k P N. Wegen Fk Œ tx P E | dpx, F q “ 0u “ F folgt
lim sup µn pF q ≤ lim sup µn pFk q “ µpFk q ÝÑ µpF q, k Ñ 8.
nÑ8
nÑ8
pcq ùñ paq : Sei f P Cb pEq. Es reicht zu zeigen, dass
ż
ż
lim sup f pxqdµn pxq ≤ f pxqdµpxq.
nÑ8
E
E
Denn, daraus folgt für p´f q anstelle von f
ż
ż
´ lim inf f pxqdµn pxq “ lim supp´f pxqqdµn pxq ≤ p´f pxqqdµpxq
nÑ8
nÑ8
E
E
und somit
ż
ż
f pxqdµn pxq ≥
lim inf
nÑ8
E
f pxqdµpxq.
E
Für f “ 0 ist nichts zu zeigen. Sei also f ‰ 0. Wir können ohne Einschränkung annehmen, dass
`}f }8
0 ≤ f ≤ 1. Anderenfalls betrachten wir f2}f
}8 . Sei k P N fest und für i P N definiere
*
"
i
.
Fi :“ f ≥
k
Dann ist Fi abgeschlossen, Fi`1 Ă Fi und es gilt
"
*
i
i`1
Fi zFi`1 “
≤f ă
.
k
k
(3.5)
Lemma 3.7. Es gilt
k
k
k
k
ÿ
ÿ
1ÿ
i
i`1
1 1ÿ
1Fi “
1Fi zFi`1 ≤ f ≤
1Fi zFi`1 “ `
1Fi .
k i“1
k
k
k
k
i“1
i“0
i“1
Beweis. Es gilt E “
k
Ť
Fi zFi`1 mit F0 “ E und Fk`1 “ H, wobei die Vereinigung disjunkt ist.
i“0
Daraus, und aus (3.5) ergibt sich die mittlere Ungleichung. Für die beiden Identitäten beachte
k
ÿ
pi ` 1q1Fi zFi`1 “
i“0
k
ÿ
pi ` 1q1Fi ´
i“0
k
ÿ
“
i“0
k´1
ÿ
pi ` 1q1Fi`1
i“0
1Fi `
k
ÿ
i“0
38
i1Fi ´
k
ÿ
i“1
i1Fi “ 1 `
k
ÿ
i“1
1Fi .
Dieses impliziert die rechte Identität. Für die linke Identität beachte 1 “
k
ř
i“0
obiger Rechnung
k
ř
i“1
i1Fi zFi`1 “
k
ř
i“1
1Fi zFi`1 woraus mit
1Fi folgt.
Die Behauptung folgt aus
ż
lim sup
f dµn ´
nÑ8
E
k
ÿ
1
1
µn pFi q
≤ lim sup
k
k nÑ8 i“1
ż
k
k
1ÿ
1ÿ
≤
lim sup µn pFi q ≤
µpFi q ≤ f dµ.
k i“1 nÑ8
k i“1
E
Satz 3.8. Seien pE, dq und pE 1 , d1 q metrische Räume, µn , µ P PpEq und h : E ÝÑ E 1 stetig.
Angenommen µn ÝÑ µ schwach, dann ist µn ˝ h´1 ÝÑ µ ˝ h´1 schwach auf E 1 .
Beweis. Sei f P Cb pE 1 q. Dann ist f ˝ h P Cb pEq.
Beispiel 3.9. Auf die Voraussetzung, dass h stetig ist kann im Allgemeinen nicht verzichtet
werden. Denn sei pxn qnPN Ă E mit xn ÝÑ x und xn ‰ x. Dann gilt δxn ÝÑ δx schwach. Wähle
hpyq “ 1txu pyq, dann gilt
#
1, hpxn q P A
´1
´1
δxn ˝ h pAq “ δxn ph pAqq “
“ δhpxn q pAq “ δ0 pAq.
0, hpxn q R A
Analog zeigen wir δx ˝ h´1 “ δhpxq “ δ1 .
Wir müssen daher eine Bedingung an die Stetigkeitsstellen von h stellen.
Satz 3.10. Seien pE, dq, pE 1 , d1 q metrische Räume, h : E ÝÑ E 1 messbar und µn , µ P PpEq mit
µn ÝÑ µ schwach. Sei
Dh :“ tx P E | h ist nicht stetig in xu.
Gilt µpDh q “ 0, so folgt µn ˝ h´1 ÝÑ µ ˝ h´1 schwach.
Beweis. Wegen
*
ď č "
1 1
1
Dh :“
x P E |Dy P E : dpx, yq ă
d phpyq, hpxqq ≥
m
n
n≥1 m≥1
folgt Dh P BpEq. Sei F Ă E 1 abgeschlossen. Dann gilt
lim sup µn ph´1 pF qq ≤ lim sup µn ph´1 pF qq ≤ µph´1 pF qq.
nÑ8
nÑ8
Sei x P h´1 pF q, dann gibt es eine Folge pxn qnPN Ă h´1 pF q mit xn ÝÑ x. Ist h stetig in x, so folgt
hpxn q ÝÑ hpxq und da F abgeschlossen ist, folgt aus hpxn q P F bereits hpxq P F . In diesem Fall
39
ist x P h´1 pF q. Falls h nicht stetig in x ist, so ist x P Dh und wir erhalten h´1 pF q Ă h´1 pF qYDh .
Daraus folgt aus der schwachen Konvergenz µn ÝÑ µ und dem Satz von Portmanteau
lim sup µn ph´1 pF qq ≤ lim sup µn ph´1 pF qq ≤ µph´1 pF qq ≤ µph´1 pF qq ` µpDh q “ µph´1 pF qq.
nÑ8
nÑ8
Nach dem Satz von Portmanteau impliziert dieses die Behauptung.
Satz 3.11. [KS07, Theorem 8.5] Seien pµn qnPN Ă PpRq und µ P PpRq gegeben und bezeichne
mit Fn ptq “ µn pp´8, tsq und F ptq “ µpp´8, tsq die dazugehörigen Verteilungsfunktionen. Dann
sind äquivalent:
(a) µn ÝÑ µ schwach für n Ñ 8.
(b) Fn ptq ÝÑ F ptq für n Ñ 8 und alle Stetigkeitsstellen t von F .
Als nächstes wollen wir Familien von Wahrscheinlichkeitsmaßen betrachten, welche die Bedingung der Folgenkompaktheit bezüglich der schwachen Konvergenz erfüllen.
Definition 3.12. Sei Γ Ă PpEq eine Familie von Wahrscheinlichkeitsmaßen.
(a) Γ heißt relativ kompakt, falls jede Folge in Γ eine schwach konvergente Teilfolge hat.
(b) Γ heißt straff, falls für alle ε ą 0 es eine kompakte Menge Kε Ă E gibt mit
µpKε q ≥ 1 ´ ε, @µ P Γ.
Lemma 3.13. Sei pµn qnPN Ă PpEq und µ P PpEq. Dann sind äquivalent:
(a) µn ÝÑ µ schwach für n Ñ 8.
(b) Für jede Teilfolge pµnk qkPN von pµn qnPN gibt es eine weitere Teilfolge pµnkl qlPN mit µnkl ÝÑ
µ schwach für l Ñ 8.
Beweis. paq ùñ pbq: Konvergiert eine Folge, so konvergiert auch jede Teilfolge gegen denselben
Grenzwert.
pbq ùñ paq: Angenommen (a) gilt nicht. Dann gibt es f P Cb pEq, ε ą 0 und eine Teilfolge
pµnk qkPN mit
ˇ
ˇ
ˇż
ˇ
ż
ˇ
ˇ
ˇ f pxqdµn pxq ´ f pxqdµpxqˇ ≥ ε, k P N.
(3.6)
k
ˇ
ˇ
ˇ
ˇ
E
E
Nach Voraussetzung gibt es eine weitere Teilfolge pµnkl qlPN mit µnkl ÝÑ µ schwach für l Ñ 8.
Für diese Teilfolge gilt
ż
ż
f pxqdµnkl pxq ÝÑ f pxqdµpxq, l Ñ 8
E
E
welches im Wiederspruch zu (3.6) steht.
40
Bemerkung 3.14. (a) ISt E kompakt, so ist Γ “ tµu für jedes µ P PpEq straff. Dann sei
An Ă E eine Folge von abgeschlossen Mengen mit An Õ E. Dann ist jedes An als abgeschlossene Menge einer kompakten Menge wieder kompakt. Die Behauptung folgt aus
µpAn q Õ µpEq “ 1 für n Ñ 8.
Ť
(b) Es gebe eine Folge von kompakten Mengen pKn qnPN Ă E mit
Kn “ E. Dann ist
n≥1
ˆN
˙
N
Ť
Ť
Kn Õ E, und wegen µ
Kn Õ µpEq “ 1 ist Γ “ tµu für jedes µ P PpEq straff.
n“1
n“1
(c) Γ “ PpRd q ist nicht straff.
Der nächste Satz stellt den Zusammenhang zu Straffheit und relativer Kompaktheit her.
Satz 3.15. (Satz von Prokhorov, [KS07, Theorem 8.9]) Sei E ein metrischer Raum. Ist Γ Ă
PpEq straff, so ist Γ relativ kompakt. Ist E zusätzlich ein Polnischer Rau, so ist Γ genau dann
straff, wenn es relativ kompakt ist.
Im folgenden führen wir einige Resulate ohne Beweis auf. Hierbei ist E ein metrischer Raum.
Definition 3.16. Es sei ρ : PpEq ˆ PpEq ÝÑ r0, 8q gegeben durch
ρpµ, νq :“ inftε ą 0 | µpF q ≤ νpF ε q ` ε, F ist abgeschlossen u
mit F ε :“ ty P E | dpy, F q ă εu. Die Abbildung ρ wird Prokhorov Metrik genannt.
Lemma 3.17. [EK86] Die Prokhorov Metrik ρ definiert eine Metrik auf E.
Satz 3.18. [EK86] Sei E ein seperabler metrischer Raum und pµn qnPN Ă PpEq, µ P PpEq.
Dann sind die folgenden Aussagen äquivalent:
(a) µn ÝÑ µ schwach für n Ñ 8.
(b) ρpµn , µq ÝÑ 0 für n Ñ 8.
Satz 3.19. [EK86] Es gelten die folgenden Aussagen.
(a) Ist E seperabel, so ist auch PpEq seperabel.
(b) Ist E vollständig, so ist auch PpEq volltändig.
Insbesondere, ist E ein Polnischer Raum, so ist auch PpEq ein Polnischer Raum.
Zum Schluß betrachten wir noch eine zusätzliche Eigenschaft von Wahrscheinlichkeitsmaßen
auf metrischen Räumen.
Definition 3.20. µ P PpEq heißt regulär, falls für jedes A P BpEq
µpAq “ suptµpKq | K Ă A kompaktu “ inftµpU q | A Ă U offen u.
41
Eine äquivalente Definition ist gegeben durch: Für jedes A P BpEq und jedes ε ą 0 gibt es
eine kompakte Menge Kε und eine offene Menge Uε mit Kε Ă A Ă Uε und
µpUε zKε q ă ε.
(3.7)
Satz 3.21. Sei E ein metrischer Raum. Dann gilt für jedes µ P PpEq
µpAq “ suptµpKq | K Ă A abgeschlossen u “ inftµpU q | A Ă U offen u.
Beweis. Es sei
K “ tA P BpEq | @ε ą 0DUε offen, DKε abgeschlossen mit Kε Ă A Ă Uε und (3.7)u .
Dann enthält K alle abgeschlossenen Mengen. Denn ist A abgeschlossen, so wählen wir
*
"
1
.
Un :“ x P E | dpx, Aq ă
n
Ş
Un . Folglich gilt lim µpUn q “ µpAq, also A P K.
Dann ist A Ă Un und A “
nÑ8
n≥1
Wir müssen zeigen, dass K “ BpEq. Hierfür reicht es zu zeigen, dass K ein Dynkin-System
ist.
• Sei ε ą 0, x0 P E fest und Uε “ E. Die Mengen der Form
Kα “ tx P E | dpx, x0 q ≤ αu
sind abgeschlossen und es gilt Kα Õ E. Folglich gilt µpKα q Õ µpEq “ 1 für α Ñ 8. Also
gibt es ein αpεq ą 0 mit µpKαpεq q ą 1 ´ ε. Dann gilt Kαpεq Ă A Ă Uε und (3.7) für diese
Mengen.
• Sei A P K und ε ą 0. Seien Kε , Uε die dazugehörigen Mengen. Dann ist K 1 :“ EzK offen,
U 1 :“ EzU abgeschlossen und es gilt U 1 Ă EzA Ă K 1 und
µpK 1 zU 1 q “ µpU zKq ă ε.
• Sei pAn qnPN Ă K eine Folge disjunkter Mengen. Sei ε ą 0. Dann gilt
˜
¸
8
8
ÿ
ď
0≤
µpAn q “ µ
An ≤ µpEq ≤ 1,
n“1
n“1
d.h. pµpAn qqn≥1 ist summierbar. Folglich gibt es ein n0 ≥ 2 mit
8
ř
n“n0
µpAn q ă 2ε . Wähle
abgeschlossene Mengen Ken und offene Mengen Uεn mit Kεn Ă An Ă Uεn und
µpUεn zKεn q ă
42
ε
2n`1
, n P N.
Dann ist Kε :“
n0Ť
´1
n“1
Kεn abgeschlossen und Uε :“
Kε Ă
8
ď
Kεn Ă
n“1
8
Ť
n“1
8
ď
Uεn offen. Ferner gilt
An Ă U ε
n“1
und
µpUε zKε q ≤
8
ÿ
µpUεn zKε q “
n“1
≤
≤
nÿ
0 ´1
nÿ
0 ´1
µpUεn zKε q `
n“1
8
ÿ
µpUεn zKε q
n“n0
n“1
µpUεn zKεn q
8
ÿ
8
ÿ
µpUεn q
`
≤ε
n“n0
nÿ
0 ´1
n“1
1
2n`1
8 ´
¯
ÿ
ε
n
`
`
µpK
q
ε
2n`1
n“n
0
8
ÿ
ε
1
`
µpAn q ≤ ε.
2 n“1 2n n“n
0
Damit ist
8
Ť
An P K.
n“1
Korollar 3.22. Sei µ P PpEq derart, dass tµu straff ist. Dann ist µ regulär.
Für den nächsten Satz brauchen wir folgendes Lemma zur Charakterisierung von Kompaktheit in metrischen Räumen.
Lemma 3.23. Sei pE, dq ein vollständiger metrischer Raum und K Ă E abgeschlossen. Dann
ist K genau dann kompakt, wenn es total beschränkt ist, d.h. für jedes ε ą 0 gibt es endlich viele
Punkte x1 , . . . , xm P E mit
m
ď
KĂ
Bε pxk q,
(3.8)
k“1
wo Bε pxk q den abgeschlossenen Ball um xk mit Radius ε bezeichnet.
Beweis. Sei K kompakt und ε ą 0. Dann ist
KĂ
ď
Uε pxq
xPK
eine offene Überdeckung von K. Es gibt daher endlich viele Punkte x1 , . . . , xm P K mit (3.8).
Umgekehrt gelte (3.8) für jedes ε ą 0. Wir zeigen, dass jede Folge in K eine konvergente
1
Teilfolge enthält. Sei pxn qnPN Ă K. Für jedes m ≥ 1 gibt es endlich viele Bälle mit Radius m
,
welche K überdecken. Mindestens einer dieser Bälle enthält unendlich viele Folgenglieder von
pxn qnPN . Für m “ 1 sei B1 der Ball mit der Eigenschaft, dass N1 :“ tn | xn P B1 unendlich
viele Elemente hat. Sei n1 P N1 beliebig. Für m “ 2 sei B2 der Ball mit der Eigenschaft, dass
43
N2 :“ tn ą n1 | xn P B1 X B2 u unendlich viele Elemente hat. Wähle n2 P N2 beliebig. Durch
Iteration erhalten wir Folgen Bm , Nm und pnm qmPN sodass
#
+
m
č
Nm`1 “ n ą nm | xn P
Bk
k“1
unendlich viele Elemente enthält und nm`1 P Nm`1 . Dann ist pxnm qmPN eine Teilfolge und es
gilt xnk P Bm für alle k ≥ m. Insbesondere gilt
dpxnk , xnl q ≤
1
, k, l ≥ m,
m
d.h. pxnm qm≥1 ist eine Cauchy Folge. Da E vollständig ist, hat diese einen Grenzwert x P E. Da
K abgeschlossen ist, liegt der Grenzwert in K.
Satz 3.24. Sei E ein Polnischer Raum. Dann ist tµu straff für jedes µ P PpEq. Insbesondere
ist jedes µ P PpEq regulär.
Beweis. Sei pan qnPN Ă E eine abzählbar dichte Teilmenge. Dann gilt für jedes δ ą 0
ď
Bδ pan q “ E.
n≥1
Damit folgt
˜
¸
ď
1 “ µpEq “ µ
Bδ pan q
˜
“ lim µ
nÑ8
n≥1
n
ď
¸
Bδ pak q .
k“1
Sei ε ą 0. Dann gibt es für jedes m ≥ 1 ein nm P N mit
˜
¸
n
m
ď
B 1 pak q ≥ 1 ´ 2´m ε.
µ
m
k“1
Sei
m
č nď
K :“
B 1 pak q.
m≥1 k“1
m
Dann ist K abgeschlossen. Für jedes δ ą 0 sei m ≥ 1 mit
KĂ
n
m
ď
B 1 pak q Ă
m
k“1
n
m
ď
1
m
≤ δ. Dann gilt
Bδ pak q.
k“1
Also ist K nach Lemma 3.23 kompakt. Die Behauptung folgt aus
˜
¸
˜
¸
n
8
m
m
ď nč
ÿ
č
c
c
c
µpK q “ µ
µ
B 1 pak q
B 1 pak q ≤
m≥1 k“1
8
ÿ
“
m“1
˜
m
˜
1´µ
n
m
ď
k“1
m“1
k“1
¸¸
B 1 pak q
m
44
≤ε
8
ÿ
m“1
m
2´m “ ε,
wo wir
n
m
č
k“1
c
B 1 pak q “
m
n
m
č
˜
pEzB 1 pak qq “ Ez
k“1
m
n
m
ď
k“1
¸
B 1 pak q
m
benutzt haben.
3.2
Konvergenz von Zufallsvariablen
Sei pE, dq ein metrischer Raum, pXn qnPN eine Folge von E-wertigen Zufallsvariablen und X eine
E-wertige Zufallsvariable. Dann ist ω ÞÝÑ pXn pωq, Xpωqq messbar bezüglich F ´ ´BpEq b BpEq.
Ferner ist px, yq ÞÝÑ dpx, yq stetig, also BpE ˆ Eq ´ ´BpRq messbar. Beachte, dass E ˆ E mit
dEˆE ppx, yq, px1 , y 1 qq :“ dpx, yq ` dpx1 , y 1 q wieder ein metrischer Raum ist. Um die Konvergenz
Xn ÝÑ X zu untersuchen, betrachten wir die Abbildung
Ω ÝÑ r0, 8q, ω ÞÝÑ dpXn pωq, Xpωqq.
Diese ist messbar, sofern BpE ˆ Eq Ă BpEq b BpEq gilt. Ohne weiteres ist dieses jedoch nicht
der Fall.
Lemma 3.25. Sei E seperabel. Dann ist E ˆ E seperabel und es gilt
BpE ˆ Eq “ BpEq b BpEq.
Hier und im folgenden ist pE, dq stets ein seperabler, metrischer Raum.
Definition 3.26. Sei pXn qnPN eine Folge von E-wertigen Zufallsvariablen und X ein weitere
E-wertige Zufallsvariable.
(a) Xn ÝÑ X is Wahrscheinlichkeit, falls dpXn , Xq ÝÑ 0 in Wahrscheinlichkeit.
(b) Xn ÝÑ X fast sicher, falls dpXn , Xq ÝÑ 0 fast sicher.
(c) Xn ÝÑ X in Lp , falls dpXn , Xq ÝÑ 0 in Lp .
(d) Xn ÝÑ X in Verteilung, falls µn :“ P ˝ Xn´1 schwach gegen µ :“ P ˝ X ´1 konvergiert.
Konvergenz in Verteilung ist, per Definition vom Bildmaß, äquivalent zu
Epf pXn qq ÝÑ Epf pXqq, n Ñ 8
für alle f P Cb pEq.
Satz 3.27. Sei pXn qnPN eine Folge von E-wertigen Zufallsvariablen und X eine weitere Ewertige Zufallsvariable. Angenommmen es gilt Xn ÝÑ X in Verteilung und X ist fast sicher
konstant. Dann gilt Xn ÝÑ X in Wahrscheinlichkeit.
45
Beweis. Es sei α P E derart, dass PpX “ αq “ 1. Sei A P BpEq beliebig, dann gilt
P ˝ X ´1 pAq “ PptX P Auq “ PptX P Au X tX “ αuq “ δα pAq.
Folglich ist P ˝ X ´1 “ δα . Sei ε ą 0 beliebig. Dann ist ty P E | dpy, αq ≥ εu abgeschlossen. Aus
dem Satz von Portmanteau folgt
lim sup PpdpXn , Xq ≥ εq “ lim sup PpdpXn , αq ≥ εq
nÑ8
nÑ8
“ lim sup P ˝ Xn´1 pty P E | dpy, αq ≥ εuq
nÑ8
´1
“P˝X
pty P E | dpy, αq ≥ εuq “ 0,
da α R ty P E | dpy, αq ≥ εu.
Satz 3.28. Sei pXn qnPN eine Folge von E-wertigen Zufallsvariablen und X eine E-wertige Zufallsvariable. Gilt Xn ÝÑ X in Wahrscheinlichkeit, so folgt Xn ÝÑ X in Verteilung.
Beweis. Sei f P Cb pEq gleichmässig stetig und ε ą 0. Dann gibt es ein δ ą 0, sodass für alle
x, y P E mit dpx, yq ă δ bereits |f pxq ´ f pyq| ă ε gilt. Dann gilt
ż
ż
|Epf pXn qq ´ Epf pXqq| ≤
|f pXn q ´ f pXq|dP `
|f pXn q ´ f pXq|dP
dpXn ,Xqăδ
dpXn ,Xq≥δ
≤ ε ` 2}f }8 P pdpXn , Xq ≥ δq .
Satz 3.29. Seien pXn qnPN , pYn qnPN Zufallsvariablen auf E und µ P PpEq. Angenommen P ˝
Xn´1 ÝÑ µ und dpXn , Yn q ÝÑ 0 in Wahrscheinlichkeit. Dann gilt
P ˝ Yn´1 ÝÑ µ, n Ñ 8.
Beweis. Sei F Ă E abgeschlossen. Für ε ą 0 sei F ε “ tx P E | dpx, F q ≤ εu und F0ε “ tx P
E | dpx, F q ă εu. Dann gilt
tYn P F u “ ptYn P F u X tdpXn , Yn q ă εuq Y ptYn P F u X tdpXn , Yn q ≥ εuq
“ ptYn P F u X tdpXn , Yn q ă εu X tXn P F0ε uq Y ptYn P F u X tdpXn , Yn q ≥ εuq
Ă tXn P F0ε u Y tdpXn , Yn q ≥ εu Ă tXn P F ε u Y tdpXn , Yn q ≥ εu.
Da F ε abgeschlossen ist folgt
lim sup PpYn P F q ≤ lim sup PpdpYn , Xn q ≥ εq ` lim sup PpXn P F ε q
nÑ8
nÑ8
“ lim sup P ˝
nÑ8
Xn´1 pF ε q
Wegen F ε Œ F für ε Ñ 0 folgt die Behauptung.
46
nÑ8
´1
ε
≤P˝X
pF q.
Wir zeigen noch einen alternativen Beweis.
Beweis. Wegen dem Satz von Portmanteau reicht es zu zeigen, dass für jede gleichmässig stetige
Funktion f : E ÝÑ R
ż
ż
´1
f pyqpP ˝ Yn qpdyq ÝÑ f pyqdµpyq, n Ñ 8
E
E
gilt. Sei ε ą 0 beliebig und wähle δ ą 0 derart, dass
ε
|f pxq ´ f pyq| ă , @x, y P E mit dpx, yq ă δ.
3
Wähle n0 P N derart, dass
ˇ
ˇ
ˇż
ˇ
ż
ˇ
ˇ
´1
ˇ f pyqpP ˝ Xn qpdyq ´ f pyqdµpyqˇ ă ε
ˇ
ˇ 3
ˇ
ˇ
E
sowie PpdpXn , Yn q ≥ δq ă
ε
3p2}f }8 `1q
E
für alle n ≥ n0 gilt. Dann folgt
ˇ
ˇ
ˇż
ˇ
ż
ˇ
ˇ
ˇ f pyqpP ˝ Yn´1 qpdyq ´ f pyqdµpyqˇ
ˇ
ˇ
ˇ
ˇ
E
E
ˇ
ˇ
ˇż
ˇ
ż
ˇ
ˇ
´1
ˇ
≤ |Epf pXn qq ´ Epf pYn qq| ` ˇ f pyqpP ˝ Xn qpdyq ´ f pyqdµpyqˇˇ
ˇ
ˇ
E
E
ż
ż
ε
≤
|f pXn q ´ f pYn q|dP `
|f pXn q ´ f pYn q|dP `
3
dpXn ,Yn q≥δ
≤ 2}f }8 PpdpXn , Yn q ≥ δq `
4
dpXn ,Yn qăδ
2ε
≤ ε.
3
Charakteristische Funktionen
Im letzten Kapitel haben wir Eigenschaften von Wahrscheinlichkeitsmaßen auf metrischen und
Polnischen Räumen untersucht. Dieses Kapitel widmet sich dem Studium von Wahrscheinlichkeitsmaßen auf E “ Rd . Für diesen Spezialfall ist es möglich jedem endlichen Maß µ auf Rd eine
komplex-wertige Funktion (charakteristische Funktion) µ
ppξq zuzuordnen. Schwache Konvergenz
von Wahrscheinlichkeitsmaßen sowie Existenz von Momenten können mithilfe der charakteristischen Funktion beschrieben werden.
47
4.1
Fouriertransformation von Funktionen
Für ξ, x P Rd sei ξ ¨x :“
d
ř
ξk xk “ xλ, Aλy das euklidische Skalarprodukt. hier und im folgenden
k“1
bezeichnet L1 pRd q den Raum aller messbaren, integrierbaren Funktionen auf Rd , d.h. für g P
L1 pRd q gilt
ż
|gpxq|mpdxq ă 8.
Rd
Definition 4.1. Sei g P L1 pRd q. Die Fouriertransformierte von g ist für ξ P Rd definiert durch
ż
ż
ż
iξ¨x
gppξq :“ e gpxqmpdxq :“ cospξ ¨ xqgpxqmpdxq ` i sinpξ ¨ xqgpxqmpdxq.
Rd
Rd
Rd
Die Definition ist wegen |eiξ¨x | “ 1 für alle ξ P Rd wohldefiniert.
Definition 4.2. Eine Funktion g : Rd ÝÑ C heißt positiv (semi-)definit, wenn für alle n P N
und alle ξ1 , . . . , ξn P Rd die Matrix pgpξi ´ ξj qq1≤i,j≤n positiv (semi-)definit ist.
Diese Definition ist äquivalent zu: Für alle n P N, alle λ “ pλ1 , . . . , λn q P Cn und alle
ξ1 , . . . , ξn P Rd gilt
n
ÿ
λj λi gpξj ´ ξi q ≥ 0.
(4.1)
i,j“1
Denn setze A :“ pgpξj ´ ξi qq1≤i,j≤n , d.h. Aij “ gpξj ´ ξi q. Dann gilt pAλqi “
n
ř
Aij λj und
j“1
folglich
xλ, Aλy “
n
ÿ
i“1
λi pAλqi “
n
ÿ
λi λj Aij “
i,j“1
n
ÿ
λi λj gpξj ´ ξi q.
i,j“1
Man beachte, dass die Matrix A insbesondere hermitsch ist, d.h. A “ AT . Es sei g eine positiv
(semi-)definite Funktion. Dann gilt:
• Für n “ 1 und λ P C folgt aus (4.1) |λ|2 gp0q ≥ 0, also gp0q ≥ 0.
ˆ
˙
gp0q gpξq
• Für n “ 2 mit ξ1 “ 0 und ξ2 “ ξ P
folgt, dass die Matrix
positiv
gp´ξq gp0q
(semi-)definit ist. Daraus folgt gp´ξq “ gpξq. Ferner muss die Determinante nicht-negativ
sein, also
gp0q2 ´ gpξqgp´ξq “ gp0q2 ´ |gpξq|2 ≥ 0
Rd
und somit |gpξq| ≤ gp0q.
Es sei Cc8 pRd q der Raum der glatten Funktionen mit kompaktem Träger. D.h. f P Cc8 pRd q, falls
f beliebig oft differenzierbar ist und f P Cc pRd q.
48
Lemma 4.3. [Wer00] Für jedes g P L1 pRd q und jedes ε ą 0 gibt es eine Funktion fε P Cc8 pRd q
mit
ż
}fε ´ g}L1 :“ |fε pxq ´ gpxq|mpdxq ă ε.
Rd
Die wichtigsten Eigenschaften der Fouriertransformierten von g sind im nächsten Satz zusammengefasst.
Satz 4.4. Es sei g P L1 pRd q. Es gelten die folgenden Eigenschaften.
ş
(a) |p
g pξq| ≤ }g}L1 und gpp0q “ gpxqmpdxq.
Rd
(b) gp ist gleichmässig stetig.
(c) gp verschwindet im Unendlichen, d.h. für alle ε ą 0 gibt es eine kompakte Menge Kε Ă Rd
derart, dass
|p
g pξq| ă ε, ξ R Kε .
(d) Ist g fast überall nicht-negativ, so ist gp positiv (semi-)definit.
Beweis. (a) Klar.
(b) Seien ξ1 , ξ2 P Rd und ε ą 0. Wähle eine kompakte Menge Kε Ă Rd derart, dass
ż
ε
|gpxq|mpdxq ă .
4
Kεc
Sei δ ą 0 mit δ ă
ε
2p1` sup |x|qp1`}g}L1 q .
Dann gilt für alle |ξ1 ´ ξ2 | ă δ
xPKε
ż
ż
iξ1 ¨x
|p
g pξ1 q ´ gppξ2 q| ≤
|e
iξ2 ¨x
´e
||gpxq|mpdxq ≤
ε
|eiξ1 ¨x ´ eiξ2 ¨x ||gpxq|mpdxq ` .
2
Kε
Rd
Es gilt
ˇ
ˇ
ˇ ξż2 ¨x
ˇ
ˇ
ˇ
ˇ
iξ1 ¨x
iξ2 ¨x
it ˇ
e dtˇ ≤ |pξ2 ´ ξ1 q ¨ x| ≤ |x| ¨ |ξ2 ´ ξ1 |
|e
´e
| “ ˇi
ˇ
ˇ
ˇ
ˇ ξ1 ¨x
woraus folgt
|p
g pξ1 q ´ gppξ2 q| ≤
ε
` }g}L1 sup |x| ¨ |ξ1 ´ ξ2 | ≤ ε.
2
xPKε
(c) Wir zeigen die Behauptung zuerst für g P Cc8 pRd q. Wähle R ą 0 derart, dass gpxq “ 0 für
R1
alle |x| ≥ R. Wähle R1 ą R und sei |ξ| ≥ R. Dann finden wir ein j P t1, . . . , du mit |ξj | ≥ ?
.
d
49
Mittels partieller Integration, wobei der Randterm wegen g P Cc8 pRd q verschwidet, erhalten wir
ż
ż
iξ¨x
eiξ¨x gpxqmpdxq
gppξq “ e gpxqmpdxq “
|x|≤R1
Rd
Beiξ¨x
ż
1
“
iξj
|x|≤R1
Daraus folgt
ż
1
gpxqmpdxq “ ´
Bxj
iξj
eiξ¨x
Bgpxq
mpdxq.
Bxj
|x|≤R1
? ›
›
›
›
1 ›› Bg ››
d ›› Bg ››
|p
g pξq| ≤
≤ 1 ›
.
|ξj | › Bxj ›L1
R Bxj ›L1
Die Behauptung folgt aus R1 ÝÑ 8. Für den allgemeinen Fall sei g P L1 pRd q, ε ą 0 und
fε P Cc8 pRd q derart, dass }g ´ fε }L1 ă ε. Die Behauptung folgt aus
|p
g pξq| ≤ |p
g pξq ´ fpε pξq| ` |fpε pξq| ≤ }g ´ fε }L1 ` |fpε pξq|.
(d) Es gilt
ˇ2
ż ˇˇ ÿ
ż ÿ
n
n
n
ˇ
ÿ
ˇ
iξj ¨x ˇ
λj e
λj λi eix¨pξj ´ξi q gpxqmpdxq “
λj λi gppξj ´ ξi q.
ˇ
ˇ gpxqmpdxq “
ˇj“1
ˇ
i,j“1
i,j“1
Rd
Rd
Wir betrachten das Beispiel einer Normalverteilung.
2
Beispiel 4.5. Es sei gpxq :“ e´α|x| mit α ą 0. Dann ist
gppξq “
Beachte, für α “
1
2
´π ¯d
2
α
|ξ|2
e´ 4α .
(4.2)
d
ist gppξq “ p2πq 2 gpξq.
Beweis. Es gilt
ż
gppξq “
e
iξ¨x ´α|x|2
e
mpdxq “
d ż
ź
2
eiξk ¨xk e´αxk mpdxq.
k“1 R
Rd
Also reicht es aus die Behauptung für d “ 1 zu beweisen. Für diesen Fall erhalten wir für ξ, x P R
¯
´
iξ 2
iξ 2
iξ
`p 2α
´α x2 ´2x 2α
q ´p 2α
q
2
e´αx eiξx “ e
ξ2
Daraus folgt
ż
e
iξx ´αx2
e
2
ξ
´ 4α
ż
R
R
50
iξ
2
e´αpx´ 2α q mpdxq.
mpdxq “ e
iξ
2
“ e´ 4α e´αpx´ 2α q .
Für das Integral erhalten wir mittels Cauchys Integralsatz (siehe [FL80]) und der Substitution
?
y “ αx
c
ż
ż
ż
iξ 2
1
π
´αpx´ 2α
´αx2
´x2
q
mpdxq “ e
mpdxq “ ?
e mpdxq “
.
e
α
α
R
R
R
Als nächstes wollen wir die Inverse Transformation finden.
Lemma 4.6. Es seien g, h P L1 pRd q. Dann gilt
ż
ż
gppξqhpξqmpdξq “ gpξqp
hpξqmpdξq.
Rd
Rd
Beweis. Mittels Fubini erhalten wir
ż
ż ż
ż
iξ¨x
gppξqhpξqmpdξq “
e gpxqhpξqmpdxqmpdξq “ gpξqp
hpξqmpdξq.
Rd
Rd Rd
Rd
Fubini ist anwendbar, da px, ξq ÞÝÑ gpxqhpξq integrierbar ist bezüglich mpdxqmpdξq.
Lemma 4.7. Für jedes g P Cb pRd q und jedes x P Rd gilt
ż
gpyq
e´
|x`y|2
4α
d
mpdyq ÝÑ gp´xq, α Ñ 0.
p4παq 2
Rd
Beweis. Übung.
Lemma 4.8. Es sei g P Cb pRd q X L1 pRd q derart, dass gp P L1 pRd q. Dann gilt
gp
ppxq “ p2πqd gp´xq, x P Rd .
2
Beweis. Sei α ą 0 und setze ϕx pξq :“ eiξ¨x e´α|ξ| . Für diese Funktion gilt nach (4.2)
ż
´π ¯d
2
2
2 ´ |ξ`x|
ϕ
px pξq “ eipξ`xq¨y e´α|y| mpdyq “
e 4α .
α
Rd
Damit erhalten wir
ż
ż
iξ¨x ´α|ξ|2
gppξqe e
px pξqmpdξq
mpdξq “ gpξqϕ
Rd
Rd
“
´π ¯d ż
2
α
2
gpξqe
´ |ξ`x|
4α
Rd
ż
d
mpdξq “ p2πq
gpξq
Rd
e´
|ξ`x|2
4α
d
p4παq 2
Betrachten wir den Grenzwert α Ñ 0, so folgt die Behauptung aus Lemma 4.7.
51
mpdξq.
Satz 4.9. Sei g P L1 pRd q. Definiere die Abbildung
ż
1
gqpxq :“
e´iξ¨x gpξqmpdξq, x P Rd .
p2πqd
Rd
Dann gilt für alle g P Cb pRd q X L1 pRd q derart, dass gp P L1 pRd q
p “ g “ gp
q.
gq
1
gpp´xq
p2πqd
für alle g P L1 pRd q gilt. Sei g P Cb pRd q X L1 pRd q mit
1 p
ppxq “ p2πq
pp´xq “ gpxq für alle x P Rd . Analog lässt sich
gp P L1 pRd q. Aus Lemma 4.8 folgt gq
dg
die andere Identität zeigen.
Beweis. Beachte, dass gqpxq “
4.2
Charakteristische Funktion für Maße
Definition 4.10. Sei µ ein endliches Maß auf Rd . Die charakteristische Funktion von µ ist die
Fouriertransformierte von µ gegeben durch
ż
µ
ppξq :“ eiξ¨x µpdxq, ξ P Rd .
Rd
Bemerkung 4.11.
8
ř
(a) Sei µ “
ak δxk mit ak ≥ 0 und xk P Rd derart, dass
8
ř
ak “ 1.
k“1
k“1
Dann ist µ ein Wahrscheinlichkeitsmaß auf Rd und es gilt
µ
ppξq “
8
ÿ
ak eiξ¨xk , ξ P Rd .
k“1
(b) Hat µ eine Dichte, d.h. µpdxq “ ppxqmpdxq, so ist
ż
ppξq “ eiξ¨x ppxqmpdxq “ pppxq.
µ
Rd
Die wichtigsten Eigenschaften sind im nächsten Satz zusammengefasst.
Satz 4.12. Es sei µ ein endliches Maß auf Rd . Dann gelten die folgenden Eigenschaften.
µpξq| ≤ µpRd q “ µ
pp0q für alle ξ P Rd .
(a) |p
p ist gleichmässig stetig.
(b) µ
(c) µ
p ist positiv (semi-)definit.
Beweis. Übung.
Wir betrachten einige Beispiele.
52
Beispiel 4.13.
(a) Benoulli Verteilung: µ “ pδ1 ` p1 ´ pqδ0 . Dann ist
µ
ppξq “ peiξ ` p1 ´ pq “ 1 ` pp1 ´ eiξ q, ξ P R.
n ` ˘
ř
n k
n´k δ . Dann ist
k
k p p1 ´ pq
(b) Binomialverteilung: µ “
k“0
ppξq “ p1 ´ p ` peiξ qn , ξ P R.
µ
1
(c) Standardnormalverteilung: Im eindimensionalen Fall sei µpdxq “ p2πq´ 2 e´
ist
ξ2
ppξq “ e´ 2 , ξ P R.
µ
d
Für den d-dimansionalen Fall sei µpdxq “ p2πq´ 2 e´
ppξq “ e´
µ
|ξ|2
2
|x|2
2
x2
2
mpdxq. Dann
. Dann gilt
, ξ P Rd .
(d) Normalverteilung im Rm : Sei µ eine Normalverteilung auf dem Rm . Dann gibt es eine
m ˆ d-Matrix A und b P Rm mit µ “ ν ˝ T ´1 , wo T pxq “ Ax ` b und
d
νpdxq “ p2πq´ 2 e´
|x|2
2
mpdxq.
Damit folgt
ż
ż
e
ppξq “
µ
iξ¨x
eiξ¨T pxq νpdxq
µpdxq “
Rm
Rd
ż
“ eiξ¨b
e
ipAT ξq¨x
1
νpdxq “ eiξ¨b e´ 2 |A
t ξ|2
1
“ eiξ¨b e´ 2 xξ,pAA
t qξy
.
Rd
1
(e) Uniforme Verteilung: Sei µpdxq “ 1p´a,aq pxq 2a
mpdxq mit a ą 0. Dann ist
#
µ
ppξq “
(f ) Cauchy Verteilung: Sei µpdxq “
sinpξaq
ξa ,
ξ‰0
1,
sonst
1
c
π c2 `x2 mpdxq
, ξ P R.
mit c ą 0. Dann gilt
ppξq “ e´c|ξ| , ξ P R.
µ
Der nächste Satz zeigt, dass die charakteristische Funktion das Maß eindeutig festlegt.
p “ νp. Dann gilt µ “ ν.
Satz 4.14. Seien µ, ν zwei endliche Maße auf Rd mit µ
53
pp0q “ νpp0q “ νpRd q. Ist µpRd q “ 0, so ist nichts zu zeigen. Sei also
Beweis. Es gilt µpRd q “ µ
µpRd q ą 0. Definiere neue Maße µ1 :“ µpR1 d q µ sowie ν 1 :“ νpR1 d q ν. Dann gilt µp1 “ νp1 . Es reicht
daher aus die Behauptung für Wahrscheinlichkeitsmaße zu beweisen.
Die kompakten Mengen bilden ein X-stabiles Erzeugendensystem der Borel-σ-Algebra BpRd q.
Es genügt also µpKq “ νpKq für alle kompakten Mengen K Ă Rd zu zeigen. Sei K Ă Rd kompakt
und
$
’
xPK
&1,
1 .
fm pxq “ 0,
dpx, Kq ≥ m
’
%
1 ´ mdpx, Kq, sonst
Dann gilt 0 ≤ fm ≤ 1, fm ist stetig und fm Œ 1K für m Ñ 8. Wir zeigen
ż
ż
fm pxqdµpxq “ fm pxqdνpxq, m P N.
Rd
(4.3)
Rd
Dann folgt mit dem Satz von Lebesgue νpKq “ µpKq. Allgemeiner zeigen wir (4.3) für alle
f : Rd ÝÑ R mit
• 0 ≤ f ≤ 1.
• f P Cc pRd q.
Sei ε ą 0 beliebig. Da f kompakten Träger hat, können wir N P N wählen mit
tx P Rd | f pxq ‰ 0u Ă r´N, N sd “: BN
c q ă ε, νpB c q ă ε. NAch dem Weierstraßschen Approximationssatz (siehe [Wer00] für
und µpBN
N
den Beweis in einer Dimension) gibt es eine Funktion
gε pxq “
m
ÿ
π
ε
cεj ei N xξj ,xy
j“1
mit cεj P C, ξjε P Zd , }gε }8 ≤ }f }8 und
sup |f pxq ´ gpxq| ≤ ε.
xPBN
Es gilt mit f |BNc “ 0 und µpBN q ≤ 1
ˇ
ˇ
ˇż
ˇ
ż
ż
ˇ
ˇ
ˇ pf ´ gε qdµˇ ≤
|f ´ gε |dµ `
|f | ` |gε |dµ
ˇ
ˇ
ˇ
ˇ d
c
BN
R
BN
c
≤ εµpBN q ` }gε }8 µpBN
q ≤ p1 ` }f }8 qε.
Analog lässt sich zeigen, dass
ˇ
ˇ
ˇż
ˇ
ˇ
ˇ
ˇ pf ´ gε qdν ˇ ≤ p1 ` }f }8 qε.
ˇ
ˇ
ˇ d
ˇ
R
54
Insgesamt erhalten wir
ˇ ˇ
ˇ
ˇ ˇ
ˇ ˇ
ˇ
ˇ ˇż
ˇ
ˇ ˇż
ˇ ˇż
ˇż
ż
ż
ˇ ˇ
ˇ
ˇ ˇ
ˇ ˇ
ˇ
ˇ f dµ ´ f dν ˇ ≤ ˇ pf ´ gε qdµˇ ` ˇ gε dµ ´ gε dν ˇ ` ˇ pgε ´ f qdν ˇ
ˇ ˇ
ˇ
ˇ ˇ
ˇ ˇ
ˇ
ˇ ˇ d
ˇ
ˇ ˇ d
ˇ ˇ d
ˇ d
Rd
R
Rd
R
R
R
ˇ
ˇ
ˇż
ˇ
ż
ˇ
ˇ
ˇ
≤ 2ε ` ˇ gε dµ ´ gε dν ˇˇ .
ˇ d
ˇ
d
R
R
Die Behauptung folgt aus
ż
gε dµ “
Rd
m
ÿ
ż
π
j“1
ε
ei N xξj ,xy dµpxq “
cεj
m
ÿ
j“1
Rd
ż
π
ε
ż
ei N xξj ,xy dνpxq “
cεj
Rd
gε dν.
Rd
Satz 4.15. [Jac01, Theorem 3.5.7] Eine Funktion g : Rd ÝÑ C ist genau dann die charakteristische Funktion von einem endlichen Maß µ auf Rd , wenn die folgenden Eigenschaften gelten:
(i) g ist stetig.
(ii) g ist positiv (semi-)definit.
In diesem Fall ist gp0q “ µpRd q. Insbesondere ist µ ein Wahrscheinlichkeitsmaß genau dann,
wenn gp0q “ 1.
p
Im Folgenden wollen wir weitere Eigenschaften von µ aus der charakteristischen Funktion µ
ableiten.
Lemma 4.16. Für jedes ϕ P L1 pRd q X Cb pRd q gibt es eine Folge pϕn qnPN Ă L1 pRd q X Cb pRd q
pn P L1 pRd q derart, dass ϕn pxq ÝÑ ϕpxq für alle x P Rd .
mit ϕ
d
|x|2
Beweis. Sei pα pxq “ p4παq´ 2 e´ 4α und
ż
ϕα pxq :“
ϕpx ´ yqpα pyqmpdyq.
Rd
Dann gilt
ż
|ϕα pyq| ≤ }ϕ}8
pα pyqmpdyq “ }ϕ}8 .
Rd
Da pα pyqmpdyq schwach gegen δ0 konvergiert, folgt ϕα pyq ÝÑ ϕpyq für alpha Ñ 8 und alle
pα “ ϕ
p ¨ ppα . Da ϕ
p beschränkt ist und ppα P L1 pRd q folgt die Behauptung.
y P Rd . Ferner gilt ϕ
Satz 4.17. Es sei µ ein endliches Maß auf Rd . Es gelten die folgenden Aussagen.
55
p P L1 pRd q, so hat µ eine Dichte 0 ≤ p P Cb pRd q, welche im Unendlichen verschwindet
(a) Ist µ
und gegeben ist durch
ż
1
ppξqmpdξq, x P Rd .
ppxq :“
e´iξ¨x µ
(4.4)
p2πqd
Rd
(b) Ist µ
p P L1 pRd q derart, dass für ein m ≥ 1
ż
|ξ|m |p
µpξq|mpdξq ă 8.
Rd
Dann hat p stetige Ableitungen bis zur Ordnung m. In diese Fall gilt für alle 0 ≤ k ≤ m
und alle 1 ≤ j1 , . . . , jk ≤ d
ż
B k ppxq
p´iqk
ppξqmpdξq.
“
e´iξ¨x ξj1 ¨ ¨ ¨ ξjk µ
Bxj1 ¨ ¨ ¨ Bxjk
p2πqd
Rd
(c) Ist
ż
|x|m µpdxq ă 8
Rd
für ein m ≥ 1. Dann hat µ
p stetige partielle Ableitungen bis zur Ordnung m und es gilt für
alle 0 ≤ k ≤ m und 1 ≤ j1 , . . . , jk ≤ d
ż
ppxiq
Bk µ
“ ik xj1 ¨ ¨ ¨ xjk ei¨x µpdxq.
Bξj1 ¨ ¨ ¨ Bξjk
Rd
Beweis. (a) Für jedes ϕ P L1 pRd q gilt ϕ ¨ µ
p P L1 pRd q und folglich
ż
ż ż
ż
iξ¨x
p
ϕpxqp
µpxqmpdxq “
ϕpxqe µpdξqmpdxq “ ϕpξqµpdξq.
Rd
Rd Rd
Rd
Man beachte, dass alle Integrale existieren und somit der Satz von Fubini anwendbar ist. Offenµ}L1 .
sichtlich definiert (4.4) eine stetige, im Unendlich verschwindende Funktion p mit |ppxq| ≤ }p
p P L1 pRd q
Wir erhalten für jedes ϕ P L1 pRd q X Cb pRd q mit ϕ
ż
ż
ż
d
p
p
pp´xqmpdxq “ ϕp´xqµ
ppxqmpdxq
p2πq
ϕpxqppxqmpdxq “ ϕpxqµ
Rd
Rd
Rd
ż
ż
“
Rd
Rd
56
ż
{
{
ϕp´¨qpxqµpdxq
“ p2πqd
{ µpxqmpdxq “
ϕp´¨qpxqp
ϕpxqµpdxq.
Rd
Aus Lemma 4.16 und dem Satz von Lebesgue folgt für alle ϕ P L1 pRd q X Cb pRd q
ż
ż
ϕpxqppxqmpdxq “ ϕpxqµpdxq.
Rd
Rd
Die Behauptung folgt aus Cc pRd q Ă L1 pRd q X Cb pRd q.
(b) Die Behauptung folgt aus der Darstellung (4.4) und denselben Argumenten wir für Teil (c).
(c) Wir zeigen nur den Fall m “ 1. Der allgemeine Fall folgt dann über Induktion. Sei ej der
Basisvektor im Rd in Richtung j. Dann ist für h ą 0
ppξ ` hej q ´ µ
µ
ppxiq
“
h
ż
eipξ`hej q¨x ´ eiξ¨x
µpdxq “
h
Rd
ż
eiξ¨x
eixj h ´ 1
µpdxq.
h
Rd
ixj h
Es gilt e h ´1 ÝÑ ixj und nach Lemma 8.1 (siehe Appendix) gibt es eine stetige Funktion Θ1
mit |Θ1 pxq| ≤ 1 derart, dass eixk h “ 1 ` ixj hΘ1 pxj hq. Daraus folgt
eixj h ´ 1
“ ixj Θ1 pxj hq
h
ˇ ix h ˇ
ˇ j
ˇ
und somit ˇ e h ´1 ˇ ≤ |xj | für alle h ą 0. Dieses liefert eine integrierbare Majorante, also folgt
aus dem Satz von Lebesgue
ż
µpξq
Bp
“ i xj eiξj ¨x µpdxq.
Bξj
Rd
Die Ableitung ist stetig, ebenfalls aus dem Satz von Lebesgue.
Bemerkung 4.18. Die Momente von µ haben die Darstellung
ż
pp0q
1 Bk µ
“
xj1 ¨ ¨ ¨ xjk µpdxq.
ik Bξj1 ¨ ¨ ¨ Bξjk
Rd
Für x P Rd setze gx pyq :“ xx, yy “ x ¨ y.
Satz 4.19. (Satz von Cramer-Wald) Seien µn , µ P PpRd q. Dann sind äquivalent:
(a) µn ÝÑ µ schwach für n Ñ 8.
(b) µn ˝ gx´1 ÝÑ µ ˝ gx´1 schwach für n Ñ 8 und alle x P Rd .
Beweis. paq ùñ pbq: Folgt aus der Stetigkeit von gx .
pbq ùñ paq: Die Familie tµn ˝ gx´1 | n P Nu ist nach Voraussetzung für jedes x P Rd relativ
kompakt und folglich straff. Seien e1 , . . . , ed P Rd die Einheitsvektoren und ε ą 0 beliebig. Dann
gibt es für jedes i “ 1, . . . , d eine kompakte Menge Ki Ă R mit
ε
pµn ˝ ge´1
qpKi q ≥ 1 ´ , n P N.
i
d
57
Setze K :“
d
Ş
i“1
ge´1
pKi q. Es ist nicht schwer zu zeigen, dass K abgeschlossen und beschränkt ist,
i
also kompakt. Ferner gilt
˜
µn pK c q “ µn
d
ď
¸
pge´1
pKi qqc
i
≤
d
ÿ
pµn ˝ ge´1
qpKic q ≤ d
i
i“1
i“1
ε
“ε
d
und folglich ist tµn | n P Nu straff. Nach dem Satz von Prokhorov ist die Folge auch relativ
kompakt. Sei pµ1n qnPN eine konvergente Folge in tµn | n P Nu und sei µ1 P PpRd q der Grenzwert.
Dann gilt auch µ1n ˝ gx´1 ÝÑ µ1 ˝ gx´1 schwach für alle x P Rd . Da µ1n ˝ gx´1 eine Teilfolge von
µn ˝ gx´1 ist, konvergiert µ1n ˝ gx´1 gegen denselben Grenzwertwie µn ˝ gx´1 , d.h. µ ˝ gx´1 “ µ1 ˝ gx´1
für alle x P Rd . Wegen
ż
ż
ppξq “ eiξ¨x µpdxq “ eit µ ˝ gξ pdtq “ µp1 pξq, ξ P Rd
µ
Rd
folgt µ “
µ1 .
R
Die Behauptung folgt aus Lemma 3.13.
Satz 4.20. (Levys Stetigkeitssatz) Seien pµn qnPN Wahrscheinlichkeitsmaße auf Rd . Dann gelten
die folgenden Aussagen.
(a) Ist µn ÝÑ µ schwach, so gilt auch µ
xn ÝÑ µ
p punktweise auf Rd .
pn pξq ÝÑ f pξq für alle
(b) Falls es eine in 0 stetige Funktion f : Rd ÝÑ C gibt derart, dass µ
d
d
p “ f und µn ÝÑ µ
ξ P R . Dann gibt es ein Wahrscheinlichkeitsmaß µ auf R mit µ
schwach.
Insbesondere gilt für jede Folge pµn qnPN Ă PpRd q und µ P PpRd q
µn ÝÑ µ schwach ðñ µ
pn pξq ÝÑ µ
ppξq, @ξ P Rd .
Beweis. (a) Klar, da x ÞÝÑ eiξ¨x stetig und beschränkt ist.
(b) Wir zeigen nur den Fall d “ 1.
Schritt 1: tµn | n P Nu ist straff.
Für alle α ą 0 gilt
żα
żα ż
ż żα
itx
µ
pn ptqdt “
e µn pdxqdt “
eitx dtµn pdxq
´α
“
´α R
ż iαx
e
R ´α
e´iαx
´
ix
ż
µn pdxq “
R
2 sinpαxq
µn pdxq.
x
R
Es folgt
żα
ż
pn ptqqdt “ 2α ´
p1 ´ µ
´α
2 sinpαxq
µn pdxq
x
R
¨
ż
“ 2α ˝1 ´
˛
˙
ż ˆ
sinpαxq
sinpαxq
‚
µn pdxq “ 2α
1´
µn pdxq.
αx
αx
R
R
58
Der Integrand ist nicht-negativ und es gilt
1´
Daraus folgt
sinpαxq
1
≥ , |αx| ≥ 2.
αx
2
żα
ˆ„
p1 ´ µ
pn ptqqdt ≥ αµn
2 2
´ ,
α α
c ˙
.
´α
Mit β “
2
α
folgt
µn pr´β, βsc q ≤
1
α
2
żα
pn ptqqdt “
p1 ´ µ
β
2
żβ
pn ptqqdt.
p1 ´ µ
´ β2
´α
pn p0q “ 1. Also gibt es zu ε ą 0 ein β ą 0
Nach Voraussetzung ist f stetig in 0 und f p0q “ lim µ
nÑ8
mit
ε
2
|1 ´ f ptq| ≤ , |t| ≤ .
4
β
Dann ist
2
2
żβ
żβ
ε
2
β
εβ 4
pn ptqqdt “
“
lim
p1 ´ µ
p1 ´ f ptqqdt ≤
nÑ8 β
2
42β
2
´ β2
´ β2
und es existiert ein n0 pεq “ n0 P N mit
ˇ
ˇ
2
2
ˇ
ˇ
ˇ
ˇ żβ
żβ
ˇ ε
ˇβ
β
ˇ
p1 ´ µ
pn ptqqdt ´
p1 ´ f ptqqdtˇˇ ă , n ≥ n0 .
ˇ2
2
ˇ 2
ˇ
ˇ
ˇ ´ β2
´ β2
2
Damit ist also
2
β
şβ
pn ptqqdt ă ε für alle n ≥ n0 , d.h.
p1 ´ µ
´ β2
µn pr´β, βsc q ≤ ε, n ≥ n0 .
Für n ă n0 gibt es ein βn ą 0 mit µn pr´βn , βn sc q ≤ ε. Sei β0 :“ maxtβ, β1 , . . . , βn0 ´1 u, so gilt
µn pr´β0 , β0 sc q ≤ ε, n ≥ 1.
Schritt 2. Sei pµnk qkPN eine Teilfolge von pµn qnPN . Dann ist tµnk | k P Nu straff und damit nach
dem Satz von Prokhorov auch relativ kompakt. Folglich gibt es eine Teilfolge pµnkl qlPN welche
schwach gegen µ1 konvergiert. Damit folgt
pnkl pξq “ µp1 pξq, ξ P R.
f pξq “ lim µ
lÑ8
Die Behauptung folgt aus Lemma 3.13.
59
4.3
Charakteristische Funktion für Zufallsvariablen
Definition 4.21. Für eine Zufallsvariable X mit Werten in Rd ist die charakteristische Funktion
definiert durch
ϕX pξq :“ Epeiξ¨X q “ P{
˝ X ´1 pξq, ξ P Rd .
Korollar 4.22. Sei X eine Zufallsvariable mit Werten in Rd . Dann gelten die folgenden Aussagen:
(a) Ist ϕX P L1 pRd q, so hat X eine Dichte p P Cb pRd q, welche im Unendlichen verschwindet
und gegeben ist durch
ż
1
ppxq “
e´iξ¨x ϕX pξqmpdξq.
p2πqd
Rd
(b) Ist ϕX P L1 pRd q und gilt für ein m ≥ 1
ż
|ξ|m |ϕX pξq|mpdξq ă 8,
Rd
so hat p stetige Ableitungen bis zur Ordnung m und für 0 ≤ k ≤ m, 1 ≤ j1 , . . . , jk ≤ d gilt
ż
B k ppxq
p´iqk
ξj1 ¨ ¨ ¨ ξjk e´iξ¨x ϕX pξqmpdξq.
“
Bxj1 ¨ ¨ ¨ Bxjk
p2πqd
Rd
(c) Es gebe ein m P N derart, dass
Ep|X|m q ă 8.
Dann hat ϕX stetige Ableitungen bis zur Ordnung m und es gilt für alle 0 ≤ k ≤ m,
1 ≤ j1 , . . . , jk ≤ d
B k ϕX pξq
“ ik EpXj1 ¨ ¨ ¨ Xjk eiξ¨X q.
Bξj1 ¨ ¨ ¨ Bξjk
Insbesondere gilt für die Momente von X die Darstellung
EpXj1 ¨ ¨ ¨ Xjk q “
1 B k ϕX p0q
.
ik Bξj1 ¨ ¨ ¨ Bξjk
Satz 4.23. Seien X, Y unabhängige Zufallsvariablen mit Werten in Rd . Dann gilt
ϕX pξqϕY pξq “ ϕX`Y pξq, ξ P Rd .
Beweis. Klar.
Satz 4.24. Sei X eine Zufallsvariable mit Werten in Rd sowie Y eine Zufallsvariable mit Werten
in Rm . Seien ϕX , ϕY , ϕpX,Y q die dazugehörigen charakteristischen Funktionen. Genau dann sind
X, Y unabhängig, wenn
ϕX pξ1 qϕY pξ2 q “ ϕpX,Y q pξ1 , ξ2 q, ξ1 P Rd , ξ2 P Rm .
60
(4.5)
Beweis. Seien X, Y unabhängig. Dann ist P ˝ pX, Y q´1 “ P ˝ X ´1 b P ˝ Y ´1 und folglich
ż
ϕpX,Y q pξ1 , ξ2 q “
eiξ1 ¨x eiξ2 ¨x P ˝ pX, Y q´1 pdx, dyq
Rd ˆRm
ż
ż
eiξ1 ¨x P ˝ X ´1 pdxq
“
eiξ2 ¨y P ˝ Y ´1 pdyq
Rm
Rd
“ ϕX pξ1 qϕY pξ2 q.
Umgekehrt gelte (4.5). Seien X 1 , Y 1 unabhängige Zufallsvariablen mit charakteristischen Funktionen ϕX sowie ϕY . Sei ϕpX 1 ,Y 1 q die charakteristische Funktion von pX 1 , Y 1 q. Dann gilt
ϕpX 1 ,Y 1 q pξ1 , ξ2 q “ ϕX 1 pξ1 qϕY 1 pξ2 q “ ϕX pξ1 qϕY pξ2 q “ ϕpX,Y q pξ1 , ξ2 q
und folglich
P ˝ pX, Y q´1 “ P ˝ pX 1 , Y 1 q´1 “ P ˝ X 1´1 b P ˝ Y 1´1 “ P ˝ X ´1 b P ˝ Y ´1 .
Korollar 4.25. Sei X “ pX1 , . . . , Xd q eine Rd -wertige Zufallsvariable. Genau dann sind X1 , . . . , Xd
unabhängig, wenn
ϕX pξq “ ϕX1 pξ1 q ¨ ¨ ¨ ϕXd pξd q, @ξ “ pξ1 , . . . , ξd q P Rd .
Bemerkung 4.26. Sei X eine Rd -wertige Zufallsvariable, A eine m ˆ d Matrix und b P Rm .
Dann hat Y :“ AX ` b die charakteristische Funktion
ϕY pξq “ eiξ¨b ϕX pAt ξq, ξ P Rm
Beispiel 4.27. (a) Cauchy-Verteilung: Seien X, Y unabhängig und Cauchy verteilt mit Parameter c ą 0, d.h. diese haben die Verteilung
µpdxq “
1
c
mpdxq.
2
π c ` x2
Sei λ P p0, 1q. Dann gilt
ϕλX`p1´λqY pξq “ ϕX pλξqϕY pp1 ´ λqξq “ e´cλ|ξ| e´cp1´λq|ξ| “ e´c|ξ| .
Also ist λX ` p1 ´ λqY wieder Cauchy verteilt mit Parameter c.
2 q, Y „ N pµ , σ 2 q mit
(b) Seien X, Y unabhängig und normalverteilt, d.h. X „ N pµX , σX
Y
Y
2
2
µX , µY P R und σX , σY ą 0. Dann ist
2
2 ξ
2
ϕX`Y pξq “ ϕX pξqϕY pξq “ eiµX ξ´σX
2 ` σ 2 q.
Also ist X ` Y „ N pµX ` µY , σX
Y
61
2
2 ξ
2
eiµY ξ´σY
2
2
ξ2
“ eipµX `µY qξ´pσX `σY q 2 .
Als nächstes zeigen wir, dass die Kovarianzmatrix und der Erwartungswert die Normalverteilung eindeutig festlegen.
Satz 4.28. Für jedes b P Rd und jede positiv (semi-)definite, symmetrische Matrix Σ gibt es
genau eine Normalverteilung mit Erwartungswert b und Kovarianzmatrix Σ.
Für den Existenzbeweis brauchen wir folgendes Lemma aus der Linearen Algebra.
Lemma 4.29. Sei Σ eine symmetrische, positiv (semi-)definite reellwertige d ˆ d-Matrix. Dann
gibt es eine reellwertige Matrix A mit Σ “ AAt .
Beweis. Jede symmetrische, reellwertige Matrix ist orthogonal diagonalisierbar. Es gibt daher
eine orthogonale Matrix S mit
SΣS t “ diagpλ1 , . . . , λd q
wo λ1 , . . . , λd die Eigenwerte von Σ bezeichnen. Da Σ positiv (semi-)definit ist, sind die Eigenwerte nicht-negativ. Definiere eine neue Matrix
a
a
1
D 2 “ diagp λ1 , . . . , λd q.
1
1
1
1
1
Dann gilt pD 2 qt “ D 2 und D 2 pD 2 qt “ D. Sei A :“ SD 2 S t . Dann gilt
1
1
1
1
AAt “ SD 2 S t pSD 2 S t qt “ SD 2 S t pS t qt pD 2 qt S t “ SDS t “ ΣT “ Σ.
Beweis. (Satz 4.28) Ist µ eine Normalverteilung mit Erwartungswert b und Kovarianzmatrix Σ,
so gilt
1
µ
ppξq “ eixξ,by e´ 2 xξ,Σξy , ξ P Rd .
Dieses zeigt die Eindeutigkeit. Für die Existenz wähle A mit Σ “ AAt und benutze die Definition
der Normalverteilung.
Satz 4.30. Sei X “ pX1 , . . . , Xd q eine normalverteilte Zufallsvariable mit Erwartungswert b P
Rd und Kovarianzmatrix Σ. Dann gelten die folgenden Aussagen:
(a) Sei a “ pa1 , . . . , ad q P Rd und definiere
Y :“
d
ÿ
ak Xk “ xa, Xy.
k“1
Dann ist Y eine normalverteilte Zufallsvariable mit Erwartungswert xa, by und Varianz
xa, Σay.
(b) Xj sind für j “ 1, . . . , d normalverteilt mit Erwartungswert bj und Varianz Σjj .
(c) Sind die Xj paarweise unkorreliert, so ist pX1 , . . . , Xd q unabhängig.
Umgekehrt, seien X1 , . . . , Xd unabhängige, normalverteilte Zufallsvariablen mit Erwartungswert
bj P R und Varianz σj2 . Dann ist X “ pX1 , . . . , Xd q normalverteilt mit Erwartungswert b “
pb1 , . . . , bd q P Rd un Kovarianzmatrix Σij “ δij σj2 .
Beweis. (a)
62
5
5.1
Grenzwertsätze
Gesetze der großen Zahlen
Sei pXn qnPN Ă L1 eine Folge von Zufallsvariablen, mn :“ EpXn q, Mn :“
werte und Sn :“
n
ř
n
ř
mk die Erwartungs-
k“1
Xk .
k“1
Definition 5.1. Die Folge pXn qnPN erfüllt das schwache Gesetz der großen Zahlen, wenn
ˆ
˙
1
|Sn ´ Mn | ≥ ε “ 0, @ε ą 0.
lim P
nÑ8
n
Die Folge Xn erfüllt das starke Gesetz der großen Zahlen, wenn
Sn ´Mn
n
ÝÑ 0 fast sicher.
Sehen wir jede Variable Xn als ein Zufallsexperiment mit Ausgang Xn an, so ist n1 Sn der
Mittelwert der Ausgänge der ersten n Experimente. Folglich ist n1 Mn der erwartete (deterministische!) Mittelwert von n1 Sn . Das Gesetz der großen Zahlen besagt, dass nach hinreichend
vielen Experimenten die Ausgänge der Experimente sich im Mittel deterministisch Verhalten.
Satz 5.2. Seien Xn P L2 unkorreliert und es gelte varpXn q ≤ C ă 8 für alle n P N und eine
Konstante C ą 0. Dann gilt
1
EppSn ´ Mn q2 q ÝÑ 0, n Ñ 8.
n2
Insbesondere gilt das schwache Gesetz der großen Zahlen.
Beweis. Es gilt EpSn q “ Mn und folglich
˘ 1
1
1 `
EppSn ´ Mn q2 q “ 2 E pSn ´ EpSn qq2 “ varpSn q
2
n
n
n
n
ÿ
C
1
varpXk q ≤ .
“ 2
n k“1
n
Aus der Tschebyscheff Ungleichung folgt
P p|Sn ´ Mn | ≥ εnq ≤
1
ε2 n 2
EppSn ´ Mn q2 q
und somit die Behauptung.
Im folgenden wollen wir zeigen, dass unter denselben Voraussetzungen bereits das starke
Gesetz der großen Zahlen gilt.
Lemma 5.3. (stochastisch schnelle Konvergenz) Sei Xn eine Folge von Zufallsvariablen mit
8
ÿ
Pp|Xk | ≥ εq ă 8, @ε ą 0.
k“1
´
Dann gilt P
¯
lim Xn “ 0 “ 1.
nÑ8
63
Beweis. Nach dem ersten Borel-Cantelli Lemma gilt
˜
¸
ˆ
˙
č ď
P lim supt|Xn | ≥ εu “ P
t|Xk | ≥ εu “ 0.
nÑ8
n≥1 k≥n
Insbesondere gilt
lim supt|Xn | ≥ εu
1“P
˜
˙c ˙
ˆˆ
¸
ď č
t|Xk | ă εu .
“P
nÑ8
n≥1 k≥n
D.h. für fast alle ω gibt es ein npωq P N sodass für alle k ≥ npωq gilt |Xk pωq| ă ε.
Satz 5.4. Seien Xn P L2 paarweise unkorreliert mit varpXn q ≤ C ă 8 für ein C ą 0 und alle
n ≥ 1. Dann gilt das starke Gesetz der großen Zahlen.
Beweis. Wir betrachten zuerst den Fall EpXn q “ 0. In diesem Fall ist Mn “ 0.
Schritt 1. Aus der Tschebyscheff Ungleichung folgt
2
k
1 1
1 ÿ
C 1
2
Pp|Sk2 | ≥ εk q ≤ 2 4 varppSk2 q q “ 2 4
varpXj q ≤ 2 2
ε k
ε k j“1
ε k
2
Insbesondere gilt
8
ÿ
8
C ÿ 1
Pp|Sk2 | ≥ k εq ≤ 2
ă 8, @ε ą 0.
ε k“1 k 2
k“1
2
Nach Lemma 5.3 gibt es N1 P F mit PpN1 q “ 0 und
lim Sk2 pωq “ 0, ω P ΩzN1 .
kÑ8
Schritt 2. Definiere eine neue Zufallsvariable
ˇ
ˇ
ˇ
ˇ
ˇ l
ˇ
k2
l
ˇÿ
ˇ
ÿ
ÿ
ˇ
ˇ
ˇ
ˇ
ˇ
ˇ.
Xj ´
Xj ˇ “
Dk2 :“
max
max
X
ˇ
j
ˇ
ˇ
ˇ
k2 ăl≤pk`1q2 ˇ
k2 ăl≤pk`1q2 ˇ
ˇ
2
j“1
j“1
j“k `1
Für jedes ε ą 0 folgt aus der Tschebyscheff Ungleichung
,˛
$ˇ
ˇ
¨
2
ˇ ÿ
ˇ
˙
ˆ
pk`1q
l
.
&
ď
ˇ
ˇ
Dk 2
ˇ
ˇ ≥ εk 2 ‚
˝
≥
ε
“
P
X
P
j
ˇ
%ˇ
k2
ˇ
l“k2 `1 ˇj“k2 `1
ˇ
ˇ
˛
¨
2
ˇ ÿ
ˇ
pk`1q
ÿ
ˇ l
ˇ
1
ˇ
˝
≤
P ˇ
Xj ˇˇ ≥ εk 2 ‚ ≤ 2 4
ε k
ˇj“k2 `1 ˇ
l“k2 `1
≤
“
C
ε2 k 4
C
2
ε k4
pk`1q2
ÿ
l“k2 `1
pl ´ k 2 q ≤
C
ε2 k 4
pk`1q2
ÿ
p2k ` 1q ≤
l“k2 `1
64
2
pk`1q
ÿ
¨
var ˝
l“k2 `1
l
ÿ
j“k2 `1
pk`1q2
ÿ `
pk ` 1q2 ´ k 2
˘
l“k2 `1
˘
4C `
8C
2
2
pk
`
1q
´
k
“ 2 2.
2
3
ε k
ε k
˛
Xj ‚
Nach Lemma 5.3 gibt es N2 P F mit PpN2 q “ 0 und
lim
kÑ8
Dk2 pωq
“ 0, ω P ΩzN2 .
k2
Schritt 3. Für n P N sei k “ kpnq P N mit k 2 ≤ n ă pk ` 1q2 . Dann gilt für alle ω P ΩzpN1 Y N2 q
ˇ
ˇ
n
ˇ
1 ˇˇ ÿ
D 2 pωq
ˇ
Xk pωqˇ ≤ Sk2 pωq ` k 2 .
|Sn pωq| ≤ ˇ
ˇ
n ˇj“1
k
Schritt 4. Für den allgemeinen Fall sei Yn :“ Xn ´ EpXn q. Dann ist Yn P L2 mit EpYn q “ 0 und
varpYn q “ varpXn q ≤ C ă 8, n P N.
Ferner gilt covpYn , Ym q “ covpXn , Xm q und
n
ÿ
n
ÿ
Sn ´ Mn “
pXk ´ EpXk qq “
Yk .
k“1
k“1
Die Behauptung folgt aus Schritt 1 – 3.
Im folgenden wollen wir die Bedingung an die Momente
varpXn q ≤ C ă 8, n P N
weiter abschwächen. Hierfür brauchen wir das zweite Borel-Cantelli Lemma.
Lemma 5.5. (Borel-Cantelli Lemma 2) Sei pAn qnPN ˜
Ă F eine Folge
¸ unabhängiger Mengen und
8
Ş Ť
ř
es gelte
PpAn q “ 8. Dann gilt Pplim sup An q “ P
Ak “ 1.
nÑ8
n“1
n≥1 k≥n
Beweis. Es gilt
¸
˜
ď č
Ppplim sup An qc q “ P
nÑ8
n≥1 k≥n
˜
k≥n
¸
č
P
k≥n
Ack
8
ź
“
k“n
PpAck q
“ lim P
nÑ8
č
Ack
.
k≥n
¸
Ş
Folglich reicht es zu zeigen, dass P
˜
Ack
¸
˜
Ack
8
ź
“
“ 0 für n ≥ 1. Dieses folgt aus
p1 ´ PpAk qq ≤
k“n
8
ź
´PpAk q
e
´
“e
8
ř
PpAk q
k“n
k“n
Lemma 5.6. (Kolmogorov Ungleichung) Seien Xn P L2 unabhängig. Dann gilt
ˆ
˙
n
1 ÿ
1
varpXk q “ 2 varpSn q.
P max |Sk ´ Mk | ≥ ε ≤ 2
1≤k≤n
ε k“1
ε
65
“ 0.
Beweis. Betrachte die Ereignisse
ˇ
#ˇ
i
i
ˇ
ˇÿ
ÿ
ˇ
ˇ
mj ˇ ă ε, 1 ≤ i ă k,
Xj ´
Ck “ ˇ
ˇ
ˇj“1
j“1
n
Ť
Dann gilt Ck X Cj “ H für k ‰ j und C “
ˇ
ˇ
+
k
k
ˇ
ˇÿ
ÿ
ˇ
ˇ
mj ˇ ≥ ε .
Xj ´
ˇ
ˇ
ˇj“1
j“1
Ck erfüllt
k“1
ˆ
˙
max |Sk ´ Mk | ≥ ε
P
“ PpCq.
1≤k≤n
Es gilt
varpSn q “
ż ˜ÿ
n
i“1
i“1
ż ˜ÿ
n
n
ÿ
Ω
≥
Xi ´
n
ÿ
Xi ´
i“1
C
“
`2
k
˜
n ż
k
ÿ
ÿ
dP “
k
mi
dP
k
ÿ
¸˜
k
ř
Xi ´
i“1
mi
i“1
mi
dP
i“1
n
ÿ
Xi ´
i“k`1
n
ÿ
Xi ´
i“k`1
k
¸2
n
ÿ
¸2
Xi ´
`
ˆ
k
k
ÿ
Xi ´
i“1
k“1 C
i“1
˜
n ż
n
ÿ
ÿ
1Ck
mi
˜
n ż
n
ÿ
ÿ
i“1
k“1 C
Die Zufallsvariablen η1 “
¸2
Xi ´
i“1
k“1 C
dP
mi
i“1
˜
n ż
k
ÿ
ÿ
k“1 C
¸2
¸
n
ÿ
mi
dP
i“k`1
¸2
mi
dP.
i“k`1
k
ř
˙
mi
n
ř
und η2 “
i“1
i“k`1
Xi ´
n
ř
sind nach Voraus-
i“k`1
setzung unabhängig. Es gilt folglich
Epη1 η2 q “ Epη1 qEpη2 q “ 0.
Damit erhalten wir
varpSn q ≥
˜
n ż
k
ÿ
ÿ
k“1 C
k
Xi ´
i“1
k
ÿ
¸2
mi
i“1
dP ≥ ε
2
n
ÿ
k“1
Lemma 5.7. Es gilt
ÿ
k: 2k ≥i
1
16 1
≤
, i P N.
2k
3 i2
2
66
PpCk q “ ε2 PpCq.
Beweis. Sei q P p0, 1q und n0 P N. Dann gilt
8
ÿ
q n “ q n0
n“n0
Für q “
1
4
und n0 P N mit
ÿ
k: 2k ≥i
lnpiq
lnp2q
8
ÿ
q n´n0 “
n“n0
´ 1 ă n0 ≤
lnpiq
lnp2q
q n0
.
1´q
folgt
ˆ ˆ
˙
˙
8
ÿ
4´n0
lnpiq
16 1
1
4
´k
≤
4
“
exp
´
´
1
2
lnp2q
“
.
≤
1
2
3
lnp2q
3
i
22k
1
´
4
k“n
0
Satz 5.8. (Erstes Kolmogorov Theorem) Seien Xn P L2 unabhängig und es gelte
8
ÿ
varpXn q
ă 8.
n2
n“1
Dann gilt das starke Gesetz der großen Zahlen.
Beweis. Wir können ohne Einschränkung der Allgemeinheit annehmen, dass EpXn q “ 0 für alle
n P N gilt. Sei ε ą 0 und
Bpεq “ tω P Ω | DN pεq P N : |Sn pωq| ă nε, @n ≥ N pεqu
8
8 č
ď
t|Sn | ă nεu.
“
N “1 n“N
"
Setze Bk pεq “
max
2k´1 ≤nă2k
1
n |Sn |
*
≥ ε . Die Kolmogorov Ungleichung impliziert
ˇ
ˇ¸
ˇ
ˇ
˜
¸
n
n
ˇÿ
ˇ
1 ˇˇ ÿ ˇˇ
ˇ
ˇ
k´1
PpBk pεqq “ P
max
ˇ Xi ˇ ≤ P k´1max k ˇ Xi ˇ ≥ ε2
ˇ
ˇ
2
≤nă2 ˇ
2k´1 ≤nă2k n ˇ
i“1
i“1
ˇ
ˇ
˜
¸
n
2k
ˇÿ
ˇ
ÿ
1
ˇ
ˇ
k´1
≤ P max ˇ Xi ˇ ≥ ε2
≤ 2 2k´2
varpXi q.
ˇ
ε 2
1≤n≤2k ˇ
i“1
i“1
˜
Daraus folgt
k
2
ÿ
1
PpBk pεqq ≤
varpXi q
ε2 22k´2 i“1
k“1
k“1
8
ÿ
8
ÿ
“
8
ÿ
1 ÿ
varpX
q
i
ε2 i“1
k
k: 2 ≥i
1
22k´2
≤
8
32 ÿ varpXi q
.
3ε2 i“1
i2
Nach dem ersten Borel-Cantelli Lemma gibt es für fast alle ω ein k0 pωq P N mit
max
2k´1 ≤nă2k
1
|Sn pωq| ă ε, k ≥ k0 pωq.
n
67
´1
Insbesondere
gilt PpBpεqq
˜
¸ “ 1 für alle ε ą 0. Also gilt auch PpBpm qq “ 1 für alle m ≥ 1 und
Ş
Ş
somit P
Bpm´1 q “ 1. Für jedes ω P
Bpm´1 q gibt es ein N pω, mq P N sodass für alle
m≥1
n ≥ N pω, mq gilt
m≥1
1
n |Sn pωq|
ă
1
m.
Eine Folge von Zufallsvariablen pXn qnPN heißt identisch verteilt, wenn P ˝ Xn´1 “ P ˝ X1´1 für
alle n ≥ 1 gilt. In diesem Fall setze m :“ EpXn q “ EpX1 q. Das starke Gesetz der großen Zahlen
ist äquivalent zu
n
1 ÿ
Xk ÝÑ m, n Ñ 8
n k“1
fast sicher. Wollen wir die Integrabilität noch weiter abschwächen, z.B. Xn P L1 , so müssen wir
annehmen dass die Folge Xn identisch verteilt ist.
Satz 5.9. (Zweites Kolmogorov Theorem, [KS07]) Seien Xn P L1 unabhängig und identisch
verteilt. Dann gilt das starke Gesetz der großen Zahlen.
Satz 5.10. (Satz von Etemadi, 1981, [Ete81]) Seien Xn P L1 paarweise unabhängig und identisch verteilt. Dann gilt das starke Gesetz der großen Zahlen.
5.2
Zentraler Grenzwertsatz
Sei Xn P L2 eine Folge von unabhängigen Zufallsvariablen mit Erwartungswert mk :“ EpXk q
n
n
n
ř
ř
ř
und Varianz σi2 :“ varpXi q. Definiere Sn :“
Xi , Mn :“
mi und Dn2 :“ varpSn q “
σi2 .
i“1
i“1
i“1
L2
Definition 5.11. (Lindeberg Bedingung) Die Folge pXn qnPN Ă
erfüllt die Lindeberg Bedingung, wenn für jedes ε ą 0 gilt
ż
n
1 ÿ
lim 2
pXi ´ mi q2 dP “ 0.
nÑ8 Dn
i“1
|Xi ´mi |≥εDn
Man beachte, ist Dn “ 0 für alle n P N, so ist Xn “ 0 fast sicher für alle n P N. Um diesen
Fall auszuschließen, können wir annehmen, dass Dn ą 0 für hinreichend große n P N gilt. Wir
werden später, unter geeigneten Bedingungen, zeigen dass Dn ÝÑ 8 gilt. Vorher brauchen wir
jedoch das nächste Lemma.
Lemma 5.12. Sei ln die Fortsetzung des natürlichen Logarithmus auf das Gebiet
"
*
1
G “ 1 ` z P C | |z| ă
,
4
d.h. es gilt
lnp1 ` zq “
n
ÿ
p´1qk`1
k“1
zk
1
, |z| ă .
k
4
Dann gibt es eine stetige Funktion Θ : tz P C | |z| ă 14 u ÝÑ C mit |Θpzq| ≤ 1 und
1
lnp1 ` zq “ z ` Θpzq|z|2 , |z| ă .
4
68
Beweis. Für z “ 0 ist nichts zu zeigen. Wir betrachten 0 ă |z| ă 41 . Dann gilt
lnp1 ` zq “
8
ÿ
p´1qk`1
k“1
Setze Θpzq :“
8
ř
k´2
p´1qk`1 z k
k“2
z2
.
|z|2
8
ÿ
z k´2 z 2
zk
.
“ z ` |z|2
p´1qk`1
k
k |z|2
k“2
Wir zeigen, dass die Reihe absolut konvergiert
ˇ ÿ
8 ˇˇ
8
8
k´2 z 2 ˇ
ÿ
2
|z|k
1 ÿ 1
ˇp´1qk`1 z
ˇ“
“ ă 1.
≤
ˇ
2ˇ
k
k
|z|
k
`
2
2
3
4
k“2
k“0
k“0
Satz 5.13. (zentraler Grenzwertsatz) Sei Xn P L2 eine Folge von unabhängigen Zufallsvaria´Mn
blen und es gelte die Lindeberg Bedingung. Dann konvergiert Sn˚ :“ SnD
schwach gegen die
n
Normalverteilung N p0, 1q auf R.
Für den Beweis können wir ohne Einschränkung der Allgemeinheit annehmen, dass mi “ 0.
Anderseits definiere Yi :“ Xi ´ mi . Für diese Zufallsvariablen ist die Lindeberg Bedingung
immernoch erfüllt. Im Beweis zeigen wir die schwache Konvergenz mittels Konvergenz der charakteristischen Funktionen. Sei ϕn die charakteristische Funktion von Xn . Das nächste Lemma
liefert hierfür eine geeignete Restgliedabschätzung.
pnq
Lemma 5.14. Es gibt Zahlen ak
derart, dass für 1 ≤ k ≤ n gilt
ˆ
ϕk
sowie
lim
ξ
Dn
n
ÿ
nÑ8
˙
“1´
ξ 2 σk2
pnq
` ak
2Dn2
pnq
|ak pξq| “ 0, @ξ P R.
k“1
Beweis. Es gibt stetige Funktionen Θ1 , Θ2 mit |Θ1 pxq|, |Θ2 pxq| ≤ 1 sowie
Θ1 pxqx2
,
2
x2 Θ2 pxqx3
“ 1 ` ix ´
`
.
2
6
eix “ 1 ` ix `
eix
69
für alle x P R. Aus diesen Entwicklungen erhalten wir
ˆ
˙ ż
ξ
ξ
ϕk
“ ei Dn Xk dP
Dn
Ω
ˆ
˙
ż
iξ
Θ1 pXk qpξXk q2
1`
Xk `
dP
“
Dn
2Dn2
|Xk |≥εDn
ˆ
ż
`
iξ
ξ2
Θ2 pXk qpξXk q3
2
1`
Xk ´
X
`
k
Dn
2Dn2
6Dn3
˙
dP
|Xk |ăεDn
ξ 2 σk2
ξ2
“1´
`
2Dn2
2Dn2
ż
p1 `
Θ1 pXk qqXk2 dP
ξ3
`
6Dn3
|Xk |≥εDn
ż
Θ2 pXk qXk3 dP.
|Xk |ăεDn
Definiere
pnq
ak
ξ2
:“
2Dn2
ż
p1 `
Θ1 pXk qqXk2 dP
ξ3
`
6Dn3
|Xk |≥εDn
Betrachten wir
n
ř
k“1
n
ξ2 ÿ
2Dn2 k“1
ż
Θ2 pXk qXk3 dP.
|Xk |ăεDn
pnq
|ak | so erhalten wir für den ersten Term aus der Lindeberg Bedingung
ż
p1 `
|Θ1 pXk q|qXk2 dP
|Xk |≥εDn
n
ξ2 ÿ
≤ 2
Dn k“1
Für den zweiten Term erhalten wir
ż
n
n
|ξ|3 ÿ
|ξ|3 ÿ
3
|Θ
pX
q||X
|
dP
≤
2
k
k
6Dn3 k“1
6Dn3 k“1
|Xk |ăεDn
ż
Xk2 dP ÝÑ 0, n Ñ 8.
|Xk |≥εDn
ż
εDn |Xk |2 dP ≤
|Xk |ăεDn
n
ε|ξ|3 ÿ 2 ε|ξ|3
σ “
.
6Dn2 k“1 k
6
Da ε beliebig war, kann dieser Term beliebig klein gemacht werden.
Eine weitere wichtige Ungleichung ist im nächsten Lemma formuliert.
Lemma 5.15. Es gilt
σk2
“ 0.
2
nÑ8 1≤k≤n Dn
lim max
(5.1)
Beweis. Für jedes ε ą 0 gilt
σk2
1
≤ max 2
2
1≤k≤n Dn
1≤k≤n Dn
ż
1
2
1≤k≤n Dn
ż
Xk2 dP ` max
max
|Xk |≥εDn
Xk2 dP.
|Xk |≤εDn
70
Der erste Term konvergiert für n Ñ 8 wegen der Lindeberg Bedingung gegen 0. Für den zweiten
Term gilt
ż
1
max 2
Xk2 dP ≤ ε2 .
1≤k≤n Dn
|Xk |≤εDn
Da ε beliebig war, folgt die Behauptung.
Kommen wir zum Beweis vom zentralen Grenzwertsatz.
Beweis. (Satz 5.13) Es reicht zu zeigen, dass
ξ2
ϕτn pξq ÝÑ e´ 2 , ξ P R.
Fixiere ξ P R. Dann gilt
˜
ϕτn pξq “ Epe
iξτn
n
ř
i Dξ
n
q“E e
Xk
¸
n
ź
“
k“1
ˆ
ϕk
k“1
Daraus folgt
ln pϕτn pξqq “
n
ÿ
ˆ
ˆ
ln ϕi
i“1
ξ
Dn
ξ
Dn
˙
.
˙˙
und somit reicht es
n
ÿ
i“1
ˆ
ln ϕi
ˆ
ξ
Dn
˙˙
ÝÑ ´
ξ2
, nÑ8
2
ξ2 σ2
(5.2)
pnq
zu zeigen. Für hinreichend große n P N ist |zk,n | ă 14 für zk,n “ ´ 2D2k ` ak (siehe (5.1). Daraus
n
folgt
˙
ˆ ˆ
˙˙ ÿ
ˆ
n
n
ÿ
ξ 2 σk2
ξ
pnq
ln ϕk
“
ln 1 ´
` ak
Dn
2Dn2
k“1
k“1
ˇ2
ˇ 2 2
n
n
n
ˇ ´ξ σk
ξ 2 ÿ 2 ÿ pnq ÿ
pnq ˇˇ
ˇ
“´ 2
σ `
a `
Θk,n ˇ
` ak ˇ
2Dn k“1 k k“1 k
2Dn2
k“1
ˇ 2 2
ˇ2
n
n
ÿ
ÿ
ˇ ´ξ σk
ξ2
pnq
pnq ˇˇ
ˇ
“´ `
ak `
Θk,n ˇ
` ak ˇ
2
2Dn2
k“1
k“1
mit Θk, n “ Θpzk,n q, |Θk,n | ≤ 1. Es reicht daher zu zeigen, dass der letzte Term gegen Null
konvergiert. Es gilt
ˇ 2 2
ˇ2
ˆ 2 2
˙ÿ
˙
n ˆ 2 2
ˇ ´ξ σk
ˇ
ξ
σ
ξ
σ
pnq
pnq
pnq
k
k
|Θk,n | ˇˇ
` ak ˇˇ ≤ max
` |ak |
` |ak | .
2
1≤k≤n 2Dn
2Dn2
2Dn2
k“1
k“1
n
ÿ
71
Die Summe ist wegen
˙
n ˆ 2 2
n
ÿ
ÿ
ξ σk
ξ2
pnq
pnq
` |ak | “
`
|ak |
2
2Dn
2
k“1
k“1
offensichtlich beschränkt. Der erste Faktor konvergiert gegen Null, welches die Behauptung zeigt.
Bemerkung 5.16. Sei K Ă R kompakt. Dann gilt mit denselben Notationen wie im letzten
Beweis
ˇ
ˇ
2ˇ
ˇ
´ ξ2 ˇ
ˇ
lim sup ˇϕτn pξq ´ e
ˇ “ 0.
nÑ8
ξPK
Der Beweis ist Übung.
Korollar 5.17. Sei Xn P L2 ein Folge von unabhängigen, identisch verteilten Zufallsvariablen
n ´nm
mit m :“ EpX1 q und 0 ă σ 2 :“ varpX1 q. Dann konvergiert S?
schwach gegen die Normalnσ 2
verteilung.
?
Beweis. Da alle Xn die gleiche Verteilung haben folgt σi2 “ σ12 und somit Dn “ nσ 2 . Ebenso
gilt Mn “ mn und
ż
ż
2
pXk ´ mk q dP “
pX1 ´ m1 q2 dP.
|X1 ´m1 |
|Xk ´mk |≥εDn
Die Lindeberg Bedingung folgt daher aus
ż
n
1
1 ÿ
pXk ´ mk q2 dP “ 2
2
Dn k“1
σ
|Xk ´mk |≥εDn
ż
pX1 ´ m1 q2 dP
?
|X1 ´m1 |≥ε σ 2 n
und dem Satz von Lebesgue wegen X1 ´ m1 P L2 .
Definition 5.18. (Lyapunov Bedingung) Eine Folge unabhängiger Zufallsvariablen Xn P L2
erfüllt die Lyapunov Bedingung, wenn es ein δ ą 0 gibt derart, dass
lim
nÑ8
1
n
ÿ
Dn2`δ
k“1
Ep|Xk ´ mk |2`δ q “ 0.
Korollar 5.19. (zentraler Grenzwertsatz, Lyapunov Bedingung) Sei Xn P L2 eine Folge un´Mn
abhängiger Zufallsvariablen, welche die Lyapunov Bedingung erfüllen. Dann konvergiert SnD
n
schwach gegen die Normalverteilung N p0, 1q.
Beweis. Sei ε ą 0 und δ ą 0 gegeben durch die Lyapunov Bedingung. Dann gilt
ż
ż
1
1
2
pXk ´ mk q dP ≤ 2
pXk ´ mk q2`δ dP
Dn2
Dn pεDn qδ
|Xk ´mk |≥εDn
|Xk ´mk |≥εDn
≤ ε´δ
Ep|Xk ´ mk |2`δ q
.
Dn2`δ
Folglich gilt die Lindeberg Bedingung.
72
Satz 5.20. (Lindeberg-Feller, [KS07]) Sei Xn P L2 eine Folge unabhängiger Zufallsvariablen
mit
σ2
lim max i2 “ 0.
nÑ8 1≤i≤n Dn
Dann sind die folgenden Aussagen äquivalent
• Die Folge Xn erfüllt die Lindeberg Bedingung.
• Die Folge
5.3
Sn ´Mn
Dn
konvergiert schwach gegen die Normalverteilung N p0, 1q.
Weitere Grenzwertsätze
Sei ppxq ≥ 0 eine Wahrscheinlichkeitsdichte. Wir schreiben
ppxq „ qpxq, |x| ÝÑ 8
falls es ein R ą 0 und eine beschränkte Funktion g gibt mit gpxq ÝÑ 0 für |x| ÝÑ 8 und
ppxq “ qpxqp1 ` gpxqq, |x| ≥ R.
Lemma 5.21. Sei p eine Wahrscheinlichkeitsdichte mit ppxq “ pp´xq,
ppxq „
c
, |x| ÝÑ 8
|x|α`1
und 0 ă α ă 2, c ą 0. Sei ϕ die charakteristische Funktion von p. Dann gilt
ϕpξq “ 1 ´ c1 |ξ|α ` op|ξ|α q, ξ Ñ 0.
(5.3)
Die Behauptung besagt, dass es eine Konstante c1 gibt derart, dass
ϕpξq ´ 1 ` c1 |ξ|α
ÝÑ 0, ξ Ñ 0.
|ξ|α
Äquivalent, es gibt eine Funktion h mit
hpξq
|ξ|α
ÝÑ 0 für ξ Ñ 0 und es gilt
ϕpξq “ 1 ` c1 |ξ|α ` hpξq
für alle hinreichend kleinen ξ P R. Wegen
ż
ż
´iξx
ϕp´ξq “ ppxqe
mpdxq “ pp´xqeiξx mpdxq “ ϕpξq
R
R
reicht es die Asymptotik nur für positive ξ zu betrachten. Im folgenden schreiben wir der einfachhalber Lebesgue Integrale wie gewöhnliche Riemann Integrale.
73
Beweis. Sei R ą 0 derart, dass
c
p1 ` gpxqq, |x| ≥ R
|x|α`1
ppxq “
für eine beschränkte Funktion g mit gpxq ÝÑ 0 für |x| Ñ 8. Der einfachhalber betrachten wir
ξ ą 0. Für 0 ă ξ ă R1 gilt
´ 1ξ
ϕpξq “
ppxqe
iξx
dx `
ppxqe
iξx
dx `
´ 1ξ
´8
1
żR
´R
ż
ż
ż8
żξ
ppxqe
iξx
ppxqe
dx `
iξx
1
ξ
R
´R
ppxqeiξx dx
dx `
“ I1 pξq ` I2 pξq ` I3 pξq ` I4 pξq ` I5 pξq.
Für I3 sehen wir, dass I3 beliebig oft stetig differenzierbar ist mit I3 p0q “
R
ş
ppxqdx und wegen
´R
ppxq “ pp´xq ist auch
żR
I31 p0q
ppxqixdx “ 0.
“
´R
Daraus folgt
żR
I3 pξq “ I3 p0q `
I31 p0qξ
2
ppxqdx ` Opξ 2 q, ξ Ñ 0.
` Opξ q “
´R
Da für jede Funktion h P Opξ 2 q bereits h P op|ξ|α q gilt, folgt
żR
ppxqdx ` op|ξ|α q, ξ Ñ 0.
I3 pξq “
´R
Für I1 erhalten wir mit y :“ ξx und dy “ ξdx
´ 1ξ
´ 1ξ
ż
ż
cp1 ` gpxqq iξx
ppxqe dx “
e dx “ cξ α
I1 pξq “
|x|α`1
´8
´8
´8
´ ¯
´1
´1
ż
ż eiy g y
ξ
eiy
α
α
“ cξ
dy ` cξ
dy.
|y|α`1
|y|α`1
iξx
´8
´ ¯
y
ξ
α`1
|y|
ż´1 1 ` g
eiy dy
´8
´ ¯
Da g beschränkt ist und g
y
ξ
ÝÑ 0 für ξ Ñ 0, folgt mit dem Satz von Lebesgue
ż´1
I1 pξq “ cξ
α
eiy
dy ` op|ξ|α q.
|y|α`1
´8
74
Analog erhalten wir
ż8
I5 pξq “
ż8
ppxqe
iξx
dx “
1
ξ
cp1 ` gpxqq iξx
e dx “ cξ α
|x|α`1
ż8
“ cξ
eiy dy
1
1
ξ
α
´ ¯
y
ξ
α`1
|y|
ż8 1 ` g
eiy
dy ` cξ α
|y|α`1
1
´ ¯
y
ξ
α`1
|y|
ż8 eiy g
ż8
dy “ cξ
1
α
eiy
dy ` op|ξ|α q.
|y|α`1
1
Für die letzten zwei Terme erhalten wir aus ppxq “ pp´xq
1
´R
ż
żξ
ppxqpeiξx ´ 1 ´ iξxqdx `
I2 pξq ` I4 pξq “
´ 1ξ
ppxqpeiξx ´ 1 ´ iξxqdx
R
1
´R
ż
żξ
ppxqdx `
`
´ 1ξ
ppxqdx.
R
Der dritte Term liefert
´ 1ξ
´R
ż
´R
ż
ppxqdx “
´ 1ξ
ż
cp1 ` gpxqq
dx “
|x|α`1
ppxqdx ´
´8
ż´1
ppxqdx ´ cξ
“
´8
ppxqdx ´ cξ
´8
´8
´R
ż
´R
ż
α
α
´ ¯
y
ξ
α`1
|y|
ż´1 1 ` g
dy
´8
1
dy ` op|ξ|α q.
|y|α`1
´8
Für den vierten Term erhalten wir analog
1
ż8
żξ
ppxqdx “
R
ż8
ppxqdx ´
R
cp1 ` gpxqq
dx “
|x|α`1
1
ξ
ż8
ż8
ppxqdx ´ cξ
R
Für den ersten Term benutzen wir eiy ´ 1 ´ iy “
75
Θ1 pyq 2
2 y
α
1
dy ` op|ξ|α q.
|y|α`1
1
mit |Θ1 pyq| ≤ 1. Weiterhin ist α ´ 1 P
p´1, 1q und somit ist
Θ1 pyq
|y|α´1
auf r´1, 0s integrierbar. Daraus folgt
´ ¯
´ξR
´R
ż 1`g y
ż
ξ
ppxqpeiξx ´ 1 ´ iξxqdx “ cξ α
peiy ´ 1 ´ iyqdy
α`1
|y|
´ 1ξ
´1
“
´ξR
ż
cξ α
2
´ ¯
y
ξ
α`1
|y|
1`g
Θ1 pyq|y|2 dy
´1
´ ¯
´ ¯
0
0
y
ż
ż
1`g ξ
1 ` g yξ
cξ α
cξ α
“
Θ1 pyqdy ´
Θ1 pyqdy
2
|y|α´1
2
|y|α´1
´1
“
ż0
cξ α
2
´ξR
Θ1 pyq
dy ` op|ξ|α q.
|y|α´1
´1
Analog zeigen wir
1
żξ
iξx
ppxqpe
cξ 2
´ 1 ´ iξxqdx “
2
¨
ż8
c1 :“ c ˝2
cospyq ´ 1
1
dy `
|y|α`1
2
Dann gilt wegen
ż1
Θ1 pyq
1
dy `
|y|α´1
2
0
1
ş
Θ1 pyq
dy ` op|ξ|α q.
|y|α´1
0
R
Setze
ż1
ż0
˛
Θ1 pyq ‚
dy .
|y|α´1
´1
ppxqmpdxq “ 1
R
ϕpξq “ 1 ` c1 ξ α ` op|ξ|α q.
Lemma 5.22. Sei pxn qnPN eine Folge reeller Zahlen mit xn ÝÑ x für n Ñ 8. Dann gilt
´
xn ¯n
lim 1 `
“ ex .
nÑ8
n
Beweis. Sei A ą 0 mit |xn |, |x| ≤ A für alle n P N. Wegen
ˇ´
ˇ ˇ´
ˇ
x n ¯n
xn ¯n ´
x ¯n
x ¯n ˇˇ ˇˇ´
ˇ
ˇ
xˇ
xˇ
1
`
´
e
≤
1
`
´
1
`
`
1
`
´
e
ˇ
ˇ ˇ
ˇ ˇ
ˇ
n
n
n
n
reicht es zu zeigen, dass der erste Term auf der rechten Seite gegen Null konvergiert. Das Letztere
folgt aus
ˇˆ
ˇ
˙n ´
ˆ
˙
ˆ
˙
n
ˇ
xn ¯ ´
x ¯n ˇˇ ÿ ˇˇ´
x ¯ˇˇ
A n´k
A k´1
ˇ 1 ` |xn |
≤
´ 1`
1`
´ 1`
ˇ 1`
ˇ¨ 1`
ˇ
n
n ˇ
n
n
n
n
k“1
ˆ
˙
A n´1
“ |x ´ xn | 1 `
.
n
76
Satz 5.23. Sei Xn eine Folge von unabhängigen Zufallsvariablen mit Verteilung
P ˝ Xn´1 pdxq “ ppxqdx, n P N.
Es gelte ppxq “ pp´xq und für ein c ą 0, 0 ă α ă 2
ppxq „
Setze Sn :“
n
1 ř
Xk .
1
n α k“1
c
, |x| Ñ 8.
|x|α`1
Dann gilt
P ˝ Sn´1 ÝÑ ν, n Ñ 8
α
schwach und die Verteilung ν ist bestimmt durch die charakteristische Funktion ψpξq “ e´c1 |ξ| .
ş
Beweis. Es sei ϕpξq “ eiξx ppxqmpdxq. Dann gilt wegen Unabhängigkeit
R
iξSn
Epe
˙˙n
ˆ ˆ
ξ
.
q“ ϕ
1
nα
Für jedes ξ P R gibt nach es (5.3) eine Folge an pξq mit nan pξq ÝÑ 0 für n Ñ 8 derart, dass
ˆ
˙
ξ
c1 |ξ|α
ϕ
` an pξq.
“1´
1
n
nα
Wir erhalten somit
ˆ ˆ
˙˙n ˆ
˙n
ξ
c1 |ξ|α
ϕ
“ 1´
` an pξq
1
n
nα
ˆ
˙
nan pξq ´ c1 |ξ|α n
“ 1`
.
n
Wegen Lemma 5.22 mit xn :“ nan pξq ´ c1 |ξ|α ÝÑ ´c1 |ξ|α “: x gilt
α
EpeiξSn q ÝÑ e´c1 |ξ| , n Ñ 8.
Die Behauptung folgt somit aus Levys Stetigkeitssatz.
Bemerkung 5.24. (a) Sei Xn P L2 eine Folge unabhängig,
identisch )verteilter Zufallsvaria!
|X
|
k
2
?k | . Dann gilt
blen mit EpX1 q “ 0 und EpX1 q “ 1. Sei Mn :“ max ?n , . . . , |X
n
ˆ
PpMn ≤ tq “ P
|Xk |
? ≤ t, k “ 1, . . . , n
n
77
n
ź
˙
“
ˆ
P
k“1
˙
?
|Xk |
? ≤ t “ Pp|X1 | ≤ ntqn .
n
Weiterhin erhalten wir
?
Pp|Xk | ą ntq “
ż
1|y|ą?nt P ˝ X1´1 pdyq
R
ż
≤
1|y|ą?nt
y2
P ˝ X1´1 pdyq
nt2
R
1
“ 2
nt
ż
y 2 P ˝ X1´1 pdyq “
?
|y|ą nt
Θn ptq
n
mit Θn ptq ÝÑ 0 für alle t ą 0. Daraus folgt
?
?
PpMn ≤ tq “ Pp|X1 | ≤ ntqn “ p1 ´ Pp|X1 | ą ntqqn
ˆ
˙
Θn ptq n
≥ 1´
ÝÑ 1, n Ñ 8.
n
Also gilt lim PpMn ≤ tq “ 1 für alle t ą 0 und somit
nÑ8
P ˝ Mn´1 ÝÑ δ0 , n Ñ 8
schwach.
Konsequenz: Der wesentliche Beitrag im zentralen Grenzwertsatz kommt von der Summe
und nicht von dem maximalen Summanden.
(b) Sei Xn wie in Satz 5.23. Für t ą 0 gilt dann
˙
ˆ
˙
ˆ
1
1
α
α
“ 1 ´ P max |Xk | ă tn
P max |Xk | ≥ tn
1≤k≤n
1≤k≤n
´ ´
¯¯n
1
“ 1 ´ P |X1 | ă tn α
´
´
¯¯n
1
“ 1 ´ 1 ´ P |X1 | ≥ tn α
.
Ferner gilt für hinreichend große n P N
1
α
ż
c
2c
mpdxq “ α .
α`1
|x|
αt n
Pp|X1 | ≥ tn q „
1
|x|≥tn α
Daher gilt
ˆ
lim P
nÑ8
max |Xk | ≥ tn
1≤k≤n
1
α
˙
ˆ
˙ ˙
ˆ
2c
2c n
“ lim 1 ´ 1 ´ α
“ 1 ´ e´ αtα ą 0.
nÑ8
αt n
Konsequenz: Der meximale Term hat in diesem Fall einen Einfluss auf die Konvergenz
in Satz 5.23.
78
Definition 5.25. Ein Wahrscheinlichkeitsmaß µpdxq auf R heißt Poissonverteilt, wenn es ein
λ ą 0 gibt mit
λk ´λ
µptkuq “
e , k “ 0, 1, . . . ,
k!
8
ř
λk
´1
d.h. µ “ e´λ
k! δk . Eine Zufallsvariable X heißt Poissonverteilt, wenn ihre Verteilung P˝X
k“0
Poissonverteilt ist.
Sei n P N. Wir betrachten n unabhängige Münzwürfe, wo 1 für Kopf und 0 für Zahl steht.
Ein Ausgang ist daher ein n-Tupel ω “ pω1 , . . . , ωn q P t0, 1un . Wir wählen
Ωn “ tω “ pω1 , . . . , ωn q P t0, 1un u
mit F “ 2Ωn und
n
ř
k“1
Pn ptωuq “ pn
n
ř
ωk
p1 ´ pn q
p1´ωk q
k“1
, ω P Ωn .
Hier ist pn P r0, 1s die Wahrscheinlichkeit bei einem der Münzwürfe Kopf zu werfen. Demnach
ist 1 ´ pn die Wahrscheinlichkeit Zahl zu werfen.
Satz 5.26. (Poissonscher Grenzwertsatz) Sei pn P r0, 1s mt npn ÝÑ λ für ein λ ą 0. Dann gilt
˜#
+¸
n
ÿ
λk ´λ
lim Pn
ω P Ωn |
ωj “ k
“
e , k P N0 .
nÑ8
k!
j“1
Beweis. Sei k P N0 fest. Wegen npn ÝÑ λ folgt pn ÝÑ 0. Wir können daher annehmen, dass
pn ă 1 gilt. Die Anzahl der Elemente in
#
+
n
ÿ
Ak :“ ω P Ωn |
ωj “ k
j“1
ist gleichbedeutend `mit
˘ der Anzahl der k-elementigen Teilmengen einer n-elementigen Menge.
Diese hat demnach nk Elemente. Für jedes ω P Ak gilt
Pn ptωuq “ pkn p1 ´ pn qn´k
und somit
ˆ ˙
n k
npn ´ 1q ¨ ¨ ¨ pn ´ k ` 1q k ´
npn ¯n´k
pn p1 ´ pn qn´k “
pn 1 ´
.
Pn pAk q “
k
k!
n
`
˘k
Wegen 1 ´ npnn ÝÑ 1 für n Ñ 8 folgt
`
˘n
´
lim 1 ´ npnn
npn ¯n´k
´λ
lim 1 ´
“ nÑ8 `
˘ “e .
npn k
nÑ8
n
lim 1 ´
nÑ8
n
Weiterhin gilt
lim npn ´ 1q ¨ ¨ ¨ pn ´ k ` 1qpkn “ lim pnpn qk “ λk .
nÑ8
nÑ8
Daraus folgt die Behauptung.
79
Korollar 5.27. Sei Xn eine Folge von unabhängigen Zufallsvariablen mit
PpXn “ 1q “ pn ,
PpXn “ 0q “ 1 ´ pn , n P N
für eine Folge pn P r0, 1s mit npn ÝÑ λ ą 0. Sei Sn “
n
ř
Xj . Dann gilt
j“1
PpSn “ kq ÝÑ
λk ´λ
e , k P N.
k!
Die Verteilung von Sn konvergiert also gegen die Poissonverteilung.
Zum Schlußbetrachten wir ein Beispiel aus der Thermodynamik.
Beispiel 5.28. Es sei VR Ă R3 eine Box mit Kantenlänge R ą 0 und uniformer Verteilung
1
mpdxq auf VR . Dann beschreibt x P VR die Position eines einzelnen Atoms. Wir betrachten
R3
ein ideales Gas aus npRq P N Atomen welche nicht miteinander wechselwirken, d.h. unabhängig
voneinander sind. Die Positionen der Atome seien x1 , . . . , xnpRq P VR . Der gemeinsame ZunpRq
standsraum ist Ω :“ VR
und wir nehmen an dass alle Atome uniform verteilt sind, d.h.
P“
1
pR3 qnpRq
mbnpRq .
Ist U Ă VR eine weitere Box, so bezeichnet
XU px1 , . . . , xnpRq q “
npRq
ÿ
1U pxk q
k“1
die Anzahl der Atome in U . Im thermodynamischen Limes betrachten wir den Grenzfall R Ñ 8
mit npRq Ñ 8 geeignet gewählt. Ziel ist es die Verteilung von XU in diesem Limes zu bestimmen. Dieses kann als Verteilung von sehr vielen Atomen in einem großen Volumen interpretiert
werden.
q
Die Wahrscheinlichkeit 1 Atom in U zu finden ist gegeben durch PpXU “ 1q “ mpU
“: pn pRq.
R3
Es gilt
npRqmpU q
npRq
npRqpnpRq “
“ mpU q 3 .
R3
R
Wir betrachten die Annahme
npRq
ÝÑ ρ, R Ñ 8.
R3
In diesem Fall sei λ “ ρmpU q. Der Poissonsche Grenzwertsatz zeigt
lim PpXU “ kq “
RÑ8
λk ´λ
e , k P N0 .
k!
Der Wert ρ ą 0 kann als Dichte des Gases interpretiert werden. Damit sit λ die mittlere Anzahl
der Atome in dem Gebiet U .
80
6
Grundlagen stochastischer Prozesse
Sei pE, Eq ein messbarer Raum.
Definition 6.1. Sei T eine Indexmenge. Ein stochastischer Prozess ist eine Familie von Zufallsvariablen X :“ pXt qtPT mit Werten in E.
(a) Für T “ Z oder T “ Z` heist X (diskreter) stochastischer Prozess.
(b) Ist T ein Intervall ra, bs Ă R oder T “ R oder T “ R` , so heißt X (Zeit kontinuierlicher)
stochastischer Prozess.
(c) Ist T ein mehrdimensionaler Raum, so heißt X auch zufälliges Feld (random field).
Für jedes ω P Ω heißt t ÞÝÑ Xt pωq Trajektorie/ Realisierung bzw. Pfad von X.
6.1
Konstruktion stochastischer Prozesse
r :“ ΩpT,
r
Sei E ein metrischer Raum und Ω
Eq der Pfadraum, d.h. die Menge aller Abbildungen
r : T ÝÑ E. Für k P N, t1 , . . . , tk P T und A P BpE k q heißt
ω
!
)
r
r P Ω | pr
ω pt1 q, . . . , ω
r ptk qq P A
Cpt1 , . . . , tk ; Aq :“ ω
Zylindermenge mit Basis A. Dann ist
Bt1 ,...,tk :“ tCpt1 , . . . , tk ; Aq | A P BpEk qu
r Es sei BpT, Eq :“ σ pBt ,...,t | t1 , . . . , tk P T, k P Nq die kleinste σ-Algebra
eine σ-Algebra auf Ω.
1
k
r
welche alle Bt1 ,...,tk enthält. Dann ist pΩpT,
Eq, BpT, Eqqq ein messbarer Raum.
Lemma 6.2. Es sei X “ pXt qtPT ein stochastischer Prozess. Die Abbildung
r
IX : Ω ÝÑ ΩpT,
Eq, ω ÞÝÑ pt ÞÝÑ Xt pωqq
ist messbar.
Beweis. Sei k P N, A P BpE k q und t1 , . . . , tk P T . Dann ist ω ÞÝÑ pXt1 pωq, . . . , Xtk pωqq messbar.
Folglich gilt
´1
IX
pCpt1 , . . . , tk ; Aqq “ tω P Ω | IX pωq P Cpt1 , . . . , tk ; Aqu
“ tω P Ω | pXt1 pωq, . . . , Xtk pωqq P Au P F.
´1
Definition 6.3. Sei X “ pXt qtPT ein stochastischer Prozess. Dann heißt P ˝ IX
Verteilung von
´1
k
pXt qtPT . Die Wahrscheinlichkeitsmaße P ˝ pXt1 , . . . , Xtk q auf E mit k P N und t1 , . . . , tk P T
heissen endlichdimensionale Verteilungen von X.
Lemma 6.4. Seien pXt qtPT und pYt qtPT zwei stochastische Prozesse. Dann sind äquivalent:
81
(a) X und Y haben diesselbe Verteilung.
(b) X und Y haben diesselben endlichdimensionalen Verteilungen.
Beweis. paq ùñ pbq : Sei k P N, t1 , . . . , tk P T und A P BpE k q. Dann gilt
P ˝ pXt1 , . . . , Xtk q´1 pAq “ P ptω P Ω | pXt1 pωq, . . . , Xtk pωqq P Auq
´1
“ pP ˝ IX
qpCpt1 , . . . , tk ; Aqq “ pP ˝ IY´1 qpCpt1 , . . . , tk ; Aqq
“ P ˝ pYt1 , . . . , Ytk q´1 pAq.
´1
pbq ùñ paq : Obige Rechnung zeigt dass P˝IX
und P˝IY´1 auf allen Zylindermengen übereinstimmen.
Da diese einen X-stabilen Erzeuger bilden, folgt die Behauptung.
r
Satz 6.5. Sei µ ein Wahrscheinlichkeitsmaß auf pΩpT,
Eq, BpT, Eqq. Definiere
r
ω q :“ ω
r ptq, t P E, ω
r P ΩpT,
Xt pr
Eq.
(6.1)
r
Dann ist pXt qtPT ein stochastischer Prozess auf pΩpT,
Eq, BpT, Eq, µq mit Verteilung µ.
Beweis. Für den ersten Teil reicht es zu zeigen, dass Xt messbar ist für jedes t P T . Sei t P T
fest und A P BpEq. Dann gilt
r
ω P ΩpT,
ω q P Au
Xt´1 pAq “ tr
Eq | Xt pr
r
“ tr
ω P ΩpT,
Eq | ω
r ptq P Au “ Cpt; Aq P BpT, Eq.
Für den zweiten Teil betrachten wir k P N, t1 , . . . , tk P T und A P BpE k q. Dann gilt
´!
)¯
´1
r
r P ΩpT,
ω q, . . . , Xtk pr
ω qq P A
µ ˝ IX
pCpt1 , . . . , tk ; Aqq “ µ ω
Eq | pXt1 pr
)¯
´!
r
r P ΩpT,
Eq | pr
ω pt1 q, . . . , ω
r ptk qq P A
“µ ω
“ µpCpt1 , . . . , tk ; Aqq
´1
und somit µ ˝ IX
“ µ.
Die Darstellung (6.1) heißt kanonische Darstellung eines stochastischen Prozesses. Insbesondere ist ein stochastischer Prozess eindeutig durch seine Verteilung festgelegt. Wir haben gesehen,
dass eine solche Verteilung eindeutig durch die endlichdimensionalen Verteilungen charakterisiert
ist. Im folgenden wollen wir untersuchen, wann eine Familie von endlichdimensionalen Verteir
lungen ein Wahrscheinlichkeitsmaß auf ΩpT,
Eq festlegt, und damit einen stochastischen Prozess
liefert.
Definition 6.6. Sei tPt1 ,...,tk P PpE k q | k P N, t1 , . . . , tk P T u eine Familie von Wahrscheinlichkeitsmaßen. Diese Familie heißt konsisten, wenn sie die folgenden Bedingungen erfüllt.
(a) Für jedes k P N, jede Permutation π von k-Elementen und jedes A “ A1 ˆ Ak P BpE k q gilt
Pt1 ,...,tk pAq “ Pπpt1 ,...,tk q pAπ1 ˆ ¨ ¨ ¨ ˆ Aπk q,
wo πpt1 , . . . , tk q “ pπ1 , . . . , πk q.
82
(b) Für alle t1 , . . . , tk , tk`1 und alle A P ApE k q gilt
Pt1 ,...,tk pAq “ Pt1 ,...,tk`1 pA ˆ Eq.
Seien t1 , . . . , tk P T mit k P N gegeben. Definiere die Projektion
r
r ptk qq.
prt1 ,...,tk : ΩpT,
Eq ÝÑ E k , prt1 ,...,tk pr
ω q “ pr
ω pt1 q, . . . , ω
Satz 6.7. (Kolmogorov’s Erweiterungssatz) Sei E ein Polnischer Raum.
r ein Wahrscheinlichkeitsmaß auf pΩpT,
r
(a) Sei P
Eq, BpT, Eqq. Dann definiert
r ˝ pr´1 pAq, t1 , . . . , tk P T, k P N, A P BpE k q
Pt1 ,...,tk pAq :“ P
t1 ,...,tk
(6.2)
eine konsistente Familie von Wahrscheinlichkeitsmaßen.
(b) Sei tPt1 ,...,tk P PpE k q | k P N, t1 , . . . , tk P T u eine konsistente Familie von Wahrscheinr auf pΩpT,
r
lichkeitsmaßen. Dann gibt es genau ein Wahrscheinlichkeitsmaß P
Eq, BpT, Eqq
mit (6.2).
Beispiel 6.8. (Unabhängig, identisch verteilte Zufallsvariablen) Sei T “ Z` und E “ R. Wähle
ein Wahrscheinlichkeitsmaß µ auf R. Sei die Familie von Wahrscheinlichkeitsmaßen Pt1 ,...,tn
gegeben durch
n
ź
Pt1 ,...,tn pAq “
µpAj q, A “ A1 ˆ ¨ ¨ ¨ ˆ An P BpRn q.
j“1
r das eindeutig beDann ist tPt1 ,...,tn | t1 , . . . , tn P Z` , n P Nu eine konsistente Familie. Es sei P
r ` , Rq mit endlichdimensionalen Verteilungen Pt ,...,tn .
stimmte Wahrscheinlichkeitsmaß auf ΩpZ
1
r
r P ΩpZ` , Rq ist eine Folge pr
Jedes ω
ωn qnPN Ă R. Der dazugehörige Prozess in der kanonischen
Darstellung ist gegeben durch
ωq “ ω
rn , n P Z` .
Xn pr
Dann ist pXn qnPZ` eine Folge von unabhängig, identisch verteilten Zufallsvariablen mit Werten
in R.
Beispiel 6.9. (Gauß–Prozesse) Ein stochastischer Prozess X “ pXt qt≥0 heißt Gauß–Prozess,
falls für alle t1 , . . . , tn ≥ 0 die endlichdimensionalen Verteilungen P ˝ pXt1 , . . . , Xtn q´1 Normalverteilt sind. Wie wir bereits gesehen haben, ist die Normalverteilung eindeutig festgelegt durch
den Erwartungswert mpti q “ EpXti q und die Konvarianzmatrix B mit Einträgen
`
˘
Bpti , tj q “ E pXti ´ mpti qqpXtj ´ mptj qq .
Die endlich-dimensionalen Verteilungen sind also festgelegt duch eine Funktion mptq und eine
symmetrische Funktion Bpt, sq derart, dass für alle t1 , . . . , tn ≥ 0 die Matrix pBpti , tj qqi,j“1,...,n
positiv semi-definit ist.
Umgekehrt gibt es zu je zwei Funktionen mptq, Bpt, sq mit obigen Eigenschaften genau einen
Gauß–Prozess pXt qt≥0 . Wählen wir speziell Bpt, sq “ mints, tu und mptq “ 0, so heißt der
dazugehörige Gauß–Prozess auch Brownsche Bewegung. Diese wird häufig auch mit pWt qt≥0
bezeichnet.
83
Satz 6.10. Sei pWt qt≥0 ein stochastischer Prozess mit Werten in R. Genau dann ist pWt qt≥0
eine Brownsche Bewegung, wenn die folgenden Eigenschaften gelten.
(a) Es gilt W0 “ 0 fast sicher.
(b) Für alle 0 ≤ s ≤ t ist Wt ´ Ws normalverteilt mit Erwartungswert 0 und Varianz t ´ s.
(c) Die Zufallsvariablen Wt0 , Wt1 ´ Wt0 , . . . , Wtk ´ Wtk´1 sind für jedes k ≥ 1 und alle 0 “
t0 ≤ t1 ≤ ¨ ¨ ¨ ≤ tk unabhängig.
Beweis. Es sei pWt qt≥0 eine Brownsche Bewegung. Dann gilt EpW02 q “ mint0, 0u “ 0 und somit
W0 “ 0 fast sicher. Seien 0 ≤ s ≤ t. Dann ist pWs , Wt q normalverteilt und somit ist auch Wt ´Ws
normalverteilt. Daraus folgt
EpWt ´ Ws q2 “ EpWt2 q ´ 2EpWt Ws q ` EpWs2 q “ mintt, tu ´ 2 mintt, su ` mints, su “ t ´ s.
Sei k ≥ 1 und 0 “ t0 ≤ t1 ≤ ¨ ¨ ¨ ≤ tk . Dann ist pWt0 , . . . , Wtk q normalverteilt. Also ist auch
pWt0 , Wt1 ´Wt0 , . . . , Wtk ´Wtk´1 q normalverteilt. Also reicht es zu zeigen, dass die Komponenten
unkorreliert sind. Sei 1 ≤ i ă j ≤ k, dann gilt
EppWti ´ Wti´1 qpWtj ´ Wtj´1 qq “ EpWti Wtj q ´ EpWti Wtj´1 q ´ EpWti´1 Wtj q ` EpWti´1 Wtj´1 q
“ mintti , tj u ´ mintti , tj´1 u ´ mintti´1 , tj u ` mintti´1 , tj´1 u
“ tj ´ tj´1 ´ tj ` tj´1 “ 0.
Umgekehrt gelten die Eigenschaften (a),(b),(c). Dann ist pWt0 , Wt1 ´ Wt0 , . . . , Wtk ´ Wtk´1 q normalverteilt und die einzelnen Komponenten sind unabhängig. Es gibt eine invertierbare Matrix
A derart, dass
pWt0 , Wt1 , . . . , Wtk qt “ ApWt0 , Wt1 ´ Wt0 , . . . , Wtk ´ Wtk´1 qt .
Folglich ist auch pWt0 , Wt1 , . . . , Wtk q normalverteilt. Es gilt mptq “ EpWt q “ EpWt ´ W0 q “ 0
und für 0 ≤ s ≤ t
Bpt, sq “ EpWt Ws q “ EppWt ´ Ws qpWs ´ W0 qq ` EppWs ´ W0 q2 q “ EpWs2 q “ s.
Sei BpZ` , Rq die kleinste σ-Algebra erzeugt urch die Zylindermengen mit T “ Z` und E “ R.
Ferner sei BpR` , Rq die kleinste σ-Algebra erzeugt durch die Zylindermengen mit T “ R` und
E “ R.
Satz 6.11. Genau dann ist A P BpR` , Rq, wenn es eine Folge ptn qnPN Ă R` und ein B P
BpZ` , Rq gibt mit
!
)
r ` , Rq | pr
r P ΩpZ
ω pt1 q, ω
r pt2 q, . . . q P B .
A“ ω
Korollar 6.12. Sei E “ R, T “ R` und C ą 0. Dann sind
!
)
r ` , Rq | |r
ω
r P ΩpR
ω ptq| ă C, t P R`
r ` , Rq | ω
und tr
ω P ΩpR
r ist stetig u keine Elemente von BpR` , Rq. Weiterhin ist
r ` , Rq ˆ R` Q pr
ΩpR
ω , tq ÞÝÑ ω
r ptq
nicht messbar.
84
6.2
Eigenschaften stochastischer Prozesse
Definition 6.13. Ein stochastischer Prozess pXt qtPT heißt messbar, wenn
pω, tq ÞÝÑ Xt pωq
messbar ist bezüglich F b BpT q ´ ´BpEq.
Sei X :“ pXt qt≥0 ein zeitkontinuierlicher stochastischer Prozess.
• X ist linksstetig, falls t ÞÝÑ Xt fast sicher linksstetig ist.
• X ist rechtsstetig, falls t ÞÝÑ Xt fast sicher rechtsstetig ist.
• X ist càdlàg, falls t ÞÝÑ Xt fast sicher rechtsstetig ist und die linksseitigen Grenzwerte
existieren.
• X ist ist stetig, falls t ÞÝÑ Xt fast sicher stetig ist.
Lemma 6.14. Sei X :“ pXt qtPT ein zeitkontinuierlicher stochastischer Prozess. Angenommen
X ist linksstetig bzw. rechtsstetig. Dann ist X messbar.
Beweis. Wir zeigen den Fall, dass X rechtsstetig ist mit T “ r0, 8q. Der allgemeine Fall geht
analog. Definiere einen neuen Prozess durch
Ytn pωq :“ X
k
2n
pωq,
k
k`1
≤tă
n
2
2n
(6.3)
mit t ≥ 0, n P N und k P N0 . Dann ist pYtn qt≥0 messbar für jedes n P N. Denn für A P BpEq gilt
)
ď „ k k ` 1˙ !
n
tpt, ωq P r0, 8q ˆ Ω | Yt pωq P Au “
,
ˆ
ω
P
Ω
|
X
k pωq P A .
2n
2n 2n
k≥0
Da X rechtsstetig ist, gilt fast sicher lim Ytn “ Xt für alle t ≥ 0. Damit ist auch X messbar.
nÑ8
Definition 6.15. Seien pXt qtPT und pYt qtPT zwei stochastische Prozesse auf demselben Wahrscheinlichkeitsraum.
(a) X ist eine Modifikation von Y , falls
PpXt “ Yt q “ 1, t P T.
(b) X und Y sind ununterscheidbar, falls
PpXt “ Yt , t P T q “ 1.
Bemerkung 6.16. (a) Ist T abzählbar, so ist X eine Modifikation von Y genau dann, wenn
X und Y ununterscheidbar sind.
(b) Ist T nicht abzählbar, so gilt immerhin: Sind X, Y ununterscheidbar, so ist X eine Modifikation von Y . Aber auch Y ist eine Modifikation von X.
85
Lemma 6.17. Seien X :“ pXt qtPT und Y :“ pYt qtPT zwei zeitkontinuierliche stochastische
Prozesse, welche beide links oder rechtsstetig sind. Ist X eine Modifikation von Y , so sind X
und Y ununterscheidbar.
Beweis. Sei Ω1 P F mit PpΩ1 q “ 1 derart, dass für alle ω P Ω1 t ÞÝÑ Xt pωq, t ÞÝÑ Yt pωq beide
links oder rechtsstetig sind. Sei S Ă T eine dichte Teilmenge. Dann gibt es für jedes t P S ein
Ωt P F mit PpΩt q “ 1 derart, dass
Xt pωq “ Yt pωq, t P S, ω P Ωt .
Wähle Ω2 :“ Ω1 X
Ş
Ωt P F, dann gilt
tPS
PpΩ2c q ≤ PpΩ1c q `
ÿ
PpΩct q “ 0
tPS
und somit PpΩ2 q “ 1. Für jedes ω P Ω2 und t P T sei ptn qnPN Ă S eine Folge mit tn ÝÑ t.
Sind X und Y linksstetig, so wählen wir ptn qnPN aufsteigend, andererseits wählen wir die Folge
absteigend. Dann gilt
Xt pωq “ lim Xtn pωq “ lim Ytn pωq “ Yt pωq.
nÑ8
nÑ8
Definition 6.18. Seien X 1 “ pXt1 qtPT , . . . , X m “ pXtm qtPT stochastische Prozesse auf einem
gemeinsamen Wahrscheinlichkeitsraum. Wir sagen dass X 1 , . . . X m unabhängig sind, falls die
σ-Algebren
´
¯
j
F X :“ σ Xtj | t P T , j “ 1, . . . , m
unabhängig sind.
Definition 6.19. Sei I Ă r0, 8q eine Indexmenge. Eine Filtration ist eine Familie von σAlgebren pFt qtPI mit den folgenden Eigenschaften:
• Ft Ă F für alle t P I.
• Fs Ă Ft für alle s, t P I mit s ≤ t.
Der Raum pΩ, F, pFt qtPI , Pq heißt filtrierter Raum.
Im folgenden betrachten wir stets den Fall I “ R` oder I “ N0 . Im Falle I “ R` ist die
folgende Definition sinnvoll.
Ť
Definition 6.20. Eine Filtration pFt qt≥0 heißt rechtsstetig, falls Ft “
Fu .
uąt
Ist eine Filtration pFt qt≥0 gegeben, so ist per Definition Ft` :“
Ş
uąt
dere ist Ft rechtsstetig genau dann, wenn Ft “ Ft` für alle t ≥ 0.
86
Ft rechtsstetig. Insbeson-
Beispiel 6.21. Sei pXt qt≥0 ein stochastischer Prozess. Die von X erzeugte Filtration ist gegeben
durch
Ft :“ σ pXs | s ≤ tq , t ≥ 0.
Definition 6.22. Sei pXt qt≥0 ein stochastischer Prozess mit Werten in E.
(a) pXt qt≥0 heißt adaptiert, falls Xt messbar bezüglich Ft ist für alle t ≥ 0.
(b) pXt qt≥0 heißt progressiv messbar, falls für alle T ą 0
r0, T s ˆ Ω Q pt, ωq ÞÝÑ Xt pωq
messbar bezüglich Bpr0, T sq b FT ´ BpEq ist.
Satz 6.23. Sei pXt qt≥0 ein stochastischer Prozess und f : E ÝÑ R beschränkt und messbar.
(a) Ist X progressiv messbar, so ist X adaptiert und messbar.
(b) Ist X adaptiert und messbar, so gibt es eine Modifikation Y von X derart, dass X progressiv
messbar ist.
(c) Ist X adaptiert und rechtsstetig, so ist X progressiv messbar.
(d) Ist X progressiv messbar, so ist f ˝ X progressiv messbar und
żt
Yt :“
f pXs qds
0
adaptiert.
(e) Ist X messbar und adaptiert, so ist f ˝ X adaptiert und messbar und Yt hat eine progressiv
messbare Modifikation.
Beweis. (a) klar.
(b) Siehe ...
(c) Approximiere X durch (6.3).
(d) Sei A P BpRq, dann gilt für alle T ą 0
tpω, tq P Ω ˆ r0, T s | f pXt pωqq P Au “ tpω, tq P Ω ˆ r0, T s | Xt pωq P f ´1 pAqu P F b Bpr0, T sq
und folglich ist f ˝ X progressiv messbar. Für festes t ist f pXs q messbar bezüglich Fs Ă Ft für
alle s P r0, ts, welches die Behauptung zeigt.
(e) f ˝ X ist messbar, als Verkettung messbarer Funktionen. Sei t ≥ 0 und A P BpEq. Dann gilt
tω P Ω | f pXt pωqq P Au “ tω P Ω | Xt pωq P f ´1 pAqu P Ft
und folglich ist f ˝ X adaptiert. Folglich ist Yt messbar und adaptiert. Die Behauptung folgt aus
(b).
87
6.3
Stoppzeiten
Definition 6.24. Eine Abbildung T : Ω ÝÑ r0, 8s heißt Stoppzeit, falls
tT ≤ tu P Ft , t ≥ 0.
Die Stoppzeit T heißt diskret, falls tT P Du “ Ω für eine abzählbare Menge D Ă r0, 8s gilt.
Für s ă t auch tT ≤ su P Fs Ă Ft und folglich
*
ď"
1
tT ă tu “
T ≤t´
P Ft
n
n≥1
(6.4)
und tT “ tu “ tT ≤ tuztT ă tu P Ft . Ist T zusätzlich diskret, so ist T eine Stoppzeit genau
dann, wenn tT “ tu P Ft für alle t P D X r0, 8q.
Lemma 6.25. Sei pTn qnPN eine Folge von Stoppzeiten, T, S weitere Stoppzeiten.
(a) mintT, Su und α ¨ T sind Stoppzeiten für α ą 1.
(b) T ist eine Stoppzeit bezüglich pFt` qt≥0 genau dann, wenn tT ă tu P Ft für alle t ≥ 0.
(c) sup Tn ist eine Stoppzeit.
nPN
(d) min Tk ist eine Stoppzeit für alle n ≥ 1.
k≤n
(e) Ist pFt qt≥0 rechtsstetig, so sind auch inf Tn , lim inf Tn und lim sup Tn Stoppzeiten.
nÑ8
nPN
nÑ8
Beweis. (a) Es gilt
tmintT, Su ≤ tu “ tT ≤ tu X tS ≤ tu P Ft .
Weiterhin gilt
*
"
t
P F t Ă Ft .
tα ¨ T ≤ tu “ T ≤
α
α
(b) Ist tT ă tu P Ft für alle t ≥ 0, so gilt tT ă t ` n´1 u P Ft`m´1 für alle n ≥ m und folglich
č
č
tT ≤ tu “
tT ă t ` n´1 u P
Ft`m´1 “ Ft` .
n≥1
m≥1
Die Umkehrung folgt aus (6.4).
Ş
(c) Es gilt tsup Tn ≤ tu “
tTn ≤ tu P Ft .
n≥1
n≥1
Ť
(d) Es gilt tmin Tk ≤ tu “
tTk ≤ tu P Ft .
k≤n
k≤n
(e) Es gilt
t inf Tn ă tu “
n≥1
ď
tTn ă tu P Ft
n≥1
und da pFt qt≥0 rechtsstetig ist, folgt die Behauptung aus (b). Wegen lim inf Tn “ sup inf Tn
nÑ8
und lim sup Tn “ inf sup Tn folgt die Behauptung.
nÑ8
m≥1 n≥m
88
m≥1 n≥m
Insbesondere lässt sich jede Stoppzeit T durch eine Folge von beschränkten Stoppzeiten
Tn :“ maxtT, nu von unten approximieren. Eine weitere nützliche Approximationseigenschaft
ist im folgenden Satz formuliert.
pnq
Satz 6.26. Für n P N sei 0 “ t0
pnq
pnq
ă t1 . . . eine Folge mit lim tk “ 8 und
kÑ8
pnq
pnq
lim supptk`1 ´ tk q “ 0.
nÑ8 kPN
Sei T eine pFt` qt≥0 Stoppzeit und
#
Tn :“
pnq
tk`1 ,
8,
pnq
pnq
tk ≤ T ă tk`1 , k ≥ 0
.
T “8
pnq
pn`1q
Dann ist Tn eine Stoppzeit und es gilt lim Tn “ T . Ist zusätzlich ptk qkPN Ă ptk
nÑ8
n ≥ 1, so gilt Tn`1 ≤ Tn .
pnq
Beweis. Sei an ptq :“ maxttk
qkPN für alle
pnq
| tk ≤ tu. Dann gilt
tTn ≤ tu “ tTn “ an ptqu “ tT ă an ptqu P Fan ptq Ă Ft .
Der zweite Teil der Behauptung ist klar.
Definition 6.27. Sei T eine Stoppzeit. Definiere
FT :“ tA P F | A X tT ≤ tu P Ft , @t ≥ 0u
und
FT ` :“ tA P F | A X tT ≤ tu P Ft` , @t ≥ 0u.
Es ist nicht schwer zu zeigen, dass FT und FT ` σ-Algebren sind. Ebenfalls ist es nicht schwer
zu zeigen, dass T messbar bezüglich FT ist, denn für r ≥ 0 gilt
tT ≤ cu X tT ≤ tu “ tT ≤ r ^ tu P Ft
und somit tT ≤ cu P FT .
Lemma 6.28. Seien T, S Stoppzeiten. Dann gelten die folgenden Eigenschaften.
(a) mintT, Su ist messbar bezüglich FT .
(b) Ist T ≤ S, so gilt FT Ă FS .
Beweis. (a) Für alle s, t ≥ 0 gilt
tS ^ T ≤ su X tT ≤ tu “ tS ^ T ≤ s ^ tu X tT ≤ tu
“ ptS ≤ s ^ tu Y tT ≤ s ^ tuq X tT ≤ tu P Ft .
Folglich gilt tS ^ T ≤ su P FT und damit ist S ^ T messbar.
(b) Sei A P FT und t ≥ 0 beliebig. Dann gilt
A X tS ≤ tu “ A X tS ≤ tu X tT ≤ tu P Ft
da A X tT ≤ tu P Ft und tS ≤ tu P Ft .
89
Sei X “ pXt qt≥0 ein stochastischer Prozess und T eine Stoppzeit. Definiere
XT : Ω ÝÑ E, ω ÞÝÑ XT pωq pωq,
wo X8 :“ x0 mit einem beliebigen (festen) Punkt x0 P E. Der zum Zeitpunkt T gestoppte
Prozess ist definiert durch
pX T qt :“ XT ^t “ Xt 1tăT ` XT 1T ≤t .
Betrachte die dazugehörigen σ-Algebren FT sowie
FT ^t “ tA P F | A X tmintT, tu ≤ su P Fs , @s ≥ 0u.
Satz 6.29. Es sei pXt qt≥0 progressiv messbar bezüglich der Filtration pFt qt≥0 . Dann gelten die
folgenden Eigenschaften.
(a) XT ist messbar bezüglich FT .
(b) X T ist pFT ^t qt≥0 sowie pFt qt≥0 progressiv messbar, wobei FT ^t eine Filtration ist.
(c) pXT `t qt≥0 ist pFT `t qt≥0 progressiv messbar, wo
FT `t “ tA P F | A X tT ` t ≤ su P Fs , @s ≥ 0u.
eine Filtration ist.
Beweis. (a) Sei t ≥ 0, dann ist T ^ t messbar bezüglich Ft . Also ist auch ω ÞÝÑ pT pωq ^ t, ωq
messbar bezüglich Ft ´ ´Bpr0, tsq b Ft . Da X progressiv messbar ist, ist auch die Komposition
ω ÞÝÑ XT pωq^t pωq messbar bezüglich Ft . Folglich gilt für A P BpEq
tXT P Au X tT ≤ tu “ tXT ^t P Au X tT ≤ tu P Ft
und somit tXT P Au P FT .
(b), (c) siehe [EK86, Chapter 2, Proposition 1.4].
Wir wollen uns abschließend mit Beispielen von Stoppzeiten beschäftigen. Es sei pXt qt≥0 ein
stoch. Prozess mit Werten in E. Gegeben A P BpEq, dann ist die Ersteintrittszeit von X in A
definiert durch
TA “ inftt ≥ 0 | Xt P Au
wo inf H :“ `8. Es sei σ eine r0, 8s-wertige Zufallsvariable. Dann ist die Ersteintrittszeit von
X in A nach σ definiert durch
Tσ,A “ inftt ≥ σ | Xt P Au.
Beachte, für σ “ 0 ist Tσ,A “ TA .
Satz 6.30. Es sei X “ pXt qt≥0 ein rechtsstetiger stoch. Prozess, pFt qt≥0 adaptiert und σ eine
pFt qt≥0 Stoppzeit. Ist A Ă E offen, so ist Tσ,A eine Stoppzeit bezüglich pFt` qt≥0 .
90
Beweis. Es gilt
tTσ,A ă tu “
ď
tXt´ 1
n≥1
n
"
*
1
P Au X σ ă t `
P Ft .
n
Es gilt ein stärkeres Resultat. Hierfür brauchen wir, dass der Wahrscheinlichkeitsraum vollständig
ist.
Definition 6.31. Ein Wahrscheinlichkeitsraum pΩ, F, Pq heißt vollständig, falls F alle Nullmengen enthält. D.h. ist A P F mit PpAq “ 0, so gilt für alle B Ă A bereits B P F.
Satz 6.32. Sei pΩ, F, Pq ein Wahrscheinlichkeitsraum und sei
N “ tA Ă Ω | DB P F : A Ă B, PpBq “ 0u.
Dann ist pΩ, F ˚ , P˚ q ein vollständiger Wahrscheinlichkeitsraum, wo
F ˚ :“ tA Y N | A P F, N P N u
eine σ-Algebra und
P˚ pA Y N q :“ PpAq, A P F, N P N
ein Wahrscheinlichkeitsmaß auf F ˚ ist.
Definition 6.33. Ein filtrierter Raum pΩ, F, pFt qt≥0 , Pq erfüllt die üblichen Bedingungen, falls
gilt:
• pΩ, F, Pq ist vollständig.
• N Ă F0 .
• pFt qt≥0 ist rechtsstetig.
Satz 6.34. Sei pΩ, F, pFt qt≥0 , Pq ein filtrierter Raum mit den üblichen Bedingungen, pXt qt≥0
ein bezüglich pFt qt≥0 progressiv messbarer stochastischer Prozess. Dann ist für jedes A P BpEq
die Ersteintrittszeit TA eine Stoppzeit bezüglich pFt qt≥0 .
7
Martingale
Definition 7.1. Es sei pMt qt≥0 ein reellwertiger, stochastischer Prozess adaptiert an eine Filtration pFt qt≥0 mit Ep|Mt |q ă 8 für alle t ≥ 0. Dann ist Mt ein
• Submartingal, falls Ms ≤ EpMt |Fs q für alle s ≤ t.
• Supermartingal, falls Ms ≥ EpMt |Fs q für alle s ≤ t.
• Martingal, falls Ms “ EpMt |Fs q für alle s ≤ t.
91
Sei pMt qt≥0 ein Submartingal, s ≤ t und A P Fs . Dann gilt
ż
ż
ż
Ms dP ≤ EpMt |Fs qdP “ Mt dP.
A
A
A
Umgekehrt pMt qt≥0 ist genau dann ein Submartingal, wenn obige Ungleichung gilt. Analog ist
pMt qt≥0 genau dann ein Supermartingal, wenn für alle A P Fs
ż
ż
Ms dP ≥ Mt dP.
A
A
pMt qt≥0 ist genau dann ein Martingal, wenn für alle A P Fs
ż
ż
Ms dP “ Mt dP.
A
A
Das nächste Lemma folgt aus der Jensen Ungleichung für bedingte Erwartungswerte.
Lemma 7.2. (a) Es sei pMt qt≥0 ein Martingal und ϕ : R ÝÑ R konvex mit Ep|ϕpMt q|q ă 8
für alle t ≥ 0. Dann ist pϕ ˝ Mt qt≥0 ein Submartingal.
(b) Es sei pMt qt≥0 ein Submartingal und ϕ : R ÝÑ R konvex und monoton steigend mit
Ep|ϕpMt q|q ă 8 für alle t ≥ 0. Dann ist pϕ ˝ Mt qt≥0 ein Submartingal.
Beweis. (a) Für s ≤ t folgt die Behauptung aus
ϕpMs q “ ϕ pEpMt |Fs qq ≤ EpϕpMt q|Fs q.
(b) Für s ≤ t folgt die Behauptung aus
ϕpMs q ≤ ϕ pEpMt |Fs qq ≤ EpϕpMt q|Fs q.
Bemerkung 7.3. Es sei pMt qt≥0 ein an die Filtration pFt qt≥0 adaptierter stochastischer Prozess. Dann gelten:
(a) Ist Mt ein Submartingal, so EpMs q ≤ EpMt q.
(b) Ist Mt ein Supermartingal, so EpMs q ≥ EpMt q.
(c) Ist Mt ein Martingal, so EpMs q “ EpMt q.
Bevor wir die allgemeine Theorie der Martingale uns ansehen, wollen wir einige Beispiele
Betrachten. Wir beginnen mit einem diskreten Beispiel.
92
Beispiel 7.4. Sei pZn qnPN0 eine Folge unabhängig, identisch verteilter Zufallsvariablen mit Z1 P
L1 und EpZ1 q “ 0. Definiere eine Filtration durch
Fn :“ σpZk | 0 ≤ k ≤ nq.
Dann ist
n
ÿ
Mn :“
Zk , n ≥ 0
k“1
ein zeitdiskretes Martingal in dem folgenden Sinne:
• Mn ist messbar bezüglich Fn und es gilt Ep|Mn |q ă 8.
• Für alle k ă n gilt
EpMn |Fk q “ Mk .
Die erste Eigenschaft ist klar. Für die zweite Eigenschaft erhalten wir
k
ÿ
EpMn |Fk q “
j“0
n
ÿ
Zj `
n
ÿ
EpZj |Fk q “ Mk `
j“k`1
EpZj q “ Mk .
j“k`1
Das nächste Beispiel ist eine zeitkontinuierliche Version.
Beispiel 7.5. Es sei pZt qt≥0 ein stetiger stochastischer Prozess, mit 0 ≤ Zt P L1 , EpZt q “ 0
sowie
żt
EpZs qds ă 8
0
für alle t ≥ 0. Definiere eine Filtration Ft :“ σpZs | s ≤ tq. Dann ist
żt
Zs pωqds, t ≥ 0
Mt pωq :“
0
ein Submartingal.
Beweis. Da Zt stetig und bezüglich Ft adaptiert ist, ist pZt qt≥0 progressiv messbar und folglich
ist Mt adaptiert. Ferner gilt nach Voraussetzung
żt
EpMt q “
EpZs qds ă 8.
0
Es sei 0 ≤ s ≤ t, dann gilt
żs
EpMt |Fs q “
żt
EpZr |Fs qdr `
0
żs
0
93
EpZr |Fs qdr ≥ Ms .
Zr dr `
EpZr |Fs qdr “
s
żt
s
Beispiel 7.6. (Brownsche Bewegung) Es sei pBt qt≥0 die Brownsche Bewegung. Definiere eine
Filtration
Ft :“ σpBs | s ≤ tq.
Dann ist pBt qt≥0 ein Martingal bezüglich pFt qt≥0 .
Beweis. Per Definition ist pBt qt≥0 adaptiert. Da Bt für t ≥ 0 Normalverteilt ist mit Varianz t,
folgt
ż
|x|2
1
Ep|Bt |q “ ?
|x|e´ 2t dx ă 8.
2πt
R
Es sei 0 ≤ s ≤ t, dann ist Bt ´ Bs wegen Unabhängigkeit der Inkremente und der Wahl der
Filtration unabhängig von Fs . Daraus folgt
EpBt |Fs q “ EpBt ´ Bs |Fs q ` EpBs |Fs q “ EpBt ´ Bs q ` Bs “ Bs .
Eine allgemeine Brownsche Bewegung definieren wir wie folgt.
Definition 7.7. Es sei pBt qt≥0 ein stochastischer Prozess und pFt qt≥0 eine Filtration. Dann
heißt pBt qt≥0 eine Brownsche Bewegung bezüglich pFt qt≥0 , falls die folgenden Eigenschaften gelten:
• B0 “ 0 fast sicher.
• Bt ´ Bs ist unabhängig von Fs und Normalverteilt mit Erwartungswert 0 und Varianz t ´ s
für alle 0 ≤ s ≤ t.
Obiges Beispiel zeigt, dass pBt qt≥0 ein Martingal bezüglich pFt qt≥0 ist. Allgemeiner ist der
nächste Satz.
Satz 7.8. Es sei pMt qt≥0 ein stochastischer Prozess adaptiert and die Filtration pFt qt≥0 mit
Ep|Mt |q ă 8 für alle t ≥ 0. Es gelte
• EpM0 q “ 0.
• Mt ´ Ms sei unabhängig von Fs für alle 0 ≤ s ≤ t.
Dann sind die folgenden stochastischen Prozesse Martingale:
(a) pMt qt≥0 .
(b) Ist EpMt2 q ă 8 für alle t ≥ 0, so ist Mt2 ´ EpMt2 q ein Martingal.
Beweis. (a) Es gilt
EpMt |Fs q “ EpMt ´ Ms |Fs q ` Ms “ EpMt ´ Ms q ` Ms “ Ms .
94
(b) Da pMt qt≥0 ein Martingal ist, folgt
EppMt ´ Ms q2 |Fs q “ EpMt2 ´ 2Mt Ms ` Ms2 |Fs q
“ EpMt2 |Fs q ` Ms2 ` 2Ms EpMt |Fs q “ EpMt2 ´ Ms2 |Fs q.
Daraus folgt
EpMt2 |Fs q “ EpMt2 ´ Ms2 |Fs q ` Ms2 “ EppMt ´ Ms q2 |Fs q ` Ms2
“ EpMt2 ´ Ms2 q ` Ms2
und somit
EpMt2 ´ EpMt2 q|Fs q “ Ms2 ´ EpMs2 q.
7.1
Martingale in diskreter Zeit
Definition 7.9. Sei pMn qnPN0 eine Folge von Zufallsvariablen auf einem filtrierten Raum pΩ, F, pFn qnPN0 , Pq
mit Mn ist messbar bezüglich Fn und Ep|Mn |q ă 8. Dann heißt pMn qnPN0 zeitdiskretes
• Submartingal, falls Mk ≤ EpMn |Fk q
• Supermartingal, falls Mk ≥ EpMn |Fk q
• Martingal, falls Mk “ EpMn |Fk q.
für alle k ă n gilt.
Lemma 7.10. Sei pMn qnPN0 eine Folge von Zufallsvariablen auf einem filtrierten Raum pΩ, F, pFn qnPN0 , Pq
mit Mn ist messbar bezüglich Fn und Ep|Mn |q ă 8. Dann gilt:
(a) Mn ist ein Submartingal ðñ Mn´1 ≤ EpMn |Fn´1 q
(b) Mn ist ein Supermartingal ðñ Mn´1 ≥ EpMn |Fn´1 q
(c) Mn ist ein Martingal ðñ Mn´1 “ EpMn |Fn´1 q.
Beweis. Wir zeigen nur den Fall eines Submartingals. Die anderen Fälle gehen analog. Die
Richtung ùñ ist klar. Für die Umkehrung sei k ă n.
Mk ≤ EpMk`1 |Fk q ≤ EpEpMk`2 |Fk`1 q|Fk q “ EpMk`2 |Fk q.
Iteration liefert nach endlich vielen Schritten die Behauptung.
Der erste Satz zeigt, dass jedes Submartingal zerlegt werden kann in die Summe von einem
Martingal und einem monoton steigenden stochastischen Prozess.
Satz 7.11. (Doob Zerlegung) Sei pXn qnPN0 ein Submartingal bezüglich einer Filtration pFn qnPN0 .
Dann gibt es zwei stochastische Prozesse pMn qnPN und pAn qnPN mit den folgenden Eigenschaften
95
• Xn “ Mn ` An , n ≥ 0.
• pMn qnPN0 ist ein Martingal bezüglich pFn qnPN0 .
• A0 “ 0, An ist messbar bezüglich Fn´1 für alle n ≥ 1.
• An ist monoton steigen, d.h.
An pωq ≤ An`1 pωq
für fast alle ω und alle n ≥ 0.
Gegeben ein weiteres Paar Mn1 und A1n mit denselben Eigenschaften. Dann gilt Mn “ Mn1 sowie
An “ A1n fast sicher.
Beweis. Angenommen wir haben Mn und An bereits konstruiert. Dann gilt für n ≥ 1
Xn´1 “ Mn´1 ` An´1
Xn “ Mn ` An .
Betrachten wir die Differenz dieser Gleichungen und bedingen auf Fn´1 , so folgt
EpXn |Fn´1 q ´ Xn´1 “ An ´ An´1 .
Also ist An eindeutig durch pXn qnPN0 sowie An´1 festgelegt. Wegen der Bedingung Mn “ Xn ´An
ist dann auch Mn eindeutig festgelegt. Beginnen wir mit M0 “ X0 und A0 “ 0, so lässt sich die
Eindeutigkeit über Induktion nachweisen.
Für die Existenz setze M0 :“ X0 , A0 :“ 0 und für n ≥ 1
An :“ EpXn |Fn´1 q ´ Xn´1 ´ An´1 , Mn :“ Xn ´ An .
Es bleibt zu zeigen, dass die so definierten Prozesse alle Bedingungen erfüllen. Die erste Bedingung folgt direkt aus der Konstruktion. Für die zweite Bedingung rechnen wir nach
EpMn |Fn´1 q “ EpXn ´ An |Fn´1 q “ EpXn |Fn´1 q ´ An
“ Xn´1 ´ An´1 “ Mn´1 .
Die dritte Bedingung folgt aus der Definition von An . Die letzte Bedingung folgt aus
An “ EpXn |Fn´1 q ´ Xn´1 ` An´1 ≥ An´1
da pXn qnPN0 ein Submartigal ist.
Satz 7.12. (Optional Sampling) Sei pXn qnPN0 ein Submartingal und T, S zwei zeitdiskrete Stoppzeiten mit S ≤ T ≤ k für ein k P N. Dann gilt
XS ≤ EpXT |FS q.
Ist pXn qnPN0 ein Martingal bzw. ein Supermartingal, so gilt “ bzw. ≥ in (7.1)
96
(7.1)
Beweis. Ist pXn qnPN0 ein Supermartingal, so ist p´Xn qnPN0 ein Submartingal. Wir zeigen daher
den Fall dass pXn qnPN0 ein Submartigal ist. Sei A P FS und 1 ≤ m ≤ n. Setze Am :“ AXtS “ mu.
Dann ist Am X tT ą nu P Fn und folglich (da pXn qnPN0 ein Submartigal ist)
ż
ż
Xn`1 dP.
Xn dP ≤
Am XtT ąnu
Am XtT ąnu
Daraus folgt
ż
ż
ż
Xn dP ≤
Am XtT ≥nu
Xn dP
Xn dP `
Am XtT “nu
Am XtT ąnu
ż
ż
≤
Xn`1 dP `
Am XtT ąnu
Xn dP
Am XtT “nu
ż
ż
Xn`1 dP `
“
Am XtT ≥n`1u
und somit
ż
Xn dP
Am XtT “nu
ż
ż
Xn`1 dP ≤
Xn dP ´
Am XtT ≥nu
Am XtT ≥n`1u
Xn dP.
Am XtT “nu
Summieren über n “ m bis k liefert mittels Teleskopsumme
ż
ż
ż
Xm dP “
Xm dP ´
Xk`1 dP
Am
Am XtT ≥mu
Am XtT ≥k`1u
¨
˛
k
ÿ
˚
“
˝
n“m
≤
k
ÿ
ż
ż
Xn dP ´
Am XtT ≥nu
‹
Xn`1 dP‚
Am XtT ≥n`1u
ż
ż
Xn dP “
n“m
XT dP.
Am
Am XtT “nu
Bilden wir jetzt die Summe von m “ 1 bis k, so folgt
ż
ż
XS dP ≤ XT dP
A
A
und somit (7.1).
Definition 7.13. Eine Familie von Zufallsvariablen pXt qtPT , wo T eine beliebige Menge ist,
heißt gleichgradig integrierbar, falls
lim sup Ep1|Xt |ąn |Xt |q “ 0.
nÑ8 tPT
97
Lemma 7.14. Eine Familie von Zufallsvariablen pXt qtPT ist genau dann gleichgradig integrierbar, wenn gilt
• sup Ep|Xt |q ă 8.
tPT
• Für alle ε ą 0 gibt es ein δ ą 0 mit
Ep1A |Xt |q ≤ ε, t P T
für alle A mit PpAq ≤ δ.
Beweis. Übung.
Bemerkung 7.15. Optional Sampling gilt im allgemeinen nur für beschränkte Stoppzeiten S ≤
T ≤ k. Ist hingegen pXn qnPN gleichgradig integrierbar, so gilt Optional Sampling für beliebige
Stoppzeiten S ≤ T .
Satz 7.16. (Doob Ungleichung) Sei pXn qnPN0 ein Submartingal. Dann gilt für alle n P N und
jedes ε ą 0
ż
1
Pp max Xi ≥ εq ≤
Xn dP ≤ EppXn q` q,
0≤i≤n
ε
max Xi ≥ε
0≤i≤n
wo pXn q` “ maxtXn , 0u.
Beweis. Sei
S “ mintk P N0 | Xk ≥ εu
mit min H :“ 8. Dann sind S ^ n ≤ n “: T beschränkte Stoppzeiten. Ferner gilt für m ≤ n
t max Xk ≥ εu X tS ^ n ≤ mu “ t max Xk ≥ εu P Fm .
0≤k≤n
1≤k≤m
Für m ą n ist t max Xk ≥ εu P Fn Ă Fm und somit
0≤k≤n
t max Xk ≥ εu X tS ^ n ≤ mu P Fm .
0≤k≤n
Daraus folgt t max Xk ≥ εu P FS^n und mit Optional Sampling
0≤k≤n
ˆ
εP
˙
max Xk ≥ ε
0≤k≤n
ż
≤
ż
Xn dP ≤ EppXn q` q.
XS^n dP ≤
max Xk ≥ε
max Xk ≥ε
1≤k≤n
0≤k≤n
Korollar 7.17. Sei pMn qnPN0 ein Martingal oder ein positives Submartingal. Dann gilt für jedes
ε ą 0 und p P r1, 8q
˜
¸
1
p
P sup |Mk | ≥ ε ≤ p Ep|Mn |p q
ε
0≤k≤n
98
Beweis. Da x ÞÝÑ |x|p konvex ist, ist p|Mn |p qnPN ein Submartingal. Folglich gilt
ˆ
˙
ż
p
p
|Mn |p dP ≤ Ep|Mn |p q.
ε P max |Mn | ≥ ε ≤
0≤i≤n
max |Mn |p ≥ε
0≤i≤n
Satz 7.18. [EK86] Sei pMn qnPN0 ein Martingal oder ein positives Submartingal. Dann gilt für
alle n P N und p ą 1
˜
¸ ˆ
˙p
p
p
E sup |Mk |
≤
E p|Mn |p q .
p´1
0≤k≤n
Beispiel 7.19. Sei pFn qnPN0 und Y P L1 . Dann definiert
Mn :“ EpY |Fn q, n P N0
ein Martingal.
Definition 7.20. Ein Martingal pXn qnPN0 heißt abgeschlossen, falls es ein M8 P L1 gibt mit
Xn “ EpX8 |Fn q.
Definiere die σ-Algebra
F8 :“ σpFn | n ≥ 0q.
Man beachte, dass F8 nicht mit F übereinstimmen muss. Sei pMn qnPN0 ein abgeschlossenes
Martingal mit M8 P L1 und definiere
1
M8
:“ EpM8 | F8 q.
Dann gilt
1
EpM8
|Fn q “ EpEpM8 |F8 q|Fn q “ EpM8 |Fn q “ Mn .
Daher können wir stets annehmen, dass M8 messbar ist bezüglich F8 .
Satz 7.21. Ein Martingal ist genau dann abgeschlossen, wenn es gleichgradig integrierbar ist.
Wir zeigen nur die gleichgradige integrierbarkeit. Die Umkehrung lässt sich in [Dud02] nachlesen.
Beweis. Sei pMn qnPN ein abgeschlossenes Martingal mit M8 P L1 messbar bezüglich F8 . Wir
müssen zeigen, dass
lim sup Ep1|Mn |ąm |Mn |q “ 0.
mÑ8 nPN
Da | ¨ | eine konvexe Funktion ist folgt
|Mn | “ |EpM8 |Fn q| ≤ Ep|M8 ||Fn q.
99
Daraus folgt Ep|Mn |q ≤ Ep|M8 |q ă 8 für alle n P N und
ż
ż
|M8 |dP.
|Mn |dP ≤
|Mn |ąm
|Mn |ąm
Sei ε ą 0 beliebig. Wegen 1|M8 |≤N ÝÑ 1 fast sicher für N Ñ 8 und dem Satz von Lebesgue
gibt es ein N mit Ep1|M8 |ąN |M8 |q ă ε. Daraus folgt
sup Ep1|Mn |ąm |Mn |q ≤ sup Ep1|Mn |ąm |M8 |q
nPN
nPN
≤ sup Ep1|Mn |ąm 1|M8 |≤N |M8 |q ` sup Ep1|Mn |ąm 1|M8 |ąN |M8 |q
nPN
nPN
≤ N sup Pp|Mn | ą mq ` Ep1|M8 |ąN |M8 |q.
nPN
Der zweite Term ist kleiner ε und für den ersten gilt
sup Pp|Mn | ą mq ≤ sup
nPN0
nPN
Ep|Mn |q
1
≤ Ep|M8 |q.
m
m
Satz 7.22. (Doob) Sei pMn qnPN0 ein abgeschlossenes Martingal. Dann gilt
Mn ÝÑ M8 , n Ñ 8
fast sicher und in L1 .
Lemma 7.23. Es sei F die Menge aller Y P L1 derart dass Y messbar bezüglch Fn für ein
n P N ist. Für jedes ε ą 0 und X P L1 pΩ, F8 , Pq gibt es Y P F mit
|EpX ´ Y q| ă ε.
Beweis. Sei K “
Ť
Fn und
nPN0
G “ tA | @ε ą 0 DB P K : PppAzBq Y pBzAqq ă εu .
Dann ist K ein X-stabiler Erzeuger von F8 und G ist ein Dynkin System.
F8 “ σpKq “ dpKq Ă G.
Die letzte Inklusion gilt da Fn P G für alle n ≥ 1.
Schritt 1. Ist X “ 1A , so wähle B P G mit PpA∆Bq ă ε. Setze Y :“ 1B P F . Dann gilt
Ep|X ´ Y |q “ PpA∆Bq ă ε.
Schritt 2. Sei X “
Bn P G mit
N
ř
n“1
an 1An mit paarweise disjunkten Mengen An P F8 und an ≥ 0. Wähle
PpAn ∆Bn q ă
ε
.
N p1 ` max |ak |q
k“1,...,N
100
Dann ist Y :“
N
ř
k“1
ak 1Bk P F und es gilt
˜
Ep|X ´ Y |q ≤ E
¸
N
ÿ
|ak ||1Ak ´ 1Bk |
k“1
N
ÿ
≤ max |ak | ¨
k“1,...,N
PpAk ∆Bk q ă ε.
k“1
Schritt 3. Sei X P L1 pΩ, F8 , Pq mit 0 ≤ X ≤ M , wo M ą 0 eine Konstante. Wähle X 1 ≥ 0
Elementarfunktion mit X 1 ≤ X und
ε
Ep|X 1 ´ X|q ă .
2
Nach Schritt 2 gibt es Y P F mit Ep|Y ´ X 1 |q ă 2ε . Daraus folgt
Ep|X ´ Y |q ≤ Ep|X ´ X 1 |q ` Ep|X 1 ´ Y |q ă ε.
Schritt 4. Sei X P L1 pΩ, F8 , Pq nicht-negativ. Dann gibt es M ą 0 mit Ep1|X|≥M |X|q ă
Ferner gibt es nach Schritt 3 ein Y P F mit Ep|Y ´ 1|X|≤M X|q ă 2ε . Daraus folgt
ε
2.
Ep|X ´ Y |q ≤ Ep1|X|≥M |X|q ` Ep|X 1|X|≤M ´ Y |q ă ε.
Der letzte Schritt folgt durch Zerlegen in Positiv und Negativteil.
Beweis. Zu ε ą 0 und M8 P L1 pΩ, F8 , Pq wähle Y8 P F mit
Ep|M8 ´ Y8 |q ≤ ε2 .
(7.2)
Sei Yn :“ EpY8 |Fn q. Dann ist pMn ´ Yn qnPN0 ein Martingal. Also ist p|Mn ´ Yn |qnPN0 ein Submartingal mit
|Mn ´ Yn | “ |EpM8 ´ Y8 |Fn q| ≤ Ep|M8 ´ Y8 | | Fn q.
Daraus folgt
Ep|Mn ´ Yn |q ≤ Ep|M8 ´ Y8 |q.
Aus Doobs Ungleichung folgt
ˆ
˙
1
1
P sup |Mn ´ Yn | ą ε ≤ sup Ep|Mn ´ Yn |q ≤ Ep|M8 ´ Y8 |q ≤ ε.
ε
ε
nPN
nPN
Nach der Wahl von F gilt Y8 “ Yn für hinreichend große n P N. Also folgt aus (7.3)
ˆ
˙
´
¯
P lim suppMn ´ Y8 q ą ε ă ε, P lim inf pMn ´ Yn q ă ´ε ă ε.
nÑ8
nÑ8
Aus Chebyscheff und (7.2) folgt
1
P p|M8 ´ Y8 | ą εq ≤ Ep|M8 ´ Y8 |q ≤ ε.
ε
101
(7.3)
(7.4)
Wir erhalten aus (7.4)
ˆ
˙
ˆ
˙
ˆ
˙
P lim suppMn ´ M8 q ą 2ε ≤ P lim suppMn ´ Y8 ą ε ` P lim suppY8 ´ M8 q ą ε ≤ 2ε
nÑ8
nÑ8
nÑ8
und analog
´
¯
P lim inf pMn ´ M8 q ă ´2ε ≤ 2ε.
nÑ8
Da ε ą 0 beliebig war folgt Mn ÝÑ M8 fast sicher für n Ñ 8.
Für die Konvergenz in L1 sei ε ą 0 fest. Da pMn qnPN gleichgradig integrierbar ist gibt es
δ ą 0 derart, dass für alle A P F mit PpAq ≤ δ
ż
ż
|M8 |dP ă ε.
sup |Mn |dP ă ε,
nPN
A
A
Da Mn ÝÑ M8 fast sicher konvergiert, gilt Konvergenz in Wahrscheinlichkeit, d.h.
Pp|Mn ´ M8 | ą εq ≤ δ
für hinreichend große n P N. Für solche großen n erhalten wir
Ep|Mn ´ M8 |q ≤ Ep|Mn |1|Mn ´M8 |ąε q ` Ep|M8 |1|Mn ´M8 |ąε q
` Ep|Mn ´ M8 |1|Mn ´M8 |≤ε q ≤ ε.
Da ε beliebig war, folgt die Behauptung.
Satz 7.24. (Doob) Sei pMn qnPN ein Martingal mit
sup Ep|Mn |q ă 8.
nPN
Dann gibt es Y P L1 mit Mn ÝÑ Y fast sicher.
Korollar 7.25. Sei pXn qnPN ein Submartingal mit
sup Ep|Xn |q ă 8.
nPN
Dann gibt es Y P L1 mit Xn ÝÑ Y fast sicher. Ist pXn qnPN gleichgradig integrierbar, so gilt
diese Konvergenz auch in L1 .
Beweis. Sei Xn “ Mn ` An die Doob Zerlegung von Xn . Da An ≥ 0 monoton steigend ist, gibt
es A8 :“ lim An P r0, 8s. Aus dem Satz der monotonen Konvergenz folgt
nÑ8
EpA8 q “ lim EpAn q ≤ sup EpAn q
nÑ8
nPN
≤ sup EpXn ´ Mn q “ sup EpXn ´ M1 q ≤ sup Ep|Xn |q ` Ep|M1 |q ă 8.
nPN
nPN
nPN
Insbesondere gilt An Õ A in L1 . Ferner gibt es M8 P L1 mit Mn ÝÑ M8 fast sicher. Daraus
folgt Xn “ Mn ` An ÝÑ M8 ` A8 fast sicher. Ist pXn qnPN gleichgradig integrierbar, so ist
Mn ÝÑ M8 in L1 und damit auch Xn ÝÑ M8 ` A8 in L1 .
102
7.2
Martingale in stetiger Zeit
In diesem Abschnitt betrachten wir Martingale pMt qt≥0 . Hier und im folgenden ist pΩ, F, pFt qt≥0 , Pq
ein filtrierter Raum mit den üblichen Bedingungen. Bisher haben wir nichts an die Pfadeigenschaften von Martingalen gefordert. Dieses ist in der Regel auch nicht notwendig wie der nächste
Satz zeigt.
Satz 7.26. [KS91] Sei pΩ, F, pFt qt≥0 , Pq ein filtrierter Raum mit den üblichen Bedingungen und
pXt qt≥0 ein Submartingal. Genau dann hat pXt qt≥0 eine Modifikation pYt qt≥0 wo pYt qt≥0 cadlag
ist. Eine solche Modifikation kann derart gewählt werden, dass Yt an Ft adaptiert ist.
Man beachte, dass im obigen Fall pYt qt≥0 wieder ein Submartingal ist. Insbesondere besitzt
jedes Martingal eine Modifikation mit rechtsstetigen Pfaden. Im Folgenden betrachten wir stets
(Sub-)Martingale mit rechtsstetigen Pfaden.
Definition 7.27. (Poisson-Prozess) Ein Poisson Prozess mit Intensität λ ą 0 ist ein stochastischer Prozess pNt qt≥0 mit den folgenden Eigenschaften.
• N0 “ 0 fast sicher.
• pNt qt≥0 ist rechtsstetig und pFt qt≥0 -adaptiert.
• Nt ´ Ns ist unabhängig von Fs fü alle 0 ≤ s ≤ t und es gilt
PpNt ´ Ns “ nq “
λn pt ´ sqn ´λ
e , n ≥ 0.
n!
rt :“ Nt ´ λt heißt kompensierter Poisson Prozess.
Der Prozess N
rt ein Martingal. Nach Definition ist N
rt
Beispiel 7.28. Ist pNt qt≥0 ein Poisson Prozess, so ist N
messbar bezüglich Ft . Wegen
EpNt q “ EpNt ´ N0 q “
8
ÿ
PpNt ´ N0 “ nqn
n“0
“ e´λ
8
8
ÿ
ÿ
λn tn
λn´1 tn´1
n “ λte´λ
“ λt.
n!
pn
´
1q!
n“0
n“1
rt P L1 . Sei 0 ≤ s ă t, dann gilt
ist Nt P L1 und somit auch N
rt |Fs q “ EpNt ´ Ns |Fs q ` EpNs ´ λt|Fs q
EpN
rs .
“ EpNt ´ Ns q ` Ns ´ λt “ λt ´ λs ´ λt ` Ns “ N
Lemma 7.29. Sei pMt qt≥0 Ă L2 ein Martingal. Dann gilt
EppMt ´ Ms q2 | Fs q “ EpMt2 ´ Ms2 | Fs q.
103
Beweis. Es gilt
EppMt ´ Ms q2 | Fs q “ EpMt2 ´ 2Mt Ms ` Ms2 | Fs q
“ EpMt2 | Fs q ´ 2Ms EpMt | Fs q ` Ms2
“ EpMt2 | Fs q ´ Ms2 q “ EpMt2 ´ Ms2 | Fs q.
rt der kompensierte
Beispiel 7.30. Sei pNt qt≥0 ein Poisson Prozess mit Intensität λ ą 0 und N
r 2 ´ λt “: Mt ein Martingal bezüglich Ft :“ σpNs | s ≤ tq.
Poisson Prozess. Dann ist N
t
Denn Mt ist per Definition messbar bezüglich Ft und es gilt
r 2 q ≤ 2EpN 2 q ` 2λt ă 8.
EpN
t
t
Folglich ist Mt P L2 . Sei 0 ≤ s ă t, dann gilt
r2 ´ N
r 2 | Fs q “ EppN
rt ´ N
rs q2 | Fs q “ EppNt ´ Ns ´ λpt ´ sqq2 | Fs q
EpN
t
s
“ EppNt ´ Ns ´ λpt ´ sqq2 q “ varpNt ´ Ns q “ λpt ´ sq.
Daraus folgt die Behauptung.
Das nächste Beispiel zeigt, dass ein solcher Prozess existiert.
Beispiel 7.31. Sei pTn qnPN eine Folge unabhängiger exponentialverteilter Zufallsvariablen mit
Parameter λ ą 0, d.h.
P ˝ Tn´1 pdtq “ λe´λt 1r0,8q ptqmpdtq.
Die Zeiten Tn werden als Ankunftszeiten interpretiert. Setze S0 “ 0 und Sn :“
n
ř
Tk . Dann be-
k“1
schreibt Sn den Zeitpunkt der n-ten Ankunft. Definiere einen N0 -wertigen stochastischen Prozess
durch
Nt :“ max tn ≥ 0 | Sn ≤ tu
mit Filtration Ft :“ σpNs | s ≤ tq. Dann ist pNt qt≥0 ein Poisson Prozess. Für einen Beweis
siehe [Chu74].
Im Folgenden brauchen wir einige Sätze aus der Integrationstheorie.
Satz 7.32. (Satz von Vitali) Es sei pXn qnPN Ă L1 und X P L1 . Dann sind äquivalent
(a) Xn ÝÑ X in L1 .
(b) Xn ÝÑ X in Wahrscheinlichkeit und pXn qnPN ist gleichgradig integrierbar.
Beweis. Siehe Maß und Integrationstheorie.
Lemma 7.33. (Scheffe’s Lemma) Sei pXn qnPN Ă L1 und X eine weitere Zufallsvariable mit
Xn ÝÑ X fast sicher. Dann sind die folgenden Aussgen äquivalent:
104
(a) pXn qnPN ist gleichgradig integrierbar.
(b) Es gilt X P L1 und
Ep|Xn |q ÝÑ Ep|X|q, n Ñ 8.
Insbesondere gilt Xn ÝÑ X in L1 .
Beweis. Es gilt fast sicher |Xn | ≤ |Xn ´ X| ` |X| und somit
0 ≤ |Xn ´ X| ` |X| ´ |Xn | ≤ |Xn | ` |X| ` |X| ´ |Xn | “ 2|X|.
(7.5)
paq ùñ pbq : Sei m P N derart, dass Ep1|Xn |≥m |Xn |q ≤ 1 für alle n P N. Dann folgt aus dem
Lemma von Fatou
Ep|X|q ≤ lim inf Ep|Xn |q
nÑ8
≤ lim inf Ep1|Xn |≥m |Xn |q ` lim inf Ep1|Xn |ăm |Xn |q ≤ 1 ` m.
nÑ8
nÑ8
Aus (7.5) folgt mit dem Satz von Lebesgue
Ep|Xn ´ X| ` |X| ´ |Xn |q ÝÑ 0, n Ñ 8.
(7.6)
Nach dem Satz von Vitali folgt Ep|Xn ´ X|q ÝÑ 0 und somit Ep|Xn |q ÝÑ Ep|X|q.
pbq ùñ paq : Aus (7.5) und dem Satz von Lebesgue folgt erneut (7.6). Wegen Ep|Xn |q ÝÑ Ep|X|q
folgt die Behauptung.
Satz 7.34. (Optional Sampling) Sei pXt qt≥0 ein cadlag Submartigal bezüglich pFt qt≥0 . Seien
S ≤ T beschränkte Stoppzeiten. Dann gilt
XS ≤ EpXT |FS q.
(7.7)
Ist pXt qt≥0 ein Martingal bzw. ein Supermartingal, so gilt “ bzw. ≥ in (7.7).
Beweis. Definiere Stoppzeiten
#
Sn pωq “
8, Spωq “ `8
k
k´1
2n ,
2n ≤ Spωq ă
k
2n
.
Dann ist Sn eine Stoppzeit mit S ≤ Sn und Sn Œ S. Definiere Tn analog. Dann gilt Sn ≤ Tn .
Lemma 7.35. (ohne Beweis) pXSn qnPN sowie pXTn qnPN sind gleichgradig integrierbar.
In diesem Fall folgt aus XSn ÝÑ XS sowie XTn ÝÑ XT fast sicher mit dem Satz von Vitali
XS , XT P L1 sowie XSn ÝÑ XS , XTn ÝÑ XT in L1 . Ist A P FS , so folgt aus S ≤ Sn auch
FS Ă FSn , und damit A P FSn . Aus dem diskreten Optional Sampling Theorem erhalten wir
ż
ż
XSn dP ≤ XTn dP, n ≥ 1.
A
A
105
Durch Grenzübergang n Ñ 8 folgt
ż
ż
XS dP ≤
XT dP.
A
A
Bemerkung 7.36. Ist pXt qt≥0 gleichgradig integrierbar, so gilt Optional Sampling für alle
Stoppzeiten S ≤ T .
Korollar 7.37. Sei pMt qt≥0 ein cadlag Martingal und T eine Stoppzeit. Dann ist M T :“
pMT ^t qt≥0 ein cadlag Martingal bezüglich pFt qt≥0 . Ist M stetig, so ist auch M T stetig.
Beweis. Wir haben bereits gesehen, dass M T adaptiert ist. Die Integrierbarkeit wurde im letzten
Satz bewiesen. Sei 0 ≤ s ă t, dann gilt
EpMtT ´ MsT |Fs q “ EpMT ^t ´ MT ^s |Fs q “ EppMpT ^tq_s ´ Ms q|Fs q.
Wegen s ≤ pT ^ tq _ s ≤ T ^ t ≤ t impliziert Optional Sampling
EppMpT ^tq_s ´ Ms q|Fs q “ EpMpT ^tq_s |Fs q ´ Ms “ Ms ´ Ms “ 0.
Die letzte Behauptung ist offensichtlich.
Korollar 7.38. Sei pXt qt≥0 ein cadlag Submartingal und T eine Stoppzeit. Dann ist X T :“
pXT ^t qt≥0 ein cadlag Submartingal bezüglich pFt qt≥0 . Ist X stetig, so ist auch X T stetig.
Beweis. Ersetze an geeigneter Stelle “ durch ≥. Die Details sind Übung.
Satz 7.39. (Doob-Ungleichung) Sei pXt qt≥0 ein cadlag Submartingal. Dann gilt für alle ε ą 0
und T ą 0
˜
¸
1
P sup Xt ≥ ε ≤ EpXT` q
(7.8)
ε
tPr0,T s
und
ˆ
P
˙
inf Xt ≤ ´ε
≤
tPr0,T s
Ist X nicht-negativ, so gilt für jedes p ą 1
˜
¸
E
sup Xtp
ˆ
≤
tPr0,T s
106
EpXT` q ´ EpX0 q
.
ε
p
p´1
˙p
EpXTp q.
(7.9)
Beweis. Wir zeigen zuerst (7.8). Da X rechtsstetig ist gilt sup Xt “ sup Xt . Wähle eine
tPr0,T sXQ
ŤtPr0,T s
aufsteigende Folge von Mengen pFn qnPN mit r0, T s X Q “
Fn . Dann gilt für 0 ă δ ă ε
n≥1
˜
¸
Xt ≥ ε
sup
P
ˆ
˙
≤ lim P max Xt ≥ δ
nÑ8
tPr0,T sXQ
tPFn
1
≤ EpXT` q.
δ
Für δ Ñ ε folgt (7.8). Die Ungleichung (7.9) folgt durch eine analoge Beweisidee. Für die letzte
Behauptung betrachten wir zuerst
˙p
ˆ
˙ ˆ
p
p
EpXTp q, n ≥ 1,
Ep sup Xt ≤
p
´
1
tPFn
welches aus der Doob Ungleichung für diskrete Submartingale folgt. Die linke Seite ist monoton
wachsend in n mit sup Xtp Õ sup Xtp “ sup Xtp . Die Behauptung folgt mit n Ñ 8.
tPFn
tPr0,T sXQ
tPr0,T s
Korollar 7.40. (Doob-Ungleichung) Sei pMt qt≥0 ein cadlag Martingal. Dann gilt für alle ε ą 0
und T ą 0
˜
¸
1
P sup |Mt | ≥ ε ≤ Ep|MT |q
ε
tPr0,T s
und für p ą 1
¸
˜
E
sup |Mt |
p
ˆ
≤
tPr0,T s
p
p´1
˙p
Ep|MT |p q.
Wir kommen zu den Martingal Konvergenzsätzen.
Satz 7.41. (Konvergenz von Submartingalen) Sei pXt qt≥0 ein cadlag Submartingal mit
sup EpXt` q ă 8.
t≥0
Dann gibt es X8 P L1 und es gilt Xt ÝÑ X8 für t Ñ 8 fast sicher.
Satz 7.42. (Konvergenz von Submartingalen) Sei pXt qt≥0 ein cadlag Submartingal. Betrachte
die Bedingungen:
(a) pXt qt≥0 ist gleichgradig integrierbar.
(b) Es gibt X8 P L1 mit Xt ÝÑ X8 in L1 .
(c) Es gibt X8 P L1 mit Xt ÝÑ X8 fast sicher und es gilt Xt ≤ EpX8 |Ft q.
Dann gilt paq ùñ pbq ùñ pcq. Ist ferner X nicht-negativ, so sind alle Bedingungen äquivalent.
Satz 7.43. (Konvergenz von Supermartingalen) Sei pXt qt≥0 ein nicht-negatives cadlag Supermartingal. Dann gibt es eine Zufallsvariable X8 mit Xt ÝÑ X8 für t Ñ 8 fast sicher.
107
˜
Es sei F8 “ σ
¸
Ť
Ft .
t≥0
Satz 7.44. (Konvergenz von Martingalen) Sei pMt qt≥0 ein cadlag Martingal. Dann sind äquivalent:
(a) pMt qt≥0 ist gleichgradig integrierbar.
(b) Es gibt M8 P L1 mit Mt ÝÑ M8 in L1 für t Ñ 8.
(c) Es gibt M8 P L1 mit Mt ÝÑ M8 fast sicher für t Ñ 8 und
Mt “ EpM8 |F8 q.
(d) Es gibt Y P L1 mit Mt “ EpY |F8 q für alle t ≥ 0.
In diesem Fall gilt M8 “ EpY |F8 q.
Zum Schluß wollen wir noch die kontinuierliche Version der Doob-Meyer Zerlegung beweisen.
Hierfür brauchen wir einige Vorbereitung.
Definition 7.45. Die σ-Algebra
P “ σ ppHt qt≥0 | pHt qt≥0 ist linksstetig und adaptiert q
heißt die σ-Algebra der vorhersehbaren Mengen. Ein stochastischer Prozess pXt qt≥0 heißt vorhersehbar (predictable), falls
Ω ˆ r0, 8q Q pω, tq ÞÝÑ Xt pωq
messbar ist bezüglich P.
Lemma 7.46. Es gilt
P “ σ ptA ˆ t0u| A P F0 u Y tA ˆ ps, ts | s ă t, A P Fs uq .
Insbesondere ist jeder vorhersehbare beschränkte stochastische Prozess pXt qt≥0 Grenzwert von
Elementarfunktionen der Form
Xt pωq “ a0 ` 1A0 pωq ` 1t0u ptq `
N
ÿ
an 1An pωq1psn ,tn s ptq
(7.10)
n“1
mit an P R, N P N, 0 ă sn ă tn , An P Fsn .
Beweis. Es sei P 1 “ σ ptA ˆ t0u| A P F0 u Y tA ˆ ps, ts | s ă t, A P Fs uq. Dann ist jede bezüglich
P 1 messbare Zufallsvariable Grenzwert von Zufallsvariablen der Form (7.10). Ferner sind diese
Elementarfunktionen linksstetig und adaptiert, woraus P 1 Ă P folgt. Umgekehrt, sei X linksstetig und adaptiert. Dann ist
pN q
Xt
:“ X0 1t0u ptq `
Nÿ
´1
k“0
pN q
X k 1p k , k`1 s ptq
N
N
N
messbar bezüglich P 1 und es gilt Xt ÝÑ Xt fast sicher für alle t und N Ñ 8. Also ist auch
X messbar bezüglich P 1 . Dieses zeigt P Ă P 1 .
108
Definition 7.47. Sei pXt qt≥0 ein stochastischer Prozess.
(a) pXt qt≥0 ist von der Klasse (D), falls die Familie
tXT | T Stoppzeit mit PpT ă 8q “ 1u
gleichgradig integrierbar ist.
(b) pXt qt≥0 ist von der Klasse (DL), falls für alle m P N die Familie
tXT | T ≤ m Stoppzeit u
gleichgradig integrierbar ist.
Lemma 7.48. Sei pXt qt≥0 ein cadlag Prozess. Es gelten die folgenden Aussagen.
(a) Ist pXt qt≥0 ein nicht-negatives Submartingal, so ist pXt qt≥0 von der Klasse (DL).
(b) Ist pXt qt≥0 von der Klasse (D), so ist pXt qt≥0 von der Klasse (DL).
(c) Ist pXt qt≥0 ein gleichgradig integrierbares Submartingal, so ist pXt qt≥0 von der Klasse (D).
(d) Ist Xt P Lp mit sup EpXtp q ă 8 und p ą 1, so ist pXt qtPr0,T s gleichgradig integrierbar.
tPr0,T s
Beweis. (a) Sei T eine beschränkte Stoppzeit mit T ≤ m P N. Aus Optional Sampling folgt
XT ≤ EpXm |FT q. Ferner ist tXT ą nu P FT und somit
Ep1tXT ąnu XT q ≤ Ep1XT ąn EpXm |FT qq “ Ep1XT ąn Xm q.
Aus Tschebyscheff und Optional Sampling folgt
PpXT ą nq ≤
1
1
EpXT q ≤ EpXm q ÝÑ 0, n Ñ 8.
n
n
Daraus lässt sich leicht die Behauptung folgern.
(b) Jede Stoppzeit T mit T ≤ m erfüllt insbesondere PpT ă 8q “ 1.
(c) Übung.
(d) Es gilt mit der Hölder Ungleichung mit p1 ` 1q “ 1
Ep|Xt |q ≤ Ep|Xt |p q ≤ sup EpXtp q ă 8
tPr0,T s
und damit sup Ep|Xt |q ă 8. Ferner gilt
tPr0,T s
¸1
˜
˘1
1
Ep1A |Xt |q ≤ Ep1qA q q pEp|Xt |p qq p ≤
`
welches die Behauptung zeigt.
109
p
sup Ep|Xt |p q
tPr0,T s
1
pPpAqq q
Wir werden später weitere hinreichende Bedingungen sehen.
Satz 7.49. (Doob-Meyer Zerlegung, [KS91]) Sei pΩ, F, pFt qt≥0 , Pq ein filtrierter Raum mit den
üblichen Bedingungen und pXt qt≥0 ein cadlag Submartingal. Dann sind aq̈uivalent:
(a) pXt qt≥0 ist von der Klasse (DL).
(b) Es gibt ein rechtsstetiges Martingal pMt qt≥0 und einen rechtsstetigen vorhersehbaren Prozess pAt qt≥0 mit
A0 “ 0, As ≤ At , s ≤ t
derart, dass
Xt “ X0 ` Mt ` At , t ≥ 0.
Ist pMt1 , A1t q eine weitere Zerlegung mit obigen Eigenschaften, so sind Mt , Mt1 sowie At , A1t ununterscheidbar. Ist zusätzlich pXt qt≥0 von der Klasse (D), so ist pMt qt≥0 gleichgradig integrierbar
und A8 :“ lim At ist integrierbar.
tÑ8
Diesen Satz zu beweisen erfordert einiges an Vorbereitung und soll hier nicht gemacht werden.
Wir werden jedoch einen wichtigen Spezialfall beweisen.
Beispiel 7.50. Dann ist pMt2 qt≥0 ein nicht-negatives Submartingal und somit von der Klasse
(DL). Die Doob-Meyer Zerlegung liefert die Existenz und Eindeutigkeit eines vorhersehbaren,
steigenden Prozesses pAt qt≥0 derart, dass Mt2 ´ M02 ´ At ein Martingal ist.
Definition 7.51. Sei pMt qt≥0 Ă L2 ein cadlag Martingal mit M0 “ 0. Dann wird der vorhersehbare, steigende Prozess pAt qt≥0 mit xM yt bezeichnet. Dieser wird Kompensator bezeichnet.
Beispiel 7.52.
• Sei pBt qt≥0 die Brownsche Bewegung. Dann ist xByt “ t.
• Sei pNt qt≥0 der Poisson Prozess mit Intensität λ ą 0. Dann ist xN yt “ λt.
Im Folgenden wollen wir die Existenz und Eindeutigkeit des Kompensators xM yt ohne
Rückgriff auf die Doob-Meyer Zerlegung beweisen. Hierfür betrachten wir den Fall von Martingalen mit stetigen Pfaden. Der allgemeine Fall von cadlag Pfaden ist wesentlich schwieriger
zu beweisen.
pnq
Satz 7.53. Sei p P r1, 8q, pMt q Ă Lp eine Familie von Martingalen mit stetigen Pfaden und
pnq
pMt qt≥0 Ă Lp ein stochastischer Prozess. Es gelte Mt ÝÑ Mt in Lp für n Ñ 8 für jedes t ≥ 0.
Dann gelten die folgenden Aussagen.
(a) pMt qt≥0 hat eine Modifikation welche ein Martingal ist.
(b) Sei p ą 1. Es gibt eine Modifikation von pMt qt≥0 , welche wir wieder mit pMt qt≥0 bezeichnen, derart dass Mt adaptiert ist, stetige Pfade hat und
˜
¸
E
pnq
sup |Mt
´ Mt |p
tPr0,T s
110
ÝÑ 0, @T ą 0.
pnq
pnq
Beweis. (a) Sei 0 ≤ s ă t. Dann gilt Ms “ EpMt |Fs q für alle n ≥ 1 und
¯p
´
¯p ´
pnq
pnq
pnq
EpMt |Fs q ´ EpMt |Fs q “ EpMt ´ Mt |Fs ≤ EppMt ´ Mt qp |Fs q.
Folglich gilt
E
¯
´´
¯p ¯
´
pnq
pnq
EpMt |Fs q ´ EpMt |Fs q
≤ E pMt ´ Mt qp
pnq
und damit EpMt |Fs q ÝÑ EpMt |Fs q für n Ñ 8 in Lp . Daraus folgt durch Grenzübergang
nÑ8
Ms “ EpMt |Fs q.
Also ist pMt qt≥0 ein Martingal.
(b) Sei T ą 0 fest. Da M pmq ´ M pnq ein Martingal ist, folgt aus der Doob Ungleichung
˜˜
¸p ¸
˜
¸
pmq
sup |Mt
E
tPr0,T s
pnq
´ Mt |
ˆ
≤
und somit
pmq
} sup |Mt
tPr0,T s
pmq
pnq
´ Mt |}Lp ≤
pnq
´ Mt |p
sup |Mt
“E
tPr0,T s
˙p
p
p´1
pmq
Ep|MT
pnq
´ MT |p q
p
pnq
pmq
}MT ´ MT }Lp ÝÑ 0
p´1
für n, m Ñ 8. Wir können daher eine Teilfolge pnk qkPN finden derart, dass
pnk`1 q
pnk q
´ MT
}MT
Folglich gilt
›
›
8
›ÿ
›
›
pnk`1 q
pnk q ›
sup |Mt
´ Mt |›
›
›
›
tPr0,T s
k“1
8
ÿ
≤
k“1
Lp
˜
8
ÿ
P
8
ř
pnk`1 q
|Mt
tPr0,T s
pnk q
´ Mt
|}Lp
¸
sup
k“1 tPr0,T s
Also konvergiert
pnk`1 q
} sup |Mt
8
8
p ÿ 1
p ÿ
pn
q
pn q
}MT k`1 ´ MT k }Lp ≤
ă8
p ´ 1 k“1
p ´ 1 k“1 2k
≤
und somit
}Lp ≤ 2´k , k ≥ 1.
pnk q
´ Mt
pn
q
|Mt k`1
´
pn q
Mt k |
“ 1.
ă8
| fast sicher gleichmässig in t P r0, T s. Insbesondere kon-
k“1
vergiert Yt :“
8
ř
pnk`1 q
pMt
pnk q
´ Mt
q fast sicher gleichmässig in t P r0, T s. Wegen
k“1
pnN q
Mt
pn1 q
“ Mt
Nÿ
´1
`
pnk`1 q
pMt
k“1
111
pnk q
´ Mt
q
pn q
pn q
konvergiert Mt N ÝÑ Mt 1 ` Yt fast sicher gleichmässig in t P r0, T s. Nach Übergang zu einer
pn q
geeigneten Teilfolge sehen wir Mt “ Mt 1 ` Yt fast sicher für alle t P r0, T s. Die rechte Seite
hat stetige Pfade und ist, da der Wahrscheinlichkeitsraum vollständig ist, adaptiert. Die letzte
Behauptung folgt aus Doobs Ungleichung wegen
˜
¸ ˆ
˙p
p
pnq
pnq
p
E sup |Mt ´ Mt |
≤
Ep|MT ´ MT |p q.
p
´
1
tPr0,T s
Lemma 7.54. Sei pMt qt≥0 Ă L1 ein adaptierter stochastischer Prozess mit cadlag Pfaden.
Genau dann ist pMt qt≥0 ein Martingal, wenn
(7.11)
EpMT q “ EpM0 q
für alle beschränkten Stoppzeiten gilt.
Beweis. Ist pMt qt≥0 ein Martingal, so gilt (7.11) nach Optional Sampling. Umgekehrt gelte
(7.11). Für konstante Stoppzeiten T “ t ≥ 0 liefert dieses
EpMt q “ EpM0 q, t ≥ 0.
Sei s ≤ t und A P Fs . Wir müssen
EpMt 1A q “ EpMs 1A q
zeigen. Wähle T “ s1A ` t1Ac . Dann ist T eine beschränkte Stoppzeit und es gilt
EpMT q “ Ep1A Ms ` 1Ac Mt q “ Ep1A Ms q ` EpMt q ´ Ep1A Mt q.
Ferner gilt
EpMT q “ EpM0 q “ EpMt q
welches die Behauptung zeigt.
Sei pMt qt≥0 Ă L2 ein Martingal mit M0 “ 0 derart, dass Mt pωq für jedes ω P Ω stetig in
t ≥ 0 ist. Sei pτn qnPN eine Folge von Zerlegungungen
pnq
0 “ t0
pnq
mit tNn ÝÑ 8,
pnq
pnq
ă t1
pnq
ă ¨ ¨ ¨ ă tNn
pnq
sup ptk`1 ´ tk q ă 8 und τn Ă τn`1 . Definiere einen Prozess
k“0,...,n
pnq
Vt
:“
ÿ
pMs1 ^t ´ Ms^t q2 ,
sPτn
wo s1 den Nachfolger von s bezeichnet.
Satz 7.55. Es gibt einen stochastischen Prozess xM yt derart, dass die folgenden Eigenschaften
gelten:
112
(a) xM yt P L1 ist adaptiert, hat stetige Pfade und ist monoton steigend. (fast sicher)
(b) Es gilt
˜
lim P
¸
sup
nÑ8
tPr0,T s
pnq
|Vt
´ xM yt | ≥ ε
“ 0, @ε ą 0, T ą 0.
(c) Mt2 ´ xM yt ist ein Martingal.
(d) Ist zusätzlich pMt qt≥0 beschränkt, d.h. c :“
sup
|Mt pωq| ă 8, so gilt
pω,tqPΩˆR`
˜
¸
sup
E
tPr0,T s
pnq
|Vt
´ xM yt |2
ÝÑ 0, @T ą 0.
Beweis. Wir betrachten zuerst den Fall, dass Mt beschränkt ist. Wir zeigen zunächst, dass
pnq
pVt qnPN für jedes t ≥ 0 eine Cauchy Folge in L2 .
pnq
pmq
Sei N P N so gross dass für m ą n ą N : t ≤ tNn ă tNm . Wegen pa ´ bq2 “ a2 ´ 2pa ´ bqb ´ b2
folgt
ÿ
ÿ `
˘
pnq
2
Mu21 ^t ´ Mu^t
´2
Vt “
Mu^t pMu1 ^t ´ Mu^t q
uPτn
uPτn
“
Mt2
ÿ
´2
Mu pMu1 ^t ´ Mu^t q
u≤τn
u≤t
ÿ
“ Mt2 ´ 2
ÿ
Mu pMs1 ^t ´ Ms^t q
u≤τn u≤său1
u≤t
sPτm
wo die letzte Gleichung aus
Mu1 ^t ´ Mu^t “
ÿ
pMs1 ^t ´ Ms^t q
u≤său1
sPτm
folgt. Analog erhalten wir
pmq
Vt
ÿ
“ Mt2 ´ 2
Ms pMs1 ^t ´ Ms^t q
s≤τm
s≤t
ÿ
“ Mt2 ´ 2
ÿ
Ms pMs1 ^t ´ Ms^t q
u≤t u≤său1
uPτn sPτm
Daraus folgt
pmq
Vt
pnq
´ Vt
ÿ
ÿ
uPτn
u≤său1
sPτm
ÿ
ÿ
“ ´2
“ ´2
pMs pMs1 ^t ´ Ms q ´ Mu pMs1 ^t ´ Ms^t qq .
pMs ´ Mu qpMs1 ^t ´ Ms^t q.
u≤t u≤său1
uPτn sPτm
113
Wir erhalten somit
˛
¨
´
pmq
E pVt
pnq 2
´ Vt
¯
q
ÿ
˚ÿ
“ 4E ˝
‹
pMs ´ Mu q2 pMs1 ^t ´ Ms^t q2 ‚,
u≤t u≤său1
uPτn sPτm
wo alle gemischten Terme wegen der Martingaleigenschaft verschwinden (nachrechnen!). Sei
(
∆N :“ sup sup sup pMs ´ Mu q2 | u P τn1 , u ≤ t, s P τm1 , u ≤ s ă u1 .
n1 ≥N m1 ąn1 ωPΩ
Da pMt qt≥0 stetige Pfade hat, gilt ∆N ÝÑ 0 fast sicher für N Ñ 8. Ferner gilt ∆N ≤ 4c2 .
Damit erhalten wir
¨
˛
´
¯
ÿ ÿ
˚
‹
pmq
pnq
E pVt
´ Vt q2 ≤ E ˝∆N
pMs1 ^t ´ Ms^t q2 ‚
u≤t u≤său1
uPτn sPτm
˛2 ˛ 12
¨ ¨
`
˘1 ˚ ˚ ÿ
≤ Ep∆2N q 2 ˝E ˝
ÿ
‹ ‹
pMs1 ^t ´ Ms^t q2 ‚ ‚
u≤t u≤său1
uPτn sPτm
˛2 ˛ 12
¨ ¨
`
˘1 ˚ ˚ ÿ
‹ ‹
“ Ep∆2N q 2 ˝E ˝
pMs1 ^t ´ Ms^t q2 ‚ ‚
s≤t
sPτm
Aus dem Satz der dominierten Konvergenz folgt Ep∆2N q ÝÑ 0. Ferner erhalten wir
˛2
¨
˛
¨
‹
˚ÿ
‹
˚ÿ
pMs1 ^t ´ Ms^t q4 ‚
pMs1 ^t ´ Ms^t q2 ‚ “ E ˝
E˝
s≤t
sPτm
s≤t
sPτm
¨
˛
˚ÿ ÿ
‹
` 2E ˝
pMs1 ^t ´ Ms^t q2 pMu1 ^t ´ Mu^t q2 ‚
uăs
s≤t
sPτm uPτm
¨
˛
˚ÿ
‹
≤ 4c2 E ˝
pMs1 ^t ´ Ms^t q2 ‚
s≤t
sPτm
`2
ÿ ÿ
său
s≤t
sPτm uPτm
“ S1 ` S2 .
114
`
˘
E pMs1 ^t ´ Ms^t q2 pMu1 ^t ´ Mu^t q2
Es gilt
¨
˛
˚ÿ
‹
S1 “ 4c2 E ˝
pMs1 ^t ´ Ms^t q2 ‚
s≤t
sPτm
“ 4c2
ÿ
`
˘
2
E Ms21 ^t ´ 2Ms1 ^t Ms^t ` Ms^t
s≤t
sPτm
“ 4c2
ÿ
`
˘
2
E Ms21 ^t ´ 2Ms^t EpMs1 ^t |Fs q ` Ms^t
s≤t
sPτm
“ 4c2
ÿ
`
˘
2
E Ms21 ^t ´ Ms^t
“ 4c2 EpMt2 ´ M02 q “ 4c2 EpMt2 q ≤ 4c4 .
s≤t
sPτm
und analog
ÿ `
ÿ `
˘
˘
E pMs1 ^t ´ Ms^t q2 pMu1 ^t ´ Mu^t q2 “
E EppMu1 ^t ´ Mu^t q2 |Fu qpMs1 ^t ´ Ms^t q2
său
uPτm
său
uPτm
ÿ
“
`
˘
2
E EpMu21 ^t ´ Mu^t
|Fu qpMs1 ^t ´ Ms^t q2
său
uPτm
ÿ
“
`
˘
2
E pMu21 ^t ´ Mu^t
qpMs1 ^t ´ Ms^t q2
său
uPτm
`
˘
“ E pMt2 ´ Ms21 ^t qpMs1 ^t ´ Ms^t q2
`
˘
`
˘
2
≤ 2c2 E pMs1 ^t ´ Ms^t q2 “ 2c2 E Ms21 ^t ´ Ms^t
.
Daraus folgt
ÿ
S2 ≤ 4c2
`
˘
2
E Ms21 ^t ´ Ms^t
“ 4c2 EpMt2 q ≤ 4c4 .
s≤t
sPτm
Insgesamt folgt
´
¯ `
˘1 ?
pmq
pnq
E pVt
´ Vt q2 ≤ Ep∆2N q 2 8c2 ÝÑ 0.
pnq
Sei Vt :“ lim Vt
nÑ8
der L2 -Grenzwert. Setze
pnq
Yt
:“ 2
ÿ
Ms^t pMs1 ^t ´ Ms^t q.
sPτn
pnq
Dann ist pYt
qt≥0 ein Martingal und es gilt
pnq
Yt
pnq
“ Mt2 ´ Vt
ÝÑ Mt2 ´ Vt , n Ñ 8
115
in L2 . Also gibt es eine Modifikation pYt qt≥0 von Mt2 ´ Vt derart, dass Y ein Martingal mit
stetigen Pfaden ist. Folglich hat Vt eine Modifikation mit stetigen Pfaden gegeben durch
xM yt “ Mt2 ´ Yt .
Insbesondere ist xM y auch adaptiert und es gilt
˜
E
sup
tPr0,T s
pnq
|Vt
(7.12)
¸
2
´ xM yt |
ÝÑ 0, n Ñ 8.
(7.13)
Betrachten wir den allgemeinen Fall. Sei
Rk pωq :“ inf tt ą 0 | |Mt pωq| ą ku .
Dann ist Rk eine Stoppzeit. Ferner gilt |Mt^Rk | ≤ k. Nach Optional Sampling ist
Mt^Rk :“ Mtk
ein beschränktes Martingal. Aus obigen Überlegungen gibt es einen stetigen, adaptierten Prozess
xM k yt “ Vtk . Es sei pVtk qpnq die Approximation von Vtk über die Zerlegung τn .
Lemma 7.56. (Diagonalfolgentrick) Es gibt es eine Teilfolge pnl qlPN und Ω0 P F0 mit PpΩ0 q “ 1
derart, dass
sup |pVsk qpnl q ´ xM k ys | ÝÑ 0, l Ñ 8, ω P Ω0 .
sPr0,ts
Beweis. Wegen (7.13) gibt es für k “ 1 eine Teilfolge pn1 plqqlPN und Ω1 P F0 mit PpΩ1 q “ 1
derart, dass
sup |pVs1 qpn1 plqq ´ xM 1 ys | ÝÑ 0, l Ñ 8, ω P Ω1 .
sPr0,ts
Wähle eine weitere Teilfolge pn2 plqqlPN von pn1 plqqlPN und Ω2 P F0 mit PpΩ2 q “ 1 derart, dass
sup |pVs2 qpn2 plqq ´ xM 2 ys | ÝÑ 0, l Ñ 8, ω P Ω2 .
sPr0,ts
Eine solche Wahl ist wegen der Konvergenz in (7.13) möglich. Iteration liefert eine Folge von
Teilfolgen pnk plqqlPN , wo pnk`1 plqqlPN eine Teilfolge von pnk plqqlPN ist, Mengen Ωk P F0 mit
PpΩk q “ 1 derart, dass
sup |pVsk qpnk plqq ´ xM k ys | ÝÑ 0, l Ñ 8, ω P Ωk .
sPr0,ts
Dann liefert Ω0 :“
Ş
Ωk sowie nplq :“ nl plq das gewünschte.
k≥1
Es gilt Rk ≤ Rk`1 fast sicher. Für R :“ lim Rk P r0, 8s gilt
kÑ8
PpR ≥ mq “ P pDk : |Mm | ≤ kq “ 1, @m P N.
116
Also ist R “ 8 fast sicher und somit Rk ÝÑ 8. Damit ist PpΩ0 X tR “ 8uq “ 1 Damit ist
#
xM k yt pωq, für k P N mit ω P tt ≤ Rk u X Ω0
,
xM yt pωq :“
0,
sonst
auf Ω0 X tR “ 8u definiert und auf dem Komplement 0. Ferner gilt
pnl q
“ 1t≤Rk pVtk qpnl q ÝÑ 1t≤Rk xM k yt
1t≤Rk Vtpnl q “ 1t≤Rk Vt^R
k
(7.14)
für l Ñ 8 auf Ω0 . Dieses zeigt, dass xM yt unabhängig von der Wahl von k ist.
Seien δ, ε ą 0 beliebig. Wähle kpδq P N derart, dass
PpRkpδq ă tq ă δ.
Dann folgt
ˆ
˙
pnq
P sup |Vs ´ xM ys | ≥ ε
0≤s≤t
ˆ
˙
ˆ
˙
pnq
pnq
“ P sup |Vs ´ xM ys | ≥ ε, Rk ă t ` P sup |Vs ´ xM ys | ≥ ε, Rk ≥ t
0≤s≤t
0≤s≤t
ˆ
˙
k pnq
k
≤ P pRk ă tq ` P sup |pVs q ´ xM ys | ≥ ε, Rk ≥ t
0≤s≤t
ˆ
˙
k pnq
k
≤ P pRk ă tq ` P sup |pVs q ´ xM ys | ≥ ε
0≤s≤t
Für den zweiten Summanden gilt nach Tschebyscheff
ˆ
˙
˙
ˆ
1
k pnq
k
k pnq
k
2
P sup |pVs q ´ xM ys | ≥ ε ≤ 2 E sup |pVs q ´ xM ys | ÝÑ 0, n Ñ 8.
ε
0≤s≤t
0≤s≤t
Daraus folgt
ˆ
lim sup P
nÑ8
˙
sup |Vspnq ´ xM ys | ≥ ε
0≤s≤t
≤ P pRk ă tq ă δ.
(7.15)
Dieses zeigt (b). Für Teil (a) bleibt es zu zeigen, dass xM yt monoton steigend ist. Sei t ≥ 0 fest,
dann gilt
ÿ
ÿ
Vspnq “
pMu1 ^t ´ Mu^t q2 “
pMu1 ´ Mu q2 ` pMs ´ Mδs pnq q2
uPτn
uPτn
u1 ≤t
wo δs pnq “ sup tu P τn | u ≤ su. Daraus folgt
ˇ
ˇ
˛
¨
ˇ
ˇ
ˇ
ˇÿ
ˇ
‹
ˇ
˚
pMu1 ´ Mu q2 ´ xM ys ˇ ≥ ε‚
P ˝ sup ˇ
ˇ
ˇ
sPr0,ts ˇ uPτn
ˇ
u1 ≤t
¸
˜
ˇ
ˇ
ˇ
ˇ
≤ P sup pMs ´ Mδs pnq q2 ` sup ˇVspnq ´ xM ys ˇ ≥ ε
sPr0,ts
sPr0,ts
˜
≤ Pp sup pMs ´ Mδs pnq q2 ≥ εq ` P
sPr0,ts
¸
ˇ
ˇ
ˇ
ˇ
sup ˇVspnq ´ xM ys ˇ ≥ ε .
sPr0,ts
117
Der
konvergiert wegen (7.15) gegen 0, der erste wegen der Stetigkeit der Pfade. Da
ř zweite Term
2
pMs1 ´ Ms q monoton wachsend in t ist, ist es auch xM yt .
sPτn
s1 ≤t
Es bleibt (c) zu zeigen. Wir zeigen dass MT2 ´ xM yT P L1 und
EpMT2 q “ EpxM yT q
für alle beschränkten Stoppzeiten gilt. Die Behauptung folgt dann aus Lemma 7.54. Wegen
(7.12) ist
Mtk ´ xM k yt “ Mt^Rk ´ xM k yt “ Mt^Rk ´ xM yt^Rk
ein Martingal für alle k P N. Insbesondere gilt für alle beschränkten Stoppzeiten T
EpMT2 ^Rk q “ EpxM yT ^Rk q.
Aus dem Satz der monotonen Konvergenz und der Submartingal Eigenschaft zusammen mit
Optional Sampling folgt
EpxM yT q “ lim EpxM yT ^Rk q “ lim EpMT2 ^Rk q ≤ EpMT2 q.
kÑ8
kÑ8
Mit dem Lemma von Fatou gilt
EpxM yT q “ lim EpMT2 ^Rk q ≥ EpMT2 q.
kÑ8
Wir erhalten also
EpxM yT q “ EpMT2 q.
Ist m P N mit T ≤ m so folgt aus Optional Sampling
2
EpMT2 q ≤ EpMm
qă8
welches die Behauptung zeigt.
8
Appendix
Lemma 8.1. Für jedes N P N0 gibt es eine stetige Funktion ΘN `1 pxq P C mit |ΘN `1 pxq| ≤ 1
derart, dass
N
ÿ
pixqn
pixqN `1
eix “
`
ΘN `1 pxq, x P R.
n!
pN ` 1q!
n“0
Beweis. Wir zeigen über Induktion, dass für alle N P N0 mit t0 “ 1 gilt
e
ix
t0
tN
0
0
ż
ż
N
ÿ
pixqn
N `1
¨ ¨ ¨ eixtN `1 dtN `1 ¨ ¨ ¨ dt1
“
` pixq
n!
n“0
118
Dann hat
żtN
żt0
ΘN `1 pxq :“ pN ` 1q!
eixtN `1 dtN `1 ¨ ¨ ¨ dt1
¨¨¨
0
0
die gewünschten Eigenschaften. Für N “ 0 gilt offensichtlich
żt0
e
ix
eixt dt.
“ 1 ` ix
0
N ÞÝÑ N ` 1: Dann gilt nach Induktionsvoraussetzung
e
ix
t0
tN
0
0
ż
ż
N
ÿ
pixqn
N `1
“
` pixq
¨ ¨ ¨ eixtN `1 dtN `1 ¨ ¨ ¨ dt1 .
n!
n“0
Für das innere Integral gilt nach N “ 0
żtN
żtN tNż`1
żtN
ixtN `1
e
dtN `1 “
0
eixtN `2 dtN `2 dtN `1 .
1dtN ` ix
0
0
0
Daraus folgt
e
ix
tN
ż`1
żt0
żtN
żt0
N
ÿ
pixqn
N `1
N `2
“
eixtN `2 dtN `2 ¨ ¨ ¨ dt1 .
` pixq
¨ ¨ ¨ 1dtN `1 ¨ ¨ ¨ dt1 ` pixq
¨¨¨
n!
n“0
0
0
0
Die Behauptung folgt, da
żtN
żt0
1dtN `1 ¨ ¨ ¨ dt1 “
¨¨¨
0
0
119
1
.
pN ` 1q!
0
Literatur
[Bil99]
Patrick Billingsley. Convergence of probability measures. Wiley Series in Probability and Statistics:
Probability and Statistics. John Wiley & Sons, Inc., New York, second edition, 1999. A Wiley-Interscience
Publication.
[Chu74] Kai Lai Chung. Elementary probability theory with stochastic processes. Springer-Verlag, New YorkHeidelberg, 1974. Undergraduate Texts in Mathematics.
[Dud02] R. M. Dudley. Real analysis and probability, volume 74 of Cambridge Studies in Advanced Mathematics.
Cambridge University Press, Cambridge, 2002. Revised reprint of the 1989 original.
[EK86]
Stewart N. Ethier and Thomas G. Kurtz. Markov processes. Wiley Series in Probability and Mathematical Statistics: Probability and Mathematical Statistics. John Wiley & Sons, Inc., New York, 1986.
Characterization and convergence.
[Ete81] N. Etemadi. An elementary proof of the strong law of large numbers. Z. Wahrsch. Verw. Gebiete,
55(1):119–122, 1981.
[FL80]
Wolfgang Fischer and Ingo Lieb. Funktionentheorie, volume 47 of Vieweg Studium: Aufbaukurs Mathematik [Vieweg Studies: Mathematics Course]. Friedr. Vieweg & Sohn, Braunschweig, 1980. Aufbaukurs
Mathematik.
[Jac01]
N. Jacob. Pseudo differential operators and Markov processes. Vol. I. Imperial College Press, London,
2001. Fourier analysis and semigroups.
[KK06] Yu. G. Kondratiev and O. V. Kutoviy. On the metrical properties of the configuration space. Math.
Nachr., 279(7):774–783, 2006.
[KS91]
Ioannis Karatzas and Steven E. Shreve. Brownian motion and stochastic calculus, volume 113 of Graduate
Texts in Mathematics. Springer-Verlag, New York, second edition, 1991.
[KS07]
Leonid B. Koralov and Yakov G. Sinai. Theory of probability and random processes. Universitext.
Springer, Berlin, second edition, 2007.
[Wer00] Dirk Werner. Funktionalanalysis. Springer-Verlag, Berlin, extended edition, 2000.
120