Ferienkurs Quantenmechanik Drehimpuls und Spin

Drehimpuls und Spin
Tag 3
10. September 2014
Seite 1
(Theoretische Physik III)
Ferienkurs Quantenmechanik
Sommersemester 2014
Fabian Jerzembeck und Christian Kathan
Fakultät für Physik
Technische Universität München
10. September 2014
Drehimpuls
und
Spin
Häug hängt unser Potential in der Schrödingergleichung nur vom Abstand unseres
Teilchens, zum Beispiel zu einem Atomkern, ab. Dann nimmt unsere stationäre Schrödingergleichung in 3 Dimesnsionen die Form
~2
∆ + V (r) Ψ(~r) = EΨ(~r),
−
2m
mit r = x2 + y 2 + z 2 , an. Diese Symmetrie können wir nutzen, indem wir das Problem in Kugelkoordinaten betrachten. Der Laplaceoperator nimmt darin folgende Form
an:
2
p
∆=
1 ∂
r2 ∂r
r2
∂
∂r
+
r2
1
∂
sin ϑ ∂ϑ
sin ϑ
∂
∂ϑ
+
r2
1
∂
2
sin ϑ ∂ϕ2
Das sieht zugegebenermaÿen (noch) nicht besser aus. Durch Einführung des quantenmechanischen Drehimpulsoperators können wir es aber weiter vereinfachen.
Anschlieÿend führen wir eine allgemeine Diskussion der Drehimpulsalgebra durch und
verwenden diese, um die Ergebnisse des Stern-Gerlach-Experiments zu interpretieren. Dazwischen schieben wir eine sehr knapp gehaltene Darstellung des WasserstoProblems ein. Zum Abschluss werfen wir einen kurzen Blick auf die Kopplung von
Drehimpulsen.
Weite Teiles dieser knappen Darstellung orientieren sich an die Vorlesung von Herrn
Prof. Ratz (SS13), sowie von Herrn Prof. Zwerger (SS14) und dem Ferienkurs 2013.
1
Drehimpuls und Spin
Tag 3
10. September 2014
Seite 2
(Theoretische Physik III)
1 Drehimpuls
Analog zum klassischen Drehimpuls denieren wir uns den (hermiteschen) Drehimpulsoperator
~ ≡ ~r × p~ = −i~(~r × ∇)
L
mit den Komponenten
∂
∂
−z
Lx = ypz − zpy = −i~ y
∂z
∂y
∂
∂
Ly = zpx − xpz = −i~ z
−x
∂x
∂z
∂
∂
−y
Lz = xpy − ypx = −i~ x
∂y
∂x
Das Betragsquadrat lautet
L2 = L2x + L2y + L2z
Für die Komponenten können wir Vertauschungsrelationen ausrechnen:
[Lx , Ly ] = [ypz −zpy , zpx −xpz ] = [ypz , zpx ]−[zpy , zpx ] − [ypz , xpz ] +[zpy , xpz ]
=
P roduktregel
| {z } | {z }
=0
=0
= y[pz , zpx ] + [y, zpx ] pz + z [py , xpz ] +[z, xpz ]py
| {z }
| {z }
=0
=
P roduktregel
=0
= yz [pz , px ] +y [pz , z] px + x [z, pz ] py + [z, x] pz py = i~(xpy − ypx ) = i~Lz
| {z }
| {z }
| {z }
| {z }
=0
=−i~
=0
=i~
Und analog
[Lx , Lz ] = −i~Lz
[Ly , Lz ] = i~Lx ,
Satz 1
In kompakter Notation:
[Li , Lj ] = i~ijk Lk
Daraus folgt dann direkt
[L2 , Li ] = 0
Die Idee ist nun gemeinsame Eigenfunktionen von Lz und L2 zu konstruieren, die
wie wir im Folgenden sehen werden, auch Eigenfunktionen vom Hamiltonoperator mit
einem radialsymmetrischen Potential sind.
2
Drehimpuls und Spin
Tag 3
10. September 2014
Seite 3
(Theoretische Physik III)
1.1 Drehimpuls in Kugelkoordinaten
(Dieser Abschnitt wird in der Vorlesung weitgehend ausgespart. Die Rechnungen werden hier dennoch präsentiert, da diese in den Standardlehrbüchern meist sehr verkürzt
dargestellt sind.)
In Kugelkoordinaten, dh
x = r sin ϑ cos ϕ
y = r sin ϑ sin ϕ
z = r cos ϑ
können wir zB die Lz -Komponente des Drehimpulses ausdrücken als
∂
∂
Lz = −i~ x
−y
=
∂y
∂x Kettenregel
∂r ∂
∂r ∂
∂ϑ ∂
∂ϕ ∂
∂ϑ ∂
∂ϕ ∂
+
+
+
+
−i~ x
−y
=
∂y ∂r
∂y ∂ϑ
∂y ∂ϕ
∂x ∂r
∂x ∂ϑ
∂x ∂ϕ
∂
∂ϑ
∂
∂ϕ
∂
∂r
∂r
∂ϑ
∂ϕ
+ x
+ x
−i~ x
−y
−y
−y
∂y
∂x
∂r
∂y
∂x
∂ϑ
∂y
∂x
∂ϕ
|
{z
}
|
{z
}
|
{z
}
(I)
(II)
(III)
p
Mit r = x2 + y 2 + z 2 folgt
∂r
x
= ,
∂x
r
Aus cos ϑ =
z
r
∂r
y
= ,
∂y
r
y
r
x
r
also (I) = x − y = 0.
folgt
z z ∂ϑ
∂ϑ
∂
∂
(II) = x
−y
= x arccos
−y
arccos
=
∂y
∂x
∂y
r
∂x
r Kettenregel
1
1z
1
1z
xyz
xyz
x q
− 3 2y − y q
− 3 2x = √
− √
=0
2
2
2
2
2r
2r
r r −z
r r2 − z 2
− 1 − zr2
− 1 − zr2
Mit tan ϕ =
y
x
folgt
∂ϕ
∂y
∂ϕ
∂x
y
y
∂
∂
(III) = x
−y
= x arctan
−y
arctan
=
∂y
x
∂x
x Kettenregel
1 1
1 y
1
y2
x
−y
− 2 =
1+ 2 =1
2
2
2
x
x
1 + xy 2 x
1 + xy 2
1 + xy 2
3
Drehimpuls und Spin
Tag 3
(Theoretische Physik III)
10. September 2014
Seite 4
Insgesamt erhalten wir für die Lz -Komponente des Drehimpulses in Polarkoordinaten
Lz = −i~
∂
.
∂ϕ
Ähnliche Rechnerei gibt uns
∂
∂
Ly = −i~ cos ϕ
− cot ϑ sin ϕ
,
∂ϑ
∂ϕ
∂
∂
Lx = −i~ sin ϕ
− cot ϑ cos ϕ
.
∂ϑ
∂ϕ
und damit
2
2
L = −~
1 ∂
sin ϑ ∂ϑ
∂
sin ϑ
∂ϑ
1 ∂2
+
sin2 ϑ ∂ϕ2
Dieser Term entspricht bis auf den Vorfaktor dem Winkelanteil des Laplaceoperators
in Kugelkoordinaten. Unseren Hamiltonoperator für das radialsymmetrische Potential
( im SP-System) können wir also schreiben als
~2 ∂
H=−
2mr2 ∂r
∂
r
∂r
2
+
L2
+ V (r)
2mr2
Da L2 und Lz nur nur auf den Winkelanteil der Wellenfunktion wirken, sehen wir
dass
0 = [H, L2 ] = [H, Lz ]
Auÿerdem gilt ja [L2 , Lz ] = 0. Es gibt also einen Satz von simultanen Eigenvektoren
von H ,L2 und Lz ! Sind diese bekannt, so lässt sich ein zentralsymmetrisches Problem
mittels Separationsansatz auf eine noch zu lösende Radialgleichung reduzieren.
1.2 Drehimpulsalgebra
Zum diese Eigenvektoren zu bestimmen, könnten wir im Ortsraum verbleiben und
die erhaltenen Dierentialgleichungen lösen 1 Im Hinblick auf die zugrunde liegende
grundsätzliche Struktur werden wir eine abstrakte, basisunabhängige Diskussion in
Dirac-Schreibweise durchführen.
Zu diesem Zweck setzen wir einen beliebigen Drehimpulsoperator J~ voraus, der die
Vertauschungsrelationen (VTR) [Jx , Jy ] = i~Jz und zyklisch erfüllt. Unser Ziel ist
es, das Spektrum (d.h. alle möglichen Eigenwerte) von J~2 und Jz (Auswahl der zKomponente absolut willkürlich!) zu bestimmen.
1 Dies
muss auch getan werden, um eine explizite Darstellung der Kugelächenfunktionen zu erhalten.
4
Drehimpuls und Spin
Tag 3
(Theoretische Physik III)
10. September 2014
Seite 5
Damit lautet unser Ansatz für die gemeinsamen (normierten) Eigenvektoren |λ, mi:
(1)
(2)
J~2 |λ, mi = ~2 λ |λ, mi
Jz |λ, mi = ~m |λ, mi ,
wobei λ und m reell angenommen werden können (→ Hermitizität).
Als erstes erklären wir sog. Auf- und Absteigeroperatoren durch
J+ := Jx + iJy
J− := Jx − iJy = J+†
. Es gelten die VTR (Übung)
[J+ , J− ] = 2~Jz ,
[Jz , J± ] = ±~J± ,
[J 2 , J± ] = 0.
Auÿerdem lässt sich J 2 = Jx2 + Jy2 + Jz2 ausdrücken als
J2 =
1
(J− J+ + J+ J− ) + Jz2 .
2
Nun beobachten wir, dass J± die Auf- und Absteigeoperatoren für die z -Komponente
des Drehimpulses sind, da
Jz (J± |λ, mi) = J± Jz |λ, mi ± ~J± |λ, mi = (m ± 1)~(J± |λ, mi)
J 2 (J± |λ, mi) = J± (J 2 |λ, mi) = λ(J± |λ, mi),
wobei wir obige VTR benutzt haben.
das heiÿt J± |λ, mi ist wieder ein Eigenzustand zu den Eigenwerten (m±1)~ und λ (unverändert, zweite Rechnung), ist also ein Vielfaches von |λ, m ± 1i. Diese Feststellung
rechtfertigt die Namensgebung von J± .
Werfen wir weiter einen Blick auf
hλ, m|
Jx2
+
L2y
!
2
2
~
|λ, mi = hλ, m| J − Jz |λ, mi = ~2 (λ − m2 ) ≥ 0,
(3)
folgt sofort die Einschränkung m2 ≤ λ.
Halten wir λ fest, so muss ein max m =: j und ein min m =: j 0 geben. Ein weiteres Aufsteigen von einem EV mit maximaler z -Komponente ist nicht möglich, was
J+ |λ, m = ji = 0 bedeutet. Durch eine geschickte Umformung
J− J+ = Jx2 + Jy2 −i (Jy Jx − Jx Jy ) = J 2 − Jz2 − ~Jz
{z
}
| {z } |
J 2 −Jz2
[Jy ,Jx ]=−i~Jz
5
(4)
Drehimpuls und Spin
Tag 3
(Theoretische Physik III)
10. September 2014
Seite 6
erhalten wir damit
0 = J− J+ |λ, m = ji =
2
− Jz2 − ~Jz |λ, m = ji = ~(λ − j 2 − j) |λ, m = ji ,
(5)
was λ = j(j + 1) bedeutet.
Die selbe Rechnung mit j 0 und J+ ↔ J− führt auf λ = j 0 (j 0 − 1). Gleichsetzen unter
Berücksichtigung von j 0 < j bedingt, dass j 0 = −j .
Nun benötigen wir einen letzten cleveren Kni: Den EV |λ, m = −ji können wir durch
ganzzahliges Anwenden des Absteigeoperators J− auf |λ, m = ji erzeugen. Insgesamt
brauchen wir j − j 0 = 2j Schritte. M.a.W. impliziert dies, dass 2j eine (positive) ganze
Zahl sein muss, was nur durch j = 0, 21 , 1, 23 , 2, . . . erfüllt wird. Gleichzeitig sind damit
auch die möglichen m zu m = −j, −j + 1, . . . , j − 1, j festgelegt.
Damit sind wir fertig und zu einer übersichtlicheren Notation benennen wir die EV um
zu |j, mi mit λ = j(j + 1). Wir fassen damit zusammen:
Die Eigenwerte eines beliebigen Drehimpulsoperators (also alle Operatoren,
die die geforderte VTR erfüllen) sind diskret und können Werte annehmen
Satz 2
ˆ ~2 j(j + 1)für J~2
ˆ ~m
mit j = 0, 21 , 1, 32 , 2, . . .,
und
für Jz mit m = −j, −j + 1, . . . , j − 1, j , d.h. (2j + 1) Werte.
Die zugehörigen Eigenvektoren sind die Zustände |j, mi.
Speziell führt eine etwas konkretere Betrachtung im Ortsraum auf die bekannten Kugelächenfunktionen :
6
Drehimpuls und Spin
Tag 3
(Theoretische Physik III)
10. September 2014
Seite 7
Die Drehimpulseigenzustände im Ortsraum sind die Kugelächenfunktionen
hϑ, ϕ|l, mi = Ylm mit
Satz 3
L2 Ylm (ϑ, ϕ) = l(l + 1)~2 Ylm (ϑ, ϕ)
Lz Ylm (ϑ, ϕ) = m~Ylm (ϑ, ϕ).
In expliziter Darstellung können sie (bereits korrekt normiert) als
s
Ylm (ϑ, ϕ) =
(l − m)!
(l + m)!
r
2l + 1 m
P (cos ϑ)eimϕ
4π l
geschrieben werden.
Als normierte Eigenfunktionen zu verschiedenen Eigenwerten von hermiteschen Operatoren bilden sie ein Orthonormalsystem auf der Sphäre S 2
ˆ
dΩYl∗0 m0 (ϑ, ϕ)Ylm (ϑ, ϕ) = δl0 l δm0 m
Dabei ist l = 0, 1, 2, ... die Drehimpuls-/Orbitalquantenzahl und m = −l, .., 0, ..l die
Magnetquantenzahl.
Explit lauten die ersten Kugelächenfunktionen
1
Y00 (ϑ, ϕ) = √
4π
r
3
Y10 (ϑ, ϕ) =
cos(ϑ)
4π
r
3
sin ϑe±iϕ
Y1,±1 (ϑ, ϕ) = ∓
8π
r
5
Y20 (ϑ, ϕ) =
(3 cos2 ϑ − 1)
16π
r
15
Y2,±1 (ϑ, ϕ) = ∓
sin ϑ cos ϑe±iϕ
8π
r
15
Y2,±2 (ϑ, ϕ) =
sin2 ϑe±2iϕ
32π
2 Energieeigenwerte vom Wasserstoatom
(Dieser Abschnitt wird in der Vorlesung aus Zeitgründen sehr knapp behandelt. Da
die Lösung des Wasserstoproblems eine der zentralen Punkte einer Einführung in die
Quantenmechanik darstellt, ndet der Leser hier eine etwas ausführlichere Zusammenfassung.)
7
Drehimpuls und Spin
Tag 3
10. September 2014
Seite 8
(Theoretische Physik III)
Wir schauen uns jetzt die Schrödingergleichung für ein gebundenes Elektron (dh E < 0)
im Coulombpotential an. In Kugelkoordinaten lautet sie
~2 ∂
−
2mr2 ∂r
∂
r
∂r
2
L2
Ze2
+
Ψ(~r) = EΨ(~r)
−
2mr2
r
Wir machen einen Separtionsansatz der Form
Ψ(~r) = REl (r)Ylm (ϑ, ϕ).
Mit der zusätzlichen Substitution REl (r) =
uEl (r)
r
erhalten wir
~2 d2 uEl
l(l + 1)~2 Ze2
−
uEl (r) = EuEl (r)
+
−
2m dr2
2mr2
r
Da die Wellenfunktion Ψ(~r) normiert sein muss, gilt
ˆ
ˆ
1=
r
2
ˆ
∗
(ϑ, ϕ)Ylm (ϑ, ϕ)
dΩYlm
∗
(r)REl (r)
drREl
|
{z
=1
=
dru∗El (r)uEl (r)
}
Wir können also uEl (r) als 1-dimensionale Wellenfunktion in dem eektiven Potential
Ve (r) = −
Ze2 l(l + 1)~2
+
r
2mr2
interpretieren. Falls l 6= 0 kommt dadurch eine Drehimpulsbarriere zustande:
Auÿer für s-Zustände (dh l = 0) ist die Wahrscheinlichkeit das Teilchen in der Nähe
des Ursprungs anzutreen sehr klein.
2.1 Asymptotisches Verhalten
Wir wollen jetzt die Funktion uEl (r) bestimmen. Schauen wir uns zunächst das asymptotische Verhalten an:
8
Drehimpuls und Spin
Tag 3
10. September 2014
Seite 9
(Theoretische Physik III)
2.1.1 für r → 0
Es dominiert der 1/r2 -Term und die Dierntialgleichung reduziert sich auf
l(l + 1)
d2 uEl
=
uEl (r).
2
dr
r2
Die allgemeine Lösung lautet u(r) = Arl+1 + Br−l . Da die Wellenfunktion normierbar
bleiben muss, kommt nur
uEl (r) ∼ rl+1
(r → 0)
in Frage.
2.1.2 für r → ∞
Für r → ∞ reduziert sich unsere DGL auf
d2 uEl
= κ2 uEl
dr2
κ2 ≡ −
2mE
>0
~2
r→∞
Unsere Denition von κ macht Sinn da wir von gebunden Zuständen (dh E < 0) reden.
Die allgemeine Lösung dieser DGL ist u(r) = Ceκr + De−κr . Zwecks Normierbarkeit
kommt diesmal nur
uEl (r) ∼ e−κr
(r → ∞)
in Frage.
2.2 Lösung
Ab jetzt führen wir die dimensionslosen Gröÿen
r
ρ ≡ κr =
2
ρ0 ≡
2m|E|
r
~2
2
Ze κ
e ~cκ
=Z
= Zα
|E|
~c |E|
s
2mc2
|E|
ein. α = ~ce 2 wird Feinstrukturkonstante genannt. Unter Beachtung von dρ = κdr wird
die DGL nach Umformung zu
2
d2
1
ρ0
− l(l + 1) 2 +
− 1 uEl (ρ).
dρ2
ρ
ρ
Zur Lösung machen wir einen Ansatz der Form
uEl (ρ) = ρl+1 e−ρ w(ρ)
9
Drehimpuls und Spin
Tag 3
(Theoretische Physik III)
10. September 2014
Seite 10
der das bekannte asymptotische Verhalten berücksichtigt. Damit bekommen wir für
w(ρ):
ρ
d2 w(ρ)
dw(ρ)
+ (ρ0 − 2l − 2)w(ρ) = 0
+
2(l
+
1
−
ρ)
dρ2
dρ
Zur Lösung machen wir einen Potenzreihenansatz:
w(ρ) =
∞
X
ak ρk
k=0
Damit erhalten wir
∞ X
ak k(k − 1)ρ
k−1
+ 2(l + 1)kρ
k−1
ak + ak (ρ0 − 2l − 2 − 2k)ρ
k
=0
k=0
und durch Koezientenvergleich
ak+1 [(k + 1)k + 2(l + 1)(k + 1)] + ak (ρ0 − 2l − 2 − 2k) ρk = 0
oder
ak+1
2(k + l + 1) − ρ0
=
ak
(k + 2l + 2)(k + 1)
Für groÿe k gilt dann
ak+1
2
∼ ,
ak
k
entspricht also ungefähr dem Verhältnis der Koezienten von der Exponentialfunktion
∞
e
2ρ
=
X (2ρ)k
k=0
Damit wäre aber
und somit
k!
w(ρ) ∼ e2ρ
(r → ∞)
uEl (ρ) ∼ eρ
(r → ∞)
nicht normierbar! Nur wenn unsere Potenzreihe abbricht bekommen wir keine Schwierigkeiten. Schauen wir unsere Rekursionsgleichung
ak+1 =
2(k + l + 1) − ρ0
ak
(k + 2l + 2)(k + 1)
an, sehen wir dass ein N existieren muss, sodass
2(N + l + 1) = ρ0 .
Das Problem ist nun prinzipiell gelöst.
10
Drehimpuls und Spin
Tag 3
10. September 2014
Seite 11
(Theoretische Physik III)
2.3 Hauptquantenzahl
n
Um weiterzumachen denieren wir die Hauptquantenzahl n als
n ≡ N + l + 1 = 1, 2, 3, ...
mit l = 0, 1, ..., n − 1
Damit gilt jetzt
2mc2
ρ0 =
−E
1/2
Zα = 2n,
wir haben also:
Satz 4
Die Energieeigenwerte für das Wasserstoatom lauten
1
Z 2 α2
En = − mc2 2
2
n
Da zu jedem n-Wert, l die Werte 0 bis n − 1 annehmen kann, und für jeden l-Wert m
die
Werte −l bis l annehmen kann, ist jeder Energieeigenwert En
Pn−1
2
l=0 (2l + 1) = n -fach entartet.
Die zugehörigen Eigenfunktionen in der Ortsbasis bezeichnen wir mit
Ψnlm (~r) = h~r|nlmi = Rnl (r)Ylm (ϑ, ϕ).
Die (normierten) Radialwellenfunktionen erhalten wir durch rücksubstituieren in der
Herleitung. Sie lauten in der allgemeinen Form
Rnl (r) = −e
−κr
(2κr)
l
(n − l − 1)!(2κ)3
2n((n + l)!)3
11
−1/2
L2l+1
n+l (2κr)
Drehimpuls und Spin
Tag 3
Mit der Bezeichnung a ≡
(Theoretische Physik III)
a0
Z
=
~2
Zme2
10. September 2014
Seite 12
lauten die ersten Radialwellenfunktionen explizit
r
R10 (r) = 2a
e a,
r
r −
−3/2
R20 (r) = 2(2a)
1−
e 2a ,
2a
r − r
1
R21 (r) = √ (2a)−3/2
e 2a ,
a
3
r
−
2r2
2r
−3/2
+
e 3a ,
R30 (r) = 2(3a)
1−
3a 27a2
√
r −r
r
4 2
(3a)−3/2
1−
e 3a ,
R31 (r) =
3
a
6a
√
2 − r
2 2
−3/2 r
R32 (r) = √ (3a)
e 3a
a
27 5
−3/2
−
3 Spin
Auÿer dem aus klassischen Systemen bekannten Bahndrehimpuls, besitzen quantenmechanische Objekte noch einen intrinsischen Drehimpuls, den Spin, ohne Entsprechung
in klassischen Systemen. Im einfachsten Fall besitzt ein Teilchen 2 Spinzustände die
wir mit Spin-up (|+i) und Spin-down (|−i) bezeichnen. Die Observablen Sx , Sy und Sz
des Spinvektors können dementsprechend durch 2 × 2-Matrizen dargestellt werden.
Als experimenteller Nachweis für den Spin dient vor allem der Stern-Gerlach-Versuch :
3.1 Das Stern-Gerlach-Experiment
~
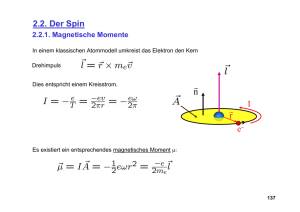
Das magnetische Moment eines geladenen Teilchens der Masse m mit Drehimpuls L
beträgt klassisch
µ
~≡
~
eL
2mc
Die potentielle Energie eines Teilchens mit dem magnetischen Moment µ
~ in einem
~
Magnetfeld B beträgt
~
−~µ · B.
~ ortsabhänWenn wir ein inhomogenes Magnetfeld nehmen, wird das Potential −~µ · B
gig. Durch so ein inhomogenes Magnetfeld schicken wir jetzt einen Strahl aus Silberatomen.
Eine Wechselwirkung der Atome mit dem Magnetfeld kann nun entweder durch das
magnetische Moment des Kerns, oder das der Elektronen geschehen: Das magnetische
Moment des Kerns ist aber vernachlässigbar da er viel schwerer ist als die Elektronen
12
Drehimpuls und Spin
Tag 3
(Theoretische Physik III)
10. September 2014
Seite 13
und die Masse im Nenner das magnetische Moment sehr klein werden lässt. Von den
Elektronen spielt nur das 5s-Elektron Elektron eine Rolle. Die Momente der restlichen
Elektronen heben sich gerade auf. Für die Quantenzahl l der 5s-Elektronen gilt aber
l = 0 und sie besitzen somit keinen Bahndrehimpuls!
Klassisch würden wir erwarten, dass das magnetische Moment der Elektronen deshalb
null ist und der Strahl somit geradlinig durch unser Magnetfeld läuft. Allerdings wird
gerade dies nicht beobachtet:
Die beobachteten 2 diskreten Werte von µz können durch Einführung eines intrinsischen halbzahligen Eigendrehimpulses, dem Spin, erklärt werden. Dieser ist ebenfalls
mit einem magnetischen Moment verknüpft und koppelt somit an das Magnetfeld. Der
Spin besitzt kein klassisches Analogon und ist somit ein komplett neues Quantenphänomen.
Nun etwas ausführlicher. Für den Spin des Elektrons (hier die Sz -Komponente) sind
anscheinend nur 2 Zustände möglich. Diese bezeichnen wir Spin-up und Spin-down.
Betrachten wir die Lz -Komponente vom Bahndrehimpuls, so sehen wir, dass
Lz = m~
− l ≤ m ≤ +l,
wobei m in ganzzahligen Schritten läuft. Wir haben also nur einen möglichen Lz -Wert
falls l = 0 und drei mögliche Lz -Werte falls l = 1.
Die Beobachtung zeigt aber nur zwei mögliche Werte für den Spin und das erhält man
formal dadurch, dass wir l = 21 setzen. Dann sind die möglichen Sz -Werte − ~2 und + ~2 ,
in Übereinstimmung mit dem Experiment.
13
Drehimpuls und Spin
Tag 3
(Theoretische Physik III)
10. September 2014
Seite 14
3.2 Formalismus
Die Observable Sz besitzt also die zwei Eigenwerte − ~2 und + ~2 . Die zugehörigen orthogonalen Eigenvektoren werden mit |+i und |−i bezeichnet. Falls wir unseren SpinOperator als 2 × 2-Matrix darstellen wollen, lauten die Eigenvektoren
1
|+i =
0
0
|−i =
.
1
Ein allgemeiner Spinor ist imAllgemeinen
eine Superposition der beiden orthogonalen
c1
Eigenzustände, d.h. |χi =
= c1 |+i + c2 |−i mit der Normierungsbedingung
c2
|c1 | + |c2 | = 1, wobei die Koezienten komplex sind.
2
2
Damit schreibt sich Sz zu
~
Sz =
2
1 0
0 −1
Als eine Form des Drehimpulses gelten/ fordern wir für den Spin die Vertauschungsrelationen
Satz 5
[Si , Sj ] = i~ijk Sk
Damit können wir uns jetzt auch eine Darstellung für Sx und Sy konstruieren. Dies
kann zum Beispiel durch Anwenden des Auf-/Absteiger-Formalismus geschehen. Damit
erhält man
Sx =
~
2
0 1
1 0
Sy =
~
2
0 −i
i 0
Das lässt sich mit den Pauli-Matrizen kompakt schreiben als
~ = ~ ~σ
S
2
wobei
T
~σ = (σx , σy , σz )
0 1
0 −i
1 0
mit σx =
, σy =
, σz =
1 0
i 0
0 −1
Für die Pauli-Matrizen gilt
[σi , σj ] = 2iijk σk
σx2 = σy2 = σz2 = 1
{σi , σj } = 2δij
Aus der zweiten Relation sehen wir, dass
3
S 2 = ~2 · 1
4
14
Drehimpuls und Spin
Tag 3
(Theoretische Physik III)
10. September 2014
Seite 15
3.3 Transformation von Spinoren unter Drehungen
In diesem Abschnitt beschränken wir uns (wie oben) auf dem Spinorraum, d.h. wir
betrachten Spin-1/2 Teilchen. Die zentrale Aufgabe ist es, die Eigenzustände von Spinprojektionen bezüglich beliebiger Raumrichtungen anzugeben. Bisher haben wir nur
diese in z -Richtung kennengelernt (das waren |+i und |−i bzgl. σz ).
~ ±i die gesuchten Zustände. Dabei gibt Ω
~
Dazu bezeichnen wir mit |Ω,
 eine beliebi
sin ϑ cos ϕ
~ =  sin ϑ sin ϕ 
ge Richtung im Ortsraum an, wobei wir die Parametrisierung Ω
verwenden. Die zu erfüllende Eigenwertgleichung lautet somit
cos ϑ
~ ±i ,
~ ·Ω
~ |Ω,
~ ±i = ± ~ |Ω,
S
2
(6)
~ |Ω,
~ ±i = ± |Ω,
~ ±i
~σ · Ω
(7)
was äquivalent zu
ist.
Es liegt nun nahe, beliebige Eigenzustände mittels Drehungen zu generieren, wobei wir
die Basis {|+i , |−i} des Spinorraums C2 festhalten. Allgemein wird durch Angabe einer
(normierten) Richtung ~n mit einem Winkel ϑ eine Drehung im Ortsraum vollständig
festgelegt. Ohne zu tief in die Darstellungstheorie der SO(3) einzusteigen, übersetzt sich
dies zu einer entsprechenden Drehung im Spinorraum. Drehungen sind dort Elemente
der SU (2) und werden parametrisiert durch
~
D~n (θ) = exp −iθ~n · S/~
= exp (−iθ~n · ~σ /2).
(8)
Starten wir bei Nord- oder Südpol (festgelegt durch unsere ursprüngliche Quantisierungsachse, also die z -Achse), so können wir mit einer Drehung um die z -Achse mit
dem Winkel ϕ und einer anschlieÿenden Drehung um die y -Achse mit θ jeden Punkt
auf der Oberäche der Einheitssphäre erreichen. Das übersetzt sich im Spinorraum zu
~ .
einer unitären Drehmatrix Dz (ϕ) · Dy (θ) =: D(Ω)
Damit können wir die Lösung formulieren:
Satz 6
Die Eigenzustände eines Spin-1/2 Teilchens in einer beliebigen Raumrichtung (Winkel ϑ und ϕ) sind
~ ±i = D(Ω)
~ |±i
|Ω,
mit der unitären 2 × 2-Drehmatrix
~ =
D(Ω)
cos
sin
ϕ
θ
e−i 2
2
ϕ
θ
e+i 2
2
ϕ − sin 2θ e−i 2
ϕ
.
cos 2θ e+i 2
Alternativ kann das Resultat durch Einsetzen in die Eigenwertgleichung auch einfach
nachgerechnet werden (Übung).
15
Drehimpuls und Spin
Tag 3
(Theoretische Physik III)
10. September 2014
Seite 16
Nochmal: Drehen wir im Ortsraum die Quantisierungsachse (z.B. falls wir die Richtung
des Gradienten des inhomogenen Magnetfeldes im Stern-Gerlach-Experiment verändern), so müssen wir gleichzeitig im Spinorraum drehen, um die korrekten Eigenzustände der Spinprojektion bzgl. der neuen Achse zu erhalten (s. Übungen).
3.4 Addition von Drehimpulsen
Zum Schluss werden wir die Addition/ Kopplung von Drehimpulsen kurz skizzieren.
Dies wird wichtig, wenn man bedenkt, dass z.B. Elektronen in Atomen sowohl einen
Bahndrehimpuls als auch einen Spin besitzen. Auch spielt dieser Formalismus eine
wichtige Rolle im Periodensystem der Elemente, um ein weiteres Beispiel zu nennen.
Betrachten wir nun zwei beliebige Drehimpulse J~1 und J~2 (und damit zwei verschiedene Hilberträume) mit ihren jeweiligen Eigenzuständen |ji , mi i, i = 1, 2. Denieren wir
nun einen Gesamtdrehimpuls J~ = J~1 + J~2 so kann der dazugehörige Gesamthilbertraum
durch die Produktzustände |j1 , m1 i ⊗ |j2 , m2 i aufgespannt werden.2 Da J~1 und J~2 vertauschbar sind, erfüllt der so denierte Gesamtdrehimpuls die Drehimpulsalgebra, d.h.
[Jx , Jy ] = i~Jz und zyklisch (so wie es sein sollte!).
Damit sind die möglichen Eigenwerte von J~2 und Jz bereits festgelegt. Gesucht sind
noch die zugehörigen Eigenzustände, ausgedrückt in der oben erwähnten Produktbasis.
Es kann nun gezeigt werden, dass insgesamt J~2 ,Jz , J~12 und J~22 untereinander kommutieren. Deshalb identizieren wir die Eigenzustände mit |j1 , j2 , j, mi. Es wird an dieser
Stelle betont, dass m1z und m2z im Allgemeinen keine guten Quantenzahlen mehr
sind!
Ein wesentliches Resultat ist nun, dass für gegebene j1 und j2 für den Gesamtdrehimpuls die Werte |j1 − j2 | ≤ j ≤ j1 + j2 möglich ist.
Als abschlieÿendes Beispiel betrachten wir nun die Kopplung zweier 1/2 Spins zu
Singlet (S = 0) und Triplet (S = 1). Hier liegt es nahe, den Gesamtdrehimpuls als Gesamtspin S~ = S~1 + S~2 zu bezeichnen. In knapper aber übersichtlicher Notation |S, mS i
erhalten wir
S = 0 Singlet :
S = 1 Triplet :
1
|0, 0i = √ (|+, −i − |−, +i)
2
|1, 1i = |+, +i
1
|1, 0i = √ (|+, −i + |−, +i)
2
|1, −1i = |−, −i
zugrunde liegende Struktur ist als Tensorraum bekannt. Die Vorlesung erlaubt aus Zeitgründen
jedoch nicht hierauf tiefer einzugehen. Auftretende Fragen können hierzu gerne in den Übungen
gestellt werden.
2 Die
16
Drehimpuls und Spin
Tag 3
(Theoretische Physik III)
10. September 2014
Seite 17
Dabei ist zu erkennen, dass der Singlet-Zustand antisymmetrisch und die TripletZustände symmetrisch sind. In den Übungen werden diese Zustände und der Umgang
mit dem Gesamtspin-Operator vertiefend behandelt.
17