2. Beschleunigte Bezugssysteme, starrer Körper und

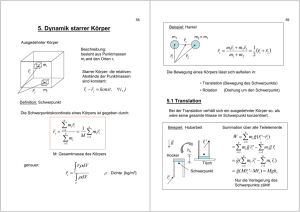
2. Beschleunigte Bezugssysteme,
starrer Körper und Himmelsmechanik
2.1. Trägheits- bzw. Scheinkräfte
Die Bewegung in einem beschleunigen Bezugssystem lässt sich mit Hilfe von sogenannten Scheinkräften beschreiben. Dazu betrachten wir zuerst ein ruhendes System KS und ein beschleunigtes
System KS’, welcher linear mit a beschleunigt wird.
In den Koordinaten von KS’ führt der eigentlich ruhende Nullpunkt von KS eine beschleunigte Bewegung durch. Für den Beobachter in KS’ scheint deshalb eine Kraft auf den Nullpunkt zu wirken.
F = ma.
Besonders wichtig sind die Trägheitskräfte von gleichförmigen Drehbewegungen:
Auf m wirkt die Kraft F = ma mit
d
ê
= vω(−êr ) = −Rω 2 êr
a = |v |
dt tang
const.
Für einen Beobachter im Massenpunkt scheint aber eine Kraft nach außen zu wirken.
Allgemein: Zerlegung in Tangential- und Normalbeschleunigung:
a(t) = êt
dv v 2
+ ên
dt
ρ
dabei ist ρ der lokale Krümmungsradius.
Allgemeine Scheinkräfte (ohne Ableitung)
a = a − ω
× (ω × r ) − 2ω × v wobei gestrichene Vektoren in der Basis des rotierenden Systems und ungestrichene in denen des
13
2. Beschleunigte Bezugssysteme, starrer Körper und Himmelsmechanik
Ruhesystem dargestellt sind. Man sieht folgende Beiträge:
1. a ⇒ reale Kräfte
2. aF = −ω × (ω × r ) ⇒ Zentrifugalbeschleunigung
3. aC = −2(ω × v ) ⇒ Coriolisbeschleunigung.
Diese treten in KS als Kräfte in Erscheinung.
Anschauliches Beispiel zur Zentrifugalbeschleunigung:
Der ruhende Punkt bewegt sich in KS’
Anschauliches Beispiel zur Coriolisbeschleunigung
Hier bewegt sich der Ball weiterhin mit v = ωR, der Erdboden aber nur mit v = ωr ⇒ Der Ball
scheint in Richtung der Drehung beschleunigt zu sein.
14
2.2. Rotierende Körper
2.2. Rotierende Körper
2.2.1. Starrer Körper
Bisher wurden nur Massenpunkte betrachtet. Bei diesen war nur die Translationsbewegung zu beachten. Bei ausgedehnten Körpern kann es auch eine rotierende Bewegung geben.
Zur Behandlung von Rotationsbewegungen führen wir das Ideal eines starren Körpers ein; das ist
ein ausgedehnter, nicht verformbarer Körper. (z.B. ein System von Massenpunkten mit konstanter
relativer Lage zueinander)
Außerdem führen wir den Drehimpuls ein:
→
= r × p = mr × v = mr × (ω × r) = ←
L
Θ ·ω
2
= mrv sin ϕ = mr2 sin2 ϕω = mr⊥
ω = Θω
→ |L|
Dabei ist Θ das Trägheitsmoment oder allgemeiner der Trägheitstensor.
Wir betrachten zuerst ein paar Beispiele:
Beispiel 1 Homogene Scheibe mit Kraft auf Mittelpunkt → keine Rotation
Beispiel 2 Inhomogene Scheibe
Wirkt bei der inhomogenen Scheibe eine Kraft auf den geometrischen Mittelpunkt, kommt es zu einer
kombinierten Translations- und Rotationsbewegung. (anschaulich kann man sich überlegen, dass die
schwerere Hälfte aufgrund iher größeren Trägheit zurückbleiben muss.) Weitere Feststellung: Wenn
der Angriffspunkt in Richtung der Kraft verschoben wird, entsteht die gleiche Bewegung. Dies wird
als Linienflüchtigkeit bezeichnet.
Zu einer reinen Drehbewegung muss die Kraft durch eine andere kompensiert werden.
15
2. Beschleunigte Bezugssysteme, starrer Körper und Himmelsmechanik
Wir erhalten F = −F
Allgemein muss (für jede Komponente des Vektors) gelten
Fi = 0
i
2.2.2. Drehmoment
Zur quantitativen Betrachtung definieren wir das Drehmoment
= r × F
M
Dies ist sinnvoll, da die Bewegung offensichtlich von der Kraft und ihrem Ansatzpunkt abhängt. Aus
der Linienflüchtigkeit schließen wir, dass die Kraft nur von r⊥ abhängt, das erreichen wir durch das
Kreuzprodukt.
Wie ändert sich nun der Drehimpuls? Wir bilden die Ableitung
d
dp dr
˙
= Θ ω
L = r ×
+
× (mr˙ ) = r × F = M
dt
dt dt konstant
0
→Die Änderung des Drehimpulses ist das Drehmoment. Ist F oder r⊥ gleich Null, so ist die Ableitung
gleich Null und L
konstant, dies bezeichnet man als Drehimpulserhaltung.
von L
2.2.3. Rotationsenergie und Trägheitsmoment
Werfen wir noch einen Blick auf die Energie. Da die Rotation eine Beweung der einzelnen Elemente
ist, können wir rechnen:
Erot =
1
i
2
mi vi2 =
i
Θ
ω 1
2
mi (ri ω) =
mi ri2 = Θω 2
2
2 i
2
1
2
Ist die Dichte als Funktion ρ(r ) gegeben, so erhält man Θ durch Integration:
2
ρ(r )r⊥
dx dy dz Θ=
K
Da häufig runde Körper behandelt werden, ist es manchmal besser, in anderen Koordinaten zu rechnen
2
• Zylinderkoordinaten Θ =
ρ(r, ϕ, z)r⊥
rdrdϕdz
16
2.2. Rotierende Körper
• Kugelkoordinaten Θ =
2 2
ρ(r, θ, ϕ)r⊥
r sin θdrdθdϕ
Dabei ist r⊥ der Abstand von r zur Drehachse.
Ein weiteres Hilfsmittel zur Berechnung von Trägheitsmomenten ist der Satz von Steiner
Es gilt für das Trägheitsmoment:
ΘA = ΘSp + M d2
Dabei ist M die Gesamtmasse.
Für die Leistung gilt:
dW
d
P =
=
dt
dt
1
Θω 2
2
= Θω ω̇ = ω L̇ = ωM
Achtung: Der Drehimpuls ist nicht absolut festlegbar!
nicht parallel zu ω
Im Allgemeinen ist auch L
17
2. Beschleunigte Bezugssysteme, starrer Körper und Himmelsmechanik
Man beachte, dass bei inhomogenen Körpern gilt
→
=←
L
Θ ·ω
Eine weitere Eigenschaft des Drehimpulses ist, dass er sich in 2 Komponenten zerlegen lässt:
• Eigendrehimpuls
• Bahndrehimpuls
Bemerkung: Massenpunkte haben keinen Eigendrehimpuls.
2.2.4. Hebelgesetz
18
2.2. Rotierende Körper
1 +M
2 = 0
Keine Bewegung, wenn M
⇔
r1 × m1g + r2 × m2g = 0. Das heißt:
r1 = −r2
m2
m1
2.2.5. Translationsbewegung starrer Körper
Frage: wie ändert sich die Bewegung des Schwerpunktes, wenn auf denen bestimmten Ort eine Kraft
wirkt?
Es gilt wie bisher
F = mgesasp
obwohl zusätzlich eine Drehbewegung entsteht!
2.2.6. Rollbedingung
Für einen rollenden Körper gilt ωR = vM , wobei vM die Schwerpunktsgeschwindigkeit ist. Falls v
konstant ist, erhalten wir die Beziehung
x
vM =
t
Bedingung für das Rollen:
vM = Rω
Herleitung: Die Zeit für eine vollen Umlauf ist gegeben durch
2πR ⇒ vM =
Wegen sBoden = SKugel
(I)
→ Winkelgeschwindigkeit
ω=
Daraus erhalten wir
2πR
s
⇒
=T
t
vM
(I)
T =
2π
T
2πR (II) 2π
=
vM
ω
(II)
⇒
ωR = vM
19
2. Beschleunigte Bezugssysteme, starrer Körper und Himmelsmechanik
2.2.7. Rotation um feste Achsen
Bisher: Betrachtung der Rotation eines freien Körpers
Jetzt: Verhalten, wenn der Körper an einem Punkt oder einer Achse fixiert wird (ohne Behinderung
einer Rotation um diesen Punkt).
→Rotation um die feste Achse, damit müssen auch alle Größen auf diese Achse bezogen werden!
• Trägheitsmoment durch Satz von Steiner
= r⊥ F = 0
• |L|
Garnrolle
Als Drehachse muss hier der Auflagepunkt betrachtet werden. Die Rolle bewegt also bei F1 und F2
in unterschiedliche Richtungen.
Bemerkung: Die Bewegung ändert sich, wenn die Kraft größer als die Reibung wird.
Übersicht: Translation und Rotation
Translation
r Ort
v = r˙ Geschwindigkeit
a = v˙ Beschleunigung
F Kraft
p = mv Impuls
m Masse
Ekin = 12 mv 2 kinetische Energie
P = F v Leistung
20
Rotation
ϕ Winkel
ω = ϕ̇ Winkelgeschwindigkeit
ω̇ = ϕ̈ Winkelbeschleunigung
Drehmoment
M
= r × p Drehimpuls
L
Θ Trägheitsmoment
Erot = 12 Θω 2 Rotationsenergie
P = M ω Leistung
2.2. Rotierende Körper
2.2.8. Bewegungsgleichungen des starren Körpers
Ein freier Körper hat 6 Freiheitsgrade. Um die Bewegung vollständig zu beschreiben braucht man
also 6 Gleichungen. Diese werden von den Vektorgleichungen
F = ma = p˙
und
= Θω
˙
M
˙ = L
geliefert.
Ein weiteres Hilfsmittel stellt die Energie dar. Die Rotations- und Translationsbewegung beeinflussen
sich ohne weitere Bedingungen (z.B. Rollen) nicht untereinander.
Nutation und Präzession
Abschneiden des Fadens → mas = FG ??
˙ = M
(für jede Komponente!) muss für das Gesamtsystem gelten. Dies lässt sich
Nein. Denn auch L
auch aus Newtonschen Gleichungen herleiten. Sei P der Nullpunkt des Systems, dann gilt
= r × F
M
• Dreifingerregel für das Kreuzprodukt
⊥L
ist |L|
= const. Der Richtung von M
entspräche eine Kippbewegung nach unten.
• Da M
˙ = d L
ein neues Drehmoment hervor, das
• Die Änderung des Drehimpulses ruft jetzt nach M
dt
zu einer Drehung um die Aufhängung führt.
auch die Richtung von M
.
• Außerdem ändert sich mit der Richtung von L
21
2. Beschleunigte Bezugssysteme, starrer Körper und Himmelsmechanik
Die Rotation um die Aufhängung erfolgt mit:
ωp ≈
dϕ
rmg
M
M
=
=
=
dt
L
ΘωF
ΘωF
Die Bewegung bezeichnet man als Präzession.
Nutation
(z.B. durch einen Schlag) läuft die Drehachse von ω
Bei einer Trennung von ω
und L
um die konstante
˙ Drehimpulsachse (L = 0).
2.3. Himmelsmechanik
2.3.1. Gravitationsgesetz
m1 m2 r12
= −F21
FG = −G 2
r12 r12
→
g=G
ME
2
RE
→ Messung durch die Gravitationsdrehwaage.
Da die Erde keine genaue Kugel, sondern am Äquator breiter ist, entsteht ein Drehmoment auf die
Erde, das zu einer Präzession führt T = ω2πp ≈ 25800a.
h
Für kleine Abstände ist E = mgh = 0 mgdz, mit mg als vom Abstand unabhängige Kraft.
Für große Abstände ist F ∝
Epot =
∞
1
r2
also
∞
F · dr =
p
p
∞
ME m
1
ME m
−G 2 dr = GME m
=0−G
r
r p
p
Fluchtgeschwindigkeit (für ein nicht angetriebenes Objekt)
Epot (∞) + Ekin (∞) = Ekin,0 + Epot,0
0
0
1
2
mvF
2
−G
ME m
RE
2GME m
= 2gRE ≈ 11, 2 · 103
RE
s
Für einen Satelliten auf einer Kreisbahn gilt Fzentrif ugal = FG . Bei RE gilt:
⇒
vF =
azentrif ugal = g =
22
v2
RE
⇒
v=
km
gRE ≈ 8
s
2.3. Himmelsmechanik
2.3.2. Die Keplerschen Gesetze
1. Planetenbahnen sind Ellipsen mit der Sonne in einem Brennpunkt
a, b Halbachsen
√
ε = a1 a2 − b2 Exzentrizität
ε für Planeten ist sehr klein → fast Kreisbahnen
Für unterschiedliche Werte für ε erhalten wir folgende Fälle:
• ε < 1 Ellipsen (z.B. wiederkehrende Kometen)
• ε = 1 Parabel
• ε > 1 Hyperbel
2. Der Fahrstrahl eines Planeten überstreicht in gleichen Zeiten gleiche Flächen
dA
1 =
|L| = const
dt
2Mpl
Dies folgt aus der Drehimpulserhaltung
3. Die Quadrate der Umlaufzeiten verhalten sich wie die dritte Potenz der großen Halbachsen a,
d.h.
T2
= const
a3
Für kreisförmige Bahnen erhalten wir mit FG = FZentrif ugal :
4π 2
Gmpl Msonne
=
m
R
pl
R2
T2
(= mpl ω 2 R)
⇒
T2
4π 2
=
= const
R3
GMSonne
23