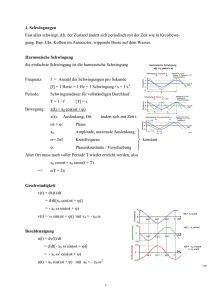
1. Schwingungen

1. Schwingungen
Physik 1 für
Maschinenbau
Seite 1
WS 05/06
Inhaltsverzeichnis
Einführung / Kinematik und Dynamik
1. Schwingungen
1. Freie Schwingung
2. Einschub: Rotation / Starrer Körper
3. Gedämpfte Schwingung
4. Erzwungene Schwingung
5. Gekoppelte Schwingungen
2. Wellen
3. Schallwellen / Akustik
4. Atomphysik
5. Kernphysik
Seite 2
Kap. 1 Schwingungen
Technische Anwendungen /
Erfahrungen
Aber auch:
• KFZ (od. MTB): Federung (mit /
ohne Dämpfung)
• Elektrischer Schwingkreis
• Vibrationen des Motors
• Motorblock auf
Schwingungsdämpfern
• Unwucht
• Regelsystem: Thermostat
• Elektromagnetische Wellen: Licht
etc.
• Energieniveaus in Atomen und
Molekülen
• Schlingerndes Schiff
• Beschreibung von
Elementarteilchen
• Uhren: Pendel, Unruhe,
Schwingquarz
• String-Theorie
• Populationen Jäger / Opfer
• Akustik: Musik, Stimmgabel, Saite,
• Wachstum von Bakterien
Luftsäule
(Nahrungsangebot / prod. Gifte)
• Erdbeben (Wellen)
• Oszillierende chemische
Reaktionen
Seite 3
1.1 Merkmale einer Schwingung
Trägheit und Rückstellkraft
Rückstellkraft Fr(t) = mg cos
Wpot, max
Wkin, max
W pot (t )  m  g  h(t )

v
mg
Die periodische Zustandsänderung
(Energieverschiebung) eines
schwingungsfähigen Elementes (Oszillators)
nennt man Schwingung; die periodische
Zustandsänderung einer Vielzahl
schwingungsfähiger Elemente nennt man Welle.
h
m
I
2
Wkin (t )  v(t )   (t ) 2
2
2
T bezeichnet die
Schwingungsdauer und
f die Anzahl der Zyklen
pro Zeiteinheit
Es gilt :
Ein träger Körper der sich an einem Minimum der
Potentiellen Energie (Ruhelage) befindet kann
durch Auslenkung aus der Ruhelage in
Schwingungen versetzt werden.
f 1 T
Seite 4
1.1 Merkmale einer freien ungedämpften
Schwingung:
h
Rückstellkraft Fr(t) = mg cos
Wpot, max
Wkin, max
W pot (t )  m  g  h(t )

v
mg
h
s
m
J
2
Wkin (t )  v (t )   (t ) 2
2
2
- Wird der Schwingung keine Energie von außen zugeführt, nennt man sie eine freie Schwingung.
- Wird der Schwingung keine Energie z.B. in Form von Reibungsenergie entzogen, nennt man
sie ungedämpfte Schwingung.
Für eine freie ungedämpfte Schwingung gilt:
W  W pot (t )  Wkin (t )  konst.
Ferner gilt:
s (t )  s (t  T )
bzw.:
h(t )  h(t  T )
Seite 5
1.1 Ungedämpftes freies Feder-MasseSystem
Kraft F
[N]
Weg s
[m]
linear
F
s

F
N 
: D    Federkonstante
s
m
degressiv
Druckfeder
Zugfeder
s
progressiv
Für eine lineare Feder gilt:
F  D  s
Ein lineares Feder-Masse-System nennt man Harmonischen Oszillator.
Aufgaben 4 bis 8
Nr. 4: Schwingende Platte
Nr. 6: Gleitkurbelgetriebe
Nr. 10: Drei Federn
Nr. 11: Anfangsbedingungen
Nr. 12: U-Rohr
Nr. 21: Standuhr
(Physikalisches Pendel)
Seite 6
1.1 Ungedämpftes freies Feder-MasseSystem
F   D  s  mg
Für die Ruhelage s0 gilt:
0
 D  s0  mg  0
oder:
mg  D  s0
F   D  s  D  s0   D  ( s  s0 )   D  s
s0
s
0
s
s
Neue Koordinaten: s00, ss
F  D  s
Schwingung ist unabhängig von konstanter äußerer Kraft, z. B.
Gewichtskraft, konstante Beschleunigung
Seite 7
1.1 Ungedämpfter freier harmonischer
Oszillator
Newtonsche Bewegungsgleichung:
Lineare Feder:
folgt:
oder:
d 2s
Fa  m  a  m  2  m  s
dt
Fa   D  s
m  s   Ds
D
s   s  0
m
Schwingungsgleichung des ungedämpften freien harmonischen Oszillators.
(lineare homogene Differentialgleichung)
Nr. 4: Schwingende Platte
Nr. 6: Gleitkurbelgetriebe
Nr. 8: Tunnel durch die Erde
Nr. 10: Drei Federn
Nr. 8: Tunnel durch die Erde
Nr. 10: Drei2.MB
Federn
11, 11.11.05
12
A8
Seite 8
1.1 Lösung der Schwingungsgleichung
(des ungedämpften freien harmonischen Oszillators)
Lösungsansatz:
s (t )  sˆ cos( 0t   0 )
 s(t )   0 sˆ sin( 0t   0 )
und
ergibt:
s(t )   sˆ cos( 0t   0 )
2
0
0
2
D

m
bzw.:
Vergleich mit
2
0 
 2  f 
T0
D
s   s  0
m
D
m
ŝ ist die Amplitude (Maximalauslenkung) der Schwingung,
0 ist der Phasenwinkel der Schwingung;
sie ergeben sich aus zwei Anfangsbedingungen.
Seite 9
1.1 Alternative:
(Lösung der Schwingungsgleichung des ungedämpften freien
harmonischen Oszillators)
Lösungsansatz:
s(t )  A cos( 0t )  B sin( 0t )
A und B ergeben sich aus den
Anfangsbedingungen.
 s(t )   0  A sin( 0t )  B cos( 0t )
ergibt:
s(t ) 
02
0
D

m
2
A cos(0t )  B sin(0t )
bzw.:
Vergleich mit
2
0 
 2  f 
T0
s 
D
s  0
m
D
m
Seite 10
1.1 Analogie elektr. / mech. Schwingung
Trägheit und Rückstellkraft
Masse und Federkraft
Spule und Kondensator
Nr. 11: Anfangsbedingungen
Nr. 12: U-Rohr
Nr. 21: Standuhr
(physikalisches Pendel)
aus Hering et al.
Seite 11
r
r
Abb. aus Physik für Ingenieure, Hering, Martin Stroher, Springer Berlin, 2004
1.1 Analogie zur Kreisbewegung
Seite 12
1.1 Analogie zur Kreisbewegung 2
sin  
 3
1!

cos   1 

e  1

1!

3!
2
2!


2
2!
5
 ...
5!
4
4!

 ...
3
3!

4
4!
 ei  cos   i sin 
 ...
i   1  i 2  1
Seite 13
dW pot
W pot
W pot
1.1 Die potentielle Energie eines
harmonischen Oszillators
 
  F  ds 
s s
s  s
s 0
s  0


   F ( s)  ds 
 Dsds
s
1 2
1
2
  Ds   Ds
2
0 2
0
s
Seite 14
Aufgabe #10: Gekoppelte Federn
A) Parallele Federn:
B) Federn in Serie:
s ges  s1  s2

F
Fges  F1  F2   D1s  D2 s
F
F

D1 D2
 1
1 
 F
 

D2 
1
D

1

Dges
 D1  D2 s


 Dges
 Dges  D1  D2
oder allgemein:
Dges   Di
i

D2
F
 1
1
1 

 

Dges  D1 D2 
oder allgemein:
1
1

Dges
i Di
Seite 15
Aufgabe #10: Gekoppelte Federn
1
1
1


Dges D1  D2 D3
 Dges 
D1  D2 D3
D1  D2  D3
Seite 16
Inhaltsverzeichnis
Einführung / Kinematik und Dynamik
1. Schwingungen
1. Freie Schwingung
2. Einschub: Rotation / Starrer Körper
3. Gedämpfte Schwingung
4. Erzwungene Schwingung
5. Gekoppelte Schwingungen
2. Wellen
3. Schallwellen / Akustik
4. Atomphysik
5. Kernphysik
Seite 17
Einschub: Kinematik der Drehbewegung starrer
Körper
 Gleichförmige Drehbewegung
0  const.
 ( t )  0  t   0
 Gleichmäßig beschleunigte Drehbewegung
  const.

d
 ( t )   0  0 t  t ;  ( t ) 
 0    t
2
dt
2
 Winkelgeschwindigkeit und –beschleunigung als Vektoren
  
v r
 

at    r
 beschreibt Änderung des
Betrags der Geschwindigkeit
Man beachte die Rechte Hand Regel!
Seite 18
Einschub: Kinematik der Drehbewegung
 Normal-Anteil der Beschleunigung
    

a n    v      r 
 beschreibt Änderung der
Richtung der Geschwindigkeit
 Gesamter Vektor der Beschleunigung
    
  
a  at  a n    r      r 

dv n
 Spezialfall: Kreisbewegung,
Winkelg. senkrecht zu Radius


r

2 
a n    r
y

v (t )

at (t )

r (t )
 (t )

an (t )
x
Seite 19
Einschub: Dynamik der Drehbewegung;
Drehmoment
 Drehmoment (= Radiusvektor x Kraftvektor)
  
M  r  F Einheit Nm

F

M

r
0; Drehpunkt
 Betrag des Drehmoments

 
 
 
M  r F sin r , F  r F sin   rF sin 
 
Rechte Winkel
Seite 20
Einschub 2: Vektoren
 a1 
  
a   a2 
a 
 3
Z.B.:
,
 b1 
  
b   b2 
b 
 3
,
 c1 
  
c   c2 
c 
 3
,…
 s1 
  
s   s2 
s 
 3
 s1   s1 t 

    
v  s   s2    s2 t 
 s   s t 
 3  3 
2
2
 s1    s1 t 

      2
2
a  v  s   s2     s2 t 
 s    2 s t 2 
 3  3

Seite 21
Einschub 2: Rechnen mit Vektoren
Summe:
 a1  b1 




a  b   a2  b2 
a b 
 3 3
Skalarprodukt:
Beispiel:
 
a b

a

b
Multiplikation
mit einem Skalar:

a a
   a1 

 
  a     a2 
  a 
3

 a1   b1 
     
 
 
a  b   a2    b2   a1b1  a2b2  a3b3  a b cos a , b


 a  b 
a b
 3  3
 
Ekin 


1 2 1
1 2
mv  m v12  v22  v32  m v
2
2
2

a
Seite 22
Einschub 2: Rechnen mit Vektoren
Vektorprodukt:
(kart. Koordinaten)
 a1   b1   a2b3  a3b2 

      
a  b   a2    b2    a3b1  a1b3 
 a  b   a b  a b 
 3  3  1 2 2 1

b
 
a b

a
 
   
a  b  a  b sin a , b
 
Spatprodukt:
(Vol. Spat)
 a1   b1   c1  a1


      
a  b  c   a2    b2    c2   b1
a  b  c  c
1
 3  3  3
   i , j ,k ai b j ck
i , j ,k
a2
b2
a3
b3
c2
c3
 
a b

c

b

a
Seite 23
Einschub 2: Rechenregeln
Es gilt:
   
a b  b a
Es gilt:
      
a  b  c  a b  a c


aber:
 
 
a  b  b  a
und:
      
a  b  c  a b  a c


Seite 24
Einschub: Massenschwerpunkt
 Schwerpunkt wird definiert zu:


1
1
1
s s   m i si   r  dm   r    dV
m i
m
m
aus Demtröder
Seite 25
Einschub: Kinetische Gesamtenergie
 Es gibt 6 Freiheitsgrade der Bewegung für Starren Körper:
Jeweils 3 für Translation und Rotation
 Separation der Bewegung in Translation und Rotation des
Schwerpunkts:
– Jede Bewegung eines starren Körpers lässt sich eine
Rotationsbewegung um den Schwerpunkt und eine
Translationsbewegung des Schwerpunkts zerlegen
 Gesamte Kinetische Energie des Starren Körpers
E Kin  ETranslation  E Rotation
1
2
ETranslation  mv s
2
1
1
2
2
2
E Rotation   mi ri  s  J   s
2 i
2
Seite 26
Einschub: Dynamik der Drehbewegung
 Massenträgheitsmoment (analog zu Masse)
I    r 2  dV speziell I   r 2  dm
 Spezialfall: Kreisbewegung mit
Radius r einer Masse m
I  m  r2
aus Demtröder
 Steiner‘scher Satz: Drehung um Achse
parallel zu einer Hauptträgheitsachse
(=Drehachse durch den Schwerpunkt),
Drehachse ist s von
Hauptträgheitsachse entfernt
I A  I S  ms
aus Dobrinski
2
Seite 27
Einschub: Einige Trägheitsmomente
aus Hering
Seite 28
Einschub: Einige Trägheitsmomente
aus Hering
Seite 29
Einschub: Dynamik der Drehbewegung starrer
Körper, Grundlegende Erfahrungen

Es gibt 3 Hauptträgheitsachsen
aus Dobrinski
1. Achse mit minimalem Trägheitsmoment
2. Achse mit maximalem Tragheitsmoment
3. Achse senkrecht zu 1. und 2.
 Kräftefreie Rotation
– Rotationsachsen gehen durch den Schwerpunkt
– Stabile Rotation bildet sich aus bei Drehung um Achse
mit minimalem und mit maximalem Trägheitsmoment.
Beispiel: Rotierender Quader
– Es treten keine Lagerkräfte auf  Auswuchten von
Drehachsen, um Lagerkräfte zu vermeiden
Seite 30
Einschub: Dynamik der Drehbewegung
 2. Newton‘sches Axiom für Drehbewegungen



M  J    J   [Nm]
– entspricht F = ma bei Translation
 Drehimpuls




L  J  ; dL  M  dt [Nms]
– entspricht p = mv bzw. dp = Fdt bei Translation
 Energie bzw. Leistung
rot
E kin


2
 J   [Nm  J]; P  M   [J/s  W]
– entspricht E = ½ mv2 bzw. P = Fv bei Translation
Seite 31
1.1 Freie Schwingung: Das Fadenpendel
 Rückstellkraft:

FR   mg sin 
3
5




  mg   

 ...    mg  


3! 5!


l
 Newton:
d 2s
d 2 (l )
d 2 ( )
Fa  m  a  m  2  m 
 ml
 m  l  
2
2
dt
dt
dt



mg
oder
Lösung:
 mg  sin   m  l   nichtlineare DGL
 mg    m  l  
 
g
  0
l
 (t )  ˆ cos(0t   0 )
mit
0 
g
l
Seite 32
1.1 Das Fadenpendel über Momente
 Rückstellmoment
M R  l  FG  sin   lmg sin 

 

M R  l  FG
3
5





  mg  

 ...    mg  


3! 5!


l


 Newton: M T  J   Trägheitsmoment
M T  m  l 2  



mg
oder
Lösung:
 lmg  sin   m  l 2   nichtlineare DGL
 mg    m  l  
 
g
  0
l
 (t )  ˆ cos(0t   0 )
mit
0 
g
l
Seite 33
1.1 Freie Schwingung: Das Torsionspendel
 Für das Rückstellmoment
des Drahtes gelte:
~
M   D

 Newton bei Rotationsbewegungen:
M   I A   I A  

Lösung:
~
I A   D

 (t )  ˆ cos(0t   0 )
~
D
    0
IA
mit
0 
~
D
IA
Seite 34
1.1 Freie Schwingung: Das physikalische Pendel
 Rückstellmoment: Kraft greift im Schwerpunkt an


3 5
M R  mgs sin   mgs  

 ...   mgs  
3! 5!


mit:
   

M  s  F  s  mg
bzw.:

M  M  s  mg  sin 
 Newton:
M   I A

 
Lösung:
mgs
  0
IA
s
 (t )  ˆ cos(0t   0 )
mit

Nr. 28: Mathematisches Pendel im Aufzug
Nr. 29: Schaukelpferd
Nr. 32.: Gedämpftes Schwingungssystem I
Nr. 33: Gedämpftes Schwingungssystem II
Nr. 34: Gedämpftes Schwingungssystem III
mgs
IA

mg

Seite 35
Inhaltsverzeichnis
Einführung / Kinematik und Dynamik
1. Schwingungen
1. Freie Schwingung
2. Einschub: Rotation / Starrer Körper
3. Gedämpfte Schwingung
4. Erzwungene Schwingung
5. Gekoppelte Schwingungen
2. Wellen
3. Schallwellen / Akustik
4. Atomphysik
5. Kernphysik
Seite 36
1.2 Gedämpfte Schwingung: Reibung
Wichtige Beispiele:
1. Coulomb-Reibung, (z.B. Gleit- und Rollreibung)
Geschwindigkeitsunabhängig:
FR= - µ FN
2. Schmiermittelreibung
Proportional zur Wurzel der Geschwindigkeit:
FR= - cv1/2
3. Stokes-Reibung oder Viskose Reibung z.B. in Flüssigkeiten
Proportional zur Geschwindigkeit:
FR= - r v
4. Newton-Reibung, z.B. Luftwiderstand
Proportional zum Quadrat der Geschwindigkeit:
FR= - cv2
Seite 37
1.2 Schwingung mit konstanter Reibung
(Coulomb-Reibung)
FR   FN
mit
gilt:

FN
m
D
s0
m
D ~
~

s  s  0
m
Ersetzten von
Ergibt:

ms   Ds  FN
~
s
und
oder
F
D
s  N  0
m
m
(inhom. lin. DGL)
s  s0  ~
s
(hom. lin. DGL)
durch
s 
Lösung
~
s (t )  ~
sˆ cos(0t   0 )
s  s0
s (t )  ( sˆ  s0 ) cos(0t   0 )  s0
mit
0 
D
m
Seite 38
1.2 Schwingungsverlauf
y(B)=y(A)-2s0
-s0
+s0
y(C)=y(B)-2s0
+s0
 Jede
Halbschwingung
findet um s0
verschobene xAchse statt
 AB: Amplitude
nimmt um 2s0 ab
 BC: Amplitude
nimmt um
weitere 2s0 ab
 Amplituden werden pro Schwingung um 4s0 kleiner 
Arithmetische Reihe  Einhüllende ist Gerade
 Schwingung kommt irgendwann zur Ruhe, muss nicht im
Nullpunkt sein
 z. B. Statistisch schwankender Einstellfehler bei
Zeigerinstrumenten
Seite 39
1.2 Schwingung mit viskoser Reibung
(Stokes-Reibung)
FR  rv  rs
Reibungskraft mit Dämpfungskonstante r proportional zur
Geschwindigkeit
 ms  rs  D  s
bzw.
s 
r
D
s   s  0
m
m
komplexer Lösungsansatz:
also z 
z (t )  zˆe
t
r
D
z   z  0 mit Rez t   s t 
m
m
r
D

 2     e t  0
m
m

r
D
 2     0
m
m
Eigenwertgleichung für den Eigenwert 
Lösung der Eigenwertgleichung:
1, 2
r
r2
D



2m
4m 2 m
1. Fall
r  2 mD
(schwache Dämpfung, Radikant < 0)
2. Fall
r  2 mD
(mittlere Dämpfung, Radikant = 0)
3. Fall
r  2 mD
(starke Dämpfung, Radikant > 0)
Seite 40
1. Fall: Schwache Dämpfung, Periodischer Fall r  2 mD
1, 2
r
r2
D



2
2m
4m
m
mit
r

2m
und
D r2

 2  02   2
m 4m
1, 2    i 02   2    i
 z (t )  zˆe (  i )t  zˆ ei0 e t e it  zˆ e t ei t 0 
Für den Realteil von s(t), der den physikalischen Schwingungsvorgang beschreibt gilt:
s(t )  sˆe t cost   0 
~ e t
Schwingfall
 Kreisfrequenz  ist kleiner
als im ungedämpften Fall
 e t ist Einhüllende
cost   0 
Seite 41
2. Fall: Aperiodischer Grenzfall
1, 2
r
r2
D



2m
4m 2 m
mit
r

2m
und
D
r2

0
2
m 4m
o  
r  2 mD
1, 2  
 s1 (t )  C1e t
eine weitere Lösung ist:
s2 (t )  C2te t
 s (t )  C1  C2t e t

Aperiodischer Grenzfall

Amplitude wird 0 bei T0: Es tritt
gerade keine Schwingung auf
z.B. Analoge Zeigerinstrumente
Anzeigenwert soll möglichst
schnell erreicht werden, ohne
dass der Zeiger zu schwingen
beginnt

T0
Seite 42
3. Fall: Starke Dämpfung, Kriechfall r  2 mD
1, 2
r
r2
D



2m
4m 2 m
r
mit  
2m
und

r2
4m 2

D
  2  02
m


   2 02 t
   2 02 t


  t
  t
 s (t )  C1e
 C2 e
 C1e
 C2 e
 Kriechfall
 Es tritt keine Schwingung
mehr auf; Amplitude wird
0 bei t > T0
 Wie in 1. und 2. auch
werden C1 und C2 über
die Anfangsbedingungen
x(0) und v(0) bestimmt
T0
Seite 43
Dämpfung bei verschiedenen
Arten der Reibung:
FR  v
n
Coulomb-Reibung
Schmiermittelreibung
Stokes-Reibung
(viskose Reibung)
Newton-Reibung
Seite 44
Wichtige Kenngrößen bei gedämpften
Schwingungen
FR  rv  rs
Die Dämpfungskonstante r ist ein Maß für die Dämpfung in frei schwingenden,
abklingenden Schwingungssystemen.
r hat die Einheit [kg/s]
Logarithmisches Dekrement:
  ln
sn
  T
sn 1
Das logarithmische Dekrement ist ein Maß für das Dämpfungsverhalten in frei
schwingenden, abklingenden Schwingungssystemen.
Das Formelzeichen ist Λ (großes Lambda).
Es errechnet sich aus dem natürlichen Logarithmus des Verhältnisses der Amplitude
zweier aufeinander folgender Ausschläge in die gleiche Richtung.
Λ ist ohne Einheiten
Seite 45
Wichtige Kenngrößen bei gedämpften
Schwingungen
Dämpfungsgrad/-maß:

m




D
0
4 2  2
Das Dämpfungsmaß (auch Dämpfungsgrad oder Lehrsches Dämpfungsmaß) ist eine Größe
für die Dämpfung einer Schwingung.  ist dimensionslos ohne Einheiten
Das Formelzeichen ist ein .
 = Abklingkonstante  / Eigenkreisfrequenz
Der doppelte Wert wird Verlustfaktor d genannt. Sein Kehrwert ist die Güte Q = 1/d
Gütefaktor:
Q
2  Energie
E 




Energieverlust / Periode  E 2
Dm
r
Seite 46
Aufgabe zu Gedämpfte Schwingung
r
Das Fahrzeug wird nun mit 240 kg beladen. Welche Eigenfrequenz
besitzt ein Vorderachsen-Federbein jetzt?
Seite 47
Aufgabe 34 zu Gedämpfte Schwingung
Seite 48
Inhaltsverzeichnis
Einführung / Kinematik und Dynamik
1. Schwingungen
1. Freie Schwingung
2. Einschub: Rotation / Starrer Körper
3. Gedämpfte Schwingung
4. Erzwungene Schwingung (Resonanz)
5. Gekoppelte Schwingungen
2. Wellen
3. Schallwellen / Akustik
4. Atomphysik
5. Kernphysik
Seite 49
Java Applet zu Erzwungenen Schwingungen
http://www.walter-fendt.de/ph14d/resonanz.htm
Seite 50
1.3 Erzwungene harmonische Schwingungen
(EHS) mit viskoser Reibung
FE  FˆE cosE t 
 Anregung eines Oszillators mit
externer Kraft:
 Bewegungsgleichung:
ms  rs  D  s  FˆE cosE t 
Trägheitskraft
Reibungskraft
Rückstellkraft
 Zur Erinnerung: Ohne externe Kraft: Gedämpfte harmonische
Schwingung mit
D r2

 2  02   2
m 4m
Seite 51
1.3 EHS (mit viskoser Reibung)
 Mit externer Kraft: Nach Einschwingzeit folgt das System
der äußeren Anregung mit der Frequenz E : System = E
 Die Amplitude dieser Schwingung mit System hängt dabei
stark von der relativen Lage  und E ab.
 Außerdem folgt die Auslenkung s der externen Kraft mit
einer gewissen Verzögerung. Es ergibt sich also eine
Phasenverschiebung  zwischen FE und s.
s  sˆ cosE t   
Seite 52
1.3 EHS (mit viskoser Reibung)
Für die stationäre Lösung (nach dem Einschwingvorgang) bedeutet das:
 mE2 sˆ cosE t     rE sˆ sinE t     Dsˆ cosE t     FˆE cosE t 
Für sehr kleine Frequenzen
(E  D m
und
E  D r )
bedeutet das:
Das System wird von der Rückstellkraft dominiert. Trägheits- und Reibungskräfte spielen
Fˆ
s  cosE t ,
D
kaum eine Rolle. Es gilt:
Für sehr große Frequenzen
(E  D m
(  0)
und
E  D r )
bedeutet das:
Das System wird von der Trägheitskraft dominiert. Rückstell- und Reibungskräfte spielen
kaum eine Rolle. Es gilt:
s
Fˆ
m
2
cosE t ,
d.h.
(   )
In beiden Fällen sind externe Kraft und Geschwindigkeit um /2 versetzt. Wegen P=FEv
nimmt das System während eines vollständigen Schwingungsdurchgangs also insgesamt
keine Energie auf.
Seite 53
1.3 EHS (mit viskoser Reibung): Resonanz (v =
maximal)
Mit wachsender Phasenverschiebung wird bei -/2 ein Wert erreicht, bei dem
externe Kraft und Geschwindigkeit in Phase sind. Jetzt nimmt das System
ständig Energie auf. Würde die zugeführte Energie nicht durch Reibung verzehrt,
dann würde die Amplitude der Schwingung unendlich werden
(Resonanzkatastrophe). Die zugeführte Leistung muss also in Mittel gleich der
Leistung durch Reibungskraft sein. D.h.:
FE v  FR v
 sˆ 
Fˆ
rE
bzw.
,
FˆE cosE t   rE sˆ sinE t   

(   )
2
Der Vergleich mit der Bewegungsgleichung ergibt, dass in diesem Fall die äußere
Kraft genau durch die Reibungskraft kompensiert wird. Das bedeutet aber auch,
dass gelten muss:
E  D m  0
Anmerkung: Im Fall  = -/2 ist zwar die Energiezufuhr maximal, die maximale
Schwingungsamplitude wird jedoch schon bei einer etwas geringeren Phasenverschiebung
2
2
erreicht, da dann die Reibung etwas kleiner ist.   0  2
Seite 54
1.3 EHS (mit visk. Reib.) RESONANZ
aus Gerthsen
 bei   02  2 2
maximale Amplitude
 Bei  = 0 nur Kraft gegen
Feder
 bei 0 maximaler
Leistungeintrag
 Bei  =   Amplitude 0
 Endliche Amplitude
durch Dämpfung 
Vermeidung
Resonanzkatastrophe
 Phasenverschiebung bei
<<0 ist KLEIN
 Phasenverschiebung bei
0 ist 90°
 Phasenverschiebung bei
>>0 ist 180°
Seite 55
1.3 EHS (mit viskoser Reibung): Resonanz
k  r Reibungskonstante
r
 2 Dämpfungsgrad
mD
aus Gerthsen
Seite 56
1.3 EHS (mit viskoser Reibung)
Die Bewegungsgleichung ms  rs  D  s  FE
mit
FE  FˆE cosE t 
bzw.
s 
r
D
F
s   s  E
m
m
m
ist eine inhomogene lineare Differenzialgleichung.
Da FE keine Konstante ist, führt eine einfache Koordinatentransformation, wie bei der
Coulomb‘schen Reibung, hier nicht auf eine homogene lineare DGL!
Für inhomogen lineare DGLn gilt folgende Regel: Kennt man eine spezielle (auch
partikulär genannte) Lösung der inhomogenen Gleichung, so ist die allgemeine Lösung
der inhomogenen Gleichung die Summe aus dieser partikulären Lösung und der
allgemeinen Lösung der dazugehörigen homogene linearen DGL:
allgemein
partikülär


st inhomogen
 st allgemein

s
t
homogen
inhomogen
oder komplex:
allgemein
partikülär


zt inhomogen
 z t allgemein

z
t
homogen
inhomogen
Seite 57
1.3 EHS (mit viskoser Reibung)
Die Lösung der dazugehörigen homogenen linearen DGL ist die Lösung des
gedämpften Schwingung mit viskoser Reibung. Diese Lösung nimmt exponentiell mit
der Zeit ab und beschreibt den „Einschwingvorgang“. Danach (d.h. für t>>1/) wird die
allgemeine Lösung der inhomogenen Gleichung nur noch von der partikulären Lösung
bestimmt. D.h. die Masse folgt dann der externen Kraft
FE  FˆE eiEt
Damit muss auch z  zˆeiE t eine partikuläre Lösung der inhomogenen DGL sein.
mit
r
D
FˆE eiEt
z  z   z 
m
m
m
iE r D  FˆE

2
folgt zˆ    E 
 
m
m m

zˆ  sˆ 
m

02
FˆE
  2
2
 E2
E

2
oder
und
FˆE
zˆ      i 2E  
m
2
0
2
E
 2 E 
  E   arctan  2
2



 0
E

Seite 58
1.3 EHS: Aufgabe 39
Seite 59
1.3 EHS: Aufgabe 40
Seite 60
Inhaltsverzeichnis
Einführung / Kinematik und Dynamik
1. Schwingungen
1. Freie Schwingung
 Einschub: Rotation / Starrer Körper
2. Gedämpfte Schwingung
3. Erzwungene Schwingung (Resonanz)
4. Überlagerte Schwingungen
5. Gekoppelte Schwingungen
2. Wellen
3. Schallwellen / Akustik
4. Atomphysik
5. Kernphysik
Seite 61
1.4.Überlagerung von Schwingungen
1.4.1 Schwingungen gleicher Frequenz
s1  sˆ1 cost  1  und s2  sˆ2 cost  2 
 sneu  sˆneu cost  neu 
mithilfe Kosinussatzes
mit
sˆneu  sˆ12  sˆ22  2sˆ1sˆ2 cos1  2 
und
sˆ1 sin1  sˆ2 sin2
tan neu 
sˆ1 cos1  sˆ2 cos2
 Neue Schwingung hat gleiche Frequenz wie die ursprüngliche Schwingungen, gilt
auch für mehr als zwei Schwingungen
 Amplitude
- hängt von Phasendifferenz ab  Interferenz
- kann von sˆneu  sˆ1  sˆ2 (  0 für 1   2   ) bis zur vollen Summe
sˆneu  sˆ1  sˆ2 (für 1   2 ) gehen
Seite 62
1.4.Überlagerung von Schwingungen
1.4.2 Schwebungen (geringer Frequenzunterschied)
Überlagerung von zwei Schwingungen gleicher Amplitude und Phase:
s1  sˆ cos1t 
und
s2  sˆ cos2t 
mit
1  2 
       
cos

cos

2
cos


Mit dem Additionstheorem

 cos

2
2

 

   2   1  2 
s  2sˆ cos 1
t  cos
t
 2
  2

gilt:
  2
Die resultierende Schwingung hat also die Frequenz neu  1
2
Die Amplitude dieser Schwingung wird mit dem Term
D.h., dass die Amplitude mit der
Schwebungsfrequenz
   2
cos  1
2

S  1  2

t

moduliert.
zunimmt und abnimmt.
Seite 63
1.4.Überlagerung von Schwingungen
f1  1,0 Hz
f2 
Tneu 
1
f neu

10
Hz  0,9091 Hz
11
2
2

s  1,04761 s
f1  f 2 1,0  0,9091
Ts 
1
1
1


s  11,0011 s
f s f1  f 2 1,0  0,9091
Seite 64
1.4.Überlagerung von Schwingungen
1.4.3 Fourieranalyse:
Jede periodische Funktion lässt sich als
Überlagerung von Schwingungen mit
ganzzahligen Frequenzverhältnissen
darstellen.
Z.B.:
s1  sˆ sint 
1
s2  sˆ sin3t 
3
1
s3  sˆ sin5t 
5
1
1
 sgesamt  sˆ sin t   sˆ sin  3t   sˆ sin  5t 
3
5
Das Spektrum (Abb. c) zeigt aus welchen
Grundfrequenzen sich die resultierende
Gesamtschwingung (Abb. b) zusammensetzt.
Seite 65
1.4.Überlagerung von Schwingungen
1.4.4 Senkrechte Bewegungsrichtungen (Lissajous-Figuren):
Seite 66
Inhaltsverzeichnis
Einführung / Kinematik und Dynamik
1. Schwingungen
1. Freie Schwingung
 Einschub: Rotation / Starrer Körper
2. Gedämpfte Schwingung
3. Erzwungene Schwingung (Resonanz)
4. Überlagerte Schwingungen
5. Gekoppelte Schwingungen
2. Wellen
3. Schallwellen / Akustik
4. Atomphysik
5. Kernphysik
Seite 67
1.5 Gekoppelte Schwingungen

Bisher:
– 1.3 Erzwungene Schwingung: Oszillator mit Einwirkung von Kraft mit
unendlichem Energievorrat
– 1.4 Überlagerung von Schwingung: Zwei Oszillatoren ohne gegenseitige
Beeinflussung
– 1.5 Zwei Oszillatoren mit ähnlichem Energievorrat mit Kopplung DK


Kopplung ist relativ „schwache“ Feder mit Federkonstante DK
zwischen den Oszillatoren D1 und D2:
DK << D1, DK << D2
Energieaustausch zwischen Oszillator 1 und 2: Energie des
Oszillators 1 wird durch die Kopplung auf den Oszillator 2
übertragen (Anstoss eines Oszillators)
– Energieübertrag schneller je „stärker“ Kopplung
– Bei gleichen Oszillatoren: Vollständiger Energieübertrag
– Bei verschiedenen Oszillatoren: Energieübertrag kehrt sich bereits vor
vollständigem Austausch um

Zwei Zustände ohne Energieübertrag (gleichzeitiges Anstossen):
– Fundamentalschwingungen / Normalmoden
– Gleichphasige Schwingung:  = 0°
– Gegenphasige Schwingung:  = 180°
Seite 68
1.5 Gekoppelte Schwingungen:
Fundamentalschwingungen
Annahme: D1 = D2 = D,
DK = konstant
und m1 = m2 = m
a) Gleichphasige Schwingung: Kopplungsfeder
entspannt, gleichzeitiges Anstoßen
1  0 
D
m
bzw. f1  f 0 
1
2
D
m
aus Hering: D oder c Fenderkonstante
b) Gegenphasige Schwingung: Mitte der Kopplungsfeder bleibt konstant, gleichzeitiges
Anstoßen
2 
D  2Dk
m
bzw.
f2 
1
2
D  2 Dk
m
Seite 69
1.5 Gekoppelte Schwingungen Überlagerung
der Fundamentalschwinungen
c) Überlagerung von Fundamentalschwingung (Schwebung):
        2 
s1  sˆ cos 1 2 t  cos 1
t

 2
  2
 1  2   1  2 
ˆ
s2  s sin
t  sin
t
  2

 2
D.h.: Oszillator 1 ist um 90° zu Osz. 2 verschoben
S  2  1
und
neu 
bzw.
2  1
2
f S  f 2  f1
f  f2
bzw. f neu  1
2
aus Hering
k
Dk
D  Dk
bezeichnet den Kopplungsgrad
Seite 70
1.5 Gekoppelte Schwingungen: Kopplungsgrad
d) Kopplungsgrad:
Unterschied der Energie von Osz 1 und Osz 2 (W1 – W2) im Verhältnis zur Mittleren
Schwingungsenergie (W1 – W2)/2., Faktor ½ kann weggelassen werden
Dk
W1  W2
f12  f 22
k

 2
W1  W2
f1  f 22 D  Dk
Je stärker Kopplungsgrad, umso stärker ist die Aufspaltung f2 – f1
Lose Kopplung. k<<1:
Starke Kopplung: k~1:
Seite 71
Aufgaben
 Nr.1: Sinusverlauf bei Federpendeln
 Nr.2: Federpendel
 Nr. 4: Schwingende Platte
 Nr. 6: Gleitkurbelgetriebe
 Nr. 8: Tunnel durch die Erde
 Nr. 10: Drei Federn
 Nr. 11: Anfangsbedingungen
 Nr. 12: U-Rohr
 Nr. 17: Eiskunstläufer
Seite 72
Aufgaben
 Nr. 21: Standuhr (physikalisches Pendel)
 Nr. 28: Mathematisches Pendel im Aufzug
 Nr. 29: Schaukelpferd
 Nr. 32.: Gedämpftes Schwingungssystem I
 Nr. 33: Gedämpftes Schwingungssystem II
 Nr. 34: Gedämpftes Schwingungssystem III
 Weitere Aufgaben: Nr. 37,39,40,42,44,45,46,47,54,
 56,57,59-63,64,65-68,71,72,73,74,77,78,
 82,84,87,88,89,90,91,93,98,101
Seite 73