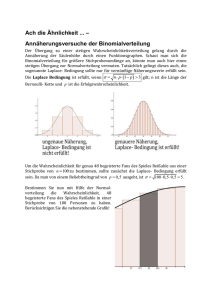
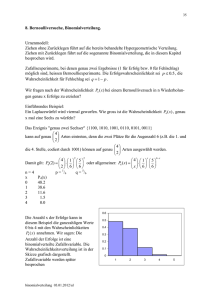
jede normalverteilung

Mathematik für MolekularbiologInnen
Vorlesung VIII
Wahrscheinlichkeitsrechnung und
Wahrscheinlichkeitsverteilungen
Übersicht
• Klassische Wahrscheinlichkeit & Kombinatorik
(La Place-Experimente, Bayes‘sche Wahrscheinlichkeit, Berechnung von
Wahrscheinlichkeit)
• Statistische Wahrscheinlichkeit &
Wahrscheinlichkeitsverteilungen
(Wahrscheinlichkeitsdichtefunktion, Binomialverteilung, Poisson-Verteilung,
Normalverteilung, (t-Verteilung))
Wahrscheinlichkeitsrechnung
• Die Wahrscheinlichkeitstheorie untersucht die möglichen Ergebnisse von
Zufallsexperimenten und sagt die Wahrscheinlichkeit von Ereignissen (E),
d.h. des Eintretens bestimmter Ergebnisse, voraus
• Laplace-Experimente sind solche mit endlicher Zahl von Elementarereignissen
von denen jedes gleich wahrscheinlich eintritt,
so der Wurf einer Münze mit E1 = Kopf und E2 = Zahl oder der Wurf eines
Würfels mit E1 = 1 Auge bis E6 = 6 Augen.
Die Gesamtheit aller Elementarereignisse definieren wir als den Ereignisraum
oder Ergebnismenge Ω mit der Wahrscheinlichkeit 1 (entspricht 100%).
Wahrscheinlichkeitstheorie
• Nach der klassischen Definition wird eine a-priori-Wahrscheinlichkeit P(A) von
Elementarereignissen vorausgesetzt, z.B. aufgrund externer Information
• Sicherheit gibt es in zwei Extremfällen: P(A) = 1, so tritt A mit Sicherheit ein. Ist
P(A) = 0, so tritt A mit Sicherheit nicht ein.
• Laplace Experiment: Wahrscheinlichkeit für das Eintreten des Ereignisses A wird
durch den Quotienten berechnet:
Zahl der günstigen Fälle
P( A ) 
Zahl der möglichen Fälle
• Beispiel: Ein fairer Würfel ist so ausbalanciert, dass jede seiner Seitenflächen beim
Werfen mit gleicher Wahrscheinlichkeit nach oben zu liegen kommt, nur die Zahlen 1-6
kommen vor, jedes dieser möglichen Resultate wird als Elementarereignis bezeichnet,
beim Würfeln gilt also:
Ω={1,2,3,4,5,6},
daher besitzen die 6 Elementarereignisse die gleiche a-priori-Wahrscheinlichkeit (p=1/6).
Für n Würfe ergeben sich 6n mögliche Elementarereignisse.
Wahrscheinlichkeitstheorie
Begriffe und Symbole aus der Mengenlehre:
A  B, A  B
A B
A\ B
A B
AɅB
...A vereinigt mit B, Schnittmenge von A und B
...A als Teilmenge von B
„ohne“, z.B. A\B…“A ohne B“ = Differenzmenge von A und B
Oder (lat. vel) „A oder B (oder beides)“; mindestens eine der
beiden beteiligten Aussagen ist wahr
„und“, logisches und, konjunkt; In der klassischen Logik ist die Konjunktion
zweier Aussagen genau dann wahr, wenn beide verknüpfte Aussagen wahr sind
Disjunktion (lat: disiunctum: getrennt): Zwei Mengen sind disjunkt wenn sie kein
gemeinsames Element besitzen, d.h. die Schnittmenge ist leer. Kennzeichnung mit Punkt.
Disjunkte Vereinigung von A = {1,2,3} und B = {4,5,6}.
Beide Mengen sind disjunkt; C ist die disjunkte Vereinigung der
Mengen A und B => C = {1,2,3,4,5,6}
ausschließende Disjunktion, „entweder – oder (aber nicht beides)“
Wahrscheinlichkeitstheorie
Vereinigung, Durchschnitt in der Mengenlehre
P( A oder B)  P( A  B)
* Wahrscheinlichkeit, dass entweder A oder B auftritt:
* Die Wahrscheinlichkeit, das A und B gleichzeitig
auftreten:
P( A und B)  P( A  B)
• Beispiel Würfel: A umfasst die Elementarereignisse bei denen der Würfel 1, 2 oder
3 zeigt und B jene mit 2,3,4; A {1,2,3} und B {2,3,4}
P( A oder B)  P( A  B)  1,2,3,4} 
4
6
* Wahrscheinlichkeit, daß A eintreten wird,
vorausgesetzt, daß B bereits eingetreten ist
P(A|B) (bezeichnet als a-posterioriWahrscheinlichkeit, Bayes‘sche Formelsiehe auch später);
P( A und B)  P( A  B)  2,3} 
2
6
P( A  B)
P( A | B) 
P( B)
P( A | B) 
P( A)  P( B | A)
P( A)  P( B | A)  P(nichtA )  P( B | nichtA )
Wahrscheinlichkeitstheorie
• Rechenregeln:
1) Die Wahrscheinlichkeitssummen aller sich gegenseitig ausschließender Ereignisse
müssen zu 1 addieren; dh PΩ= 1
z.B. Würfel: P(1)+P(2)+P(3)+P(4)+P(5)+P(6)=1
2) Für beliebige Ereignisse A und B gilt die allgemeine Additionsregel. P(A und B) muß
subtrahiert werden, da es sonst doppelt gezählt wird;
P(A oder B)= P(A) + P(B)-P(A∩B) bzw.
bei sich ausschließenden Ereignissen: P(A oder B)= P(A) + P(B)
• Beispiel Würfel: A umfasst die Elementarereignisse bei denen der Würfel 1, 2 oder
3 zeigt und B jene mit 2,3,4; A {1,2,3} und B {2,3,4}
P( A oder B)  P( A)  P( B)  P( A  B) 
3 3
3 3 2 4
  P( A  B)    
6 6
6 6 6 6
P( A und B)  P( A  B)  2,3} 
2
6
Wahrscheinlichkeitstheorie
• Rechenregeln:
3) Subtraktionsregel für komplementäre Wahrscheinlichkeit: P(A)=1 - P(nicht A).
z.B. fairer Würfel: P(1)= 1- P(2) - P(3) - P(4) - P(5) – P(6) =1 - 1/6 - 1/6 - 1/6 - 1/6 - 1/6 =
1/6;
P(A) = 1 - P(nicht A).
4) Sind zwei Ereignisse A und B voneinander unabhängig, gilt die spezielle
Multiplikationsregel. A und B sind unabhängig, wenn das Vorkommen von A
keinen Einfluss auf die Wahrscheinlichkeit hat, dass B eintreffen wird.
P(A und B)= P(A)*P(B)
z.B. fairer Würfel; 2 Würfe. Wie hoch ist die Wahrscheinlichkeit dass eine ‚1‘ und
eine ‚2‘ gewürfelt wird: P(‚1‘ und ‚2‘) = P(1)*P(2) = 1/6 * 1/6= 1/36
Wahrscheinlichkeitstheorie
Definitionen, Axiome und daraus abgeleitete Gesetze
• Axiome der Wahrscheinlichkeitstheorie (Kolmogorow, 1930)
 Jedes Ereignis hat als Wahrscheinlichkeit P eine reelle Zahl mit 0  P  1
 Das sichere Ereignis ist die vereinigte Ergebnismenge mit der
Wahrscheinlichkeit P (Ω) = 1
 Inkompatible Ereignisse sind exklusiv disjunkte Mengen (wenn z.B. E1  E2 ).
Die Wahrscheinlichkeit der Vereinigung inkompatibler Ereignisse ist die
Summe der Einzelwahrscheinlichkeiten: P( E1 
 E2 )  P( E1 )  P( E2 )
Elementarereignisse sind notwendigerweise inkompatibel, also exklusiv
• Für Laplace-Experimente mit n gleich wahrscheinlichen Elementarereignissen
h
gilt:
h
1 sowie für die Vereinigung
P
(
E
)

P
(
E
)

P( Ei ) 

h
i
von h der n Ereignisse:
n
n
i 1
Beispiel: Einmaliger Wurf eines Würfels
P (1 Auge) = 1/6
P (1 Auge oder 3 Augen) = 2/6
Wahrscheinlichkeitstheorie
Definitionen, Axiome und daraus abgeleitete Gesetze
• Die Verkettung, also das gleichzeitige Eintreten, zweier Ereignisse kann als
Schnittmenge zweier Ereignis-Teilmengen angesehen werden.
Die Verbund-Wahrscheinlichkeit ist das Produkt der Einzelwahrscheinlichkeiten:
P( E1  E2 )  P( E1 )  P( E2 | E1 )  P( E2 )  P( E1 | E2 )
bzw.
P( E1  E2 )  P( E1 )  P( E2 )
abhängige Ereignisse
unabhängige Ereignisse
Beispiel: Einmaliger Wurf zweier Würfel W
P (W1 = 1 Auge und W2 = 3 Augen) = 1/6 ∙ 1/6 = 1/36
• Die Verkettung inkompatibler Ereignisse hat die Wahrscheinlichkeit 0
Beispiel: Für den einmaligen Wurf eines Würfels ist P (1 Auge und 3 Augen) = 0
• Wahrscheinlichkeit für die Vereinigung kompatibler Ereignisse (mit Schnittmenge)
P( E1  E2 )  P( E1 )  P( E2 )  P( E1  E2 )
• Die exklusive Vereinigung kompatibler Ereignisse hat die Wahrscheinlichkeit:
.
P( E1  E2 )  P( E1 )  P( E2 )  2  P( E1  E2 )
Wahrscheinlichkeitstheorie
Bedingte Wahrscheinlichkeit in der Mengenlehre
*Wahrscheinlichkeit, daß A eintreten wird, vorausgesetzt, daß B bereits eingetreten ist
P(A|B) (bezeichnet als a-posteriori-Wahrscheinlichkeit, Bayes‘sche Formel);
falls A und B unabhängig sind (d.h. P(A|B)=P(A), erhalten wir die spezielle
Multiplikationsregel: P(A∩ B)=P(A)*P(B).
P( A  B)
P( A | B) 
P( B)
P( A)  P( B | A)
P( A | B) 
P( A)  P( B | A)  P(nichtA )  P( B | nichtA )
Wahrscheinlichkeitstheorie
Bayes‘sche Gesetz
P( A | B) 
P( A  B)
P( A)  P( B | A)

P( B)
P( A)  P( B | A)  P(nichtA )  P( B | nichtA )
Beispiel: Autoimmunthyreoiditis (eine Schilddrüsenerkrankung) hat 0,1% der männlichen
Bevölkerung befallen. In einem diagnostischen Test werden 99% der infizierten m. Personen
korrekt identifiziert (bei 1% fällt der Test negativ aus). Allerdings werden 2%
fälschlicherweise als infiziert diagnostiziert. Ein zufällig gewählter Einwohner erhält ein
positives Resultat. Wie hoch ist die Wahrscheinlichkeit, dass er tatsächlich infiziert ist?
Lösungsweg: A: Infektion, B: positiver Test; Wie hoch ist P(A|B)?
P(A)=0,001 …. Wahrscheinlichkeit der Infektion (kranksein);
P(B|A)=0,99 …Wahrscheinlichkeit eines positiven Tests bei Infektion
P(nichtA)=0,999; P(B|nichtA)=0,02
P( A | B) 

P( Krank und Positiv )

P( Krank und Positive )  P(Gesund und positiv )
0,001 0,99
0,00099

 0,0472
0,001 0,99  0,999  0,02 0,00099  0,01998
Antwort:
Die Wahrscheinlichkeit einer
Infektion bei einem positiven
Test beträgt ca. 5%!
Wahrscheinlichkeitstheorie
Beispiel I: Berechnung von Wahrscheinlichkeiten
Aufgabe: Vereinfachend soll die Evolution von Genen als Zufallsvorgang betrachtet
werden, so dass das Auftreten von DNA-Basen an einer bestimmten Sequenzposition
ein Elementarereignis darstellt. Außerdem behaupten wir, jede der n = 4 Basen sei
gleich wahrscheinlich. Berechnen Sie die Wahrscheinlichkeit, dass
(a) eine Sequenzposition Adenin (A) aufweist
Lösung: P (S1 = A) = 1/n = ¼ = 0,25
(b) eine Sequenzposition A oder Thymin (T) aufweist
Lösung: P (S1 = A  T) = P(A oder T)= P(A) + P(T)-P(A∩T) =
¼ + ¼ + 0 = ½ = 0,5
(c) eine Sequenzposition irgend eine der 4 Basen (B) aufweist
Lösung: (c)
P (S1 = B) = P (Ω) =P(A)+P(T)+P(G)+P(C) = 1
Wahrscheinlichkeitstheorie
Beispiel I: Berechnung von Wahrscheinlichkeiten
(d) eine Sequenzposition zugleich A und T aufweist
Lösung: Die Verkettung inkompatibler Ereignisse hat die Wahrscheinlichkeit 0
P (S1 = A  T) = 0
(e) zwei aufeinanderfolgende Positionen beide A aufweisen
Lösung: spezielle Multiplikationsregel, 2 Ereignisse sind voneinander unabhängig
P(A und B)= P(A)*P(B)
P (S1 = A  S2 = A) = ¼ ∙ ¼ = 1/16 = 0,0625
(f) von 2 aufeinanderfolgenden Positionen die eine oder die andere (o. beide) A aufweisen
Lösung:
1 1 1
7
P( S1  A  S2  A)  P( S1  A)  P( S 2  A)  P( S1  A  S 2  A) 
    0,4375
4 4 16 16
(g) von 2 aufeinanderfolgenden Positionen entweder die eine oder die andere A aufweist
Lösung:
 S 2  A)  P( S1  A)  P( S 2  A)  2  P( S1  A  S 2  A)
P( S1  A 

1 1 1 3
    0,375
4 4 8 8
Wahrscheinlichkeitstheorie
Kombinatorik
• Beim Errechnen von Wahrscheinlichkeiten komplexer Ereignisse ist eine
Aufzählung der Fälle oft schwer oder weitschweifig (oder auch beides). Um die
damit verknüpfte Arbeit zu erleichtern, benutzt man grundlegende Prinzipien,
die in einem Kombinatorik genannten Gebiet untersucht werden.
• Die Kombinatorik kennt verschiedene Typen von Anordnungen und
Auswahlmöglichkeiten von Objekten: Permutation, Kombination und Variation
Einschub: n Fakultät
• n Fakultät, geschrieben als n! ist definiert durch
n!= n(n-1)(n-2)….1
• Definition: 0!=1
z.B.
5! 5  4  3  2 1  120
Wahrscheinlichkeitstheorie
Kombinatorik
 Kombination: Möglichkeiten der Auswahl von unterscheidbaren Objekten
ohne Berücksichtigung der Reihenfolge d.h. {a,b} = {b,a}
unterschieden wird danach, ob Objekte mehrfach verwendet werden dürfen
– für die k-fache Auswahl von n Objekten mit Wiederholung von Objekten gilt
(Kombination mit Zurücklegen (Repetition)):
(n  k  1)!
C 
k! (n  1)!
k
n
Beispiel:
Die Buchstaben a, b, c (n = 3).
(3  2  1)! 4! 24
2
C


 6
Zwei werden ausgewählt (k = 2)
3
2! (3  1)!
möglich:
2! 2!
a,a ; a,b ; a,c ; b,b ; b,c ; c,c
– für die k-fache Auswahl von n Objekten ohne Wiederholung (Kombination ohne
Zurücklegen (also ein Anordnungsproblem) gilt:
Cnk 
n!
k! (n  k )!
Cn2 
n (n  1)
2
(Spezialfall k = 2)
Beispiel:
möglich:
C42 
a, b, c (n = 3) mit k = 2.
(Paarungen einer Vierergruppe)
a,b ; a,c; b,c ;
3!
3  2 1

3
2! (3  2)!
2
4
Wahrscheinlichkeitstheorie
Kombinatorik
 Variation: Möglichkeiten der Auswahl von unterscheidbaren Objekten
mit Berücksichtigung der Reihenfolge d.h. {a,b}  {b,a}
– für die k-fache Auswahl von n Objekten mit Wiederholung von Objekten, bzw. anders
betrachtet: die Variation von n Objekten auf k Positionen (vgl. Zahlenschloss), gilt:
Vnk  n k
Beispiel:
möglich:
a, b, c (n = 3). Zwei werden ausgewählt (k = 2)
a,a ; a,b ; a,c ; b,a ; b,b ; b,c ; c,a ; c,b ; c,c
V32  32  9
– für die k-fache Auswahl (auf einmal) von n Objekten ohne Wiederholung gilt:
Vnk 
n!
(n  k )!
Vn2  n (n  1)
(Spezialfall k = 2)
Beispiel:
möglich:
a, b, c (n = 3) mit k = 2
a,b ; a,c ; b,a ; b,c ;
c,a ; c,b
V32 
3!
6
1!
 Permutation: Möglichkeiten der Anordnung von unterscheidbaren Objekten
– für die Anordnung von n Objekten auf n Positionen (d.h. Mischen aller Objekte) gilt:
Pn  n !
Beispiel:
möglich:
a, b, c (n = 3).
a,b,c ; a,c,b ; b,a,c ; b,c,a ; c,a,b ; c,b,a
P3  3!  6
Anmerkung: Alle diese 6 Permutationen entsprechen einer einzigen Kombination
(ohne Wiederholung), da C33  1
Wahrscheinlichkeitstheorie
Beispiel II: Kombinatorische Bestimmung von Wahrscheinlichkeiten
• Aufgabe: Ausgehend von Beispiel I (DNA, 4 Basen), bestimmen sie alle Fälle kombinatorisch,
also dass
(a) S1 = A
(b) S1 = A oder S1 = T
(c) S1 = B (-*-)
(d) S1 = A und S1 = T
• Lösung: Wieviele Möglichkeiten gibt es prinzipiell?
(a) – (d) Von 4 Basen (n = 4) wählen wir eine (k = 1) für die erste/einzige Position aus –
Anordnung ohne Berücksichtigung der Reihenfolge.
Es kommt also die Betrachtung von Kombinationen oder Variationen in Frage.
Im Fall von k = 1 sind sowohl die Unterscheidung der Reihenfolge als auch die
Frage nach Wiederholungen gegenstandslos. Alle 4 Fälle (Kombination oder
Variation mit oder ohne Wiederholung) ergeben 4 Möglichkeiten, vgl. Formeln.
C41 
(n  k  1)! 4! 1 2  3  4
 
4
k! (n  1)! 3! 1 2  3
oder
V41  n k  41  4
• Die Wahrscheinlichkeit ist die Zahl erlaubter/betrachteter Möglichkeiten
geteilt durch die Zahl insgesamt vorhandener Möglichkeiten, also:
(a) -A- = 1 von 4 Möglichkeiten; P = 0,25
-A-C-G-T-
Wahrscheinlichkeitstheorie
Beispiel II: Kombinatorische Bestimmung von Wahrscheinlichkeiten
• Lösung b-d:
•Anzahl der Möglichkeiten (siehe vorige Folie) = 4
• Die Wahrscheinlichkeit ist die Zahl erlaubter/betrachteter Möglichkeiten
geteilt durch die Zahl insgesamt vorhandener Möglichkeiten, also:
(b) S1 = A oder S1 = T
d.h. -A- oder -T- = 2 von 4 Möglichkeiten; P = 0,5
(c) S1 = B (-*-); B eine Sequenzposition irgend eine der 4 Basen (B) aufweist
also -*- (A,C,G,T) = 4 von 4 Möglichkeiten; P = 1
-A-C-G-T-
(d) S1 = A und S1 = T ; eine Sequenzposition zugleich A und T aufweist,
also S1 = A und S1 = T
0 von 4 Möglichkeiten; P = 0 (A+T können nicht gleichzeitig eine Position einnehmen)
Wahrscheinlichkeitstheorie
Beispiel II: Kombinatorische Bestimmung von Wahrscheinlichkeiten
• Aufgabe: Ausgehend von Beispiel I, bestimmen sie alle Fälle kombinatorisch, also dass
(e) S1 = A und S2 = A (-A-A-)
(f) S1 = A und/oder S2 = A (-A-*- sowie -*-A-)
-A-A-A-C-A-G(e) – (g) Von 4 Basen (n = 4) wählen wir zwei (k = 2) für die beiden Position aus. -A-T-C-AEs kommt nur die Betrachtung von Variationen in Frage, weil z.B.
-C-Cdie Sequenz -A-T- eine andere ist als -T-A- . Wiederholungen von Basen sind
-C-Goffensichtlich erlaubt.
-C-T-G-AVnk  n k also hier: V42  42  16
-G-C• Die Wahrscheinlichkeit entspricht der Zahl erlaubter/betrachteter
-G-GMöglichkeiten geteilt durch die Zahl insg. vorhandener Möglichkeiten.
-G-T-T-AAbzählen ergibt:
-T-C(e) -A-A- = 1 von 16 Möglichkeiten ; P = 0,0625
-T-G(f) -A-*- oder -*-A- = 7 von 16 Möglichkeiten; P = 0,4375
-T-T(g) -A-*- oder -*-A- ohne -A-A- = 6 von 16 Möglichkeiten; P = 0,375
(g) entweder S1 = A oder S2 = A (-A-*- sowie -*-A-, ohne -A-A-)
Lösung: Variation: Möglichkeiten der Auswahl von unterscheidbaren Objekten
mit Berücksichtigung der Reihenfolge
Statistische Wahrscheinlichkeit
Die statistische Definition der Wahrscheinlichkeit
• Die Verknüpfung der Wahrscheinlichkeitstheorie (und der Kombinatorik) mit
der Statistik führt zur übergeordneten mathematischen Disziplin der Stochastik.
• Der Wahrscheinlichkeitsbegriff lässt sich statistisch definieren, indem die
a-priori-Wahrscheinlichkeiten für Ereignisse durch die Häufigkeiten des
Eintretens von Ergebnissen ersetzt werden.
• Wird in einem Zufallsexperiment eine Münze 100 mal geworfen, wäre ein
mögliches Ergebnis 43 mal Kopf und 57 mal Zahl (relativ 0,43 zu 0,57).
Strebt die Zahl der Würfe gegen unendlich, dann nähern sich die relativen
Häufigkeiten 50% an, was mit P (Kopf) = P (Zahl) = 0,5 interpretiert werden kann.
Somit ist die Wahrscheinlichkeit der Grenzwert der relativen Häufigkeit eines Ereignisses
für eine Grundgesamtheit, d.h. für unendlich große Zahl N von Beobachtungen.
P( Ei )  lim
N 
f i ( Ei )
f (E )
 lim iK i
N 
N
 fi
i 1
z.B. Münzwurf: K = 2
(E1 = Kopf; E2 = Zahl)
Statistische Wahrscheinlichkeit
Diskrete und stetige Wahrscheinlichkeitsverteilungen
• So wie die Wahrscheinlichkeit als Grenzwert der relativen Häufigkeit eines
Ereignisses angesehen werden kann, so stellt eine Wahrscheinlichkeitsverteilung
die theoretische („ideale“) Grenzform der relativen Häufigkeitsverteilung dar,
welche man für verschiedene Werte einer Zufallsvariable erhält
• Nimmt eine Zufallsvariable X diskrete Werte an, dann wird sie als diskrete
Zufallsgröße bezeichnet. Jeder Wert von X entspricht einem Ereignis mit einer
Wahrscheinlichkeit p (X). Es handelt sich bei p (X) um eine Funktion, die als
Wahrscheinlichkeitsfunktion (bzw. Häufigkeitsfunktion) bezeichnet wird.
• Wahrscheinlichkeitsverteilungen werden graphisch wie Häufigkeitsverteilungen
als Histogramme dargestellt. Handelt es sich um eine diskrete Zufallsgröße, so
werden korrekterweise Linien statt Balken gezeichnet, um die Punktualität der
X-Werte hervorzuheben
Statistische Wahrscheinlichkeit
Diskrete und stetige Wahrscheinlichkeitsverteilungen
• Beispiel: Der Wurf zweier Würfel ergibt Augensummen von 2 bis 12. Diese Summen sind
Ereignisse, also Werte der diskreten Zufallsvariablen X. Die Wahrscheinlichkeiten p (X)
sind Funktionswerte der Wahrscheinlichkeitsfunktion (Anwendung der
Multiplikationsregel) und ergeben sich aus den Variationsmöglichkeiten (Vnk = nk=62=36)
der beiden Augenzahlen.
X
2
3
4
5
6
7
8
9
10
11
12
p (X)
1/36
2/36
3/36
4/36
5/36
6/36
5/36
4/36
3/36
2/36
1/36
Wahrscheinlichkeitsverteilung
Häufigkeitsverteilung (N = 20)
• Im Falle einer sehr großen Zahl von Beobachtungen nähert sich die Häufigkeitsverteilung
den p(X)-Werten an, d.h. bei 9000 Würfen würde man 1000mal die Augensumme 5
erwarten, da p (5) = 4/36 = 1/9.
Statistische Wahrscheinlichkeit
Diskrete und stetige Wahrscheinlichkeitsverteilungen
• Im Falle stetiger Variablen verwendet man Balken-Histogramme mit Rechteckflächen oder die flächengleichen Häufigkeitspolygone, um die relative
Häufigkeit zu repräsentieren (vgl. VL 7).
• Im Grenzfall großer Zahlen erhält man die durch eine Kurve beschriebene
Wahrscheinlichkeitsfunktion p (X).
große N
Histogramm
Häufigkeitspolygon
Stichprobe
Kurve der
Wahrscheinlichkeitsfunktion
Grundgesamtheit
Statistische Wahrscheinlichkeit
Dichtefunktion und kumulative Verteilungsfunktion
• Der Grenzfall einer relativen Häufigkeitsverteilung (von stetigen Variablen) für
hinreichend kleine Klassenintervalle wird auch als Dichtefunktion bezeichnet.
Eine stetige Wahrscheinlichkeitsfunktion p (X) ist kann somit als eine
Wahrscheinlichkeitsdichtefunktion betrachtet werden.
• Die Flächen von Histogramm-Balken bzw. Flächen unter Häufigkeitspolygonen
geben die Häufigkeiten für bestimmte Intervalle der Variablen an.
Die Summation dieser (Teil-)Flächen entspricht also der Ermittlung
kumulativer Häufigkeiten, repräsentiert durch eine Summenkurve (vgl. VL 7).
• Wie im Folgenden gezeigt, ersetzt im Fall von Dichtefunktionen die Integration
den Vorgang der Summation, so dass man zur kumulativen Verteilungsfunktion
gelangt.
große N
Summen“kurve“
Kurve der kumulativen
Verteilungsfunktion
Statistische Wahrscheinlichkeit
Dichtefunktion und kumulative Verteilungsfunktion
• Im Fall stetiger Funktionen ist die Fläche unter dem Funktionsgraphen zwischen
zwei Grenzen durch ein bestimmtes Integral gegeben
• Bezogen auf Verteilungs-Dichtefunktionen im Allgemeinen und auf die
Wahrscheinlichkeitsfunktion p (X) im Speziellen bedeutet dies:
Der Anteil an der Gesamthäufigkeit für alle (Zufalls-)Variablenwerte X zwischen den
Grenzen a und b, d.h. die Wahrscheinlichkeit, dass X innerhalb dieses Intervalls liegt,
ist gegeben durch das bestimmte Integral

b
a
p ( X ) dx
welches der Bedingung genügt, dass



p( X ) dx  1
• Dieses Integral berechnet sich über die kumulative Verteilungsfunktion P (X).
P (X) ist die Stammfunktion von p (X), und es gilt:
P( X ) 

X

p( X ) dx
woraus folgt:

b
a
p( X ) dx  P(b)  P(a)
Statistische Wahrscheinlichkeit
Intervall-Wahrscheinlichkeit als Häufigkeitsanteil
• Allgemein ist die Wahrscheinlichkeit einer Zufallsgröße X, innerhalb bestimmter
Grenzen zu liegen, gleich dem bestimmten Integral der Wahrscheinlichkeitsfunktion p (X).
Die markierte Fläche gibt
die Wahrscheinlichkeit
dafür an, dass X im Intervall
zwischen a und b liegt
• Da die Wahrscheinlichkeitsfunktion der Grenzfall einer relativen Häufigkeitsverteilung ist, gibt die kumulative Häufigkeit einer Grundgesamtheit in Gestalt
von P (X) direkt die Intervall-Wahrscheinlichkeiten an
Die Wahrscheinlichkeit, dass eine
höchstens 50 Jahre alte Person aus
der Beispiel-Bevölkerung „gezogen“
wird beträgt ca. 73%, weil 73% der
Bevölkerung 50 alt oder jünger sind
X
Statistische Wahrscheinlichkeit
Median von Dichtefunktionen
• Der Median T teilt die Fläche einer Häufigkeitsverteilung in zwei gleich
große Hälften (vgl. VL 7). Übertragen auf eine Dichtefunktionen p (X) folgt:
T


p ( X ) dx  P(T )  0,5
Der Median T erfüllt die Bedingung, dass die Fläche links des Wertes X = T gerade 50% der
Gesamthäufigkeit ausmacht. Es ist der Wert X, an dem die kumulative Verteilungsfunktion
gerade den Funktionswert P (T) = 0,5 annimmt
Mittelwert von Dichtefunktionen
• Der Mittelwert μ einer Funktion p (X) wird berechnet :
 



X  p ( X ) dx
Wahrscheinlichkeitsverteilungen
a) Die Binomialverteilung
• Die Binomialverteilung ist eine Wahrscheinlichkeitsverteilung für eine
diskrete Zufallsvariable X (diskrete Daten), die für einen einzelnen
Versuch die binären Werte (Ergebnisse) 0 und 1 (Erfolg, Mißerfolg)
annehmen kann.
• Die Wahrscheinlichkeit für X = 1 („Erfolg“) z.B. Münze = Kopf; Kind =
Mädchen, beträgt p, die Wahrscheinlichkeit für X = 0 („Misserfolg“)
beträgt q = 1 – p (Gegenwahrscheinlichkeit)
• Die Binomialverteilung ergibt sich für ein Zufallsexperiment mit N
Versuchen („Würfen“) aus den Wahrscheinlichkeiten p (X), wobei X
nun die Zahl der Erfolge angibt und N – X die Zahl der Misserfolge.
• Ist N groß und weder p noch q nahe bei Null, kann die
Binomialverteilung durch eine Normalverteilung angenähert werden.
Wahrscheinlichkeitsverteilungen
a) Die Binomialverteilung
• Die Werte von p (X) berechnen sich dabei wie folgt aus den Kombinationen
von Erfolg und Misserfolg (Auswahl von X Erfolgen aus N Ereignissen):
p (X )  C  p q
X
N
X
NX
N!

p X qNX
X !( N  X )!
• Der Binomialkoeeffizient C X berechnet die Anzahl möglicher
N
Kombinationen, mit denen wir in N Versuchen X Erfolge haben.
Anmerkung: In der Literatur gibt es unterschiedliche Schreibweisen des Binomialkoeffizienten,
z.B. NCX,  n , beachten Sie also die jeweilige Schreibweise/Definition in Ihren Unterlagen.
k 
 
Wahrscheinlichkeitsverteilungen
Symmetrische Binomialverteilung
• Bei der symmetrischen (p = q = 0,5) Binomialverteilung hängen die
Wahrscheinlichkeiten nur von den Kombinationsmöglichkeiten ab und es
ergeben sich Verteilungen nach dem Pascal‘schen Dreieck
56
N = 1 : p(X) =
∙ 0,5
N = 2 : p(X) =
∙ 0,25
N = 3 : p(X) =
∙ 0,125
N = 4 : p(X) =
∙ 0,0625
N = 5 : p(X) =
∙ 0,03125
70
28
8
1
• Wie am Beispiel-Histogramm für N = 8 zu sehen, gleicht sich die Form der
symmetrischen Binomialverteilung für große N der Normalverteilung an.
Anmerkung: N ist hier nicht die Zahl der Beobachtungen, sondern die Zahl möglicher
diskreter Werte. Wenn also dieses N gegen unendlich konvergiert, wird die Verteilung
quasi-stetig. Stetige (Zufalls-)Variablen werden durch die Normalverteilung beschrieben.
Wahrscheinlichkeitsverteilungen
Symmetrische Binomialverteilung
N!
• Die Binomialverteilung ist symmetrisch,
p ( X )  CNX  p X  q N  X 
p X qNX
X !( N  X )!
wenn p = q = 0,5; so beim fairen Münzwurf
Erfolgserlebnis X = Kopf
• Es ergeben sich beispielsweise folgende Verteilungen für N = 1, 2, 3 Versuche:
N = 1 : X = 0, 1 ; in beiden Fällen ist C11= C10 = 1 (da 1! = 1 und 0! = 1)
1!  1 
p (0) 
 
0!1!  2 
N = 2 : X = 0, 1, 2
2!  1 
p (0) 
 
0! 2!  2 
0
2
1 1
  
2 4
0
1
1
1 1
  
2 2
0
1!  1   1  1
p (1) 
   
1! 0!  2   2  2
1
1
2!  1   1  2
p (1) 
   
1!1!  2   2  4
2!  1 
p (2) 
 
2! 0!  2 
2
0
1 1
  
2 4
N = 3 : X = 0, 1, 2, 3
3!  1 
p (0) 
 
0! 3!  2 
0
3
1 1
  
2 8
1
2
3!  1   1  3
p (1) 
   
1! 2!  2   2  8
3!  1 
p (2) 
 
2!1!  2 
2
1
1 3
  
2 8
3!  1 
p (3) 
 
3! 0!  2 
3
0
1 1
  
2 8
Wahrscheinlichkeitsverteilungen
Eigenschaften der Binomialverteilung
• Sämtliche Charakteristika der Binomialverteilung hängen von den Parametern
N, p und q ab, wie in folgender Tabelle ersichtlich.
Anmerkung: Da sich Wahrscheinlichkeitsverteilungen auf Grundgesamtheiten beziehen,
verwendet man als Symbole für die Lagemaßzahlen griechische Buchstaben.
Mittelwert
  Np
Varianz
 2  Npq
Standardabweichung
  Npq
Momentenkoeffizient
der Schiefe
3 
q p
Npq
(Momentenkoeffizient
der Kurtosis)
4 
1  6 pq
Npq
Binomialverteilungskurven
(http://www.statistik.tuwien.ac.at)
Wahrscheinlichkeitsverteilungen
Beispiel I: Binomialverteilung ermitteln
• Aufgabe: In einer Spezies trete eine genetische Variation mit dominantem Phänotyp mit
der Wahrscheinlichkeit p = 0,3 auf. Berechnen Sie die Verteilung der positiven Phänotypen
(Erfolg, X) unter 4 Nachkommen, mit Angabe der Kombinationen von X und 0 (Misserfolg).
• Lösung:
Wir überlegen uns als erstes die Werte, welche die Zufallsvariable X annehmen kann.
N = 4, da 4 Nachkommen betrachtet werden. X kann also 0, 1, 2, 3 und 4 betragen.
Die Zahl kombinatorischen Möglichkeiten entnehmen wir dem Pascal‘schen Dreieck
X = 0: C = 1 : 0000
N=1
N=2
N=3
N=4
X = 1: C = 4 : X000 ; 0X00 ; 00X0 ; 000X
X = 2: C = 6 : XX00; X0X0; X00X; 0XX0; 0X0X; 00XX
X = 3: C = 4 : XXX0; XX0X; X0XX; 0XXX
X = 4: C = 1 : XXXX
Wahrscheinlichkeitsverteilungen
Beispiel I: Binomialverteilung ermitteln
• Lösung:
Wir überlegen uns als erstes die Werte, welche die Zufallsvariable X annehmen kann.
N = 4, da 4 Nachkommen betrachtet werden. X kann also 0, 1, 2, 3 und 4 betragen.
Die Zahl kombinatorischen Möglichkeiten entnehmen wir dem Pascal‘schen Dreieck
X = 0: C = 1 : 0000
N=1
X = 1: C = 4 : X000 ; 0X00 ; 00X0 ; 000X
N=2
N=3
X = 2: C = 6 : XX00; X0X0; X00X; 0XX0; 0X0X; 00XX
N=4
X = 3: C = 4 : XXX0; XX0X; X0XX; 0XXX
X = 4: C = 1 : XXXX
Berechnung: Binomialkoeffizient: 4 Nachkommen (N=4); z.B. 2 positive Ereignisse (pos.
Phänotyp; X=2)
z.B.: C NX 
N!
X ! ( N  X ) !
4 Nachkommen, 2 positive Ereignisse (X)
C42 
4!
24

 6
2! 2!
4
Wahrscheinlichkeitsverteilungen
Beispiel I: Binomialverteilung ermitteln
• Nun können die Wahrscheinlichkeiten anhand der Binomialverteilungs-Formel mit p = 0,3
und q = 0,7 berechnet werden (N=4). Es ergibt sich, wie erwartet, eine asymmetrische
Verteilung (rechtsschief).
p ( X )  CNX  p X  q N  X 
p (0) 
N!
p X qNX
X !( N  X )!
4!
 (0,3)0  (0,7) 4  1 (0,3)0  (0,7) 4  0,240
0!4  0!
p (1)  4  (0,3)1  (0,7)3  0,412
p (3)  4  (0,3)3  (0,7)1  0,076
p (2)  6  (0,3)2  (0,7)2  0,264
p (4)  1  (0,3) 4  (0,7)0  0,008
  Np  4  0,3  1,2
Mittelwert
Momentenkoeffizient der Schiefe
3 
q p

Npq
0,7  0,3
 0,436
4  0,7  0,3
Wahrscheinlichkeitsverteilungen
b) Die Poissonverteilung
• diskrete Wahrscheinlichkeitsverteilung
• Poisson-Verteilung bsd. bei der Berechnung von seltenen Ereignissen.
• λ. Erwartete Ereignishäufigkeit (wieviele Ereignisse finden im Mittel im Zeitintervall statt)
• Die Poisson-Verteilung Pλ hat für kleine Mittelwerte λ eine stark asymmetrische Gestalt
• die Binomialverteilung kann zur Poisson-Verteilung vereinfacht werden, wenn N sehr groß
(zumindest N>10) wird und p die Gegenwahrscheinlichkeit (1-p) sehr stark übersteigt
(p<0,1, p=λ/N; Np<5) (die meisten Binomialverteilungen haben relativ kleine N und
einigermaßen ausgeglichen p und q Werte, vgl. Münzwurf)
• Bei grossen λ ähnelt die Poisson-Verteilung einer Gaußschen Normalverteilung
e    X
p( X ) 
X!
Mittelwert
μ=λ
Varianz
σ2 = λ
Standardabweichung
σ=( λ)1/2
Momentenkoeffizient
der Schiefe
α3 = 1/(( λ)1/2)
http://knol.google.com/k/poisson-verteilung#
Wahrscheinlichkeitsverteilungen
b) Die Poissonverteilung
• Ein Zufallsexperiment hat eine sehr kleine unbekannte Trefferwahrscheinlichkeit p.
Das Experiment wird N-mal (genaue Zahl unbekannt) unabhängig voneinander
durchgeführt. Bekannt ist jedoch die im Mittel auftretende Trefferzahl λ.
Die Wahrscheinlichkeit bei einer
konkreten N-maligen Ausführung des
Experiments genau k Treffer zu
erzielen berechnet sich aus:
pk 
k
k!
e 
• Beispiel: Ein α-Strahler emitiert in der Zeitspanne von 7,5 s im Mittel 3,87α-Teilchen.
Wie groß ist die Wahrscheinlichkeit, dass in diesem Zeitraum genau 5 Teilchen
detektiert werden?
• Lösung: Menge radioaktives Material, N-Atome (sicher sehr groß). Positive Ereignis:
Emission eines α-Teilchens, im Mittel (λ) 7,5 daher gilt: p= λ/N= sehr klein =>
Anwendung der Poisson-Verteilung:
pk 
k
k!
e 
3,875 3,87

e
 0,151  15,1%
5!
Wahrscheinlichkeitsverteilungen
c) Die Normalverteilung
• Die Normalverteilung (Gauss-Verteilung, Glockenkurve“, normal distribution) ist
eine (bzw. die wichtigste) Wahrscheinlichkeitsverteilung für stetige Daten
(Variablen). Beispielsweise sind zufällig gestreute physikalische Größen, darunter
Messwerte (ohne systematische Fehler) normalverteilt.
• Die Wahrscheinlichkeitsfunktion p (X)
der Normalverteilung (Dichtefunktion)
hat die Gleichung
1
Y 
e
 2

...Mittelwert
 ...STABW
( X  )2
2 2
• Die Standardform der Normalverteilung liegt vor, wenn μ = 0 und σ2 = 1
1
Y 
1  2X2
e
2
Wichtig: Jede Normalverteilung kann
auf die Standardform
gebracht werden (Z-Transformation),
indem die standardisierte Variable z
(für die x-Achse) verwendet wird:
Z = (X - μ) / σ (vgl. VL 7)
Y
z
Wahrscheinlichkeitsverteilungen
Die Normalverteilung
allgemein

Maximalstelle
P(Maximalwert)
Wendestellen
68.26%
95.45%
99.73%
standardisiert
0
1
 2
1
 0,399
2
 
1
(Momentenkoeffizient
der Kurtosis)
3
Momentenkoeffizient
der Schiefe
0
• Die Gesamtfläche unter der Kurve ist Eins; dh. die Fläche unter der Kurve, die zwischen zwei
Ordinaten bei X=a und X=b , liegt (a<b), stellt die Wahrscheinlichkeit dar, dass X zwischen a
und b liegt (Flächenangabe in der Abbildung).
• Es existiert keine elementare, also analytisch bestimmbare, Stammfunktion zur
Normalverteilungs-Funktion. Für die Standard-Normalverteilung sind die numerisch
ermittelten Werte der kumulativen Verteilungsfunktion jedoch tabelliert.
Ist N groß und weder p noch q nahe bei Null, kann die
Binomialverteilung durch eine Normalverteilung angenähert werden.
z
X  Np
Npq
Wahrscheinlichkeitsverteilungen
Die Normalverteilungstabelle (Z-Verteilung)
1
Y 
1  2X2
e
2
Gesamtfläche unter der Kurve =1
68.26%
95.45%
99.73%
Unterschiedliche Tabellen Standardnormalverteilung:
• a) Prozentuelle Anteile der
Standardnormalverteilung links vom tabellierten zWert (bzw. X-Wert)
• b) Prozentuelle Anteile der
Standardnormalverteilung startend bei 0 (0-Z)
Grafik: http://wirtschaft.fhduesseldorf.de/fileadmin/personen/lehrbeauftragte/schmei
nk/Normalvert_beide.pdf
Wahrscheinlichkeitsverteilungen
Die Normalverteilungstabelle
Für z=1,95: Fläche=0,9744 => 97,44%
Für z=0,00: Fläche=0,5000 => 50,00%
Für z=-1,95:
Für z=-1,95: Fläche=1-0,9744 =0,0256
=> 2,56%
Grafik: www.sts.uzh.ch/static/courses/statistik/folien/v16_4.pdf
Wahrscheinlichkeitsverteilungen
Die Normalverteilungstabelle (Z-Verteilung)
Kumulative Fläche von 0 bis Z.
Für z=0,00:
Fläche=0,0000
=> 00,00%
Für z=1,00 : Fläche=0,3413 => 34,13%
Im Bereich μ ± σ (entspricht z=-1 bis z=+1
(durch die Normierung)) befinden sich ca
2* 34,13 % ~ 68 %
68,26%
95,45%
99,73%
Wahrscheinlichkeitsverteilungen
Beispiel II: Anwendung der Normalverteilung
• Aufgabe:
Wir betrachten eine Grundgesamtheit von Personen, deren IQ als normalverteilt
angenommen wird, mit einem Mittelwert von 100 und einer Standardabweichung von 15.
(a) mit (ca.) welcher Wahrscheinlichkeit wählt man eine Person, die genau IQ 100 hat?
(b) welchen Wert hat der IQ 95 in Standardeinheiten?
(c) welcher Anteil der Grundgesamtheit besitzt einen IQ größer als 130?
Da der IQ ganzzahlige Werte aufweist, haben wir es eigentlich mit einer diskreten
Verteilung zu tun, allerdings sind offensichtlich etwa 100 ± 50 Werte, sprich N = 100
Werte für die Variable X möglich, die quasi-stetige Näherung ist also gültig.
a) Lösung:
IQ = 100 ist der Mittelwert μ der Normalverteilung, dort liegt die maximale
Wahrscheinlichkeit mit dem Wert Maximalwer t 
oder: μ ± 0,03 ≈
≈ 2*0,012 ≈ 0,024 ≈2,4%
1
1

 0,0266
 2 15 2
(2,66%)
Wahrscheinlichkeitsverteilungen
Beispiel II: Anwendung der Normalverteilung
• Aufgabe:
Wir betrachten eine Grundgesamtheit von Personen, deren IQ als normalverteilt
angenommen wird, mit einem Mittelwert von 100 und einer Standardabweichung von 15.
(a) mit (ca.) welcher Wahrscheinlichkeit wählt man eine Person, die genau IQ 100 hat?
(b) welchen Wert hat der IQ 95 in Standardeinheiten?
(c) welcher Anteil der Grundgesamtheit besitzt einen IQ größer als 130?
• Lösung:
b)
Z  (X -  ) /  
95  100
  0,333
15
c) IQ von 130 in Standardeinheiten: Z  (X -  ) /   130  100  2
15
dh. wir suchen den Anteil aller Personen mit X > 2σ.
Normalverteilungstabelle (ab Mitte) bei z=2,00: 0,4772,
innerhalb von μ ± 2σ liegen 95,44 % innerhalb der
Aussenbereiche insgesamt 4,56%, an jeder Flanke also
2,28%, d.h. 2,28% besitzten einen IQ größer als 130.
oder Normalverteilungstabelle ‚von links‘:
bei z=2,00: 0,97725; unser gesuchter Wert =
=1-0,97725=0,02275 ≈ 2,28%
95.44%
Wahrscheinlichkeitsverteilungen
• Gibt es aufgrund wahrscheinlichkeitstheoretischer Überlegungen einen
Hinweis auf die Verteilung einer Grundgesamtheit, so ist es möglich,
diese erwarteten Verteilungen an Häufigkeitsverteilungen anzupassen.
Verwendet werden dazu die Daten, die man aus der Stichprobe der
Grundgesamtheit erhalten hat.
• Die Güte der Anpassung (goodness of fit) der theoretischen Verteilung zu
testen, wird dann der χ2-Test (Chi-Quadrat-Test) verwendet