V2 Felder (Funktionen mehrerer unabhängigen Variablen) Orts

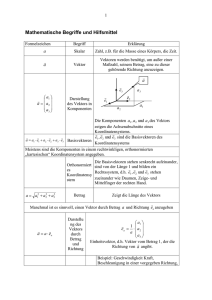
V2 Felder (Funktionen mehrerer unabhängigen Variablen)
Orts- und zeitabhängige physikalische Größen werden durch "Felder" beschrieben.
Beispiel: Maxwell-Gleichungen der
Elektrodynamik:
Vektor-Analysis: nützlichen Identitäten
Ziel der folgenden Abschnitte ist, elementare Rechenoperationen für Felder
einzuführen.
Beispiel 1: Temperatur im Zimmer
Menge aller Punkte im Zimmer
= Temperatur am Punkt
Beispiel 2: Zeitabhängige Temperatur im Zimmer
Zeitintervall
= Temperatur am Punkt
zur Zeit
Beispiel 3: Luftfluss durch Tunnel
= Luftgeschwindigkeit am Punkt
Beispiel 4: Ferromagnet
zur Zeit
Menge aller Vektoren mit Betrag = 1
= 'Magnetisierung' am Punkt
zur Zeit
Allgemeine mathematische Struktur eines 'Feldes':
'Basismannigfaltigkeit'
'Zielmannigfaltigkeit'
'Skalarfeld'
Beispiele: Temperatur, Druck, Dichte
'Vektorfeld'
Beispiele: Luftfluss, Magnetfeld,
Elektrisches Feld, Gravitationskraftfeld
Skalarfeld:
(z.B. Höhe eines Gebirges)
Vektorfeld:
(z.B. Stromfluss im Wassertank)
Vektorfeld:
(z.B. Stromfluss an Wasseroberfläche)
Wie ändern sich Felder als Funktion v.
Wie bildet man Ableitungen von Feldern?
?
C3: Partielle Ableitungen
C3 Partielle Ableitungen
Betrachte
(Skalarfeld)
Beispiel für d=3, mit
C3.1 Partielle Ableitung:
wie ändert sich
als Funktion v. nur
einer der Variablen,
, wenn die
anderen Variablen
festgehalten
werden?
Wie ändert sich
als Funktion v. nur einer der Variablen,
Definition: 'Partielle Ableitung von
am Punkt
nur
?
, nach
':
ändert sich, um
In Vektornotation:
Lineare Näherung:
eher unüblich
Alternative
Notationen:
Lieblingsnotation
von JvD
Merkregel: Index oben 'im Nenner der Ableitung' = Index unten in Kurznotation!
Beispiele:
[Index, nicht Potenz!]
C3.2 Mehrfache partielle Ableitungen (rekursive Definition)
Gemischte
partielle
Ableitungen:
Beispiel v.
Seite C3a:
gleich!
(falls f stetige Ableitungen bis
mindestens zur 2.ten Ordnung besitzt)
Satz v. Schwarz: Für hinreichend glatte Funktionen sind part. Ableitungen vertauschbar:
V3 Skalare Felder
Beispiel: Höhenfeld
Kontur-Linien:
Dort, wo Konturlinien dicht liegen, ist es "steil".
Funktion ändert sich am schnellsten in Richtung
senkrecht zu den Konturlinien.
Frage: Welcher Vektor gibt diese Richtung an?
Antwort:
Gradient:
(wird im Folgenden eingeführt)
[für Figur wurde c=1 gewählt]
V3.1 Totales Differential
Wie ändert sich eine Funktion
an einem gegebenen Punkt
in eine vorgegebene Richtung
?
'totales Differential' liefert die Antwort:
vergleiche
"Mutter aller
Ableitungen",
(C1b.3)
Das totale Differential
ist eine 'Maschine', definiert bei
, die einen Vektor
und als Antwort eine Zahl 'ausspuckt', nämlich die differenzielle Änderung v. f bei einem
'frisst'
-Schritt.
Falls
Allgemein gilt:
(Begründung: Seite 3d)
Beispiel: Höhenfeld
nachdifferenziert nach
Anmerkung: trotz des "d" in der Notation, ist das totale Differential im Allgemeinen nicht
infinitessimal klein! Es ist nur dann klein, wenn der Vektor im Argument klein ist:
z.B.:
nur, falls
Begründung für (V3b.3):
explizit für
:
subtrahiere und addiere dieselbe Größe
vernachlässigbar!
(5) eingesetzt in (2)
Analog folgt
(V3b.3) für
beliebiges d
Kompaktnotation: (C3a.3)
V3.2 Gradient
Das totale Differential
'wirkt linear auf seinen
Argument-Vektor':
(1) und (2) lassen sich kompakt schreiben, wenn wir der Funktion f einen neuen Vektor zuordnen:
Def: 'Gradient v.
am Punkt
i-Komponente des
Gradienten-Vektors:
Skalarproduktnotation:
:
Beispiel (d=2): Höhenfeld:
vergleiche
(VC3.1)
für (1):
für (2):
(siehe Fig, Seite V3a !)
Geometrische Interpretation des Gradienten-Vektors
Skizze in d = 2 Dimensionen, zur Veranschaulichung:
(sei ein Einheitsvektor, Richtung beliebig)
zeigt in Richtung
maximaler Steigung
Steigung in
-Richtung
Höhen-, Konturlinien:
= konst.
maximal falls
zeigt in Richtung maximaler Steigung v.
0 falls
steht
Beispiel:
(allgemeiner: Höhenflächen)
auf den Höhenlinien v.
Sei
mit
Analog für die anderen
Komponenten, also:
= nach 'aussen'
gerichteter
Einheitsvektor
Zusammenfassung C3: Partielle Ableitungen
Partielle Ableitung:
Satz v. Schwarz:
Totales Differential:
Kettenregel:
Zusammenfassung V2: Konzept eines Feldes
Zusammenfassung V3: Skalarfelder, Gradient
Totales Differential: differentielle Änderung von
bei
durch einen
-Schritt:
Gradient:
zeigt in Richtung maximaler Steigung v.
steht
auf den 'Höhenflächen' v.