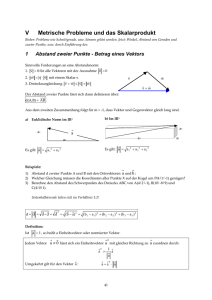
Inhalte Didaktik der Linearen Algebra und Analytischen Geometrie
Werbung
Jürgen Roth Didaktik der Linearen Algebra und Analytischen Geometrie Modul 12a: Fachdidaktische Bereiche juergen-roth.de/lehre/did_linalg_anageo/ Jürgen Roth • Didaktik der Linearen Algebra und Analytischen Geometrie Kapitel 5: Skalarprodukt • 5.1 Inhalte Didaktik der Linearen Algebra und Analytischen Geometrie 0 Organisatorisches 1 Ziele und Inhalte 2 Algebraisieren des Anschauungsraums 3 Modellieren und Angewandte Mathematik 4 Kegelschnitte 5 Skalarprodukt – Längen und Winkel messen Jürgen Roth • Didaktik der Linearen Algebra und Analytischen Geometrie Kapitel 5: Skalarprodukt • 5.2 Didaktik der Linearen Algebra und Analytischen Geometrie Kapitel 5: Skalarprodukt – Längen und Winkel messen Jürgen Roth • Didaktik der Linearen Algebra und Analytischen Geometrie Kapitel 5: Skalarprodukt • 5.3 Inhalte Kapitel 5: Skalarprodukt 5.1 Aspekte des Skalarprodukts im MU 5.2 Skalarprodukt und Messen 5.3 Arithmetischer Zugang zum Skalarprodukt 5.4 Geometrische Deutung des Skalarprodukts 5.5 Produktive Übungen und systematische Variation 5.6 Geometrische Eigenschaften des Skalarprodukts 5.7 Skalarprodukt im Kontext Jürgen Roth • Didaktik der Linearen Algebra und Analytischen Geometrie Kapitel 5: Skalarprodukt • 5.4 Inhalte Kapitel 5: Skalarprodukt 5.1 Aspekte des Skalarprodukts im MU 5.2 Skalarprodukt und Messen 5.3 Arithmetischer Zugang zum Skalarprodukt 5.4 Geometrische Deutung des Skalarprodukts 5.5 Produktive Übungen und systematische Variation 5.6 Geometrische Eigenschaften des Skalarprodukts 5.7 Skalarprodukt im Kontext Jürgen Roth • Didaktik der Linearen Algebra und Analytischen Geometrie Kapitel 5: Skalarprodukt • 5.5 Aspekte des Skalarprodukts im Mathematikunterricht Schacht, F. (2014): Ganz schön verMESSEN! – Das Skalarprodukt aus der Perspektive des Messens. Praxis der Mathematik in der Schule 56(55), S. 32-38 Idee: Längen und Winkel messen Geometrische Deutung Arithmetischer Zugang Skalarprodukt Jürgen Roth • Didaktik der Linearen Algebra und Analytischen Geometrie Zahlen und Vektoren vermessen Kontext und produktive Übungen Kapitel 5: Skalarprodukt • 5.6 Skalarprodukt Skalarprodukt: Weitere Struktur in einem Vektorraum Um in einem Vektorraum Längen und Winkel messen zu können, muss eine weitere Struktur, das Skalarprodukt, hinzugefügt werde. ⇒ Euklidischer Vektorraum Anwendungen des Skalarprodukts Abstandsbestimmung Punkt ↔ Gerade, Ebene ↔ Gerade paralleler Geraden (z. B. zur Flächenberechnung) Windschiefer Geraden Berechnung von Schnittwinkeln Gerade ↔ Gerade, Ebene ↔ Ebene Prüfen auf Orthogonalität Gerade ↔ Gerade, Ebene ↔ Ebene Bestimmung Normalenvektor, Normalengleichung einer Ebene Jürgen Roth • Didaktik der Linearen Algebra und Analytischen Geometrie Kapitel 5: Skalarprodukt • 5.7 Inhalte Kapitel 5: Skalarprodukt 5.1 Aspekte des Skalarprodukts im MU 5.2 Skalarprodukt und Messen 5.3 Arithmetischer Zugang zum Skalarprodukt 5.4 Geometrische Deutung des Skalarprodukts 5.5 Produktive Übungen und systematische Variation 5.6 Geometrische Eigenschaften des Skalarprodukts 5.7 Skalarprodukt im Kontext Jürgen Roth • Didaktik der Linearen Algebra und Analytischen Geometrie Kapitel 5: Skalarprodukt • 5.8 Skalarprodukt und Messen Schmidt et al. (2010). Mathematik Neue Wege. Arbeitsbuch für Gymnasien – Lineare Algebra – Analytische Geometrie. Braunschweig: Schroedel, S. 140-142 Jürgen Roth • Didaktik der Linearen Algebra und Analytischen Geometrie Kapitel 5: Skalarprodukt • 5.9 Skalarprodukt und Messen Schmidt et al. (2010). Mathematik Neue Wege. Arbeitsbuch für Gymnasien – Lineare Algebra – Analytische Geometrie. Braunschweig: Schroedel, S. 140-142 Jürgen Roth • Didaktik der Linearen Algebra und Analytischen Geometrie Kapitel 5: Skalarprodukt • 5.10 Skalarprodukt und Messen Schmidt et al. (2010). Mathematik Neue Wege. Arbeitsbuch für Gymnasien – Lineare Algebra – Analytische Geometrie. Braunschweig: Schroedel, S. 140-142 Jürgen Roth • Didaktik der Linearen Algebra und Analytischen Geometrie Kapitel 5: Skalarprodukt • 5.11 Skalarprodukt und Messen Schmidt et al. (2010). Mathematik Neue Wege. Arbeitsbuch für Gymnasien – Lineare Algebra – Analytische Geometrie. Braunschweig: Schroedel, S. 140-142 Jürgen Roth • Didaktik der Linearen Algebra und Analytischen Geometrie Kapitel 5: Skalarprodukt • 5.12 Skalarprodukt und Messen Schmidt et al. (2010). Mathematik Neue Wege. Arbeitsbuch für Gymnasien – Lineare Algebra – Analytische Geometrie. Braunschweig: Schroedel, S. 140-142 Jürgen Roth • Didaktik der Linearen Algebra und Analytischen Geometrie Kapitel 5: Skalarprodukt • 5.13 Skalarprodukt und Messen Schmidt et al. (2010). Mathematik Neue Wege. Arbeitsbuch für Gymnasien – Lineare Algebra – Analytische Geometrie. Braunschweig: Schroedel, S. 140-142 Jürgen Roth • Didaktik der Linearen Algebra und Analytischen Geometrie Kapitel 5: Skalarprodukt • 5.14 Inhalte Kapitel 5: Skalarprodukt 5.1 Aspekte des Skalarprodukts im MU 5.2 Skalarprodukt und Messen 5.3 Arithmetischer Zugang zum Skalarprodukt 5.4 Geometrische Deutung des Skalarprodukts 5.5 Produktive Übungen und systematische Variation 5.6 Geometrische Eigenschaften des Skalarprodukts 5.7 Skalarprodukt im Kontext Jürgen Roth • Didaktik der Linearen Algebra und Analytischen Geometrie Kapitel 5: Skalarprodukt • 5.15 Arithmetischer Zugang: Bsp. Modelleisenbahnbau Filler, A. (2011). Elementare Lineare Algebra. Heidelberg: Spektrum Akademischer Verlag, S. 100 Preis 2,40 € 2,70 € 6,29 € 17,98 € 17,98 € 12,98 € Jürgen Roth • Didaktik der Linearen Algebra und Analytischen Geometrie Kapitel 5: Skalarprodukt • 5.16 Arithmetischer Zugang: Bsp. Modelleisenbahnbau Filler, A. (2011). Elementare Lineare Algebra. Heidelberg: Spektrum Akademischer Verlag, S. 100/122 Preis 2,40 € 2,70 € 6,29 € 17,98 € 17,98 € 12,98 € Teilevektor Stückliste Erg.- 15 sortiment 2: 8 ๐2 = 1 2 2 4 Preisvektor 2,40 2,70 6,29 ๐ิฆ = 17,98 17,98 12,98 Gesamtpreis eines Sortiments Summe der Produkte einander entsprechender Komponenten des Teile- und des Preisvektors 15 ⋅ 2,40 + 8 ⋅ 2,40 + 1 ⋅ 6,29 + 2 ⋅ 17,98 + 2 ⋅ 17,98 + 5 ⋅ 12,98 = 187,73 (in €) Die Produktsumme, die den Gesamtpreis ergibt, nennen wir Skalarprodukt der Vektoren ๐๐ und ๐. Jürgen Roth • Didaktik der Linearen Algebra und Analytischen Geometrie Kapitel 5: Skalarprodukt • 5.17 Arithmetischer Zugang: Definition Skalarprodukt Filler, A. (2011). Elementare Lineare Algebra. Heidelberg: Spektrum Akademischer Verlag, S. 122 Definition Als Skalarprodukt zweier Vektoren ๐ข, ๐ฃิฆ ∈ โ๐ mit ๐ข1 ๐ฃ1 ๐ข2 ๐ฃ2 ๐ข= โฎ und ๐ฃิฆ = โฎ ๐ข๐ ๐ฃ๐ wird die Summe der Produkte der einander entsprechenden Komponenten von ๐ข und ๐ฃิฆ bezeichnet: ๐ ๐ข ⋅ ๐ฃิฆ = ๐ข1 ⋅ ๐ฃ1 + ๐ข2 ⋅ ๐ฃ2 + โฏ + ๐ข๐ ⋅ ๐ฃ๐ = เท ๐ข๐ ⋅ ๐ฃ๐ ๐=1 Jürgen Roth • Didaktik der Linearen Algebra und Analytischen Geometrie Kapitel 5: Skalarprodukt • 5.18 Arithmetischer Zugang: Definition Skalarprodukt Filler, A. (2011). Elementare Lineare Algebra. Heidelberg: Spektrum Akademischer Verlag, S. 122 Bemerkungen Der Name Skalarprodukt kommt daher, dass zwei Vektoren ein Skalar, d. h. eine reelle Zahl zugeordnet wird. Beim Rechnen mit Vektoren treten damit nun drei Arten von Produkten auf, für die jeweils das Zeichen „⋅“ verwendet wird: das Produkt zweier reeller Zahlen, das Produkt eines Vektors mit einer reellen Zahl, das Skalarprodukt zweier Vektoren. Was das Zeichen „⋅“ jeweils bedeutet, ergibt sich aus der Art von Objekten (Vektoren oder reelle Zahlen), zwischen denen es steht. Jürgen Roth • Didaktik der Linearen Algebra und Analytischen Geometrie Kapitel 5: Skalarprodukt • 5.19 Inhalte Kapitel 5: Skalarprodukt 5.1 Aspekte des Skalarprodukts im MU 5.2 Skalarprodukt und Messen 5.3 Arithmetischer Zugang zum Skalarprodukt 5.4 Geometrische Deutung des Skalarprodukts 5.5 Produktive Übungen und systematische Variation 5.6 Geometrische Eigenschaften des Skalarprodukts 5.7 Skalarprodukt im Kontext Jürgen Roth • Didaktik der Linearen Algebra und Analytischen Geometrie Kapitel 5: Skalarprodukt • 5.20 Geometrische Deutung des Skalarprodukts Filler, A. (2011). Elementare Lineare Algebra. Heidelberg: Spektrum Akademischer Verlag, S. 55 Abstand zweier Punkte der Ebene Für den Abstand zweier Punkte ๐1 ๐ฅ1 ; ๐ฆ1 und ๐2 ๐ฅ2 ; ๐ฆ2 der Ebene ergibt sich mit dem Satz des Pythagoras: ๐1 ๐2 = ๐ฅ2 − ๐ฅ1 2 + ๐ฆ2 − ๐ฆ1 2 Jürgen Roth • Didaktik der Linearen Algebra und Analytischen Geometrie Kapitel 5: Skalarprodukt • 5.21 Geometrische Deutung des Skalarprodukts Filler, A. (2011). Elementare Lineare Algebra. Heidelberg: Spektrum Akademischer Verlag, S. 55 Abstand zweier Punkte des Raums Für den Abstand zweier Punkte ๐1 ๐ฅ1 ; ๐ฆ1 ; ๐ง1 und ๐2 ๐ฅ2 ; ๐ฆ2 ; ๐ง2 des Raums ergibt sich (zweimaliges Anwenden des Satzes des Pythagoras): ๐1 ๐2 = ๐ฅ2 − ๐ฅ1 2 + ๐ฆ2 − ๐ฆ1 Jürgen Roth • Didaktik der Linearen Algebra und Analytischen Geometrie 2 + ๐ง2 − ๐ง1 2 Kapitel 5: Skalarprodukt • 5.22 Geometrische Deutung des Skalarprodukts Filler, A. (2011). Elementare Lineare Algebra. Heidelberg: Spektrum Akademischer Verlag, S. 124 Darstellung von Vektoren Der Abstand zweier Punkte ๐1 ๐ฅ1 ; ๐ฆ1 ; ๐ง1 und ๐2 ๐ฅ2 ; ๐ฆ2 ; ๐ง2 des Raums entspricht der Länge des Pfeils ๐1 ๐2 . Wird ein Vektor ๐ิฆ durch den Pfeil ๐1 ๐2 repräsentiert, dann kann man diesen Vektor auch so darstellen: ๐ฅ๐ ๐ฅ2 − ๐ฅ1 ๐ิฆ = ๐1 ๐2 = ๐ฆ๐ = ๐ฆ2 − ๐ฆ1 ๐ง๐ ๐ง2 − ๐ง1 Jürgen Roth • Didaktik der Linearen Algebra und Analytischen Geometrie Kapitel 5: Skalarprodukt • 5.23 Geometrische Deutung des Skalarprodukts Filler, A. (2011). Elementare Lineare Algebra. Heidelberg: Spektrum Akademischer Verlag, S. 124 Betrag (Länge) eines Vektors Bildet man das Skalarprodukt eines Vektors ๐ฅ๐ ๐ฅ2 − ๐ฅ1 ๐ิฆ = ๐1 ๐2 = ๐ฆ๐ = ๐ฆ2 − ๐ฆ1 ๐ง๐ ๐ง2 − ๐ง1 mit sich selbst, so erhält man ๐ิฆ ⋅ ๐ิฆ = ๐ฅ๐ ⋅ ๐ฅ๐ + ๐ฆ๐ ⋅ ๐ฆ๐ + ๐ง๐ ⋅ ๐ง๐ = ๐ฅ2 − ๐ฅ1 = 2 + ๐ฆ2 − ๐ฆ1 ๐ฅ2 − ๐ฅ1 2 2 + ๐ง2 − ๐ง1 + ๐ฆ2 − ๐ฆ1 2 2 + ๐ง2 − ๐ง1 2 2 = ๐1 ๐2 2 Definition Als Betrag eines Vektors ๐ฃิฆ bezeichnet man die Wurzel aus dem Skalarprodukt dieses Vektors mit sich selbst: ๐ฃิฆ = ๐ฃิฆ ⋅ ๐ฃิฆ = Jürgen Roth • Didaktik der Linearen Algebra und Analytischen Geometrie ๐ฃิฆ 2 Kapitel 5: Skalarprodukt • 5.24 Inhalte Kapitel 5: Skalarprodukt 5.1 Aspekte des Skalarprodukts im MU 5.2 Skalarprodukt und Messen 5.3 Arithmetischer Zugang zum Skalarprodukt 5.4 Geometrische Deutung des Skalarprodukts 5.5 Produktive Übungen und systematische Variation 5.6 Geometrische Eigenschaften des Skalarprodukts 5.7 Skalarprodukt im Kontext Jürgen Roth • Didaktik der Linearen Algebra und Analytischen Geometrie Kapitel 5: Skalarprodukt • 5.25 Produktive Übungen nutzen die systematische Variation Schacht, F. (2014): Ganz schön verMESSEN! – Das Skalarprodukt aus der Perspektive des Messens. In: Praxis der Mathematik in der Schule, Heft 55, 56. Jahrgang, S. 32-38 Jürgen Roth • Didaktik der Linearen Algebra und Analytischen Geometrie Kapitel 5: Skalarprodukt • 5.26 Produktive Übungen nutzen die systematische Variation Schacht, F. (2014): Ganz schön verMESSEN! – Das Skalarprodukt aus der Perspektive des Messens. Praxis der Mathematik in der Schule 56(55), S. 32-38 Jürgen Roth • Didaktik der Linearen Algebra und Analytischen Geometrie Kapitel 5: Skalarprodukt • 5.27 Inhalte Kapitel 5: Skalarprodukt 5.1 Aspekte des Skalarprodukts im MU 5.2 Skalarprodukt und Messen 5.3 Arithmetischer Zugang zum Skalarprodukt 5.4 Geometrische Deutung des Skalarprodukts 5.5 Produktive Übungen und systematische Variation 5.6 Geometrische Eigenschaften des Skalarprodukts 5.7 Skalarprodukt im Kontext Jürgen Roth • Didaktik der Linearen Algebra und Analytischen Geometrie Kapitel 5: Skalarprodukt • 5.28 Geometrische Eigenschaften des Skalarprodukts Filler, A. (2011). Elementare Lineare Algebra. Heidelberg: Spektrum Akademischer Verlag, S. 126f Satz über die Orthogonalität von Vektoren Zwei Vektoren ๐ข und ๐ฃิฆ sind genau dann orthogonal, wenn ๐ข ⋅ ๐ฃิฆ = 0 gilt. Beweis Von zwei Vektoren ๐ฅ๐ข ๐ฅ๐ฃ ๐ข = ๐ฆ๐ข und ๐ฃิฆ = ๐ฆ๐ฃ ist keiner der Nullvektor. ๐ง๐ข ๐ง๐ฃ (Wenn ๐ข = ๐ิฆ oder ๐ฃิฆ = ๐, ิฆ dann folgt ๐ข ⋅ ๐ฃิฆ = 0 direkt aus der Definition des Skalarprodukts.) Betrachte die Pfeile ๐๐ und ๐๐ die Repräsentanten von ๐ข bzw. ๐ฃิฆ sind und deren Anfangspunkt der Koordinatenursprung ist. Die Vektoren ๐ข und ๐ฃิฆ sind genau dann orthogonal, wenn das Dreieck โ๐๐๐ bei ๐ rechtwinklig ist. Nach dem Satz des Pythagoras und seiner Umkehrung ist das genau dann der Fall, wenn ๐๐ 2 + ๐๐ 2 = ๐๐ 2 gilt. Jürgen Roth • Didaktik der Linearen Algebra und Analytischen Geometrie Kapitel 5: Skalarprodukt • 5.29 Geometrische Eigenschaften des Skalarprodukts Filler, A. (2011). Elementare Lineare Algebra. Heidelberg: Spektrum Akademischer Verlag, S. 127 Satz über die Orthogonalität von Vektoren Zwei Vektoren ๐ข und ๐ฃิฆ sind genau dann orthogonal, wenn ๐ข ⋅ ๐ฃิฆ = 0 gilt. Beweis (Fortsetzung) Zu zeigen: ๐๐ 2 + ๐๐ 2 = ๐๐ 2 ๐๐ 2 = ๐ข 2 ๐๐ 2 = ๐ฃิฆ 2 ๐๐ 2 = ๐ฃิฆ − ๐ข 2 = ๐ฅ๐ฃ − ๐ฅ๐ข 2 + ๐ฆ๐ฃ − ๐ฆ๐ข 2 + ๐ง๐ฃ − ๐ง๐ข 2 = ๐ฅ๐ฃ2 − 2๐ฅ๐ข ๐ฅ๐ฃ + ๐ฅ๐ข2 + ๐ฆ๐ฃ2 − 2๐ฆ๐ข ๐ฆ๐ฃ + ๐ฆ๐ข2 + ๐ง๐ฃ2 − 2๐ง๐ข ๐ง๐ฃ + ๐ง๐ข2 = ๐ฅ๐ข2 + ๐ฆ๐ข2 + ๐ง๐ข2 + ๐ฅ๐ฃ2 + ๐ฆ๐ฃ2 + ๐ง๐ฃ2 − 2 ⋅ (๐ฅ๐ข ๐ฅ๐ฃ + ๐ฆ๐ข ๐ฆ๐ฃ + ๐ง๐ข ๐ง๐ฃ ) = ๐ข 2 + ๐ฃิฆ 2 − 2 ⋅ ๐ข ⋅ ๐ฃิฆ = ๐๐ 2 + ๐๐ 2 − 2 ⋅ ๐ข ⋅ ๐ฃิฆ Damit gilt ๐๐ 2 + ๐๐ 2 = ๐๐ 2 genau dann, wenn ๐ข ⋅ ๐ฃิฆ = 0. Genau in diesem Fall sind die Vektoren ๐ข und ๐ฃิฆ orthogonal. ๏ผ Jürgen Roth • Didaktik der Linearen Algebra und Analytischen Geometrie Kapitel 5: Skalarprodukt • 5.30 Geometrische Eigenschaften des Skalarprodukts Filler, A. (2011). Elementare Lineare Algebra. Heidelberg: Spektrum Akademischer Verlag, S. 124ff Cauchy-Schwarzsche Ungleichung Für beliebige Vektoren ๐ข und ๐ฃิฆ gilt: ๐ข ⋅ ๐ฃิฆ ≤ ๐ข ⋅ ๐ฃิฆ Satz über das Skalarprodukt kollinearer Vektoren Für zwei kollineare und gleichorientierte Vektoren ๐ข und ๐ฃิฆ gilt: ๐ข ⋅ ๐ฃิฆ = ๐ข ⋅ ๐ฃิฆ Für zwei kollineare und entgegengesetzt orientierte Vektoren ๐ข und ๐ฃิฆ gilt: ๐ข ⋅ ๐ฃิฆ = − ๐ข ⋅ ๐ฃิฆ Jürgen Roth • Didaktik der Linearen Algebra und Analytischen Geometrie Kapitel 5: Skalarprodukt • 5.31 Geometrische Eigenschaften des Skalarprodukts Filler, A. (2011). Elementare Lineare Algebra. Heidelberg: Spektrum Akademischer Verlag, S. 128 Skalarprodukt und Winkel zwischen Vektoren Der Betrag des Skalarprodukts zweier Vektoren ist also maximal, wenn die Vektoren kollinear und minimal (nämlich Null), wenn die Vektoren orthogonal sind. Damit liegt nahe, dass das Skalarprodukt von den Beträgen und dem Zwischenwinkel der Vektoren anhängt. Der Winkel zwischen zwei Vektoren ๐ข und ๐ฃิฆ ist der Winkel zwischen zwei repräsentierenden Pfeilen ๐๐ und ๐๐ mit demselben Anfangspunkt ๐. Jürgen Roth • Didaktik der Linearen Algebra und Analytischen Geometrie Kapitel 5: Skalarprodukt • 5.32 Geometrische Eigenschaften des Skalarprodukts Filler, A. (2011). Elementare Lineare Algebra. Heidelberg: Spektrum Akademischer Verlag, S. 128 Skalarprodukt und Winkel zwischen Vektoren Lot von ๐ auf die Gerade ๐๐ fällen. ๐1 ist der Lotfußpunkt. ๐ฃิฆ = ๐ฃิฆ1 + ๐ฃิฆ2 (vgl. Abbildungen) ๐ข ⋅ ๐ฃิฆ = ๐ข ⋅ ๐ฃิฆ1 + ๐ฃิฆ2 = ๐ข ⋅ ๐ฃิฆ1 + ๐ข ⋅ ๐ฃิฆ2 = ๐ข ⋅ ๐ฃิฆ1 # =0 wegen ๐ข⊥๐ฃ2 ๐ข und ๐ฃิฆ1 können abhängig von ihrem Zwischenwinkel ๐ (mit 0 ≤ ๐ ≤ 180°) gleich (๐ < 90°) oder entgegengesetzt (90° < ๐ < 180°) orientiert sein. Jürgen Roth • Didaktik der Linearen Algebra und Analytischen Geometrie Kapitel 5: Skalarprodukt • 5.33 Geometrische Eigenschaften des Skalarprodukts Filler, A. (2011). Elementare Lineare Algebra. Heidelberg: Spektrum Akademischer Verlag, S. 128 Skalarprodukt und Winkel zwischen Vektoren Seien ๐ข und ๐ฃิฆ1 gleichorientiert, dann gilt nach dem Satz über das Skalarprodukt gleichorientierter, kollinearer Vektoren: ๐ข ⋅ ๐ฃิฆ1 = ๐ข ⋅ ๐ฃิฆ1 ∗ Im rechtwinkligen Dreieck Δ๐๐1 ๐ gilt cos ๐ = |๐ฃ1 | ๐ฃ bzw. ๐ฃิฆ1 = ๐ฃิฆ ⋅ cos ๐ # ∗ ∗∗ ∗∗ Damit folgt: ๐ข ⋅ ๐ฃิฆ = เธ ๐ข ⋅ ๐ฃิฆ1 = เธ ๐ข ⋅ ๐ฃิฆ1 = เธ ๐ข ⋅ ๐ฃิฆ ⋅ cos ๐ Jürgen Roth • Didaktik der Linearen Algebra und Analytischen Geometrie Kapitel 5: Skalarprodukt • 5.34 Geometrische Eigenschaften des Skalarprodukts Filler, A. (2011). Elementare Lineare Algebra. Heidelberg: Spektrum Akademischer Verlag, S. 128 Satz Für das Skalarprodukt zweier Vektoren ๐ข und ๐ฃ, ิฆ ihre Beträge ๐ข , ๐ฃิฆ und den Winkel ๐ = ∠ ๐ข, ๐ฃิฆ gilt: ๐ข ⋅ ๐ฃิฆ = ๐ข ⋅ ๐ฃิฆ ⋅ cos ๐ ∗ Jürgen Roth • Didaktik der Linearen Algebra und Analytischen Geometrie Kapitel 5: Skalarprodukt • 5.35 Geometrische Eigenschaften des Skalarprodukts Filler, A. (2011). Elementare Lineare Algebra. Heidelberg: Spektrum Akademischer Verlag, S. 128 Winkel zwischen zwei Vektoren ๐ฅ๐ข ๐ฅ๐ฃ Wenn ๐ข = ๐ฆ๐ข und ๐ฃิฆ = ๐ฆ๐ฃ zwei Vektoren des Raumes sind, ๐ง๐ข ๐ง๐ฃ dann ergibt sich: cos ∠ ๐ข, ๐ฃิฆ ๐ข ⋅ ๐ฃิฆ = = ๐ข ⋅ ๐ฃิฆ ๐ฅ๐ข ⋅ ๐ฅ๐ฃ + ๐ฆ๐ข ⋅ ๐ฆ๐ฃ + ๐ง๐ข ⋅ ๐ง๐ฃ ๐ฅ๐ข2 + ๐ฆ๐ข2 + ๐ง๐ข2 ⋅ ๐ฅ๐ข2 + ๐ฆ๐ข2 + ๐ง๐ข2 Jürgen Roth • Didaktik der Linearen Algebra und Analytischen Geometrie Kapitel 5: Skalarprodukt • 5.36 Präsenzübung Winkelbestimmung Bestimmen Sie den Winkel zwischen der Seite ๐ด๐ต und der Raumdiagonalen [๐ด๐บ]. Lösungshinweis 4 4 ๐ด๐ต = 0 , ๐ด๐ต = 3 0 2 ๐ด๐ต ⋅ ๐ด๐บ 4⋅4+0⋅3+0⋅2 16 cos ∠ ๐ด๐ต, ๐ด๐บ = = = 2 2 2 2 2 2 4 ⋅ 29 4 +0 +0 ⋅ 4 +3 +2 ๐ด๐ต ⋅ ๐ด๐บ ⇒ ∠ ๐ด๐ต, ๐ด๐บ ≈ 42° Jürgen Roth • Didaktik der Linearen Algebra und Analytischen Geometrie Kapitel 5: Skalarprodukt • 5.37 Inhalte Kapitel 5: Skalarprodukt 5.1 Aspekte des Skalarprodukts im MU 5.2 Skalarprodukt und Messen 5.3 Arithmetischer Zugang zum Skalarprodukt 5.4 Geometrische Deutung des Skalarprodukts 5.5 Produktive Übungen und systematische Variation 5.6 Geometrische Eigenschaften des Skalarprodukts 5.7 Skalarprodukt im Kontext Jürgen Roth • Didaktik der Linearen Algebra und Analytischen Geometrie Kapitel 5: Skalarprodukt • 5.38 Skalarprodukt im Kontext Schacht, F. (2014): Ganz schön verMESSEN! – Das Skalarprodukt aus der Perspektive des Messens. Praxis der Mathematik in der Schule 56(55), S. 32-38 Nägel und Schrauben Eine Firma produziert Nägel und Schrauben, die im Verkauf jeweils 1 € (Nägel) bzw. 2 € (Schrauben) kosten. Du kaufst 10 Nägel und 10 Schrauben – es entsteht ein Gesamtbetrag von 30 €. Solche Rechnungen lassen sich mit Kostenvektoren und Stückzahlvektoren darstellen, die sich miteinander verknüpfen lassen: 10 1 ⋅ = 10 ⋅ 1 + 10 ⋅ 2 = 30 10 2 a) Angenommen, du möchtest für 30 € Schrauben & Nägel kaufen. Welche Möglichkeiten hast du jeweils, Schrauben für 2 € und Nägel für 1 € zu kaufen? Stelle unterschiedliche Stückzahlvektoren auf und zeichne sie in der Ebene ein. b) Begründe inwiefern die verschiedenen Stückzahlvektoren zusammenhängen. Was fällt dir auf? c) Zeichne den Kostenvektor 12 im Koordinatensystem ein. Wie hängt dieser mit den Stückzahlvektoren zusammen? Jürgen Roth • Didaktik der Linearen Algebra und Analytischen Geometrie Kapitel 5: Skalarprodukt • 5.39 Skalarprodukt im Kontext Jürgen Roth • Didaktik der Linearen Algebra und Analytischen Geometrie Kapitel 5: Skalarprodukt • 5.40
