12 Die komplexen Zahlen

– 269 –
12
Die komplexen Zahlen
Motivation: Die Gleichung x2 = −1 hat in R keine Lösung. Deshalb definieren wir die ima-
ginäre Einheit i mit der Eigenschaft i2 = −1. Ferner vereinbaren wir, dass mit dieser Zahl“
”
genauso gerechnet wird wie mit reellen Zahlen.
Beispiel 12.1
a) (4 + 3i) + (2 − i) = (4 + 2) + (3i − i) = 6 + 2i.
b) (4 + 3i) · (2 − i) = 4 · 2 + 4 · (−i) + 3i · 2 + 3i · (−i) = 8 − 4i + 6i − 3 |{z}
i2 = 11 + 2i.
=−1
Definition 12.1 Die Zahl z = a + ib mit a, b ∈ R heißt komplexe Zahl. Ist z = a + ib,
so heißt a der Realteil von z, geschrieben a = Re z, und b heißt der Imaginärteil von z,
geschrieben b = Im z. Die Menge der komplexen Zahlen bildet mit den Verknüpfungen +, ·
einen Körper, das heißt, es kann mit den komplexen Zahlen gerechnet werden wie in R. Der
Körper der komplexen Zahlen wird mit C bezeichnet.
Bemerkung: Ist der Imaginärteil eine komplexen Zahl Null: z = a + 0i, so ist diese Zahl reell.
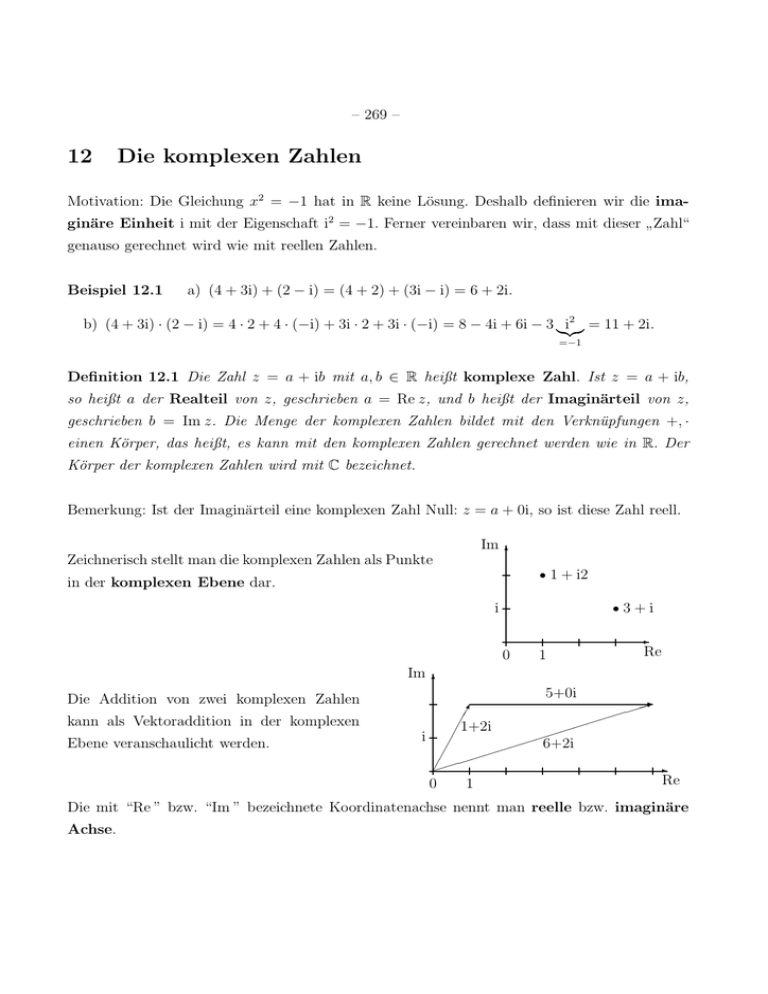
Im
Zeichnerisch stellt man die komplexen Zahlen als Punkte
6
s 1 + i2
in der komplexen Ebene dar.
i
s3 + i
-
0
Im
Die Addition von zwei komplexen Zahlen
Re
5+0i
1
1+2i
6+2i
kann als Vektoraddition in der komplexen
Ebene veranschaulicht werden.
6
1
i
0
1
Re
Die mit “Re ” bzw. “Im ” bezeichnete Koordinatenachse nennt man reelle bzw. imaginäre
Achse.
– 270 –
Beispiel 12.2
a) (4 − 3i) − (1 + 5i) = 3 − 8i.
!
b) Die Gleichung z 2 = a = (−1) · (−a) mit a ∈ R hat in C immer zwei Lösungen, falls
a 6= 0:
√
i) a > 0 : z1,2 = ± a
√ 2
√ 2
√
−a (denn ±i −a = (±i)2
−a = −(−a) = a)
ii) a < 0 : z1,2 = ±i |{z}
>0
√
a) Das Wurzelzeichen
war für reelle Zahlen dadurch eindeutig defi√
niert, dass festgelegt wurde, dass a > 0 für a > 0 gelten soll. Bei komplexen Zahlen ist
Bemerkung 12.1
eine solche Festlegung nicht möglich, da es keine “natürliche” Definition von “z > 0” bei
komplexen Zahlen gibt.
b) Die Potenzen mit ganzzahligen Exponenten ≥ 0, wie sie in Abschnitt 1.3 eingeführt wur-
den, sind auch für komplexe Basen definiert, und die dort formulierten Regeln gelten auch
für komplexe Basen. Für weitere Definitionen und Regeln, die wir in diesem Abschnitt
brauchen, wie etwa
z −n :=
1
für n ∈ N, (z · w)m = z m · w m für m ∈ Z, (z w )m = z w·m für m ∈ Z
zn
(12.1)
wurde für reelle z und w die allgemeine Potenzdefinition (5.10) verwendet. Bei komplexen
Größen z, w ∈ C brauchte man dazu z.T. den Logarithmus von komplexen Zahlen, der
uns bisher nicht zur Verfügung steht. Daher leiten wir diese Formeln ohne Verwendung
von (5.10) her:
1
ist eine sinnvolle Definition; denn die formale Anwendung der Multiplaktionsregel
zn
(1.3) ergibt für n ∈ N:
1
z n · z −n = z n−n = z 0 = 1 = z n · n .
z
Für n ∈ N gilt:
z −n :=
n
n
(z · w)n = (z · w) · (z · w) · · · (z · w) = z| · z{z· · · z} · w
| · w{z· · · w} = z · w ,
|
{z
}
n−mal
(z · w)−n =
n−mal
n−mal
1
1
1
1
= n n = n · n = z −n · w −n ,
n
(z · w)
z ·w
z w
– 271 –
(z · w)0 = 1 = z 0 · w 0 ,
n−mal
z
}|
{
w
+
w
+
·
·
·
+
w
= z w·n ,
(z ) = z| · z{z· · · z } = z
w n
w
w
w
n−mal
(z w )−n =
und
1
(z w )n
=
1
z w·n
= z −w·n = z w·(−n)
3
(z w )0 = 1 = z w·0 .
Beispiel 12.3 Die Gleichung
az 2 + bz + c = 0
mit a, b, c ∈ R
hat folgende Lösungen z ∈ C (Mitternachtsformel):
a) b2 − 4ac > 0 : z1,2 =
−b ±
√
b2 − 4ac
2a
−b
2a√
−b ± i 4ac − b2
=
2a
b) b2 − 4ac = 0 : z1 = z2 =
c) b2 − 4ac < 0 : z1,2
Definition 12.2 Es sei z := a + ib. Dann heißt z := a − ib die konjugiert komplexe Zahl
√
zu z. Ferner heißt |z| := a2 + b2 der Betrag von z.
Im
6
z1 s
s
z
i
|z|
0
= a + ib
-
Re
1
sz
= a − ib
z1 s
3
Eigentlich müsste man bei Aussage und Beweis der 3. Regel etwas sorgfältiger sein (vergl. (12.18), (12.19)
und (12.20)). Für die Anwendungen in diesem Abschnitt genügen aber diese saloppen Formulierungen.
– 272 –
Beispiel 12.4
z = 2 − 3i,
a) z := 2 + 3i,
b) Ist z = a reell, so gilt |z| =
√
|z| =
√
2 2 + 32 =
√
13.
a2 + 0 = |a|.
c) z · z = (a + ib)(a − ib) = a2 − (ib)2 = a2 − i2 b2 = a2 + b2 = |z|2 ⇒ z · z = |z|2 .
d) (4 − 3i) · (4 − 3i) = (4 − 3i) · (4 + 3i) = 42 − (3i)2 = 16 + 9 = 25.
e) z + z = a + ib + a − ib = 2 a = 2 Re z,
z − z = a + ib − a + ib = 2i b = 2i Im z
Bei einem Quotienten von zwei komplexen Zahlen macht man durch Erweiterung mit dem konjugiert Komplexen des Nenners den neuen Nenner reell und kann so die Division durchführen.
Beispiel 12.5
(1 + 5i)(4 + 3i)
4 − 15 + i(20 + 3)
11 23
1 + 5i
=
=
=− +
i
4 − 3i
(4 − 3i)(4 + 3i)
25
25 25
Für den Betrag gilt wie im Reellen:
|z · z | = |z1 | · |z2 |,
1 2
z1 |z1 |
=
z2 |z2 | für z2 6= 0,
|z1 + z2 | ≤ |z1 | + |z2 |
(12.2)
Erweiterung der Exponentialfunktion: Die in (11.8) angegebene Reihe für die Exponentialfunktion ist auch für dann überall konvergent, wenn x ∈ R durch z ∈ C ersetzt wird. Also ist die
Exponentialfunktion durch
z
e := exp z :=
∞
X
zk
k=0
=1+z+
k!
z2 z3
zn
+
+···+
+···
2!
3!
n!
z∈C
(12.3)
sinnvoll definiert, wobei u.a. auch die wichtige Eigenschaften
ez1 +z2 = ez1 ez2 , e−z2 =
ez1
1
z1 −z2
z1 −z2
und
e
für z1 , z2 ∈ C
=
e
e
=
ez2
ez2
(12.4)
(vergl. (5.4) und (5.5)) erhalten bleiben. Ein anderer wichtiger Zusammenhang ergibt sich
ebenfalls aus (12.3). Für ein reelles ϕ gilt nämlich:
eiϕ =
∞
X
(iϕ)k
k=0
k!
=
∞
X
k=0, k
gerade
(iϕ)k
+
k!
k=0, k
∞
X
ungerade
(iϕ)k
k!
– 273 –
=
∞
∞
∞
X
X
X
(iϕ)2ν+1
(i2 )ν ϕ2ν
(i2 )ν · i · ϕ2ν+1
+
=
+i
.
(2ν)!
(2ν + 1)! ν=0 (2ν)!
(2ν + 1)!
ν=0
ν=0
∞
X
(iϕ)2ν
ν=0
=
∞
X
(−1)ν ϕ2ν
ν=0
(2ν)!
+i
∞
X
(−1)ν ϕ2ν+1
ν=0
(2ν + 1)!
.
Die beiden letzten Reihen erkennen wir wieder als die Taylorreihen für den Cosinus und den
Sinus (vergl. (11.10) und (11.11)), und damit erhalten wir die wichtige als Eulersche Relation
bekannte Beziehung:
eiϕ = cos ϕ + i sin ϕ für ϕ ∈ R.
Bemerkung 12.2
(12.5)
a) Es gilt e0i = cos 0 + i sin 0 = 1 = e0 und darüberhinaus sogar für l ∈ Z
e2lπi = cos(2lπ) + i sin(2lπ) = 1 + i · 0 = 1
(12.6)
Daraus folgt unmittelbar nach (12.4):
eiϕ+2lπi = eiϕ · e2lπi = eiϕ · 1 = eiϕ .
(12.7)
eiϕ ist also eine 2π–periodische Funktion von ϕ ∈ R .
b) Es gilt ez 6= 1 für z ∈
/ {2lπi|l ∈ Z}.
c) Es gilt 1/eiϕ = e−iϕ = cos(−ϕ) + i sin(−ϕ) = cos ϕ − i sin ϕ = eiϕ für ϕ ∈ R.
d) Für α, ϕ ∈ R gilt:
eα+iϕ = eα eiϕ = eα (cos ϕ + i sin ϕ) = eα cos ϕ + ieα sin ϕ
(12.8)
und damit, da eα > 0 ist,
α+iϕ
|e
Im
q
| = |e | |cos ϕ + i sin ϕ| = e cos2 ϕ + sin2 ϕ = eα .
α
α
(12.9)
Insbesondere ist |eiϕ | = 1 für ϕ ∈ R, und ϕ ∈ R kann als Winkel intepretiert werden:
6
iϕ

se = cos ϕ + i sin ϕ

3


sin ϕ



ϕ
|
{z
} -
0
cos ϕ
Re
– 274 –
Dabei ist der Winkel im Bogenmaß anzugeben; denn es ist z.B. e90i = −0.45 + 0.89i und
nicht = cos 90◦ + i sin 90◦ = i
e) eiπ = cos π + i sin π = −1 + i · 0 = −1.
f)
eikπ
k
= eiπ = (−1)k =
(
+1
−1
für k ∈ Z und k gerade
für k ∈ Z und k ungerade
Die Formel (12.9) bietet eine zweite für viele Anwendungen zweckmäßige Darstellungsmöglichkeit der komplexen Zahlen; denn für z 6= 0 ist |z/|z|| = |z|/|z| = 1 und damit kann z/|z| durch
eiϕ dargestellt werden. Wir erhalten so die Polardarstellung
z
z = |z| ·
= reiϕ (= r cos ϕ + ir sin ϕ) mit r = |z|.
|z|
(12.10)
Dabei ist auch r = |z| = 0 zugelassen, wobei dann aber ϕ beliebig gewählt werden könnte.
Außerdem ist wegen (12.7) ϕ für z 6= 0 erst dann eindeutig bestimmt, wenn wir uns auf ein
Periodenintervall festlegen. Es gibt dafür verschiedene Möglichkeiten. Auf die unten gewählte
Im
i
Umrechnungsformel passt das Intervall −π < ϕ ≤ π.
6
z

s
3

r = |z| 

ϕ
|
{z
0
b := Im z



} Re
1 a := Re z
Aus den Beziehungen
b = r sin ϕ ≥ 0 für 0 ≤ ϕ ≤ π, b = r sin ϕ < 0 für −π < ϕ < 0 und a = r cos ϕ = r cos(−ϕ)
ergibt sich dann die folgende Umrechnung auf Polardarstellung:
(12.7)
z := a + ib = r · eiϕ
= r · ei(ϕ+2·l·π) , l ∈ Z mit
r = |z| =
√
a2 + b2 und ϕ =
(
arccos(a/r)
− arccos(a/r)
für b ≥ 0,
für b < 0,
(12.11)
– 275 –
wobei der arccos – entsprechend der Auswertung in Rechnern – Werte zwischen 0 und π annimmt. Der oben bestimmte Winkel ϕ liegt tatsächlich zwischen (−π) und π. Bei anderen
Umrechnungsformeln erhält man u.U. einen anderen Bereich für ϕ.
Beispiel 12.6 z1 := 1 + 2i, z2 := −1 + 2i, z3 := −1 − 2i:
√
1
∧
r1 = 5, b1 = 2 ≥ 0 ⇒ ϕ1 = arccos √ = 1.11(= 63.4◦ )
5
√
−1
∧
r2 = 5, b2 = 2 ≥ 0 ⇒ ϕ2 = arccos √ = 2.03(= 116.6◦ )
5
√
−1
∧
r3 = 5, b3 = −2 < 0 ⇒ ϕ3 = − arccos √ = −2.03(= −116.6◦ )
5
Aus der Polardarstellung kann man dann
die kartesische Darstellung leicht zurückgewinnen:
√
z1 =
√
z2 =
√
z3 =
Im
6
−1 + 2i s
KA
A
A i
A
A A
−1 0
−1 − 2i s
5 (cos 1.11 + i sin 1.11)
= 0.99 + 2.00 i
5 (cos 2.03 + i sin 2.03)
= −0.99 + 2.00 i
5 (cos(−2.03) + i sin(−2.03)) = −0.99 − 2.00 i
s 1 + 2i
-
1
Re
Mit den Rechenregeln für die Exponentialfunktion folgt sofort:
Satz 12.1 Es sei z1 = r1 eiϕ1 , z2 = r2 eiϕ2 . Dann gilt
a) z1 z2 = r1 eiϕ1 r2 eiϕ2 = r1 r2 ei(ϕ1 +ϕ2 ) (Beträge werden mult., Winkel addiert),
b)
z1
r1 eiϕ1
r1
=
= ei(ϕ1 −ϕ2 ) (Beträge werden dividiert, Winkel subtrahiert),
iϕ
2
z2
r2 e
r2
c) Für m ∈ Z und z1 6= 0 gilt: z1m = r1m eimϕ1 (Betrag hoch m, Winkel mit m multipliziert).
– 276 –
Bei der letzten Formel spielt die Periodizität wegen m ∈ Z keine Rolle; denn es gilt, da mit m
und l auch m · l ganzzahlig ist:
eim(ϕ1 +2lπ) = eimϕ1 e2mlπi = eimϕ1 .
Beispiel 12.7
z1
z2
a) Sei a 6= 0, a = r eiϕ . Die Gleichung z 2 = a besitzt die zwei Lösungen
)
√ iϕ/2
re
=
√
⇒ z1,2 = ± r eiϕ/2 .
√ iϕ/2 iπ
√ iϕ/2
√ i(ϕ+2π)/2
re
=
re e
= − re
=
b) Berechnung von hohen Potenzen komplexer
16
23/2 eiπ/4
(2 + 2i)16
√
=
z =
=
20
(−1 − 3i)20
(2e−2iπ/3 )
= 24 e52iπ/3 = 16e17iπ+i(π/3)
=
π
π
= −16 cos + i sin
=
3
3
Zahlen:
23·16/2 · e16iπ/2
220 · e−2·20iπ/3
= 224−20 ei(4π−(−40π/3))
16e17iπ ei(π/3)
−16
= 16 · (−1)17 eiπ/3
!
√
√
1
3
= −8 − 8 3i
+i
2
2
Ermittlung der verwendeten Polardarstellungen: 2 + 2i = 23/2 · eiπ/4 ; denn es gilt:
√
√
r1 := |2 + 2i| = 22 + 22 = 23 = 23/2
und Im (2 + 2i) = 2 ≥ 0 ⇒ ϕ1 = arccos(2/23/2 ) = π/4
√
3i = 2 · e−2iπ/3q; denn es gilt:
√
√
√
r2 := | − 1 − 3i| = 12 + ( 3)2 = 1 + 3 = 2
√
√
und Im (−1 − 3i) = − 3 < 0 ⇒ ϕ2 = − arccos(−1/2) = −2π/3
−1 −
Für die Behandlung der Differentialgleichungen im nächsten Abschnitt brauchen wir schließlich
noch die Ableitungsformel
d tλ
e = λetλ ,
(12.12)
dt
die für eine komplexe Konstante λ und eine reelle Variable t gültig ist, was am Besten über die
Exponentialreihe zu beweisen ist:
∞
∞
∞ k−1 k−1
X
d tλ
t λ
d X (tλ)k X d tk λk
e =
=
=λ
dt
dt k=0 k!
dt k!
(k − 1)!
k=0
k=1
k−1=:l
=
λ
∞ l l
X
tλ
l=0
l!
= λetλ .
– 277 –
Außerdem benötigen wir noch die Beziehung
ez = exp(Re z − iIm z) = exp(Re z) · exp(−iIm z)
= exp(Re z) · (cos(−Im z) + i sin(−Im z)) = exp(Re z) · (cos(Im z) − i sin(Im z))
= exp(Re z) · (cos(Im z) + i sin(Im z)) = exp(Re z) · exp(iIm z)
= exp(Re z)) · exp(iIm z)
= ez
(12.13)
Bei der Herleitung der Formel wurde neben der Eulerschen Relation (12.5) und der Formel
(12.4) die folgenden Regel benutzt: Für α ∈ R und z ∈ C gilt:
Re (αz) = Re (α(Re z + iIm z)) = Re (αRe z + iαIm z))
= αRe z
Im (αz) = Im (α(Re z + iIm z)) = Im (αRe z + iαIm z))
(12.14)
= αIm z
Schließlich gilt bei komplexwertigen Funktionen einer reellen Veränderlichen:
d
d
d
Re
f (x)
= Re
(Re f (x) + iIm f (x)) = Re
Re f (x) + i
dx
dx
dx
d
=
Re f (x),
dx
d
d
d
f (x)
= Im
(Re f (x) + iIm f (x)) = Im
Re f (x) + i
Im
dx
dx
dx
d
=
Im f (x),
dx
d
Im f (x))
dx
d
Im f (x))
dx
(12.15)
d.h. Realteilbildung und Ableitung sowie Imaginäteilbildung und Ableitung sind vertauschbar.
Der nun folgende letzte Teil von Kapitel 12 wird im Sommersemester 2010 nicht in der Vorlesung
und in der Übung behandelt und ist daher für die Klausuren im 2. Halbjahr 2010 und im 1.
Halbjahr 2011 nicht klausurrelevant.
Die Umrechnung in die Polardarstellung erweist sich als besonders günstig bei der Bestimmung
von Wurzeln aus einer komplexen Zahl. Wenn wir nämlich von der Polardarstellung ausgehen,
√
erhalten wir für n ∈ N durch “unkritisches” Übertragen von (5.15): n z = z 1/n = (reiϕ )1/n =
r 1/n eiϕ/n . Wir müssen aber berücksichtigen, dass wir ϕ auf ein Periodenintervall festgelegt
haben. Berücksichtigt man die Periodizität von eiϕ , so erhält man für z 6= 0 nicht eine Wurzel
– 278 –
sondern genau n verschiedene Wurzeln, was wir durch einen Index kennzeichnen:
√
1/n
iϕ 1/n
i(ϕ+2kπ) 1/n
n
z k= z
=
r
·
e
:=
r
·
e
k
k
= r 1/n · ei(ϕ+2kπ)/n = r 1/n · eiϕ/n · e2ikπ/n ,
k = 0, 1, . . . , n − 1,
(12.16)
wobei für die konkrete Ausrechnung einer der letzten beiden Ausdrücke zur Auswahl steht.
Dass die genannten n Werte für k reichen, sieht man sofort, wenn man zu k ein ganzzahliges
Vielfaches von n addiert:
ei(ϕ+2(k+nl)π)/n = ei(ϕ+2kπ)/n · e2nlπi/n = ei(ϕ+2kπ)/n · e2lπi = ei(ϕ+2kπ)/n · 1 = ei(ϕ+2kπ)/n
für l ∈ Z. Nun ist aber die in (12.16) benutzte Potenzierung einer komplexen Zahl mit einem
Exponenten ∈
/ Z eigentlich noch nicht erlaubt. Wir können mit Hilfe von (12.4) aber leicht
!
klären, dass mit (12.16) tatsächlich alle Lösungen der Gleichung w n = z erfasst sind:
Wir prüfen dazu, wann eine beliebige komplexe Zahl 6= 0, die wir durch wir durch
w := ̺1/n · eiϕ/n · e2ikπ/n ,
̺ > 0, k ∈ R,
!
darstellen können, eine Lösung der Gleichung w n = z ist: Aus (12.4) folgt
n iϕ/n n 2ikπ/n n
̺
w n = ̺1/n
e
e
= ̺n/n · einϕ/n · e2iknπ/n = ̺ · eiϕ · e2ikπ = z · · e2ikπ = z
r
⇔̺=r∧k ∈Z .
Da wir oben gezeigt haben, dass man k noch weiter einschränken kann, erhalten wir, dass mit
!
den (12.16) angegebenen komplexen Zahlen alle Lösungen von w n = z erfasst sind.
Beispiel 12.8 Es sollen die dritten Wurzeln der komplexen Zahl (−1 + 2i) bestimmt werden.
Dazu brauchen wir die bereits in Beispiel 12.6 bestimmte Polardarstellung:
√
−1 + 2i = 5 · e2.03i .
Damit gilt
√ 1/3 i(2.03+2kπ)/3 √
2.03 + 2kπ
2.03 + 2kπ
6
, k = 0, 1, 2,
+ i sin
( −1 + 2i)k = ( 5) · e
= 5 cos
3
3
√
3
und wir erhalten die drei Wurzeln:
√
( 3 −1 + 2i)0 = 1.31 · (cos 0.68 + i sin 0.68) = 1.02 + 0.82i
– 279 –
√
( 3 −1 + 2i)1 = 1.31 · (cos 2.77 + i sin 2.77) = −1.22 + 0.47i
√
( 3 −1 + 2i)2 = 1.31 · (cos 4.87 + i sin 4.87) = 0.20 − 1.29i
Wir führen jetzt analog zu (5.10) die Potenzen ein, bei denen sowohl die Basis als auch der
Exponent eine komplexe Zahl ist: Für die komplexe Zahl
z = r·exp(iϕ)(= exp(ln r) exp(iϕ) = exp(ln r+i(ϕ+k·2π)), r > 0, −π < ϕ ≤ π, k ∈ Z, (12.17)
definieren wir
(z w )k := exp(w ln r + i · (ϕ + k · 2π) · w),
w ∈ C, k ∈ Z .
(12.18)
Es ist also nicht wie im Reellen z w eindeutig zu definieren, sondern man muss berücksichtigen,
dass z = r · exp(i(ϕ + k · 2π)) für alle k ∈ Z gilt und erhält so u.U. unendlich viele Potenzen
z.B. bei
(z13.12 )k := exp (3.12 · ln r1 + i · (ϕ1 + k · 2π) · 3.12)
= exp(3.12 · ln r1 ) · exp(3.12 i ϕ1) · exp(6.24kiπ),
k ∈ Z,
wobei z1 , r1 und ϕ1 die Größen aus Beispiel 12.8 sind. Auch bei der Basis e müsste man die
Definition (12.18) anwenden, also
(ew )k := exp(1 · w + i · (0 + k · 2π) · w) = (exp w) · exp(k · 2π · w),
k ∈ Z.
Die früher angegebene und allgemein übliche Gleichsetzung ew := exp w ist also eigentlich nicht
korrekt. Trotzdem werden wir sie in den nächsten Kapiteln, bei denen die Mehrdeutigkeit ignoriert werden kann, verwenden. Bei ganzzahligen Exponenten m ∈ Z kann die Mehrdeutigkeit
ohnehin ignoriert werden: Für die in der Polardarstellung (12.17) gegebene komplexe Zahl z
erhalten wir für m ∈ Z:
(z m )k := exp(m ln r+i·(ϕ+k·2π)·m) = exp(m ln r)·exp(i·m·ϕ)·exp(k·m·i·2π) = r m ·exp(i·m·ϕ)


(r · exp(iϕ)) · (r · exp(iϕ)) · · · (r · exp(iϕ)) = (r · exp(iϕ))m
für m ∈ N


|
{z
}



m−mal
0
=
r · exp(i · 0 · ϕ) = 1 = (r · exp(iϕ))0
für m = 0



1
1
1


= −m
=
= (r · exp(iϕ))m für (−m) ∈ N
 −m
−m
−m
r exp(i · (−m) · ϕ)
r · (exp(i ϕ))
(r · exp(i ϕ))
– 280 –
für alle k ∈ Z , d.h. (z m )k ist von k unabhängig und stimmt mit der in Abschnitt 1.3 bzw. in
(12.4) gegebenen Definition von z m überein.
Mit der Potenzdefinition (12.18) lassen sich – soweit nicht schon geschehen – die in (5.15)
gesammelten Potenzrechenregeln ins Komplexe übertragen:
Für a := r exp(iϕ), r > 0, −π < ϕ ≤ π und b := ̺ exp(iψ), ̺ > 0, −π < ψ ≤ π erhalten wir
(az )0 · (aw )0 = exp(z ln r + izϕ) · exp(w ln r + iwϕ) = exp(z ln r + izϕ + w ln r + iwϕ)
= exp((z + w) ln r + i(z + w)ϕ)
= (az+w )0
(az )0 · (bz )0 = exp(z ln r + izϕ) · exp(z ln ̺ + izψ) = exp(z(ln r + ln ̺) + iz(ϕ + ψ))
= exp(z ln(r · ̺) + iz(ϕ + ψ))

z


 ((a · b) )0 für − π < ϕ + ψ ≤ π
=
((a · b)z )1 für ϕ + ψ > π


 ((a · b)z ) für ϕ + ψ ≤ −π
−1
(a−z )0 = exp((−z) ln r + i(−z)ϕ) = exp(−(ln r + iϕ)z) =
1
exp((ln r + iϕ)z)
1
(az )0
exp(z ln r + izϕ)
=
= exp(z ln r + izϕ − (w ln r + iwϕ))
exp(w ln r + iwϕ)
= exp((z − w) ln r + i(z − w)ϕ)
=
(az )0
(aw )0
= (az−w )0
exp(z ln r + izϕ)
(az )0
=
= exp(z ln r + izϕ − (z ln ̺ + izψ))
(bz )0
exp(z ln ̺ + izψ)
= exp(z ln(r − ̺) + iz(ϕ − ψ))

z


 ((a/b) )0 für − π < ϕ − ψ ≤ π
=
((a/b)z )1 für ϕ − ψ > π


 ((a/b)z ) für ϕ − ψ ≤ −π
−1
(12.19)
– 281 –
Um eine Formel für (az )w herzuleiten, benötigen wir noch einen Zwischenschritt: Mit a :=
r exp(iϕ), r > 0, −π < ϕ ≤ π und z = x + iy, x, y ∈ R gilt
(az )0 = exp(z ln r + izϕ) = exp(x ln r − yϕ + i(y ln r + xϕ))
Im Allgemeinen ist (y ln r + xϕ) nicht im Intervall (−π, π], sondern in einem ”passend” verschobenen Intervall, d.h. es gibt eine ganze Zahl l, die von a und z abhängt, mit
−π + 2lπ < y ln r + xϕ ≤ π + 2lπ .
Damit erhalten wir
((az )w
0 )l = exp ((x ln r − yϕ + i(y ln r + xϕ))w)
= exp((z ln r + izϕ)w) = exp(zw(ln r + iϕ))
= (azw )0
(12.20)