noch wichtige Theorie zum Winkel zum selber lernen

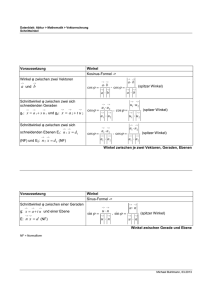
Winkelberechnungen
a) Winkel 0 < α < 180° zwischen zwei Vektoren a und b :
cos α =
a b
a⋅b
b) Schnittwinkel α zweier Geraden g1 : X = P1 + s ⋅ u1 und g 2 : X = P2 + t ⋅ u 2 :
Als Schnittwinkel zwischen g1 und g2 wird der kleinere der beiden möglichen
Winkel definiert, d.h. 0 < α < 90° . Dies erreicht man bei der Rechnung durch
positive Werte (kleinstenfalls Null) für cos α . Die Berechnungsformel lautet
(beachten Sie den Betrag im Zähler):
cos α =
u1 u 2
u1 ⋅ u 2
c) Schnittwinkel α zweier Ebenen
Ermitteln Sie die Normalenvektoren n1 und n 2 der Ebenen. Der Schnittwinkel der
beiden Ebenen ist gleich dem Schnittwinkel zweier sich schneidender Normalen
der Ebenen, also 0 < α < 90° , also:
cos α =
n1 n 2
n1 ⋅ n 2
d) Schnittwinkel α einer Geraden und einer Ebene
Auch hier gilt per Definition: 0 < α < 90°
Zwischen n und u liegt β (hier einfach so bezeichnet) aber nicht α .
Es gilt: β = 90° - α
cos β = cos(90° − α ) = sin α =
Formelsammlung
n u
n⋅u
(die letzte Gleichung ist gut für die Aufgaben)