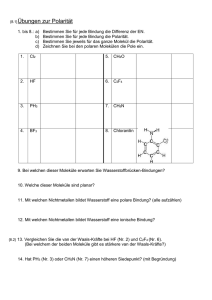
BPC I Praktikum

BPC I Praktikum
Theoretische Grundlagen zu den Experimenten
(1)
(2)
(3)
(4)
(5)
(6)
(7)
NMR
ATR-FTIR
ITC
Enzymkinetik
GC
Fluoreszenz
Docking
NMR
Kernspezifische Eigenschaften: Eigendrehimpuls, Spin und magnetisches Moment
Elektronen haben ein intrinsisches magnetisches Moment. Auch Protonen haben ein
magnetisches Moment, das jedoch ca. 2000mal schwächer ist als das des Elektrons. Daher
spielt das kernmagnetische Moment für die Reaktivität eines Moleküls keine Rolle. Dennoch
macht es ein wichtiges spektroskopisches Verfahren möglich. Das magnetische Moment
wird von einem Spin (Quantenzahl des Drehimpulses) erzeugt. Während ein Elektron immer
die Spinquantenzahl 1/2 aufweist, können Kernspins ein ganz-zahliges Vielfaches von 1/2
annehmen, da mehrere Protonen vorhanden sind, die jeweils eine Spinquantenzahl von 1/2
aufweisen. Der Eigendrehimpuls
P =  I ⋅ ( I + 1)
der Atomkerne steht in direktem Zusammenhang mit der Spinquantenzahl I. Dabei gilt
 = h / 2π , wobei h = 6,626 ⋅ 10−34 Js das Plancksche Wirkungsquantum ist. I kann Werte von
0 bis 6 annehmen, wobei der Kernspin I=0 NMR Inaktivität bedeutet.
Der Kerndrehimpuls P erzeugt immer ein magnetisches Moment
µ = γ ⋅ P = gN ⋅ βN ⋅ P = gN ⋅
e⋅
⋅P
2mPr oton
Der Kerndrehimpuls P und das magnetische Moment µ sind über das gyromagnetische
oder magnetogyrische Verhältnis γ proportional verknüpft.
e = 1,6 ⋅ 10−19 C ist die Elementarladung und mPr oton = 1,672 · 10-27 kg = 1836,152 · m Elektron ist
die Masse des Protons, die wesentlich größer ist als die des Elektrons, weshalb das
kernmagnetische Moment wesentlich geringer ist. β N = 5,051 ⋅ 10−27 J / T ist das
Kernmagneton und der Kern-g-Faktor g N eine für den jeweiligen Atomkern charakteristische
dimensionslose Zahl. γ = g N ⋅ β N ist das gyromagnetische Verhältnis. Je größer der Wert für
γ , desto nachweisempfindlicher ist die Substanz in der NMR Spektroskopie. Kerne mit
einem großen γ Wert werden daher als NMR empfindlich, solche mit einem kleinen Wert für
γ als NMR-unempfindlich bezeichnet.
Anhand der Formel ist ersichtlich, dass Kerne ohne Spin kein magnetisches Moment
aufweisen. Solche Kerne sind zum Beispiel 12C und 16O. Um sie im NMR Spektrometer zu
detektieren, müssen diese Elemente Isotopenmarkiert werden, damit sie einen Spin
aufweisen. Insgesamt beeinflusst sowohl die Form des Kerns als auch das Verhältnis
zwischen Protonen und Neutronen im Kern die NMR Empfindlichkeit.
Wechselwirkung zwischen Kerndrehimpuls und externem Magnetfeld
Bringt man nun ein Teilchen mit Kernspin in ein externes,
homogenes, statisches Magnetfeld B0, so wird sich sein
Kerndrehimpulsvektor in diesem Feld aufgrund seines
magnetischen Momentes ausrichten. Die Ausrichtung des zuvor
zufallsverteilten Kerndrehimpulses entspricht einer
Richtungsquantelung (siehe Abbildung 1). Der
Drehimpulsvektor P nimmt einen bestimmten Winkel α zur
Richtung des Magnetfelds B0 ein. Die Z-Komponente des
Drehimpulsvektors
pz= m ⋅ 
Abbildung 1 Übersicht über die
Ausrichtung von P in B0 in
Abhängigkeit von m
steht in Verbindung mit der magnetischen Quantenzahl m. Der Drehimpuls orientiert sich
also im Raum so, dass seine Komponente in Feldrichtung (PZ) ein m-Faches von  ist. M
kann Werte von I, I-1,… bis –I annehmen. Für die Z-Komponente des magnetischen
Moments gilt somit
µz = γ ⋅ m ⋅ 
Ein magnetisches Moment, das nicht parallel zum Magnetfeld
ausgerichtet ist, erfährt eine Kraft. Das resultierende
Drehmoment ist gegeben durch
Γ = µ × B0
Und befindet sich somit senkrecht zur µ − B0 Ebene. So wird
eine Bewegung von μ auf der Oberfläche eines Kegels um die
Richtung des Magnetfeldes (Z-Komponente des gedachten
Koordinatensystems) bewirkt (Präzession: siehe Abbildung 2). Abbildung 2 dicker Pfeil
entspricht P. er rotiert entlang
Die Frequenz
ω0 = 2π ⋅ f = γ ⋅ B0
der Fläche eines Kegels um B0
Mit der das magnetische Moment um die Z-Achse präzidiert heißt Lamorfrequenz. Diese
Frequenz ist kernspezifisch und nimmt linear mit der Magnetfeldstärke zu. Radiowellen
dieser Frequenz bewirken die Resonanz des Spinsystems. Solche werden bei der Messung
zusätzlich eingestrahlt um den Winkel α der Drehung so zu verändern, sodass der Vektor in
der Nähe der xy-Ebene liegt, wo er messbar ist. Auf der Z-Achse ist der Kerndrehimpuls
nicht zu messen, da das magnetische Moment sehr gering ist und vom viel größeren
externen Magnetfeld überlagert wird.
Die Anzahl der energetischen Niveaus
Energetisch gesehen bedeutet eine Ausrichtung des
Atomkerns eine Aufspaltung in Energieniveaus (Zeeman
Effekt). Es gibt für einen Spin I , der zuvor zufällig im Raum
ausgerichtet war, exakt 2 I + 1 verschiedene Energieniveaus
in einem äußeren Magnetfeld B0. Für das Wasserstoffatom gilt
I = 1 2 , wodurch 2 mögliche Energieniveaus möglich sind
(siehe Abbildung 3). Der Abstand der Energieniveaus nimmt
linear mit der Magnetfeldstärke zu. Für Wasserstoff gibt es
den energetisch niedrigeren Zustand α bzw. + 1 2 , der
Abbildung 3 Aufteilung der
Energieniveaus. Energiedifferenz
zwischen Niveaus steigt mit B0
parallel zum Magnetfeld ausgerichtet ist und den energiereicheren, antiparallelen Zustand β
bzw. + 1 2 . Es herrscht ein thermisches Equilibrium der Absolutmagnetisierung, wenn alle
Spins im α oder β Zustand vorliegen, diese Zustände aber untereinander wechseln können.
Die Energie der Niveaus und ihre Verteilung
Die Energie eines Teilchens
E = − µ Z B0 = −γ ⋅ PZ ⋅ B0 = −γ ⋅ m ⋅  ⋅ B0
ist der Stärke des äußeren Magnetfeldes proportional. Da es auch stets 2I+1 verschiedene m
Werte und damit Orientierungsmöglichkeiten für das magnetische Moment gibt, lassen sich
die Energien der zwei möglichen Niveaus berechnen:
1
Eα / β = ± γ ⋅  ⋅ B0
2
Für das Wasserstoffatom ergibt sich so eine Energiedifferenz, das so genannte ZeemanSplitting von
1 
1

∆E =  − γ ⋅ B0 ⋅  ⋅ +  −  − γ ⋅ B0 ⋅  ⋅ −  = −γ ⋅  ⋅ B0 ,
2 
2

welche aufgebracht werden muss, um vom α in den β Zustand zu gelangen.
Die Population der Spin ½ Teilchen teilt sich proportional zur Zeeman-Energie ΔE und zur
thermischen Energie der Teilchen (führt zur Vermischung der Zustände) in beide
Energieniveaus auf. Die Populationsverteilung entspricht einer Boltzmann-Verteilung
∆E
−
β
= e kT
α
So kommt es zu einer Überschussmagnetisierung der Gesamtprobe. Es liegen mehr Spins
im Zustand α als im Zustand β. Dies ist per NMR detektierbar, wobei zu beachten ist, dass
das beobachtete Signal immer der Gesamtüberschuss-Magnetisierung aus allen Spins der
Probe entspricht. Die Überschussmagnetisierung ist jedoch sehr gering und nimmt mit der
Stärke des Magnetfelds zu.
Einstellung der Überschussmagnetisierung
Wird eine Probe in ein Magnetfeld eingebracht, stellt
sich die Überschussmagnetisierung jedoch nicht sofort
ein. Die räumliche Orientierung bleibt zunächst
unverändert. Spins verhalten sich wie Magneten und
beeinflussen sich daher über ihr Magnetfeld gegenseitig
(dipolare Kopplung). Da sich die Teilchen in Lösung sehr
schnell bewegen erfahren sie so ein leicht zeitlich
fluktuierendes Magnetfeld. Dadurch fluktuiert auch die
Drehachse der Spins. Das fluktuierende Magnetfeld
setzt sich aus dem starken äußeren und den sie jeweils
umgebenden Magnetfeldern zusammen. Wenn eine
Komponente des Magnetfeldes mit der Lamorfrequenz
um die Spins oszilliert, kann durch Resonanz-Effekt der
Drehachsen-Fluktuation ein Übergang zwischen den
Energieniveaus ausgelöst werden, indem die
Drehachse immer stärker fluktuiert, bis sie letztlich
nahezu parallel oder antiparallel zur Z-Achse steht.
Dadurch, dass die Vektoren jedoch nicht kohärent um
die Z-Achse präzidieren, ist die Nettomagnetisierung
(siehe Abbildung 4) exakt auf der Z bzw. der –Z Achse
Abbildung 4 dicker Pfeil entspricht der
Nettomagnetisierung; sie ergibt sich aus
den nicht kohärent rotierenden einzelnen
Kerndrehimpulsvektoren. Im α Zustand
liegen mehr Kerndrehimpulsvektoren vor.
Hier liegt demnach die
Überschussmagnetisierung
vorzufinden. Wie bereits beschrieben ist hier jedoch
aufgrund des externen Magnetfeldes keine
Überschussmagnetisierung messbar.
So wird mit der Zeit die energetisch günstigere
Überschussmagnetisierung erzeugt. Dieser Prozess
kann über einen exponentiellen Anstieg der
Nettomagnetisierung
t
− 

T1 

M Z (t ) = M eq 1 − e




Abbildung 5 Einstellung der
Überschussmagnetisierung, nach
Einstellung des externen Magnetfeldes
beschrieben werden (siehe Abbildung 5), wobei T1 „Spin Lattice Relaxation“ Konstante
genannt wird. Sie muss mittels eines Experiments bestimmt werden. M eq ist die
Magnetisierung im Equilibrium (Gleichgewicht).
Messung der Überschussmagnetisierung, Radiofrequenz-Pulstechnik
Wenn sich die Überschussmagnetisierung nun eingestellt hat, muss sie nun detektierbar
gemacht werden, indem die Magnetisierung von der Z bzw. –Z Achse in die xy-Ebene
geklappt wird. Dies geschieht durch einen 90° Puls. Ist der Kerndrehimpulsvektor in der xyEbene angelangt erzeugt die Magnetisierung ein zeitlich veränderliches Magnetfeld. Dieses
erzeugt einen Strom in der fest installierten Detektorspule. Dieser erzeugt ein messbares FID
Signal. Bei einem Puls handelt es sich um eine elektromagnetische Welle der
Lamorfrequenz einer bestimmten Dauer und Intensität. Diese Welle entspricht einem mit der
Lamorfrequenz rotierenden Vektor. Wechselwirkt dieser mit dem Kerndrehimpulsvektor, der
ebenfalls mit der Lamorfrequenz rotiert, so kommt es zur Resonanz und der Winkel α des
Kerndrehimpulsvektors zur Z-Achse verändert sich.
longitudinale Relaxationszeit T1 und transversale Relaxationszeit T2
Diese Relaxationszeiten sind unterschiedlichen Ursprunges, bewirken jedoch beide eine
Abnahme der Signalintensität mit der Zeit. Die T1 Relaxationszeit beschreibt die Zeit, die der
Drehimpuls-Vektor benötigt seine xy-Komponenten zu verlieren, indem er zurück zur ZAchse relaxiert. Für das Verständnis um die T2 Relaxationszeit stellt man sich die in der
NMR letztlich gemessene Nettomagnetisierung als Summe der Einzelmagnetisierungen vor.
Alle Spins präzidieren mit ihrer Lamorfrequenz um die Z-Achse. Da die Lamorfrequenz
jedoch Magnetfeldabhängig ist und sich die Spins in leicht unterschiedlichen magnetischen
Umgebungen befinden, geht die Kohärenz der Einzelspins mit der Zeit verloren, weil die
Lamorfrequenz fluktuiert. Diese Kohärenz macht jedoch die Überschussmagnetisierung und
somit die Intensität des Signals aus. Liegt absolut keine Kohärenz vor, befindet sich die
Nettomagnetisierung wieder auf der Z-Achse, weshalb sie nicht mehr zu detektieren ist.
Beide Relaxationszeiten lassen sich durch Experimente bestimmen. Im Folgenden soll nur
das „Inversion-Recovery“ Experiment zur Bestimmung von T1 erläutert werden.
Inversion-Recovery Experiment zur Spin-Gitter Relaxation (T1)
Zunächst wird durch einen 180° Puls die Nettoüberschussmagnetisierung um 180°, von der
Z-Achse auf die -Z-Achse gedreht. Dazu wird eine Radiowelle mit der Resonanzfrequenz der
zu drehenden Spins eingestrahlt. So wandert die Nettoüberschussmagnetisierung von oben
entlang der Z-Achse nach unten, indem sich der Winkel α des Kerndrehimpulsvektors durch
Resonanzeffekt vergrößert, bis die Rotation des Überschuss-Kerndrehimpulsvektors um die
–Z Achse erfolgt (energetisch ungünstiger Zustand), anstatt um die Z-Achse (energetisch
günstiger Zustand). Aus dieser energetisch invertierten Lage (die Boltzmann-Verteilung
wurde umgekehrt) relaxiert das Spinsystem zurück in den Ausgangszustand, indem die
Nettoüberschussmagnetisierung wieder entlang der Z-Achse nach oben wandert.
Abbildung 6 Übersicht über das
Inversion-Recovery Experiment.
Zunächst schiebt ein 180° Puls die
Überschussmagnetisierung auf –Z.
Unterschiedliche Zeiten des Wartens
vor dem 90° Puls bewirken ein
unterschiedliches Signal nach diesem
90° Puls.
Die Rückkehr in den energetischen Gleichgewichtszustand wird durch die Änderung der
Schwingungszustände der Moleküle ermöglicht. Die Dauer der Relaxationszeit hängt somit
auch von der Molekülbewegung ab. Stimmt die Molekülbewegung nicht mit der
Resonanzfrequenz überein bewirkt ein fluktuierendes Magnetfeld zu einer höheren
Wahrscheinlichkeit die Entstehung einer Rotations-Frequenz ungleich der Lamorfrequenz,
wodurch die T1 Relaxationszeit groß wird. Wenn die Molekülbewegung und die
Resonanzfrequenz ideal harmonieren, ist die Relaxationszeit minimal. Die Molekülbewegung
hängt von der Temperatur (Molekülbewegung steigt) und der Viskosität (Molekülbewegung
sinkt) des Lösungsmittels ab (Hierzu siehe auch Diskussionsteil).
Nachdem eine gewisse Zeit nach dem 180° Puls vergangen ist, kann nun ein 90° Impuls
eingestrahlt werden, der die Magnetisierung in die xy-Ebene bringt. Erst in dieser Position
(transversal) kann die Magnetisierung beobachtet werden. Dieses Experiment muss nun für
mehrere Zeiten τ zwischen dem 180° und dem 90° Impuls durchgeführt werden, bis
diejenige Zeit gefunden ist, für die kein Signal mehr detektierbar ist. Diese Zeit wird benötigt,
um die invertierte Anfangsnettomagnetisierung des Spins (-MZ) genau auf 0 zu bringen. Für
die Inversion-Recovery (T1 Relaxation) lässt sich die Magnetisierung wie folgt beschreiben:
t
−

T1

M Z (t ) = M eq 1 − 2e






Der resultierende Graph ist in folgender Abbildung 7 zu sehen.
Abbildung 7 Abhängigkeit der Signal-Intensität
zwischen 180° Puls und 90° Puls
a (τ ) von der Zeit τ
Spin Echo Experiment zur Spin-Spin Relaxation (T2)
Bei t = 0 werde die Magnetisierung mit einem π/2 bzw. 90° Puls in die x-Richtung gedreht
und beginnt zu präzedieren. Die Inhomogenität des Feldes bewirkt, dass die
Präzessionsfrequenz ebenfalls nicht einheitlich ist. Das bedeutet, dass die einzelnen
Teilmagnetisierungen sich schon bald planar um B0 verteilt haben und sich gegenseitig
kompensieren. In obigem Bild ist dies mit zwei Teilmagnetisierungen (rot und blau)
dargestellt, die im rotierenden Koordinatensystem schneller (blau) bzw. langsamer (rot) als
die mittlere Präzessionsfrequenz sind. Der mit der Verzögerung τ auf den ersten Impuls
folgende π bzw. 180° Puls vertauscht die vorauseilenden Teilmagnetisierungen mit den
zurückgebliebenen. Vorausgesetzt, die Präzessionsgeschwindigkeit bleibt konstant, treffen
sich alle Teilmagnetisierungen wieder in der ursprünglichen Richtung, wenn die Verzögerung
τ ein weiteres Mal abgelaufen ist. Das Messsignal sieht wie die rote Linie im oberen
Diagramm in Abb. 1 aus. Das Zusammentreffen nach 2τ äußert sich als Wiederanstieg des
Signals und wird als Echo bezeichnet.
Die T2 läuft schneller ab als die T1:
 − Tt
M Y (t ) = M eq  e 2






FID Signal, Fouriertransformation, Frequenz-Spektrum
Der Strom, welcher in der Spule erzeugt wird, ist auf dem Monitor als FID (free induction
decay) zu sehen. Es handelt sich um eine Sinusförmige Kurve, welche die Intensität in
Abhängigkeit der Zeit darstellt. Die Intensität entspricht den einer bestimmten Zeit
zugeordneten Aufenthaltsorten (innerhalb der xy-Ebene) aller kohärenten
Kerndrehimpulsvektoren, die um die Z-Achse rotieren. Wenn sich die Spule (siehe Abbildung
8) in Richtung der –x Achse befindet, erzeugt der Kerndrehimpulsvektor, wenn er sich auf
der –x Achse befindet eine Maximalintensität, auf der x-Achse erzeugt er ebenso eine
Maximalintensität, mit umgekehrtem Vorzeichen. Auf der y-Achse ist die Intensität jeweils 0.
Die Sinuskurve schwächt aufgrund der Relaxation (Kerndrehimpulsvektor verlässt die xy-
Abbildung 9 nach der FT resultierendes typisches NMR-Spektrum,
deren Piks anhand der Farbmarkierung bestimmten Gruppen eines
Moleküls zugeordnet werden konnten
Ebene und verliert an Kohärenz) mit der Zeit ab.
Dieses Zeitdomänensignal wird nun mittels Fouriertransformation in ein Frequenzspektrum
umgewandelt. Dazu wird aus der erhaltenen FID-Funktion ein Produkt mit einer SinusFunktion und über dieses Produkt ein Integral gebildet. Sind beide Faktoren gleich so ist das
Integral maximal, es resultiert ein Peak im Frequenzspektrum (siehe Abbildung 9). Sind sie
nicht gleich, heben sie sich zu null auf. Jeder Peak bei einer bestimmten Frequenz kann im
Frequenzspektrum einer bestimmten chemischen Gruppe zugeordnet werden
Fourier Transformation
Jedes Proton hat eine unterschiedliche Larmorfrequenz, je nachdem in welcher chemischen
Umgebung sie sich befinden; Bei einer NMR Messung werden alle Frequenzen gleichzeitig
eingestrahlt, weshalb auch alle H Atome angeregt werden, wodurch sich ihre
Kerndrehimpulsvektoren mit ihrer Larmorfrequenz (nach einem 90° Puls) innerhalb der xy
Ebene um die Z Achse drehen; jedes einzelne Proton induziert dadurch einen Wechselstrom
in der Spule mit seiner Larmofrequenz, wodurch es im FID zu einer Überlagerung aller
Larmorfrequenzen kommt; daher lassen sich aus dem zeitdomänen Signal des FID nicht
einfach die Frequenzen ableiten;
Die Fourier Transformation ist eine mathematische Operation, mit der die Zeitdomänen
Information der F(t) Funktion (FID) in die Frequenzdomänen Information der F(omega)
Funktion (Spektrum) umgewandelt wird;
Das FID stellt eine periodische Funktion dar, die sich durch eine Reihe harmonischer
Funktionen annähern lässt:
Es wird das Produkt zwischen f(t) und dem sinusteil, sowie dem cosinusteil gebildet;
Dabei werden alle Frequenzen einmal für den sinusteil (Punktsymmetrisch) und einmal für
den cosinusteil (Achsensymmetrisch) durchprobiert; ist z.b. der sinusteil für eine bestimmte
Frequenz gleich der Funktion f(t), so ergibt das Produkt der beiden Funktionen eine
maximale Intensität; es resultiert somit ein Peak; genauso wird das mit dem cosinusteil
gemacht;
F(omega) ist eine komplexe Größe, weshalb man nach der FT zwei Spektren erhält; einen
Realteil (durch den cosinusteil) und einen Imaginärteil (durch den sinusteil)
Zeitfunktion (links) und Frequenzfunktion (rechts) für zwei um 90° phasenverschobene
Signale. Die obere Frequenzfunktion ist das Absorptionsspektrum oder der Realteil, und die
untere ist das Dispersionsspektrum oder der Imaginärteil. In der Praxis ergibt die
Fouriertransformation zunächst eine Kombination der beiden Frequenzfunktionen (jedes
Signal liefert 2 Peaks), aus denen man durch Phasenkorrekturen die reinen Absorptions- und
Dispersionsspektren berechnet. Bei der Phasenkorrektur wird aus dem einen Teil das für die
Praxis relevante Absorptionsspektrum berechnet (enthält 1 Peak je Signal), während der
andere Teil, das Dispersionsspektrum, die um 90° phasenverschobenen Signale enthält.
Nachteile und Vorteile der NMR Spektroskopie
Nachteil: Der Energieabstand zwischen den Niveaus ist im Vergleich zu kT sehr gering.
Dadurch wird der Nachweis der Energieabsorption erheblich erschwert, da die Niveaus
annähernd gleich besetzt sind (siehe Boltzmann-Verteilung). Das NMR Signal wird so nur
durch einen sehr kleinen Anteil der Kernspins erzeugt. Daher sind sehr starke Magneten
notwendig, um eine Erhöhung der Energieabstände der Niveaus zu bewirken.
Vorteil: Das Magnetfeld entspricht nicht dem angelegten Magnetfeld, sondern einem lokalen
Magnetfeld. Dieses lokale Magnetfeld wird von der Elektronenverteilung an dem
untersuchten Atom und an benachbarten Atomen beeinflusst. Die so genannte chemische
Verschiebung bewirkt die Differenz zwischen dem externen und dem induzierten Magnetfeld.
Daher weisen H-Atome in verschiedenen Molekülen auch verschiedene Lamorfrequenzen
auf (siehe Abschnitt 12: chemische Verschiebung)
Vorteil: Einzelne magnetische Dipole wechselwirken miteinander. Dies bewirkt die
Aufspaltung der Energieniveaus von Systemen mit zwei Spins und die Entstehung von
Multiplettspektren. Diese liefern unmittelbare Informationen über die Struktur eines Moleküls
(Die Einführung in das Thema „Multiplettspektren“ in diesem Protokoll wurde übergangen, da
es im Rahmen des Versuches keine Rolle spielt)
Die chemische Verschiebung
Die Ursache der chemischen Verschiebung ist die magnetische Suszeptibilität der
Elektronen, die den jeweiligen Atomkern umgeben. Die magnetische Suszeptibilität gibt die
Fähigkeit der Magnetisierung in einem externen Magnetfeld an. Das resultierende induzierte
Magnetfeld führt zu einer teilweisen Abschirmung des externen Magnetfeldes. Die
Abschirmwirkung wird von der Elektronendichte beeinflusst.
Die chemische Verschiebung für ein isoliertes Atom:
Die Richtung des induzierten Magnetfeldes ist der des externen entgegengesetzt und
proportional. Man spricht von einer diamagnetischen Reaktion
Binduziert = −σ ⋅ B0
Die Proportionalitätskonstante ist die Abschirmkonstante σ . Das Gesamt-Magnetfeld ist die
Summe aus induziertem und externem Magnetfeld
BGesamt = (1 − σ ) ⋅ B0
Somit ergibt sich eine neue Resonanzfrequenz in Abhängigkeit der Abschirmkonstante
(welche durch die das betrachtende Atom umgebenen Elektronendichten bestimmt wird)
ω0 = 2π ⋅ f = γ ⋅ B0 ⋅ (1 − σ )
Da der Wert für die Abschirmkonstante mit zunehmender Ordnungszahl und somit auch
Elektronendichte ansteigt, verringert also eine ansteigende Elektronendichte die
Resonanzfrequenz.
Die chemische Verschiebung für ein Atom in einem Molekül
σ ändert sich, sobald benachbarte Atome oder Gruppen die Elektronendichte des
betrachtenden Atoms verringert oder erhöht. Ursache für diese chemische Verschiebung
sind erstens die Elektronegativität benachbarter Gruppen und zweitens die Magnetfelder
benachbarter Gruppen. Dies führt zu einer Frequenzverschiebung, die Rückschlüsse auf die
Umgebung des Atoms und somit die Struktur des Moleküls zulässt.
Hier wird die chemische Verschiebung δ definiert als dimensionslose Größe (ppm-1) zur
Beschreibung der Frequenzverschiebung in Bezug auf eine festgelegte Referenzverbindung.
Dabei gilt die Betrachtung immer einem bestimmten Atom, wie zum Beispiel 1H.
δ (1H )
ppm
=
f − f ref
f ref
=
(γ ⋅ B0 ⋅ (1 − σ ) ) − (γ ⋅ B0 ⋅ (1 − σ ref ) )
γ ⋅ B0 ⋅ (1 − σ ref )
=
γ ⋅ B0 ⋅ (σ ref − σ )
≈ σ ref − σ
γ ⋅ B0 ⋅ (1 − σ ref )
Die Referenz ist im Falle der NMR Spektroskopie des 1H die Verbindung Tetramethylsilan
(CH3)4Si.
ATR-FTIR
Spektroskopie
Die spektroskopischen Techniken beruhen auf den Übergängen zwischen verschiedenen
erlaubten Energie- bzw. Quantenzuständen von Molekülen oder Atomen aufgrund ihrer
Wechselwirkung mit elektromagnetischer Strahlung. In den meisten Experimenten, wie auch
hier, misst man eine Abschwächung oder Verstärkung der einfallenden Strahlung, die durch
Anregung von Atomen oder Molekülen oder ihren Rückfall in Zustände niedrigerer Energie
ausgelöst wurde, als Funktion der Wellenlänge oder Frequenz. Ein grundlegendes Ergebnis
der Quantenmechanik ist die diskrete Natur der Energiespektren von Atomen und Molekülen.
Solche können nur jene Energiebeträge aufnehmen und abgeben, welche der Differenz
zwischen zwei Energieniveaus entsprechen. Das Energiespektrum ist somit für jede
chemische Substanz einzigartig. Es muss nur in die Struktur der jeweiligen Substanz
übersetzt werden. Da die Energiespektren quantenmechanischer Systeme diskret sind,
setzen sich die Absorptions- und Emissionsspektren aus einzelnen Linien zusammen. Dabei
ist jede Linie einem Übergang zwischen zwei erlaubten Energieniveaus eines Systems
zugeordnet. Die Frequenz hängt mit den, am Übergang beteiligten, Energieniveaus über
h ⋅ f = E2 − E1 zusammen. Bei der IR Spektroskopie regen Frequenzen im IR Bereich
Schwingungen an (Übergang zwischen Schwingungsniveaus), wobei gleichzeitig auch
Rotation angeregt wird (reine Rotationsanregung würde durch Strahlungen im
Mikrowellenbereich geschehen)
Die Spektroskopie erlaubt es mit 13 Größenordnungen der Photonenenergie zu arbeiten
(von Mikrowellen bis Röntgenstrahlung):
Spektroskopieart
NMR
Kernspinübergang
Wellenlänge
Radiowellen:
λ = 10 nm
Energieabstand
E = 10 −8 kJ / mol
9
Rotationsspektroskopie
Anregung der
Translation
Übergang im
?
?
Mikrowellen:
E = 10−2 kJ / mol
Vibrationsspektroskopie
Elektronenspektroskopie
Rotationsniveau
Übergang im
Vibrationsniveau
Elektronischer
Übergang
λ = 105 nm
Infrarotwellen:
λ = 103 nm
Ultraviolett:
λ = 450nm
E = 103 kJ / mol
E = 3 ⋅ 105 kJ / mol
Spektroskopiker verwenden anstelle der Wellenlänge oder Frequenz die Wellenzahl, den
Kehrwert der Wellenlänge in reziproken Zentimetern: ν~ = 1 / λ [cm −1 ] . Die Frequenz
entspricht so: f = ν~ ⋅ c [ s −1 ] .
Wechselwirkung von elektromagnetischer Strahlung mit Molekülen
permanente und dynamische Dipolmomente
Licht ist eine elektromagnetische Welle, die sich mit aufeinander senkrecht stehenden
elektrischen und magnetischen Feldkomponenten fortpflanzt. Nehmen wir ein zweiatomiges,
dipolares Molekül. Die beiden Atome, über die Bindung verbunden, schwingen um den
Gleichgewichtsabstand x und erzeugen so ein periodisch in der Zeit veränderliches
dynamisches Dipolmoment. Wenn nun das äußere elektrische Feld und die Schwingung des
Dipolmoments (deren Frequenz sich ständig verändert) die gleiche Frequenz besitzen und
sich in Phase befinden, kann das Molekül Energie aus dem Feld aufnehmen. Alle
Schwingungen von Molekülen mit Symmetriezentrum, die symmetrisch zu diesem Zentrum
erfolgen sind IR-inaktiv, da sie lediglich ein über die Zeit unveränderliches dynamisches
Dipolmoment aufweisen. Die entsprechende Absorption ist zu schwach um im Spektrum
sichtbar zu sein. Dafür lässt sich die Emission der entsprechend IR-inaktiven Bindung
messen. Diese liefert ein Raman-Spektrum. Symmetrische Gruppen können demnach
mittels Raman-Spektrum, asymmetrische mittels IR-Spektrum nachgewiesen werden.
Die Größe des permanenten Dipolmoments ist abhängig von der Bindungslänge und dem
Ausmaß der Ladungsverschiebung zwischen den zwei polarisierten Komponenten eines
Dipols. Die Ladungsverschiebung hängt von den überlappenden Elektronendichten beider
Atome ab und ist somit vom Kernabstand abhängig. Bei der Schwingung des Moleküls
entsteht zusätzlich ein dynamisches Dipolmoment, wodurch sich das Gesamtdipolmoment
verändert. Da die Amplitude der Schwingung nur einem kleinen Bruchteil der Bindungslänge
entspricht, ist das dynamische Dipolmoment wesentlich kleiner als das permanente.
Die Energieabsorption eines Moleküls im Infrarotbereich wird durch das dynamische
Dipolmoment bestimmt (Die Energie wird von der Vibration aufgenommen). Die
Energieabsorption eines Moleküls im Mikrowellenbereich wird durch das permanente
Dipolmoment bestimmt (Die Energie wird von der Rotation aufgenommen). Da wesentlich
weniger Energie für eine Anregung der Rotation ausreicht als für die Anregung der Vibration
ist mit einem Energieübergang im Vibrationsbereich auch immer ein Übergang der Rotation
verbunden.
Genauer: wann ist eine Bindung IR aktiv und wann nicht?
Damit ein Molekül IR-Strahlung absorbieren kann, muss sich das Dipolmoment durch die
Schwingungs- bzw. Rotationsbewegungen ändern (also ein dynamischer Dipol vorliegen);
dies ist für alle permanenten Dipole gewährleistet; aber auch solche Moleküle, die kein
permanentes Dipol aufweisen, können ein dynamisches Dipolmoment haben;
Anhand der Grundschwingungen eines linearen dreiatomigen Moleküls (z.B. wie CO2) wird
die Änderung des Dipolmomentes dargestellt.
Abbildung: symmetrische valenzschwingung (Dipolmoment ändert sich nicht)
Tatsächlich ist die symmetrische Valenzschwingung des gestreckten Moleküls nicht infrarotaktiv, da diese Schwingung keine Änderung des Dipolmomentes bewirkt. Die beiden
Sauerstoffatome bewegen sich simultan vom zentralen Kohlenstoffatom weg oder auf dieses
zu. Es tritt keine periodische Gesamtänderung der Ladungsverteilung auf. Die
Ladungsschwerpunkte der positiven und negativen Ladung fallen in jeder Phase der
Schwingung zusammen. Das Dipolmoment ist gleich Null.
Abbildung: antisymmetrscihe Valenzschwingung (Dipolmoment ändert sich)
Während der antisymmetrischen Valenzschwingung hingegen ändert sich das Dipolmoment
und es tritt Infrarotabsorption auf. Ein Sauerstoffatom entfernt sich vom Kohlenstoffatom,
währenddessen sich das andere Sauerstoffatom dem zentralen Kohlenstoffatom nähert. Die
Ladungsverteilung verändert sich damit periodisch.
Abbildung: Deformationsschwingung (Dipolmoment ändert sich)
Ähnlich ist es auch bei der Deformationsschwingung. Diese ist ebenfalls infarot-aktiv, da sich
aufgrund der mit der Schwingung auftretenden gewinkelten Struktur die Dipolmomente
während der Schwingung ändern.
Betrachtet man zusätzlich die Raman-Aktivitäten der Schwingungen des oben gezeigten
dreiatomigen linearen Moleküls, so erkennt man, dass keine Schwingung gleichzeitig
Raman-aktiv und Infrarot-aktiv ist.
Absorptions- und Emissionsraten
Insgesamt gibt es drei unterschiedliche Wechselwirkungen zwischen Licht und Molekül. Bei
der Absorption regt ein einfallendes Photon einen Übergang zu einem höheren
Energieniveau an. Bei der stimulierten Emission fällt ein angeregter Zustand unter
Aussendung eines Photons auf ein nieder energetisches Niveau zurück. Absorption und
stimulierte Emission werden von einem Photon ausgelöst, das auf ein Molekül auftrifft. Bei
der stimulierten Emission stimmen Phase und die Ausbreitungsrichtung mit dem einfallenden
Photon überein (kohärente Photonenemission). Die spontane Emission ist ein zufälliges
Ereignis, wobei die entsprechende Übergangsrate mit der Dauer des angeregten Zustands
zusammenhängt. Die emittierten Photonen sind nicht kohärent. Ihre Phase und
Ausbreitungsrichtung sind zufallsverteilt.
Absorptionsrate und stimulierte Emission sind proportional zur Strahlungsdichte bei einer
bestimmten Frequenz ρ ( f ) . Die spontane Emission ist von dieser unabhängig, da sie durch
elektromagnetischen Feldern der Vakuumfluktuation ausgelöst wird und nicht von der im
Versuch eingestrahlten Photonenmenge. Für ein genaueres Verständnis der spontanen
Emission siehe Literatur der Quantenelektrodynamik (quantenfeldtheoretische Beschreibung
des Elektromagnetismus). Jeder dieser drei Übergangsraten ist abhängig von der Anzahl der
Moleküle im jeweiligen Zustand (Grundzustand oder angeregter Zustand: N1 oder N2). Es
müssen immer so viele Übergänge vom Grundzustand in den angeregten Zustand
geschehen, wie sie vom angeregten in den Grundzustand stattfinden:
Stimuliert:
B1→2 ⋅ ρ ( f ) N 1 = B2→1 ⋅ ρ ( f ) N 2 ,
Spontan:
A1→2 ⋅ ρ ( f ) N 2 = A2→1 ⋅ ρ ( f ) N 2
wobei B und A Proportionalitätskonstanten darstellen. Die Proportionalitäts-konstanten
stehen wie folgt im Zusammenhang
B1→ 2 = B2 →1 , A1→2 = A2→1
A2 →1 8π ⋅ h ⋅ f 3
=
und
B2 →1
c3
Schwingungsmodi und Schwingungsübergänge,
harmonische und anharmonische Schwingungen von Molekülen
Die wahrscheinlichsten Übergänge in der Schwingungsspektroskopie
Da Übergänge zwischen einem Zustand n=0 zu einem anderen Zustand n=1 nur dann
stattfinden können, wenn Zustand n=0 auch in ausreichender Menge existiert, ist es wichtig
zu wissen welche der unendlich vielen Schwingungsniveaus eine nennenswerte
Besetzungswahrscheinlichkeit aufweist. Bei Raumtemperatur befinden sich fast alle
Moleküle einer makroskopischen Probe im Schwingungsgrundzustand, da
N1
<< 1
N0
(bei höheren Temperaturen wird das Verhältnis größer; Die Berechnung kann mit der
Boltzmann- Verteilung
Ni = N0 ⋅ gi ⋅ e
−
E
K B ⋅T
durchgeführt werden). Daraus folgt, dass diese Moleküle Strahlung bestimmter Frequenzen
von ihren Schwingungsgrundzuständen n=0 absorbieren. Nun ist die Frage, welche
Endzustände möglich sind. Für einen harmonischen Oszillator gilt die Auswahlregel Δn=1.
Da einzig der Schwingungsgrundzustand nennenswert besetzt ist, beobachtet man einen
Übergang n=0  n=1. Oberschwingungen bzw. Oberton-Übergänge (Δn>1) sind wesentlich
schwächer, unwahrscheinlicher, treten aber dennoch auf.
Die verschiedenen Schwingungsmodi
Im Allgemeinen lassen sich alle Schwingungen grob folgenden Typen zuordnen. Man
unterscheidet erstens die Valenzschwingungen oder auch Streckschwingungen ν
(Bindungslängen werden geändert, mehr Energie zur Anregung notwendig) von den
Deformationsschwingungen oder auch Scherschwingungen (Bindungswinkel variieren,
weniger Energie zur Anregung notwendig)
Betrachtet man die Streckschwingungen, so ist eine Einteilung in symmetrische
Schwingungen ν S (verlaufen unter Wahrung der Molekülsymmetrie) und antisymmetrische
Schwingungen ν as (Symmetrieelemente gehen verloren) möglich.
Betrachtet man hingegen die Scherschwingung, so unterscheidet man ebene (Schwingung
innerhalb einer Ebene) von nichtebenen (die drei zueinander schwingenden Atome bilden
keine Ebene) Schwingungen. Die rocking- (Pendel-) und wagging- (Kipp-) Schwingungen
tragen das Kürzel γ , die bending- und twist- Schwingungen tragen das Kürzel δ .
Spricht man von entarteten Schwingungen, so meint man unterschiedliche Schwingungen,
die bei derselben Wellenlänge absorbieren und somit zu demselben Absorptionspeak
beitragen.
Im Versuch sollen vor allem antisymmetrische und symmetrische Streckschwingungen
untersucht werden. Die Frequenzen für diese Schwingungen lassen sich mit folgenden
Gleichungen berechnen
f antisym =
1
2π
k1 + 2k 2
µ
f sym =
1
2π
k1
µ
Anhand der Formeln sieht man, dass der antisymmetrische Modus der Streckschwingung die
höhere Frequenz, also die höhere Wellenzahl aufweist.
Übersicht über Schwingungsmodi zur Analyse der Wasser- und Lipidspektren
In der folgenden Tabelle sind alle möglichen Schwingungsmodi in Wasser aufgelistet.
In der folgenden Tabelle sind alle möglichen Schwingungsmodi in Lipiden aufgelistet
Der harmonische Oszillator in der klassischen Physik
Es handelt sich um ein mechanisches System (z.B. zwei Massen über eine Feder
verbunden) der klassischen Physik, das ein Potentialminimum besitzt und bei einer
Auslenkung x aus diesem Minimum eine dieser Auslenkung proportionale Rückstellkraft F
erfährt. Diese Tatsache wird im Hooke’schen Gesetz dargestellt:
F ( x) = −kx ,
wobei k die Federkonstante des Oszillators darstellt. Ein harmonischer Oszillator besitzt ein
quadratisches, also parabelförmiges Potential (ist die Funktion für die zur Streckung der
Feder benötigte Energie):
V ( x) =
1 2
kx
2
In Schwerpunktkoordinaten wandelt sich das Bild des Systems von zwei Massen, die mit
einer Feder der Federkonstanten k verbunden sind, zu einem System einer reduzierten
Masse, die mit einer Feder der gleichen Stärke mit einer unbeweglichen Wand verbunden
ist. Diese Transformation wird durchgeführt, weil lediglich die relative Bewegung dieser
beiden Massen in Bezug zueinander, nicht aber ihre individuellen Bewegungen
interessieren. So reduziert sich die Beschreibung der Schwingung auf eine einzige
Koordinate, dem Massenschwerpunkt xSP. Die Positionen x1/2 der Massen m1/2 sind nun nicht
mehr nötig. Ein zweiatomiges Teilchen der reduzierten Masse
µ=
m x + m2 x 2
m1 ⋅ m2
, wobei x SP = 1 1
m1 + m2
m1 + m2
beschreibt im Oszillatorpotential eine Sinusschwingung der Frequenz:
ω = 2πf =
k
µ
Die Frequenzen die bei zweiatomigen Molekülen in der Schwingungsspektroskopie zu
beobachten sind, hängen demnach von zwei Materialparametern ab: der Kraftkonstanten k
und der reduzierten Masse µ (entsprechen den Materialparametern Rotationskonstante B
und Bindungslänge r bei der Rotationsspektroskopie).
Man kann das Potential daher auch schreiben als:
V ( x) =
1
µω 2 x 2
2
In einem harmonischen Oszillator sind die Potentiale immer äquidistant. Außerdem gibt es
keinen Grenzwert für die Potentiale. Eine unendlich große Energiemenge, welche von einem
harmonischen Oszillator aufgenommen wird, führt zu einem unendlich großen Potential. Die
im Potential n des klassischen harmonischen Oszillators gespeicherte Energie kann jeden
beliebigen Wert annehmen (anders als im quantenmechanischen Fall). Es handelt sich um
Potentiallinien, das heißt alle Abstände x um den Gleichgewichtsabstand herum, die sich im
erlaubten Bereich (innerhalb der Potentialfunktion) befinden, haben eine gleiche
Wahrscheinlichkeit. Der Zustand n=0 hat eine verschwindende Breite, weshalb keine
Schwingung vorliegt (Die Energie ist 0).
Der harmonische Oszillator in der Quantenphysik
In der Quantenphysik können alle Teilchen auch als Wellen betrachtet werden. Daher lässt
sich das um die Gleichgewichtslage schwingende Welle-Teilchen der Masse µ durch eine
Menge von Wellenfunktionen Ψn (x) beschreiben. Um die einzelne Wellenfunktion für das
Potential n zu erhalten und die entsprechenden erlaubten Energien zu ermitteln muss die
Schrödinger Gleichung
E n Ψn ( x) = −
 2 d 2 Ψn ( x) kx 2
⋅
+
⋅ Ψn ( x)
2µ
2
dx 2
gelöst werden. Die Lösung liefert die Eigenfunktionen der verschiedenen Energieniveaus,
wie z.B. die Eigenfunktion des Niveaus n=0:
α 
Ψ0 ( x) =  
π 
1/ 4
⋅ e −(1 / 2 )αx , wobei α =
2
kµ
2
Man erkennt, dass der niedrigste Zustand (absoluter Nullpunkt der Temperatur ist erreicht)
eine von 0 verschiedene Energie besitzt, die so genannte Nullpunktenergie:
E0 =
1
ω
2
Das Teilchen ist demnach bei dem absoluten Nullpunkt nicht exakt bei x=0 lokalisiert (im
Gegensatz zum klassischen harmonischen Oszillator), sondern weist eine
Nullpunktsschwingung entsprechend der nullten Eigenfunktion auf, wodurch es um x=0
herum verschmiert ist. Aus den Eigenfunktionen folgt direkt, dass im quantenmechanischen
Fall nicht alle beliebige Energien möglich sind, sondern lediglich die für das Potential n nach
folgender Beziehung entsprechende:
1
1


E (n) = hf  n +  = ω  n + 
2
2


In der Abbildung ist das Quadrat der Eigenfunktionen in einem Graphen, der das Potential
(Energie) gegen die Verschiebung aus dem Gleichgewichtsabstand x=0 zeigt aufgetragen.
Das Quadrat der Eigenfunktion entspricht der Wahrscheinlichkeitsdichte, also der
Wahrscheinlichkeit zu der sich das Teilchen in einer bestimmten Auslenkung um den
Gleichgewichtsabstand liegt (in der klassischen Physik handelt es sich um Linien, da alle
Auslenkungen gleichwahrscheinlich sind). Die rote Parabel entspricht der Potentialfunktion.
Außerhalb dieser liegen die verbotenen Zustände.
Der anharmonische Oszillator
Die Potentialfunktionen der Moleküle weichen vom einfachen harmonischen Potential ab.
Eine analytische Annäherung an die Molekülpotentiale, die anharmonischen Charakters sind,
stellt das Morse- Potential dar:
V ( R) = De ⋅ [1 − e −α ⋅( R − Re ) ]2 .
De ist die Dissoziationsenergie in Bezug auf das Potentialminimum. Re ist der entsprechende
Kernabstand. Das heißt im anharmonischen Oszillator führt eine unendlich große
Energiemenge zur Dissoziation des Moleküls. Die einzelnen Potentiale sind nicht mehr
äquidistant. Deren Abstände nehmen mit zunehmender Energie ab (Energiedifferenz
zwischen den einzelnen Schwingungszuständen wird kleiner). Der Steifeparamter α ist
definiert durch:
α = k / 2 De
Die Bindungsenergie D0 wird in Bezug auf das niedrigste erlaubte Energieniveau definiert,
das ungleich 0 ist. Die einzelnen Energieniveaus für dieses Potential sind mit
1  (h ⋅ f ) 2 
1

⋅n + 
E ( n) = h ⋅ f  n +  −
2
4 De 
2

2
gegeben. Der zweite Term ist der Korrekturterm für den anharmonischen Oszillator. Die
möglichen Energien werden in der Morse Potentialkurve als horizontale Linien im
klassischen Fall oder als Quadrat der Eigenfunktionen im quantenmechanischen Fall
dargestellt. Das Minimum der Funktion entspricht dem Gleichgewichtsabstand der Kerne,
wie beim harmonischen Oszillator. Um das Potentialminimum herum stellt das Harmonische
Potential (Parabel) deshalb eine gute Näherung an das Morse-Potential dar.
Prinzip der FTIR Spektroskopie und Aufbau des Spektrometers
Das FTIR Spektrometer ist eine Apparatur, bestehend aus einer Polychromatischen
Lichtquelle, einem Michelson-Interferometer, einer Kammer, welche während der Messung
die zu analysierende Probe enthält und einem Detektor.
Das Michelson-Interferometer
Bei Einem Interferometer handelt es sich um einen
optischen Aufbau, der dazu dient Lichtbündel zu trennen,
sie räumlich gegeneinander zu verschieben und wieder
zu überlagern. Das einfachste Interferometer ist das
Michelson-Interferometer.
Der Strahlengang im Interferometer findet wie folgt statt.
Das einfallende, parallele Lichtbündel (1) wird an der aktiven Schicht (3) eines Strahlenteilers
(2) in zwei gleich intensive Teile aufgespaltet. Ein Teil reflektiert am Strahlenteiler zu einem
festen Spiegel (4), der sich am Referenzarm des Interferometers befindet. Der andere Teil
transmitiert zu einem sich ständig hin und her bewegenden Spiegel (5), der sich im Messarm
befindet. Beide Teile werden am jeweiligen Spiegel zum Strahlenteiler zurück reflektiert und
wiedervereinigt, wobei beide Teilbündel eine Laufzeitdifferenz bzw. Weglängendifferenz
x = 2 ⋅ (d1 − d 2 )
aufweisen. Daher kommt es zur Interferenz. Durch den Einbau eines Interferometers ist es
möglich aus einer Dauerlichtquelle aus polychromatischem Licht mittels dem beweglichen
Spiegel einen Licht-Impuls pro Zeit los zusenden.
bei gleichzeitiger Anregung der Probe mit allen Wellenlängen durch polychromatisches Licht,
würde der Detektor die gemessenen Intensitäten nicht den einzelnen λ zuordnen können, da
alle gleichzeitig ankommen. Die Spiegelposition im Interferrometer codiert für die einzelnen
Wellenlängen. Dadurch kommen die Intensitäten in unterschiedlicher Reihenfolge am
Detektor an und können den einzelnen Wellenlängen zugeordnet werden. Eine manuelle
Einstrahlung aller einzelnen Wellenlängen nacheinander würde jedoch zu viel zeit in
Anspruch nehmen!
Monochromatische Interferenz
Aus der Bewegung des Spiegels (5) folgernd, verschiebt sich die aus dem Messarm
kommende Welle gegen die des Referenzarms. Beide Wellen interferieren zu einer
resultierenden Welle. Im Fall der optischen Weglängendifferenz null beider Arme
überlagern sich beide Wellen so konstruktiv, sie verstärken sich. Entspricht die
optische Weglängendifferenz genau einer halben Lichtwellenlänge, so erfolgt die
Überlagerung destruktiv (Auslöschung). Das Licht, welches das Interferometer
letztlich verlässt, schwankt daher kosinusförmig über der Spiegelverschiebung.
Wenn der eine der beiden Spiegel mit konstanter Geschwindigkeit kontinuierlich bewegt
wird, dann variiert die Strahlungsintensität am Detektor nach der Kosinusfunktion
 2π 
I ( x) = 0,5 I 0 ⋅ cos
x  = I (ν~ ) ⋅ cos(2πν~x)
λ


Hierin sind λ die Wellenlänge und x die Weglängen- bzw. Laufzeitdifferenz der
elektromagnetischen Welle (auch Retardierung genannt).
Polychromatische Interferenz
Da Spektrometer Licht vieler Wellenlängen verarbeiten, entsteht die oben beschriebene
Interferenz für jede Wellenlänge. Entsprechend überlagern sich die einzelnen Wellenlängen
zusätzlich. Der Nullpunkt des Spiegelwegs (x=0) ist der Ort an dem beide
Interferometerarme gleich lang sind. Dort besitzen alle Wellen die Phasendifferenz Null und
überlagern sich deshalb konstruktiv. Die Intensität ist maximal. Bei größer werdender
Weglängendifferenz interferieren die einzelnen Wellenlängen destruktiv. Es kommt zur
Auslöschung.
Überlagert man alle Wellenlängen (Kontinuum) des an der Messung beteiligten Lichts, ergibt
sich die vom Detektor erfasste Intensität als Integral über die Bandbreite B.
I ( x) = ∫ [I (ν~ ) cos(2πν~x)]dν~
B
Die Bandbreite ist der nutzbare Wellenzahlbereich eines Spektrometers. Die Bandbreite
umfasst alle von der Lichtquelle zum Detektor gelangenden und im spektralen
Empfindlichkeitsbereich des Detektors liegenden Wellenzahlen. Die Bandbreite ist limitiert
durch die Empfindlichkeit des Detektors, der verwendeten Fenster oder des verwendeten
Strahlenteilers.
ATR (abgeschwächte Totalreflexion)
Bei dieser, im Praktikum verwendeten Methode wird die vom Interferometer kommende
Strahlung durch einen Lichtwellenleiter geführt. Im Innenraum dieses Lichtwellenleiters findet
die abgeschwächte Totalreflexion statt.
Totalreflektion bedeutet, dass die gesamte Energie eines einfallenden Lichtstrahls an der
Grenze zwischen zwei Medien (vom optisch dichteren zum optisch dünneren Medium bzw.
vom Medium mit einem größeren Brechungsindex zum Medium mit einem kleineren
Brechungsindex) reflektiert wird, wenn der für die Medien charakteristische Einfallswinkel
überschritten wird. Bei der abgeschwächten Totalreflektion dringt der Lichtstrahl, abhängig
vom Einfallswinkel, der Wellenlänge des Lichtstrahls und den Brechungsindizes der Medien,
bis in eine bestimmte Tiefe in das optisch dünnere Medium, also der IR-Probe ein.
λ
dp =
2π ⋅ n1
n
sin θ −  2
 n1
2



2
Dort wird ein Teil der Strahlung absorbiert. Nur der nicht absorbierte Teil wird vom Detektor
am Ende des Strahlengangs detektiert. Das Strahlenmodell hat an der Grenzfläche
zwischen IR Probe und Lichtwellenteiler keine Gültigkeit. Es bildet sich an dieser
Grenzfläche ein evaneszentes Feld, das in die Probe eindringt und exponentiell abfällt!
Die Differenz zwischen eingestrahlter Intensität jeder bestimmten Wellenlänge und nicht
absorbierter Intensität jeder bestimmten Wellenlänge bildet das Absorptionsspektrum, das
erst mittels eines Rechners durch Fouriertransformation aus dem Interferogram errechnet
werden muss. So ist das Absorptionsspektrum, dass mittels Reflektionstechnik erzeugt wird
den gewöhnlichen Absorptionsspektren, die mittels Durchstrahltechnik erzeugt werden,
nahezu identisch.
Der Vorteil dieser Methode liegt darin, dass bei einem großen Proberaum (besseres
Absorptionsvermögen) nur wenig Probe (nicht teuer) benötigt wird. Außerdem können
Oberflächen, ohne zerstört zu werden und andere Proben, die für die Durchstrahltechnik zu
stark absorbieren oder zu dick sind, analysiert werden
Evaneszentes Feld
Erfolgt zwischen zwei Medien (ATR-Kristall - optisch dichter und Probe - optisch dünner)
aufgrund unterschiedlicher Brechungsindizes Totalreflexion, dann fällt die
Strahlungsintensität hinter der Grenzfläche nicht abrupt ab, sondern dringt in die Probe ein
und pflanzt sich parallel zur Grenzfläche als evaneszente Welle fort. Sie tritt an der
Grenzfläche wieder aus und durchdringt den ATR-Kristall. Die Abschwächung des
evaneszenten Feldes erfolgt exponentiell mit zunehmendem Abstand von der Grenzfläche.
Absorbiert die Probe die Strahlung, beobachtet man eine Schwächung der Totalreflexion und
es sind ATR-Spektren messbar. Aufgrund der vorhandenen Abhängigkeit der Eindringtiefe
von der Wellenlänge (Absorptionsbanden werden im ATR-Spektrum mit größeren
Wellenlängen intensiver) müssen ATR-Spektren korrigiert werden, um transmissionsähnliche
Spektren zu erhalten.
Die nicht propagierende Komponente des Nahfeldes wird als evaneszentes Feld bezeichnet.
Es fällt exponentiell zur Oberflächennormalen des strahlenden Körpers ab. Jedes
beleuchtete Objekt erzeugt also ein evaneszentes und ein propagierendes Feld [Cou 94].
Ein rein evaneszentes Feld kann man z.B. im Fall von Totalreflexion beobachten. Ein im
Medium mit Brechungsindex n1 propagierender Lichtstrahl trifft auf die Grenzfläche zum
, so daß der
optisch dünneren Medium ( n2<n1) mit einem Einfallswinkel
Strahl totalreflektiert wird. Aufgrund der Stetigkeitsbedingung kann auf der Seite des
dünneren Mediums das Feld nicht abrupt Null sein, sondern es fällt exponentiell in den
Halbraum n2 ab [Hec 98]. Sei z.B. die Grenzfläche in der (x,y)-Ebene bei z=0. Dann ist die zKomponente des Wellenvektors kz komplex und das evaneszente Feld
ist senkrecht zur Oberfläche stark exponentiell gedämpft. Es ist i.a. bereits bei einem
Abstand
komplett verschwunden. Gerade dieses Feld enthält Informationen über
Strukturen unterhalb der Auflösungsgrenze.
Die Fouriertransformation
Der Rechner muss nun die Fouriertransformation durchführen, um aus einem Interferogram
ein Spektrum zu erstellen. Das Interferometer liefert eine Gleichung für die
Absorptionsintensität in Abhängigkeit von der Retardierung x.
Nun formen wir diese Gleichung so um, dass ein unbestimmtes Integral (Intervall ist
unendlicher Wellenzahlbereich) entsteht, indem wir die Fensterfunktion D (ν~ ) multiplikativ im
Integral ergänzen.
Diese Funktion entspricht der Fourierkosinustransformation. Da es sich um eine gerade
Funktion handelt, lässt sich diese invertieren:
Diese Inverse Fourierkosinustransformation entspricht nun, da es sich um eine gerade
Funktion handelt und somit die Sinusteile der Eulerschen Funktion
entfallen, der komplexen Fouriertransformation
Diese Formel liefert nun einen Graphen, der dem Einstrahlspektrum entspricht. Das
Einstrahlspektrum einer Probe ist das Spektrum, das der Energieverteilung entspricht, die
durch den Detektor aufgenommen wird. Im Einstrahlspektrum sind alle Gerätefunktionen wie
die Energie-Verteilungsfunktionen der Lichtquelle, die Transmission des Spektrometers
selbst und die Empfindlichkeit des Detektors enthalten.
Um diese Gerätefunktionen zu filtern, bedarf es einer Aufnahme des Spektrums der leeren
Probekammer. Dieses Spektrum wird vom Probenspektrum subtrahiert, um ein möglichst
reines Spektrum zu erhalten. Das nun auf dem Bildschirm erscheinende Spektrum zeigt
Peaks einer bestimmten Intensität an den Wellenzahlen, an denen die Probe zu dieser
Intensität absorbiert.
graphische /physikalische Erklärung der Fourriertransformation:
Bei der Fouriertransformation in der IR-Spektroskopie wird wie folgt das Spektrum
berechnet. I(x) ist das vom Detektor erzeugte FID. Es wird mit den cosinus-Funktionen einer
jeden Frequenz multipliziert. Die Integrale des Produkts aus dem FID und jeder einzelnen
Frequenz werden nun berechnet und gegenübergestellt. Wenn die Frequenz genau dem FID
entspricht, so ist das Integral maximal. Je höher die Überlappung der entsprechenden
Frequenz mit dem FID, desto größer wird das Integral.
Findet keine Überlappung statt und ist der Unterschied zwischen FID und entsprechender
Frequenz zu groß, so ist dass Integral des Produkts sehr klein oder null (negative Anteile
und positive Anteile heben sich auf).
Werden die Integrale nun in einem Graphen gegen die entsprechende Frequenz
aufgetragen, so entsteht das Fouriertransformierte Signal, das Spektrum. In diesem Beispiel
handelt es sich um einen einzigen Peak, da das maximale integral für eine einfache
Kosinusfunktion erreicht wird und für alle niedrigeren und höheren Frequenzen dieser
Kosinusfunktion eine geringere Überlappung erreicht wird. Für komplexere FIDs gibt es
natürlich mehrere Maxima, da für keine einfache Frequenz eine perfekte Überlappung
stattfinden wird.
Das Lambert Beersche Gesetz
Im Allgemeinen verwendet man in der Absorptionsspektroskopie elektromagnetische
Strahlung einer geeigneten Wellenlänge, die auf ein Probevolumen geschossen wird. In den
chemischen Substanzen im Probevolumen finden die Übergänge zwischen Rotations-,
Schwingungs- und Elektronenzustände statt. Die Intensität I 0 (λ ) der einfallenden Strahlung
wird beim Durchgang durch ein Längenelement der Länge d des Probevolumens
abgeschwächt. Diese Abschwächung wird durch das Lambert-Beer’sche Gesetz
beschrieben:
I (λ ) = I 0 (λ ) ⋅ e −ε ( λ )⋅c⋅d

E (λ ) = − log
I (λ )
= ε (λ ) ⋅ c ⋅ d
I 0 (λ )
Hier ist c die Konzentration des absorbierenden Mediums in mol/l. ε (λ ) ist der molare
Absorptionskoeffizient. Er entspricht der Steigung der Geraden „spezifische Absorption bei
der Wellenlänge λ vs. c“. Ermittelt werden kann er durch Photometrie einer
Verdünnungsreihe des Stoffes. Das Absorptionsvermögen nimmt mit ε (λ ) , c und d zu und ist
Proportional zu
I (λ )
.
I 0 (λ )
Durch die Methode der ATR ist die Länge d erheblich erhöht, weshalb die Absorption sehr
hoch ist, obwohl nur sehr wenig Probe vorhanden ist
Dichroismus
Dichroismus ist ein optischer Effekt, der bewirkt, dass ein Mineral in Abhängigkeit von der
Blickrichtung in zwei verschiedenen Farben erscheint. In der Infrarot Spektroskopie wird
dieser Effekt zur Bestimmung von Orientierungen verwendet!
Materialien haben eine oder mehrere ausgezeichnete optische Achsen. Verschiedene
Eigenschaften unterscheiden sich hierbei, ob man sie parallel zur optischen Achse
(außerordentlich) oder senkrecht dazu (ordentlich) betrachtet. Zeigt das Material zwei
unterschiedliche Absorptionsverhalten bezüglich dieser Achsen, also wird z. B. je nach
Polarisation des durchscheinenden Lichtes eine andere Farbe absorbiert, wird dieses
Verhalten Dichroismus genannt. Das Wort Dichroismus leitet sich aus dem griechischen
Wort Dichroos für „zweifarbig“ ab. Die Mehrfarbigkeit wird allgemeiner als Pleochroismus
bezeichnet
Der Dichroismus wurde 1939 von Peter Debye entdeckt. Hierbei wird unterschieden, welche
Art von Polarisation das einfallende Licht hat. Es gibt den linearen Dichroismus, bei dem das
Material von linear polarisiertem Licht durchschienen wird. Daneben wird mit
Zirkulardichroismus die Differenz der Absorptionskoeffizienten für links bzw. rechts zirkular
polarisiertes Licht beim Durchgang durch optische aktive Verbindungen beschrieben
Zirkulardichroismus ist eine spezielle spektroskopische Messung, um die Struktur optisch
aktiver Moleküle aufzuklären. Dazu verwendet man zirkular polarisiertes Licht. Ein optisch
aktives Molekül absorbiert nun das zirkular rechts polarisierte Licht im Vergleich zu dem
zirkular links polarisierten Licht unterschiedlich stark. Diese Differenz wird für jede
Wellenlänge gemessen und man erhält das gewünschte Spektrum. Dieses sollte für die
Enantiomere eines Moleküls spiegelbildlich ausfallen. Besonders gerne wird die Methode bei
biologischen Substanzen wie Aminosäuren und Zuckern, aber auch bei Untersuchungen zu
Helix-Strukturen von Peptiden benutzt. Hier sind allerdings die Röntgenstrukturanalyse und
NMR-Spektroskopie weitaus besser bei der Strukturaufklärung.
zirkular polarisiertes Licht
Eine elektromagnetische Welle ist zirkular polarisiert, wenn der elektrische Feldvektor an
jedem Punkt im Raum als Funktion der Zeit einen Kreis beschreibt. Eine zirkular polarisierte
Welle lässt sich als eine Überlagerung zweier senkrecht aufeinander stehender, linear
polarisierter Wellen mit gleichem Wellenvektor und gleicher Amplitude sowie einem
Phasenversatz von 90 Grad darstellen. Erzeugen kann man eine zirkular polarisierte Welle
durch Beleuchtung eines λ/4-Plättchens mit einer linear polarisierten Welle
λ/n-Plättchen
Eine Wellen- oder Verzögerungsplatte (auch: λ/n-Plättchen) ist ein optisches Gerät, das die
Polarisation und Phase von passierendem Licht ändern kann.
Ein λ/4-Plättchen ist eine spezielle Wellenplatte, die das Licht in einer Richtung um eine
viertel Wellenlänge – bzw. π/2 – gegen die dazu senkrechte Richtung verzögert. Es kann
aus linear polarisiertem Licht zirkular oder elliptisch polarisiertes Licht machen und aus
zirkular polarisiertem Licht wieder linear polarisiertes.
Ein λ/2-Plättchen ist ebenfalls eine spezielle Wellenplatte, die das Licht wie oben um eine
halbe Wellenlänge – bzw. π – verzögert. Es kann die Polarisationsrichtung von linear
polarisiertem Licht drehen.
Die Verschiebung kommt dadurch zustande, dass das Licht in zwei senkrecht stehende
Polarisationsrichtungen zerlegt werden kann, die die Wellenplatte mit unterschiedlicher
Geschwindigkeit passieren, deren Phasen also gegeneinander verschoben werden. Ein
solches Plättchen besteht typischerweise aus einem doppelbrechenden Kristall (z. B. Kalzit)
mit passend gewählter Dicke und Ausrichtung
Bei einer Wellenplatte handelt es sich um eine dünne Scheibe von optisch anisotropem
Material, also Material, welches für unterschiedlich polarisiertes Licht verschiedene
Ausbreitungsgeschwindigkeiten c/n (bzw. verschiedene Brechzahlen n) in verschiedenen
Richtungen aufweist. Oft verwendete Materialien sind optisch einachsig, das heißt es gibt
zwei zueinander senkrechte Achsen im Kristall, entlang derer sich die Brechzahlen
unterscheiden. Man nennt diese ordentliche (das Licht ist senkrecht zur optischen Achse
polarisiert) und außerordentliche Achse (das Licht ist parallel zur optischen Achse
polarisiert). Die Schwingungsrichtung des Lichtes, bei der eine Welle die größere
Ausbreitungsgeschwindigkeit hat, heißt „schnelle Achse“, die dazu senkrecht stehende
Richtung entsprechend „langsame Achse“.
Licht, welches parallel zur schnellen Achse polarisiert ist, benötigt weniger Zeit zum
Durchlaufen des Mediums als Licht, welches senkrecht dazu polarisiert ist. Man kann sich
das Licht in zwei Komponenten senkrecht (ordentlicher Strahl) und parallel
(außerordentlicher Strahl) zur optischen Achse aufgeteilt vorstellen, die nach dem
Durchlaufen des Plättchens eine Phasenverschiebung von
aufweisen. Dabei ist d die Dicke des Plättchens und λ die Wellenlänge des eingestrahlten
Lichtes. Die beiden Strahlen überlagern sich hinter dem Kristall (Interferenz) zum
ausgehenden Licht. Durch die (kohärente) Überlagerung dieser beiden Strahlen ergibt sich
dann eine neue Polarisation des Lichtes (Frequenz und Wellenlänge bleiben erhalten; siehe
nächster Abschnitt). Wie man an der Formel sieht, ist eine solche Wellenplatte also immer
nur für eine bestimmte Wellenlänge ausgelegt. Es sei noch bemerkt, dass die Aufspaltung in
zwei Strahlen nur eine Art Rechentrick ist. In der Realität überlagern sich diese beiden
Strahlen natürlich an jeder Stelle des Kristalls. Die Elektronen um die Kristallatome bilden
lokale und momentane Dipole, die in einer Überlagerung der beiden Polarisationsrichtungen
der Strahlen schwingen.
Lipide und Membranen
Die Glycerolipide, die aus einem Glycerinbaustein und daran veresterten Acylresten
bestehen spielen bei dem Aufbau der Membranen und als Speicherstoff eine entscheidende
Rolle. Speicherlipide sind Triacylglycerine, Membranlipide sind Diacylglyceride mit polarer
Kopfgruppe als dritten Substituenten. Je nach Art des dritten Substituenten spricht man von
Phospholipiden (Substituent: Phosphatguppe mit polarem Rest wie Cholin), Sulfolipiden
(Substituent: Sulfatgruppe mit polarem Rest) oder Glykolipiden (Substituent: Saccharide).
Ein weiterer Membranbaustein sind Sphingolipide, bei denen Sphingosin statt Glycerin das
Grundgerüst darstellt. Hier befindet sich jeweils ein Acyl-Rest verestert an die Amidgruppe
des Sphingosins. Auch hier unterscheidet man je nach polarer Kopfgruppe drei Typen
voneinander: Ceramide (Substituent: Wasserstoff), Sphingomyelin (Substituent:
Phosphatguppe mit polarem Rest wie Cholin) oder Glykosphingolipide (Substituent:
Saccharide)
Außerdem gibt es Plasmalogene Lipide. Solche unterscheiden sich von Phospholipiden
lediglich durch den Rest in sn1 Position. Dieser enthält eine O-Alkyl oder eine O-Alkenyl
Etherfunktion.
Als dritte Hauptgruppe gehören zu den Lipiden die so genannten Isoprenoide bzw.
Terpenoide. Jene lassen sich noch einmal in Carotinoide und Steroide einteilen. Steroide
weisen als Grundgerüst vier miteinander verbundene Kohlenstoffringe auf. Das wichtigste
Steroid für die Membranen ist Cholesterin. Carotinoide bestehen aus 8 Isopreneinheiten und
kommen ausschließlich in Pflanzen vor. Man unterscheidet sie nochmals in Carotine und
Xanthophylle, welche zusätzlich Sauerstofffunktionen tragen. Carotinoide sind Pigmente und
Steroide werden häufig als Hormone verwendet.
Die Fluidität der Membran hängt von der Membranzusammensetzung sowie von der
Temperatur ab. Bei tiefen Temperaturen gibt es einen parakristallinen Zustand. Oberhalb
einer Transition-Temperatur wird die Membran flüssig. Ungesättigte Fettsäuren erhöhen die
Membranfluidität (behindern den parakristallinen Zustand, da die Doppelbindungen die
gerade kette der Fettsäure abknicken und somit die restlichen geradkettigen Fettsäuren
sterisch „wegschieben“), da sie den Schmelzpunkt der Membran herabsetzen. Langkettige
Fettsäuren erniedrigen die Membranfluidität, da sie den Schmelzpunkt der Membran
erhöhen.
Der Cholesteringehalt der Membran beeinflusst ebenso die Membranfluidität. Unterhalb der
Transition-Temperatur erhöht Cholesterin die Fluidität, während oberhalb der TransitionTemperatur die Membranfluidität erniedrigt wird. Cholesterin beeinflusst das
Schmelzverhalten allosterisch, sodass der Phasenübergang nicht plötzlich stattfindet,
sondern nach und nach (sigmoidal) über ein Temperaturintervall.
Extremophile Organismen, welche bei extrem hohen Temperaturen leben, weisen eine ganz
andere Membranzusammensetzung auf, als Organismen normaler Habitate. Dies ist
lebensnotwendig. Damit die Membranen bei hohen Temperaturen noch eine ausreichende
Integrität aufweisen, müssen sie einen großen Anteil an Cholesterin und gesättigte
langkettige Fettsäuren aufweisen. Des Weiteren besitzen die Lipide der extremophilen
Organismen Etherbrücken anstelle von Esterbrücken. Häufig kommen auch Monolayer
anstelle von Bilayer vor.
ITC
Thermodynamik und Spontanität von Reaktionen
Eine chemische Reaktion läuft immer dann spontan (exergonisch) ab, wenn ∆G , die
Änderung der Gibbs Energie zwischen Edukten und Produkten negativ ist.
∆G = ∆H − T∆S
für p=const. und T=const.
Spontane Reaktionen werden demnach durch exotherme Enthalpien und
Entropieerhöhungen angetrieben. Aufgrund der großen Dichte und Komplexität der Moleküle
in einer Zelle, bedarf es einer hohen Interaktions-Selektivität. Der größte Teil dieser
Selektivität liefert die Thermodynamik. Intramolekulare Interaktionen erlauben die
Proteinfaltung, während intermolekulare Interaktionen die Substrat-Wahrnehmung der
Enzyme ermöglicht.
In diesem Praktikum wird der Frage nachgegangen, warum aus thermodynamischer Sicht
die Bindung zwischen Ligand und Enzym zustande kommt. Es ist klar, dass ∆G für die
Protein-Ligand Bindung negativ ist. Doch wird jener von der Enthalpie, der Entropie oder
beidem angetrieben?
Calmodulin (CaM) und RNAse A
In der ITC kann z.B. die Faltung eines Proteins beobachtet
werden, um zu ermitteln, ob der Faltungsprozess von der
Enthalpie oder der Entropie getrieben wird. Dies lässt sich am
Beispiel des Proteins Ca-Rinder-Calmodulin erforschen. Es
handelt sich um ein 16kD Ca2+-bindindes Protein, das eine
Schlüsselkomponente des Ca2+-second-messenger Systems
darstellt. Es kontrolliert demnach viele biochemische Prozesse
einer Zelle. In Abwesenheit von Calcium ist dieses Protein
größtenteils ungefaltet. Ist Calcium vorhanden, so faltet sich das
Protein schnell zu einer organisierten Struktur, je nachdem ob es 2 oder 4 Ionen gebunden
hat. Diese Calcium-abhängige Faltung von Calmodulin wird in vielen biochemischen
Reaktionsketten als regulatorischen An bzw. Ausschalter verwendet. So werden über
Calmodulin regulierte Proteine (zelluläre Enzyme und transmembrane Ionentransporter) erst
aktiviert, wenn ein aktiviertes Calmodulin an sie bindet und so eine Reaktionskaskade ein
bzw. ausschaltet.
Außerdem lässt sich mittels ITC die Frage beantworten,
weshalb Liganden an Enzyme binden. Im Praktikum wird
dieser Frage am Beispiel der Bindung von CMP an das
Enzym RNAse nachgegangen. RNAse ist eine
Endonuklease und gehört zu den Hydrolasen. Sie spaltet die
bereits in die Proteinsequenz übersetzte single stranded
RNA am Zuckergerüst von ungepaarten C und U Resten
am 3’ Ende des Stranges in ihre einzelnen Monomere, damit
diese neue RNA aufbauen können. CMP ist also ein Produkt der RNAse. Es handelt sich um
ein relativ kleines Protein aus 124 Aminosäuren mit einem Molekulargewicht von 13,7kDa.
Aufgrund der Tatsache, dass in unserem Experiment keine RNA in Lösung vorhanden ist,
aber auch keine RNA aufgebaut werden kann, weil die dafür notwendige Energie fehlt, wird
CMP von dem Enzym RNAse zwar gebunden, aber nicht umgesetzt. Die Bindung erfolgt mit
einer bestimmten Affinität, sodass entweder Energie frei wird oder Energie benötigt wird,
während die Protein-Ligand Bindung entsteht. Dieser Energiebetrag ist mittels ITC messbar.
Funktion und Prinzip der ITC
Es wird im Versuch RNAse mit CMP titriert und die Enthalpieänderung ∆H für die
Ligandenbindung festgehalten. Die Daten, welche die Titration liefert, geben einen
Aufschluss darüber, welche Kräfte die Ligandenbindung antreiben.
Die Enthalpieänderung während der Interaktion von Makromolekülen kann über ITC am
direktesten bestimmt werden. Bei einem typischen Experiment wird der Titrator L (bekannter
Konzentration) in eine Lösung von M titriert und dabei die Änderung der Enthalpie des
gesamten adiabatischen Systems gemessen. Die Assoziationskonstante Ka und die
Stöchiometrie n des Komplexes kann ebenso durch ITC ermittelt werden. Wenn die ITC bei
verschiedenen Temperaturen durchgeführt wird, erhält man zusätzlich die Änderung der
Wärmekapazität bei konstantem Druck.
Ein solches Kalorimeter besteht aus zwei identischen Zellen aus Wärmeleitendem Material,
umgeben von einem adiabatischen Mantel (siehe Abbildung).
Die Referenzzelle (enthält gepuffertes H2O) besitzt einen Heizer, der auf die gewünschte
Temperatur für das Experiment eingestellt wird. Die Probenzelle (enthält die gepufferte
Probe) besitzt zwei Heizer. Der erste Heizer ist identisch mit dem Heizer der Referenzzelle.
Der zweite Heizer (Feedback Heizer) ist dafür verantwortlich auf thermische Fluktuationen,
die während dem Experiment erzeugt werden, zu reagieren. Beide Zellen sind mit einem
Thermoelement (meist: 2000-6000 Bimetall Kabeln; aus je mehr Bimetallkabeln dieses
Thermoelement besteht, desto genauere Messungen von ΔT sind möglich) verbunden, das
die Temperaturdifferenz zwischen den Zellen ermittelt.
Die Probenzelle ist zugänglich mit einer langen Spritze. Das Experiment wird bei einer
konstanten Temperatur durchgeführt, indem der Titrator L in der Spritze in die Lösung mit
dem Makromolekül M der Probenzelle titriert wird. Der Inhalt der Probenzelle bewegt sich
ständig, um den Mischvorgang aller Reaktanden zu beschleunigen.
Nach jeder Zugabe einer kleinen Menge L, wird durch die Interaktion von L und M Hitze frei
oder verbraucht. Diese Temperaturänderung wird über das Thermoelement gemessen. Die
Temperaturdifferenz wird ausgedrückt in derjenigen elektrischen Kraft [J/s], die benötigt wird
um eine konstante Temperatur zwischen der Proben- und der Referenzzelle mittels
Feedback Heizer wieder herzustellen.
Wenn die Temperatur in der Probenzelle mit der Zugabe des Titrators steigt, nimmt der
Heizer die frei gewordene Energie des exothermen Mischprozesses auf und kühlt somit die
Probenzelle. Wenn die Temperatur sinkt, muss der Heizer die Probenzelle auf die
Anfangstemperatur erwärmen. Der Prozess ist hier endotherm. Es liegt nahe, dass die
ersten Titrationen exothermer sein werden, als die letzten Titrationen, da je höher die
Konzentration des Titrators in der Probenzelle ist, desto mehr L-M Komplexe liegen vor.
Nach jeder Titration befinden sich weniger freie Proteine in Lösung, weshalb mit jeder
Titration immer weniger der titrierten Liganden auch an ein Protein binden. Nach einer
bestimmten Anzahl an Titrationen, wird kein zusätzlicher Ligand mehr an Proteine binden
können. Das dynamische Gleichgewicht zwischen L-M und freiem L und M hat sich
eingestellt. (siehe Abbildung).
Warum sind nun zwei Zellen für die Messung notwendig? Nur mit einer Referenzzelle ist
eine Messung bei geringen Temperaturunterschieden, also bei geringen Konzentrationen
und Volumina der Probe möglich. Wenn man nur eine Zelle hätte, müsste man ΔT aus der
Differenz der Temperaturen vor und nach der Titration messen. Die Referenz wäre hier
jeweils die nicht adiabatische Umgebung. Nicht adiabatisch bedeutet, dass ein
Wärmeaustausch mit an dem System angrenzenden Bereichen des Universums möglich ist.
Es resultiert daher ein größerer absoluter Fehler bei der Messung, da die Wärmemenge der
nicht adiabatischen Umgebung nicht konstant ist. Nur wenn die Messungen mit großen
Konzentrationen und Volumina durchgeführt werden würden könnte dieser Absolutfehler
relativ betrachtet gering ausfallen. Dies würde allerdings erheblich mehr kosten und
aufwändiger sein.
Die ITC Apparatur, welche wir im Praktikum nutzen, besteht aus einem „control block“, an
dem drei wichtige Daten abzulesen sind: die momentane Temperatur am Thermoelement,
die Zellen Feedback Temperatur und die Mantel Feedback Temperatur. Außerdem gibt es
einen „measure block“, an dem die Main-Heater ein bzw. ausgeschaltet werden. Sie sorgen
für eine konstante Anfangstemperatur im Mantel. Während der Messung wird der MainHeater immer ausgeschaltet.
Protein-Ligand Wechselwirkung und ITC
Im einfachsten Fall hat ein Protein nur eine Bindungsstelle, an die ein Ligand andocken
kann. Die Stöchiometrie und die entsprechende Gleichgewichtskonstante lassen sich einfach
beschreiben:
P + L ⇔ PL
K=
[ PL]
[ L] ⋅ [ P ]
Die Gleichgewichtskonstante steht in direkter Verbindung zur freien Gibbs Energie
K =e
−
∆G
RT
Diese wiederum lässt sich in enthalpische und entropische Beiträge zerlegen
∆G = ∆H − T∆S = − RT ⋅ ln K
Im Prinzip kann man die Reaktionsenthalpie mittels Van’t Hoff Gleichung ermitteln, da wir die
Temperaturänderung und die Änderung der Gleichgewichtskonstante kennen.
∆H R0
 ∂ ln K 
=


2
 ∂T  p RT

 RT 2 ∂ ln K 

∆H R0 = 
∂
T

p
In einer anderen Form enthält diese Beziehung sowohl die Reaktionsenthalpie, als auch die
Entropie:
ln K = −
∆H R0 1 ∆S R0
⋅ +
R T
R
In einem Graphen, der lnK gegen den Reziprokwert der Temperatur aufträgt, ist also
−
∆H R0
∆S R0
die Steigung und
der Schnittpunkt mit der lnK Achse.
R
R
Die Temperatur lässt sich im Experiment einfach einstellen und zuordnen. Nun muss der
Wert für die Gleichgewichtskonstante zur entsprechenden Temperatur ermittelt werden.
K kann nur ermittelt werden, wenn das Verhältnis zwischen Protein-Ligand Komplex und
freiem Protein und freiem Liganden bekannt sind.
K=
[ PL]
[ P][ L]
Dieses Verhältnis lässt sich zum Beispiel über Absorptionsverschiebungen messen, aber
auch zahlreiche andere Werte (z.B. Fluoreszenz, NMR, UV) lassen sich beobachten und
liefern ein Verhältnis zwischen gebundenem und freiem Protein. So lässt sich die obige
Gleichung wie folgt verallgemeinern.
K=
θD −θX
θX
=
θX −θN 1−θX
Dabei ist θ X der aktuell beobachtete Parameter (z.B. Absorption einer bestimmten
Wellenlänge) und θ N und θ D jeweils die zu Beginn und am Ende der Interaktion
beobachteten Parameter .
Wir gehen im Experiment davon aus, dass jeder Temperatur Zuwachs von einem
Wärmeeffekt Q bewirkt wird. Zu Beginn des Experiments ist die Temperatur konstant,
weshalb Qinitial null zu setzen ist. Die Gesamtwärmemenge, die benötigt wird, damit alle
Liganden binden ist die Bindungsenthalpie.
K=
Qtotal − qi
∆H bind − qi
=
qi − Qanfang
qi
Die Wärmemenge q, welche im Titrationsprozess i entsteht, steht in Zusammenhang mit
dem Volumen der Zelle, der Konzentration des Protein-Ligand-Komplexes im Schritt i, der
Anzahl der Bindungsstellen des Proteins n und natürlich der Bindungsenthalpie selbst.
q i = n ⋅ [ PL]i ⋅ V Zelle ⋅ ∆H bind
Die Wärmemenge des Titrationsprozesses i entspricht der Fläche unter dem Peak des
entsprechenden Schrittes (das Integral über alle Piks demnach der Bindungsenthalpie). So
ist auch die Gesamtwärmemenge bekannt. Nun wird die Gleichgewichtskonstante für die
Ligandenbindung Kbind, die Bindungsenthalpie ∆H bind und der Wert für n im
Computerprogramm so eingestellt, dass die gemessenen Werte am besten beschrieben
werden können bzw. die erhaltene Kurve am besten gefittet wird. So sind wir auch in der
Lage aus der Bindungsenthalpie die Bindungsentropie rechnerisch zu ermitteln.
∆S bind =
(∆H bind − ∆Gbind )
T
Nachdem alle Werte für mehrere Temperaturen bestimmt wurden, kann die Protein-Ligand
Wechselwirkung aufgrund folgender Beziehungen thermodynamisch exakt beschrieben
werden.
∆c p bind =
∂∆H bind ∂T∆Sbind
=
∂T
∂T
Die Wärmekapazität entspricht diejenige Wärmemenge, die nötig ist, um ein mol eines
Stoffes um 1K zu erwärmen. Es handelt sich dabei um eine Materialkonstante. Ist ∆c p bind
negativ bedeutet dies, dass mit zunehmender Temperatur immer weniger Wärmeenergie
aufgebracht werden muss, um eine Erwärmung um 1K zu bewirken.
1. Bestimmung der einzelnen Parameter
A.) Bestimmung von ΔH0
Die molare Reaktionsenthalpie ΔH0 kann direkt gemessen werden, wenn man sicher sein
kann, dass der gesamte hinzu titrierte Ligand auch gebunden wird, also gilt:
∆[ L] gebunden = ∆[ L]titriert
dies ist bei einem einfachen Bindungsmodell mit n unabhängigen gleichartigen
Bindungsstellen am Beginn der Titration der Fall; Voraussetzung ist, dass
n ⋅ K A ⋅ [ P] >> 1 (Protein muss hohe Affinität, und ausreichend vorhanden sein)
Somit resultiert aus der Beziehung: q i = n ⋅ [ PL] i ⋅ V Zelle ⋅ ∆H bind

∆H bind =
qi
n ⋅ [ L]titriert ⋅ VZelle
∆H bind kann alternativ auch wie K und n über eine mathematische Näherung bestimmt
werden;
B.) Bestimmung von KA und n
Zur Bestimmung der Bindungsparameter K und n wird die Auftragung qi vs. ∆[ L]titriert _ i
(tatsächlich aufgetragen ist die Zeit t, welche ∆[ L]titriert repräsentiert) für einen Satz von
Vorgaben für die Parameter ∆H bind , n und K rechnerisch simuliert (Annahme eines
bestimmten Bindungsmodells); Die Parameter werden softwaregestützt solange variiert, bis
eine gute Übereinstimmung der simulierten Kurve mit dem Experiment erzielt ist; für ∆H bind
kann ein fester Wert eingesetzt werden, um die Anzahl an Variablen zu verringern
(Berechnung siehe oben)
C.) Bestimmung von ΔGbind und ΔSbind
Über K können nun diese Werte anhand folgender Beziehungen errechnet werden:
ΔSbind positiv: Ligand verdrängt Wassermoleküle aus Bindungstasche
ΔSbind negativ: Flexibilität von Seitenketten wird eingeschränkt
D.) Bestimmung von Δcp
Wird das ITC Experiment für unterschiedliche Temperaturen durchgeführt, so kann Δcp
aufgrund der T-Abhängigkeit von ΔH berechnet werden:
Cp groß: apolare, hydrophobe Seitenketten in Bindungstasche
Cp klein: polare, ionisierte Seitenketten in Bindungstasche
Die resultierende Kurve
in der vom Computer berechneten resultierenden Kurve ist ΔH die Differenz vom h öchsten
Wert zum niedrigsten Wert der sigmoidalen Kurve; n ist der x Wert des Wendepunkts; K
(Assoziation) lässt sich einfach für jeden Titrationsschritt berechnen: K =
qtotal − qi
; je
qi
größer das K für den gesamtprozess, desto sigmoidaler ist die Kurve
Molare Rate = [injizierter Ligand] / [Protein]
Gegenüberstellung: Differential Scanning Calorimetry (DSC)
In dieser Methode wird die Referanzzelle kontinuierlich aufgeheizt (0,5-1,5K/min). Die
Temperatur der Probenzelle wird durch Heizen der Temperatur der Referenzzelle angepasst.
Die Probenzelle enthält bereits eine bestimmte Menge Protein und Ligand (keine Titration).
Es wird der Unterschied im Heizstrom zwischen Probenzelle und Referenzzelle in
Abhängigkeit von der Temperatur gemessen; dadurch kann direkt die Änderung der
Wärmekapazität bei konstantem Druck bestimmt werden;
Enzymkinetik
Geschwindigkeitsgesetz und Reaktionsordnung
Im Gegensatz zur Thermodynamik, welche untersucht wann eine Reaktion stattfindet und wo
das Gleichgewicht dieser Reaktion liegt, beschäftigt sich die Kinetik mit der
Reaktionsgeschwindigkeit. Die Reaktionsgeschwindigkeit ist immer proportional zur
Konzentration der Reaktanden:
v = k ⋅ cn
Die Geschwindigkeitskonstante k bildet dabei die Proportionalitätskonstante. Diese
beinhaltet ebenso die Temperaturabhängigkeit der Geschwindigkeit. N ist die
Reaktionsordnung, nach der die Reaktion klassifiziert wird. Die Reaktionsordnung ist im
Geschwindigkeitsgesetz der Exponent der Produktkonzentration, der beschreibt von wie
vielen Edukten die Produktbildung abhängt. Dabei spielen nur solche Edukte eine Rolle,
deren Konzentration nicht konstant ist.
Die Reaktion von Glucose und ATP zu Glucose-6-phosphat mittels Hexokinase ist eine
Reaktion zweiter Ordnung, da die Produktbildung von den Konzentrationen von ATP und
Glucose abhängt. Da in biologischen Systemen die ATP-Konzentration jedoch nahezu
konstant gehalten wird, spricht man von einer Reaktion pseudo erster Ordnung. In der
Kinetik wird der Verbrauch des Edukts A oder die Zunahme des Produkts P gemessen,
weshalb eine Differentielle Schreibweise möglich ist (hier für eine Reaktion erster Ordnung):
v=−
d [ P]
d [ A]
= k ⋅ [ A] = k ⋅ [ A0 − P ] = +
dt
dt
Enzymatisch katalysierte Reaktionen: Michaelis Menten Kinetik
Im ersten Reaktionsschritt wird aus Substrat und Enzym ein Enzym-Substrat Komplex
gebildet. Es handelt sich um eine vor gelagerte Gleichgewichtsreaktion. Im zweiten
Reaktionsschritt werden aus dem Enzym-Substratkomplex das Enzym und das Produkt
freigesetzt.
Wendet man die Differentialschreibweise auf die Bildung des Enzymsubstratkomplexes an
folgt:
d [ ES ]
= k1 ⋅ [ E ][ S ] + k − 2 [ E ][ P] − k −1 ⋅ [ ES ] − k 2 ⋅ [ ES ]
dt
Aufgrund der Tatsache, dass das Produkt in vivo schnell weiter reagiert und in vitro in
kleinen Konzentrationen vorliegt, lässt sich der Term k-2 vernachlässigen:
d [ ES ]
= k1 ⋅ [ E ][ S ] − k−1 ⋅ [ ES ] − k2 ⋅ [ ES ]
dt
Durch die Annahme des quasi-stationären Zustands (die Konzentration des Enzym-SubstratKomplexes erreicht einen Sättigungswert und bleibt über einen gewissen Zeitraum konstant)
resultiert:
d [ ES ]
= k1 ⋅ [ E ][ S ] − (k−1 + k2 ) ⋅ [ ES ] = 0
dt
Nach einer äquivalenten Umformung erhalten wir die Michaelis-Menten Konstante
k −1 + k 2 [ E ][ S ]
=
= KM
k1
[ ES ]
Nun betrachten wir die Geschwindigkeit der Produktbildung, also die
Reaktionsgeschwindigkeit bezüglich des Produkts
v=
d [ P]
= k2 [ ES ] − k− 2 [ E ][ P]
dt
Auch hier ist der Term k-2 aus genannten Gründen zu vernachlässigen
v=
d [ P]
= k2 [ ES ]
dt
Der limitierende Faktor für den Reaktionsumsatz stellt die Enzymkonzentration dar, weil
diese wesentlich geringer ist, als die Substratkonzentration.
[ E ] frei = [ E ]total − [ ES ]
Durch einsetzen und umformen der bisher erläuterten Gleichungen erhält man unter
Berücksichtigung, dass die Maximalgeschwindigkeit
v max = k 2 [ E ]total
Ist, die Michaelis-Menten-Gleichung
v = k 2 [ E ]total ⋅
[S ]
K M + [S ]
Diese Gleichung lässt sich auf alle
Enzymreaktionen anwenden. Sie zeigt einen
hyperbolischen Sättigungsverlauf, wobei ihre
beiden Asymptoten dem Vmax (reale Asymptote
bei positiver Reaktionsgeschwindigkeit) und dem
–KM Wert (imaginäre Asymptote bei negativer
Substratkonzentration) entsprechen. Wenn die
Substratkonzentration dem KM Wert gleicht, liegt die Hälfte der Enzyme als Enzym-SubstratKomplex vor, was bedeutet, dass die Halbmaximale Reaktionsgeschwindigkeit erreicht ist.
Man sieht, dass die Reaktionsgeschwindigkeit bei geringen Substratkonzentrationen
proportional zu [S] verläuft. Bei hohen Substratkonzentrationen, ist sie jedoch [S]unabhängig. Es wird die Maximalgeschwindigkeit des Enzyms erreicht. Nun ist die
Enzymkonzentration limitierend für die Gesamtreaktionsgeschwindigkeit.
Messung der Daten und Auswertung
Um die charakteristischen Werte KM und vmax
eines Enzyms zu bestimmen, müssen einige
Messungen durchgeführt werden. Um die
Produktbildung zu verfolgen, bedient man sich
der Photometrie. In manchen Reaktionen haben
die Edukte andere Absorptionsmaxima als die
Produkte. Dadurch lässt sich die Zunahme der
relativen Absorption in dem
Wellenlängenbereich, bei dem die Produkte
absorbieren, direkt mit der Konzentrationszunahme der Produkte korrelieren. So erhält man
einen Graphen, welcher die Extinktion gegen die Zeit darstellt.
Die Anfangssteigung dieses Graphen entspricht der Reaktionsgeschwindigkeit. Die
Steigungen später entsprechen zwar ebenso Reaktionsgeschwindigkeiten, sind aber nicht
aussagekräftig, da die Geschwindigkeit erstens mit zunehmender Produktbildung abnimmt
und zweitens durch den Substratverbrauch nicht mehr der Anfangssubstratkonzentration,
zuzuordnen ist.
Führt man diese photometrische Messung mit unterschiedlichen Substratkonzentrationen
durch, lässt sich ein Diagram erstellen, dass die Substratkonzentration der
Reaktionsgeschwindigkeit zuordnet. Die Anfangssteigung, also die
Reaktionsgeschwindigkeit, ist dann am größten, wenn die Substratkonzentration sehr hoch
ist. Insofern kann das Enzym die maximale Reaktionsgeschwindigkeit vmax erst bei einer
unendlich hohen Substratkonzentration erreichen.
Dieser Graph entspricht der Michaelis-Menten Kinetik. Allerdings lassen sich hier die
charakteristischen Werte KM und vmax nur erahnen, da sie die Asymptoten des hyperbolen
[E]
= [ ES ]
total
wird. Ursache
Graphen darstellen. Vmax wird in der Realität nie erreicht, da nie
hierfür ist, dass die Affinität des Enzyms zum Substrat nie stark genug ist, damit alle Enzyme
als Enzym-Substratkomplex vorliegen. Um dennoch die Werte exakt ermitteln zu können
werden die Graphen linearisiert. Hier gibt es unterschiedliche Möglichkeiten, wobei jede
seine Vor- und Nachteile hat. Diskutiert und angewendet werden im Praktikum die folgenden
zwei Linearisierungen.
Lineweaver-Burk Darstellung
Diese Darstellung entspricht einer Linearisierung mittels doppelreziproker Darstellung.
v = v max ⋅

[S ]
K M + [S ]

1
1 K M + [S ]
1
1
=
⋅
=
v v max
[S ]
v v max


K
⋅  M + 1

 [S ]
1 KM 1
1
=
⋅
+
v v max [ S ] v max
1
1
v
In dieser Darstellung entspricht der Schnittpunkt mit der v Achse genau max . Der
KM
1
1
−
K M . Die Steigung ist vmax . Problematisch bei dieser
Schnittpunkt mit der [ S ] Achse ist
Darstellung ist, dass die Geschwindigkeitswerte bei den niedrigen Substratkonzentrationen
den größten Fehler aufweisen. Diese sind jedoch die aussagekräftigsten und daher
wichtigsten Werte, da sie den Messdaten am Anfang des Michaelis-Menten-Plots
entsprechen. Diese Daten liefern die genauesten Geschwindigkeits-Werte. Spätere Werte für
die Geschwindigkeit sind verfälscht, da hier die Maximalgeschwindigkeit des Enzyms
aufgrund bereits vorhandener Produkte nicht erreicht wird.
 sie sind deshalb wichtig, weil nur bei niedrigen Substratkonzentrationen die
angenommene quasi-Stationarität auch tatsächlich vorhanden ist; größere
Substratkonzentrationen haben einen höheren systematischen Fehler (Annahme falsch); die
kleineren allerdings einen hohen statistischen Fehler!
Eadie-Hofstee Darstellung
Diese Darstellung basiert auf der Lineweaver-Burk Gleichung. Sie ergibt sich durch
äquivalente Umformung
v
KM
K
vK M
1
1
v
 max = M + 1  v max =
=
+
+ v max
+ v  v = −K M
v v max ⋅ [ S ] v max
[S ]
v
[S ]
[S ]
v
Hier entspricht der Schnittpunkt mit der v Achse genau vmax. Der Schnittpunkt mit der [S ]
vmax
K
Achse ist M . Die Steigung ist − K M . Problematisch bei dieser Darstellung ist, dass v in
beide Koordinaten eingeht. Daher konvergieren alle Fehler im Ursprung. Die Fehler sind
nicht mehr einzuschätzen.
Theoretischer Hintergrund zur betrachteten Reaktion
Die in diesem Praktikumsversuch betrachtete Reaktionsfolge wird von den Enzymen
Hexokinase und Glucose-6-phosphat-Dehydrogenase katalysiert. Die Hexokinase-Reaktion
beinhaltet die Umwandlung von Glucose unter ATP-Verbrauch zu Glucose-6-Phosphat
(Eingangsreaktion in die Glykolyse). Die Glucose-6-phosphat-Dehydrogenase spielt im
Pentosephosphatweg eine entscheidende Rolle. Sie wandelt das überschüssige Glucose-6Phosphat unter Erzeugung von NADPH+H+ zu 6-Phosphoglucono-δ-lacton um.
Betrachtet man die Folge beider Reaktion, ist wichtig festzustellen, dass die Affinität der
Hexokinase zu Glucose wesentlich geringer ist, als die Affinität der Glucose-6-phosphatDehydrogenase zu Glucose-6-Phosphat. Dies bedeutet erstens, dass die Hexokinase die
Geschwindigkeit der Reaktionsfolge bestimmt und zweitens, dass somit die Kinetik der
NADPH-Synthese im zweiten Schritt identisch ist mit der Glucose-Umsetzung im ersten
Schritt. Somit lässt sich die NADPH-Synthese messen und mit der Glucose Umsetzung
direkt korrelieren. Zweitens liegt in unserem Fall ATP und NADP+ im Überschuss vor. Somit
ist sichergestellt, dass die gesamte Glucosemenge, welche im Reagenz vorhanden ist, auch
zu Glucose-6-Phosphat und weiter zu 6-Phosphoglucono-δ-lacton unter NAPH+H+
Erzeugung reagiert. Die gebildete NAPH+H+ Menge entspricht also der Glucose-Menge die
sich zu Beginn der Reaktion im Reagenz befand.
Die NADPH-Synthese ist in einem Photometer direkt messbar über die Zunahme der
spezifischen Extinktion bei 340nm (siehe folgende Abbildung)
Gaschromatographie
Das Prinzip der Chromatographie
Die Chromatographie ist ein in der Chemie sehr häufig verwendetes Trennverfahren. Die
Auftrennung eines Stoffgemisches erfolgt in allen chromatographischen Methoden durch die
unterschiedliche Verteilung seiner Einzelbestandteile zwischen der stationären und der
mobilen Phase. Dabei strömt die mobile Phase durch die stationäre Phase. Je nachdem, ob
ein Einzelbestandteil mehr mit der mobilen oder mehr mit der stationären Phase
wechselwirkt, desto weiter bzw. kürzer wandert er in der stationären Phase. Nachdem der
Einzelbestandteil sichtbar gemacht wurde (Detektion am Ende der stationären Phase in der
Gaschromatographie oder Anfärbung bei der Dünnschichtchromatographie), kann es
aufgrund der Wanderungsstrecke innerhalb einer bestimmten Zeit bzw. der
Wanderungsdauer auf der Strecke der stationären Phase einem bestimmten Stoff
zugeordnet werden.
Die Gaschromatographie selbst dient zur Auftrennung von unzersetzt verdampfbaren
Stoffgemischen. Hier dient als mobile Phase ein Inertgas mit guten Strömungseigenschaften
(z.B. Stickstoff, Helium oder Wasserstoff). Dieses Trägergas wird durch eine Säule mit
definiertem Innendurchmesser geleitet. Die 25-50m lange und 0,5mm dünne Säule (Metall
oder Quarzglas) ist mit einem bestimmten Material (Polysiloxane oder Polyethylen-Glykole),
der stationären Phase, ausgekleidet und zu einer Spule aufgewickelt.
Der Bau eines Gaschromatographen
Ein GC besteht aus drei wesentlichen Bauteilen: Injektor, Trennsäule im GC Ofen und
Detektor (siehe Abbildung 1)
Abbildung 1 Aufbau eines
Gaschromatographen. (1) Druckbehälter
mit Trägergas; (2) Injektor; (3) Trennsäule
zur Spule aufgewickelt; (4) Detektor; (5)
Chromatogramm
Der Injektor und die mobile Phase
Die in einem niedrig siedenden Lösungsmittel
gelöste Probe wird durch das Septum des in
unserem Praktikum verwendeten Split-Injektors
(siehe Abbildung 2) über eine Hamilton Pipette in
die Vaporisations-Kammer eingespritzt. Diese
wird auf ca. 170° erhitzt, damit die Probe
schnellstmöglich vollständig verdampft. Das
obere „Septum purge outlet“, dient dazu
Überreste des durchstochenen Gummi-Septums
abzusaugen, sodass es nicht in die Probe gerät.
Das darauf folgende „Carrier Gas inlet“ ist die
Verbindung zu einem externen TrägergasBehälter. Dieser enthält in unserem Fall
Wasserstoff. Sobald die Probe in den Injektor
Abbildung 2 Aufbau eines Split Injektors
eingespritzt wurde, wird der Startbutton betätigt,
und das Trägergas strömt ein. Es kommt zur
Vermischung des Trägergases mit der Substanz. Der Split outlet dient dazu, überflüssiges
Trägergas-Proben Gemisch zu entfernen. Nur ein sehr geringer Teil der Probe gelangt
letztlich in die Trennsäule (column).
Die Trennsäule und die stationäre Phase
Die Substanzen werden durch das Trägergas (Säulenvordruck) in die Trennsäule
transportiert, welche in den GC Ofen eingebaut ist. Der GC Ofen dient dazu, die Säule
präzise zu temperieren. Das Proben-Trägergas Gemisch sublimiert zunächst in der Säule
wieder, wenn die Temperatur des Ofens unterhalb der Siedetemperatur aller Bestandteile
der Probe liegt. Nun wird ein bestimmtes Temperaturprogramm gefahren, das heißt der Ofen
erwärmt sich langsam, sodass alle Bestandteile erst nach und nach verdampfen, sodass sie
letztlich weiter entfernt voneinander wandern (dies verhindert ein Überschneiden der Peaks
und erleichtert die Auswertung). Man unterscheidet zwei verschiedene Arten von
Trennsäulen: beschichtete und gepackte. Beschichtete Trennsäulen haben im Inneren
lediglich eine Schicht stationäre Phase aufgelagert. Bei gepackten Trennsäulen hingegen
kleidet die stationäre Phase das gesamte Volumen der Trennsäule aus. Die Trennsäule
selbst kann aus Metall oder Glas bestehen. In
unserem Fall handelt es sich um eine beschichtete
Säule aus Glas (FSOT: fused silica open tubular;
siehe nebenstehende Abbildung 3).
Sie besteht aus einer stabilisierenden Schicht aus
fusioniertem Silikat und einem äußeren PolyimidMantel, der für die Flexibilität der Säule sorgt. Nur so
kann sie zu einer Spule aufgewickelt werden. Die
stationäre Phase ist auf die Silikat-Schicht
aufgelagert. Gebräuchlich sind Polysiloxane und
Polyethylen-Glykole (siehe Abbildung 4), wobei
unsere Säule eine Polyethylen-Glykolschicht als
stationäre Phase aufweist.
Abbildung 3 Aufbau eines FSOTs
Abbildung 4 links: Polysiloxane mit
unterschiedlichen Resten; oben: Struktur
der Polyethylen-Glykole
Der Detektor und das Signal
Am Ende der Säule befindet sich ein Detektor, der ein elektronisches Signal erzeugt, wenn
eine Substanz das Trennsystem verlässt. So wird ein typisches Chromatogramm erzeugt. Es
gibt zahlreiche Detektoren, welche jeweils nur selektiv verschiedene Stoffe detektieren
können und auch nur mit bestimmten
Trägergasen kompatibel sind. Im
Gaschromatographen, der in unserem
Versuch verwendet wurde, befindet sich ein
Flammen-Ionisations-Detektor (FID; siehe
nebenstehende Abbildung 5).
Dieser kann lediglich C-C und C-H
Abbildung 5 Aufbau eines FlammenBindungen detektieren. Dieser Detektor
Ionisations-Detektors (FID)
ionisiert die Moleküle der Probe, die aus der
Trennsäule kommen und Sauerstoffmoleküle,
die aus einem externen Behälter
synthetischer Luft (80% Stickstoff, 20%
Sauerstoff) mit der aus der Säule
hervortretenden Probe vermischt werden.
Außerdem wird Wasserstoff als Brenngas beigemischt. Durch die Ionisation der
Sauerstoffmoleküle entstehen Sauerstoffradikale, die sofort mit den ionisierten
Kohlenstoffatomen und Wasserstoffatomen reagieren. Die hierbei frei werdende spezifische
Energie erzeugt einen spezifischen Strom, dessen Intensität gemessen und an den
Computer zur Auswertung weitergegeben wird. Eine Messung erzeugt somit einen Punkt im
Chromatogramm. Ein typisches Chromatogramm (siehe Abbildung 6) eines FI-Detektors ist
im Folgenden abgebildet. Die Zuordnung der Peaks zu den Stoffen erfolgt aufgrund
bekannter Retentionszeiten. Die Fläche unterhalb des Peaks entspricht der Menge des
Stoffes innerhalb des Gemisches. Je breiter der Peak ist, desto verzerrter, also schlechter ist
das Chromatographische Ergebnis (hierzu siehe Abschnitt 6: Die Güte der Trennung)
Totzeit und Retentionszeit
Die Zeit, die das Trägergas benötigt,
um die ganze Säule zu durchströmen,
nennt man die Totzeit t0 des Systems.
Sie liegt bei ca. einer Minute. Im
Idealfall wechselwirkt das Trägergas
gar nicht mit der stationären Phase, so
dass die Totzeit lediglich von Vordruck
(mit dem das Trägergas durch die Säule Abbildung 6 typisches Chromatogramm mit einer
Zuordnung der einzelnen Piks zu den zugehörigen
gedrückt wird) und vom
Strömungswiderstand der Säule abhängt. Verbindungen aufgrund der Retentionszeiten
Die zu trennenden Stoffe müssen chemisch auf die stationäre Phase abgestimmt sein. Im
Gegensatz zu den Trägergasen zeigen die meisten chemischen Stoffe daher eine
Wechselwirkung mit der stationären Phase. Diese brauchen daher länger, um die Säule zu
passieren. Die Totzeit beschreibt also auch diejenige Zeit, die sich ein Analyt in der mobilen
Phase aufhält. Die Nettoretentionszeit beschreibt im Gegensatz dazu die Zeit, die sich ein
Analyt in der stationären Phase aufhält. Die Retentionszeit t R ist die Zeit, die ein Analyt zum
passieren der Säule benötigt, also die Summe aus Totzeit und Nettoretentionszeit.
Die Retention einer Substanz durch die stationäre Phase wird durch drei Aspekte bestimmt:
Die Stärke der Wechselwirkung (z.B. Van-der-Waals, H-Brücken oder Dipol-Moment
Wechselwirkungen) der Substanz mit der stationären Phase beschreibt die Neigung in der
stationären Phase zu bleiben. Der Siedepunkt der Substanz beschreibt die Neigung in der
mobilen Phase zu bleiben. Die Diffusionseigenschaften der Substanz beschreiben die
Beweglichkeit der Substanz in beiden Phasen.
Von außen kann auf die Retention einer Substanz am einfachsten durch TemperaturVeränderungen am Ofen und Veränderungen der Flussrate der mobilen Phase eingewirkt
werden. Eine Temperaturerhöhung bewirkt eine höhere kinetische Energie der Teilchen,
weshalb alle Retentionszeiten verkürzt werden. Wird die Flussrate erhöht, so erhöht sich
auch die Geschwindigkeit der mobilen Phase. Dementsprechend verkürzt sich die
Retentionszeit. Mit der Verkürzung der Retentionszeit reduziert sich allerdings die
Trenneffizienz, weshalb bei geringen Flussraten und bei geringst-möglichen Temperaturen
(knapp oberhalb der Siedetemperatur) aufgetrennt wird.
Biophysikalischer Hintergrund der Auftrennung
Ist ein Stoff A dazu in der Lage sich zwischen zwei nicht mischbaren Phasen physikalisch zu
verteilen, findet das Nernst’sche Verteilungsgesetz Anwendung. Es besagt, dass diese
Verteilung zu einem Gleichgewicht mit dem Nernst’schen Verteilungskoeffizienten
K=
c A ( Phase2) c Aflüssig
= gas
c A ( Phase1)
cA
führt. K ist lediglich von der Temperatur abhängig. Dabei ist zu beachten, dass der Quotient
aus der Menge X der Komponente A in der Phase 1 und der Menge X der Komponente A in
der Phase 2 immer konstant ist
X Aflüssig
= const.
X Agas
Der Retentionsfaktor oder auch Kapazitätsfaktor k ' wird genutzt, um die Wanderungsrate
eines Analyten anhand durch folgende Beziehung zu beschreiben.
k' A =
t R − t0
t0
Um die Trennung von zwei Substanzen auf der Säule zu beschreiben, wird ein
Selektivitätsfaktor
α=
B
k ' B t R − t0
= A
k ' A t R − t0
definiert. Bei der Verwendung dieser Formel, soll Stoff A schneller diffundieren als Stoff B.
Der Selektivitätsfaktor ist daher immer größer als 1.
Die Güte der Trennung
Die Güte der Trennung lässt sich anhand der resultierenden Peaks im Chromatogramm
ersehen. Eine ideale Trennung zeigt Peaks mit verschwindender Breite und großer
Intensität. Das heißt alle Moleküle eines Stoffes, der zuvor im Gemisch vorlag, kommen
exakt zum selben Zeitpunkt am Ende der Trennkapillare an. Je breiter die Peaks, desto
schlechter die Auftrennung. Je unsymmetrischer die Peaks sind, desto unsauberer (Probe
wurde z.B. zu langsam injiziert) wurde gearbeitet. Um die Trenneffizienz anhand der
Peakbreite theoretisch vorauszusagen wurden zwei Modelle entwickelt, die im Folgenden
erläutert werden sollen. Neben der Peakbreite korreliert die Trenneffizienz außerdem mit der
Retentionszeit. Je größer diese ist, desto besser ist die Auftrennung, da die Peaks der
einzelnen Stoffe weiter voneinander entfernt sind und sich somit die Flächen weniger bis
nicht überschneiden. Mit größerer Retentionszeit werden jedoch die Peaks breiter. Es muss
also eine optimale Einstellung zwischen Retentionszeit durch u.a. Flussrate und Breite der
Peaks gefunden werden, je nachdem wie weit die Peaks der Stoffe im Chromatogramm
ohnehin auseinander liegen.
Das Theoretische Plattenmodell
Das theoretische Plattenmodell beschreibt die Vorstellung, dass eine Trennkapillare aus
einer großen Anzahl aufeinander folgender theoretischer Platten besteht. In jeder Platte
findet ein neuer Trennprozess statt, der eine neue Gleichgewichtseinstellung der zu
trennenden Stoffe in der mobilen und stationären Phase bewirkt. Stellt man sich die
Trennkapillare wie beschrieben vor, lässt sich die Trenneffizienz exakter beschreiben: Sie
nimmt mit der Anzahl N der theoretischen Platten zu (je mehr, desto besser) und mit der
Höhe (HETP = Höhenäquivalent) der theoretischen Platten ab (je kleiner, desto besser). Es
resultiert folgende Beziehung zur Länge L der Trennkapillare
HETP =
L
N
Die Anzahl der theoretischen Platten kann aufgrund des Peaks im Chromatogramm
berechnet werden.
5,55 ⋅ t R
N=
2
b1 / 2
2
Hierzu ist die Halbwertsbreite b1/2 relevant. Sie lässt sich einfach anhand eines Peaks im
Koordinatensystem ermitteln, wie die folgende Abbildung 7 zeigen soll. Die Halbwertsbreite
ist der Abstand zwischen den zwei x Werten, deren zugehörige y Werte auf der halben Höhe
der Amplitude liegen.
Abbildung 7 Die Halbwertsbreite
entspricht der Breite des Peaks
auf der halben Intensität.
Die Ratentheorie
Das Plattenmodell geht davon aus, dass die Gleichgewichtseinstellung in jeder Platte sofort
geschieht, also keine Zeit benötigt wird. Eine realistischere Beschreibung für die Prozesse
innerhalb der Trennkapillare liefert die Ratentheorie. Sie konzentriert sich auf die
Beschreibung der Zeit, die für das Lösen des zu trennendes Gemisches benötigt wird, bis
sich ein Gleichgewicht zwischen stationärer und mobiler Phase eingestellt hat. Für die
resultierende Peakbreite ist also die Elutionsrate (Elution ist der Transport einer Substanz
durch eine chromatographische Säule durch kontinuierliche Zugabe von mobiler Phase) von
großer Bedeutung. Außerdem spielen die Anzahl der unterschiedlichen Wege, die das Gas
einschlagen kann eine wichtige Rolle.
Die Raten-Theorie führte zu der Entwicklung der Van-Deemter Gleichung, welche das
Höhenäquivalent mit 4 Parametern beschreibt:
HETP = A +
A: [m]
B: [m*ml/min]
B
+ Cv
v
C: [m*min/ml]
v: [ml/min]
v ist hier die durchschnittliche lineare Gasgeschwindigkeit der mobilen Phase (=Flussrate).
Sie kann am Chromatographen eingestellt werden und ist somit bekannt. A, B und C sind
spezielle Parameter. A ist die Wirbeldiffusionskonstante (Eddy Diffusion). Sie ist unabhängig
von der Gasgeschwindigkeit und berücksichtigt, dass das Gas unterschiedliche Wege
einschlagen kann. Diese Konstante spielt jedoch nur bei gepackten Säulen (Säulen, bei
denen die stationäre Phase den Hohlraum vollständig auskleidet) eine bedeutende Rolle, da
hier viel mehr Wege möglich sind. Bei beschichteten Säulen, wie wir sie im Praktikum
verwendet haben, ist der Wert dieser Konstante sehr klein. B ist die
Längsdiffusionskonstante (Longitudinale Diffusion). Um diese zu veranschaulichen, stellt
man sich einen Stoff in der Kapillare als ovaler Tropfen vor, dessen Dichte in der Mitte am
größten, vorne und hinten am geringsten ist. Wird nun die Flussrate erhöht, so driften die
einzelnen Moleküle dieses Tropfen durch Ausgleichsdiffusion in Bereiche niedriger Dichte
bzw. Konzentration weniger auseinander, da weniger Zeit dazu zur Verfügung steht. Der
Tropfen vergrößert sich weniger. Die Breite des Peaks wird geringer. Die Flussrate verhält
sich hier also antiproportional mit der Konstante zum Höhenäquivalent. Die Longitudinale
Diffusion hängt ab von der Temperatur und dem Trägergas. C ist die
Stoffübergangskonstante. Sie beschreibt de Interaktion des Stoffes in der stationären Phase
und die Möglichkeit des Übergangs in die mobile Phase. Je schneller die Flussrate, desto
größer ist der Widerstand für den Übergang von der stationären Phase in die mobile Phase.
Der Übergang erfolgt daher statistisch gesehen später, was eine Verbreiterung der Peaks
zur Folge hat. Mit der Flussrate nimmt auch der Widerstand, und somit die Konstante zu. Sie
verhalten sich proportional zum Höhenäquivalent. Die Stoffübergangskonstante ist abhängig
vom Trägergas und der Dicke der stationären Phase.
Der Van-Deemter Plot
Anhand dieser Beziehung lässt sich die ideale Flussrate, die einen minimalen Wert für HETP
liefert, bestimmen. Es ist das Minimum des v -HETP Plots.
(1)
Bildung der Ableitungen:
HETP (v) = A +

B
∂HETP
= − 2 +C
v
∂v
∂HETP 2 B
= 3
v
∂v∂v
(2)
Notwendige Bedingung:
−
und
∂HETP
=0
∂v
B
C
B
B
+ C = 0  C = 2  Cv 2 = B  v =
2
v
v
(3)
Hinreichende Bedingung:
2B
 B


 C


(4)
3
> 0  Minimum bei v =
∂HETP
≠0
∂v∂v
 v=
B
∂HETP 2 B
in
= 3
C
v
∂v∂v
B
C
Berechnung der HETP Koordinate: v =
HETP(v) = A +
B
+ Cv
v
B
B
in HETP (v) = A + + Cv
C
v
B1 / 2
B ⋅ C1 / 2 C ⋅ B1 / 2
B
B
B
+C
= A + 1/ 2 + C ⋅ 1/ 2 = A +
+
B
C
B1 / 2
C1 / 2
C
B
C1 / 2
C
= A + B1 / 2 ⋅ C1 / 2 + C 1 / 2 ⋅ B1 / 2 = A + 2(C ⋅ B )
1/ 2
= A + 2 CB
In der folgenden Abbildung 8 ist der Graph gezeigt. Man kann erkennen wie sich das
Höhenäquivalent aus den einzelnen Konstanten additiv zusammensetzt. Das Minimum der
Ergebnis-Kurve (rot) entspricht exakt den Koordinaten
[
 B

 | A + 2 CB
C


]
Abbildung 8 Auftragung des Höhenäquivalents H gegen die Flussrate u. ein
typischer Van-Deemter Plot ist hier rot gezeigt. Die drei Parameter, von denen der
Van-Deemter Plot abhängt, sind ebenfalls eingezeichnet Es ist bei kleinen
Flussraten gut die Abhängigkeit von der Diffusionskonstante und bei großen
Flussraten gut die Abhängigkeit von der Stoffaustauschkonstanten zu erkennen.
Anwendung der Gaschromatographie
Die Gaschromatographie findet ihre Anwendung in Bereichen u.a. der Medizin (klinische
Diagnostik: Auftrennung von Blut), Lebensmittelchemie (Typisierung von Lebensmitteln
aufgrund ihrer Zusammensetzung) und Umweltanalytik (Untersuchung von AerosolTreibgasen). Dies sind nur einige Beispiele. In der Biochemie eignet sich die
Gaschromatographie zur Analyse der Proteine. Es kann der prozentuale Gehalt der
einzelnen Aminosäuren in einem Protein bestimmt werden. Da Gaschromatographen
lediglich eine maximale Temperatur von 250°C unterstützen, Proteine jedoch eine erheblich
höhere Siedetemperatur haben, ist eine Auftrennung der Proteine an sich nicht möglich.
Auch Aminosäuren haben einen Siedepunkt von weit über 250°C. Meistens kommt es durch
solch hohe Temperaturen auch zur Zersetzung, weshalb ebenso keine
Gaschromatographische Auftrennung erfolgen kann. Mittels Totalhydrolyse eines Proteins
und anschließender Derivatisierung der Carboxylgruppe mit einem Ester wird der Siedepunkt
jedoch soweit herabgesetzt, dass eine Auftrennung möglich ist. Das Verhältnis der Integrale
der einzelnen Peaks ergibt das Verhältnis zu dem die einzelnen Aminosäuren im Protein
vorkommen.
Fluoreszenz
Fluoreszenz: Übergänge zwischen elektronischen und Schwingungs- Zuständen
Bei der Fluoreszenz handelt es sich um eine Strahlung, ausgehend von einem
fluoreszierenden Molekül. Sie wird ausgelöst, indem dieses Molekül zunächst ein Photon
absorbiert und so vom elektronischen und Schwingungsgrundzustand in den ersten
elektronischen Zustand und je nach Photonenenergie in einen höheren Schwingungszustand
angeregt wird. Innerhalb von Femtosekunden relaxiert das System in den untersten
Schwingungszustand des ersten angeregten elektronischen Zustandes zurück. Die
freiwerdende Energie entspricht einer Wärmestrahlung (interne Konversion: internal
conversion). Von hier aus wird ein Photon emittiert. Das System gelangt so in den
elektronischen Grundzustand und durch weitere schnelle interne Konversion in den
Schwingungsgrundzustand. Dadurch, dass durch die zweimalig auftretende interne
Konversion Energie verloren geht, kann das emittierte Photon nicht dieselbe Energie
aufweisen, wie das absorbierte. Es resultiert eine Rotverschiebung der Fluoreszenzstrahlung
relativ zur absorbierten Strahlung. Dieses Phänomen wird als Stokes-Shift nach seinem
Entdecker beschrieben
Mittels des Franck Condon Prinzips kann der wahrscheinlichste Übergang zwischen
verschiedenen Schwingungszuständen unterschiedlicher elektronischer Zustände berechnet
werden. Die Berechnung geht davon aus, dass die Zeit für den Übergang der Elektronen
zwischen den beiden Niveaus so schnell stattfindet (10-15s), dass sich der Kernabstand nicht
ändern kann, da eine Kernschwingungsperiode länger dauert (10-13s). Die
Elektronenbewegung ist aufgrund der geringeren Masse des Elektrons in einer solchen
Geschwindigkeit möglich. Betrachtet man das Energieschema des quantenmechanischen
Morse-Potentials (siehe Abbildung 1), erkennt man die direkte Konsequenz dieser Annahme.
Die Elektronen aus dem Schwingungsgrundzustand landen nicht im
Schwingungsgrundzustand des höheren elektronischen Niveaus, sondern in einem sich
darüber befindenden Schwingungszustand. Der Pfeil, welcher für diesen Übergang steht,
verläuft dabei senkrecht nach oben. Man spricht von einem vertikalen Übergang. Ob der
Übergang nun hin zum Schwingungszustand n, n+1 oder n-1 stattfindet ist
wahrscheinlichkeitsverteilt. Die Verteilung der Übergangsintensitäten (vom
Schwingungsgrundzustand hin zu diesen oberen Schwingungszuständen des elektronisch
höheren Niveaus) in einer makroskopischen Probe hängt davon ab, welcher
Schwingungszustand bei einem vertikalen Übergang auch den wahrscheinlichsten (je größer
die Amplitude der Eigenfunktion eines Schwingungsniveaus für einen bestimmten Abstand
ist) Schwingungsabstand hat und in welchem Abstand sich das Elektron gerade im aktuellen
Schwingungsgrundzustand befindet.
Abbildung 1, Energieschema des quantenmechanischen Morse-Potentials; links:
wahrscheinlichster Übergang nach dem Franck Condon Prinzip; rechts: Wanderung eines
Elektrons zwischen den Zuständen bis zum Ausgangspunkt
Auf der x Achse ist der Kernabstand aufgetragen; er ist abhängig von der Kernschwingung
(kann vernachlässigt werden, da sie sehr langsam ist) und der Schwingung der
Bindungselektronen; würde die Schwingung der Kerne zueinander schneller sein, als die
Elektronen für den Übergang zwischen ihren elektronischen Niveaus benötigen, so würde
kein vertikaler Übergang stattfinden; das Elektron würde also zufällig in einem beliebigen
Schwingungszustand landen; angeregt werden mittels Fluoreszenz die Pi Elektronen in das
Pi* Orbital; dadurch steigt der mittlere Abstand der Kerne voneinander an (Antibindendes
Orbital hat geringere Überlappung); Die Lebensdauer des angeregten Zustands (Elektron im
Pi*) beträgt ca. 10ns (d.h. nach Abstellen der Anregungsquelle erlischt die Fluoreszenz
sofort); im Unterschied zur Phosphoreszenz bleibt der Spin des Elektrons bei allen
Übergängen erhalten!
Die Photonen-Emission findet immer aus dem S1 statt, weshalb das Emissionsspektrum
unabhängig von der Anregungswelle ist; höhere elektronische zustände gehen immer durch
interne Konversion (Wärmestrahlung) in den S1 Zustand über;
 Der Triplettzustand n liegt energetisch unterhalb des Singulettzustandes n. Ursache ist,
dass für den Übergang in den unteren S Zustand vom Triplett-1 Zustand aus weniger
Energie frei wird als vom Sigulett-2 Zustand aus. Es wird deshalb weniger Energie frei, da
Energie dafür verloren geht, den Spin umzudrehen. Diesen Energiebetrag nennt man
Spinpaarungsenergie.
Auch das Jablonski-Diagramm veranschaulicht die Prozesse der Photonen -Absorption und
–Emission, wobei Rotationsübergänge eine Ebene unter den Vibrationsübergängen sind und
deshalb in diesem Diagram nicht abgebildet werden (siehe Abbildung 2). Im Folgenden soll
auf den Prozess der Phosphoreszenz eingegangen werden.
Abbildung 2, Jablonski Diagram der möglichen quantenmechanischen Übergänge
Phosphoreszenz
Phosphoreszenz ist ähnlich der Fluoreszenz ebenfalls eine Strahlung, ausgehend von
phosphoreszierenden Molekülen. Während die Fluoreszenz-Strahlung direkt während der
Einstrahlung von Licht messbar ist, und schon Mikrosekunden danach nicht mehr, so
ermöglicht die Phosphoreszenz ein mitunter sehr langes Nachleuchten. Dieses entsteht
dadurch, dass vom ersten elektronischen angeregten Zustand kein Photon emittiert wird,
sondern zunächst ein Interkombinationsprozess (internal crossing), bei dem sich der Spin
des Elektrons umkehrt, stattfindet (S1 Zustand geht in T1 Zustand über). Es handelt sich um
ein höheres metastabiles Energieniveau (Triplett-Zustand), in dem das Elektron nun
„gefangen“ ist. Interkombinationsprozesse sind eigentlich quantenmechanisch verboten und
geschehen selten und zufällig, mit einer bestimmten Wahrscheinlichkeit. Die Rückkehr in den
elektronischen Grundzustand ist nur durch einen weiteren Interkombinationsprozess
möglich, der den Triplett-Zustand durch Spinumkehr und Photonen-Emission in den
Singulett-Zustand überführt. Da die gesamte Phosphoreszenz-Strahlung aufgrund ihrer
Abhängigkeit von einer Wahrscheinlichkeitsverteilung mitunter erst Sekunden oder länger
nach der Einstrahlung des Lichts abgestrahlt wird, eignet sie sich nicht für unsere
Messungen. Es würde eine zu lange Zeit beanspruchen.
Typische Lebensdauern der Phosphoreszenz betragen millisekunden bis sekunden und
werden daher eher durch mögliche Deaktivierungsprozesse begrenzt als durch die
eigentliche Emission des Photons;
Messung der Phosphoreszenz Lebensdauer
ich sollte erklären, wie man die tripplett lebensdauer messen kann, wenn keine
Phosphoreszenz stattfindet (das war so eine Knobelaufgabe, wo man keine Ahnung von
haben muss ;)). Bin erst nach vielen Hilfestellungen draufgekommen. Man nutzt einfach zwei
gepulste Laser, einen intensiven und einen schwächeren, der es nicht schafft in den Triplet
zustand anzuregen. der schwächere Laser läuft im dauerfeuer, sodass man die ganze zeit
ein Fluoreszenzsignal hat, dann kommt der starke Laserpuls. Dadurch werden Elektronen in
den Tripletzustand angeregt. Dementsprechend schwächt sich die Fluoreszenz ab. wenn die
Elektronen nun nach und nach wieder strahlungsfrei in den Grundzustand übergehen
werden sie wieder von dem schwachen Laser angeregt wodurch das Fluoreszenzsignal
wieder zunimmt.
 Als Konkurrenz zur Lumineszenz (Fluoreszenz + Phosphoreszenz) können weitere zwei
Möglichkeiten der Relaxation in den Grundzustand stattfinden
Fluoreszenzlöschung (Quenching)
Fluoreszenzlöschung meint die strahlungslose Desaktivierung des angeregten Zustands des
Fluorophors durch Quencher Moleküle, wodurch die Fluoreszenzintensität reduziert wird
(geringere Quanten-Ausbeute). Fluoreszenzlöschung kann über verschiedene Prozesse
erfolgen (Energietransfer, Elektronen- bzw. Protonentransfer, chemische Reaktionen im
Anregungszustand);
Die Löschung geschieht entweder durch Kollision des Fluorophors mit dem Quencher
(dynamische Fluoreszenzlöschung) oder durch Komplexbildung zwischen beiden Molekülen
(statische Fluoreszenzlöschung). Die Effektivität beider Prozesse ist von der Konzentration
der Löschermoleküle abhängig. In beiden Prozessen ist der direkte molekulare Kontakt
zwischen Fluorophor und Quencher erforderlich. Quenching-Messungen geben daher
Aufschluss über die Zugänglichkeit eines Fluorophors (z.B. in einem Protein oder einer
Membran) und über die Diffusionsgeschwindigkeiten des Quenchers.
Fluorophore und Fluoreszenzintensität
Man unterscheidet intrinsische von extrinsischen Fluorophoren. Erstere sind in vivo
vorkommende fluoreszierende Moleküle, letztere sind synthetisch hergestellte. Alle
Fluorophore weisen delokalisierte Pi Elektronensysteme auf, die in der Lage sind Photonen
zu absorbieren; Wichtige intrinsische fluoreszierende Moleküle sind die aromatischen
Aminosäuren Tryptophan, Tyrosin und Phenylalanin, sowohl die Kofaktoren FMN, FAD und
NADH. In gefalteten Proteinen ist lediglich die Fluoreszenz der Tryptophane relevant (macht
90% der Fluoreszenzemission des Proteins aus), da die der Tyrosine gequencht wird
(Energietransfer von Tyrosin auf Tryptophan oder durch Wasserstoffbrücken über die OH
Gruppe auf die Lösungsmittelumgebung) und die der Phenylalanine sehr schwach ist. Als
typische Quencher fungieren Sauerstoff, Acrylamid und Amine. Auch die Aminosäuren
desselben Proteins können ein Quenchen der Tryptophanfluoreszenz bewirken, was zu einer
Intensitätssteigerung der Fluoreszenz proportional zum Denaturierungsprozess führt.
Fluoreszenzanisotropie
Ein Fluorophor absorbiert bevorzugt Photonen, deren elektrische Feldvektoren parallel zum
Übergangsmoment des Fluorophoren ausgerichtet sind. Die Übergangsmomente für
Absorption und Emission eines Fluorophoren haben jeweils definierte Orientierungen. In
einer isotropen Lösung nehmen die Moleküle alle Orientierungen mit gleicher
Wahrscheinlichkeit ein. Strahlt man mit polarisiertem Licht ein, so werden von allen
Molekülen nur diejenigen angeregt, deren Absorptionsübergangsmoment parallel zum
ausgerichteten elektrischen Feldvektor des einfallenden Lichtes steht. Aus dieser
Photoselektion, welche die Fluoreszenzintensität im Vergleich zur „normalen“ Fluoreszenz
erheblich verringert, resultiert eine partiell polarisierte Fluoreszenzemission, die daraus
resultiert, dass diese angeregten Moleküle ihrerseits Licht emittieren, deren elektrischer
Feldvektor parallel zu ihrem Emissionsübergangsmoment steht.
Zweck der Fluoreszenzspektroskopie
Fluoreszenzspektroskopie ist eine sehr leistungsfähige Untersuchungsmethode, um
dynamische Eigenschaften der Lösungen von Biomolekülen zu untersuchen. Dies liegt vor
allem in der hierfür günstigen Lebensdauer der angeregten Zustände. Innerhalb dieser
Zeitspanne können sich viele molekulare Prozesse ereignen, die das Erscheinungsbild des
Fluoreszenzspektrums beeinflussen und damit Informationen über eben diese molekulare
Prozesse, an denen man ja interessiert ist, geben. Die Parameter, die das
Fluoreszenzspektrum beeinflussen sind von allen Prozessen, die innerhalb der Lebensdauer
des angeregten Zustands stattfinden, abhängig. So z.B. Kollisionen mit Quenchern,
Rotationsdiffusion, Bildung von Komplexen mit Lösungsmittelmolekülen oder anderen
gelösten Stoffen sowie der Einfluss der Lösungsmittelrelaxation. Diese Prozesse können
Moleküle mit einschließen, die zum Zeitpunkt der Anregung über 100 Å vom Fluorophoren
entfernt sind.
Rotationsdiffusion der Fluoreszenzanisotropie
Wie oben erwähnt kann man durch Einstrahlung von polarisiertem Licht eine polarisierte
Lichtemission erzeugen. Die Größe der theoretischen Polarisation, die durch den Winkel
zwischen den Übergangsmomenten für Absorption und Emission bestimmt wird, kann im
Experiment durch verschiedene Faktoren vermindert werden. Einer dieser Faktoren ist die
Rotationsdiffusion. Rotieren die Moleküle in Lösung sehr viel langsamer als die Lebensdauer
des angeregten Zustands beträgt, so tritt die Lichtemission schneller ein, als dass die
Fluoreszenzanisotropie durch die Rotation merklich beeinflusst werden könnte. Rotieren die
Moleküle sehr viel schneller, so mittelt sich der Effekt der Rotation auf das
Fluoreszenzspektrum heraus. Ist die Rotationsgeschwindigkeit wie im Fall von Proteinen in
wässriger Lösung in der Größenordnung der Fluoreszenzlebensdauern, so ändern sich die
Orientierungen der Moleküle, während sie sich im angeregten Zustand befinden und damit
auch die Orientierung des Emissionsübergangsmoments. Dadurch wird die gemessene
Anisotropie bzw. Polarisation des emittierten Lichtes von der theoretischen (d.h. ohne
Rotation) abweichen. Es folgt, dass Messungen von Fluoreszenzanisotropie empfindlich auf
alle Faktoren sein werden, welche die Rotationsrate der Fluorophoren beeinflussen.
Quenchen der Fluoreszenz durch molekularen Sauerstoff
Stößt ein Fluorophor im angeregten Zustand mit einem Sauerstoffmolekül zusammen, so
relaxiert das Fluorophor ohne die Emission eines Photons in den Grundzustand. Die
durchschnittliche Weglänge, die ein Sauerstoffmolekül innerhalb von 10ns diffundieren kann
beträgt nach Einstein Dx2 = 2Dt. Setzt man für den Diffusionskoeffizienten D den Wert für
Sauerstoff ein (D = 2,5 10-5 cm2/s) so erhält man Dx = 70 Å. Dies ist mit der Dicke einer
biologischen Membran oder dem Durchmesser eines Proteins vergleichbar. Mit
Fluorophoren, die eine längere Lebensdauer aufweisen, kann die Sauerstoffdiffusion via
gemessene Fluoreszenzintensität über (noch) längere Abschnitte verfolgt werden.
Lösungsmittelrelaxation
Die Lösungsmittelrelaxation bewirkt in polaren Lösungsmitteln eine Rotverschiebung der
Fluoreszenz (unpolare Lösungsmittel verschieben das Fluoreszenzmaximum hin zu
kleineren Wellenlängen). Dies geschieht, weil die angeregten elektronischen Zustände eine
stärkere Polarisation (höheres Dipolmoment) aufweisen und daher mit den Molekülen des
polaren Lösungsmittels wechselwirken (höherer Solvatationsgrad), was zu einer
Energieerniedrigung des angeregten Zustandes führt. Diese Energieerniedrigung entspricht
einer erheblichen Rotverschiebung (Stokes shift), welche abhängig ist von der
Polarisierbarkeit und Viskosität des Lösungsmittels sowie von der Ladungsverteilung im
Grund- und ersten angeregten Zustand des Fluorophors. Ist das Lösungsmittel sehr viskos,
erfolgt die Lösungsmittelrelaxation nicht während der Lebensdauer des angeregten Zustands
(Rotverschiebung wird daher reduziert); normalerweise erfolgt die Lösungsmittelrelaxation in
einer Zeit von einer Pikosekunde;
Wenn Tryptophane in der hydrophoben Tasche des Proteins liegen, bewirken sie also die
Maximalintensität der Fluoreszenz bei einer anderen Wellenlänge als, wenn die Tryptophane
an der Proteinoberfläche liegen, wie es im denaturierten Zustand der Fall ist. sind sie der
polaren wässrigen Umgebung ausgesetzt, zeigen sie Fluoreszenzmaxima bei ca. 350-353
nm; ist Trp vom wässrigen Medium abgeschirmt zeigen sie eine Blauverschiebung im
Fluoreszenzmaximum;
So lässt sich der Denaturierungsprozess korrelieren mit der Zunahme der Rotverschiebung
bzw. der Verschiebung des Fluoreszenzmaximums. Anders formuliert: die
Fluoreszenzintensität bei einer höheren Wellenlänge nimmt zu, während die
Fluoreszenzintensität bei einer niedrigeren Wellenlänge abnimmt. Damit lassen sich
Aussagen über die Proteinstabilität machen;
Fluoreszenz- Resonanz-Energietransfer (FRET)
Es ist möglich, dass die Energie des angeregten
Zustands eines Fluorophors (Donor-Fluorophor) direkt
und strahlungslos (über Dipol-Dipol Wechselwirkung) auf
ein anderes Molekül (Akzeptor-Fluorophor) übertragen
wird. FRET kann über ein Quenchen (verringern) der
Fluoreszenz des ersten Farbstoffes und die Zunahme
der Fluoreszenzintensität des zweiten, nicht direkt
angeregten Farbstoffes detektiert werden (siehe
Abbildung 3: Prinzip der Wechselwirkung
Abbildung 3). Damit ein FRET stattfinden kann,
zwischen einem Fluorophorenpaar,
müssen 3 Kriterien erfüllt werden.
Auslösung des FRET
1.) Das Emissionsspektrum des Fluorophors
muss dem Absorptionsspektrum des Moleküls entsprechen, das die Energie
aufnimmt (Überlappung der Spektren)
2.) Der Abstand r zwischen den beiden Farbstoffen darf nicht größer als 6-8nm sein, da
die Effizienz der Energieübertragung antiproportional zu r6 ist.
3.) Donor und Akzeptor müssen parallele elektronische Schwingungsebenen aufweisen
(in Lösung aufgrund der Molekülbewegung meist erfüllt)
Aufgrund dieser Bedingungen haben sich bestimmte FRET Fluorophorenpaare entwickelt,
wie z.B. CFP (Zyan fluoreszierendes Protein) und YFP (gelb fluoreszierendes Protein),
dessen überlappendes Spektrum in der folgenden Abbildung 4 gezeigt werden soll.
Abbildung 4: grau hinterlegt die Überlappung des
CFP Emissionsspektrums mit dem YFPAbsorptionsspektrum
Aus der Größe der überlappenden Fläche lässt sich die maximale FRET-Effizienz herleiten.
Außerdem hängt die FRET Effizienz vom Förster-Radius R0 und vom Abstand r des
Fluorophorenpaars ab.
R06
E= 6
R0 + r 6
Der Förster-Radius R0 beschreibt denjenigen Abstand zwischen beiden Fluorophoren, bei
dem die Energieübertragung zu 50% erfolgt. Er entspricht für das Paar CFP-YFP 4,9nm und
ist lediglich von den eingesetzten Fluorophoren abhängig (bewegt sich immer im nm
Bereich):
Der Förster Radius wird theoretisch berechnet und dann auf das FRET Experiment
angewandt.
Auch die Aminosäuren Tyrosin und Tryptophan lassen sich als FRET Fluorophorenpaare
nutzen, weshalb Abstände zwischen solchen Aminosäuren innerhalb eines Proteins
bestimmbar sind. FRET dient hauptsächlich zum Nachweis von Protein-Protein, ProteinNukleinsäure und Nukleinsäure-Nukleinsäure Wechselwirkungen. Die Interaktion zwischen
zwei Proteinen kann beobachtet werden, indem an das erste Protein ein Donor-Fluorophor
und an das zweite Protein ein Akzeptor-Fluorophor über Kopplungsreaktionen (meist über
Thiobindungen an Cysteine) bindet. So entsteht ein FRET-Signal, dessen Effizienz je nach
Abstand der modifizierten Proteine variiert (bewegen sie sich voneinander weg, wird die
Effizienz geringer, bewegen sie sich aufeinander zu, wird die Effizienz höher). So kann der
Abstand zwischen beiden Proteinen berechnet und über die Zeit Signaltransduktionswege
oder Dimerisierungen aufgeklärt werden. Darüber hinaus ist die Vermessung von ProteinKonformationsänderungen möglich, wenn Donor- und Akzeptor-Fluorophor an dasselbe
Protein gebunden sind. Die Konzentrationsbestimmung von Nukleinsäuren ist ebenso über
FRET möglich. Dabei werden während der PCR (Polymerase Kettenreaktion) mit Donorbzw. Akzeptor-Fluorophoren markierte Oligonukleotide im Überschuss hinzu gegeben. Diese
dienen als Hybridsonden, welche während eines PCR Zyklus spezifisch an die DNA binden
und somit eine double-stranded Hybrid-DNA erzeugen, bei der sich Donor- und AkzeptorFluorophor sehr nahe kommen. So steigt mit Zunahme der double-stranded Hybrid-DNA
Konzentration proportional auch die Fluoreszenz des Akzeptor-Fluorophors (siehe Abbildung
5).
Abbildung 5: 1: vor einem
PCR Zyklus liegen die
Oligonukleotide frei vor; 2:
danach sind die
Hybridsonden in einer
double-stranded DNA
eingebaut und bewirken
FRET
 Zur Untersuchung von Protein-Ligand WW dienen FRET, intrinsische Fluorophore und
Anisotropie Messungen; Protein-Protein-WW können über Anisotropie Messungen nur
schwer beobachtet werden, da Rotation zu langsam;
Grün fluoreszierendes Protein (GFP)
Das für unseren Versuch verwendete Protein trägt die
Bezeichnung GFP. Es wurde aus der Leuchtqualle Aequoria
victoria isoliert. Es besteht aus 238 Aminosäuren mit einem
Molekulargewicht von 26,9 kDa und stellt somit ein eher
kleines Protein dar. Strukturell besteht es aus einem mittels
Enzym post-translational gebildetem Chromophor, das durch
Zyklisierung und Oxidation dreier Aminosäure Reste entsteht
(Ser65-Tyr66-Gly67) und einer β-Fass Struktur, welche sich
um das Chromophor herum befindet (siehe Abbildung 6).
Abbildung 6: Tertiärstruktur von GFP
Das unmodifizierte GFP weist zwei Absorptionsmaxima auf. Eines befindet sich bei 395nm,
das andere bei 475nm. Das Fluoreszenzmaximum liegt bei 509nm. Das besondere an GFP
ist, dass es sich in Zellen überexprimieren lässt, weshalb es in der Fluoreszenzmikroskopie
exakt lokalisiert werden kann. Nun lässt sich GFP mit beliebigen anderen Proteinen Genspezifisch fusionieren. Somit kann eine räumliche und zeitliche Verteilung eines jeden
Proteins in einem Organismus über die empfindliche Laser-Fluoreszenzmikroskopie verfolgt
werden. Es handelt sich heutzutage um eine Standardmethode der Zellbiologie, vor allem
auch deshalb, weil GFP in nahezu allen eukaryotischen Zellen als nicht toxisch einzustufen
ist.
Auf eine Denaturierung des Proteins, folgt auch eine
Zerstörung des Chromophors. Die Folge ist der Verlust der
Fähigkeit Fluoreszenz zu zeigen. In der FRET wird GFP
ebenso verwendet, wobei hier als Fluorophorenpaar
Rhodamin 6G (siehe Abbildung 7) zum Einsatz kommt.
Rhodamin 6G weist eine Quantenausbeute von 95% auf,
was bedeutet, dass 95% aller absorbierten Photonen und
Fluoreszenzphotonen umgewandelt werden. Außerdem ist
die Wahrscheinlichkeit eines Interkombinationsprozess
Abbildung 7: Struktur von Rhodamin 6G
äußerst gering. Rhodamine liegen also selten im nicht
fluoreszierenden, langlebigen Triplett-Zustand vor.
Kinetik des Denaturierungsprozesses
Die Denaturierung eines Proteins beschreibt den Verlust der Tertiärstruktur und der damit
verbundenen biologischen Funktion. Sie kann durch Hitze, Säure, Base, Schwermetallionen,
Detergentien (=Tenside) und anderen Denaturierungsmittel erfolgen. Die Denaturierung ist,
solange nicht abgeschlossen, reversibel. Ist das Protein jedoch vollständig denaturiert, ist es
auch evtl. irreversibel zerstört. Die Denaturierung zerstört neben der Tertiärstruktur auch die
Sekundärstruktur und die Quartiärstruktur. Die Primärstruktur jedoch bleibt erhalten (keine
Spaltung kovalenter Peptidbindungen). Der Denaturierungsprozess verläuft kooperativ
(Effekt der Allosterie). Es resultiert somit ein sigmoidaler Zusammenhang zwischen der
Intensität des Denaturierungsfaktors (zum Beispiel Konzentration des Detergentiums oder
Temperatur) und dem Denaturierungsgrad des Proteins. In der Folgenden Abbildung 8 wird
dies über die Veränderung der relativen Absorption bei 260nm, die wie später genauer
erläutert wird mit dem Denaturierungsgrad direkt proportional korreliert, über ein
Temperaturintervall verdeutlicht.
Abbildung 8: sigmoidaler Zusammenhang zwischen der
Intensität des Denaturierungsfaktors (hier Temperatur) und
Denaturierungsgrad (hier indirekt über die relative
Absorption bei 260nm dargestellt)
Bekannte und häufig in der Biochemie verwendete Denaturierungsmittel sind Harnstoff und
SDS (Natriumdodecylsulfat). In unserem Versuch findet Guanidiniumhydrochlorid (GuHCl)
als Denaturierungsmittel seine Anwendung.
Vorteile und Anwendung der Fluoreszenzspektroskopie
(Zusammenfassung und Ergänzung)
Fluoreszenzspektroskopie ist die wichtigste Spektroskopie Methode in der Biochemie. Sie
erlaubt die Unersuchung von Einzelmolekülen und sehr kleinen Mengen Probe sowohl in
vitro als auch in vivo. Es können thermodynamische (Bindungskonstanten,
Faltungsgleichgewichte), kinetische (Faltungskinetik) und dynamische
(Rotationskorrelationszeit) Parameter gemessen werden.
Wie bereits beschrieben, können über FRET Abstände von Proteinen gemessen werden und
somit Signaltransduktionswege und Dimerisierungen aufgeklärt werden. Darüber hinaus
können Konformations-Veränderungen und Entfaltungsprozesse beobachtet werden.
In der FCS (Fluoreszenz-Korrelations-Spektroskopie) können Diffusionskonstanten,
Konzentrationen und Bindungen zwischen verschiedenen diffundierenden Spezies
gemessen werden.
Außerdem ist eine Einzelmolekülfluoreszenzspektroskopie möglich. Hier werden einzelne
Moleküle sichtbar gemacht, indem mittels eines Konfokalmikroskopes die Größe des
Detektionsvolumens auf unter einen Femtoliter begrenzt wird. Dadurch befindet sich bei
geeigneter Verdünnung im Durchschnitt weniger als ein fluoreszenzaktives Teilchen im
Detektionsvolumen. So können emittierte Photonen einem bestimmten Teilchen zugeordnet
werden und charakterisieren somit die Eigenschaften des Teilchens, welche in der Analyse
einer Probe verborgen bleiben würden. In einer Probe können evtl. nur wenige
Einzelmoleküle den Hauptteil der gemessenen Fluoreszenzintensität ausmachen, während
die anderen nur schwach fluoreszieren.
Docking
Computerchemie: Das strukturbasierte Design von Liganden
Durch die genaue Kenntnis über die dreidimensionale Struktur von Proteinen, die durch die
Aminosäuresequenz determiniert ist, und über ihre Wirkungsweise (geometrisch und
chemisch komplementäre Anlagerung kleiner Moleküle, im folgenden als Liganden
bezeichnet, an biologische makromolekulare Zielstrukturen, häufig Proteine, im folgenden als
Rezeptoren bezeichnet, bewirkt einen Eingriff in die Abfolge von Stoffwechsel- und
Signaltransduktionsprozessen und löst somit einen physiologischen Effekt aus) 1 ist es der
modernen Wissenschaft möglich gezielter Wirkstoffe herzustellen. Früher wurden große
Mengen an Substanzen willkürlich auf ihre Wirksamkeit getestet. Diesen Prozess, dessen
Anwendung selbst heutzutage teilweise noch unverzichtbar ist, wird als Screening (häufig:
HTS = Hochdurchsatz-Screening) bezeichnet. Heute ist bekannt, dass die Wirksamkeit
bestimmter Stoffe auf ihre Inhibitions-Wirkung auf bestimmte Proteine zurückzuführen ist.
Da außerdem bekannt ist, dass der Inhibitor exakt in die dreidimensionale Struktur des zu
inhibitierenden Enzyms passen muss (Modell des Schlüssel-Schloss Prinzips bzw. des
induced fits), lassen sich, wenn die Enzym-Struktur bereits aufgeklärt wurde, einige wenige
ideale Inhibitoren am Computer designen, welche im Anschluss synthetisiert und im
Experiment getestet werden. Der Materialverbrauch ist demnach erheblich geringer.
Die Zukunft des Experimentierens wird also stark in silico liegen, wobei in vitro und in vivo
Experimente den in silico Experimenten nur noch in reduzierter Form folgen. Diese in silico
Experimente werden als strukturbasiertes Liganden-Design bezeichnet (im Gegensatz zu
Wirkstoff-Design, da bei jenem außerdem die Optimierung von Faktoren wie Absorption,
Verteilung, metabolische Stabilität, Ausscheidung [zusammen: ADME Eigenschaften]
Lösungsmittelverhalten, toxikologisches Profil, pharmazeutische Eigenschaften und
Synthesekosten u.a. eine Rolle spielen), da sie lediglich die Stärke eines Liganden in einem
in vitro Experiment optimieren sollen. So können sich auch Liganden, die sich im
strukturbasierten Design und im Folgenden in vitro Experiment als ideal erwiesen haben,
aufgrund von geringer Bioverfügbarkeit und metabolischer Instabilität als nicht optimales
Medikament herausstellen (wie der HIV-Protease Inhibitor DMP323). Der darauf folgend
entwickelte Wirkstoff DMP450 zeigt eine hohe Plasmaproteinbindunng (hängt von Lipophilie
und Ladung ab), welche die Wirkung der Liganden in vivo erheblich herabsetzt. Grob
zusammengefasst ist der Weg zu einem idealen Wirkstoff durch mehrere Abschnitte
charakterisiert, die im Folgenden noch einmal graphisch zusammengefasst werden sollen.
Abbildung 1
Überblick über das Wirkstoff Design
Das HTS kann zum Teil durch
strukturbasiertes Liganden Design
(in silico) ersetzt oder kombiniert
werden, um den Arbeitsaufwand zu
minimieren. Die Strukturaufklärung
erfolgt mittels NMR oder
Röntgenstrukturanalyse. Die Testung
entspricht den in vitro Experimenten.
Ist diese erfolgreich kommt die
Voraussetzung für in silico Experimente: Strukturaufklärung
Um in silico Experimente durchführen zu können, müssen die Strukturen der jeweiligen
Moleküle und Enzyme exakt bekannt sein. Dabei spielt die Konformation der Atome im
Molekül, sowie die Elektronendichte eine große Rolle. Solche Informationen werden durch
röntgenographische Methoden (z.B. Protein-Ligand-Kristallographie), KryoElektronenmikroskopie und auch eingeschränkt (aufgrund der Größe von Proteinen ist
mehrfache Isotopenmarkierung notwendig) durch NMR-spektroskopische Methoden
ermittelt, welche Substanzbibliotheken durchmustern (Screening) und somit günstige
Templates identifizieren, die anschließend in silico optimiert werden können, so dass die
Bindungsstärke des Liganden maximal wird. Jene kann nun über kompetetive Inhibierungsoder Bindungsassays in vitro gemessen werden, was das in silico Experiment verifiziert und
falsifiziert.
Die Kristallographie spielt bei der Strukturaufklärung von Proteinen und Protein-Ligand
Komplexen eine erhebliche Rolle, weshalb nun auf dieses Verfahren näher eingegangen
werden soll. Die Züchtung des Kristalls eines Rezeptor-Substrat Komplexes ist leider nicht
möglich, da das Substrat sehr schnell wieder frei gegeben wird. Daher sind Inhibitoren als
Liganden dieser Rezeptoren nicht wegzudenken, um kristallographische Untersuchungen an
solchen Komplexen durchführen zu können. Ist das zu untersuchende Protein (bzw. der
Protein-Ligand Komplex) kristallisiert, folgt das eigentliche kristallographische
Röntgenbeugungsexperiment, welches die Positionen und Intensitäten der im
Beugungsmuster des Kristalls gemessenen Beugungen liefert. Nachdem die
Strukturfaktoramplituden mittels Quadratwurzel der Intensitäten berechnet wurden und die
Phasen der Strukturfaktoren bekannt sind, kann mittels Fouriertransformation eine
dreidimensionale Matrix aus Zahlen, welche den lokalen Elektronendichten entsprechen,
berechnet werden. Diese Matrix wird nun anhand eines bestimmten Atommodels mittels
Kristallograph in eine Struktur übersetzt (große Elektronendichten bedeuten schwere
Atome). Dieser Vorgang ist iterativ (ein Teil der Struktur wird aufgebaut und anschließend
durch Veränderung der Atomkoordinaten mittels Verfeinerungsprogramm verbessert) und
durch mehrere Randparameter eingeschränkt. Dieser iterative Prozess ist notwendig, da
durch Röntgenstrahlung nur schwer zwischen Elementen ähnlicher Ordnungszahl
unterschieden werden kann und daher manche Gruppen ein fast identisches Signal liefern.
Die resultierende Struktur liefert nun ihrerseits eine Matrix-Karte aus Elektronendichten, in
der weitere Einzelheiten erkannt werden können. Neben den Koordinaten weisen die Atome
auch einen Temperaturfaktor auf, der die Fehlerordnung im Kristall charakterisiert. Er liefert
demnach einen Hinweis auf die Verlässlichkeit des entsprechenden Modellteils. Ist er hoch,
bedeutet dies, dass nur eine geringe Elektronendichte gemessen wurde und die Koordinaten
daher ein hohes Fehlerintervall aufweisen. Die Auflösung von solchen Matrix-Karten liegt
selten unterhalb von 1,5 Å, meist bei 2-3 Å. Erst ab einer Auflösung von 1,2 Å, kann die
Position polarer H-Atome bestimmt werden. Der Fehler korreliert wie bereits erwähnt mit
dem Temperaturfaktor, aber auch direkt mit der Auflösung. Bei einer Auflösung von 2,5 Å
liegt der Fehler bei ca. 0,4 Å. Ein Temperaturfaktor von 20 Å2 bedeutet eine mittlere
Verschiebung aus der Gleichgewichtsposition von 0,5 Å. Eine solche resultierende
verbesserte kristallographische Matrix wird nun in so genannten PDB Dateien gespeichert,
auf die ich später noch zu sprechen kommen werde (Einleitung Abschnitt 7).
Qualität der Protein-Ligand Bindung
Ob ein Ligand nun exakt in die Bindungstasche des Proteins passt, ist noch nicht
ausschlaggebend für eine ideale Protein-Ligand Bindung. Die sterische Kompatibilität ist
vielmehr Grundvorrausetzung für die Bindung. Hinzu kommt die energetische Erkennung
zwischen den Partnern. Betrachtet wird im Folgenden die nicht-kovalente Assoziation eines
Liganden an seinen Rezeptor.
Raq + Laq ↔ RLaq
Die Bindungsaffinität selbst ist durch die Bindungskonstante Ki zugänglich und setzt sich aus
entropischen und enthalpischen Beträgen zusammen. Beide können die Ligandenbindung
antreiben, wie Messungen an unterschiedlichen Protein-Ligand-Wechselwirkungen durch
ITC bestätigt haben. Die Bindungskonstante entspricht der Dissoziationskonstante, welche
gleich dem reziprokem Wert der Assoziationskonstante ist.
KA =
1
1
[ RL]
=
=
K D K I [ R ] ⋅ [ L]
∆G = − RT ln K A = ∆H 0 − T∆S
Die Dissoziationskonstante K für die Ligandenbindung an ein Protein liegt in einem Bereich
von 10-2 M (niederaffin: ΔG=-10kJ/mol) bis 10-12 M (hochaffin: ΔG=-70 kJ/mol) bei einer
Temperatur von 298 K. Wodurch diese unterschiede in der Bindungsaffinität zustande
kommen, soll im folgenden Abschnitt 4 behandelt werden.
Wechselwirkungen zwischen Ligand und Protein
enthalpische und entropische Beiträge
Bei der nicht-kovalenten Bindung eines Liganden an seinen Rezeptor spielen
elektrostatische (= Coulomb-) und Van-der-Waals Wechselwirkungen für die enthalpischen
Beiträge zur Bindungsaffinität eine große Rolle. Entropische Beiträge liefern
Solvatisierungseffekte des Lösungsmittels und Entstehung oder Verlust neuer Freiheitsgrade
im Liganden oder Rezeptor. Außerdem können durch die Bindung induzierte konformelle
Strukturveränderungen in Rezeptor und/oder Ligand ausschlaggebend für die
Bindungsaffinität sein.
kovalente Bindungen
Wie so eben beschrieben, sollen nur nicht kovalente Wechselwirkungen zwischen Liganden
und Rezeptoren betrachtet werden. Um einen Vergleich der Bindungsenergien und -längen
zu ermöglichen, möchte ich hier dennoch auf die kovalenten Bindungen eingehen. Eine C-C
Einfachbindung hat einen Energiegehalt von 340kJ/mol. Eine C=C Doppelbindung hingegen
weist einen im Vergleich zum doppelten Energiegehalt einer C-C Einfachbindung geringeren
Energiewert auf (ca. 610kJ/mol), da es zu einer Verzerrung der Elektronendichten kommt
und sich deshalb die π-Orbitale nicht so gut wie die σ-Orbitale überlappen. Bei der CΞC
Dreifachbindung resultiert somit ein noch geringerer Energiewert von ca. 800 kJ/mol. Die CC Einfachbindung ist 154 pm lang, die C=C Doppelbindung ist mit 133 pm wesentlich kürzer,
da wegen der Orbital- Überlappung die Atome dichter liegen müssen. Eine C-H Bindung ist
ca. 110 pm lang. Am stabilsten sind C-C Bindungen bei einem Winkel von 120°.
Die Bedeutung der Wasserstoffbrücke
Wasserstoffbrücken kommen durch die anziehende Wechselwirkung zwischen einem an ein
elektronegativeres Atom gebundenes Wasserstoffatom und einem weiteren
elektronegativem Atom (kann auch ein π-Elektronensystem sein) zustande. Die Länge der
Wasserstoffbrücke liegt zwischen 1,7 (in reinem HF) und 3,2A (teilweise in Proteinen). Sie ist
für einen Winkel zwischen den drei Punkten X~H-X (X ist elektronegatives Atom; - ist
kovalente Bindung; ~ ist H-Brücke) von 180° am stabilsten, kann sich allerdings bis zu einem
Winkel von 135° ausbilden.
Das Coulomb’sche Gesetz findet bei der Beschreibung aller elektrostatischen
Wechselwirkungen seine Anwendung und ist in folgender Gleichung dargestellt.
V =
1
4π ⋅ ε 0 ⋅ ε M
⋅
q1 ⋅ q 2
r2
V ist das Potential mit dem sich die Teilchen anziehen, q sind die Ladungen der Teilchen und
r ist der Abstand. ε 0 ist die Permittivität (= dielektrische Leitfähigkeit) des Vakuums, welche
die Abschirmung elektrostatischer Wechselwirkungen beschreibt. In einem Medium ist die
elektrostatische Bindungsstärke über ε 0 hinaus zusätzlich von der Dielektrizitätskonstanten
ε M des umgebenden Mediums abhängig. Im Vakuum gilt ε M = 1 . Hohe Werte für ε M (etwa
80) sind an der Grenzfläche Protein-Lösungsmittel zu finden, weshalb hier die
Wechselwirkung wesentlich geringer ist, als im Inneren des Proteins ( ε M Werte von 2-8 sind
hier häufig). In polarer Umgebung sind Wasserstoffbrücken also schwächer, als in apolarer.
Bei der Protein-Ligand Bindung müssen bereits bestehende H-Brücken des freien Proteins
aufgebrochen werden, wobei neue H-Brücken zwischen Protein und Ligand entstehen. Ob
der H-Brücken Austausch zur Bindungsaffinität beiträgt, hängt von den Enthalpien der HBrücken im freien Protein und im Protein-Ligand-Komplex ab. Eine Wechselwirkung
zwischen einem Wasserstoffatom und einem elektronegativeren Partner in apolarer
Umgebung liefert einen enthalpischen Beitrag von ca. ∆G = (−5 ± 2,5)kJ / mol . Die Energie,
die aufgebracht werden müsste um Wasserstoffbrücken von H2O in reinem Wasser zu
spalten, beträgt ∆G = (17,5 ± 2,5)kJ / mol . Im Allgemeinen sind die Energien der
Wasserstoffbrückenbindungen von sehr vielen Faktoren abhängig (Länge der Bindung,
Bindungswinkel, stärke der Polarisation des H-Atoms bzw. Differenz der Elektronegativitäten
zwischen Wasserstoff und seinem elektronegativem Partner), weshalb jene zwischen 1 und
50 kJ/mol schwanken können.
Salzbrücken und spezielle H-Brücken
Die geladenen proteinogenen Aminosäuren weisen bei einem physiologischen pH-Wert von
7,4 die unterschiedlichsten Protonierungsgrade auf. Arginin und Lysin sind protoniert,
während Asparagin- und Glutaminsäure deprotoniert vorliegen. Der Protonierungsgrad kann
je nach lokaler elektrostatischer Veränderung in der Umgebung variieren. Sind Reste
unterschiedlicher Ladung in direkter Reichweite, kommt es zur Ausbildung von Salzbrücken.
Salzbrücken können auch spezielle Wasserstoffbrücken sein (siehe Abbildung). Die
enthalpischen Beiträge von ladungsunterstützten Wasserstoffbrücken und Salzbrücken
betragen ca. ∆G = (−15 ± 5)kJ / mol . Diese sind nicht zu verwechseln mit den
Wasserstoffbrücken in polarer Umgebung, die wesentlich schwächer sind. Bei
ladungsunterstützten H-Brücken liegen jeweils zwei unterschiedlich geladene Reste in einer
sonst apolaren Umgebung vor, die miteinander wechselwirken. In polarer Umgebung würde
diese Wechselwirkung erheblich abgeschwächt, da die Wassermoleküle ebenso mit den
geladenen Resten wechselwirken (ständiger Umbau der H-Brücken). Beispiele für
ladungsunterstützte H-Brücken sind in folgender Abbildung zu sehen.
Abbildung 2
Ladungsunterstützte H-Brücken
Es werden grob 2 Typen von H-Brücken
unterschieden: solche in polarer Umgebung und
solche in apolarer Umgebung. Letztere sind
wesentlich stärker. Kommt bei H-Brücken in
apolarer Umgebung hinzu, dass sie durch eine
Ladung am Nachbaratom verstärkt werden, so
In einem Salz-Kristall sind die Bindungsenergien wesentlich höher. Die NaCl Bindung im
Kristall ist 250kJ/mol stark. In Lösung wird sie erheblich abgeschwächt, da die
Wassermoleküle die Ladungen der Gegenionen voneinander abschirmen.
weitere elektrostatische Wechselwirkungen
So genannte π-π-Wechselwirkungen zwischen aromatischen Systemen in Ligand und den
Seitenketten der aromatischen Aminosäuren des Proteins liefern ebenso einen bedeutenden
Beitrag zur Affinität des Liganden an seinen Rezeptor. Außerdem sind die
Wechselwirkungen von Kation und π-Elektronen-System nicht zu vergessen. Kation-πSysteme liefern einen um 10kJ/mol größeren Beitrag zur Bindungsaffinität als normale
Salzbrücken. Außerdem können koordinative Bindungen funktioneller Gruppen von Liganden
an Metallionen des Proteins die Affinität erheblich erhöhen.
Van-der-Waals Wechselwirkung
Die Van-der-Waals-Kräfte tauchen zwischen allen Molekülen auf und können durch das
Lennard-Jones-Potential beschrieben werden. Es erklärt die intermolekularen
Wechselwirkung zweier ungeladener nicht-kovalent verbundener Teilchen. Dabei spielen ein
anziehender Faktor und ein abstoßender Faktor eine Rolle. Somit lässt sich das LennardJones-Potential in zwei Anteile gliedern. Der anziehende Anteil entspricht
V =−
C
r6
In dieser Gleichung ist V das Potential der Wechselwirkung und r der Abstand zwischen den
Teilchen. C entspricht einem externen Term, welcher stoffspezifische Konstanten (u.a. die
Ionisierungsenergie) enthält. Der abstoßende Teil lässt sich durch
V =
C
r 12
beschreiben. Es resultiert das so genannte Lennard-Jones-(12,6)-Potential, das nun wie folgt
aus diesen beiden zusammengesetzten Gleichungen beschrieben werden kann
 σ 12  σ  6 
V (r ) = 4ε ⋅   −   
 r 
 r  
Das Potentialminimum der resultierenden Kurve ist ε . Die Nullstelle (für V=0) der Kurve ist
bei einem Abstand r = σ abzulesen. σ wird auch als Van-der-Waals Radius definiert. Es
existiert auch die folgende Schreibweise für das Lennard-Jones-(12,6)-Potential:
 reqm
V (r ) = ε ⋅ 
 r
12

r
 − 2 ⋅  eqm

 r






6



Hier ist reqm = 21 / 6 σ der Abstand des Energieminimums vom Ursprung. Dies soll die
folgende Abbildung noch einmal veranschaulichen.
Abbildung 3
Das Lennard-Jones-Potential
Die Abbildung zeigt die zwei Komponenten des
Lennard-Jones-Potentials in einer unterbrochenen
Linie und die resultierende Summe aus beiden
Komponenten. Das Minimum ist bei V (r ) = ε
abzulesen. Dieses Potentialminimum ist bei einem
idealen Abstand
reqm = 21 / 6 σ vorzufinden. Die Nullstelle ist
σ und
entspricht gleichzeitig den Van-der-Waals Radien.
Die Van-der-Waals Wechselwirkung trägt mit einer Energie von ca. ∆G = (−2,5 ± 2)kJ / mol
zur Bindungsaffinität bei. Aufgrund der hohen Anzahl mit der diese Wechselwirkung auftritt
spielt diese eine bedeutende Rolle bei der Rezeptor-Ligand-Bindung.
Der anziehende Term
Die Ursache des anziehenden Terms des Lennard-Jones-Potentials sind die 3
verschiedenen Van-der-Waals Kräfte, und zwar die Keesom-Wechselwirkung zwischen zwei
Dipolen, die Debye-Wechselwirkung zwischen einem Dipol und einem polarisierbaren
Molekül und die Londonsche Dispersionswechselwirkung.
Ursache ist jeweils das Auftreten eines fluktuierenden Dipolmomentes. Dazu kommt es, weil
die Elektronen um einen Atomkern herum ständig in Bewegung sind, weshalb sich die
Ladungsverteilung mit der Zeit ändert. Wird der Schwerpunkt der negativen Ladung vom
Schwerpunkt der positiven Ladung, der sich immer im Kern befindet getrennt, so liegt ein
Dipol vor. Wenn sich nun zwei Moleküle mit einem solchen temporären Dipol nahe genug
kommen, können sie miteinander elektrostatisch wechselwirken. Dabei induziert die negativ
polarisierte Seite des Teilchens 1 eine Abstoßung der Elektronen der zugewandten Seite des
Teilchens 2. Der Minuspol eines temporären Dipols influiert (von Influenz = Ladungstrennung
innerhalb eines ungeladenen Leiters durch ein elektrisches Feld) also beim Nachbarmolekül
einen Pluspol. Es kommt zur Van-der-Waals Wechselwirkung zwischen dem temporärem
Dipol des Teilchens 1 und dem influierten Dipol des Teilchens 2 durch Synchronisation der
Elektronenbewegungen beider Teilchen.
Der abstoßende Term
Elektronen, die zu den Fermionen gehören, stoßen sich aufgrund der gleichen Ladung ab.
Daher gilt je näher sich zwei Atome kommen, desto mehr überlappen sich ihre Orbitale und
desto energetisch ungünstiger wird der Zustand. Es lässt sich berechnen, dass bei
antisymmetrischen Wellenfunktionen die Wahrscheinlichkeit beide Elektronen am selben Ort
vorzufinden null ist (im Gegensatz zu symmetrischen Wellenfunktionen). Außerdem ist der
durchschnittliche Abstand beider Teilchen antisymmetrischer Wellenfunktionen größer als
mit symmetrischen Wellenfunktionen. Ergo ist bei gleichsinnig geladenen Teilchen eine
antisymmetrische Wellenfunktion erheblich günstiger.
Das Pauli Prinzip fasst dies in einem Postulat zusammen: „Wellenfunktionen, die ein
Mehrelektronensystem beschreiben, müssen beim Austausch von zwei beliebigen
Elektronen das Vorzeichen wechseln. Solche Wellenfunktionen sind de facto
antisymmetrisch.“ Wenn die Wellenfunktionen der überlappenden Elektronen-Orbitale
antisymmetrisch sind, so liegt automatisch eine parallele Spinkonstellation vor. Fermionen
(Teilchen mit halbzahligem Spin), die denselben Raum belegen, dürfen jedoch nicht in allen
vier Quantenzahlen übereinstimmen (Pauli-Verbot, welches sich direkt aus dem Pauli Prinzip
ableiten lässt). Daher ist die Überlappung der Orbitale mit Elektronen gleichen Spins
quantenmechanisch verboten, weshalb es zur sehr starken Pauli Repulsion zwischen
Atomen mit geringen Abständen zueinander kommt.
Solvatisierungseffekte
Bei der Betrachtung der entropischen Beiträge zur Qualität der Protein-Ligand
Wechselwirkung spielen die Lösungsmittelmoleküle eine entscheidende Rolle. Diese
bewirken Solvatisierungs- und Desolvatisierungsprozesse, im Falle von Wasser
(De-)Hydratisierungsprozesse. Wassermoleküle bilden in reiner Phase des flüssigen
Zustands ein Netzwerk aus H-Brücken-Donoren und -Akzeptoren. Dabei bildet ein
Wassermolekül 3-4 H-Brücken aus. Befindet sich ein Stoff, z.B. ein Protein in wässriger
Lösung, so bildet sich eine Hydrathülle. Die Wassermoleküle dieser Hülle wechselwirken mit
dem Protein, anstatt untereinander H-Brücken auszubilden.
Im Allgemeinen kommt es bei der Hydratisierung einer Substanz zu einer Verringerung der
Anzahl an H-Brücken. Die resultierenden H-Brücken (z.B. der Solvatationssphäre von Argon:
∆G = 2,6kJ/mol ) sind jedoch stärker als diejenigen in der reinen Wasserphase (
∆G = 2kJ/mol ). Daher kompensiert sich der enthalpische Beitrag nahezu zu null (wenige
starke statt viele schwache H-Brücken). Da die Wassermoleküle der Hydrathülle in ihrer
Bewegungsfreiheit erheblich eingeschränkt sind, erniedrigt sich jedoch die Entropie (höhere
Ordnung). Wenn nun ein Ligand eine hydrophobe Oberfläche des Proteins bedeckt, werden
Solvensmoleküle freigesetzt. Die Protein-Ligand-Bindung wird also entropisch getrieben.
Dies wird auch als Hydrophober Effekt beschrieben, der u.a. auch ausschlaggebend für die
Proteinfaltung und die Ausbildung von Biomembranen ist. Da der Beitrag des hydrophoben
Effekts zur freien Enthalpie ΔG proportional zu der begrabenen hydrophoben Fläche ist, lässt
sich dieser Wert auf ca. ∆G = (−0,175 ± 0,075)kJ/molA 2 quantifizieren.
Nicht zu verwechseln mit diesem entropischen Beitrag ist der Verbrückungs-Effekt, den
Wassermoleküle der Hydrathülle um das aktive Zentrum herum aufweisen können. Dieser ist
enthalpischer Natur. Die Wassermoleküle im unbesetzten aktiven Zentrum verbrücken
Protein und Ligand miteinander (solvensvermittelte Wechselwirkung), bevor es zu einer
Bindung zum Protein-Ligand-Komplex kommt. Die Überführung eines Wassermoleküls aus
der umgebenden Wasserphase in das Bindungsepitop (Rezeptor-Wasser-Ligand Komplex)
setzt sich aus dem entropischen ungünstigen Betrag von - T∆S = 9kJ/mol bei 298K und dem
enthalpisch günstigen Betrag von ∆H = −16kJ/mol zusammen. Die solvensvermittelte
Wechselwirkung zwischen Protein-Wasser und Wasser-Ligand liefert also einen
energetischen Beitrag von ∆G = −7 kJ/mol zur Bindungsaffinität. Die Wassermoleküle des
Bindungsepitops dienen darüber hinaus als Mediatoren zur Anpassung an die
unterschiedlichen Ligand-Strukturen, während die Proteinstruktur nahezu, aber nicht absolut
(wie in Abschnitt 4.8 gezeigt) unverändert bleibt.
Mobilität und Beweglichkeit durch Freiheitsgrade
Bei der Bindung von Ligand und Rezeptor gehen immer auch 3 Freiheitsgrade der
Translation und 3 der Rotation verloren, wodurch 6 neue Vibrationsfreiheitsgrade entstehen.
Unter Anwendung der Trouton’schen Regeln resultiert, dass eine solche Einschränkung ein
Entropieverlust von ∆S = −420J/molK bedeutet. Die Praxis zeigt jedoch, dass es sogar
möglich ist, dass Liganden ihre Mobilität im gebundenen Zustand beibehalten und durch
zusätzliche Proteinbewegung die Ligand-Bindung sogar entropisch gefördert wird (in diesem
Fall sind keine elektrostatischen Wechselwirkungen möglich, da der Ligand innerhalb der
Bindungstasche rotiert und ist eine Selektivität bei der katalysierten Reaktion nahezu
auszuschließen).
Torsionsfreiheitsgrade, welche nicht zu den 3n Freiheitsgraden eines n-atomigen Moleküls
zählen, spielen eine große Rolle bei der Betrachtung der Bindungsaffinität. Jede frei
drehbare Bindung weist einen solchen Freiheitsgrad auf. Bei der Bindung geht dieser
verloren. Es muss also erreicht werden, dass diese Torsionsfreiheitsgrade von ideal
bindenden Inhibitoren schon in Lösung eingeschränkt werden (Doppelbindungen,
Ringsysteme, sterische Hinderung).
intramolekulare Konformationsänderungen
Um eine ideale Bindung eines Inhibitors zu ermöglichen, wird jener so designt, dass er
bereits in Lösung in derjenigen Konformation vorliegt, in der er auch an den Rezeptor bindet.
So wird durch die Bindung keine neue, energetisch ungünstigere Konformation erzwungen,
die eine größere Spannung aufweist und somit die Bindungsaffinität reduzieren würde.
Neben der Konformation des Inhibitors spielen auch Strukturveränderungen des Rezeptors
eine Rolle. Obwohl früher geglaubt wurde, dass Proteine starr sind (Hypothese des starren
Rezeptors), hat sich dies als großer Irrtum herausgestellt. Die Dynamik von Protein-Ligand
Wechselwirkungen wurde bei der Analyse von Proteinen (z.B. HIV-Revertase) entdeckt,
welche mehrere strukturell unterschiedliche Liganden (Nevirapin ist Inhibitor, der sich
strukturell sehr von den Substraten α-APA und HEPT unterscheidet) aufweisen.
Abbildung 4
Substrate der HIV-Revertase
Die drei Strukturen, welche an das
Enzym HIV-Revertase am selben aktiven
Die Bindung aller dieser drei Liganden ans aktive Zentrum erfolgt durch unterschiedliche
konformelle Veränderungen, sowohl des Liganden als auch des Proteins, sodass immer
dieselben drei Aminosäurereste hydrophob mit den Liganden wechselwirken können. So
werden die Cα Positionen in diesem Fall um bis zu 2,7 Å verschoben. Die elektrostatischen
Wechselwirkungen variieren hingegen stark. Dies ist ein Hinweis darauf, dass hydrophobe
Wechselwirkungen für die sterische Komplementarität, die elektrostatischen hauptsächlich
für die Erkennung aus größerer Entfernung verantwortlich sind.
Das Enzym DFPase
Im Praktikumsversuch wird ein Inhibitor mittels strukturbasiertem Designverfahren für das
Enzym DFPase entwickelt. Die DFPase kommt unter anderem in Kopfganglien und dem
Riesenaxon (Axone der Kalmaren, die in der Regel 100-1000mal größer sind als bei
Mammalia) vor und besteht aus 314 Aminosäuren mit einem Molekulargewicht von 35 kDa.
Es wurde aus loligo vulgaris extrahiert, einem häufig vorkommenden Kalmar.
Die Struktur der DFPase
Die DFPase ist ein globuläres Protein mit einem in einer mittels Oberflächenstrukturmodellierten Abbildung gut sichtbarem aktivem Zentrum (siehe Abbildung). In der nativen
Form enthält die DFPase zwei Calciumionen, wobei eines für die strukturelle Stabilität des
Enzyms, das andere für die katalytische Aktivität benötigt wird.
Die Oberflächenstruktur des aktiven Zentrums zeigt, dass die Struktur des Enzyms sehr gut
mit der Struktur des Substrats wechselwirken kann, weshalb es zu einer relativ hohen
Affinität zum Substrat kommt.
Abbildung 5
Oberflächenstruktur des aktiven
Zentrums der DFPase mit gedocktem
DFP
Die Oberflächenstruktur zeigt die
äußersten Grenzen der Orbitale der
einzelnen Atome des Enzyms. Die
verschiedenen Farben kennzeichnen
die Atomart, zu dem die Orbitale
gehören (rot: Sauerstoff, cyan:
Wasserstoff, blau: Stickstoff, grau:
Kohlenstoff, gelb: Schwefel, grün:
Kalzium)
Die Sekundärstruktur des Enzyms entspricht sechs antiparallelen β Faltblättern, die
zusammen einen sechsblättrigen Β-Propeller bilden.
Abbildung 6
Sekundärelemente der DFPase,
Aufsicht
Es sind die zwei Calcium Ionen im
Zentrum des Enzyms und die
i
ll l β F l bl
k
Nervenkampfstoffe: Die Substrate der DFPase
Die Funktion und der Reaktionsmechanismus des Enzyms sind noch nicht vollständig
aufgeklärt, wohl aber ist bekannt, welche Substrate umgesetzt werden können. Die DFPase
spaltet Organophosphat-Verbindungen wie unter anderem DFP (Diisopropylfluorophosphat),
aber auch Tabun, Sarin, Soman und Cyclohexylsarin (siehe Abbildung 7). Viele dieser
Organophosphat-verbindungen gehören zur Gruppe der Ultragifte, die als Nervenkampfstoffe
verwendet werden. Zur Anwendung kommen diese als Aerosol, es handelt sich nicht um
Gase.
Abbildung 7
Substrate der DFPase
Außer DFP gehören die in dieser
Abbildung aufgelisteten Substrate alle
zur Klasse der Nervenkampfstoffe .Es
h d l i h b i ll S b
Nervenkampfstoffe sind Inhibitoren der Acetylcholinesterase, die sich im synaptischen Spalt
befindet. Die Übertragung eines ankommenden Nervenreizes von einem präsynaptischen
Neuron zu einem postsynaptischen Neuron erfolgt durch Ausschüttung des
Neurotransmitters Acetylcholin (ACh) aus dem Synapsenendknöpfchen mittels synaptischer
Vesikel des präsynaptischen Axons und durch die Bindung von ACh an Rezeptoren der
postsynaptischen Membran. Diese Bindung bewirkt die Liganden-abhängige Öffnung der
Ionenkanäle des postsynaptischen Neurons, wodurch es zur Änderung des
Membranpotentials kommt. Der Nervenreiz wurde über die Synapse weitergeleitet. Das
Enzym Acetylcholinesterase spaltet nun ACh in Acetat und Cholin, sodass der
Nervenimpuls ca. 1ms anhält. Diese Moleküle werden wieder vom Synapsenendknöpfchen
phagocytiert. Wird die Acetylcholinesterase durch Substrate der DFPase blockiert wird ACh
nicht mehr gespalten. Da es in dieser Form jedoch nicht zurück ins Synapsenendknöpfchen
transportiert werden kann, bleibt es im synaptischen Spalt und bewirkt durch die dauerhafte
Bindung an den Rezeptor der postsynaptischen Membran eine Dauerreizung des
postsynaptischen Neurons. Diese Dauerreizung bewirkt den Verlust der Kontrolle über
sämtliche motorischen Muskelfunktionen und führt letztlich zum Tod durch Atemversagen.
Zum Herzstillstand kommt es nicht, da das Herz andere Neurotransmitter hat und somit nicht
ausschließlich von der Aktivität der Acetylcholinesterase abhängig ist. Außerdem ist der
Herzmuskel aufgrund einer doppelt so langen Refraktärphase (20ms anstatt 10ms im
Skelettmuskel) nicht tetanisierbar (kann nicht krampfen), da die Kontraktion des
Herzmuskels noch vor dem Ende der Refraktärphase beendet ist.
Der Reaktionsmechanismus der DFPase Reaktion
Das Enzym spaltet eine Reihe von Organophosphat-Verbindungen durch Hydrolyse. Der
exakte Mechanismus ist noch nicht verstanden, jedoch sind einige Prinzipien der SubstratUmsetzung bereits deutlich geworden. Das für die katalytische Aktivität benötigte Calcium
Ion (positiv geladen) der Bindungstasche koordiniert den an das Phosphoratom gebundene
Sauerstoff (negativ geladen) des Substrats. Dadurch kommt es zur Polarisierung innerhalb
des Substrats (die Elektronen werden zum Sauerstoff hin gezogen, wodurch das
Phosphoratom partial positiv geladen wird). Nun kann ein Wassermolekül bzw. ein OH- Ion
nukleophil an das Phosphat angreifen. Dieser Angriff resultiert in einem fünffach
koordinierten Übergangszustand, aus dem letztlich die elektronegative Gruppe (meist Fluor)
entlassen wird.
Abbildung 8
Reaktionsgleichung der DFPase-Reaktion Diese Reaktionsgleichung zeigt die
Hydrolyse von DFP.
Auto Dock 4.0
Unser in silico Experiment wird mit dem Programm Auto Dock 4.0 durchgeführt. Im
Folgenden soll die Arbeitsweise von diesem Programm genauer betrachtet werden.
Berechnung der Bindungsenergie
Das Programm liefert als Ergebnis eines Docking Experiments die Bindungsenergie ΔG,
welche sich aus mehreren Komponenten zusammensetzt. Gemessen werden zunächst die
Wechselwirkungen zwischen Rezeptor und Ligand (Van-der-Waals, H-Brücken und
elektrostatische Wechselwirkungen). Bei der Bindung des Liganden an seinen Rezeptor, der
in Lösung in seiner günstigsten Konformation vorliegt, kann eine Konformationsänderung
auftreten, dessen ΔG ebenso berechnet wird.
Außerdem werden die Anzahl der Torsionsfreiheitsgrade berücksichtigt. In Lösung haben
alle n-atomigen Moleküle zusätzlich zu den 3n Freiheitsgraden (3 Translation, 2-3 Rotation,
und Vibration; Bsp. CO2 hat 2 Scherschwingungen und 2 Streckschwingungen, da es nur 2
Rotationsfreiheitsgrade aufweist, H2O hat eine Scherschwingung weniger, weil es 3
Rotationsfreiheitsgrade aufweist) an jeder drehbaren Bindung einen Torsionsfreiheitsgrad,
bei dem eine Atom-Gruppe im Molekül rotiert. Diese gehen bei der Bindung an den Rezeptor
verloren, weshalb die Bindung entropisch ungünstig ist.
Als vierte Komponente wird die Energie der Solvatisierung vorhergesagt. Hierzu wird ein
thermodynamischer Kreisprozess zu Hilfe genommen. Es wird ΔG f ür die Bindung im
Vakuum berechnet, außerdem für die Solvatisierung des gebundenen Rezeptor-Ligand
Komplexes und der ungebundenen Komponenten. Die Gibbs Energie für die Bindung in
Lösung erhält das Computerprogramm nun über die Subtraktion des ΔG Wertes f ür die
Solvatisierung des Rezeptor-Ligand Komplexes von dem ΔG Wert f ür die Solvatisierung der
ungebundenen Komponenten. Dies ist daher möglich, weil ΔG eine Zustandsgröße und
daher vom Weg unabhängig ist. Dies sei in folgender Abbildung veranschaulicht.
Abbildung 9
Thermodynamischer Kreisprozess der Solvatisierung
Ein weiterer Term (unbound system energy) ist bei der aktuellsten Version von Auto-Dock
hinzugekommen, dessen Funktion uns bisher unbekannt ist. Die zugrunde liegenden
Gleichungen aller Berechnungen sind hochkomplex. Die Addition aller Terme ergibt die
Mastergleichung. Das resultierende ΔG soll sehr genau der freien Enthalpie des
Bindungsprozesses entsprechen. Im Folgenden ist die Mastergleichung gezeigt.
Abbildung 10
Die Mastergleichung von Auto-Dock
Gezeigt werden die einzelnen Terme für
die Berechnung der freien Gibbs Energie
für die Van-der-Waals WW, für HBrücken, für elektrostatische WW, für die
Torsionsfreiheitsgrade und die
Solvatation. Es fehlt der bei Auto Dock
4.0 neu hinzugekommene Term für die
Das Ergebnis ist nur eine Näherung
Das Ergebnis ist allerdings nicht exakt. Auto Dock berechnet zwar die Solvatisierung über
den thermodynamischen Kreisprozess, berücksichtigt aber nicht einzelne
Lösungsmittelmoleküle, weshalb es sich nur um eine Annäherung handelt. Außerdem wird
angenommen, dass der Rezeptor starr ist, was ebenso nicht korrekt ist. Auch der Rezeptor
kann seine Konformation leicht verändern und weist geringe, in wenigen Fällen sogar große
Bewegungen auf, welche die Bindung beeinflussen könnten (wie in Abschnitt 4.8 gezeigt).
Außerdem berechnet Auto Dock 4.0 die Interaktionsenergie zwischen Rezeptor und Ligand
durch molekülmechanische Ansätze, die sich von den tatsächlich quantenmechanischen
Vorgängen sehr unterscheiden können. Es kommt hinzu, dass Auto-Dock nicht alle
Konformationen berücksichtigt, sondern nur stichprobenartig einige auswählt. Das
gefundene Ergebnis ist demnach nur zu einer gewissen Wahrscheinlichkeit das tatsächliche
ΔG Minimum. Darüber hinaus liegen in der Zelle noch eine große Bandbreite anderer
Moleküle vor, die um die Wechselwirkung mit dem aktiven Zentrum (Ionen, andere Proteine)
oder der Bindung an diesem aktiven Zentrum (strukturell ähnliche Moleküle, Inhibitoren) mit
dem Liganden konkurrieren. Zudem berechnet Auto-Dock nur die Interaktions-Energie
zwischen Liganden und Rezeptor in einer bestimmten Position des aktiven Zentrums. Die
Wahrscheinlichkeit mit der der Ligand nun tatsächlich in dieses Zentrum gelangt bleibt
unberücksichtigt. So kann ein rein hydrophober Ligand eine sehr große Wechselwirkung mit
einem rein hydrophoben Zentrum erreichen. Wenn allerdings die gesamte Oberfläche des
Proteins hydrophob ist, so ist die Wahrscheinlichkeit, dass der Ligand im aktiven Zentrum
landet erheblich eingeschränkt. Hinzu kommt, dass innerhalb der in der .pdb Datei
gespeicherten Struktur Fehler sein können, wie bereits in Abschnitt 2.1 diskutiert wurde. Dies
kann ebenso zu verfälschten Einschätzungen über die Bindungsaffinität führen. Aufgrund all
dieser Vernachlässigungen und Annäherungen sind spätere in vitro (ITC) und in vivo
Experimente nicht wegzudenken.
Die Funktion von Auto-Grid 4.0
Um die Berechnung der energetisch günstigsten Position des Liganden zu beschleunigen,
wird von Auto Dock ein engmaschiges Gitter als Hilfsmittel verwendet. Die Größe des Gitters
und der Abstand der Gitterpunkte werden im Programm festgelegt. Die Position des Gitters
wird über das aktive Zentrum gelegt. Wenn das Unterprogramm Auto-Grid seine Rechnung
beginnt, werden in jeden Gitterpunkt alle im Liganden vorhandenen Atomtypen in Form eines
„Testatoms“ eingesetzt und die auf ihn wirkende Energie berechnet. Ebenso wird mit den
„Testladungen“ zur Berechnung der elektrostatischen Wechselwirkungen verfahren. Es
resultieren die Gitterenergien der einzelnen Gitterpunkte je Testatom bzw. Testladung. Im
eigentlichen Docking werden diese Gitterenergien verwendet, um die Gesamtenergie der
Rezeptor-Ligand-Wechselwirkung zu berechnen. Dabei können Atome auch zwischen den
Gitterpunkten positioniert werden, wobei hier ein Mittelwert der Energien der umgebenden
Gitterpunkte als Energiewert genommen wird.
Der Suchalgorithmus während des Docking-Prozesses
Während des Dockings werden die Bindungsgeometrien (Konformation: Bindungswinkel,
Bindungsabstände, Torsionswinkel) und die Position des Liganden (Translation und
Rotation) stichprobenartig und willkürlich variiert. Daher gilt, dass die gefundene Position des
Liganden, welches ein ΔG Minimum für die Bindung aufweist nur zu einer bestimmten
Wahrscheinlichkeit das tatsächliche Minimum ist.
Zur Findung des Minimums werden zwei Methoden miteinander kombiniert: der GenotypAlgorithmus und der Phänotyp-Algorithmus bilden zusammen den hybriden Suchalgorithmus
von Auto-Dock. Die folgende Abbildung soll diesen veranschaulichen.
Abbildung 11
Schematische Darstellung des hybriden
Suchalgorithmus’ von Auto Dock 4.0
Die untere Linie stellt den Genotyp dar, der
die Suche an den Phänotyp weitergibt. Der
Phänotyp Algorithmus startet die lokale
Suche nach einem Minimum. Im Genotyp
Zunächst wird im Genotyp-Algorithmus ein bestimmter Bezugspunkt im Gitter ausgewählt,
der als „Parent“ bezeichnet wird. Alle Atome des Liganden richten sich nach diesem
Bezugspunkt aus. Diese Ausrichtung resultiert in einer bestimmten Rezeptor-Ligand
Interaktionsenergie. Nun wird diese Position beibehalten und der Phänotyp-Algorithmus
aktiviert. Dadurch werden die Positionen der einzelnen Atome im Raum zueinander und
somit die Bindungslängen und Winkel willkürlich verändert, so dass der zuvor gesetzte
Bezugspunkt leicht verändert wird. Dadurch wird auch die zuvor berechnete Energie
verändert. Ist die neu berechnete Energie kleiner als die vorherige werden die
Atompositionen weiter in dieselbe Richtung verändert. Ist sie größer werden sie die Richtung
der Positionsänderung variieren. Die Entfernungen, welche die Atome pro Schritt in diesem
Algorithmus zurücklegen, werden von Schritt zu Schritt kleiner. Somit verändert sich die
Interaktions-Energie auch immer geringfügiger.
Der Phänotyp-Algorithmus läuft solange weiter, bis ein lokales Energie-Minimum gefunden
wurde oder eine zuvor festgelegte Abbruchskondition vorliegt. Abbruchskondition kann zum
Beispiel eine bestimmte Anzahl sein, mit der die Energie neu berechnet werden soll. Das
lokale Minimum ist nun das Ergebnis des ersten Phänotyp Algorithmus. Dieses wird
zwischengespeichert und an den Genotyp-Algorithmus weitergegeben, wodurch eine erste
Child-Generation im Genotyp erzeugt wurde. Aufgrund der Tatsache, dass sich der
Phänotyp direkt auf den Genotyp auswirkt, wird hier vom Lamark’schen hybriden
Suchalgorithmus gesprochen. Der Genotyp kann seinen Bezugspunkt auch durch Mutation
willkürlich verändern. Der Bezugspunkt der Child-Generation wird nun erneut an den
Phänotyp Algorithmus weiter gegeben, um ein weiteres Minimum zu detektieren.
Da die Wechselwirkung zwischen Molekülen von sehr vielen Faktoren abhängig ist, resultiert
für einen durchschnittlichen Liganden ein 30-40 dimensionaler Graph, in der jede Dimension
ein Minimum hat. Daher ist es wichtig mehrmals zurück in den Genotyp-Algorithmus zu
gehen, um mehrere lokale Minima zu detektieren. Je öfter in den Genotyp-Algorithmus
gewechselt wird, desto wahrscheinlicher ist es das globale Minimum zu finden. Dabei spielt
natürlich auch die breite des Minimums eine Rolle. Ist das globale Minimum schmal,
verringert sich die Wahrscheinlichkeit seiner Detektion, wie bei einem Blick auf die SchemaDarstellung deutlich wird.
Die PDB, Corina und PyMol
Die Struktur des Proteins wird online aus der PDB (Protein-Data-Bank:
http://www.rcsb.org/pdb/home/home.do) herunter geladen. Die PDB lebt durch die
Strukturaufklärung mittels Röntgenstrukturanalyse und den anderen genannten
strukturaufklärenden Methoden (siehe Abschnitt 2.1). Fachleute sind sich uneinig, ob die
.pdb Dateien wirklich verlässlich sind. Es handelt sich um die größte Datenbank der Welt.
Dennoch ist ihre Validität aufgrund einer unterschiedlich großen Fehlerrate in den Strukturen
umstritten. Im Gegensatz dazu verbessern sich die Auflösungen der in der PDB hinterlegten
Dateien ständig, was die Fehlerrate senkt, Fehler jedoch nicht ausschließt. Aufgrund der
Tatsache, dass wir den Liganden selbst entworfen haben, ist es sehr unwahrscheinlich, dass
wir die Struktur in einer .pdb finden werden. Daher müssen wir für unsere Liganden die .pdb
Datei selbst erstellen. Hierzu wird das Webprogramm Corina (http://www2.chemie.unierlangen.de/software/corina/free_struct.html) verwendet. Dabei wird die Struktur gezeichnet
und anschließend in einen eindeutigen Smiley-Code übersetzt, welcher nach Bestätigung
über einen Start Button in eine energieminimierte dreidimensionale Struktur übertragen und
in einer .pdb Datei gespeichert wird, die nun herunterladen werden kann.
Wenn das ΔG Minimum für die Rezeptor-Ligand-Bindung mittels Auto-Dock gefunden wurde,
kann die zu diesem Minimum korrelierte Liganden-Struktur und die Struktur des fixen
Rezeptors exportiert werden. Die exportierten Strukturen lassen sich nun mittels Pymol
komfortabel betrachten. In diesem Programm lassen sich mittels Wizzard ebenso u.a.
Bindungswinkel und Bindungslängen messen und andere elementare Operationen
durchführen (siehe Material und Methoden).