Formelsammlung Mathematik – Realschule an der Holbeinstraße

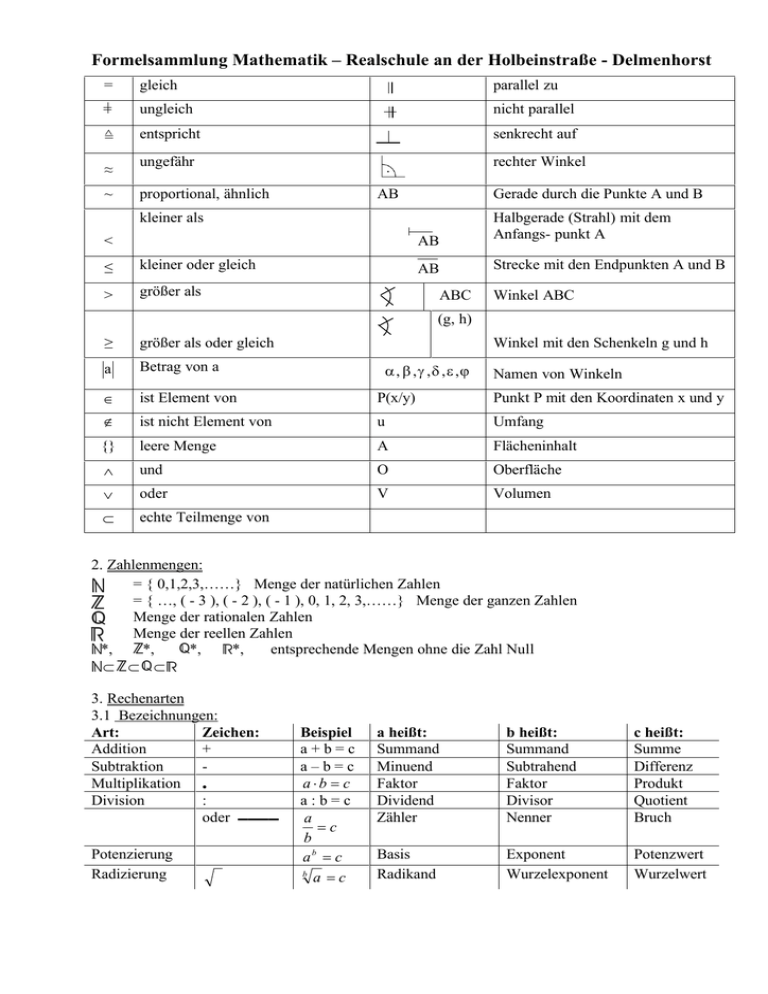
Formelsammlung Mathematik – Realschule an der Holbeinstraße - Delmenhorst
=
gleich
parallel zu
=
ungleich
nicht parallel
^
=
entspricht
senkrecht auf
≈
~
ungefähr
rechter Winkel
.
proportional, ähnlich
AB
Gerade durch die Punkte A und B
kleiner als
<
≤
kleiner oder gleich
>
größer als
AB
Halbgerade (Strahl) mit dem
Anfangs- punkt A
AB
Strecke mit den Endpunkten A und B
ABC
Winkel ABC
(g, h)
≥
größer als oder gleich
Winkel mit den Schenkeln g und h
a
Betrag von a

ist Element von
P(x/y)
Punkt P mit den Koordinaten x und y

ist nicht Element von
u
Umfang
{}
leere Menge
A
Flächeninhalt

und
O
Oberfläche

oder
V
Volumen

echte Teilmenge von
 ,  ,  ,  ,  ,
Namen von Winkeln
2. Zahlenmengen:
= { 0,1,2,3,……} Menge der natürlichen Zahlen
= { …, ( - 3 ), ( - 2 ), ( - 1 ), 0, 1, 2, 3,……} Menge der ganzen Zahlen
Menge der rationalen Zahlen
Menge der reellen Zahlen
*,
*,
*,
*,
entsprechende Mengen ohne die Zahl Null
  
3. Rechenarten
3.1 Bezeichnungen:
Art:
Zeichen:
Addition
+
Subtraktion
Multiplikation ●
Division
:
oder ▬▬▬▬
Potenzierung
Radizierung
Beispiel
a+b=c
a–b=c
ab  c
a:b=c
a
c
b
ab  c
b
a c
a heißt:
Summand
Minuend
Faktor
Dividend
Zähler
b heißt:
Summand
Subtrahend
Faktor
Divisor
Nenner
c heißt:
Summe
Differenz
Produkt
Quotient
Bruch
Basis
Radikand
Exponent
Wurzelexponent
Potenzwert
Wurzelwert
3.2 Hierarchie der Rechenarten:
 Klammern ausrechnen oder vereinfachen.
 Potenzierung und Radizierung durchführen.
 Punktrechnung ausführen.
 Klammern auflösen.
 Strichrechnung ausführen.
4. Klammern:
4.1 Klammern auflösen:
a+(b–c)=a+b–c ; a–(b–c)=a–b+c
4.2 Multiplikation:
a  b c  d   ac  ad  bc  bd
4.3 Ausklammern:
ab  ac  ad  a  b  c  d 
4.4 Binomische Formeln:
a  b2  a 2  2ab  b 2 ; a  b 2  a 2  2ab  b 2 ;
5. Potenzen, Wurzeln:
a x  a y  a x y
a x : a y  a x y
a 
x y
n
n
 a xy
a  n b  n a b
a : n b  n a :b
n m
a x  b x  a  b 
a  n m a
x
n
a : b  a : b 
a1  a
a0  1
1
a x  x
a
x
x
x
n
a  b a  b   a 2  b 2
am 
a a
 a
n
1
n
6. Quadratische Gleichungen:
Normierte Form: x 2  px  q  0
2
Lösungen:
Satz des Vieta:
p
 p
   q
2
2
x1  x 2   p und x1  x 2  q
x1, 2  
7. Prozent- und Zinsrechnung:
p
G
100
p
Promillerechnung: W 
G
1000
K  pt
Zinsrechnung:
Z
100  360
Prozentrechnung:
8.
8.1
W 
Wachstum:
Exponentielles Wachstum:
p 

Gn  G0  q n ; q  1 

 100 
t ist die Zeit in Tagen
m
8.2
Zinseszinsrechnung:
p 

K n  K 0  q n ; q  1 

 100 
9.
Statistik, Wahrscheinlichkeit:
Arithmetisches Mittel:
w  w2  w3  ....  wn
w 1
n
2
2
2
Standardabweichung:
w1  w  w2  w  ....  wn  w
s
n
Fakultät:
n! n  n  1 n  2 ....  3  2  1
Binominalkoeffizient:  n 
n!
  
 k  k!n  k !

 



10. Dreiecke:
10.1
allgemeines Dreieck:
      180 0
.
u=a+b+c
A
10.2
a  ha b  hb c  hc


2
2
2
rechtwinkliges Dreieck:
.
2
Höhensatz:
hhy  q  p
Kathetensatz:
kq  hy  q
2
2
.
k p  hy  p
Satz des Pythagoras:
10.3
2
2
gleichseitiges Dreieck:
.
11.
11.1
2
hy  k q  k p
Vierecke:
Quadrat:
ha 
a 3
2
A
a2  3
4
11.2 Rechteck:
u  2  a  2  b  2  a  b 
u  4a
A  a  a  a2
.
A  a b
e  a2  b2
e  A 2
11.3
Parallelogramm:
11.4 Raute:
.
11.5
u  2  a  2  b  2  a  b
u  4a
A  a  ha  b  hb
A  a  ha 
Trapez:
11.6 Drache:
u  abcd
m  ( g1  g 2 ) : 2
g  g 2  h
A 1
2
A  mh
12.
e f
2
u  2  a  c 
A
e f
2
regelmäßiges Sechseck:
M: Mittelpunkt des Umkreises und Inkreises
R: Radius des Umkreises
ha : Radius des Inkreises
a 3
2
u  6a
A  1,5  a 2  3
ha 
13.
Kreis:
13.1 Kreis:
r
d
13.2 Kreisring:
d  2r
u  d
u  2  r
A   r2   
d2
4
13.3 Kreisausschnitt, Kreisbogen::
  r 
b
180 0
  r 2  b  r
A

2
360 0
14.
Strahlensatz; Ähnlichkeit:
AB║AõBõ

2
A    r1  r2
ZA' ZB '

ZA ZB
k: Abbildungsmaßstab
ZA' B ' A'

ZA
BA
A'  k 2  A
a'  k  a
V '  k 3 V
2

15.
Würfel
O  6  a2
V  a3
e  a 3
16.
Quader
O  2  a  b  a  c  b  c 
V  a bc
e  a2  b2  c2
17.
gerades Prisma
M  uG  h
(M: Mantelfläche)
O  2G  M
(G: Grundfläche)
V  Gh
18.
Zylinder
M  2  r  h
O  2  G  M  2    r  r  h 
V   r2 h
19.
Pyramide
OGM
V 
20.
Gh
3
Kegel
M  r s
s
O  G  M    r  r  s 
V 
 r2 h
3
21.
Kugel
O  4   r 2
V 
4   r 3
3
22. Pyramidenstumpf
O  G1  M  G 2
.
.
V 
h
 G1  G1  G 2  G 2
3


23. Kegelstumpf:
M    s  r1  r2 
V 
 h
2
2
 r1  r1  r2  r2
3

O  G1  G 2  M


O    r1  r2  s  r1  r2 
2
2
24. Trigonometrie:
24.1 rechtwinkliges Dreieck:
sin  
Gegenkathete von 
Hypotenuse
cos  
Ankathete von a
Hypotenuse
tan  
Gegenkathete von 
Ankathete von 
25.2 allgemeines Dreieck:
a
b
c


 2r
sin  sin  sin 
a 2  b 2  c 2  2  b  c  cos 
b 2  a 2  c 2  2  a  c  cos 
c 2  a 2  b 2  2  a  b  cos 
A
a  b  sin  a  c  sin  b  c  sin 


2
2
2
A  2  r 2  sin   sin   sin 

26. Funktionen:
26.1 Proportionale Funktionen:
x  m x
y  mx
26.2 Lineare Funktionen:
x  m xb
y  m x b
y(0/b) (y-Achsenschnittpunkt)
26.3 Quadratische Funktionen:
x  a  x2  b  x  c
y  a  x2  b  x  c
S: Scheitelpunkt
26.4 Potenzfunktionen:
x  xn
y  xn
26.5 Exponentialfunktionen:
x  a bx
y  a bx