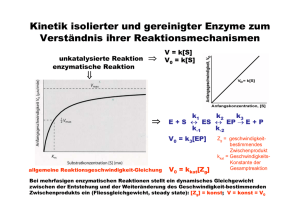
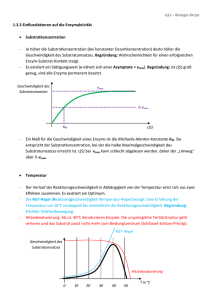
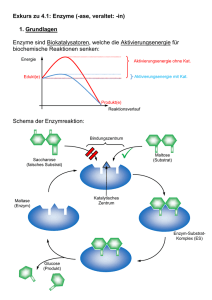
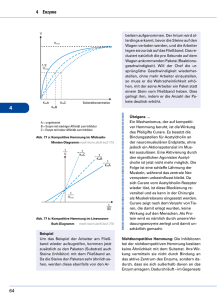
E S ES K - LIMES

Vertiefendes Seminar zur Vorlesung Biochemie I
04.12.2015
Bearbeitungg Übungsblatt
g
6
Gerhild van Echten-Deckert
Fon. +49-228-732703
Homepage:
http://www.limes-institut-bonn.de/forschung/arbeitsgruppen/unit-3/
Energiediagramm einer Reaktion  Enzym
Abhängigkeit der
Geschwindigkeit einer
Enzym katalysierten
Enzym-katalysierten
Reaktion von der
Substratkonzentration.
Wie verändern sich die Konzentrationen der Teilnehmer im Verlaufe einer einfachen
MM-Reaktion?
Michaelis--MentenMichaelis
Menten-Modell
E +S
frei
k+1
k-1
ES
k+2
a)
b)
E +P
frei
k-2
V0  k2 *[ ES ]
k1 :[[
V f  k1 *[ E ]*[ S ]
Vd  k1 *[ ES ]  K 2 [ ES ]
Anfangsgeschwindigkeiten : k-2 = 0
Fließgleichgewicht : [ES] = C
1 L
]
s mol
1
k1 :[ ]
s
Fließgleichgewicht : [ES] ist konstant  Vf=Vd
 k1 *[ E ]*[ S ]  [ ES ](k2  k1 )
[ E ]*[ S ] k1  k2

 K M ; Michalis-Menten-Konstante
[ ES ]
k1
[ ES ]
[S ]

;  [ E ]  [ Et ]  [ ES ]
[ Et ] K M  [ S ]
[ ES ]  [ Et ]*
[S ]
K M  [S ]
[S ]
V0  k2 [ Et ]*
KM  [S ]
Bei Substratsättigung  [ES]=[Et]
Vmax  k2 [ Et ]  V0  Vmax *
[S ]
KM  [S ]
Michalis-Menten-Gleichung
Michaelis--MentenMichaelis
Menten-Modell
Alternative Michaelis-Menten-Gleichung :
KM
Vmax
Vmax  V0
Oder : V0 
 [S ]
KM
V0
1
In vitro, [S] Überschuss , [E] begrenzend
[S ]
v
Vmax
V0  Vmax
1 V max
2
KM
[S]
[S ]
K M  [S ]
Grenzfälle :
[S ]
v steigt fast linear mit [S]
KM
a)
Für [S]  KM  V0  V max
b)
Für [S] = KM V0  1 2 V max Definition von KM :
v halbmaximale
Substratkonzentration
c)
Für [S]  KM 
V0  V max
v maximal, Grenzwert
Bestimmung von KM und Vmax : Lineweaver
Lineweaver--Burk
[S ]

V0  Vmax *
K M  [S ]
Für
1
1
1
0

V0
[S ]
KM
Für
1
1
1
0 
[S ]
V0 Vmax
K
1
1
1

 M *
V0 Vmax Vmax [ S ]
Die Geschwindigkeit einer Michaelis-Menten
Reaktion als Funktion der Substratkonzentration
Lineweaver–Burk
i
k Auftragung
A f
Michaelis--MentenMichaelis
Menten-Modell
E +S
frei
k+1
k-1
ES
k+2
k-2
E +P
frei
Für k-11  k+2

(ES zerfällt schneller in E + S als in E + P)
k1  k2
 1 sec

KM 


1
sec
*
l
mol


k1
k  1 Dissoziationskonstante von ES
KM 
k 1
KM-Werte einiger Enzyme
Enzym
Substrat
Chymotrypsin
Lysozym
-Galactosidase
Threonin-Deaminase
Carboanhydrase
Penicillinase
Pyruvat carboxylase
Acetyl-L-tryptophanamid
Hexa N Acetylglucosamin
Hexa-N-Acetylglucosamin
Lactone
Threonin
CO2
Benzylpenicillin
Pyruvat
HCO3ATP
Arginin
tRNA
ATP
Arginin t-RNA Synthetase
KM
5x10-3M
6x10-66M
4x10-3M
5x10-3M
8x10-3M
5x10-5M
4x10-4M
1x10-3M
6x10-5M
3x10-6M
4x10-7M
3 10-44M
3x10
Je kleiner KM desto stabiler ES, desto höher Affinität von E für S
Vmax  k2 *[ Et ]
 k2  Wechselzahl *[
Carboanhydrase : diffusionskontrolliert
Acetylcholinesterase auch :
S  Moleküle
]  k2  kcat
E  Moleküle *sec
HCO3- + H+
H2O + CO2
O
O
O
N
Enzym
Carboanhydrase
Acetylcholinesterase
+ H2O
O
600000
25000
2000
Lactat-Dehydrogenase
1000
DNA-Polymerase I
HO
N
[s-1]
Penicillinase
Chymotrypsin
+
100
15
Tryptophan-Synthetase
2
Lysozym
0,5
Maximale Wechselzahlen
einiger Enzyme
Michaelis--MentenMichaelis
Menten-Modell
kcat
KM
Katalytische Leistungsfähigkeit eines Enzyms
Für [S] << KM (in vivo) gilt : Et  Efrei und aus
V  k2 *[ ES ]
I in II 
wird
[ ES ] [ Et ]*[ S ]
KM
(I)
(II)
k2
*[ S ]*[ Et ]
V
KM
k2
 k1
KM
[ Et ]*[ S ]
[ ES ] 
K M  [S ]
;
1
k1

K M k1  k2
(diffusionskontrolliert), da :
Und
k2 k2 * k1

K M k1 * k2
k2
k1  k2
stets kleiner als 1
 k+2=kkcat kann
k
maximal
i l k+1 erreichen
i h (wenn
(
k-1<< k+2) ddann iistt E diffusionskontrolliert:
diff i k t lli t
 k+1 max = 108-109 M-1s-1
Kinetische Messungen zum EnzymEnzym-Optimum
Plot : v als Funktion von pH
• Veränderung der Nettoladung z.B. –COO- zu –COOH
• Wendepunkt bei pH ca
ca. 6 deuten oft auf ein Histidin
• Wendepunkt bei pH ca. 3,5 deuten auf Aspartat oder Glutamatrest
Temperatureffekte
• bis 40°C Verdoppelung von V bei Erhöhung von je 10°C
• Später Inaktivierung durch Denaturierung
Substratkonzentration
• häufigg „Produkthemmung“
„
g durch unspezifische
p
Bindung,
g, ggf.
gg
Blockade des aktiven Zentrums
• pS = - log [S]
Enzymkinetik (Inhibitoren)
1.
2.
Irreversible Inhibitoren
Suizid-Inhibitoren
Reversible Inhibitoren
(a) kompetitive Inhibitoren : Substratanaloga (EtOH bei MeOH od.Glykolod Glykol Vergiftung),
Vergiftung)
Übergangszustandsanaloga
(b) nichtkompetitive Inhibitoren
Angriffspunkte:

Aktives Zentrum, Inhibitoren werden durch das Substrat verdrängt

I Bereichen
In
Be ei he außerhalb
ße h lb des
de aktiven
kti e Zentrums
Ze t

Keine Verdrängung durch das Substrat

Erniedrigung der Wechselzahl
Unterschied zw einem kompetitiven und einem nichtkompetitiven Inhibitor
Reversible Inhibitoren
Kompetitiv
K
i i (aktives
( ki
Zentrum,
Z
häufigster
hä fi
Typ)
T ):
• reversible Bindung, aber kein Umsatz
• Erschwerung des Substratzutritts
• keine Veränderung des Katalyseeigenschaften Vmax wird
nicht verändert
Kompetitive Inhibition
E k
Erkennung
d
durch
h ki
kinetische
ti h M
Messung : KM steigt
t i t
Vmax unverändert
1
1
=
V
KM (1 + [I]/KI)
1
Vmax
[S]
+
Vmax
Kompetitive Inhibition
A double reciprocal plot of enzyme kinetics in the presence (blue, red) and absence
(green) of a competitive inhibitor. Vmax is unaltered whereas KM is increased
Nichtkompetitive Hemmung
Nichtkompetitive Hemmung
Unkompetitive Hemmung
Erkennung durch kinetische Messung : KM unverändert
Vmax fällt
• häufig bei zwei oder mehr Substraten
• keine Blockade oder Verdrängung des Substrats
• Enzym wird auch unabhängig vom Substrat inaktiviert
• Effekt : scheinbare Verringerung der Enzymkonzentration
• meist kein Effekt auf KM
• unkompetitive Inhibitoren binden nur an den ES-Komplex
Unkompetitive Hemmung in der Lineweaver-Burk Auftragung
Gemischt-kompetitive Hemmung in der Lineweaver-Burk Auftragung
Kinetik allosterischer Enzyme in Anwesenheit
positiver bzw. negativer allosterischer Effektoren
K-Typ:
v-Typ:
vmax-konstant
KM-ändert
ä d t sich
i h±
KM-konstant
vmax-ändert sich ±
Substratbindung an ein allosterisches Protein: SYMMETRIE-MODELL
Jaques Monod
Jeffries Wyman
Jean-Pierre
Jean
Pierre Changeux
“Alles oder Nichts”
“Konzertiertes Modell”
Substratbindung an ein allosterisches Protein: SEQUENZ-MODELL
Daniel Koshland
“Induced
Induced fit
fit”
Wirkung allosterischer Effektoren auf die kooperative Substratbindung
eines dimeren Enzyms
niedrigaffin
hochaffin
1) Michaelis-Menten kinetics and calculation of KM & Vmax
KM = 4.6 µM
Vmax = 12.8
12 8 nmol/min
http://www.graphpad.com/guides/prism/6/curve-fitting/index.htm?reg_michaelis_menten_enzyme.htm
2. Zugabe von 4 µM eines kompetitiven Inhibitors
KI = 1.5µM
http://www.graphpad.com/faq/file/P4-Competitive%20inhibition.pdf