Lassen Sie uns mit einem kleinen praktischen Beispiel beginnen

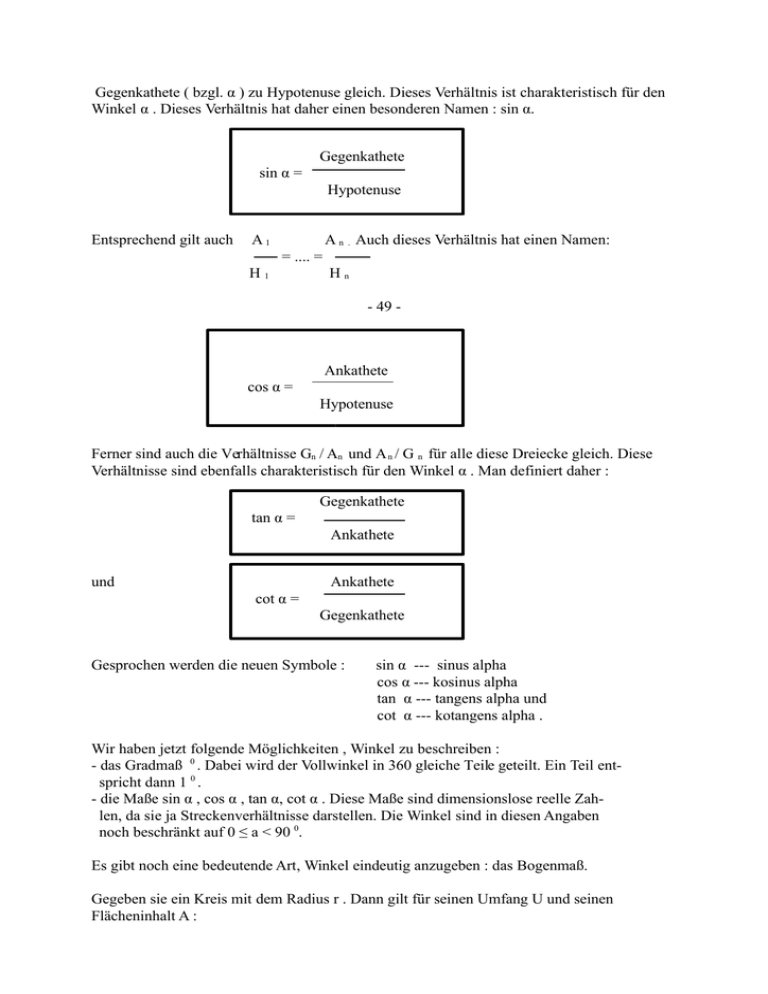
Gegenkathete ( bzgl. α ) zu Hypotenuse gleich. Dieses Verhältnis ist charakteristisch für den
Winkel α . Dieses Verhältnis hat daher einen besonderen Namen : sin α.
Gegenkathete
sin α =
Hypotenuse
Entsprechend gilt auch
A1
A n . Auch dieses Verhältnis hat einen Namen:
= .... =
H1
Hn
- 49 -
Ankathete
cos α =
Hypotenuse
Ferner sind auch die Verhältnisse Gn / An und A n / G n für alle diese Dreiecke gleich. Diese
Verhältnisse sind ebenfalls charakteristisch für den Winkel α . Man definiert daher :
Gegenkathete
tan α =
Ankathete
und
Ankathete
cot α =
Gegenkathete
Gesprochen werden die neuen Symbole :
sin α --- sinus alpha
cos α --- kosinus alpha
tan α --- tangens alpha und
cot α --- kotangens alpha .
Wir haben jetzt folgende Möglichkeiten , Winkel zu beschreiben :
- das Gradmaß 0 . Dabei wird der Vollwinkel in 360 gleiche Teile geteilt. Ein Teil entspricht dann 1 0 .
- die Maße sin α , cos α , tan α, cot α . Diese Maße sind dimensionslose reelle Zahlen, da sie ja Streckenverhältnisse darstellen. Die Winkel sind in diesen Angaben
noch beschränkt auf 0 ≤ a < 90 0.
Es gibt noch eine bedeutende Art, Winkel eindeutig anzugeben : das Bogenmaß.
Gegeben sie ein Kreis mit dem Radius r . Dann gilt für seinen Umfang U und seinen
Flächeninhalt A :
U = 2 π r = d r und A = π r 2 .
Dabei ist π ≈ 3,1415927.... die sogenannte Kreiszahl. Sie ist wie etwa √ 2 eine irrationale
Zahl, hat also eine unendliche nichtperiodische Dezimaldarstellung. Man erhält sie, indem
man den Umfang eines Kreises durch dessen Durchmesser teilt.
b
α
+
r=1
- 50 Betrachten wir den Kreis mit dem Radius r = 1, den Einheitskreis . Der Winkel a schneidet
aus dem Umfang des Kreises einen Bogen b aus. Die Länge dieses Bogens ist abhängig von
der Größe des Winkels a . Es verhält sich nun der Winkel a zu 360 0 ( Vollwinkel ) wie der
Bogen b zum Gesamtumfang des Einheitskreises
U= 2p 1 .( Der Radius ist 1 !) Etwas abstrakter in einer Gleichung formuliert lautet dieser
Zusammenhang :
α
b
=>
=>
=
360 0
Einige Beispiele :
2 πα
b=
πα
=
360 0
2π
α
in 0
1800
im Bogenmaß
180 0
π
0
90
π/2
60 0
π/3
0
30
π/6
45 0
π/4
0
40
0,6981317...
Das Bogenmaß findet man auf dem Taschenrechner in der Einstellung < RAD >, das Gradmaß
in der Einstellung < DEG >.
Ordnet man jedem Winkel a seinen Wert sin a zu, so spricht man von der Sin-Funktion
( entsprechend Cos-, Tan-, Cot-Funktion ). Dabei spielt es keine Rolle, ob der Winkel α im
Gradmaß oder Bogenmaß angegeben ist. Der Oberbegriff für die Sin- , Cos- , Tan- , und CotFunktion ist Winkelfunktionen .
Der Definitionsbereich der Winkelfunktionen ist, wie oben gesagt, beschränkt auf Winkel <
90 0, denn im rechtwinkligen Dreieck gibt es keinen Winkel a , der 90 0 oder größer ist. Die
Winkelsumme im Dreieck ist 180 0. Da aber im rechtwinkligen Dreieck ein Winkel schon 90 0
beträgt, bleibt für die anderen beiden zusammen nur noch 90 0 über.
Wir wollen nun die Definition der Winkelfunktionen erweitern, sodass die neue Definition mit
der alten verträglich ist.
Gegeben sei ein beliebiger Punkt P auf dem Peripherieteil des Einheitskreises im
1. Quadranten. Seine Koordinaten bilden mit dem Radius, der nach P weist,
einrechtwinkliges Dreieck.
P(x|y)
1
In diesem rechtwinkligen Dreieck gilt
Gegenkathete
y
sin α =
=
Hypotenuse
1
sin α
oder y = sin α
α
cos α
Entsprechend leitet man ab:
x = cos α
- 51 -
Man kann also den y - Wert ( die Ordinate ) des Punktes P als sin - Wert des Winkels α deuten,
und den x - Wert ( die Abszisse ) deutet man als cos α . Damit ist man nicht mehr an Winkel
bis 90 0 gebunden. Für α können jetzt beliebige Winkel gewählt werden. Der Winkel α = 720 0
z.B. bedeutet ein zweimaliges Umlaufen gegen den Uhrzeigersinn. Ein Umlauf mit dem
Uhrzeigersinn liefert negative Winkel, etwa
α = - 30 0. Wir haben somit eine neue Definition für sin α und cos α gefunden, die mit der
alten Definition verträglich ist:
y = sin α
x = cos α,
wobei x,y die Koordinaten
des Punktes P auf dem Einheitskreis sind, der zum Winkel a gehört.
Nach dem Satz des Pythagoras leitet man sofort die wichtige Beziehung
sin 2 α + cos 2 α = 1.
Schreibt man sin α , so ist der Winkel im 0 - Maß gemeint, schreibt man sin x , so wird der
Winkel im Bogenmaß angegeben.
β
β
β β
-α
α
Aus der Zeichnung ließt man ab
sin α = sin ( 180 0 - α )
cos α = - cos ( 180 0 - α )
Für eine Kreisumdrehung "wieder
holen" sich die alten Funktions
werte. sin α = sin ( α + 180 0 ) und
cos α = cos ( α + 180 0 ). Oder im
Bogenmaß formuliert
sin x = sin ( x + 2π )
cos x = cos ( x + 2π )
Auch bei k-maliger Umdrehung kehren die gleichen Funktionswerte wieder.
sin x = sin ( x + kπ )
cos x = cos ( x + kπ ) , k = ± 1; ± 2 ; .....
Der Winkel β in der obigen Zeichnung ist gleich 90 0 - α. Es gilt sin β= cos α . Und damit
cos α = sin ( 90 0 - α ) oder
cos x = sin ( π / 2 - x ) .
Ferner gilt
cos ( β + 90 0 ) = sin β
cos (x + π / 2 ) = sin x
und
cos x = sin ( x - π / 2 ).
Aus den letzten beiden Beziehungen geht hervor, dass sich jeder der beiden Funk- 52 tionsgraphen aus dem anderen durch Parallelverschiebung um p / 2 bzw. - p / 2 Einheiten in
Richtung der x - Achse darstellen läßt.
Die Sin-Funktion und die Cos-Funktion haben beide den Definitionsbereich IR. Der
Wertebereich beider Funktionen ist nach oben und unten beschränkt. Die Funktionswerte sind
kleiner oder gleich 1 , aber größer oder gleich – 1.
P´
P
tan x
1
x
sin x
0
1
Tangens ist im rechtwinkligen Dreieck definiert worden als Verhältnis von Gegenkathete zu
Ankathete. Wählen wir nun die Länge der Ankathete gleich 1, dann gibt die Länge der
Gegenkathete den Tangens des Winkels an. In der obigen Zeichnung hat die Ankathete des
Dreiecks 01P' die Länge 1. Die Gegenkathete liegt dann auf der Tangente an den Kreis durch
1. ( Daher der Name Tangens !) Das gilt für jeden Winkel, mit Ausnahme von α = 90 0 und
α = 270 0 bzw x = π / 2 und x = (3 / 2)π und entsprechende Vielfache davon.
- 53 Aus der Zeichnung sieht man auch, dass nach dem Strahlensatz gilt :
sin x : tan x = cos x : 1
sin x
tan x =
cos x
,
für cos x ≠ 0
Schnittpunkte :
Häufig kommt es vor, daß sich die Graphen zweier Funktionen schneiden . Man möchte dann
die Koordinaten der Schnittpunkte berechnen. Nehmen wir zunächst das Beispiel zweier
Geraden. Die Geraden seien gegeben durch
g 1 : y = 2x - 4 und g 2 : y = 1/2 x + 1/2.
Zunächst ist klar, daß der Schnittpunkt S ( x s | y s ) auf beiden Geraden liegt. Also erfüllen
seine Koordinaten beide Gleichungen. y s = 2 x s - 4 ^ y s = 1/2 x s + 1/2.
Da die y s - Werte in diesen beiden letzten Gleichungen gleich sind, es sind ja in beiden Fällen
der y - Wert des Schnittpunktes, sind auch die rechten Terme gleich.
2 x s - 4 = 1/2 x s + 1/2
( man spricht von der Gleichsetzungsmethode )
2 x s - 1/2 x s = 1/2 + 4
3/2 x s = 9 / 2
x s= 3
| ( 2/3) [ Multiplik.m.d. Kehrzahl ]
Der x - Wert des Schnittpunktes ist also x s = 3 . Den zugehörigen y - Wert erhält man, indem
man diesen x - Wert in eine der beiden obigen Gleichungen einsetzt.
ys=2(3)-4=2
Der Schnittpunkt hat also die Koordinaten S ( 3 | 2 ).
Die beiden Geraden h 1 : y = 2x - 4 und h 2 : y = 2x + 3 können keinen Schnittpunkt haben,
da sie parallel verlaufen und nicht identisch sind. Das zeigt auch die Rechnung. Anwendung
der Gleichsetzungsmethode ( Indizes sind weggelassen ):
2x - 4 = 2x + 3
2x - 2x = 4 + 3
0=7!
Das ist ein Widerspruch ! Es gibt also keinen
gemeinsamen Punkt.
Beispiel Gerade - Parabel. g : y = 1/2 x - 1/2 und p : y = - 1/2 x 2 + 5x - 19/ 2
Auch hier geht man davon aus, daß der Schnittpunkt auf beiden Graphen liegt.
Anwendung der Gleichsetzungsmethode :
1/2 x - 1/2 = - 1/2 x 2 + 5x - 19/ 2
- 1/2 x 2 + 5x - 19/ 2 - 1/2x + 1/2 = 0
| ( - 2)
x 2 - 10x + 19 + x - 1 = 0
x 2 - 9x + 18 = 0
Wir sehen, das bei dieser Problemlösung die Rechnung auf eine quadratische Gleichung führt,
- 54 die wir mit bewährter Methode ( p-q-Formel ) lösen können .
x 1/2 = 9/2 ± √ 81 / 4 - 72/ 4 =9/2 ± 3/2
x 1= 6
;
x 2= 3
Es gibt also zwei Schnittpunkte P1 ( 6 | ?) und P 2 ( 3 | ? ). Die zugehörigen y - Werte bestimmt
man wieder durch Einsetzen der x - Werte in die Geraden - oder Parabelgleichung. Bequemer
ist das Einzetzen in die Geradengleichung .
y = 1/2 ( 6 ) - 1 /2 = 3 - 1/2 = 2,5
P1 ( 6 | 2,5 )
Und
y = 1/2 ( 3) - 1/2 = 2/2 = 1
P 2( 3 | 1 )
Die Schnittpunkte zweier Parabeln bestimmt man entsprechend, indem man die Parabelterme
gleichsetzt und die Lösungen der so entstandenen Bestimmungsgleichung berechnet. Hat eine
solche Gleichung keine Lösung, dann besitzen die Parabeln auch keine gemeinsamen Punkte.
Und was Sie sonst noch wissen sollten !
Das Produktzeichen Π
Das Produkt 3• 4• 5 z.B. wird abkürzend mit dem Produktzeichen folgendermaßen
geschrieben :
4
Π ( i + 1) = (2 + 1 )( 3 + 1) ( 4 + 1) ,
i=1
wobei, wie man sieht, für i nacheinander die Zahlen 2 bis 4 eingesetzt werden.
P ist dabei der griechische Groß-Buchstabe für p ( gesprochen pi bzw großpi )
Ein besonderes Produkt stellt das Produkt der ersten n natürlichen Zahlen dar.
Es wird mit n ! ( gesprochen n-Fakultät ) bezeichnet:
n
n ! = 1• 2• 3• .....• n = Π i
i=1
Z. B. gilt : 3 ! = 1•2 • 3 = 6
4 ! = 1• 2 • 3 • 4 = 3 ! 4 = 24
5 ! = 1•2 • 3 • 4 • 5 = 4 ! 5 = 120
6 ! = 5 ! 6 = 720
7 ! = 6 ! 7 =5040
Allgemein gilt :
(n+1)!=n!(n+1)
Diese Formel nennt man auch Rekursionsformel, weil sich ( n +1 ) ! auf n ! zurückbezieht.
n ! ordnet jeder natürlichen Zahl eindeutig eine natürliche Zahl zu . Man spricht daher auch
von der Fakultätsfunktion. Aus Zweckmäßigkeitsgründen definiert man noch : 0 ! = 1 Damit
ist der Definitionsbereich IN Ụ { 0 } = IN 0. Der Wertebereich ist IN. Die Fakultätsfunktion ist
streng monoton steigend. Sie steigt, wie wir schon an den wenigen Beispielen sehen,
- 55 ungeheuer schnell an. [ Normale Taschenrechner sind bei 70 ! schon überfordert !! ]
Das Summenzeichen ∑
Mit dem Summenzeichen ∑ ( gr. Zeichen für S ; gesprochen : Sigma ) fasst man Summen
zusammen :
n
Z. B. 1 + 2 + 3 +4 + .... + n = ∑ i ;
i=1
n
Sind alle Summanden gleich, dann gilt :
∑
a = a + a + ... + a = n a
i=1
Aus den Rechenregeln der Addition ( Subtraktion ) folgt :
n
∑ ( a i + b i ) = a 1 + b 1 + a 2 + b 2 + .... + a n + b n
= a 1 + a 2 +... + an + b 1 + b 2 +.... b n
i=1
| ( Kommutativgesetzt )
n
=
n
∑ a i+
i=1
∑ bi
i=1
Entsprechend schließt man für die Subtraktion.
Durch Ausklammern des gemeinsamen Faktors erhält man :
n
n
∑ c a i = c a 1 + c a 2 + ..... c a n = c ( a 1 + ..... + a n ) = c ∑ a i
i=1
i=1
Mit diesen neuen Symbolen können wir uns nun den Binomialkoeffizienten zuwenden. Wir
erinnern uns, dass damit die Zahlen des Pascalschen Dreiecks gemeint sind. Man kann diese
Koeffizienten auch mit Hilfe der Fakultäts - Funktion berechnen. Dazu führen wir folgende
Definition ein :
n
Für k ≤ n heißt
n
( sprich n über k ) ein Binomialkoeffizient mit:
k
n ( n - 1 )( n - 2 ) ....... ( n - k + 1 )
=
k
n (n - 1).... ( n - k + 1)
=
n!
=
1· 2· 3 ..... ·( k - 1 ) k
k!
k!(n-k)!
Folgende Gesetzmäßigkeiten kann man sofort durch Einsetzen in die obige Gleichung
bestätigen :
- 56 1.
n
2.
n
=1
0
n
3.
n
n
=
k
=
n-k
=n
n-1
1
Der Binomische Lehrsatz kann nun so formuliert werden :
n
(a+b)n = Σ
n
k
a
n-k
bk =
k=0
n
0
a nb 0 + n
1
a n-1b 1 + n
2
a
n-2
b 2 + ..+ n a
k
n-k
b k + .. + n
bn
n
Einige Beispiele zur Verdeutlichung :
(a+b)2 = 2
a 2b 0 +
2
ab+ 2
a 0b 2
2
=1
2
=2
2
=1
0
1
2
;
0
1
2
= a 2 + 2 ab + b 2
(a+b)4=
a 4b 0 + 4 a 3b 1 + 4 a 2b 2 + 4 a b 3 + 4 a 0b 4
1
2
3
4
4
0
a 4 + 4 a 3b + 6 a 2b2 + 4 a b 3 + b 4
=
Der Vorteil dieser Darstellung gegenüber der Herleitung mit dem Pascalschen -Dreieck ist der,
dass man in dieser Darstellung direkt nach irgendeinem n entwickeln kann, während man zur
Entwicklung von (a + b ) n die Koeffizienten bzgl. ( n - 1 ) kennen muß. Lautet der Binom (a b ) [ ( a - b ) n ], dann wechselt ( alterniert ) das Vorzeichen, beginnend mit + . Kurz : " + " , " " , " + " , " - " ,.....
Beträge und Abstände
Den Betrag einer reellen Zahl | a | hatten wir weiter oben folgendermaßen definiert :
|a|=
a für a > 0
0
für a = 0
- a für a < 0
Den Betrag kann man auch als Abstand der Zahl a vom Nullpunkt auf dem Zahlenstrahl
deuten.
|b|
|
-b
|a|
|
0
|
a
- 57 -
| a - b | stellt den Abstand zwischen a und b dar. Die Ungleichung | x - 3 | ≤ 2 gilt für alle
Zahlen x , die von 3 um weniger als 2 Einheiten entfernt liegen, oder gerade 2 Einheiten
entfernt. Die Ungleichung läßt sich demnach auch folgendermaßen formulieren :
1 ≤ x ≤5 .
Wenn das Zeichen " = " an den Grenzen mit angegeben wird, spricht man auch von einem
abgeschlossenen Intervall, fehlt das Gleichheitszeichen, also 1 < x < 5 , so ist das Intervall
nach beiden Seiten offen. Die Grenzen 1 und 5 gehören dann nicht zum Intervall ( in diesem
Beispiel ). Entsprechnd nennt man das Intervall 1 < x ≤ 5 links offen - rechts abgeschlossen .
Das Intervall | x - x 0 | ≤ d stellt man auf dem Zahlenstrahl so dar :
|
x 0- d
|
x0
|
x 0+ d
Beträge haben folgende Eigenschaften :
|-a|=|a|
|ab|=|a||b|
-|a|≤a≤|a|
|a+b|≤|a|+|b|
( Dreiecksungleichung )
Geometrischer Anhang
C
Dreieck
γ
b
a
α
β
A
c
B
Die Ecken werden mit großen Buchstaben bezeichnet ( gegen den Uhrzeigersinn, Analoguhr ),
die den Eckpunkten gegenüberliegenden Seiten mit kleinen Buchstaben . Die Bezeichnung der
Seiten entsprechen den Bezeichnungen der gegenüberliegenden Punkte. Die Winkel erhalten
die entsprechnenden kleinen griechischen Buchstaben, wie aus der Zeichnung er sichtlich. Die
Winkelsumme im Dreieck beträgt 180 0. α + β + γ = 180 0.
Ist ein Winkel im Dreieck, etwa γ = 90 0 , dann nennt man das Dreieck rechtwinklig.
Die dem Winkel γ anliegenden Seiten nennt man Katheten - hier a und b - , die dem rechten
Winkel gegenüberliegende Seite nennt man Hyptenuse - hier c.
- 58 Im rechtwinkligen Dreieck gilt der Satz des Pythagoras :
a2+b2 = c2
( Kurzform ! )
Zwei Dreiecke nennt man ähnlich , wenn sie in ihren Winkeln übereinstimmen.
C
C`
b
α
a
β
A
b`
c
a`
B
α
β
A`
c`
B`
0
Da die Winkelsumme im Dreieck 180 beträgt, ist die Ähnlichkeit zweier Dreiecke schon
gegeben, wenn diese in zwei Winkeln übereinstimmen. In ähnlichen Drei- ecken gelten
folgende Beziehungen :
a`:a=b`:b=c`:c
oder anders ausgedrückt
a`
b`
=
a
oder
a
a`
a
b`
c
=
b
a`
b
c`
c
=
c`
=
b
c
b`
=
c`
Die Verhältnisse entsprechender Seiten sind gleich !
Aus diesen Erkenntnissen folgen unmittelbar die bedeutenden Strahlensätze .
C`
γ
C
γ
β
α
β
B
B`
Werden zwei von einem Punkt S ausgehende Strahlen von zwei Parallelen geschnitten, so
gelten folgende Verhältnisse :
SB : SC = SB ` : SC ` ( 1. Strahlensatz )
oder
SB : SB ` = SC : SC `
Und
SB : SB ` = BC : B `C `
( 2. Strahlensatz )
- 59 -
Die beiden Dreiecke S B C und S B ` C ` sind ähnlich, da sie in ihren Winkeln
übereinstimmen. Diese Beziehungen gelten auch für die nachfolgende Zeichnung .
B`
C
β
α
S
α
β
C`
B
Flächeninhalt und Umfang
Rechteck :
a
b
Umfang :
U = 2a + 2b = 2 ( a + b )
Flächeninhalt : A = a b
Parallelogramm :
Ein Viereck, bei dem die jeweils gegenüberliegenden Seiten parallel sind, nennt man
Parallelogramm.
a
h = Höhe
b
Grundlinie
Wenn man in diesem Parallelogramm das rechte Stark umrandete Dreieck abschneidet und
links wieder anträgt, so ändert man den Flächeninhalt nicht. Die neu entstandene Figur ist ein
Rechteck, dessen Flächeninhalt Grundlinie þ Höhe ist. Also gilt für das Parallelogramm :
Umfang :
U = 2a + 2b = 2 ( a + b )
Flächeninhalt : A = a ha ( Seitenlänge mal Länge der
zugehörigen Höhe )
- 60 -
Dreieck :
h
Jedes Parallelogramm läßt sich durch eine Diagonale in zwei kongruente
( deckungsgleiche ) Dreiecke zerlegen. Deckungsgleiche Dreiecke sind aber auch
flächengleich . Daher gilt für das Dreieck :
Umfang :
U=a+b+c
Flächeninhalt : A = g h
2
Trapez :
D
c
C=B´
a
A´
m
h
A
a
B
c
D´
Ein Viereck mit zwei parallelen Seiten nennt man Trapez. Dreht man das Trapez ABCD um
180 0 um den Punkt S, so erhält man das Parallelogramm AD`A`D. Dieses Parallelogramm
setzt sich also aus zwei kongruenten ( und somit flächengleichen Trapezen ) zusammen . Der
Flächeninhalt dieses Parallelogramms ist aber
A = Grundlinie þ Höhe = ( a + c ) h. Daher gilt :
Umfang :
U=a+b+c+d
Flächeninhalt : A = ( a + c ) h = m h,
2
- 61 -
wobei ( a + c ) / 2 = m ist. ( vergl. Zeichnung ) m = Mittellinie - Verbindungslinie der
Mittelpunkte der beiden Schenkel des Trapezes.
Kreis :
Umfang
:
Flächeninhalt :
U=2πr=dπ
A=π r2
- 62 -
Lexikon
absolut
Addition
äquivalent
alternieren
assotiativ
Basis
Binom
lat. absolvere ( part. absolutum)
lat. addere ( ad - zu; dare - geben )
lat. aequus - gleich ; valere - gelten
lat. alternare
lat. associare
gr. basiV ( basis )
lat./gr ( bis - zweimal, nomoV(nomos)
Differenz
Diskriminante
distributiv
Dividend
Division
Divisor
Exponent
Faktor
kommutativ
Logarithmus
lat.
lat.
lat.
lat.
lat.
lat.
lat.
lat.
lat.
lat.
differentia
lat. discriminare
distribuere
dividendus ( numerus )
dividere
"
exponere
facere
commutare
logos
arithmos
( numerus ) minuendus
multiplicandus ( numerus )
lat. multiplicare
"
negare
per annum
ponere ( part. positum )
potentia
productum
proportio
quadratus
quotiens
radix ; radicandus (numerus)
rational
lat.
ratio
reziprok
Subtrahend
Subtraktion
Term
lat.
lat.
lat.
lat.
reciprocare
( numerus ) subtrahendus
subtrahere
terminus
Minuend
Multiplikand
Multiplikation
Multiplikator
negativ
p.a.
positiv
Potenz
Produkt
Proportion
quadratisch
Quotient
Radikand
lat.
lat.
lat.
lat.
lat.
lat.
gr.
gr.
lat.
lat.
loslösen, unabhängig
hinzufügen
gleichwertig
abwechseln
verbinden
Grundlage, Grundzahl
Gesetz) zweigliedriger
Ausdruck
Unterschied
trennen
verteilen
die zu teilende Zahl
teilen
Teiler
heraussetzen
der, der etwas macht
vertauschen
Verhältnis
Zahl
die zu vermindernde Z .
die zu vervielfältig . Z .
vervielfältigen
Vervielfältiger
verneinen
pro Jahr
setzen ; festgesetzt
Macht
Hervorgebrachtes
Ebenmaß
viereckig
wie oft
Wurzel ; die Zahl, aus der
die Wuzel gezogen wird
Maßstab,Verhältnis,
Bruch
zurückwenden
die abzuziehende Z.
abziehen
Ausdruck