Kinetik des Massenpunktes
Werbung

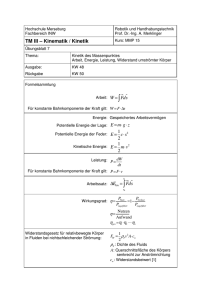
Technische Mechanik II Kinetik des Massenpunktes Prof. Dr.-Ing. Ulrike Zwiers, M.Sc. Fachbereich Mechatronik und Maschinenbau Hochschule Bochum WS 2009/2010 Kinetik des Massenpunktes Übersicht 1. Kinematik des Massenpunktes 2. Kinematik des starren Körpers 3. Kinetik des Massenpunktes ◦ Grundgesetze der Dynamik - Newtonsche Axiome - Klassifizierung von Kräften - Wichtige Kraftgesetze der Mechanik ◦ Arbeit, Energie und Leistung ◦ Impuls und Drehimpuls 4. Kinetik des starren Körpers 5. Stossprobleme Prof. Dr. U. Zwiers BTM2 2/24 Kinetik des Massenpunktes Grundgesetze der Dynamik 1/14 Grundlegende Begriffe Kinetik Lehre der Kräfte, die auf sich bewegende Körper wirken Kraft Physikalische Größe, die eine Bewegungsänderung bewirkt und durch drei Eigenschaften bestimmt ist: Betrag, Richtung und Angriffspunkt. Arten von Kräften: ◦ Einzelkraft ◦ Volumenkraft ◦ Flächenkraft ◦ Linienkraft Prof. Dr. U. Zwiers BTM2 3/24 Kinetik des Massenpunktes Grundgesetze der Dynamik 2/14 Grundlegende Begriffe (Forts.) Masse Physikalische Grundgröße, die proportional der Stoffmenge eines Körpers ist und die Trägheit des Körpers gegenüber einer Änderung seines Bewegungszustandes sowie die Anziehung zu anderen Körpern bezeichnet Masse eines homogenen Körpers: Masse eines inhomogenen Körpers: m = ρV Z m = ρ(r) dV V ρ → Massendichte Prof. Dr. U. Zwiers BTM2 4/24 Kinetik des Massenpunktes Grundgesetze der Dynamik 3/14 Grundlegende Begriffe (Forts.) Impuls Physikalische Größe, die als Maß für den Bewegungszustand eines Körpers dient: p = mv Superpositionsprinzip der Kräfte Wirken auf einen Punkt (oder einen starren Körper) mehrere Kräfte F 1 , F 2 , . . . , F n , so addieren sich diese vektoriell zu einer resultierenden Kraft F auf: n X Fi F = i=1 Prof. Dr. U. Zwiers BTM2 5/24 Kinetik des Massenpunktes Grundgesetze der Dynamik 4/14 Newtonsche Axiome 1. Axiom: Trägheitsprinzip Jeder Körper beharrt in seinem Zustand der Ruhe oder der gleichförmigen Bewegung, wenn er nicht durch einwirkende Kräfte gezwungen wird, seinen Zustand zu ändern. F = n X Fi = 0 v = const ⇒ i=1 Inertialsystem Bezugssystem, in dem das Trägheitsprinzip gilt Beschleunigte Bezugssysteme sind keine Inertialsysteme! Prof. Dr. U. Zwiers BTM2 6/24 Kinetik des Massenpunktes Grundgesetze der Dynamik 5/14 Newtonsche Axiome (Forts.) 2. Axiom: Aktionsprinzip Die Änderung der Bewegung ist der Einwirkung der bewegenden Kraft proportional und geschieht nach der Richtung derjenigen geraden Linie, nach welcher jene Kraft wirkt. dp dt d(mv) dt dm dv v+m dt dt = F = F = F Bewegungsgleichung eines Teilchens konstanter Masse: m a = F Prof. Dr. U. Zwiers BTM2 7/24 Kinetik des Massenpunktes Grundgesetze der Dynamik 6/14 Newtonsche Axiome (Forts.) 3. Axiom: Reaktionsprinzip Die Wirkung ist stets der Gegenwirkung gleich, oder die Wirkungen zweier Körper aufeinander sind stets gleich und von entgegengesetzter Richtung. F 1→2 = −F 2→1 Schnittprinzip Das Gleichgewicht eines mechanischen Systems bleibt bei einem gedachten Schnitt durch das System erhalten, wenn an der Schnittstelle als Ersatz für die entfernten Teile die auftretenden Schnittkräfte berücksichtigt werden. Prof. Dr. U. Zwiers BTM2 8/24 Kinetik des Massenpunktes Grundgesetze der Dynamik 7/14 Klassifizierung von Kräften Trägheitskräfte Kräfte in beschleunigten Bezugssystemen, die der Beschleunigungsrichtung entgegen wirken. F T = −m a Prinzip von d’Alembert Im beschleunigten Bezugssystem befindet sich die Summe der auf einen Körper wirkenden eingeprägten Kräfte jederzeit im Gleichgewicht mit der Summe aller Trägheitskräfte. F + FT = 0 Prof. Dr. U. Zwiers BTM2 9/24 Kinetik des Massenpunktes Grundgesetze der Dynamik 8/14 Klassifizierung von Kräften (Forts.) Zwangskräfte Normal zur Bahn eines Massenpunktes wirkende Kräfte, die eine geführte Bewegung erzwingen Lagerkräfte Kontaktkräfte Fx FN Prof. Dr. U. Zwiers Fy BTM2 10/24 Kinetik des Massenpunktes Grundgesetze der Dynamik 9/14 Klassifizierung von Kräften (Forts.) Eingeprägte Kräfte Von außen auf einen Körper einwirkende Kräfte, die ihre Ursache in physikalischen Gesetzen haben bzw. deren Verlauf vorgegeben ist Beispiele: Gewichtskraft, Federkraft, Reibungskraft, Windkraft Widerstandskräfte Tangential zur Bahn eines Massenpunktes wirkende Kräfte, die eine Bewegung verhindern bzw. erschweren und der Bewegungsrichtung entgegengesetzt wirken Beispiele: Federkraft, Reibungskraft, Dämpferkraft Prof. Dr. U. Zwiers BTM2 11/24 Kinetik des Massenpunktes Grundgesetze der Dynamik 10/14 Wichtige Kraftgesetze der Mechanik m1 m2 , R2 Γ = 6.673 · 10−11 m3 kg s2 Gravitationskraft FΓ = Γ Gewichtskraft FG = m g , g = 9.81 Federkraft FF = k(ℓ − ℓ0 ) , k Federkonstante ℓ0 ungespannte Federlänge ℓ0 m s2 ∆ℓ ℓ FF Prof. Dr. U. Zwiers BTM2 12/24 Kinetik des Massenpunktes Grundgesetze der Dynamik 11/14 Wichtige Kraftgesetze der Mechanik (Forts.) Dämpferkraft d Dämpferkonstante ẋ Geschwindigkeit FD = d ẋ , ẋ FD Haftreibung FR ≤ µ0 FN , µ0 Haftreibungskoeffizient FN Normalkraft Gleitreibung FR = µ FN , µ Gleitreibungskoeffizient FN Normalkraft Prof. Dr. U. Zwiers BTM2 13/24 Kinetik des Massenpunktes Grundgesetze der Dynamik 12/14 Wichtige Kraftgesetze der Mechanik (Forts.) Reibungskegel ̺0 µ0 = tan ̺0 µ = tan ̺ ̺ v Wirkungslinie der Kontaktkraft innerhalb des Reibungskegels Prof. Dr. U. Zwiers Kontaktkraft Wirkungslinie der Kontaktkraft auf dem Mantel des Reibungskegels BTM2 Kontaktkraft 14/24 Kinetik des Massenpunktes Grundgesetze der Dynamik 13/14 Wichtige Kraftgesetze der Mechanik (Forts.) Rollreibung FR = µR FN , µR Rollreibungskoeffizient FN Normalkraft Stokes-Reibung FR = 6π r η v , r Partikelradius η Viskosität des Fluids v Partikelgeschwindigkeit Newton-Reibung FR = Prof. Dr. U. Zwiers 1 cW ρ A v 2 , 2 cW Widerstandskoeffizient ρ Dichte des Fluids A Körperquerschnitt v Körpergeschwindigkeit BTM2 15/24 Kinetik des Massenpunktes Grundgesetze der Dynamik 14/14 Wichtige Kraftgesetze der Mechanik (Forts.) Seilreibung µ0 S1 α S2 Haftung ist gewährleistet, wenn die Seilkraft S2 innerhalb der folgenden Grenzen liegt: S1 e−µ0 α ≤ S2 ≤ S1 eµ0 α Prof. Dr. U. Zwiers BTM2 16/24 Kinetik des Massenpunktes Arbeit, Energie und Leistung 1/8 Mechanische Arbeit Arbeit Energie, die durch eine Kraft längs eines Weges auf einen Körper übertragen wird: Zr2 W = F T dr r1 Sonderfall: konstante Kraft entlang einer geraden Strecke W = F T ∆r Reaktionskräfte verrichten keine Arbeit! Prof. Dr. U. Zwiers BTM2 17/24 Kinetik des Massenpunktes Arbeit, Energie und Leistung 2/8 Mechanische Arbeit (Forts.) Verschiebungsarbeit Arbeit, die von einer Kraft F ′ = −F gegen eine Kraft F ohne Beschleunigung des Körpers verrichtet wird Reibungsarbeit W ′ = FR ∆s , FR Reibungskraft ∆s zurückgelegte Strecke Hubarbeit W ′ = mg h , mg Gewichtskraft h Verformungsarbeit W ′ = Prof. Dr. U. Zwiers Höhenunterschied k (ℓ − ℓ0 )2 , k Federkonstante 2 ℓ0 ungespannte Federlänge BTM2 18/24 Kinetik des Massenpunktes Arbeit, Energie und Leistung 3/8 Mechanische Arbeit (Forts.) Konservative Kraft Kraft, die eine vom Weg unabhängige Arbeit verrichtet, so dass aufgewandte Arbeit durch die Umkehrung des Weges vollständig wiedergewonnen werden kann Beispiele: Federkraft, Gewichtskraft Dissipative Kraft Kraft, die eine vom Weg abhängige Arbeit verrichtet, so dass aufgewandte Arbeit durch die Umkehrung des Weges nicht wiedergewonnen werden kann Beispiele: Reibungskraft, Dämpferkraft Prof. Dr. U. Zwiers BTM2 19/24 Kinetik des Massenpunktes Arbeit, Energie und Leistung 4/8 Mechanische Arbeit (Forts.) Beschleunigungsarbeit Arbeit, die eine Kraft F verrichtet, wenn sie einen Körper der Masse m von v0 auf v1 beschleunigt: m 2 W = v1 − v02 2 Energie Fähigkeit eines Körpers, Arbeit zu verrichten Arbeit → Vorgang (Heben, Verformen, Beschleunigen) Energie → Zustand gespeicherter Arbeit Prof. Dr. U. Zwiers BTM2 20/24 Kinetik des Massenpunktes Arbeit, Energie und Leistung 5/8 Energieformen der Mechanik Kinetische Energie Energie, die ein Körper aufgrund seiner Bewegung besitzt (Bewegungsenergie): 1 T = mv 2 2 Potentielle Energie Energie, die ein Körper aufgrund seiner Lage in einem konservativen Z Kraftfeld besitzt: U = − F T dr + const Lageenergie eines um h angehobenen Körpers U = mg h Verformungsenergie einer um ∆ℓ gespannten Feder 1 U = k ∆ℓ2 2 Prof. Dr. U. Zwiers BTM2 21/24 Kinetik des Massenpunktes Arbeit, Energie und Leistung 6/8 Mechanische Leistung Leistung Zeitliche Änderung der Arbeit: P = Leistung einer Kraft F : dW dt P = F Tv Wirkungsgrad Verhältnis von abgegebener Leistung (Nutzleistung) zu zugeführter Leistung: Pab η= Pzu Idealer Prozess: ηideal = 1 Realer Prozess: ηreal < 1 Prof. Dr. U. Zwiers BTM2 22/24 Kinetik des Massenpunktes Arbeit, Energie und Leistung 7/8 Erhaltungssätze Arbeitssatz Die Arbeit, die Kräfte zwischen zwei Bahnpunkten verrichten, entspricht der Änderung der kinetischen Energie: W01 = T1 − T0 Gültigkeit: beliebige Systeme Energiesatz Die Summe aus kinetischer und potentieller Energie ist konstant, d. h. die Gesamtenergie eines Körpers ist an zwei beliebigen Bahnpunkten stets dieselbe: U0 + T0 = U1 + T1 = const Gültigkeit: abgeschlossene (konservative) Systeme Prof. Dr. U. Zwiers BTM2 23/24 Kinetik des Massenpunktes Arbeit, Energie und Leistung 8/8 Erhaltungssätze (Forts.) Verallgemeinerter Energiesatz Die Differenz der mechanischen Energie eines Körpers an zwei verschiedenen Bahnpunkten entspricht der Arbeit der nichtkonservativen (dissipativen) Kräfte: U0 + T0 + Wd01 = U1 + T1 Gültigkeit: beliebige Systeme Leistungssatz Die Leistung einer einwirkenden Kraft entspricht der zeitlichen Änderung der kinetischen Energie: dT P = dt Gültigkeit: beliebige Systeme Prof. Dr. U. Zwiers BTM2 24/24