0 - Ruhr-Universität Bochum

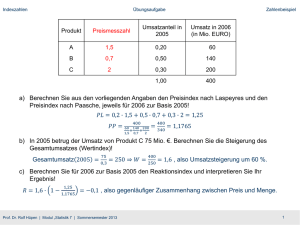
WISTA
WIRTSCHAFTSSTATISTIK
PROF. DR. ROLF HÜPEN
FAKULTÄT FÜR
WIRTSCHAFTSWISSENSCHAFT
Seminar für Theoretische Wirtschaftslehre
Vorlesungsprogramm 02.07.2013
Theorie der Indexzahlen
1.
2.
3.
4.
5.
Konstruktion von Indizes
Laspeyres- und Paasche-Preisindex
Mengenindex, Wertindex, Reaktionsindex
Umbasierung und Verkettung von Indexreihen
Aggregation und Zerlegung
Literatur:
Degen, Horst / Lorscheid, Peter: Statistik-Lehrbuch, 2. Aufl., München-Wien 2002, S. 108113.
Mosler, Karl und Schmid, Friedrich: Beschreibende Statistik und Wirtschaftsstatistik, 4. Aufl.,
Berlin-Heidelberg-New York 2009, S. 127-141.
von der Lippe, Peter: Deskriptive Statistik, Stuttgart 1993, Online-Ausgabe, S. S. 355-392.
Übungsaufgaben:
WS00/01–A3, WS01/02–A1d), WS05/06–A3, SS08–A3, SS09–A5, SS11–A5.
Prof. Dr. Rolf Hüpen | Modul „Statistik I“ | Sommersemester 2013
Indexzahlen
Einführung
Indexzahlen (Indizes)
= gewogene Mittelwerte von Messzahlen
● Ziel: Quantifizierung der durchschnittlichen (zeitlichen) Veränderung einer Vielzahl
gleichartiger Tatbestände mit einer einzigen Zahl.
● Beispiele: Preisindex, Mengenindex, Wertindex, Aktienindex, Produktionsindex
Notation:
𝑡 = Berichtsjahr
0 = Basisjahr
𝑖 = 1, … , 𝑛 = Güter
𝑝𝑖 𝑡 = Preis des Gutes 𝑖 im Zeitpunkt 𝑡
𝑞𝑖 𝑡 = umgesetzte Menge des Gutes 𝑖 im Zeitpunkt 𝑡
𝑞𝑖 𝑡
= 𝑞1 𝑡 , … , 𝑞𝑛 𝑡
𝑝𝑖 𝑡
= Preismesszahl
𝑝𝑖 0
= Warenkorb im Zeitpunkt 𝑡
𝑞𝑖 𝑡
= Mengenmesszahl
𝑞𝑖 0
Prof. Dr. Rolf Hüpen | Modul „Statistik I“ | Sommersemester 2013
𝑝𝑖 𝑡 ∙𝑞𝑖 𝑡
= Wertmesszahl
𝑝𝑖 0 ∙𝑞𝑖 0
2
Indexzahlen
Einführung
Zahlenbeispiel:
Jahr
t
2005
2006
2007
0
1
2
Gut 1
Preis Menge
q1
p1
10
10
15
5
20
10
Gut 2
Preis Menge
p2
q2
5
20
4
24
3
30
Gut 3
Preis Menge
p3
q3
3
9
5
3
5
2
Gut 1
Gut 2
Gut 3
Jahr
2005
2006
2007
Preismesszahl, Basis 2005, pi(t)/pi(0)
1
1
1
1,5
0,8
1,66666667
2
0,6
1,66666667
2005
2006
2007
Mengenmesszahl, Basis 2005, qi(t)/qi(0)
1
1
1
0,5
1,2
0,33333333
1
1,5
0,22222222
Wertmesszahl, Basis 2005, pi(t)qi(t)/[pi(0)qi(0)]
2005
1
1
1
2006
0,75
0,96
0,55555556
2007
2
0,9
0,37037037
Prof. Dr. Rolf Hüpen | Modul „Statistik I“ | Sommersemester 2013
3
Indexzahlen
Einführung
Aufgabe:
Zusammenfassung der einzelnen Messzahlen für alle 𝑛 Güter durch geeignete Mittelwerte zur Beschreibung
der Preis-, Mengen oder Wertentwicklung.
 Preisindex, Mengenindex oder Wertindex.
Konstruktion des Mittelwertes:
z. B. beim Preisindex : Gewichtung entsprechend der Bedeutung des jeweiligen Gutes erforderlich 
einfaches arithmetisches Mittel nicht aussagefähig  gewichtetes arithmetisches Mittel GAM.
𝑛
𝐺𝐴𝑀 =
𝑖=1
𝑝𝑖 𝑡
𝑝𝑖 0
𝑛
𝑖=1 𝑤𝑖
𝑤𝑖 ∙
Wahl der Gewichte:  Bedeutung der Güter  Umsatz- bzw. Mengengerüst:
𝑤𝑖 = 𝑝𝑖 ∙ 𝑞𝑖
Datierung der Gewichte: Mengengerüst aus Basis- oder Berichtsperiode?
Laspeyres: Mengengerüst des Basisjahres  Ausgaben im Basisjahr 
𝑤𝑖 = 𝑝𝑖 0 ∙ 𝑞𝑖 0
Paasche: Mengengerüst des Berichtsjahres für die im Basisjahr gewählten n Güter  fiktive Ausgaben
im Basisjahr 
𝑤𝑖 = 𝑝𝑖 0 ∙ 𝑞𝑖 𝑡
Prof. Dr. Rolf Hüpen | Modul „Statistik I“ | Sommersemester 2013
4
Indexzahlen
Preisindex von Laspeyres
Preisindex von Laspeyres
(Étienne Laspeyres 1834 – 1913)
Drei Darstellungsmöglichkeiten:
(1) Allgemeine Gewichte:
𝑤𝑖 = 𝑝𝑖 0 ∙ 𝑞𝑖 0 = Ausgaben (oder Umsatz) Gut 𝑖 im Basisjahr
𝑃𝐿 0, 𝑡 =
(2) Normierte Gewichte:
𝑔𝑖 = 𝑤𝑖
1
∙
𝑤𝑖
𝑤𝑖 ∙
𝑝𝑖 𝑡
𝑝𝑖 0
𝑤𝑖 = Ausgabenanteil Gut 𝑖 an Gesamtausgaben im Basisjahr
𝑃𝐿 0, 𝑡 =
𝑔𝑖 ∙
𝑝𝑖 𝑡
𝑝𝑖 0
(3) Aggregatform (Summenform):
𝑃𝐿 0, 𝑡 =
𝑝𝑖 𝑡 ∙ 𝑞𝑖 0
𝑝𝑖 0 ∙ 𝑞𝑖 0
Nr. (3) ist die bekannteste Darstellungsform des Preisindexes von Laspeyres: Der Warenkorb des Basisjahres
𝑞𝑖 0 wird mit Preisen des Berichtsjahres bewertet  fiktive Ausgaben für den alten Warenkorb im
Berichtsjahr / tatsächliche Ausgaben im Basisjahr.
In der Praxis multipliziert man 𝑃𝐿 0, 𝑡 mit 100 und erhält Prozentgrößen. Im Basisjahr ist dann wegen
𝑃𝐿 0,0 = 1 der Indexstand = 100.
Prof. Dr. Rolf Hüpen | Modul „Statistik I“ | Sommersemester 2013
5
Indexzahlen
Zahlenbeispiel
Preisindex von Laspeyres
Berechnung auf der Basis der Aggregatform:
Gut 1
Gut 2
Gut 3
Jahr
Preis
Menge
Preis
Menge
Preis
Menge
t
p1
q1
p2
q2
p3
q3
0
10
10
5
20
3
9
1
15
5
4
24
5
3
2
20
10
3
30
5
2
𝑃𝐿0 = 1

Indexstand = 100
𝑃𝐿1 =
15∙10+4∙20+5∙9
10∙10+5∙20+3∙9
= 1,2115

Indexstand = 121,15
𝑃𝐿2 =
20∙10+3∙20+5∙9
10∙10+5∙20+3∙9
= 1,3436

Indexstand = 134,36
Prof. Dr. Rolf Hüpen | Modul „Statistik I“ | Sommersemester 2013
6
Indexzahlen
Zahlenbeispiel
Preisindex von Laspeyres
Berechnung mit allgemeinen Gewichten:
Preismesszahlen
Jahr
Gut 1
Gut 2
Gut 3
t
p1(t)/p1(0)
p2(t)/p2(0)
p3(t)/p3(0)
0
1
1
1
1
1,5
0,8
1,66666667
2
2
0,6
1,66666667
Gut 1
100
Allgemeine Gewichte
(Ausgaben im Basisjahr)
Gut 3
Gut 2
100
27
𝑃𝐿0 = 1
𝑃𝐿1 =
100∙1,5+100∙0,8+27∙1,6
227
𝑃𝐿2 =
100∙2+100∙0,6+27∙1,6
227
= 1,2115
= 1,3436
Prof. Dr. Rolf Hüpen | Modul „Statistik I“ | Sommersemester 2013
Summe
227

Indexstand = 100

Indexstand = 121,15

Indexstand = 134,36
7
Indexzahlen
Zahlenbeispiel
Preisindex von Laspeyres
Berechnung mit normierten Gewichten:
Jahr
t
0
1
2
Preismesszahlen
Gut 1
Gut 2
p1t/p10
p2t/p20
1
1
1,5
0,8
2
0,6
Gut 3
p3t/p30
1
1,66666667
1,66666667
Normierte Gewichte
(Ausgabenanteile im Basisjahr)
Gut 1
0,44053
Gut 2
0,44053
Gut 3
0,11894
Summe
1
𝑃𝐿0 = 1

Indexstand = 100
𝑃𝐿1 = 0,44053 ∙ 1,5 + 0,44053 ∙ 0,8 + 0,11894 ∙ 1, 6 = 1,2115

Indexstand = 121,15
𝑃𝐿2 = 0,44053 ∙ 2 + 0,44053 ∙ 0,6 + 0,11894 ∙ 1, 6 = 1,3436

Indexstand = 134,36
Prof. Dr. Rolf Hüpen | Modul „Statistik I“ | Sommersemester 2013
8
Indexzahlen
Preisindex von Laspeyres
Zusammenhang zwischen den Darstellungsformen:
(3)
Aggregatform
(1)
Allgemeine Gewichte
(2)
Normierte Gewichte
Preismesszahl
𝑃𝐿 0, 𝑡 =
𝑝𝑖 𝑡 ∙ 𝑞𝑖 0
𝑝𝑖 0 ∙ 𝑞𝑖 0
=
Allgemeines Gewicht =
Ausgaben für Gut im Basisjahr
𝑝𝑖 𝑡
∙ 𝑝𝑖 0 ∙ 𝑞𝑖 0
𝑝𝑖 0
𝑝𝑖 0 ∙ 𝑞𝑖 0
=
𝑝𝑖 𝑡
𝑝𝑖 0 ∙ 𝑞𝑖 0
∙
𝑝𝑖 0
𝑝𝑖 0 ∙ 𝑞𝑖 0
Normiertes Gewicht =
Ausgabenanteil für Gut i an den
Gesamtausgaben im Basisjahr
Der Preisindex von Laspeyres lässt sich also als gewichtetes arithmetisches
Mittel der einzelnen Preismesszahlen schreiben.
Prof. Dr. Rolf Hüpen | Modul „Statistik I“ | Sommersemester 2013
9
Indexzahlen
Interpretation
t
Interpretation:
(1)
(2)
0
1
2
𝑃𝐿 0, 𝑡
1
1,2115
1,3436
𝑃𝐿 0, 𝑡
∙ 100
100
121,15
134,36
1
2
21,15 %
34,36 %
1
2
21,15 %
10,90 %
𝑃𝐿 0, 𝑡 − 1
Preisveränderungsrate
vom Basisjahr 0 zum
Berichtsjahr 𝑡
Inflationsrate im
Vorjahresvergleich
Preisindex von Laspeyres
𝑃𝐿 0, 𝑡 − 𝑃𝐿(0, 𝑡 − 1)
𝑃𝐿 0, 𝑡 − 1
𝑃𝐿 0, 𝑡
=
−1
𝑃𝐿 0, 𝑡 − 1
(3)
Jahresdurchschnittliche
Inflationsrate im
Zeitraum 𝑡2 − 𝑡1
𝑃𝐿 0, 𝑡2
𝑃𝐿 0, 𝑡1
Prof. Dr. Rolf Hüpen | Modul „Statistik I“ | Sommersemester 2013
1
𝑡2 −𝑡1
−1
𝑡1 = 0
𝑡2 = 2
⇒ 𝑡2 − 𝑡1 = 2
134,36
100
1
2
− 1 = 15,91 %
10
Indexzahlen
Interpretation
t
Interpretation:
(4) „Kaufkraft“, Binnenwert
des Geldes
1
𝑃𝐿 0, 𝑡
(5) Kaufkraftänderungsrate
im Vergleich zum
Basisjahr
𝑃𝐿 0,0 − 𝑃𝐿 0, 𝑡
𝑃𝐿 0, 𝑡
(6) Kaufkraftänderungsrate
im Vorjahresvergleich
𝑃𝐿 0, 𝑡 − 1 − 𝑃𝐿 0, 𝑡
𝑃𝐿 0, 𝑡
=
=
(7) Jahresdurchschnittliche
Kaufkraftänderungsrate
im Zeitraum 𝑡2 − 𝑡1
Preisindex von Laspeyres
0
1
2
𝑃𝐿 0, 𝑡
1
1,2115
1,3436
𝑃𝐿 0, 𝑡
∙ 100
100
121,15
134,36
1
0,8254
0,7443
- 17,46 %
- 25,57 %
- 17,46 %
- 9,83 %
𝑃𝐿 0,0
−1
𝑃𝐿 0, 𝑡
𝑃𝐿 0, 𝑡 − 1
−1
𝑃𝐿 0, 𝑡
𝑃𝐿 0, 𝑡1
𝑃𝐿 0, 𝑡2
Prof. Dr. Rolf Hüpen | Modul „Statistik I“ | Sommersemester 2013
1
𝑡2 −𝑡1
−1
𝑡1 = 0
𝑡2 = 2
⇒ 𝑡2 − 𝑡1 = 2
100
134,36
1
2
− 1 = − 13,73 %
11
Indexzahlen
Preisindex von Laspeyres
Vorteile des Preisindexes von Laspeyres:
● Nur die Preise 𝑝𝑖 𝑡 müssen neu erhoben werden, das Gewichtungsschema bzw. der
Warenkorb 𝑞𝑖 0 bleiben konstant.  Einfache und kostengünstige Berechnung.
● Bei gleichem Basisjahr 0 sind 𝑃𝐿 0, 𝑡 und 𝑃𝐿 0, 𝑡′ direkt vergleichbar.
Nachteile des Preisindexes von Laspeyres:
● Mit zunehmender Entfernung vom Basisjahr veraltet der Warenkorb. Neue
Verbrauchsgewohnheiten und neue Produkte werden nicht berücksichtigt.
● Relativ teurer gewordene Güter werden durch relativ billiger gewordene (teilweise) ersetzt:
Substitutionseffekt, Laspeyres-Effekt, „rationales Verbraucherverhalten“.
● Somit ist der Warenkorb nach einigen Jahren nicht mehr repräsentativ für das
Verbraucherverhalten.
Konsequenz:
● Warenkorb in regelmäßigen Abständen aktualisieren oder
● Preisniveau am Mengengerüst des Warenkorbes in der Berichtsperiode messen
 Preisindex von Paasche.
Prof. Dr. Rolf Hüpen | Modul „Statistik I“ | Sommersemester 2013
12
Indexzahlen
Preisindex von Paasche
Preisindex von Paasche
(Hermann Paasche 1851 – 1925)
Fünf Darstellungsmöglichkeiten:
(1) Allgemeine Gewichte 𝑤𝑖 𝑡 = 𝑝𝑖 𝑡 ∙ 𝑞𝑖 𝑡 = tatsächliche Ausgaben für Gut 𝑖 im Berichtsjahr
𝑃𝑃 0, 𝑡 =
𝑤𝑖 𝑡
𝑝 0
𝑤𝑖 𝑡 ∙ 𝑖
𝑝𝑖 𝑡
 Gewichtetes harmonisches Mittel der Preismesszahlen mit allgemeinen Gewichten 𝑤𝑖 𝑡 .
(2) Normierte Gewichte 𝑔𝑖 𝑡 = 𝑤𝑖 𝑡
𝑤𝑖 𝑡 = Ausgabenanteil für Gut 𝑖 im Berichtsjahr
1
𝑃𝑃 0, 𝑡 =
𝑝 0
𝑔𝑖 𝑡 ∙ 𝑖
𝑝𝑖 𝑡
 Gewichtetes harmonisches Mittel mit normierten Gewichten 𝑔𝑖 𝑡 .
(3) Aggregatform (Summenform)
𝑃𝑃 0, 𝑡 =
𝑝𝑖 𝑡 ∙ 𝑞𝑖 𝑡
𝑝𝑖 0 ∙ 𝑞𝑖 𝑡
Bekannteste Darstellungsform des Preisindexes von Paasche: Tatsächliche Ausgaben für den Warenkorb im
Berichtsjahr / fiktive Ausgaben im Basisjahr, für das das Mengengerüst des Berichtsjahres unterstellt wird.
Prof. Dr. Rolf Hüpen | Modul „Statistik I“ | Sommersemester 2013
13
Indexzahlen
Preisindex von Paasche
Preisindex von Paasche
(Hermann Paasche 1851 – 1925)
Fünf Darstellungsmöglichkeiten (Fortsetzung)
(4) Fiktive Gewichte 𝑓𝑖 𝑡 = 𝑝𝑖 0 ∙ 𝑞𝑖 𝑡 = fiktive Ausgaben für Gut 𝑖 im Basisjahr
𝑃𝑃 0, 𝑡 =
(5) Fiktive normierte Gewichte ℎ𝑖 𝑡 = 𝑓𝑖 𝑡
Gesamtausgaben im Basisjahr
1
∙
𝑓𝑖 𝑡
𝑝𝑖 𝑡
𝑝𝑖 0
𝑓𝑖 𝑡 = fiktiver Ausgabenanteil für Gut 𝑖 an den fiktiven
𝑃𝑃 0, 𝑡 =
Prof. Dr. Rolf Hüpen | Modul „Statistik I“ | Sommersemester 2013
𝑓𝑖 𝑡 ∙
ℎ𝑖 𝑡 ∙
𝑝𝑖 1
𝑝𝑖 0
14
Indexzahlen
Preisindex von Paasche
Zusammenhang zwischen den Darstellungsformen:
(3)
Aggregatform
𝑃𝑃 0, 𝑡 =
(1)
Allgemeine Gewichte
𝑝𝑖 𝑡 ∙ 𝑞𝑖 𝑡
𝑝𝑖 0 ∙ 𝑞𝑖 𝑡
=
𝑝𝑖 𝑡 ∙ 𝑞𝑖 𝑡
=
𝑝𝑖 𝑡 ∙ 𝑞𝑖 𝑡
𝑝𝑖 𝑡
𝑝𝑖 0
Allgemeines Gewicht =
Ausgaben für Gut i im Berichtsjahr
Preismesszahl
(2)
Normierte Gewichte
1
𝑝𝑖 𝑡 𝑞𝑖 𝑡
𝑝𝑖 𝑡 𝑞𝑖 𝑡
𝑝𝑖 𝑡
𝑝𝑖 0
Normiertes Gewicht =
Ausgabenanteil für Gut i an den
Gesamtausgaben im Berichtsjahr
Der Preisindex von Paasche ist mithin das gewichtete harmonische Mittel
der einzelnen Preismesszahlen.
Prof. Dr. Rolf Hüpen | Modul „Statistik I“ | Sommersemester 2013
15
Indexzahlen
Zahlenbeispiel
Preisindex von Paasche
Berechnung auf der Basis der Aggregatform:
Jahr
Gut 1
15∙5+4∙24+5∙3
10∙5+5∙24+3∙3
𝑃𝑃2 =
20∙10+3∙30+5∙2
10∙10+5∙30+3∙2
Gut 3
Preis
Menge
Preis
Menge
Preis
Menge
t
p1
q1
p2
q2
p3
q3
0
10
10
5
20
3
9
1
15
5
4
24
5
3
2
20
10
3
30
5
2
𝑃𝑃0 = 1
𝑃𝑃1 =
Gut 2
= 1,0391
= 1,1719
Prof. Dr. Rolf Hüpen | Modul „Statistik I“ | Sommersemester 2013

Indexstand = 100

Indexstand = 103,91

Indexstand = 117,19
16
Indexzahlen
Zahlenbeispiel
Preisindex von Paasche
Berechnung mit allgemeinen Gewichten:
Preismesszahlen
Jahr
Gut 1
Gut 2
Gut 3
t
p1(t)/p1(0)
p2(t)/p2(0)
p3(t)/p3(0)
0
1
1
1
1
1,5
0,8
1,66666667
2
2
0,6
1,66666667
Allgemeine Gewichte (Ausgaben im Berichtsjahr)
t
Gut 1
Gut 2
Gut 3
Summe
1
75
96
15
186
2
200
90
10
300

Indexstand = 100
= 1,0391

Indexstand = 103,91
= 1,1719

Indexstand = 117,19
𝑃𝑃0 = 1
𝑃𝑃1 =
186
75 96 15
+ +
1,5 0,8 1,6
𝑃𝑃2 = 200
2
300
+
90 10
+
0,6 1,6
Prof. Dr. Rolf Hüpen | Modul „Statistik I“ | Sommersemester 2013
17
Indexzahlen
Zahlenbeispiel
Preisindex von Paasche
Berechnung mit normierten Gewichten:
Preismesszahlen
Jahr
Gut 1
Gut 2
Gut 3
t
p1(t)/p1(0)
p2(t)/p2(0)
p3(t)/p3(0)
0
1
1
1
1
1,5
0,8
1,66666667
2
2
0,6
1,66666667
Normierte Gewichte (Ausgabenanteile im Berichtsjahr)
t
Gut 1
Gut 2
Gut 3
Summe
1
0,4032
0,5161
0,0806
1
2
0,6667
0,3
0,3333
1
𝑃𝑃0 = 1
𝑃𝑃1 = 0,4032
1
0,5161 0,0806
+
+
1,5
0,8
1,6
𝑃𝑃2 = 0,6
2
1
+
0,3 0,3
+
0,6 1,6
= 1,0391
= 1,1719
Prof. Dr. Rolf Hüpen | Modul „Statistik I“ | Sommersemester 2013

Indexstand = 100

Indexstand = 103,91

Indexstand = 117,19
18
Indexzahlen
Preisindex von Paasche
Vorteil des Preisindexes von Paasche:
● Reagiert auf aktuelle Änderungen im Mengengerüst des Warenkorbes
Nachteile des Preisindexes von Paasche:
● Im Berichtsjahr sind sowohl die Preise als auch die Mengen zu erheben.
 aufwändige Berechnung.
● 𝑃𝐿 0, 𝑡 und 𝑃𝐿 0, 𝑡′ sind wegen der wechselnden Gewichte kaum vergleichbar.
Verwendung:
● zur Preisbereinigung (Deflationierung gesamtwirtschaftlicher Aggregate).
● als Kontrollindex für den Laspeyres-Index.
Prof. Dr. Rolf Hüpen | Modul „Statistik I“ | Sommersemester 2013
19
Indexzahlen
Preisbereinigung
Preisbereinigung:
Division einer gesamtwirtschaftlichen Wertgröße durch einen Paasche-Preisindex. Ergebnis:
Wertgröße in konstanten Preisen des Basisjahres (= reale Größe).
Beispiel Bruttoinlandsprodukt (BIP)
𝑛
𝐵𝐼𝑃𝑡 𝑛𝑜𝑚𝑖𝑛𝑎𝑙 =
𝑝𝑖 𝑡 ∙ 𝑞𝑖 𝑡
𝑖=1
𝑃𝑃𝑡 =
𝐵𝐼𝑃𝑡 𝑟𝑒𝑎𝑙
𝑝𝑖 𝑡 ∙ 𝑞𝑖 𝑡
𝑝𝑖 0 ∙ 𝑞𝑖 𝑡
𝐵𝐼𝑃𝑡 𝑛𝑜𝑚𝑖𝑛𝑎𝑙
=
=
𝑃𝑃𝑡
𝑛
𝑝𝑖 0 ∙ 𝑞𝑖 𝑡
𝑖=1
Ergebnis: Bruttoinlandsprodukt in Preisen des Basisjahres („Festpreisbasis“)
Neuerdings gebräuchlich: „Vorjahrespreisbasis“. Dabei wird immer das jeweilige Vorjahr als
Basisjahr für PP gewählt, d. h. die Basis wechselt ständig.
Prof. Dr. Rolf Hüpen | Modul „Statistik I“ | Sommersemester 2013
20
Indexzahlen
Preisbereinigung
Zwischen nominalem und realem Bruttoinlandsprodukt besteht also folgender Zusammenhang:
𝐵𝐼𝑃𝑡 𝑛𝑜𝑚𝑖𝑛𝑎𝑙 = 𝑃𝑃𝑡 ∙ 𝐵𝐼𝑃𝑡 𝑟𝑒𝑎𝑙
Leitet man diese Gleichung logarithmisch ab, erhält man:
dln 𝐵𝐼𝑃𝑡 𝑛𝑜𝑚𝑖𝑛𝑎𝑙 = dln(𝑃𝑃𝑡 ) + dln 𝐵𝐼𝑃𝑡 𝑟𝑒𝑎𝑙
Für die Wachstumsraten gilt deshalb (näherungsweise):
𝑊𝑅 𝐵𝐼𝑃𝑡 𝑛𝑜𝑚𝑖𝑛𝑎𝑙 = 𝑊𝑅 𝑃𝑃𝑡 + 𝑊𝑅 𝐵𝐼𝑃𝑡 𝑟𝑒𝑎𝑙
Also
Nominale Wachstumsrate = Reale Wachstumsrate + Inflationsrate
Prof. Dr. Rolf Hüpen | Modul „Statistik I“ | Sommersemester 2013
21
Indexzahlen
Weitere Indizes
Weitere Indizes:
Ausgehend von 3 Formen (Preis, Menge, Wert) und 2 Typen (Laspeyres, Paasche) können die folgenden
Indizes berechnet werden:
●
𝑃𝐿 0, 𝑡 :
Preisindex nach Laspeyres
●
𝑃𝑃 0, 𝑡 :
Preisindex nach Paasche
●
𝑀𝐿 0, 𝑡 :
Mengenindex nach Laspeyres
●
𝑀𝑃 0, 𝑡 :
Mengenindex nach Paasche
●
𝑊 0, 𝑡 = 𝑊𝐿 0, 𝑡 = 𝑊𝑃 0, 𝑡 :
Wertindex
Berechnung der Mengen- und Wertindizes, z. B. in der Aggregatform:
𝑀𝐿 0, 𝑡 :
𝑝𝑖 0 ∙ 𝑞𝑖 𝑡
𝑝𝑖 0 ∙ 𝑞𝑖 0
Es gilt:
𝑊 0, 𝑡 = 𝑃𝐿 0, 𝑡 ∙ 𝑀𝑃 0, 𝑡 = 𝑀𝐿 0, 𝑡 ∙ 𝑃𝑃 0, 𝑡
𝑀𝑃 0, 𝑡 :
𝑝𝑖 𝑡 ∙ 𝑞𝑖 𝑡
𝑝𝑖 𝑡 ∙ 𝑞𝑖 0
𝑊 0, 𝑡 :
𝑝𝑖 𝑡 ∙ 𝑞𝑖 𝑡
𝑝𝑖 0 ∙ 𝑞𝑖 0
Verwendung des Wertindexes: z. B. als Index für die Lebenshaltungskosten (Ein Preisindex ist dafür nicht
geeignet!)
Prof. Dr. Rolf Hüpen | Modul „Statistik I“ | Sommersemester 2013
22
Indexzahlen
Vergleich Laspeyres - Paasche, Reaktionsindex
Vergleich Laspeyres – Paasche
Fall (1): Preise und Mengen verändern sich überwiegend gegenläufig.
 Nachfrager substituieren relativ teurer gewordene durch relativ billiger gewordene
Güter  „rationales Verbraucherverhalten“ hat sich durchgesetzt  überwiegend
„Käufermärkte“. Dieser Befund muss sich dann niederschlagen in den beiden
äquivalenten Ungleichungen:
𝑃𝐿 0, 𝑡 > 𝑃𝑃 0, 𝑡 ⇔ 𝑀𝐿 0, 𝑡 > 𝑀𝑃 0, 𝑡
Fall (2): Preise und Mengen verändern sich überwiegend gleichläufig.
 Anbieter erhöhen bei gestiegener Nachfrage die Preise  „rationales
Anbieterverhalten“ (Gewinnmaximierung) hat sich durchgesetzt  überwiegend
„Verkäufermärkte“. Dieser Befund muss sich dann niederschlagen in den beiden
äquivalenten Ungleichungen:
𝑃𝐿 0, 𝑡 < 𝑃𝑃 0, 𝑡 ⇔ 𝑀𝐿 0, 𝑡 < MP 0, 𝑡
Prof. Dr. Rolf Hüpen | Modul „Statistik I“ | Sommersemester 2013
23
Indexzahlen
Vergleich Laspeyres - Paasche, Reaktionsindex
Dies lässt sich quantifizieren durch den Reaktionsindex 𝑅 0, 𝑡 :
𝑅 0, 𝑡 = W 0, 𝑡 ∙ 1 −
𝑃𝐿 0, 𝑡
𝑃𝑃 0, 𝑡
= W 0, 𝑡 ∙ 1 −
𝑀𝐿 0, 𝑡
𝑀𝑃 0, 𝑡
Somit gilt:
●
𝑅 0, 𝑡 < 0

rationales Verbraucherverhalten, Käufermärkte
●
𝑅 0, 𝑡 > 0

rationales Anbieterverhalten, Verkäufermärkte
Am Vorzeichen des Reaktionsindexes lässt sich also die Richtung des Zusammenhangs
zwischen Preis- und Mengenänderung ablesen.
Ferner gilt:
𝑊 0, 𝑡 = 𝑀𝐿 0, 𝑡 ∙ 𝑃𝐿 0, 𝑡 + 𝑅 0, 𝑡
Prof. Dr. Rolf Hüpen | Modul „Statistik I“ | Sommersemester 2013
24
Vergleich Laspeyres – Paasche Preisindex, Reaktionsindex
Indexzahlen
Fall (1)
Fall (2)
p
p
A1
A0
A0
G1
p1
p0
G1
p1
p0
G0
G0
N1
N0
N0
0
q1
q0
q
0
• Preis und Menge verändern sich gegenläufig.
• Bewegung entlang der Nachfragekurve.
• „rationales Verbraucherverhalten“, Käufermarkt
𝑃𝐿 > 𝑃𝑃
𝑃𝐿
𝑅 = 𝑊 ∙ 1 − 𝑃𝑃
<0
Prof. Dr. Rolf Hüpen | Modul „Statistik I“ | Sommersemester 2013
q
(𝑁1 > 𝑁0 , z. B. wegen höheren Einkommens)
(𝐴1 < 𝐴0 , z. B. wegen höherer Kosten)
𝑝1 > 𝑝0 und 𝑞1 < 𝑞0
q1
Rechtsverschiebung der Nachfragekurve
Linksverschiebung der Angebotskurve
→
q0
→
𝑝1 > 𝑝0 und 𝑞1 > 𝑞0
• Preis und Menge verändern sich gleichläufig.
• Bewegung entlang der Angebotskurve.
• „rationales Anbieterverhalten“, Verkäufermarkt
𝑃𝐿 < 𝑃𝑃
𝑃𝐿
𝑅 = 𝑊 ∙ 1 − 𝑃𝑃
>0
25
Indexzahlen
Zahlenbeispiel
Zahlenbeispiel
Ursprungswerte:
Gut 1
Gut 2
Gut 3
Jahr
t
Preis
p1
Menge
q1
Preis
p2
Menge
q2
Preis
p3
Menge
q3
2005
0
10
10
5
20
3
9
2006
1
15
5
4
24
5
3
2007
2
20
10
3
30
5
2
Indexzahlen:
Jahr
t
PL
PP
W
R
ML
MP
2005
0
100
100
100
0
100
100
2006
1
121,15
103,91
81,94
-13,59
78,85
67,64
2007
2
134,36
117,19
132,16
-19,37
112,78
98,36
Prof. Dr. Rolf Hüpen | Modul „Statistik I“ | Sommersemester 2013
26
Indexzahlen
Übungsaufgabe
Zahlenbeispiel
Übungsaufgabe:
Einem Unternehmen, das drei Produkte, A, B und C, verkauft, liegen hinsichtlich der Entwicklung
der Verkaufspreise und für die Umsätze in den Jahren 2005 und 2006 folgende Angaben vor:
Produkt
Wachstumsrate des
Verkaufspreises in %
Umsatzanteil in
2005
Umsatz in 2006
(in Mio. EURO)
A
50 %
0,20
60
B
- 30 %
0,50
140
C
100 %
0,30
200
a) Berechnen Sie aus den vorliegenden Angaben den Preisindex nach Laspeyres und den
Preisindex nach Paasche, jeweils für 2006 zur Basis 2005!
b) In 2005 betrug der Umsatz von Produkt C 75 Mio. €. Berechnen Sie die Steigerung des
Gesamtumsatzes (Wertindex)!
c) Berechnen Sie für 2006 zur Basis 2005 den Reaktionsindex und interpretieren Sie Ihr
Ergebnis!
Prof. Dr. Rolf Hüpen | Modul „Statistik I“ | Sommersemester 2013
27
Indexzahlen
Umbasierung und Verkettung
Umbasierung und Verkettung von Indexzahlen
Umbasierung
Umstellung eines Indexes I von einer alten Indexbasis (0) auf eine neue Indexbasis (1) nach der
Formel:
𝐼 1, 𝑡 =
𝐼 0, 𝑡
𝐼 0,1
● Formel entspricht der einer Umbasierung von einfachen Messzahlen.
● Werden die Indizes in Prozent ausgedrückt, ist die rechte Seite mit 100 zu multiplizieren.
● Da 𝐼 0,1 eine Konstante ist, ist die neue Indexreihe 𝐼 1, 𝑡 ein konstantes Vielfaches der alten
Indexreihe 𝐼 0, 𝑡 .
● Ist die Umbasierung mit einer Revision der Reihenauswahl (Preisvektor) oder des
Wägungsschemas (Gewichtung) verbunden, spricht man (ab Periode 1) von einer
Neuberechnung.
Prof. Dr. Rolf Hüpen | Modul „Statistik I“ | Sommersemester 2013
28
Indexzahlen
Umbasierung und Verkettung
Umbasierung (Fortsetzung)
● In der Regel handelt es sich um Näherungslösungen, weil die gebräuchlichen Indexzahlen
nicht verkettbar sind. Beispiel: Neuberechnung eines Preisindexes von Laspeyres zur Basis
1 ergibt:
𝑝𝑖 𝑡 ∙ 𝑞𝑖 1
𝑃𝐿 1, 𝑡 =
𝑝𝑖 1 ∙ 𝑞𝑖 1
● Dagegen liefert die Anwendung der Umbasierungsformel:
𝑃𝐿 1, 𝑡 =
𝑝𝑖 𝑡 ∙ 𝑞𝑖 0
𝑝𝑖 0 ∙ 𝑞𝑖 0
𝑝𝑖 1 ∙ 𝑞𝑖 0
𝑝𝑖 0 ∙ 𝑞𝑖 0
=
𝑝𝑖 𝑡 ∙ 𝑞𝑖 0
𝑝𝑖 1 ∙ 𝑞𝑖 0
● Die beiden Ergebnisse werden sich nur dann wenig unterscheiden, wenn die Struktur der
Warenkörbe in den Zeitpunkten 0 und 1 ähnlich ist.
Prof. Dr. Rolf Hüpen | Modul „Statistik I“ | Sommersemester 2013
29
Indexzahlen
Umbasierung und Verkettung
Verkettung
Bildung einer langen Reihe zur Basis 0 aus zwei einzelnen Reihen zur Basis 0 und zur Basis 1
nach der Formel:
𝐼 0, 𝑡 = 𝐼 0,1 ∙ 𝐼 1, 𝑡
Die Formel entspricht einer äquivalenten Umformung der Formel zur Umbasierung. Daher gelten
alle oben angeführten Bemerkungen auch zur Verkettung.
Prof. Dr. Rolf Hüpen | Modul „Statistik I“ | Sommersemester 2013
30
Indexzahlen
Umbasierung und Verkettung
Beispiel aus von der Lippe, Deskriptive Statistik, S. 389, Beispiel 10.11:
Jahr
𝟏𝟐𝟎
= 𝟏, 𝟐
𝟏𝟎𝟎
𝟏𝟏𝟖
= 𝟏, 𝟏𝟖
𝟏𝟎𝟎
Erhobene Werte
Index A
Index B
Lange Reihen
Index C
Index A
Index B
Index C
100
83,33
70,62
1980
100
1985
120
100
120
100
84,75
1986
125
105
126
105
88,98
1987
109
130,8
109
92,37
1988
112
134,4
112
94,92
1989
116
98
139,2
116
98,31
1990
118
100
141,6
118
100
1991
103
145,85
121,54
103
1992
105
148,68
123,9
105
Prof. Dr. Rolf Hüpen | Modul „Statistik I“ | Sommersemester 2013
31
Indexzahlen
Umbasierung und Verkettung
Übungsaufgabe
Übungsaufgabe:
Mit Beginn des Jahres 2008 hat das Statistische Bundesamt den
Verbraucherpreisindex von der bisherigen Basis 2000 = 100 auf
die neue Basis 2005 = 100 umgestellt. Die nebenstehende
Tabelle zeigt ausgewählte Indexstände des alten und des neuen
Indexes.
Bei den Antworten zu den folgenden Fragen sind Inflationsraten
und Kaufkraftänderungsraten in Prozent anzugeben und die
Endergebnisse auf zwei Nachkommastellen zu runden.
a)
Wie hoch war die Inflationsrate im Jahr 2001, wie hoch war
sie 2007?
b)
Führen Sie den alten Index (Basisjahr 2000) bis zum Jahr
2007 fort.
c)
Berechnen Sie für den Zeitraum 2000 bis 2007 die
jahresdurchschnittliche Inflationsrate.
d)
Um wie viel Prozent ist die Kaufkraft im Jahr 2007 geringer
als im Jahr 2000?
e)
Begründen Sie, warum in regelmäßigen Abständen eine
Revision und Umbasierung des Preisindexes erforderlich ist.
Prof. Dr. Rolf Hüpen | Modul „Statistik I“ | Sommersemester 2013
Verbraucherpreisindex für
Deutschland
Jahr
Indexstand
2000 = 100
2000
100,0
2001
102,0
2002
103,4
2003
104,5
2004
106,2
2005
108,3
2005 = 100
100,0
2006
101,6
2007
103,9
32
Indexzahlen
Aggregation und Zerlegung
Aggregation und Zerlegung von Indizes
Beispiel: Preisindex von Laspeyres
n Güter, 2 Gruppen: 𝑖 = 1, … , 𝑘, 𝑘 + 1, … , 𝑛
𝑘
𝑃𝐿1 0, 𝑡 =
𝑘
𝑝𝑖 𝑡 𝑞𝑖 0
𝑖=1
𝑛
𝑝𝑖 0 𝑞𝑖 0
𝑃𝐿2 0, 𝑡 =
𝑖=1
𝑛
𝑝𝑖 𝑡 𝑞𝑖 0
𝑖=𝑘+1
𝑝𝑖 0 𝑞𝑖 0
𝑖=𝑘+1
Normierte Gewichte der Gruppen im Basisjahr:
𝑘
𝑤1 =
𝑛
𝑝𝑖 0 𝑞𝑖 0
𝑖=1
𝑛
𝑝𝑖 0 𝑞𝑖 0
𝑖=1
𝑤2 =
𝑛
𝑝𝑖 0 𝑞𝑖 0
𝑖=𝑘+1
𝑝𝑖 0 𝑞𝑖 0
𝑖=1
Dann gilt für den Gesamtindex: 𝑃𝐿 0, 𝑡 = 𝑤1 ∙ 𝑃𝐿1 0, 𝑡 + 𝑤2 ∙ 𝑃𝐿2 0, 𝑡
d. h. der Gesamtindex lässt sich als gewichtetes arithmetisches Mittel der Teilindizes
berechnen, wobei die Ausgabenanteile im Basisjahr als Gewichte heranzuziehen sind.
Prof. Dr. Rolf Hüpen | Modul „Statistik I“ | Sommersemester 2013
33