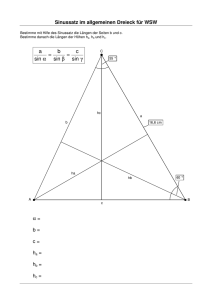
Sinussatz – Herleitung

Arbeitsblatt: Sinussatz – Herleitung
Mathematik / Geometrie / Berechnungen an Dreiecken / Sinussatz und Cosinussatz
Arbeitsblätter zum Ausdrucken von sofatutor.com
Sinussatz – Herleitung
1
Gib den Sinussatz an.
2
Ergänze die Herleitung des Sinussatzes.
3
Berechne die fehlenden Größen c , β und γ.
4
Leite alle fehlenden Größen her.
5
Bestimme den Winkel γ und die Seite c im vorgegebenen Dreieck.
6
Berechne die Entfernung von Anna zu dem Heißluftballon.
+
mit vielen Tipps, Lösungsschlüsseln und Lösungswegen zu allen Aufgaben
Das komplette Paket, inkl. aller Aufgaben, Tipps, Lösungen und Lösungswege
gibt es für alle Abonnementen von sofatutor.com
Schau das Video zur Aufgabe: http://www.sofatutor.at/v/11/aRK
© 2016 sofatutor GmbH, Berlin. Alle Rechte vorbehalten. V63
1
Arbeitsblatt: Sinussatz – Herleitung
Mathematik / Geometrie / Berechnungen an Dreiecken / Sinussatz und Cosinussatz
von 6
Gib den Sinussatz an.
Wähle die richtigen Formeln aus.
A
a
sin(α)
=
b
sin(β)
B
c
sin(β )
=
b
sin(γ)
Schau das Video zur Aufgabe: http://www.sofatutor.at/v/11/aRK
© 2016 sofatutor GmbH, Berlin. Alle Rechte vorbehalten. V63 | E11563
C
a
sin(α)
=
c
sin(γ)
D
a
sin(β )
=
c
sin(γ)
Arbeitsblatt: Sinussatz – Herleitung
Mathematik / Geometrie / Berechnungen an Dreiecken / Sinussatz und Cosinussatz
Unsere Tipps für die Aufgaben
1
von 6
Gib den Sinussatz an.
1. Tipp
Im Sinussatz sind drei Verhältnisse gleich.
Er kann auch als drei Gleichungen geschrieben werden.
2. Tipp
Der Sinussatz besagt, dass das Verhältnis einer Seite zu dem Sinus des gegenüberliegenden Winkels
immer gleich ist.
Schau das Video zur Aufgabe: http://www.sofatutor.at/v/11/aRK
© 2016 sofatutor GmbH, Berlin. Alle Rechte vorbehalten. V63
Arbeitsblatt: Sinussatz – Herleitung
Mathematik / Geometrie / Berechnungen an Dreiecken / Sinussatz und Cosinussatz
Lösungen und Lösungswege für die Aufgaben
1
von 6
Gib den Sinussatz an.
Lösungsschlüssel: A, C
Der Sinussatz lautet:
a
sin(α )
=
b
sin(β)
=
c
.
sin(γ)
Das heißt, dass jeweils die Verhältnisse einer Seite zu dem Sinus
des gegenüberliegenden Winkels immer gleich sind.
Der Sinussatz kann auch in die folgenden Verhältnisse aufgeteilt
werden:
a
sin(α )
a
sin(α )
b
sin(β)
=
=
=
b
,
sin(β)
c
oder
sin(γ)
c
.
sin(γ)
Schau das Video zur Aufgabe: http://www.sofatutor.at/v/11/aRK
© 2016 sofatutor GmbH, Berlin. Alle Rechte vorbehalten. V63