Mechanik der Flüssigkeiten und Gase F
Werbung
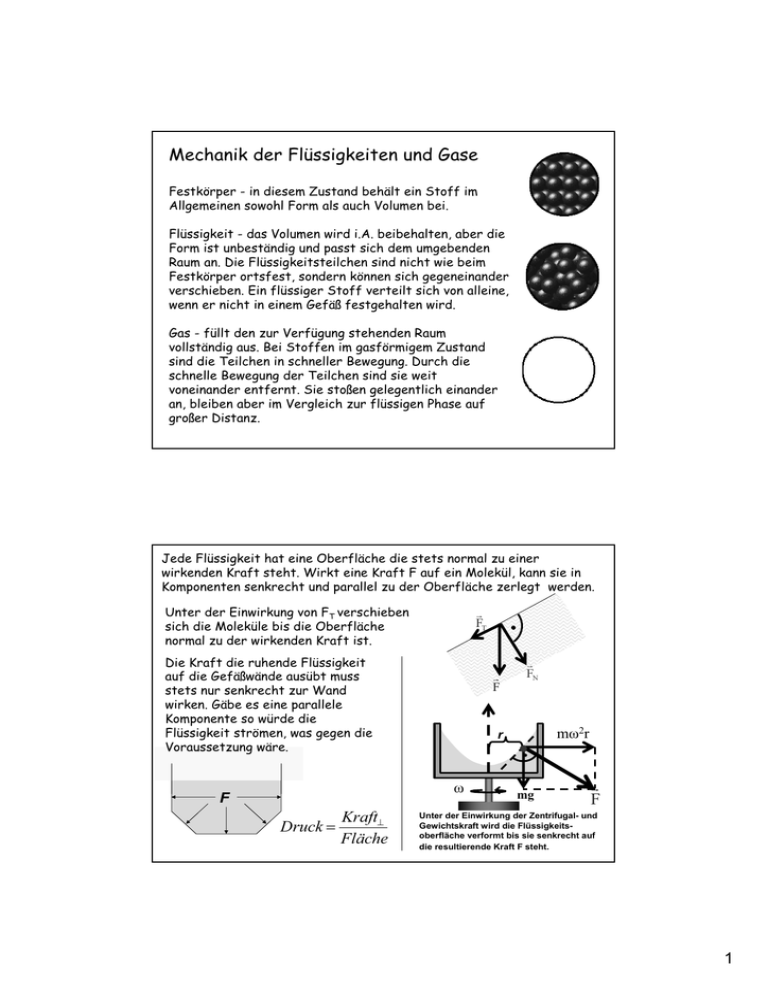
Mechanik der Flüssigkeiten und Gase Festkörper - in diesem Zustand behält ein Stoff im Allgemeinen sowohl Form als auch Volumen bei. Flüssigkeit - das Volumen wird i.A. beibehalten, aber die Form ist unbeständig und passt sich dem umgebenden Raum an. Die Flüssigkeitsteilchen sind nicht wie beim Festkörper ortsfest, sondern können sich gegeneinander verschieben. Ein flüssiger Stoff verteilt sich von alleine, wenn er nicht in einem Gefäß festgehalten wird. Gas - füllt den zur Verfügung stehenden Raum vollständig aus. Bei Stoffen im gasförmigem Zustand sind die Teilchen in schneller Bewegung. Durch die schnelle Bewegung der Teilchen sind sie weit voneinander entfernt. Sie stoßen gelegentlich einander an, bleiben aber im Vergleich zur flüssigen Phase auf großer Distanz. Jede Flüssigkeit hat eine Oberfläche die stets normal zu einer wirkenden Kraft steht. Wirkt eine Kraft F auf ein Molekül, kann sie in Komponenten senkrecht und parallel zu der Oberfläche zerlegt werden. & FT Unter der Einwirkung von FT verschieben sich die Moleküle bis die Oberfläche normal zu der wirkenden Kraft ist. Die Kraft die ruhende Flüssigkeit auf die Gefäßwände ausübt muss stets nur senkrecht zur Wand wirken. Gäbe es eine parallele Komponente so würde die Flüssigkeit strömen, was gegen die Voraussetzung wäre. & F Druck KraftA Fläche m2r r F & FN mg & F Unter der Einwirkung der Zentrifugal- und Gewichtskraft wird die Flüssigkeitsoberfläche verformt bis sie senkrecht auf die resultierende Kraft F steht. 1 HYDROSTATIK – Lehre der strömungsfreien Flüssigkeiten und Gase Druck : p F A 1N m2 >p@ 1 Pa 1Pa = 1Pascal Andere Druckeinheiten: 1 Bar =100000 Pa; 1 mm Hg = 1 Torr Einige Zahlenwerte: Luftdruck – 1E5 Pa; Wasserleitung – 400 kPa A1 & F1 A2 Hydraulische Presse Ann. Inkompressibilität, Schwerkraft (Flüssigkeit) vernachlässigbar s2 dV1 A1 ds1 dV2 dW1 F1 ds1 dW2 pA F2 ds2 & F2 s1 A2 ds2 F1 A1 F2 A2 Gesamter Hydrostatischer Druck Die Betrachtung der Druckverhältnisse in einer ruhenden Flüssigkeit muss vervollständigt werden indem wir auch den Schweredruck berücksichtigen. Dazu benutzen wir den Begriff der Dichte (U) = Masse (m) / Volumen (V) ein. 0 p1 F U A h g pS U h g In nach oben geöffneten Gefäßen wirkt zusätzlich der äußere atmosphärische Druck (pA) auf die Flüssigkeitsoberfläche. Für den gesamten hydrostatischen Druck (p) gilt dann: p3 h* p F=m*.g F A Der Schweredruck (pS) hängt nur von der Höhe Flüssigkeitssäule und von der Dichte (U ) ab. p2 h mg p pA U g h Das hydrostatische Paradoxon 2 Messung des atmosphärischen Druckes (pA) mit dem Barometer Der Luftdruck wird auch manchmal in Torr angegeben (1 Torr= 1mm Hg. 760Torr = 101325 Pa. Der Luftdruck hängt vom Wetter und der Höhe ab. Torricelli beobachtete, dass das Hg-Niveau in geschlossenen Glasröhren immer gleich ist. & FA Das Prinzip des Archimedes Auf einen in einer Flüssigkeit eingetauchten Körper wirkt eine Auftriebskraft FA, deren Betrag gleich der Gewichtskraft der verdrängten Flüssigkeitsmenge ist. & FA & mFL g & U FL V g Auftriebskraft U Körper ! U Fl mK Körper sinkt U Körper K Fl & mK g U Fl Körper schwebt U Körper U Fl Körper schwimmt Aräometer 3 HYDRODYNAMIK Zur Vereinfachung der Überlegungen nehmen wir an, dass: 1. Die Flüssigkeit ist inkompressibel 2. Es wirken keine Kräfte zwischen den Molekülen der Flüssigkeit DIE KONTINUITÄTSGLEICHUNG & v1 Strömung ideale Flüssigkeit F1 's1 W1 I A1 'V1 't & v2 ' s1 p1 A1 's1 ' s2 A2 I p1 'V1 ª m 3 º Volumen« » strom ¬ s ¼ 's 's1 A2 2 't 't A1 v1 A2 v2 A1 DIE BERNOULLISCHE GLEICHUNG Durch die Annahme, dass eine reibungsfreie Strömung vorliegt können Energieumwandlungen nur zwischen der kinetischen und potentiellen Energie erfolgen. Zwischen Position 1 und 2 gibt es eine Differenz an potentieller und kinetischer Energie. 'E pot 'mg (h2 h1 ) 'Ekin 'm 2 2 (v2 v1 ) 2 Dieser Energiezuwachs stammt von der Netto-Volumenarbeit:: 'W F1 ' s1 F2 ' s 2 weil F pA ( p1 p 2 ) ' V und ( p1 p 2 ) ' V U 'm / 'V ' mg ( h2 h1 ) p1 U g h1 'm 2 2 ( v 2 v1 ) 2 1 U v12 2 Das ist die Energieerhaltung ! p2 U g h2 1 U v2 2 2 4 Die Flüssigkeit strömt durch eine Verengung. Wie hoch ist der Druck in der Flüssigkeit in der Verengung ? & & v 2 v U 1 p1 Ugh 2 p1 p U U v v1 ȡ & v 2 2 p Ugh 2 (v 2 v1 ), wegen v v1 2 ist p1 p p p Nach dem Prinzip: Erzeugung des Unterdruckes durch hohe Strömungsgeschwindigkeiten funktionieren viele Vorrichtungen. -'p p p1 Konsequenz der Bernoullischen Gleichung und Anwendungen Zerstäuber FlächeA1 v1't v groß p klein FlächeA2 'h v2't v2 wenn A1 !! A2 v1 | 0 U v2 2 v2 2 U g (h2 h1 ) 2 g 'h 5 Strömungsvorgänge in Flüssigkeiten und Gasen Laminare und turbulente Strömungen Kräfte auf Körper in Strömungen Widerstrandsbeiwert Tragflügel Strömende Flüssigkeiten (Gase) Hydrodynamik beschreibt das Strömen von Flüssigkeiten in Röhren bzw. das Umströmen von Körpern. Das Strömen von Flüssigkeiten wird durch innere und durch äußere Kräfte verursacht. Äußere Kräfte: Schwerkraft, Druckdifferenzen zwischen verschiedenen Strömungsquerschnitten. Sie wirken auf jedes Volumselement des Fluides. Innere Kräfte wirken nur bei realen Flüssigkeiten. Sie sind für die Viskosität verantwortlich und werden Reibungskräfte genannt. 6 Innere Reibung in Flüssigkeiten und Gasen Reibung - physikalische Kraft, die einer Relativbewegung zwischen zwei einander berührenden Körpern entgegenwirkt. Innere Reibung tritt auf bei Bewegung der Atome bzw. Moleküle eines Stoffes gegeneinander. Innere Reibung bewirkt die Zähigkeit (Viskosität) in Flüssigkeiten und Gasen. Die innere Reibung kann ähnlich der Reibung zwischen festen Körpern mittels einer Reibungskraft beschrieben werden. Diese Reibungskraft behindert die relative Bewegung zwischen den Flüssigkeitsteilchen. F v A; F v v; F v 1 z v z F z A v F K A z K >K @ Viskosität (K) 1N s m 2 1Pa s Typische Viskositätswerte (in mPa.s bei 20 °C) Stoffeigenschaft einer Flüssigkeit resultiert und ist abhängig von den zwischen den Molekülen wirkenden Kräften. charakterisiert das Fließverhalten einer Flüssigkeit beim Fließen gleiten die Moleküle aneinander vorbei Was passiert also bei der realen Rohrströmung ? Es gibt ein Druckabfall entlang des Rohres (Kapillare) 7 Hagen-Poiseuillesches Gesetz Bei einer Strömung durch eine Röhre haftet die äußere Schicht der Flüssigkeit an der Rohwand. Damit die nächste Flüssigkeitsschicht vorbeiströmt erzeugt der Druck p eine Kraft die der Schicht eine Geschwindigkeit erteilt. Daraus resultiert, dass Geschwindigkeit im Zentrum am höchsten ist und nimmt zu den Wänden hin ab. Das Strömungsprofil wird parabolisch (für sog. laminare Strömung). p1 Die Volumsstromstärke (Volumen / Zeit) durch eine Röhre mit Radius R und Länge l bei einer gegebenen Druckdifferenz 'p ist gegeben durch: p2 Q V Volumen Zeit S 'p 1 4 R 8 l K Beim Durchfließen der Röhre hängt die Durchflußmenge von der 4-Potenz des Radius ab. 1. Durchflußmenge ist proportional der Druckdifferenz 2. Durchflußmenge ist umgekehrt proportional zu der Rohrlänge und Zähigkeit Qv 'p 1 4 R l K 3. Durchflußmenge ist proportional zu der 4. Potenz des Radius des Rohres Punkt 3 bedeutet, dass bei gegebener Länge und Druck, jedoch bei halbem Radius die Durchflußmenge auf 1/16, das sind 6.6% sinkt. Bedeutung für den Bluttransport im Körper: das Blut strömt vom Herzen über die Aorta und über verschieden lange und dicke Arterien bis in diverse Organe. Die Kapillaren mit etwa 8 Pm Durchmesser sind die kleinsten Blutgefäße, jedoch findet der größte Druckabfall in den sog. Arteriolen statt. Der Durchmesser der Arteriolen ist Dank der Muskelhülle veränderlich. Wird ein Gefäß um 20% erweitert, so ändert sich sein Radius von R auf 1.2 R. Das bedeutet eine Vergrößerung des Volumenstromes um mehr als das Doppelte: (1,2 R) 4 / R 4 2,07 8 Druckverteilung beim Menschen Beim liegen ist die Druckverteilung in den großen Arterien ziemlich homogen (etwa 100 Torr = 133 mBar). Im Stehen ist die Druckverteilung aufgrund des Schweredruckes des Blutes inhomogen. Laminare Strömung Die Geschwindigkeit der Flüssigkeitsschichten von der Wand bis zur Achse des Rohres nimmt kontinuierlich zu. Laminare Strömungen haben ein parabolisches Strömungsprofil. Die Flüssigkeitsteilchen unmittelbar an der Gefäßwand sind in Ruhe. Die Stromlinien verlaufen parallel. Die mittlere Geschw. v = vmax/2 Im Rohr Umströmung einer Kugel (Uni Leipzig) 9 Turbulente Strömung Steigt die Stömungsgeschwindigkeit an, beginnen sich die Flüssigkeitsschichten zu verwirbeln - es entsteht eine turbulente Strömung. Das Geschwindigkeitsprofil flacht ab, da sich die Flüssigkeitsteilchen auch quer zur Rohrachse bewegen. Der Strömungswiderstand steigt an. Der Übergang in die turbulente Strömungsform hängt von der Viskosität, von der Dichte, vom Gefäßradius und von der mittleren Geschwindigkeit der Strömung ab. Turbulente Umströmung einer Kugel Die Reynoldszahl Re Re - eine nach dem Physiker Reynolds benannte dimensionslose Kennzahl einer Strömung. Sie stellt das Verhältnis von Trägheits- zu Reibungskräften (Zähigkeit) dar. Re U vd K U - Dichte des Mediums K - Zähigkeit des Mediums v – Strömungsgeschwindigkeit d – charakteristische Länge Überschreitet die Reynoldszahl einen kritischen Wert wird eine bis dahin laminare Strömung anfällig gegen kleinste Störungen. Oberhalb des kritischen Wertes gibt es dann einen Umschlag von laminarer zur turbulenten Strömung. Dieser Wert beträgt typischerweise Re (kritisch)~1000 – 3000. Praktische Formulierung von Re für Luft (NTP) - Achtung Einheiten: Re # 6,6.v.d (v in (cm/s); d in (cm) 10 Luftwiderstand (Widerstandskraft) FW 1 U cW A v 2 2 U.... Luftdichte in kg/m3 cW... Luftwiderstandsbeiwert (dimensionslos) A..... Stirnfläche in m2 v...... Geschwindigkeit in m/s 11 Kräfte am Tragflügel c d c …Zugkraft d … Widerstrandskraft Wieso gibt es diese Druckunterschiede ? Tragfläche Druckveränderung durch unterschiedliche Anstellwinkel 12 Lilienthal – Polardiagramm. Bestimmung des Anstellwinkels A cA W U v2 S 2 U v2 cW S 2 Oberflächenspannung und Kapillarität photo by Harold Davis 13 Oberflächenspannung Eine Flüssigkeit wird von anziehenden Kräfte, welche zwischen benachbarten Molekülen wirken, den Kohäsionskräften, zusammengehalten. Molekül im Inneren der Flüssigkeit seine Nachbarmoleküle sind allseitig etwa gleichmäßig verteilt. Damit heben sich die auf das betrachtete Teilchen wirkenden Kräfte auf – die resultierende Kraft ist im Mittel Null. Molekül nahe bei der Oberfläche – hier fehlt ein Teil der Wechselwirkungen mit anderen Molekülen der Flüssigkeit. Wechselwirkung mit den Molekülen des darüberliegenden Gases findet statt - diese Kräfte sind i.a. schwächer o resultierende Kraft auf das Molekül ist nach innen, senkrecht zur Oberfläche gerichtet. MINIMAL - Um ein Molekül aus dem Inneren der Flüssigkeit an die Oberfläche zu bringen, muß gegen die Resultierende der molekularkräfte Arbeit geleistet werden - es bedarf einer zusätzlichen Energie. Der umgekehrte Vorgang ist mit einem Gewinn von Energie verbunden o die Oberflächenmoleküle haben das Bestreben, die Flüssigkeitsoberfläche klein zu halten o Minimalflächen FLÄCHEN 14 Vergrößert man die Oberfläche einer Flüssigkeit, so muss man - eben aufgrund der Oberflächenspannung - eine Arbeit verrichten. Die Oberflächenspannung wird nun so definiert: Der Quotient aus der Arbeit, die zur Vergrößerung der Oberfläche verrichtet werden muss zu dem Oberflächenzuwachs. Die Oberflächenspannung kann daher auch als Oberflächenenergie bezeichnet werden. V l 'W 'A F 'x 2'x l F 2l ªN º «¬ m »¼ 'x Einige Werte bei 20°C für die Oberflächenspannungen : Aceton 23.3 mN/m; Quecksilber 476 mN/m; Wasser 72.75 mN/m Kapillarität Durch die Oberflächenspannung verursachtes Verhalten von Flüssigkeiten in engen Röhren (Hohlräumen). Beim (senkrechten) Eintauchen einer engen Röhre (Kapillare) in eine benetzende Flüssigkeit, z. B. Glas in Wasser, steigt die Flüssigkeit in dem Kapillarrohr hinauf (Kapillaraszension). Für eine nicht benetzende Flüssigkeit, z. B. Quecksilber, sinkt diese im Kapillarrohr ab und steht dort tiefer als die Flüssigkeit außerhalb der Kapillare (Kapillardepression). Die Ursache für diese Phänomene ist das Verhältnis von Kohäsionskräften zwischen den Flüssigkeitsmolekülen und Adhäsionskräften zwischen Flüssigkeit und Kapillarwand. 15











