86 § 6 Die Kreiszahl π und das Problem der Quadratur des Kreises

86
§ 6 Die Kreiszahl π und das Problem der Quadratur des Kreises
Berechnungen von Kreisumfang U und Kreisinhalt F bei gegebenem Radius r (bzw.
Durchmesser d) werden schon seit den Anfängen der Mathematik betrieben. Man hat
sehr schnell erkannt, dass sowohl U als auch F proportional zu d bzw. r2 sind.
Stimmen beide Proportionalitätsfaktoren überein und wie groß sind der bzw. die Faktoren? Dass in beiden Fällen derselbe Faktor vorliegt, war schon Archimedes (* um 287
v. Chr. in Syrakus, †212 in v. Chr. in Syrakus) bekannt. Es gibt ein hübsches Argument dafür, das schon bei Leonardo da Vinci im 16. Jh. vorkommt, aber auch in alten
japanischen Schriften:
Wir zerlegen die Kreisfläche F in 4, 8, allgemein 2n gleichgroße Sektoren und bilden daraus
jeweils die skizzierte Fläche vom Inhalt 2F , die bei zunehmend feinerer Unterteilung einem
Rechteck mit dem Inhalt U · r immer ähnlicher wird. Ist nun
U = c1 · d
und
F = c2 · r 2 ,
so folgt im Grenzwert
c2 · r 2 = F =
r
r
· U = · c1 · d = c1 · r 2 ,
2
2
also c1 = c2 .
Die gemeinsame Proportionalitätskonstante heißt seit William Oughtred31 und L. Euler (unabhängig voneinander ?) π von dem Anfangsbuchstaben des griechischen Wortes
πριϕ´ρια für Peripherie. Bis 1735 schreibt Euler noch p statt π; seit 1737 benutzt er
nur noch den Buchstaben π.
31
William Oughtred wurde am 5.3.1575 in Eton geboren, studierte in Cambridge, wurde 1603 zum
Priester geweiht und 1608 Pfarrer in Albury. Ab 1628 wurde er zum Erzieher eines Adligen bestellt, und
er verfasste für diesen den ”Clavis mathematicae”, der erstmals 1647 gedruckt erschien. Diese Schrift
übte großen Einfluss auf die Mathematik in England aus. Oughtred verstarb am 30.6.1660 in Albury.
87
a) Näherungsweise Berechnung von π
Alles ist also klar, wenn man π bestimmt hat. Aber das ist nicht ganz so einfach. Ein paar
Näherungen für π aus der Geschichte:
Wir finden in der Bibel im Alten Testament, 1. Buch von den Königen, Kap. 7, Vers 23:
”Und er machte ein Meer, gegossen zehn Ellen weit, von einem Rande zum anderen, rund
umher, und fünf Ellen hoch, und eine Schnur dreißig Ellen lang war das Maß rings um.”
Hieraus resultiert: π ≈ 3.
Bei den Ägyptern finden wir im Rechenbuch des Ahmes (ca. 1900 v. Chr.) wegen der
Vorliebe für Stammbrüche:
2
16
= 3, 16049 3827 (mit einem Fehler von ca. 0.5 %).
π≈
9
Archimedes gibt als erster Abschätzungen für die Zahl π an. Er vergleicht den Kreisumfang mit den Seitenlängen von ein- bzw. umbeschriebenen regelmäßigen n−Ecken. Das
einbeschriebene regelmäßige 6-Eck hat den Umfang 6r = 3d, woraus sich sofort π > 3
ergibt. Durch Betrachtung des regelmäßigen 96−Ecks erhält Archimedes
3
1
10
<π<3 ,
71
7
d.h.
3.14084 50704 22535 21126 76056 33802 81690 < π < 3.142857 .
Archimedes wurde um 287 v. Chr. in Syrakus geboren. Es gilt als sicher, dass er einige
Zeit in Alexandria weilte, da die Mehrzahl
seiner Schriften in Form von Briefen aus Syrakus an Mathematiker in Alexandria erhalten sind, wie z.B. an Konon von Samos oder
Eratosthenes. Archimedes starb 212 v. Chr.
während der Einnahme seiner Geburtsstadt
Syrakus durch die Römer, nachdem er ihre 2 Jahre dauernde Verteidigung durch die
Konstruktion ballistischer Apparate aktiv
und erfolgreich unterstützt haben soll.
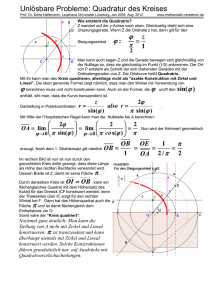
Wir wollen den Weg von Archimedes nachzeichnen. Dazu bezeichnen wir den halben
Umfang des regelmäßigen Kn −Ecks mit Kn = 3 · 2n−1 , das den Kreis mit Radius 1
umschreibt, mit an ; ferner sei bn der halbe Umfang des regelmäßigen Kn −Ecks, das in den
Kreis mit Radius 1 einbeschrieben ist. Dann können wir mit Hilfe der trigonometrischen
Funktionen folgende Beziehungen festhalten (vgl. Skizze):
88
an = Kn · tan(
π
)
Kn
und
bn = Kn · sin(
π
).
Kn
Daraus erhalten wir
π
π
)
und
bn+1 = 2 · Kn · sin(
).
2 · Kn
2 · Kn
Hieraus ergeben sich die Beziehungen
1
1
2
+
=
und
an+1 · bn = (bn+1 )2 ,
an b n
an+1
die Archimedes natürlich nicht mit Hilfe der trigonometrischen Funktionen, sondern aus
Flächenbetrachtungen erzielte.
Um die beiden letzten Gleichungen einzusehen, benutzen wir hier und auch spter die
π
folgenden Beziehungen für trigonometrische Funktionen mit dem Argument θ ∈]0, [:
2
θ
θ
θ
θ
sin θ = 2 sin cos , cos θ = cos2 − sin2 ,
2
2
2
2
und
θ
θ
1 + cos θ = 2 cos2
und 1 − cos θ = 2 sin2 .
2
2
Es gilt
cos Kπn
1
1
π
1
1
+
=
+
=
1 + cos
an b n
Kn sin Kπn
Kn sin Kπn
Kn sin Kπn
Kn
an+1 = 2 · Kn · tan(
=
2
2 π
π cos
Kn sin Kn
2Kn
=
2
2
π =
2Kn tan 2Kn
an+1
89
und
an+1 bn = 2Kn
=
sin 2Kπ n
cos 2Kπ n
Kn sin
4Kn2 sin2
π
2Kn
sin 2Kπ n
π
π
π
= 2Kn2
cos
π 2 sin
Kn
cos 2Kn
2Kn
2Kn
= b2n+1 .
Aus diesen Formeln kann man ”iterativ” die Zahlen an und bn berechnen. Es ist nämlich
an+1 =
2an bn
an + b n
und bn+1 =
p
an+1 bn .
√
3 √
Nach heutigen Überlegungen ergibt sich wegen a1 = 3 · 3 und b1 = · 3 für das
2
√
√
regelmäßige Sechseck a2 = 2 · 3 und b2 = 3. Archimedes wählt als Näherung für 3
3180
265
. Mit diesem Wert erhalten wir a3 =
≈ 3.215 und
den etwas kleineren Wert
153
989
9540
(b3 )2 =
, d.h. b3 ≈ 3.106. Wenn man weiter fortfährt und die auftretenden Wurzeln
989
durch kleinere bzw. größere rationale Zahlen ersetzt, so ergeben sich die oben angegebenen
10
1
unteren und oberen Schranken b6 = 3
und a6 = 3 .
71
7
Die Zahl π mit den ersten 20 korrekten Dezimalstellen nach dem Komma lautet
3.14159 26535 89793 23846 ... .
Lange gebräuchlich war die Näherung
1
π ≈ 3 = 3.14285 7 (mit einem Fehler von ca. 0.04 %) .
7
a) Klaudius Ptolemaios32 benutzt einen Wert, der zwischen den obigen Schranken
liegt, d.h.
17
= 3.1416 < 3.14285 . . . .
3.14084 . . . < π ≈ 3
120
b) In China finden wir bei Zu Chong-Zhi (430 – 501) die Näherung
π≈
355
= 3.14159 29203 53982 30088 49557 52212 38938 05309
113
73451 32743 36283 18584 07079 64601 76991 15044
24778 76106 19469 02654 86725 66371 68
mit einem Fehler < 2.7 · 10−7 . (Der Dezimalbruch hat die bei Nenner 113 maximale
Periodenlänge 112.)
32
Klaudius Ptolemaios wurde um 85 in Ptolemaios in Ägypten geboren. Über sein Leben lassen
sich einige Daten nur aus seinen Werken erschließen. Die in seinem Hauptwerk ”Almagest” verwendeten
eigenen Beobachtungen wurden in Alexandria durchgeführt und erstreckten sich von März 127 bis Februar
141. Ptolemaios starb um 165.
90
c) Diese Näherung findet sich auch bei Valentin Otho33 . Für Otho ergab sich diese
22
377
Zahl aus den Werten
und
durch ”Subtraktion”
7
120
355
377 − 22
=
.
113
120 − 7
d) Leonardo von Pisa (vgl. S. 18) findet um 1220 durch Betrachtung des 96−Ecks:
π≈
864
= 3.1418 .
275
e) Ludolph van Ceulen34 berechnet π im Jahre 1596 auf 20 Stellen nach dem Komma.
Nach ihm nennt man π auch oft Ludolphsche Zahl. Die Zahl π mit den ersten 20
korrekten Dezimalstellen nach dem Komma lautet
3.14159 26535 89793 23846 ... .
Posthum veröffentlichte seine Frau eine Arbeit mit 32 Stellen nach dem Komma
(1615).
f) Ohne Kommentar geben wir eine Möglichkeit zur Berechnung von π an:
1
1
1
1
−
+
−
+ −...
π = 16
3
5 · 55 7 · 57
5 3·5
1
1
1
1
− 4
−
+
−
+ −... .
239 3 · 2393 5 · 2395 7 · 2397
Wir erhalten
16
4
−
≈ 3.18326 3598 ,
5
239
16
4
4
16
−
−
+
≈ 3.14059 7029
5
375 239 3 · 2393
16
16
16
4
4
4
−
+ 6 −
+
−
≈ 3.14162 1029
3
5
375 5
239 3 · 239
5 · 2395
und
16
16
16
16
4
4
4
4
−
+ 6 −
−
+
−
+
≈ 3.14159 1772 .
7
3
5
5
375 5
7·5
239 3 · 239
5 · 239
7 · 2397
g) Wir könnten die Jagd nach mehr Stellen weiter verfolgen: im Jahre 1705 sind 72
Stellen, Im Jahr 1794 sind 140 Stellen, im Jahr 1874 sind 526 Stellen, 1947 sind 808
und 1967 sind 500000 Stellen bekannt.
33
Valentin Otho wurde um 1550 in Magdeburg geboren. Ab 1576 war er Professor für ”Höhere Mathematik” (Astronomie) in Wittenberg. 1581 wurde er unter Beschuldigung des Kryptokalvinismus seines
Amtes enthoben. Er starb 1605 in Heidelberg
34
Ludolph van Ceulen wurde am 28.1.1540 in Hildesheim geboren. Er war Mathematik-Lehrer in Breda, Amsterdam, Delft, Arnheim und Leiden. Ab 1600 war er Inhaber einer Professur für Kriegsbaukunst
in Leiden. Er starb am 31.12.1610 in Leiden
91
h) Heute sind noch mehr Stellen bekannt. Zur numerischen Berechnung von π siehe
”Ramanuian, Modular Equations, and Approximations to Pi” bei
http://www.cecem.sfu.ca/organics/papers/borwein,
vorher erschienen in American Math. Monthl. 96 (3), 1989. Hier findet sich auch der
berühmte superschnelle Algorithmus:
Mit den Startwerten
√
a0 = 6 − 4 2
√
y0 =
2−1
wird für n ∈ N0 iteriert
yn+1 =
1 − (1 − yn4 )1/4
,
1 + (1 − yn4 )1/4
2
an+1 = (1 + yn+1 )4 an − 22n+3 yn+1 (1 + yn+1 + yn+1
).
Dann gilt für alle n ∈ N0
0 < an −
1
n
< 16 · 4n e−2·4 π ,
π
grob gesagt vervierfacht sich die Anzahl der richtigen Stellen in jedem Schritt:
1
π
1
0 < a2 −
π
1
0 < a3 −
π
1
0 < a4 −
π
0 < a1 −
< 8 · 10−10
< 6 · 10−42
< 3 · 10−172
< 2 · 10−695
Eine Berechnung mit einem (alten) Taschenrechner TI-30 ergibt z.B.
√
a0 = 6 − 4 2 ≈ 0.3431458
√
y0 =
2 − 1 ≈ 0.4142136
p
1 − 4 1 − y04
0.007442
p
y1 =
≈
≈ 0.0037349
4
4
1.992558
1 + 1 − y0
a1 = (1 + y1 )4 a0 − 23 y1 (1 + y1 + y12 ) ≈ 0.3483011− ≈ 0.0299912 ≈ 0.3183099
und damit
1
≈ 3.1415926 .
a1
92
i) Es gibt zahlreiche ”Merkregeln” bzw. Gedichte, die helfen sollen, sich die ersten
Stellen von π zu merken. Dabei gibt die Anzahl der Buchstaben der einzelnen Worte
die entsprechende Ziffer von π an. Hier seien zwei Beispiele genannt, ein Vers in
deutscher Sprache und eine ”Merkregel” in englischer Sprache:
Wie, o dies π
macht ernstlich so vielen viele Müh’,
lernt immerhin Jünglinge, leichte Verselein,
wie so zum Beispiel dies dürfte zu merken sein!
Man kann Jünglinge auch durch Mägdelein ersetzen. Dieser Vers liefert dann 23
Stellen nach dem Komma, wogegen die folgende Merkregel ”nur” 14 Stellen nach
dem Komma liefert:
How I need a drink - alcoholic of course - after the heavy lectures involving quantum
mechanics!
Da die Ziffernfolge von π den Charakter von Zufallszahlen hat, benutzt man sie häufig
als Testprogramm.
b) Quadratur des Kreises
Neben diese mehr rechnerischen Probleme stellen wir nun ein geometrisches. Nach Plato
sind die einzigen legitimen Hilfsmittel des Geometers Zirkel und Lineal. Also kann sich
der Geometer an folgender Aufgabe versuchen:
Quadratur des Kreises: Ein gegebener Kreis ist allein mit Zirkel und Lineal in ein
flächengleiches Quadrat zu verwandeln.
Diese Aufgabe gehört zu den 3 wichtigen Aufgaben der antiken Mathematik; die beiden
anderen lauten:
Delisches Problem (der Würfelverdoppelung): Konstruiere mit Zirkel und Lineal einen
Würfel mit dem doppelten Volumen des Einheitswürfels.
Winkeldreiteilung: Teile mit Zirkel und Lineal einen beliebigen Winkel in drei gleich
große Teile.
Der vollständige Nachweis, dass die Quadratur des Kreises nicht lösbar ist, gelang erst
Lindemann im Jahre 1882.
Bis dahin gab es viele Versuche, die (natürlich) nur Näherungen brachten, z.B. aus Indien
von Śulbasútras (schriftlich fixiert etwa 500 v. Chr.):
Will man zu einem Kreis ein flächengleiches Quadrat finden, ziehe man vom Durchmesser
2
ab. Das ist die gesuchte Quadratseite. (Hieraus folgt: π ≈ 3.0044.)
15
Nun einige Bemerkungen zu der Frage, welche Zahlen mit Zirkel und Lineal konstruierbar
sind. Wir gehen vom Koordinatensystem aus, betrachten es als komplexe Zahlenebene
und überlegen uns, welche Punkte – ausgehend von (0, 0) und (1, 0) – mit Zirkel und
Lineal konstruierbar sind. Zunächst sind alle ganzen Zahlen Z := {0, ±1, ±2, ±3, . . .}
93
konstruierbar, dann alle Zahlen der Form in mit der imaginären Einheit i und n ∈ Z.
1
Mit Hilfe des Strahlensatzes können wir alle Stammbrüche mit n ∈ N konstruieren und
n
m
mit m ∈ Z und n ∈ N. Ferner läßt sich mit Hilfe des Satzes
damit auch alle Brüche
n
√
von Pythagoras zeigen, dass sich alle Zahlen der Form n mit n ∈ N konstruieren lassen.
Mit Hilfe
oder des Kathetensatzes im rechtwinkligen Dreieck können wir
p√des Höhensatzes
√
4
auch
n = n mit n ∈ N konstruieren. Wir wollen uns überlegen, welche Zahlen nicht
konstruierbar sind. Dazu folgende
Definition
Eine komplexe Zahl x ∈ C heißt algebraisch, wenn x eine Gleichung der Form
an xn + an−1 xn−1 + . . . + a1 x + a0 = 0
mit ganzen Zahlen ai ∈ Z erfüllt, die nicht alle Null sind. Anders gesagt: x ist Nullstelle
eines von Null verschiedenen Polynoms P ∈ Z[X] (d.h. mit ganzen Koeffizienten).
Eine komplexe Zahl x heißt transzendent, wenn sie nicht algebraisch ist.
Im Jahre 1882 bewies Carl Louis Ferdinand Lindemann, dass π transzendent ist. Man
weiß inzwischen auch, dass neben e auch eπ mit
e = lim (1 +
n→∞
1 n
) ≈ 2.71828
n
ebenfalls transzendent ist. Es ist aber noch nicht einmal bekannt, ob eπ oder e+π irrational
ist.
Carl Louis Ferdinand Lindemann wurde
am 12.4.1852 in Hannover geboren. Nach
einem Studium in Göttingen, Erlangen,
München, Paris und London promovierte er
1873 bei Felix Klein in Erlangen. 1877 wurde er Privatdozent in Würzburg und noch
im gleichen Jahr Professor an der Universität Freiburg. 1883 wurde er an die Universität Königsberg und 1893 an die Universität München berufen, wo er bis zu seiner
Emeritierung 1923 tätig war. Lindemann
verstarb am 6.3.1939 in München.
Es gibt auch einen bekannten Philosophen unter der ”Kreisquadrierern”: Thomas Hobbes35 war bis zu seinem Tod nicht zu überzeugen, dass er nur eine Näherungslösung
gefunden hatte.
35
Hobbes wurde am 3.4.1588 in Westport (Malmesbury) geboren. Er studierte von 1603 bis 1608 in
Oxford und lebte ab 1610 lange in Frankreich und Italien. Er erteilte als Hofmeister auch mathematischen Unterricht. Hobbes lernte u.a. R. Descartes und G. Galilei kennen. Hobbes war Mitbegründer der
Aufklärung. Er kehrte 1651 nach England zurück und starb am 4.12.1679 in Hardwick (Devonshire).
94
Wir wollen so vollständig wie möglich in diesem Abschnitt ”beweisen”, dass die Quadratur
des Kreises mit Zirkel und Lineal unmöglich ist.
Der erste Schritt dazu ist die Algebraisierung der Aufgabe. Wir behandeln das Problem
im Koordinatensystem des R2 . Was bedeutet ”Konstruierbarkeit” algebraisch?
Ist eine Anzahl von Punkten gegeben oder schon konstruiert, so kann man mit Zirkel und
Lineal
– eine Gerade durch zwei (verschiedene) dieser Punkte legen,
– einen Kreis um einen der Punkte schlagen, dessen Radius der Abstand zweier Punkte
ist.
Neu konstruierbare Punkte sind genau die Schnittpunkte solcher Kreise und Geraden (und
evtl. sind nicht alle diese Punkte neue Punkte).
Im Koordinatensystem mit den Koordinaten (x, y) sehen diese Objekte so aus:
(1) Eine Gerade durch (x1 , y1 ) 6= (x2 , y2 ) ist die Menge aller (x, y) mit
(y2 − y1 )x + (x1 − x2 )y = x1 y2 − x2 y1 ,
q
(2) ein Kreis um (x1 , y1 ) mit Radius r = (x2 − x3 )2 + (y2 − y3 )2 ist die Menge aller
(x, y) mit
(x − x1 )2 + (y − y1 )2 = r2 ,
d.h.
x2 + y 2 − 2x1 x − 2y1 y = r2 − x21 − y12 .
Schnittpunkte bestimmen bedeutet: zwei Gleichungen mit zwei Unbekannten lösen, die
vom Typ (1) oder (2) sind. Für die Koordinaten bedeutet das:
Lemma
Die Koordinaten eines neu konstruierbaren Punktes sind Lösungen von linearen oder quadratischen Gleichungen, deren Koeffizienten durch sogenannte Körperoperationen (Addition, Subtraktion, Multiplikation bzw. Division) aus Koordinaten ”alter” Punkte hervorgehen.
Beweis:
(1) Für Schnittpunkte von zwei Geraden ist das klar. Da nicht beide Koeffizienten von
x, y Null sind, kann man etwa nach y auflösen
y=
y2 − y1
x2 y1 − x1 y2
·x+
x2 − x1
x2 − x 1
und in die zweite Geradengleichung einsetzen.
(2) Schnittpunkt(e) von Kreis und Gerade: Man löst die Geradengleichung wie in (1)
auf; durch Einsetzen in die Kreisgleichung ergibt sich eine quadratische Gleichung
mit Koeffizienten der gewünschten Art.
95
(3) Schnittpunkt(e) von zwei Kreisen: Zu lösen ist das Gleichungssystem
x2 + y 2 − 2x1 x − 2y1 y = r12 − x21 − y12
x2 + y 2 − 2x2 x − 2y2 y = r22 − x22 − y22 .
Durch Subtraktion beider Gleichungen entsteht eine Geradengleichung
2(x2 − x1 )x + 2(y2 − y1 )y = r12 − r22 + x22 − x21 + y22 − y12 .
(Wegen (x1 , y1 ) 6= (x2 , y2 ) können nicht beide Koeffizienten von x bzw. y Null sein,
so dass wir nach x oder y auflösen können und wir sind damit in Fall (2).)
Ist nun ”der” Kreis zur Quadratur vorgelegt, so haben wir anfangs nur seinen Radius,
d.h. 2 Punkte, o.E. (0, 0), (1, 0). Nach dem Lemma ist plausibel, dass alle endlichen
Konstruktionen einen gewissen Rahmen nicht verlassen. Für unsere Zwecke genügt der
Nachweis, dass Koordinaten stets algebraisch bleiben.
Eine etwas genauere Analyse des Prozesses zeigt, dass nur Punkte konstruierbar sind, die
sich aus√Quadratwurzeln von Quadratwurzeln von ... aufbauen lassen. Eine Strecke der
Länge 3 2 ist nicht konstruierbar. Damit ist auch das Delische Problem mit Zirkel und
Lineal unlösbar. Ebenso kann man zeigen, dass das Problem der Winkeldreiteilung (im
Allgemeinen) mit Zirkel und Lineal nicht lösbar ist.
Beispiele
(1) Alle rationalen Zahlen x =
qx − p = 0.
p
mit p ∈ Z, q ∈ N sind algebraisch, denn es ist
q
√
(2) Nicht nur rationale Zahlen sind algebraisch, z.B. ist x = 10 algebraisch wegen
p
x2 − 10 = 0. x ist aber nicht rational, denn die Annahme x = liefert 10q 2 = p2 ;
q
nun endet p2 im Dezimalsystem auf gerade viele Nullen (wenn die Anzahl der Nullen
die Zahl 0 ist, so wird 0 als gerade Zahl betrachtet!) und 10q 2 auf ungerade viele,
was ein Widerspruch ist.
(3) Die komplexe Einheit x = i ist algebraisch wegen x2 + 1 = 0.
π
π
+ i sin ist für jedes n ∈ N algebraisch, da nach der Formel von Moivre36
n
n
gilt: x2n − 1 = 0.
(4) x = cos
36
Abraham de Moivre wurde am 26.5.1667 in Vitry in der Champagne geboren. Mit Mathematik
beschäftigte sich Moivre fast ausschließlich autodidaktisch. Als Hugenotte gelang ihm 1688 die Emigration
nach London, wo er sich bis ins hohe Alter seinen Lebensunterhalt durch Privatunterricht in Mathematik
verdiente, aber auch Spieler und Spekulanten in Kaffeehäusern beriet. 1707 bewies er einen Satz, in dem
er implizit die nach ihm benannte Formel (cos α + i sin α)n = cos nα + i sin nα verwandte. Moivre starb
am 27.11.1754 in London.