ap , b., v - L`Arpenteur

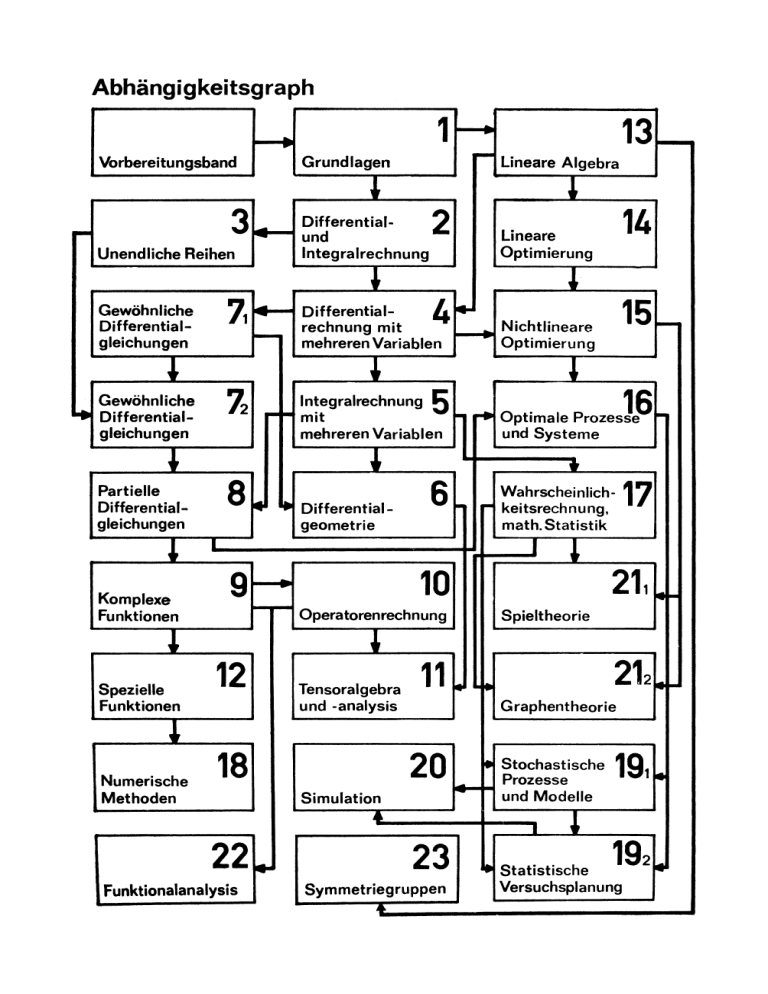
Abhängigkeitsgraph
Vorbereitungsband
-
~
,
, ..
4
Differential71 40- rechnung
mit
Gewöhnliche
Differentialgleichungen
-
mehreren Variablen
~
72
Gewöhnliche
~ Differential-
~-
gleichungen
~
,
8~
•
Differentialgeometrie
,
und Systeme
•
~r--
12
,
10
Operatorenrechnung
Tensoralgebra
und -analysis
18
Funktionalanalysis
211 ~212 ~-
~
Graphentheorie
20
•
...
Symmetriegruppen
,
~ Stochastische
~
Prozesse
und Modelle
I
23
•
Spieltheorie
11 •
Simulation
22 ~
,
Wahrscheinlich-17
- keitsrechnung,
math. Statistik
I
9~
15 -
Nichtlineare
Optimierung
~ Optimale Prozes1ß -
6~
~
Numerische
Methoden
~.
I
~
Spezielle
Funktionen
5
14
Lineare
Optimierung
----
Integralrechnung
mit
mehreren Variablen
13 io-
Lineare Algebra
~
Partielle
Differentialgleichungen
Komplexe
Funktionen
2
Integralrechnung
Unendliche Reihen
,
I""""
Grundlagen
3 .- Differentialund
,
1~
191.
192 ..
• Statistische
Versuchsplanung
MATHEMATIK FÜR INGENIEURE, NATURWISSENSCHAFTLER,
ÖKONOMEN UND LANDWIRTE· ÜBUNGSAUFGABEN 1
Herausgeber: Prof. Dr. o. Beyer, Magdeburg . Prof. Dr. H. Erfurth, Merseburg
Prof. Dr. o. Greuelt . Prof. Dr. C. Großmann, Dresden
Prof. Dr. H. Kadner, Dresden· Prof. Dr. K. ManteufTel, Magdeburg
Prof. Dr. M. Schneider, Karl-Marx-Stadt . Doz. Dr. G. Zeidler, Berlin
PROF. DR. H. WENZEL
OL DIPL.-MATH. G. HEINRICH
Übungsaufgaben zur
Analysis 1
4. AUFLAGE
ä3
LEIPZIC
BSB B. G. TEUBNER VERLAGSGESELLSCHAFf
1990
Das Lehrwerk wurde 1972 begründet und wird seither herausgegeben von:
Prof. Dr. Otfried Beyer, Prof. Dr. Horst Erfurth, Prof. Dr. Otto Greuel t, Prof. Dr. Horst Kadner,
Prof. Dr. Karl Manteuffel, Doz. Dr. Günter Zeidler
Außerdem gehören dem Herausgeberkollektiv an:
Prof. Dr. Manfred Schneider (seit 1989), Prof. Dr. Christian Großmann (seit 1989)
Verantwortlicher Herausgeber dieses Bandes:
Dr. sc. nat. Karl Manteuffel, ordentlicher Professor für mathematische Methoden der Operationsforschung an der Technischen Universität "Otto von Guericke", Magdeburg
Autoren:
Dr. rer. nat. habil. Horst Wenzel, ordentlicher Professor rur Analysis an der Technischen Universität
Dresden (Abschnitte 7.-10. und 14.-16.)
Oberlehrer Dipl.-Math. Gottfried Heinrich, Lehrer im Hochschuldienst an der Technischen Universität Dresden (Abschnitte 1.-6. und 11.-13.)
Wenzel, Horst:
Übungsaufgaben zur Analysis I/H. Wenzel; G. Heinrich. 4.Aufl. - Leipzig: BSB Teubner, 1990. - 76 S.: 34 Abb.
(Mathematik rur Ingenieure, Naturwissenschaftler, Ökonomen und
Landwirte; Übungsaufgaben 1)
NE: Heinrich, Gottfried:; GT
ISBN 978-3-322-00366-9
ISBN 978-3-322-94555-6 (eBook)
DOI 10.1007/978-3-322-94555-6
Math. Ing. Nat. wiss. Ökon. Landwirte, Ü 1
ISSN 0138-1318
©
BSB B. G. Teubner Verlagsgesellschaft, Leipzig, 1987
4. Auflage
VLN 294-375/45/90 . LSV 1034
Lektor: Jürgen Weiß
GesamtherstelJung: INTERDRUCK Graphischer Großbetrieb Leipzig,
Betrieb der ausgezeichneten Qualitätsarbeit, 111/18/97
00600
Vorwort
Die vorliegenden Übungsaufgaben sind für den Einsatz im Direkt- und Fernstudium
an Universitäten und Hochschulen gedacht. Da die Aufgaben inhaltlich an die Bände 1,
2,3 und 6 der Reihe "Mathematik für Ingenieure, Naturwissenschaftler, Ökonomen und
Landwirte" angeschlossen sind, können sie vom Leser auch zum Selbststudium herangezogen werden. Zum Zwecke der Motivation wird neben innermathematischen Problemstellungen auch mit einfachen naturwissenschaftlichen, technischen und ökonomischen
Sachverhalten gearbeitet.
Bei der Erarbeitung dieses Übungsheftes wurden die Erfahrungen aus den Mathematiklehrveranstaltungen an der Technischen Universität Dresden und an anderen Hochschulen der DDR genutzt. Wir danken für die eingegangenen Hinweise, die alle sorgfältig geprüft und in der Regel berücksichtigt wurden.
Unser besonderer Dank gilt den Herren Oberlehrer Dipl.-Math. Helmut Ebmeyer
(Technische Universität Dresden, Mitarbeit bei den Abschnitten 1.-6. und 11.-13.)
und Dr.-Ing. Ralf Kuhrt (Humboldt-Universität Berlin, Mitarbeit bei den Abschnitten 7.-10. und 14.-16.). Sie haben wertvolle Hinweise aus der Sicht des Fernstudiums gegeben.
Aufgaben mit höherem Schwierigkeitsgrad oder umfangreicherem Rechenaufwand sind
mit einem Stern gekennzeichnet.
Für Hinweise und Vorschläge, die der Verbesserung der Aufgabensammlung dienen,
sind wir stets dankbar.
Dresden, April 1986
H. Wenzel
G. Heinrich
Inhalt
l.
2.
Logik . . . . . . .
Beweisprinzipien
3.
4.
Zahlen . . . .
Kombinatorik
Mengen ...
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
Funktionen
Zahlenfolgen
Grenzwerte und Stetigkeit
Ableitungen . . . . . . . .
Anwendung des Ableitungsbegriffs .
Das unbestimmte Integral
Das bestimmte Integral . ; . . . . .
Uneigentliche Integrale . . . . . . .
Unendliche Reihen mit konstanten Gliedern
Potenzreihen . . . . . . . . . . . . .
Fourierreihen und Fourierintegrale
Lösungen und Lösungshinweise ........
15.
16.
5
6
7
10
13
14
21
22
23
26
30
33
39
41
42
45
. 48
Logik
1.
(Bd.l,3.)
1.1. Welche der folgenden schriftlichen Gebilde bzw. Formulierungen sind Aussagen;
man bestimme gegebenenfalls ihren Wahrheitswert.
a) 2 + 1 = 15,
b)
Je
d) Halten Sie mal bitte!
e)
d:~:)
x2
dx,
=
c) 2216091 -1 ist eine Primzahl.
120.
f) Warum ist
~
größer als I?
Am 30. September 1993 wird es in Vitte keinen Verkehrsunfall geben.
Das ist stets ein günstiges Angebot!
3C2H sOH + PCl3 ~ 3C2H sCI + P(OHh.
Wenn ein rechtwinkliges Dreieck gleichseitig ist, so hat eine Kathete die Länge
Zwei rechtwinklige Dreiecke sind ähnlich, wenn die Differenz der spitzen Winkel des
einen Dreiecks gleich der entsprechenden Differenz des anderen Dreiecks ist.
1) Aller Irrtum ist maskierte Wahrheit.
m) Ig 7 ist eine rationale Zahl.
g)
h)
i)
j)
k)
..fi.
1.2. Folgende Aussagen sollen betrachtet werden:
p: "Die Ware ist verdorben",
q: "Die Ware darf nicht verkauft werden".
Es sind verbal alle Fälle anzugeben, in denen die Aussagenverbindung "p = q" wahr ist.
1.3. Welche der folgenden Aussagen sind wahr, wenn p und auch q wahr sind?
a) p
1\
b) Pl\q,
ij,
e) p v ij,
d) p=q,
g) (p v ij)
c) (pl\q),
f) (p 1\ q),
I\P,
h) (p=q).
1.4. Man gebe jeweils eine Aussage p an, so daß mit q: "Das Parallelogramm D ist ein
Quadrat", gilt:
=
=
a) q, p, aber nichtp
q,
b) p = q, aber nicht q = p,
c) p
~
q.
1.5. Welche der folgenden Implikationen sind für beliebige reelle Zahlen a, b, c, d stets
wahr?
a) (a> b) =(a2 > b 2),
b) (a> b > C > 0) = (a 2 > ab > b 2 > bc> c 2),
c) [Ca - b)2 + 2ab > a 2 + b 2 ] =(a 2 > 12ab),
d) (a> b) 1\ (c < d)
(a - c> b - d),
=
e) (ab> cd)
= (:
>
~)
(b, d =F 0).
1.6. Man bilde die Negation von:
a) Eine notwendige Bedingung dafür, daß zwei Dreiecke kongruent sind, ist, daß sie gleichen Flächeninhalt haben.
b) Zu jedem Mann gibt es mindestens eine Frau, die ihn nicht liebt.
6
2. Beweisprinzipien
1.7. Man gebe die Wahrheitstafeln folgender Aussagenverbindungen an:
a) p 1\ (q V r),
b) (p~q) ~r,
c) (p~q)~q,
d) [pvq]I\[~].
Wie können demnach c) und d) vereinfacht dargestellt werden?
1.8. Mit Hilfe von Wahrheitstafeln zeige man:
a) (p~q)<=>(pvq),
b) (p v q) -(p 1\
c)
d)
e)
f)
(p
1\
[(P
[p
q) -(p V
1\
q)
(p 1\ q)] -[p -q],
r)] -[(p 1\ q) v (p 1\ r)],
r)] -[(p v q) 1\ (p V r)].
V
(q
V
[p v (q
1\
1\
q),
q),
1.9. Z(x, y) sei eine Aussageform. Man bilde die Negation von:
a) VxVy: Z(x,y),
b) Vx3y: Z(x,y),
d) 3x 3y: Z(x,y).
c) 3x Vy: Z(x,y),
1.10. Es seien x und y Variable für reelle Zahlen. Man bestimme die Wahrheitswerte
von:
a) VxVy:y=x 2 ,
b) Vx3y:y=x 2 ,
c) 3x Vy: y = x 2 ,
e) Vy 3x: y = x 2 ,
d) 3x3y:y=x 2,
f) 3yVx:y=x 2 •
Ändert sich die Lösung in dem Fall, daß x und y Variable für komplexe Zahlen sind?
Beweisprinzipien
2.
(Bd. 1,4.)
2.1. Man zeige, daß für die endliche geometrische Reihe die Darstellung
I -
1 + q + q2 + ... + qn = {
qn+!
1(n
q
falls q
,
+ 1),
* 1 ist,
für n E N, q reell,
falls q = 1 ist,
gilt. Welche Situationen ergeben sich beim Grenzübergang n ~ oe ?
±
2.2. Beweisen Sie durch vollständige Induktion:
a)
k2
k~!
=
n(n + 1)(2n + 1)
6'
n
b)
L (2k -
d)
L
n
k~!
n+!
e) 3·
L (2k -1)2 = 4n
k~l
3
+ 12n 2 + lln + 3,
1) = n 2 ,
k~l
k
n+2
--2k =2 - - 2
n '
3. Zahlen
f)
i:. kxk=
7
X
{
x-I
(
xn
-l)
nxn_~
n(n+l)
k=1
2
~
sin2nx
g) L.. cos (2k -1) x = 2 .
k= 1
h)
1
k= 1
'V k
r..>.[n
x'* 1,
für
x = 1,
(x'* m1f, m ganze Zahl),
SIDX
n
L
für
(n = 2,3, ... ).
2.3. Für welche natürlichen Zahlen n gilt:
b) 2n > 2n + 1,
a) n!;;; 3n,
d) 4n > n 4 (man benutze das Ergebnis b»,
265n ?
f) 6;;a 4n2 + 121 .
2.4. Durch indirekten Beweis zeige man, daß
ff
a)
..f3:
b)
c)
d)
e)
(a 2 + b 2)2;;; 4ab(a - b)2 für beliebige reelle Zahlen a, b gilt,
für reelle Zahlen a, b mit 0< a < b die Ungleichung {b - .ja <
log2 6, 1 + 3
1- 2
irrationale Zahlen sind,
die Gleichung eX = 0 für keine reelle Zahl x eine Lösung hat,
..[b-""i gilt,
die Umkehrfunktion einer streng monoton fallenden Funktion ebenfalls streng monoton fallend ist,
f)* .fi für jede Primzahl p irrational ist.
2.5.· Man untersuche die durch
n
y(x) =
L Ca. .=1
xb.)2
gegebene Parabel auf ihre Nullstellen und leite daraus die Cauchy-Schwarzsche Ungleichung
n
n
v=1
11=1
L a/ L b/
3.
ab (a
p ,
b., v = 1, ... , n, beliebige reelle Zahlen).
Zahlen
(Bd. 1, 5.)
3.1. Für welche reellen Zahlen x gilt:
a) x + 2 >4 - x,
b) 3 - 2x > x - 9,
8
3. Zahlen
x-2
d) 4 + 2x
3x+2
x-l<
-x-2 '
b) x 2 + X - 6 < 0,
c)
-6x 2 + 13x < 6,
x2 - 9
e) --5-~2,
f) 2x+ 1 ~2x,
e) 3 _ 2x ~ 2,
g) 5 - 2x ~ 3,
h) x 2 + 6x + 4
x2 + X +6
4x+ 3
2x-4
f)
< x,
> 1.
3.2. Gesucht sind alle reellen Zahlen x, für die gilt:
a) 5x - x 2 ~ 0,
x-2
d) x + 3 < 2x,
g) (x - a)(a - x)
3x+ 5
x-
< 2ax,
aE
R\
h) x 3 - 4x 2 - 52x
> 80.
3.3. Man bestimme alle reellen Werte x, für die gilt:
a)
I~
e)
12:~341<1,
x - 21 = ; ,
b) Ix - 41 < 6,
f)
l;x~35!>3,
h) 2Ix-71<7(x+2)+15x+21,
j)* 12 -Ix + 11 - Ix + 211 = 1,
~ 4,
c) 11 + xl
g)
d) 12x + 11 = Ix - 11 + 1,
Ix-11+lx+51~4,
0* 11-12-lxlll=1,
k)* Ilx + 11 - Ix + 311 < 1.
3.4. Welche reellen Werte von x erftillen die Ungleichung:
a) Inlx+41>1,
b) V4x-x 2 -4 >3,
e). e1-1x'-tl> 1,
f)
Isin(2x+3)1~ ~,
c) Itanxl< 1,
g)*
d) 11+lgxl<3,
x<~,
a>O?
3.5. In der x,y-Ebene skizziere man den Lösungsbereich von:
b) (x - 1)2 (y + 5) > 0,
a) y ~ 1 - x und 2y < 5x + 1,
d) y ~ 2 - x 2 und x 2 + (y - 2)2 = 4,
e) Ix - llY ~ 1,
f) y - e 1xl > 0,
g) lxi + lyl ::;;; I (l> 0).
c) l.xyl = 1,
3.6. Man überlege sich, daß lai ~ la + bl + Ibl für beliebige reelle Zahlen a, b gilt und
weise damit die Ungleichung Hal-Ibll ::;;; la + bl nach.
3.7. Zeigen Sie, daß für nichtnegative Zahlen a, b,
a)
~ +b~2
c) ~
ra,
C,
d gilt:
eb > 0),
+ [bd : ; ; ~(a + b) (c + d).
3.8. Mittels vollständiger Induktion beweise man die Ungleichung
n
n
Il= (1 + aa ~ 1 + La"
i
1
i - 1
wenn die a, reelle Zahlen sind mit a, ::;;-1 und a,' aj
gleichungstyp erhält man für al = a2 = ,', = an?
~ 0
für i, j
=
1,2, "" n, Welchen Un-
9
3. Zahlen
a) Zl = 1 + i f3, Z2 = 1 - i,
c) Zl = 4 - 5i, Z2 = 4 + 5i,
b) Zl = 2 + 3i, Zz = 3 - 5i,
d) zl=i, z2=-2-4i.
3.10. Welche komplexe Zahl ist das Spiegelbild von Z =F
a)
c)
d)
e)
°
bei Spiegelung
am Ursprung,
b~ an der reellen Achse,
an der imaginären Achse,
an der Winkelhalbierenden des I. und III. Quadranten,
an der Winkelhalbierenden des 11. und IV. Quadranten?
3.11. Welche der folgenden Ungleichungen sind richtig?
a) -2F < 5,
c) F + 2 > 0,
b) (i + 2)2 > 0,
d) sin Ip ~ leitpi ,
e) (1 + i)4 > 0,
f) 1{21 i - 61 < 17 + 3il.
3.12. Von der komplexen Zahl Z bestimme man Real- und Imaginärteil:
1
a) Z = i + 1 '
d)
Z
3 + 2i
b) Z = 1+i'
c) Z =
( 1 + i )2
1- i '
= (2i + l)(i - 2) + 1
(2 - i)2 - 2 + i '
g) Z = 64· (sin21p + i f3 +
i) Z = re itp mit
COS2 1p
r = 2 f3:
Ip
r
= -
h) Z = re itp
6,
~
mit
r = 4,
Ip
=
~ 1I,
1I
3.13. Berechnen Sie den absoluten Betrag und das Argument der komplexen Zahlen, und
geben Sie die trigonometrische und die exponentielle Form an:
a) Z = i + 1,
d)
z
=
g) z=
1 + 2i
2- i '
b) Z =
f3 + i,
c) z = - ; + i-/[ ,
e) z
2- i
3i + (i - 1)2 '
f)z=i+3+~'
1+·
(1 - i)2
l+i
3.14. Man stelle folgende Zahlen in trigonometrischer Form und in der Gestalt x + iy
dar:
a) (1 - i)6,
e)
b)e3m,
(i - f3)8,
3 . f3)6
h) ( 2+1-2- ,
f)
c)(2-if3Y,
d)e 2- 6m,
Cb-f3 +ib+f3Y,
i) e
3+i~·
3
g) e 4 -
i · 3•5",
10
4. Kombinatorik
3.15. Geben Sie die komplexen Zahlen ZI = 4i, Zl =.f2 + .j6i, Z3 = 3.f3 - 3i,
Z4 = - 3 - 3i in exponentieller Darstellung an! Berechnen Sie mit deren Hilfe:
a)
Z~
Z5=-,
ZI
3.16. Für welche Punkte z = x + iy der Gaußschen Zahlenebene gilt:
c) Iz + 4i - 31 = 3,
b) 0<.f2 Im(z) < Izl,
d) Iz + 2 - il
~
z
e) - = 1
2,
g) Iz + 11 ~ 21z - 11,
z
'
1
1
f) Iz + 11 ~ Iz - 11,
i) Re(z2) = e (e reell),
h)-+-:-=1
z
z
'
k) Iz + 2il > 12z + iI,
m)* (z - Z)2 - (z + Z)2 = e (e reell).
j) Izl + Re(z) = 1,
I) Sz· z + 18Im(z) ~ 4Re(z2),
3.17. Bestimmen Sie alle verschiedenen Werte
geben!
a)
d)
b + 12i,
Vi,
Wj,
j = 0, 1, ... , (n - 1), die sich für
b) ~8 -ISi ,
c) V-2+2i,
e)
f)
V-8 + i8.f3,
'!fi er-
Vs + 8i.
3.18. Man löse die Gleichungen:
a)
Z6 =
1,
b)
Z4
c)
Z3 =
8i,
d)
Z4 =
e) Z5 + 10 - Si = 0,
g) (z - 3i)6 + 64 = 0,
i) Z2 - 2iz + 8 = 0,
= -1,
f) z2(1
~ Ci.ß - 1),
+ i) = 2z,
h) Izl=z·z,
j) Z2 - Z + iz - i = 0.
3.19. Welche Kurven besitzen in der Gaußschen Zahlenebene folgende Parameterdarstellungen:
(a
'*' 1,
a
> 0, 0::;:; t ~ 2n)?
Man gebe für a = 2 eine Skizze an!
3.20.* Für die durch die Gleichung Iz 2 - 11 = 1 bestimmte Punktmenge ist eine Parameterdarstellung in der Form z = z(qJ) = r(qJ) ei'l' anzugeben.
4.
Kombinatorik
(Bd. 1, 6.)
4.1. Sechs Personen werden namentlich in eine Liste eingetragen. Auf wie viele verschiedene Arten der Reihenfolge ist das möglich?
4. Kombinatorik
11
4.2. Bei der Herstellung eines Maschinenteils sind 7 Arbeitsgänge notwendig. N ach dem
ersten Arbeitsgang folgen 4 Arbeitsgänge, die in beliebiger Reihenfolge durchgeführt werden können. Eine weitere Bearbeitung ist aber erst nach Abschluß der ersten fünf Arbeitsgänge möglich. Die Reihenfolge der zwei restlichen Arbeitsgänge ist wiederum beliebig.
Wie viele Bearbeitungsreihenfolgen sind bei der Herstellung des Maschinenteils möglich?
4.3. a) Wie viele verschiedene dreibuchstabige "Wörter" lassen sich aus 5 verschiedenen
Buchstaben bilden, wenn kein Buchstabe mehrfach auftreten darf?
b) Wie groß ist die Anzahl der Wörter aus a), wenn die Buchstaben mehrfach auftreten
dürfen?
4.4. Wie viele neue "Wörter" lassen sich durch Umstellen der Buchstaben aus dem Wort
"ANANAS" gewinnen?
4.5. Für den Besuch der EOS bewerben sich aus einer Schule acht Mädchen und zwölf
Jungen. Sechs Mädchen und acht Jungen können nur ausgewählt werden. Wieviel verschiedene Möglichkeiten der Auswahl unter den Bewerbern gibt es?
4.6. Wie viele Ziehungen sind bei ,,6 aus 49" möglich, für die ein abgegebener Tip genau
einen "Dreier" ergibt?
4.7. Ein Kind baut durch Übereinanderlegen von 2 roten, 3 schwarzen und 4 weißen Baukastensteinen gleicher Form "Türme".
a) Wie viele verschiedene Türme sind möglich?
b) Wie groß ist die Anzahl der Türme, die mit einem weißen Stein beginnen?
4.8. Eine Lieferung von 25 Geräten, die durch ihre Fabrikationsnummern unterscheidbar
sind, enthält 4 fehlerhafte Geräte.
a) Wie viele verschiedene Stichproben vom Umfang 5 sind möglich?
b) Wie viele Stichproben vom Umfang 5 gibt es, die genau zwei fehlerhafte Geräte enthalten?
c) Wie viele Stichproben vom Umfang 5 gibt es, die höchstens ein fehlerhaftes Gerät enthalten?
d) Wie viele Stichproben vom Umfang 5 gibt es, die mindestens ein fehlerhaftes Gerät
enthalten?
4.9. Eine Sendung von 12 Erzeugnissen enthält 3 beschädigte Erzeugnisse.
a) Wie viele verschiedene Stichproben vom Umfang 4 sind möglich?
b) Wie viele Stichproben vom Umfang 4 gibt es, die mindestens ein beschädigtes Erzeugnis enthalten?
c) Wie viele Stichproben vom Umfang 4 gibt es, die höchstens zwei einwandfreie Erzeugnisse enthalten?
4.10. In einer Schachtel sind 4 Bleistifte und 11 Buntstifte. Wie viele Möglichkeiten gibt
es, daß beim zufälligen Herausgreifen von 5 Stiften höchstens 2 Buntstifte erfaßt werden?
4.11. Ein Parkplatz bestehe aus einer Reihe von 18 Boxen für PKW. Er sei durch Abstellen von 6 Trabant, 2 Fiat, 4 Wartburg, 5 Skoda und einem Volvo belegt. Die Fahrzeuge
sind durch ihr polizeiliches Kennzeichen alle unterscheidbar.
12
4. Kombinatorik
Wie viele verschiedene Möglichkeiten gibt es, daß
a) alle Skodas nebeneinander stehen,
stehen?
b) alle PKW vom gleichen Typ nebeneinander
4.12. Wie groß ist die Anzahl der möglichen "Bilder", die sich bei einem Wurf auf 9 - in
üblicher Weise aufgestellte - Kegel ergeben können?
4.13. Die Qualität von 8 Erzeugnissen wird überprüft ("Gut-schlecht-prüfung").
a) Wie viele verschiedene Prüfungsprotokolle sind insgesamt möglich?
b) Wie viele Prüfungsprotokolle enthalten das Element "gut" genau sechsmal?
4.14. An einem Pferderennen sind 8 Pferde beteiligt. Wie viele verschiedene Möglichkeiten gibt es, eine Vorhersage über die drei erstplazierten Pferde
a) ohne Angabe ihrer Reihenfolge,
b) mit Angabe ihrer Reihenfolge zu treffen?
4.15. Bei einem Versuch sind drei verschiedene Ergebnisse möglich. Dieser Versuch wird
zehnmal wiederholt. Wie viele verschiedene Versuchsprotokolle sind insgesamt möglich?
4.16. Eine Münze wird n-mal geworfen. Bestimmen Sie die Anzahl der verschiedenen
möglichen Versuchsausgänge!
4.17. Wie viele Diagonalen gibt es in einem regelmäßigen Zwölfeck?
4.18. Zur Kennzeichnung von Kraftfahrzeugen wird bekanntlich ein System aus Buchstaben und Ziffern verwendet.
a) Man bestimme für das System "Zwei Buchstaben - vier Ziffern" die Anzahl der Möglichkeiten, zu einer fest vorgegebenen Buchstabenkombination (z. B. IA) Kraftfahrzeuge durch verschiedene Ziffernkombinationen zu kennzeichnen.
b) Wie viele Möglichkeiten der Kennzeichnung von Kraftfahrzeugen gibt es insgesamt
für das System "Zwei Buchstaben - vier Ziffern"?
c) Wie ändert sich die unter b) berechnete Anzahl bei Verwendung des Systems "Drei
Buchstaben - drei Ziffern"?
4.19. Ein Gütekontrolleur entnimmt einem Posten von N Teilen (auch "Grundgesamtheit" oder "Los" vom Umfang N genannt), in dem sich MAusschußteile befinden, nacheinander ohne Zurücklegen n Teile (eine sog. Stichprobe ohne Zurücklegen vom Umfang n). Zwei Stichproben werden als gleich angesehen, wenn sie aus denselben Teilen
bestehen.
a) Man bestimme die Anzahl N k verschiedener Stichproben, die genau kAusschußteile
enthalten (k = 0,1,2, ... , n);
b) Man ermittle die Anzahl M j der Stichproben, die mindestens ein Ausschußteil enthalten.
c) Man berechne die entsprechenden Werte für N = 100, M = 3, n = 5.
4.20.* Auf einem Schachbrett sind acht verschiedene Türme so aufzustellen, daß keiner
dieser Türme einen anderen schlagen kann.
a) Wie viele derartige Aufstellungen gibt es?
b) Wieviel Zeit würde man benötigen, wenn man alle derartigen Aufstellungen ausführen
würde und pro Anordnung nur 1 Sekunde benötigen würde?
13
5. Mengen
c) Wie viele Möglichkeiten gibt es überhaupt, acht verschiedene Türme auf einem
Schachbrett aufzustellen?
d) Man ermittle das Verhältnis der unter a) und c) errechneten Anzahlen und interpretiere das Ergebnis!
5.
Mengen
(Bd. 1, 7.)
5.1. Es
A
werde
= Ulj = 1(2)15},
a) A u B,
b) M"-.if,
die
B
M
Universalmenge
=
{ili = 1(1)15}
und
ihre
Teilmengen
= {klk = 6(2)12}, C = {2, 3, 5, 12, 13} betrachtet. Man bestimme:
A n B, A, C, C n B, if n C,
C"-.A, (M',C)nC, B"-..CAuC).
5.2. Gegeben sind im R 1 die Mengen A
=
C='(-l; (0).
{x E R 1: -7
~
x < 5}, B
=
[0; 5],
Ermitteln Sie die folgenden Mengen:
a) Au B u C,
f) B "-. C,
b) A n C,
g) A n C,
d) An B,
e) ifnA,
i) CA u if) n C.
c) B u C,
h) if u C,
5.3. Die Mengen A = {xlix - 11 < 2}, B = {xl x-I< 2x + 7}, C = {xl 4,5 > Ix + 3,51}
sind Teilmengen der Universalmenge R 1. Man bestimme:
a) AnB,
b) A"-.B,
AnC,
B"-.A,
BnC,
B"-.C,
AuB,
C"-.B,
AuC,
A"-.C,
BuC,
C"-..A.
A,
if,
AuC,
AnC,
5.4. Man begründe, daß rur beliebige Mengen A und B gilt:
a) AnBc:Bc:AuB,
c)
b) AuB=B~Ac:B,
d) A c B ~ if cA.
AnB=A~AcB,
5.5. Es wird eine Menge M betrachtet. A, B seien beliebige Teilmengen von M. Man
stelle die Menge aller Elemente von M dar, die
a)
b)
c)
d)
e)
nicht zu A und B gleichzeitig gehören,
zu A gehören, aber nicht zu B,
nicht zu 1; aber zu B gehören,
die nicht "nur zu A oder nur zu B" gehören,
die entweder nur zu A oder nur zu B gehören.
5.6. Es sei A = {a, b, c, d, e} und B = {MIM cA}. Man entscheide, welche der folgenden
Aussagen wahr, welche falsch sind:
a E B,
f) {al cA,
a)
b) {b} E B,
g) 0 E B,
c) {al E A,
h) 0 c B,
d) A E B,
i) {0} c B.
e) Ac B,
5.7. A, B, C, D seien beliebige Mengen. Untersuchen Sie die folgenden Gleichungen und
begründen Sie, welche der Beziehungen wahr und welche falsch sind!
a) CA "-. B) u CB "-.. A) = CA u B) "-. CA n B),
b) Au CB"-.C) = CA u B)"-..(C"-.A),
c) A u CB"-. C) = (A u B) "-. CA u Cl,
14
d)
e)
f)
g)
h)
6. Funktionen
A n (B"- C) = (A u B) "- (A n C),
(A"-B)n(C"-D)=(AnC)"-(BuD),
[A n (A "-B») n C= (A n C)"-B,
(A u B)"-(Cu D) = (A "-C) u (B"-D),
A "- (B "- C) = (A " B) u (A n C).
5.8. A, B, C seien Teilmengen der Universalmenge M. Man vereinfache die folgenden
Ausdrücke!
a) A "-(A "-B),
b) An (B"-A),
d) (B"-A)u(A"-B)u(AnB),
f)* A "- [A "- [B "- (B "- C)j),
c) An (B"-A),
e) M"- [(M"-A) n B),
g)* (A "- B) n [(A n B) u (A "- C»).
5.9. P(A) sei die Potenzmenge von A und An := {ili = l(l)n,
nE
N}.
a) Man bestimme P(A 1), P(A 2), P(A 3 ).
b) Wieviel Elemente besitzt P(A n )?
c)* Die Elemente von P[P(ß») und P[ P(A 1)] sind anzugeben.
5.10. In der x,y-Ebene skizziere man die Produktmenge A x B für:
A = {xix E [0; 1] v x = 3}, B = {YlY E [1; 3] v y = 4},
b) A = {I, 2, 3}, B = [2; 4) u {5},
c) A = [1; 3] u (4; 5), B = [0; 2] u [4; 7).
d)* Ist die Gleichung (A x C) "- (B x C) = (A "- B) x C für beliebige Mengen A, B, C
stets erftillt?
a)
5.11. Als symmetrische Differenz zweier Mengen A und B erklärt man die Menge
A A B := (A u B) "- (A n B).
Man bestimme die symmetrische Differenz der Mengen A und B fiir:
a)
A={xlx 2 >1},
b)
A={(x,Y)lx2+y2~2},
c)*
A={(x,Y)IIXI+IYI~ ~}.
d)
e)
Zeigen Sie, daß A A B = (A "- B) u (B "- A) gilt.
Für die Mengen An aus 5.9. bestimme man AnAA m.
6.
B={XJJx+ ;J<l}.
B={(x,y)lx2+y2~1},
B= {(x,y)lmax{lxl, IYI} <I}.
Funktionen
(Bd. 1, 9.)
6.1. Sind durch folgende Zuordnungsvorschriften Funktionen Y = f(x) erklärt?
a) y = {
X2 + 1,04
3x - 1,2
lnx
c) lyl= x 2 +1'
für
fiir
x~l,
x ~ 1,6,
x ~ 1,6,
b) y
=
{2 für
x für
d) arctany=e~lxl,
x'*' 0,
x 2 = x,
xER\
15
6. Funktionen
e) y2 =
g) y = { e - ;,
°
f) tany = x,
X,
für
x > 0,
für
x ~ 0.
6.2. Man skizziere die Bilder der Funktionen y = f(x) mit x E R 1
= x + lxi,
a)
y
c)
y = (x -1)2'
e)
y = lnlxl,
g)
x
y=sin-,
n
j)
y= xlxl
1
x'*' 1,
x ,*,0,
n = 1, 2, 3,
+.[;2,
!)I,
m)* y=lsin2(x+
= Ix - 21 + 3x 2,
b)
y
d)
y = xL l'
f)
(x - 2)2
h)
y = 2 cosnx,
k)
Y = 4 sin(2x - 7),
1
lxi '*' 1,
+ (y + 1)2 = 4 mit
1
n)* Y =1 sinx
x'
y~
-1,
n = 1,2,3, i) y = cos (x +
1) Y = sin 1x -
;),
~ I,
x ,*,0.
6.3. Gegeben sind die Funktionen Yl(t) = al cos (wt + 11'1), Y2(t) = a2 cos (wt + 11'2) und
+ Y2(t) = a· cos(wt + 11'). Man gebe a und 11' in Abhängigkeit von al, a2, 11'10
y(t) = Yl(t)
1fJ2 an, wobei al
~ 0,
a2
~
°
und -
~ < 11'1,
11'2 <
~
gelten soll.
6.4. Bestimmen Sie
a) f(x - 1), f(x) - 1, - f(x), f( - x), 2f(x), f(2x), wenn f(x) = x-./x"+T ist,
b) N(x)], g[f(2)], J1g(x)], f[
g( ~)].
g[g(x)], g[rrf(32815)] für f(x) = x 3 - x und
g(x) = sin2x.
6.5. Welche der nachfolgenden Ausdrücke sind sinnvoll?
. rr
)
a arcslnT'
c) arccos
[~
b) cos 2 ~ - sin2 ~
12
12 '
(e +
!)].
d) tan 2 ( arccos
rr2
f) arcsin (x 2 + x
e) arccosT'
g) arcsin (sin x
~) ,
+ 2),
+ 1).
6.6. Man gebe an, welche der folgenden Ausdrücke definiert sind und vereinfache diese:
a) arsinh(; - 21e)'
b) arsinhO,
d) arcosh1,
e) artanhO,
1)
e4 g) artanh ( e4 + 1 '
c) arcoshO,
e2
+1)
h) arcoth ( e2 - 1. '
f) artanhrr,
i) arcoth (-1).
16
6. Funktionen
6.7. Skizzieren Sie für den jeweils größtmöglichen Definitionsbereich die Bilder der
~), f(~) , wenn
Funktionen y = fex), If(x)l, f(lxl}, f(x 2), [f(x)]2, f(
a) fex)
x,
=
d) fex) = lnx,
rx
g) fex) =
1
b) f(x)=~,
c) f(x) = eX,
e) fex) = sinx,
f) fex) = arctanx,
ist.
6.8. Von folgenden Funktionen y = fex) sind im R 1 der größtmögliche Definitionsbereich zu ermitteln, der zugehörige Wertebereich anzugeben und eine Skizze anzufertigen:
a)
y=~,
c)
y=
e)
y=n
b)
1
~'
für
~
1
y - ~Ixl- x '
d) y
n<x;:;;n+1
f). y = 4 - bx 2 -
3x 2 + Ix - 21,
=
(n ganz),
+3,
g) y=~(x-a)(x-b)
h)
y=.;x+2 - b - x ,
i) y = In (x - 1) - In x,
j)
y=ln(1-
1)
y=
n)
y = arcsin (ln x),
X
~),
k) y
b + sinx,
(a;:;; b),
- xl
In 123 +
x '
=
m)y = In sinx,
0) y =
1
f i--x .
6.9. Gesucht sind der größtmögliche Definitionsbereich und der zugehörige Wertebereich von y = fex) im R 1.
a)
d)
x
x+1
y = x 2 + 3x + 2 '
Y
=
[h+.2_ 2
VT-2x
1
y=
i)
y = In [a
=
~
e) y=ln(2-4sin 2 x),
'
X2+6X+ 4
-1
x2+ x - 6
'
g)
k)* y
b) y = - - - ,
3-
- rx-=1],
-J2- Ix
L
-
2!,
5x - x 2
~
Ig
4
'
h) y =
')*
a> 1,
X -
J
1)* Y
=
.
a) x
=
(2 -
2t + 3,
b) x=1-5t C,
d) x
y=
y=3+t 2 ,
= cos2t, y = sin t,
x +1
y=arcsm~,
rc;;s rx .
6.10. Gegeben sind die Parameterdarstellungen x
t2 -
f) y=ln(3-[x+7),
= x(t),
y = (t), tE R 1:
2t + 1,
c) x=cos2t,
y=sin 2 t,
17
6. Funktionen
f) x=2tanht
1 sm
. 2 t.
Y = "2
g) x = cos t,
y=_2_
cosht'
,
Bestimmen Sie den Wertebereich der Funktionen x(t) und y(t), und geben Sie nach Elimination von t Darstellungen der Gestalt F(x, y) = 0 bzw. y = f(x) an. Folgern Sie daraus
das Bild der zu den Parameterdarstellungen gehörenden Kurven.
6.11. Welche Kurven werden in der x,y-Ebene durch folgende Parameterdarstellungen
beschrieben? Geben Sie jeweils eine parameterfreie Darstellung der Kurvengleichung an
(a, b, xo, Yo const)!
a) x(t) = Xo + a cos t, y(t) = Yo + b sin t (a, b > 0; tE [O,2n]),
b) x(s) = Xo + s, y(s) = Yo + S2, SE R 1,
c) x(t)=xo+acosht, y(t)=Yo+bsinht (a,b>0,tER1),
d) x(u)=
co~u'
y(u)=btanu
~n)"{;})
(a,b>o;uE(-;,
6.12. Skizzieren Sie die in Polarkoordinatendarstellung r = r(q;) gegebenen Kurven:
a) r = 5,
b) r = q;
c) r = e"',
q; E R 1,
(q;?; 0),
d) r = 2 cos q;,
e) r=2a(1+cosq;),
q;E[O,2n],
q; E
( - ;, ;],
a>O.
6.13. Gesucht sind die Nullstellen folgender Funktionen y = f(x) mit x
1
e'
E R 1:
a)
Y = eX 2 -
c)
y = 19 (x 2 + 10x - 4) - 19 x - 1,
d)
y=1+~8x+1-~LOx+6,
e) y=(4cos 2 x-1)sinx-l,
3
y = 2(sin x - cos x) - sinx· sin (2x),
g) y = sinh2 X - 3 + 4 tanh2 x,
f)
2 VX
C2·
__
b) y = 102x - 101· lOx + 100,
h)* y = ~ x + 2 - ~ x + 4 +..;-;+3,
x?; 1,
i)* y = x - ; + arccos (sin x).
x?; - 2,
6.14. Welche der folgenden Funktionen (bei größtmöglichem Definitionsbereich) sind
gerade, welche sind ungerade und welche haben keine dieser Eigenschaften?
5
.
1
d) y=x+-
a) y=e- x,
b) y=x +7x,
c)
y=xsinx,
e) y = eCosx,
f) y = (x + 2)2,
g)
y=x(e-x+e X ), h) y=arcsinx,
i) y = arccos x,
j) Y =
k)
y - (x 3 + x)lsinxl '
1) y = Ix - 11
~lx4 + al ,
+ ~X2 + 2x + 1,
m) y
_
=
x'
lxi cosx
In[x +
P+!J.
1
e X -1
n) y = - 1
eX + 1
x
'
2 Wenzel, Ueb. Analysis 1
x
2
0)* y = - - + - .
eX -1
18
6. Funktionen
6.15. Gegeben ist die Funktiony=f(x), xe(-a,a), a>O. Weisen Sie die Gültigkeit
von f(x) = g(x) + u(x) nach, dabei ist g(x) eine gerade und u(x) eine ungerade Funktion. Bestimmen Sie g(x) und u(x) für:
a) f(x) = Xl + 2x 2 + 1,
b) f(x) = eX ,
c) f(x} = arcsinx,
e} f(x}
X
a = 1,
d} f(x} = 1- x'
a = 1,
Ix - 11 + Ix + 11·
=
6.16. Untersuchen Sie von den Funktionen y = f(x}, xe Rl, das Monotonieverhalten
und geben Sie den Wertebereich an. Welche Funktionen sind beschränkt?
a
a} y = ~,
x
x+3
c} y = - 4 _ x'
e) y =
Xl -
1
b) y = x2 _ 6x + 10 '
'* 0, a '* 0,
x'* 4,
6x 2 + 12x - 8,
g} y = arctan (
2x 2 + 3x +
x2
1)
'
x>O,
d) y =
x.Jx2,
f) y=
1-.f9"+h,
1 + ~9 + 3x
h} y=lnlsinxl,
Xii:;;
x,*k1t,
-3,
keG.
6.17. Welche der für x e Rl erklärten Funktioneny = f(x) sind periodisch? Falls Periodizität vorliegt, versuche man, die primitive Periode p zu ermitteln. Außerdem untersuche
man, ob die Funktionen nach unten bzw. nach oben beschränkt sind und gebe in diesen
Fällen Schranken an. Für welche Funktionen ergibt sich daraus die Beschränktheit?
a) y
=
~
sin (x + 3),
b) y = _ecos4x,
c) y = cos (2 -1tx),
d) y=sinh(x+sinx),
1
e) y
=
2 + sinx'
f) y = ln [2 sin 2 x + 1],
g) y
=
cos 2 3x + 1,
h) y = (cos 3x + 1)2,
sinx + cosx
coshx
'
J') Y = 1 1 2 '
+tan x
k) y=-+ sm 2 x + - -
1.
. x
x
1) y = sm
2 + cos],
m)y = 6sin1tx + cos2x,
n)y=cot2;+ISinxl,
')
1
Y=
cos2x
2 '
2
X
'* -21t + k 1t,
kE G,
x*2k1t,
kEG.
6.18. Welchen Wertevorrat haben die Funktionen y = fex)? Skizzieren Sie die Graphen
und geben Sie - falls vorhanden - die Umkehrfunktion y = Q1(x) an:
3
a) y = x,
XE
b
1
R ,
c) y = In(x 2 - 4),
lxi> 2,
)y={ (X+2)2+1
d) y =
2x + 8
rur
rur
';-;:=1 + rx+1,
xE[-2,l],
XE
xii:;;
(1, 3],
1,
19
6. Funktionen
_ 2x + 5
e) y-~,
f) y = eCOShx,
I
xER "-{3},
XE R \
g) y=2- 3x + 1,
h) y=sin(arcsinx),
xE[-1,1],
i) y = ; -
xER\
~ ~X2 -
4,
lxi
~ 2.
6.19. Geben Sie die Umkehrfunktion an von:
rx -4 ,
rx +1
a)
y=f(x) =
c)
x-2
y = fex) = x + 4 '
e)
g= g(8) = In
x~O,
b)
y = h(t) = er sinh t,
x* -4,
d)
Y = g(t) =
{fg
38- 2 '
--
g)* y = fex) = cos X,
2
8>3'
tER!,
.rt=2 ,
(i+4
f)* y = fex) = sinx,
t~
2,
x E [; rr,
~ rr] ,
XE [-2rr, -rr].
6.20. Man stelle die folgenden Funktionen durch algebraische Funktionen in Abhängigkeit von x dar:
a) y = fex) = sin (2 arcsinx), -1 ~ x~, 1,
b) y = f(x) = sin(arccos
~),
lxi ~ 1.
6.21. Berechnen Sie mittels Homerschema die Werte von P(x) an den angegebenen Stellen und bestimmen Sie die Zerlegung von P(x) in reelle Elementarfaktoren.
a) P(x)=2x s +4x 4 -4x 3 -8x 2 +2x+4; xo=1, xI=-1, x2=-2, x3=2,
xo= -3,
XI = -2,
c) P(x) = x 4 + 3x 3 - 2x 2 -12x - 8; Xo = -2, XI = 2, X2 = 3,
d) P(x) = x 6 -19x 4 + 44x 2 + 64; Xo = {3, XI = -{3, X2 = i,
e) P(x) = X S - 12x 4 + 56x 3 -120x 2 + 100x; Xo = 4, XI = 3 + i.
6.22. Ermitteln Sie von den gebrochen rationalen Funktionen y = fex) die Nullstellen,
Polstellen Geweils Vielfachheit angeben) und Lücken. Geben Sie die Asymptoten an, und
skizzieren Sie den Graphen von f und die Asymptote.
x2+ X
-
2
a) y = (x - 1)(x + 1)2 (X + 2) ,
x 3 -7x+6
+3 '
d) y =
x 4 + 4x 3 + 2x 2 - 4x - 3
x(x - 2)(x + 3)
,
f) y = (x2
c) y = x2 - 4x
e) y =
g) y =
2·
Xl -
b) y =
XS-
x 3 + X -1
x 2 -1
'
3x 2 - 4x + 12
x' + 5x + 6
'
x 3 - x' - x + 1
x'
'
x 2 -1
+ x)(x - 3)2 '
x 4 - 8x 2 + 16
h) y = (x2 - 3x - 10)(x + 1) ,