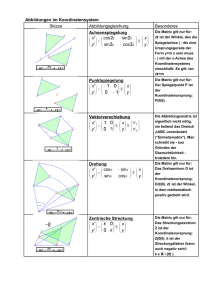
Mathematische Methoden der Physik Prof. Dr. Ludger Santen

Mathematische Methoden
der Physik
Prof. Dr. Ludger Santen
Kontakt: Ludger Santen, Universität des Saarlandes, Geb. E2 6, Zi. 4.15
[email protected]
http://www.uni-saarland.de/campus/fakultaeten/professuren/
naturwissenschaftlich-technische-fakultaet-ii/theoretische-physik/
professuren-theoretische-physik-fr-71/prof-dr-ludger-santen.html
letzte Aktualisierung: 13. Januar 2011
1
Inhaltsverzeichnis
1 Komplexe Zahlen
1.1 Komplexe Zahlen und die komplexe Ebene . . . . .
1.2 Die vier Grundrechenarten mit komplexen Zahlen . .
1.2.1 Addition und Subtraktion . . . . . . . . . . .
1.2.2 Multiplikation . . . . . . . . . . . . . . . . .
1.2.3 Division . . . . . . . . . . . . . . . . . . . .
1.3 Eigenschaften komplexer Zahlen . . . . . . . . . . .
1.3.1 Die komplex konjugierte Zahl . . . . . . . .
1.3.2 Betrag und Argument komplexer Zahlen . . .
1.4 Komplexe Zahlen und die Exponentialfunktion . . .
1.4.1 Die Polardarstellung komplexer Zahlen . . .
1.4.2 Multiplikation und Division in Polarform . .
1.4.3 de Moivres Theorem . . . . . . . . . . . . .
1.5 Trigonometrische Funktionen . . . . . . . . . . . . .
1.5.1 Additionstheoreme . . . . . . . . . . . . . .
1.6 Die n-te Wurzel von 1 . . . . . . . . . . . . . . . . .
1.7 Der komplexe Logarithmus . . . . . . . . . . . . . .
1.8 Hyperbolische Funktionen . . . . . . . . . . . . . .
1.9 Hyperbolische Umkehrfunktionen – Areafunktionen
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
2 Elemente der linearen Algebra
2.1 Vektorräume . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.1.1 Lineare Gleichungen . . . . . . . . . . . . . . . . . .
2.1.2 Vektorräume: Definition und Beispiele . . . . . . . . .
2.2 Linearkombinationen, lineare Hülle und erzeugende Systeme .
2.3 Lineare (Un-) Abhängigkeit . . . . . . . . . . . . . . . . . . .
2.4 Vektorräume und Basis . . . . . . . . . . . . . . . . . . . . .
2.5 Lösen linearer Gleichungssysteme . . . . . . . . . . . . . . .
2.6 Matrizen . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.6.1 Rechenoperationen mit Matrizen . . . . . . . . . . . .
2.6.2 Determinanten . . . . . . . . . . . . . . . . . . . . .
2.6.3 Matrixinversion . . . . . . . . . . . . . . . . . . . . .
2.6.4 Matrizen: Definitionen und Eigenschaften . . . . . . .
2.6.5 Das Eigenwertproblem . . . . . . . . . . . . . . . . .
2.6.6 Entartete Eigenwerte . . . . . . . . . . . . . . . . . .
2.6.7 Eigenvektoren und Eigenwerte einer normalen Matrix
2.6.8 Basiswechsel und Ähnlichkeitstransformationen . . .
2.6.9 Diagonalisierung von Matrizen . . . . . . . . . . . . .
3 Differentialrechnung im Rn
3.1 Funktionen mehrerer Variablen . . . . . . . . . . . . . . .
3.2 Das totale Differential und die totale Ableitung . . . . . .
3.3 Exakte und inexakte Differentiale . . . . . . . . . . . . .
3.4 Rechenregeln für partielle Ableitungen . . . . . . . . . . .
3.5 Variablentransformation . . . . . . . . . . . . . . . . . . .
3.6 Taylor-Entwicklung . . . . . . . . . . . . . . . . . . . . .
3.7 Stationäre Punkte von Funktionen mit mehreren Variablen
3.8 Extrema mit Nebenbedingungen . . . . . . . . . . . . . .
2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
5
5
6
6
6
6
7
7
7
8
8
9
10
10
12
13
13
14
15
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
16
16
16
17
18
18
19
20
23
23
24
25
26
28
29
30
31
32
.
.
.
.
.
.
.
.
35
35
36
37
37
38
39
40
41
4 Integralrechnung im Rn
4.1 Zweidimensionale Integrale . . . . . . . . . . . . . .
4.2 Dreifachintegrale . . . . . . . . . . . . . . . . . . .
4.3 Variablentransformation . . . . . . . . . . . . . . . .
4.3.1 Transformationen im R2 . . . . . . . . . . .
4.3.2 Variablentransformation in Dreifachintegralen
5 Vektoranalysis
5.1 Der Gradient . . . . . . . . . . . . . . . .
5.2 Raumkurven und Kurvenintegrale . . . . .
5.3 Länge und Bogenlänge . . . . . . . . . . .
5.4 Skalare Kurvenintegrale . . . . . . . . . . .
5.5 Vektorielle Kurvenintegrale . . . . . . . . .
5.5.1 Verhalten bei Umparametrisierung:
5.6 Konservative Vektorfelder und Potential . .
5.7 Weitere Vektoroperatoren . . . . . . . . . .
5.8 Oberflächenintegrale . . . . . . . . . . . .
5.9 Das vektorielle Oberflächenintegral . . . .
5.10 Der Integralsatz von Gauß . . . . . . . . .
5.11 Der Integralsatz von Stokes . . . . . . . . .
3
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
43
43
44
45
45
47
.
.
.
.
.
.
.
.
.
.
.
.
49
49
49
50
51
51
52
52
53
54
57
59
60
Vorbemerkungen
Die Vorlesung Mathematische Methoden der Physik ist weder eine Mathematik- noch eine Physikvorlesung. Sie stellt vielmehr eine Vielzahl von Rechenmethoden für die Vorlesungen der
theoretischen und experimentellen Physik zur Verfügung.
Dieses Konzept hat einige praktische Konsequenzen:
Training: Sie lernen nicht zu schwimmen, wenn Sie regelmäsig Wettkämpfe im Fernsehen
schauen. Sie lernen es auch nicht, wenn Sie Freunden beim Schwimmen zusehen. Sie
müssen selber schwimmen und das ist am Anfang schwer! Leichter wird es, wenn Ihnen
ein Trainer Tipps gibt.
Gleiches gilt für die mathematischen Methoden. Sie müssen selber rechnen, rechnen, rechnen! Lassen Sie sich aber bei Problemen von Ihren Trainern (Übungsgruppenleiter, Tutor,
Kommilitonen) helfen.
Tutorien: Die Vorlesung mathematische Methoden der Physik baut auf das Abiturwissen aus
dem Mathematik-Grundkurs auf, also auf die Rechenmethoden, die wir im Vorkurs noch
einmal wiederholt haben. Sollten Sie damit noch Probleme haben, sollten Sie sich bemühen, die Probleme schnell zu beseitigen, eventuell mit Hilfe des Tutoriums.
Ausrichtung: Physik wird in dieser Vorlesung nur eine untergeordnete Rolle spielen, insbesondere werden Sie keine physikalischen Übungsaufgaben lösen. Dies hat den Grund, dass
die Übertragung des physikalischen in ein geeignetes mathematisches Problem häufig den
Schwierigkeitsgrad der Aufgabe erhöht und eigens eingeübt werden muss. Der geeignete
Ort, um diese Fähigkeit zu üben, sind die Module der theoretischen und experimentellen
Physik.
Zur Vorlesung wird ein Skript veröffentlicht, das Sie für die Lösung der Übungen nutzen können. Sollten Sie zusätzlich Bedarf an einem Lehrbuch haben, gibt es eine reiche Auswahl an
geeigneten Lehrbüchern. Eine unvollständige Auswahl finden Sie in folgender Liste:
1. Rainer Wüst, Höhere Mathematik für Mathematiker und Physiker, Bde 1& 2, Wiley VCH,
2003
2. Christian B. Lang, Norbert Puckler, Mathematische Methoden in der Physik, Spektrum
Akademischer Verlag, 2005.
3. Helmut Fischer, Helmut Kaul, Mathematik für Physiker 1-3, Teubner, 2005
4
1 Komplexe Zahlen
Durch die Einführung komplexer Variablen ist es für beliebige algebraische Gleichungen möglich, die Wurzeln der Gleichung anzugeben. Damit entfällt eine Einschränkung die im Körper
der reellen Zahlen besteht.
Die Einführung der komplexen Zahlen hat aber nicht nur den Lösungsraum algebraischer Gleichungen erweitert, sondern auch viele analytische Rechnungen stark vereinfacht, wie wir in
einem späteren Abschnitt dieser Vorlesung sehen werden.
1.1 Komplexe Zahlen und die komplexe Ebene
Obwohl komplexe Zahlen in sehr vielen Bereichen auftreten, begegnen sie uns am natürlichsten
als Wurzeln von Polynomen. Dies wollen wir am Beispiel der quadratischen Gleichung
z2 − b z + c = 0
.
(1)
diskutieren. Die Gleichung (1) hat die beiden Lösungen1
z1/2 =
i
p
1h
b ± b2 − 4c .
2
(2)
Wenn der Ausdruck unter der Wurzel (die Diskriminante) positiv ist, also b2 − 4c > 0 gilt, sind
die beiden Lösungen reelle Zahlen. Für b2 − 4c < 0 steht man allerdings vor dem Problem, dass
es im Körper der reellen Zahlen keine Lösung der obigen Gleichung gibt. Um nun trotzdem eine
Lösung der Gleichung angeben zu können, muss man also den Zahlenraum erweitern. Dazu
führt man eine neue Art von Zahl ein, die sog. imaginäre Einheit
i mit der Definition
i2 = −1 .
(3)
Mit dieser Vereinbarung lässt sich nun auch für b2 − 4c < 0 eine Lösung angeben
z1/2 =
i
p
1h
b ± i 4c − b2 .
2
(4)
Ganz allgemein schreiben wir komplexe Zahlen in der Form
z = x + iy ,
(5)
wobei x und y reelle Zahlen sind. Man nennt√x den Realteil und y den Imaginärteil von z. In
dem vorigen Beispiel ist x = b/2 und y = ± 4c − b2 /2. Man schreibt für den Real- und den
Imaginärteil auch
x = Re(z)
y = Im(z).
und
(6)
Der Fundamentalsatz der Algebra sagt uns auch, daß ein Polynom wie in Gl. (1) immer eine
Lösung hat, nur ist diese manchmal komplex. Ist das Polynom von Grade 3 und höher, also
vom Grade n, so sagt uns der Fundamentalsatz, daß es n-Lösungen gibt, die aber nicht alle ver2
schieden seinen
√ müssen. Im speziellen Beispiel hat das Polynom z − 4z + 5 = 0 die Lösungen
z1/2 = 2 ± 16 − 20/2 = 2 ± i.
1 Zur Erinnerung: Gleichung (1) kann umgeschrieben werden in (z − b/2)2 + c − b4 /4 = 0 bzw. (z − b/2)2
p
p
c. Zieht man daraus die Wurzel, so folgt z − b/2 = ± b2 /4 − c bzw. z = b/2 ± b2 /4 − c .
5
= b2 /4 −
1.2 Die vier Grundrechenarten mit komplexen Zahlen
1.2.1 Addition und Subtraktion
Die Addition zweier komplexer Zahlen z1 und z2 ergibt im allgemeinen wieder eine komplexe
Zahl. Dabei werden die Realteile xi und die Imaginärteile yi separat addiert.
z1 + z2 = (x1 + iy1 ) + (x2 + iy2 ) = (x1 + x2 ) + i(y1 + y2 ) .
(7)
Dies hat eine gewisse ähnlichkeit zu Vektoren, wo die Addition komponentenweise ausgeführt
wird. Man kann sich auch sofort davon überzeugen, daß aus der Gültigkeit des Assoziativ- und
Kommutativgesetzes für die Addition reeller Zahlen, diese Gesetze ebenso für komplexe Zahlen
folgen.
z1 + z2 = z2 + z1
(Kommutativgesetz)
z1 + (z2 + z3 ) = (z1 + z2 ) + z3
(Assoziativgesetz)
(8)
(9)
1.2.2 Multiplikation
Die Multiplikation zweier komplexer Zahlen ergibt gewöhnlich auch wieder eine komplexe
Zahl. Das Produkt erhält man, indem man alles ausmultipliziert und sich daran erinnert, daß
i2 = −1 gilt.
z1 z2 = (x1 + iy1 )(x2 + iy2 )
= x1 x2 + ix1 y2 + iy1 x2 + i2 y1 y2
= (x1 x2 − y1 y2 ) + i(x1 y2 + x2 y1 ).
(10)
Das Produkt der beiden Zahlen z1 = 3 + 2i und z2 = −1 − 4i ist demnach
z1 z2 = (3 + 2i)(−1 − 4i)
= −3 − 2i − 12i − 8i2
= 5 − 14i
Wie für reelle Zahlen, so gelten auch für die Multiplikation komplexer Zahlen das Kommutativund das Assoziativgesetz
z1 z2 = z2 z1
(z1 z2 )z3 = z1 (z2 z3 ) .
(11)
1.2.3 Division
Der Quotient zweier komplexer Zahlen ist
z3 =
z1 x1 + iy1
=
z2 x2 + iy2
.
Dies möchte man natürlich wieder in der Form z3 = x3 + iy3 mit x3 , y3 ε R darstellen und erweitert hierfür einfach den Quotienten mit (x2 − iy2 ).
z1
z2
=
=
(x1 + iy1 )(x2 − iy2 ) (x1 x2 + y1 y2 ) + i(x2 y1 − x1 y2 )
=
(x2 + iy2 )(x2 − iy2 )
x22 + y22
x1 x2 + y1 y2
x2 y1 − x1 y2
+i 2
x22 + y22
x2 + y22
6
(12)
1.3 Eigenschaften komplexer Zahlen
1.3.1 Die komplex konjugierte Zahl
Zu einer komplexen Zahl z = x + iy wird noch die komplex konjugierte Zahl z∗ = x − iy
niert.
Es gelten einige nützliche Rechenregeln. Für z = x + iy gilt
defi-
(z∗ )∗ = z
z + z∗ = 2x
z − z∗ = 2iy
(13)
1.3.2 Betrag und Argument komplexer Zahlen
Da jede komplexe Zahl z = x + iy als geordnetes Paar reeller Zahlen betrachtet werden kann,
lassen sich solche Zahlen durch Punkte in der xy-Ebene, der sogenannten komplexen Ebene
(Argand Diagramm) darstellen. Eine komplexe Zahl die z.B. durch den Punkt P = (3, 4) in der
xy-Ebene repräsentiert wird, kann daher als (3, 4) oder 3 + 4i gelesen werden. Für jede komplexe
Zahl gibt es genau einen Punkt in der Ebene. Umgekehrt entspricht jedem Punkt der Ebene eine
komplexe Zahl. Manchmal bezeichnet man die x und y-Achse als relle bzw. imaginäre Achse
und die komplexe Ebene als z-Ebene.
Abbildung 1: Punkt in der komplexen Ebene.
Der Abstand des Punktes (x, y) vom Ursprung (0, 0) entspricht der Länge des Vektors~r = (x, y),
was wir als den Betrag der komplexen Zahl interpretieren. Der Betrag einer komplexen Zahl
wird also definiert durch:
p
| z |= x2 + y2 .
(14)
Wenn man die komplex konjugierte Zahl benutzt, kann man den Betrag auch in der Form
p
√
| z |= z · z∗ = (x + iy)(x − iy)
(15)
angeben. Mit dem Argument einer komplexen Zahl arg(z) wird der Winkel φ = arg z in Abb. 1
bezeichnet
y
arg(z) = arctan( ) .
(16)
x
Durch Konvention wird dieser Winkel entgegen des Uhrzeigersinnes positiv gewählt.
Zur Illustration betrachten wir das konkrete Beispiel z = 2 − 3i. Der Betrag dieser komplexen
Zahl ist
q
√
| z |= 22 + (−3)2 = 13
7
und ihr Argument
3
arg(z) = arctan(− ) ∼ −56, 3◦ = −0.98279
2
1.4 Komplexe Zahlen und die Exponentialfunktion
Nachdem wir die einfachen Rechenregeln für komplexe Zahlen diskutiert haben, müssen wir uns
mit elementaren Funktionen komplexer Variablen beschäftigen. Dies ist eigentlich die Aufgabe
der Funktionentheorie, die wir in einem späteren Abschnitt ausführlicher diskutieren werden.
Eine wichtige Voraussetzung für eine sinnvolle Definition komplexer Zahlen ist, dass sie für
verschwindenden Imaginärteil wieder in die entsprechende reelle Funktion übergehen.
Eine komplexe Funktion von besonderer Bedeutung ist die Exponentialfunktion. Die komplexe
Exponentialfunktion ist eng mit den trigonometrischen Funktionen verknüpft, woraus sich einige
wichtige Rechenregeln ergeben.
Die Reihendarstellung der komplexen Exponentialfunktion gilt auch für komplexe Zahlen:
∞
ez =
∑
k=0
zk
.
k!
(17)
Aus dieser Tatsache, die im Rahmen der Funktionentheorie ausführlicher diskutiert wird, lassen
sich einige nützliche Zusammenhänge herleiten.
1.4.1 Die Polardarstellung komplexer Zahlen
Im folgenden wählen wir ω = iφ mit reeller Variable φ . In diesen Fall ist dann ω rein imaginär
und exp(ω) = exp(iφ ). Wir nutzen nun die Reihendarstellung (17) der Exponentialfunktion aus
und schreiben davon die ersten Summanden hin
i
i2
i3
φ + φ2 + φ3 +...
1!
2!
3!
i
i2 2 i3 3
exp (−iφ ) = 1 − φ + φ − φ + . . .
1!
2!
3!
exp (iφ ) = 1 +
,
.
(18)
Nutzen wir noch die Regel i2 = −1, so bekommen wir mit
i2 2 i4 4
φ + φ + . . .)
2!
4!
φ2 φ4
= 2(1 −
+
− . . .)
2! 4!
exp (iφ ) + exp (−iφ ) = 2(1 +
(19)
wieder eine reelle Zahl! Offensichtlich sind für reelles φ die komplexen Zahlen z = eiφ und
z = e−iφ konjugiert komplex zueinander, also z∗ = (eiφ )∗ = e−iφ . Demzufolge gilt
z + z∗ = eiφ + e−iφ = 2 Re{eiφ }
z − z∗ = eiφ − e−iφ = 2i Im{eiφ }
.
Für den Betrag von eiφ folgt mit der Regel (14)
|z|2 = |eiφ |2 = zz∗ = eiφ e−iφ = eiφ −iφ = e0 = 1
Offensichtlich beschreibt eiφ einen Kreis mit Radius 1 in der komplexen Ebene.
8
(20)
Abbildung 2: graphische Darstellung der Eulerformel
Mit z = x +iy = eiφ sieht man aus Abb. 1 daß x = cos φ und y = sin φ . Daraus folgt die Eulersche
Formel
cos φ + i sin φ = eiφ .
(21)
Hier sieht man nun auch, daß es sich z.B. für z = iφ = iωt bei eiωt um eine Schwingung handelt.
Die Exponentialfunktion in dieser Schreibweise ist daher bei der Untersuchung von Schwingungen unentbehrlich.
Insbesondere folgt sofort
eiπ = −1,
eiπ/2 = i
und
ei0 = ei2π = 1.
Mit der Darstellung (21) kann man auch leicht eine altbekannte Formel neu ableiten
1 = |z|2 = (cos φ + i sin φ )(cos φ − i sin φ )
= cos2 φ + sin2 φ = 1
.
Darüberhinaus läßt sich jede komplexe Zahl in dieser sogenannten Polardarstellung
z = reiφ
schreiben, wobei r und φ reell sind. Das Argument arg(z) = φ ist in dieser Darstellung trivial
abzulesen.
1.4.2 Multiplikation und Division in Polarform
Die Multiplikation und Division komplexer Zahlen wird in Polardarstellung ausgesprochen einfach. Das Produkt der komplexen Zahlen z1 = r1 eiφ1 und z2 = r2 eiφ2 ist mit den Regeln für die
Exponentialfunktion durch
z1 z2 = r1 eiφ1 r2 eiφ2 = r1 r2 ei(φ1 +φ2 )
(22)
gegeben. Daraus folgen auch unmittelbar |z1 z2 | = |z1 | · |z2 | und arg(z1 z2 ) = arg(z1 ) + arg(z2 ).
Insbesondere ist auch die Division komplexer Zahlen in Polardarstellung sehr einfach
z1 r1 eiφ1
r1
r1
=
= eiφ1 e−iφ2 = ei(φ1 −φ2 )
iφ
2
z2 r2 e
r2
r2
.
Die Beziehungen |z1 /z2 | = |z1 |/|z2 | und arg(z1 /z2 ) = arg z1 − arg z2 folgen.
9
(23)
1.4.3 de Moivres Theorem
Ein recht wichtiges Theorem für sin und cos folgt aus der einfachen Identität (eiφ )n = einφ .
Schreibt man dies in der sin- und cos-Darstellung, so ist dies äquivalent mit
n
(cos φ + i sin φ )n = eiφ = einφ = cos(nφ ) + i sin(nφ ) .
(24)
1.5 Trigonometrische Funktionen
De Moivres Theorem zeigt deutlich den Zusammenhang zwischen (komplexer) Exponentialfunktion und den trigonometrischen Funktionen. Diesen Zusammenhang werden Sie beispielsweise bei der Lösung von Schwingungsgleichungen oder der Herleitung von Additionstheoremen nutzen können.
Wir betrachten nun mit die komplexen Darstellungen von sin und cos:
cos φ
=
sin φ
=
1 iφ
(e + e−iφ )
2
1 iφ
(e − e−iφ ) ,
2i
(25)
welche unmittelbar aus (21) und (20) folgen. Mit Gl. (18) erhält man auch Reihendarstellungen
für cos und sin
cos φ
=
(−1)k 2k
φ
k=0 (2k)!
sin φ
=
∑ (2k + 1)! φ 2k+1
∞
(26)
∑
∞
(−1)k
.
(27)
k=0
Entsprechend folgt auch für tan und cot eine Exponentialdarstellung.
tan φ
=
cot φ
=
sin φ
1 eiφ − e−iφ
,
=
cos φ
i eiφ + e−iφ
cos φ
eiφ + e−iφ
= i iφ
.
sin φ
e − e−iφ
(28)
Ersetzt man nun φ = nΘ, so folgt auch für den n-fachen Winkel Θ zusammen mit z = eiΘ
1 n 1
1 inΘ
cos(nΘ) =
e + e−inΘ =
z + n
2
2
z
1 n 1
1 inΘ
−inΘ
(29)
z − n
sin(nΘ) =
=
e −e
2i
2i
z
Anwendungsbeispiele
1) überlagerung zweier Schwingungen gleicher Frequenz ω, welche gegeneinander Phasenverschoben sind. Die Gesamtschwingung ist dann
f (t) = A1 sin(ωt + ϕ1 ) + A2 sin(ωt + ϕ2 )
i
1 h i(ωt+ϕ1 )
=
A1 e
− e−i(ωt+ϕ1 ) + A2 ei(ωt+ϕ2 ) − e−i(ωt+ϕ2 )
2i
1
1 i(ωt+ϕ1 ) =
e
A1 + A2 ei(ϕ2 −ϕ1 ) − e−i(ωt+ϕ1 ) A1 + A2 e−i(ϕ2 −ϕ1 )
2i
2i
1 i(ωt+ϕ1 ) =
e
A1 + A2 ei(ϕ2 −ϕ1 ) + konj. komplex
2i
10
Nun kann man den Vorfaktor umschreiben und man erhält mit
−η A1 + A2 ei(ϕ2 −ϕ1 ) = A eiϕ
(30)
wieder eine komplexe Zahl, die sich leicht mit den bisherigen Regeln berechnen läßt.
Abbildung 3: Modellverstärker für den Input x(t) = 0.2sin(t) (durchgezogene Linie) und dem
Output y(t) = 0.3sin(t) + 0.5sin2(t). Ein ähnliches Verhalten zeigen auch nichtlineare optische Frequenzverdoppler.
Abbildung 4: Eine Überlagerung zweier leicht verstimmter Schwingungen y = cos(x) +
cos(1.1x). Das Ergebnis ist eine Schwebung.
Das Endsignal hat also die gleiche Frequenz, aber eine andere Amplitude und ist phasenverschoben
f (t) = A cos(ωt + ϕ) .
(31)
2) Betrachten wir einen Verstärker mit einem Input-Signal x(t) = x0 cos(ωt) und der Eigenschaft, daß der Output mit dem Input wie folgt zusammenhängt
y(t) = B(x + f x2 ) = B(x0 cos(ωt) + x02 cos2 (ωt)) .
(32)
Um daran zu erkennen, welche Frequenzen im Output sind, muß man z.B. ausrechnen, wie
cos2 (ωt) mit der ursprünglichen Frequenz zusammenhängt.
3) Ein anderes Problem von großer Bedeutung betrifft die überlagerung von zwei Schwingungen
mit zwei leicht verstimmten Frequenzen:
f (t) = A1 cos((ω + ∆ω)t + ϕ1 ) + A2 cos(ωt + ϕ2 ) .
Das Resultat ist eine Schwebung. In der Akustik ist dieses Phänomen gut hörbar.
11
(33)
1.5.1 Additionstheoreme
Die Herleitung von Additionstheoremen im Körper der reellen Zahlen ist häufig kompliziert.
Durch die Beziehung zwischen komplexer Exponentialfunktion und den trigonometrischen Funktionen kann man dagegen diese Theoreme sehr leicht herleiten. Wir wollen dies an einigen Beispielen diskutieren. Wir betrachten dazu:
sin(x + y) =
1 i(x+y)
e
− e−i(x+y)
2i
.
(34)
Von exp(i(x + y)) brauchen wir nur den Imaginärteil und zur Umformung dieses Ausdruckes
verwenden wir die Produktregel für Exponentialfunktionen und die Euler-Formel (21)
ei(x+y) = eix eiy = (cos x + i sin x)(cos y + i sin y)
= i(sin x cos y + cos x sin y) + cos x cos y − sin x sin y
(35)
Subtrahieren wir hiervon noch exp(−i(x + y)) so bleibt nur der Imaginärteil übrig. Insgesamt
bekommen wir dadurch
sin(x + y) = sin x cos y + cos x sin y
.
(36)
Ein weiteres Problem, das man durch das Theorem von de Moivre leicht lösen kann, ist sin 3Θ
und cos 3Θ durch Potenzen von cos Θ und sin Θ auszudrücken. Wir erhalten
cos 3Θ + i sin 3Θ = (cos Θ + i sin Θ)3
= (cos3 Θ − 3 cos Θ sin2 Θ) + i(3 sin Θ cos2 Θ − sin3 Θ).
Vergleichen wir die die Real- und Imaginärteile auf beiden Seiten, so bekommen wir
cos 3Θ = cos3 Θ − 3 cos Θ sin2 Θ
= cos3 Θ − 3 cos Θ(1 − cos2 Θ)
= 4 cos3 Θ − 3 cos Θ
(37)
und
sin 3Θ = 3 sin Θ cos2 Θ − sin3 Θ
= 3 sin Θ(1 − sin2 Θ) − sin3 Θ
= 3 sin Θ − 4 sin3 Θ
.
(38)
Ein weiteres Beispiel ist cos3 Θ, das wir mit z = eiΘ und Gl. (20) leicht berechnen können
cos3 Θ =
=
=
=
1
1
(z + )3
3
2
z
1 3
1 1
(z + 3z + 3 + 3 )
8
z z
1
1 3 1
3
(z + 3 ) + (z + )
8
z
8
z
3
1
cos(3Θ) + cos Θ
4
4
(39)
Potenzen von sin x und cos x führen offensichtlich zu höheren Harmonischen wie cos(3x) und
umgekehrt lassen sich höhere harmonische Funktionen durch Potenzen der Grundfrequenz ausdrücken. An dem oben genannten nichtlinearen Verstärker wird dann eine Frequenzmischung
deutlich. Auf diese und ähnliche Weise lassen sich eine Reihe weiterer nützlicher Beziehungen
ableiten, die in Formelsammlungen aufgelistet werden.
12
1.6 Die n-te Wurzel von 1
Die Gleichung z2 = 1 hat die beiden bekannten Lösungen z = ±1. Nachdem uns die komplexen
Zahlen bekannt sind, können wir auch alle Lösung von zn = 1 beschaffen. Nach dem Fundamentalsatz der Algebra gibt es für jedes Polynom n-ten Grades n Lösungen. Wir wissen auch schon,
daß
e2iπk = cos(2πk) + i sin(2πk) = 1
(40)
falls k ∈ Z Demzufolge können wir schreiben
zn = e2ikπ
(41)
oder
z = e2iπk/n
.
(42)
Dies bedeutet, die Lösungen von zn = 1 sind
z1,2,...,n = 1, e2iπ/n , . . . , e2i(n−1)π/n ,
(43)
wobei wir hier k = 0, 1, 2, . . . , n − 1 verwenden. Größere Werte von k ergeben keine neuen Lösungen, sondern sind nur eine Duplizierung der vorhandenen Lösungen.
Betrachten wir als Beispiel die Lösungen der Gleichung z3 = 1. Wenden wir nun Formel (43)
an, so erhalten wir z1 = 20i , z2 = e2iπ/3 , z3 e4iπ/3 . Für k = 3, also z4 = e6iπ/3 = e2iπ = 1 = z1 , nur
eine Wiederholung von z1 .
Es ist auch keine überraschung, daß wir auch |z|3 = |z3 | finden, da alle Wurzeln auf dem Einheitskreis liegen und damit den Betrag 1 haben.
1.7 Der komplexe Logarithmus
Die Umkehrfunktion der Exponentialfunktion exp(x) = y ist der Logarithmus
x = ln y
(44)
falls x, y ∈ R.
Der Logarithmus ist auch die Umkehrfunktion der Exponentialfunktion für komplexe Zahlen.
Für den Logarithmus einer komplexen Zahl z schreiben wir
w = ln z
mit
z = ew
(45)
Jetzt können wir die Regeln für die Exponentialfunktion ausnutzen, um den Logarithmus eines
Produktes komplexer Zahlen
z1 · z2 = ew1 ew2 = ew1 +w2
(46)
zu berechnen
ln(z1 z2 ) = w1 + w2 = ln(z1 ) + ln(z2 ) .
(47)
Nehmen wir eine komplexe Zahl auf dem Einheitskreis, so wissen wir bereits, dass
z = eiφ = ei(φ +2πk) .
(48)
Diese Vieldeutigkeit wirkt sich auch auf den Logarithmus aus und es folgt
ln z = ln r + i(φ + 2π) .
13
(49)
Um die Vieldeutigkeit zu vermeiden, schränkt man das Argument arg(z) = φ auf −π < φ ≤ π
ein und nennt ln(z) bei dieser Einschränkung den Hauptwert.
Und was ist ln(−i)? Hier schreiben wir zuerst −i in Exponentialform um
π
ln(−i) = ln ei(−π/2+2nπ) = i − + 2πn
,
(50)
2
mit einer natürlichen Zahl n. Dies bedeutet ln(−i) = −i π2 , 3i π2 , . . . Für den Hauptwert gilt ln(−i) =
− π2 i.
1.8 Hyperbolische Funktionen
Was bedeutet eigentlich cos(iφ ) oder sin(iφ )? Mit dieser Wahl eines rein imaginären Argumentes im cos und sin werden die Exponenten von e in Gl. (25) reell und es folgt eine neue Klasse
von Funktionen:
1 −φ
cos(iφ ) =
(e + e+φ ) =: cosh φ
2
1 −φ
(e − e+φ ) =: sinh φ .
(51)
i sin(iφ ) =
2
Die beiden Funktionen cosh φ und sinh φ bezeichnet man als ”Cosinus Hyperbolicus” oder ”Hyperbelcosinus” bzw. ”Sinus Hyperbolicus” oder ”Hyperbelsinus”. Diese hyperbolischen Funktionen sind die komplexen Analoga zu den trigonometrischen Funktionen. Neben den beiden
fundamentalen Funktionen gibt es in Analogie zu den trigonometrischen Funktionen die verbleibenden hyperbolischen Funktionen
sinh x
ex − e−x
= x
cosh x e + e−x
cosh x ex + e−x
coth x =
= x
sinh x
e + e−x
1
2
sechx =
=
cosh x ex + e−x
1
2
,
(52)
cosechx =
=
sinh x ex − e−x
siehe Abb. 5. Folgende Beziehungen zwischen trigonometrischen und Hyperbelfunktionen sind
noch ganz hilfreich
tanh x =
cosh x = cos(ix)
i sinh x = sin(ix)
cos x = cosh(ix)
i sin x = sinh(ix) .
(53)
ähnlich zu den Relationen zwischen verschiedenen trigonometrischen Funktion lassen sich auch
Hyperbelfunktionen durch andere Hyperbelfunktionen ausdrücken. Gehen wir von cos2 x+sin2 x =
1 aus und benutzen (53) so folgt mit cosh2 x = cos2 (ix) und sinh2 x = − sin2 (ix)
cosh2 x − sinh2 x = 1 .
(54)
Einige andere Identitäten können ebenso abgeleitet werden.
sech2 x = 1 − tanh2 x
cosech2 x = coth2 x − 1
sinh(2x) = 2 sinh x cosh x
cosh(2x) = cosh2 x + sinh2 x
14
(55)
Abbildung 5: Graphen der verschieden hyperbolischen Funktion deren analytische Darstellung im Text angegeben ist.
1.9 Hyperbolische Umkehrfunktionen – Areafunktionen
Die Umkehrfunktion von y = sinh x nennen wir x = arsinh y. Wir sind nun an der expliziten Form
dieses Ausdruckes interessiert. Hierfür drückt man ex durch Linearkombinationen von cosh x und
sinh x aus.
ex = cosh
p x + sinh x
=
1 + sinh2 x + sinh x
p
=
1 + y2 + y .
(56)
Wenden wir auf beide Seiten den Logarithmus an, so folgt der explizite Ausdruck für die Umkehrfunktion
p
x = arsinh(y) = ln( 1 + y2 + y) .
(57)
Auf ähnliche Weise erhält man
p
x = arcosh(y) = ln( y2 − 1 + y)
(58)
für |y| > 1. Die Umkehrfunktion von tanh(x) nennen wir analog artanh(y) und die explizite Form
ist
1
1+y
x = artanh(y) = ln
.
(59)
2
1−y
15
2 Elemente der linearen Algebra
Wobei die Beweiskraft einzig vom Geschick der Beweisinszenierung abhängt
(worunter nicht nur Beweisrhetorik, Beweisinstallierung und Beweismarketing zu verstehen sind, sondern auch die Verwandlung der
Wirklichkeit in einen beweisäquivalenten Zustand).
Heinrich Steinfest - Cheng
2.1 Vektorräume
In der Schule und im Vorkurs sind Ihnen einige wichtige Eigenschaften von Vektoren vorgestellt
worden. Wir betrachten an dieser Stelle den Zusammenhang zwischen linearen Gleichungssystemen, Vektorräumen und Matrizen.
2.1.1 Lineare Gleichungen
Lineare Gleichungen sind von der Form:
L(u) = v,
mit den Vektoren u und v
Beispiele solcher Systeme gibt es häufig in der Physik:
(i) Schwingungsgleichung:
bzw.
d
d2
u(t) + a
u(t) + b u(t) = v(t)
2
dt dt
d2
d
+a
+ b u(t) = v(t)
dt 2
dt
(ii) Potentialgleichung:
d2
d2
u(x,
y)
+
u(x, y) = v(x, y)
dx2
dy2
2
d
d2
+ 2 u(x, y) = v(x, y)
dx2
dy
bzw.
(iii) Vertrauter dürfte Ihnen die Form
2x1 + x2 − x3 = y1
−7x1 − 5x2 + 3x3 = y2
sein, mit


x1
u =  x2  ,
x3
v=
y1
y2
,
16
L(u) =
2x1 + x2 − x3
−7x1 − 5x2 + 3x3
.
Diese Probleme haben gemeinsam, dass für die Abbildung
L : u 7→ L(u)
gilt:
L(α1 u1 + α2 u2 ) = α1 L(u1 ) + α2 L(u2 ).
Dies sind die definierenden Eigenschaften von linearen Abbildungen. Einige Eigenschaften von
linearen Abbildungen sind direkt offensichtlich:
(i) Die homogene Gleichung L(u) = 0 besitzt immer die triviale Lösung u = 0
(ii) Sind u1 und u2 Lösungen der homogenen Gleichung, so ist auch jede Linearkombination
α1 u1 + α2 u2 eine Lösung. Die Lösungen bilden einen Vektorraum.
(iii) Ist u0 eine spezielle Lösung der homogenen Gleichung L(u) = 0, so erhält man sämtliche
Lösungen durch u = uh + u0 , wobei uh sämtliche Lösungen der homogenen Gleichung
durchläuft.
Mit der Einführung von linearen Abbildungen sind offenbar einige Begriffe verbunden, die
wir näher diskutieren wollen. Außerdem werden wir uns mit der Lösbarkeit von linearen Gleichungssystemen beschäftigen.
2.1.2 Vektorräume: Definition und Beispiele
Definition:
Einen nichtleere Menge V heißt Vektorraum über R bzw. über C, wenn auf V einen Addition und einen Multiplikation mit Zahlen aus R bzw. C erklärt ist, sodass die Rechenregeln der
Vektorräume gelten. Im einzelnen wird ein Vektorraum durch folgende Eigenschaften bestimmt:
Wenn u, v, w ∈ V gilt, dann ist auch u + v ∈ V . Ferner entlält V ein ausgezeichnetes Element 0.
Es gelten dann die Regeln:
(A1 ) (u + v) + w = u + (v + w)
(A2 ) u + v = v + u
(A3 ) u + 0 = u
(A4 ) Die Gleichung u + x = v besitzt stets genau eine Lösung x. Mit u ∈ V , α ∈ R (bzw. α ∈ C)
gehört auch α · u zu V und es gilt:
(S1 )
(S2 )
(S3 )
(S4 )
(α + β ) · u = α · u + β · u
α · (u + v) = α · u + α · v
α · (β · u) = (α · β ) · u
1·u = u
Die Elemente von V nennen wir Vektoren. Die Elemente des zugrundeliegenden Zahlenkörpers
R bzw. C Skalar (z.B. α, β ). Das neutrale Element der Addition 0 nennen wir Nullvektor .
Beispiele:
• Rn und Cn sind Vektorräume über R bzw. C. Dies gilt auch für n = 1, wobei dann der
Unterschied zwischen Vektoren und Skalaren nicht mehr besteht.
17
• Funktionenräume:
M ist eine nichtleere Menge, K einer der Zahlenkörper R bzw. C. Dann ist
F (M , K) = { f : M 7→ K}
mit
f + g : x 7→ f (x) + g(x)
α · f : x 7→ α · f (x)
ein Vektorraum über K.
Definition: Teilräume
Ist V ein Vektorraum über K, so nennen wir U einen Unterraum bzw. Teilraum, wenn mit
u, v ∈ U auch jede Linearkombination α · u + β · v zu U gehört, mit α, β ∈ K. Weiterhin setzen
wir vorraus, dass U eine nichtleere Teilmenge von V ist.
Beispiele:
• {0} ist immer Teilraum von V , genauso wie V selbst.
• Die Lösungen x = (x1 , x2 , ..., xn ) ∈ Rn der Gleichung
a1 · x1 + ... + an · xn = 0
bilden einen Teilraum des Rn .
Übungsaufgabe: Gilt dies auch für a1 · x1 + ... + an · xn = mit t 6= 0?
2.2 Linearkombinationen, lineare Hülle und erzeugende Systeme
Definition: Linearkombination
Jeder Vektor der Form
n
α1 v1 + α2 v2 + ... + αn vn =
∑ αk vn
mit
αi ∈ K
k=1
heißt Linearkombination der Vektoren v1 , ..., vn ∈ V .
Definition: Aufspann bzw. lineare Hülle
Die Menge aller Linearkombinationen aus v1 , ..., vn heißt ihr Aufspann bzw. ihre lineare Hülle
span{v1 , ..., vn }.
Der Aufspann ist ein Teilraum von V .
2.3 Lineare (Un-) Abhängigkeit
Definition:
Vektoren v1 , ..., vn eines K-Vektorraums V heißen linear abhängig (l.a.), falls es Skalare (α1 , ..., αn ) ∈
K gibt, die alle nicht Null sind, sodass
α1 v1 + α2 v2 + ... + αn vn = 0
Andernfalls heißen sie linear unabhängig.
18
Beispiele:
(i) Die Vektoren


1
e1 =  0  ,
0


0
e2 =  1  ,
0


0
e3 =  0 
1
sind linear unabhängig.
(ii) Sind die Vektoren


1
 0 

u=
 −1  ,
0


0
 1 

v=
 1 ,
−2


3
 −1 

w=
 −4 
2
des R4 linear unabhängig? Wir müssen dazu offenbar die Gleichung
x1 u + x2 v + x3 w = 0
lösen, bzw. in Koordinaten
x1 + 3x3 =0
−x1 + x2 − 4x3 =0
−2x2 + 2x3 =0.
Folglich
x2 − x3 = 0 ⇒ x2 = x3 und − x1 − 3x3 = 0.
Offenbar ist x1 = 3 und x2 = x3 = −1 Lösung des homogenen Gleichungssystems. Die
Vektoren sind also linear abhängig.
2.4 Vektorräume und Basis
Definition:
Ein geordnetes n-Tupel B = (v1 , ..., vn ) von Vektoren des K-Vektorraums V heißt eine Basis
von V , wenn sich jeder Vektor v ∈ V als Linearkombination
v = α1 v1 + ... + αn vn
in eindeutiger Weise darstellen lässt. Die durch v eindeutig bestimmten Zahlen α1 , ..., αn heißen
die Koordinaten von v bezgl. der Basis B. Sie werden zu einem Koordinatenvektor


α1


(v)B =  ... 
αn
zusammengefasst.
Satz:
B = (v1 , ..., vn )
ist genau dann eine Basis, wenn v1 , ..., vn ein linear unabhängiges Erzeugendensystem ist.
Bemerkung:
Es sei U = span{v1 , ..., vn } ein Teilraum von V , dann ist v1 , ..., vn ein Erzeugendensystem für
U.
19
Beweis:
(i) Es sei B = (v1 , ..., vn ) eine Basis. Nach Definition gilt V = span{v1 , ..., vn }. Jeder Vektor
v ∈ V muss sich mit eindeutig bestimmten Koeffizienten aus den v1 , ..., vn bestimmen
lassen. Dies gilt auch für den Nullvektor. Damit folgt aus
α1 v1 + ... + αn vn = 0
⇒
α1 , ..., αn = 0
und somit die lineare Unabhängigkeit.
(i) Es seien v = α1 v1 + ... + αn vn = β1 v1 + ... + βn vn zwei Darstellungen von v. Mit
(α1 − β1 )v1 + ... + (αn − βn )vn = 0
folgt aus der linearen Unabhängigkeit von v1 , ..., vn ; α1 = β1 , ..., αn = βn , also die Eindeutigkeit.
Satz: Dimension eines Vektorraums
Besitzt ein Vektorraum V eine Basis aus n Vektoren, so besteht auch jede andere Basis aus n
Vektoren. n ist gleichzeitig die Dimension des Vektorraums V . Also
dim V = n
Bemerkung:
Für V = {0} gilt dim V = 0, besitzt V keine endliche Basis, so bezeichnen wir ihr als unendlichdimensional.
Basisergänzungssatz: Ist b1 , ..., bn ein Erzeugendensystem von V und sind a1 , ..., an lin. unabhängige Vektoren in V , die keine Basis von V bilden, so lassen sich die a1 , ..., an durch Hinzufügen geeigneter bk zu einer Basis von V ergänzen.
Basisauswahlsatz:
Besitzt der Vektorraum V 6= {0} ein endliches Erzeugendensystem b1 , ..., bn , so lässt sich aus
diesem eine Basis für V auswählen.
2.5 Lösen linearer Gleichungssysteme
Ein lineares Gleichungssystem (LGS) mit m Gleichungen für n Unbekannte hat die Form
a11 x1 + a12 x2 + . . . + a1n xn = b1
..
.
am1 xm + am2 xm + . . . + amn xm = bm
Gegeben sind in diesem Problem die Koeffizienten aik ∈ K und die Zahlen bk ∈ K. Gesucht sind
alle Vektoren x(x1 , ..., xn ) ∈ Kn , die die obige Gleichung erfüllen.
Rangbedingung zur Lösbarkeit: Lineare Gleichungssysteme in der obigen Form können kompakt durch Ax = b geschrieben werden, mit der Koeffizientenmatrix




x1
a11 . . . a1n



..  ,
A =  ...
x =  ...  ∈ Kn .
. 
xn
am1 . . . amn
Der Rang einer Matrix bestimmt sich aus:
20
(i) der Maximalzahl linear unabhängiger Zeilenvektoren (Zeilenrang)
(ii) der Maximalzahl linear unabhängiger Spaltenvektoren (Spaltenrang)
(iii) der Dimension des Bildraums der linearen Abbildung x 7→ Ax,
Kn 7→ Km
Beispiel: Die Matrix


1 −2 4 0 5
A =  −2 1 −1 2 −6 
−1 −1 3 2 −1
hat den Rang 2, da die ersten beiden Vektoren linear unabhängig sind und die dritte Zeile die
Summe der ersten beiden ist.
Rangbedingung:
Hat V die Dimension n, W die Dimension m so ist die lineare Abbildung L : V 7→ W genau
dann in jektiv (eineindeutig), wenn Rang(L) = n und genau dann sur jektiv, wenn Rang(L) = m.
Bemerkung:
Für eine injektive Abbildung gilt, dass jedem Bild höchsten ein Urbild zuzuordnen ist, d.h. dass
aus f (x1 ) = f (x2 ) stets x1 = x2 und aus x1 6= x2 f (x1 ) 6= f (x2 ) folgt. Für eine surjektive Abbildung f M 7→ N gilt, dass N die Bildmenge von f ergibt, d.h. dass für jedes y ∈ N die Gleichung
f (x) = y mindestens einen Lösung aus M existiert.
Das LGS Ax = b ist also eindeutig lösbar, wenn Rang(A) = n und universell lösbar, wenn
Rang(A) = m ist .
Eliminationsverfahren:
Gesucht: Alle Lösungen des LSG
4x2 + 4x3 + 3x4 − 2x5 = 16
−3x1 − 3x2 + 3x3 + x4 − 2x5 = − 2
2x2 + 2x3 + 3x4 − 4x5 = 14
4x1 − x2 − 9x3 − 2x4 − x5 = − 5
1. Schritt: Umstellung der Gleichungen (nur noch Koeffizenten), Vertauschung der Zeilen I&II
−3 −3 3
1 −2 −2
0
4
4
3 −2 16
0
2
2
3 −4 14
4 −1 −9 −2 −1 −5
2. Schritt: Normierung der Kopfzeile
1 1 −1 − 13 23 23
0 4
4
3 −2 16
0 2
2
3 −4 14
4 −1 −9 −2 −1 −5
21
3. Schritt: Elimination von x1 aus der Zeile IV durch Multiplikation der Kopfzeile mit (−4) und
Addition zur 4. Zeile
2
2
1 1 −1 − 13
3
3
0 4
4
3
−2 16
0 2
2
3
−4 14
2
− 23
0 −5 −5 − 3 − 11
3
3
4. Schritt: Normierung der Kopfzeile im Restsystem
3
1
1
4
2
2
3
−5 −5 − 23
− 21
−4
− 11
3
4
14
− 23
3
5. Schritt: Eliminatione von x2 aus den letzten beiden Gleichungen
((−2)· bzw 5· erste Zeile)
1 1 43 − 21 4
0 0 32 −3 6
37 37
0 0 37
3
12 − 6
6. Schritt: Die Koeffizienten von x3 verschwinden. Das obige Schema führt dann auf das Restsystem
3
−3 6
2
37
− 37 37
12
6
3
und schließlich nach Normierung der Kopfzeile und Elimination von x4 (und x5 ) in der unteren
Zeile
1 −2 4
0 0 0
7. Schritt: Zeilenstufenform
1
0
0
0
1 −1 − 13
3
1 1
4
0 0
1
0 0
0
2
3
2
3
1 −2 4
−2 4
0 0
bzw.
1
2
2
x1 + x2 − x3 + − x4 + x5 =
3
3
3
3
1
x2 + x3 + x4 − x5 = 4
4
2
x4 − 2x5 = 4
8. Schritt: Auflösen der Gleichung in Zeilenstufenform. Mit der Festlegung x3 = s und x5 = t
ergibt sich


 
 
1
1
2
 1 
 −1   −1 

 

 
 



x=
 0 +s 1 +t  0 .
 4 
 0   2 
1
0
0
22
2.6 Matrizen
2.6.1 Rechenoperationen mit Matrizen
(i) Matrizen werden elementweise addiert, die Addition ist (daher) kommutativ und assoziativ, d.h.
A+B = B+A
A + (B +C) = (A + B) +C.
(ii) Multipliziert man eine Matrix mit einer Konstanten, so werden alle Elemente mit der
Konstanten multipliziert.
B = αA
⇔
bi j = ∧ik α · ai j .
(iii) Die Multiplikation von Matrizen erfolgt nach der Regel „Zeile mal Spalte“:
AB = C
⇔
Ci j = ∑ aik bk j
k
Aus der Rechenregel ergibt sich sofort, dass die Zahl der Spalten von A der Zahl der Zeilen
von B entsprechen muss.
(iv) Für die Matrixmultiplikation gilt das Distributiv- aber nicht das Kommutativgesetz.
Beispiel:
0 1
1 0
A=
B=
1 0
0 −1
0 · 1 + 1 · 0 0 · 0 + 1 · (−1)
0 −1
AB =
=
1 · 1 + 0 · 0 1 · 0 + 0 · (−1)
1 0
0 1
BA =
6= AB
−1 0
Die Matrixmultiplikation ist also nicht-kommutativ!
Bemerkung:
Die obigen Matrizen sind zwei der drei Pauli − Matrizen, die die Komponenten des quantenmechanischen Spinoperators bilden.
Definition: Der Kommutator [A, B] ≡ AB − BA misst die Differenz zwischen den beiden Produkten von A, B.
Spezielle Matrizen:
(i) Nullelement
(ii) Einheitsmatrix
A = 0 ⇔ ai j = 0
A = 1 ⇔ ai j = δi j
(
0, wenn i 6= j
δi j =
1, wenn i = j
23
mit
Kronecker- Delta
Es gilt offenbar A0 = 0A = 0 und A1 = 1A = A.
Bemerkung:
Bei Matrizen treten einige Eigenschaften auf, die man von der Multiplikation von gewöhnlichen
Zahlen nicht kennt. Gegeben seien die Matrizen:
1 2
10 4
A=
B=
3 6
−5 2
0 0
22
44
;
BA =
⇒
AB =
0 0
−11 −22
Das Produkt der Matrizen ergibt die Nullmatrix, obwohl keine der beiden Matrizen Null ist.
Damit kann also auch AC = AD gelten, obwohl C 6= D.
2.6.2 Determinanten
Die Determinante einer 2x2 Matrix wird definiert durch
a11 a12 := a11 a22 − a21 a12
det(A) = a21 a22 Bem.: Das lineare Gleichungssystem
a11 a12
Au = v
mit
A=
;
a21 a22
u=
u1
u2
;
v=
v1
v2
ist genau dann universell und eindeutig lösbar, wenn det(A)6= 0.
Laplacescher Entwicklungssatz
Die Determinante einer nxn Matrix A = (ai j ) kann man durch Entwicklung nach der i-ten Zeile
n
det(A) = |A| =
∑ (−1)i+ j ai j Ai j j=1
bzw. der k-ten Spalte
n
det(A) = |A| =
∑ (−1) j+k a jk A jk j=1
berechnen.
Mit: Ai j ist eine (n-1) x (n-1) Matrix, die durch Streichung der i-ten Zeile und der j-ten Spalte
aus A hervorgeht.
Beispiel Determinante einer 3x3 Matrix (Entwicklung nach der ersten Spalte)
a11 a12 a13 a21 a22 a23 = a11 a22 a23 − a21 a12 a13 + a31 a12 a13
a22 a23
a32 a33 a32 a33 a31 a32 a33 Eigenschaften von Determinanten
(i) det(A) = det(AT )
(ii) Für nxn Matrizen gilt: det(AB)= det(A)*det(B)
24
(iii) det(A−1 )= (det(A))−1
Determinantenformen
Definition: Eine Abbildung F:Kn x...xKn → K(n > 1) heißt
(i) Multilinearform auf Kn , wenn F in jedem der n Argumente (Spalten) linear bei festgehaltenen
restlichen Spalten ist:
F(..., αx + β y, ...) = αF(..., x, ...) + β F(..., y, ...)
(ii) Alternierende Multilinearform falls (i) gilt und
F(..., ai , ..., a j , ...) = −F(..., a j , ..., ai , ...)
(iii) Determinantenform falls (i) und (ii) erfüllt sind und F(e1 , ..., en ) = 1 für die kanonische
Basis e1 , ..., en des Kn gilt. (ei Einheitsvektor in i-Richtung)
Bemerkungen:
(i) Für alternierende Multilinearformen gilt
F(a1 , ..., an ) = 0
falls a1 , ..., an linear abhängig sind.
Insbesondere gilt natürlich, dass F(a1 , ..., an ) = 0 falls ai = ak für i 6= k, bzw. ai = αak .
(ii) Die Determinante ändert sich nicht, wenn ein Vielfaches einer Zeile von einer anderen Zeile
subtrahiert wird. Damit lässt sich die Matrix durch Umformungen auf obere Dreiecksform bringen, ohne dass sich die Determinante ämdert. Die Determinante ergibt sich dann einfach aus der
Multiplikation der Diagonalelemente.
Bsp.:
a
a
det 11 12
a21 a22
a12
= det a11
0 a22 − a21 a12
a11
= a11 (a22 − a21 a12 ) = a11 a22 − a21 a12
a11
2.6.3 Matrixinversion
Für quadratische Matrizen A kann man eine Matrix A−1 suchen, sodass AA−1 = A−1 A = 1.
Die inverse Matrix lautet:
A−1
ij
=
1
C ji
det(A)
mit der Kofaktormatrix
C ji = (−1)i+ j Mi j
und dem Minor Mi j , d.h. die Determinante der Streichmatrix. Offenbar ist die Matrix nur dann
invertierbar, wenn det(A) 6= 0. Da det(AA−1 ) = det(1) = 1 gilt, erhalten wir
det(A−1 ) =
1
.
det(A)
Ferner gilt: (AB)−1 = B−1 A−1 wegen (AB)−1 (AB) = B−1 A−1 AB = B−1 B = 1
25
Beispiel: Bestimmung der Inversen der Matrix A


2
4
3
A =  1 −2 −2 
−3 3
2
Kofaktoren:
−2 −2
= −4 + 6 = 2 = 4 = C11
M11 = det
3
2
1 −2
M12 = det
= 2 − 6 = −4 = −C12
−3 2
Insgesamt erhalten wir:


2
4 −3
C =  1 13 −18 
−2 7 −8
det(A) = 2 · 2 + 1 · 1 + (−3) · (−2) = 11
und


2
1
−2
T
C
1
 4
13
7 
A−1 =
=
det(A) 11
−3 −18 −8
Bemerkung:
Ist die Koeffizientenmatriz eines LGS invertierbar, so kann man die Lösung des GS einfach
durch Matrizinversion bestimmen.
⇒
Ax = b
x = A−1 b
2.6.4 Matrizen: Definitionen und Eigenschaften
• Die Spur einer Matrix:
Die Spur einer Matrix Sp(A) bzw. tr(A) ist die Summe ihrer Diagonalelemente
Sp(A) = tr(A) = ∑(A)ii = ∑ aii
i
i
Es gilt:
tr(AB) = ∑ Aik Bki = ∑ Bki Aik = tr(BA)
ik
ik
Allgemeiner gilt:
Die Spur ist invariant gegenüber zyklischer Vertauschung von Matrixprodukten, also
tr(A1 A2 ...An ) = tr(An A1 ...An−1 )
• Die transponierte Matrix:
AT : AT
ij
= (A) ji . Es gilt (AB)T = BT At .
• Die komplex-konjugierte Matrix:
A∗ bzw. A, die die Elemente a∗i j enthält.
• Die hermitisch konjugierte Matrix (bzw. adjungierte Matrix):
26
A+ = AT
∗
• Die Diagonalmatrix:
Nur die Diagonalelemente sind verschieden von Null.
• Die symmetrische Matrix:
A = AT
Die antisymmetrische Matrix:
A = (−1)AT
• Die relle Matrix:
A = A∗
Die imaginäre Matrix:
A = −A∗
• Die orthogonale Matrix:
AT = A−1 (für eine quadratische Matrix, z.B. die Drehmatrix)
• Die hermitische Matrix:
A+ = A
Die antihermitische Matrix:
A+ = −A
• Die unitäre Matrix:
A+ = A−1
• Die nilpotente Matrix:
für n > n0 gilt An = 0
• Die singuläre Matrix:
Matrix deren Determinante verschwindet (nicht invertierbar)
27
2.6.5 Das Eigenwertproblem
Die Mutiplikation eines Vektors mit einer Matrix ist im Allgemeinen eine Drehstreckung, d.h.
Richtung und Betrag des Vektors werden geändert. Liegt der Vektor aber parallel zur Drehachse, wird nicht seine Richtung, sondern ausschließlich sein Betrag geändert. Also gilt für einen
solchen Vektor v
Av = λ v.
(60)
Vektoren v, die die Gleichung (60) erfüllen, nennt man Eigenvektoren der Matrix A und den
Skalierungsfaktor seinen Eigenwert. Zur Bestimmung von λ und v betrachtet man die homogene
Gleichung
(A − λ 1) v = 0,
die direkt aus (60) folgt.
Eine nichtlineare Lösung dieses homogenen Gleichungssystems kann offenbar nur dann erfolgen, wenn det (A − λ 1) verschwindet. Die Bedingung
det (A − λ 1) = 0
(61)
führt für eine n × n Matrix auf ein Polynom n-ten Grades in λ , das über den Körper C n
(nicht notwendigerweise verschiede) Lösungen besitzt. Diese Lösungen sind die Eigenwerte des
Problems. Das Polynom, das sich aus der Eigenwert- bzw. Säkulargleichung (61) ergibt, wird
charakteristisches Polynom genannt.
Beispiel: Bestimmung der Eigenwerte der Matrix A mit


1 1 −3
A =  1 1 −3  .
3 −3 −3
Die Säkulargleichung zur obigen Matrix lautet
1−λ
det (A − λ 1) = det 1
3
⇒
1
1−λ
−3
−3
−3
−3 − λ
= 0.
(1 − λ )2 (−3 − λ ) − (1 · (−3) · 3) + (−3 · 1 · (−3)) − 9(1 − λ ) − (−3 − λ ) + 9(1 − λ ) = 0
(1 − 2λ + λ 2 )(−3 − λ ) − 9 + 9 + 3 + λ = 0
−3 − λ + 6λ + 2λ 2 − 3λ 2 − λ 3 + 3 + λ = 0
−λ 3 − λ 2 + 6λ = 0
−λ (λ − 2)(λ + 3) = 0
Die Eigenwerte lauten demnach λ1 = 2, λ2 = 0 und λ3 = −3.
Es bleibt also noch die Aufgabe die Eigenvektoren zu bestimmen. Dazu setzt man die Eigenwerte
ein und löst das zugehörige homogene Gleichungssystem. Wir wollen dies am Beispiel von oben
explizit durchführen.
Für den Eigenwert λ1 = 2 ergibt sich das folgende Gleichungssystem:
28
−x1 + x2 + 3x3 = 0
x1 + x2 − 3x3 = 0
| +1· Zeile I
3x1 − 3x3 − 3x3 = 0
| +3· Zeile I
−x1 + x2 + 3x3 = 0
0 =0
⇒
4x3 = 0
x3 = 0 ⇒ x1 = x3 = t
Der zugehörige Eigenvektor lautet also


t
x1 =  t  .
0
Es ist nützlich mit normierten Eigenvektoren zu arbeiten, sodass
!
|x1 | = 2t 2 = 1
1
t=√
2
⇒
Damit lautet der normierte Eigenvektor


1
1
x1 = √  1  .
2
0
Analog ergibt sich für die übrigen Eigenvektoren


1
1 
−1 
x2 = √
und
3
1


1
1 
−1  .
x3 = √
6
−2
Bemerkung:
Die Menge der Eigenwerte und Eigenvektoren einer Matrix nennt man auch das Eigensystem.
Die Eigenwerte von A und AT stimmen überein, die zugehörigen Eigenvektoren nicht unbedingt.
Dies bedeutet, dass linke und rechte Eigenvektoren nicht übereinstimmen müssen.
2.6.6 Entartete Eigenwerte
Wir wenden uns wiederum einem Beispiel zu. Es sei
0 1
A=
.
−1 2
⇒
!
det (A − λ 1) = (−λ )(−2 − λ ) + 1 = (1 + λ )2 = 0
⇒
λ1,2 = −1
Der einzige Eigenvektor dieser Matrix ist
1
x1 = √
2
1
−1
.
Die 2 × 2 Matrix A ist ein Beispiel für eine nicht-hermitische Matrix, bei der das Eigensystem
eine niedrigere Dimension hat als die Matrix. Die geometrische Multiplizität, d.h. die Zahl der
Eigenvektoren zu einem Eigenwert ist also in diesem Fall geringer als die algebraische Multiplizität.
29
2.6.7 Eigenvektoren und Eigenwerte einer normalen Matrix
Wir wollen nun die Eigenschaften verschiedener Matrizen mit den Eigenschaften von Eigenvektoren und -werten in Verbindung bringen. Dazu betrachen wir zunächst normale Matrizen, d.h.
Matrizen für die gilt
A+ A = AA+
Bemerkung:
Unitäre und hermitische Matrizen sind gleichzeitig normale Matrizen (bzw. orthogonale und
symmetrische Matrizen im Falle reeller Matrizen).
Es sei nun x Eigenvektor zum Eigenwert λ , also gilt
(A − λ 1) x = 0.
Mit B = A − λ 1 gilt dann Bx = 0 = x+ B+ ., also insgesamt
x+ B+ Bx = 0
Explizit ergibt sich
B+ B = (A − λ 1)+ (A − λ 1) = A+ − λ ∗ 1 (A − λ 1) = A+ A − λ ∗ A − λ A+ + λ λ ∗ = 0.
Wegen AA+ = A+ A ergibt sich, dass B+ B = BB+ . Damit erhalten wir
+
x+ B+ Bx = x+ BB+ x = B+ x B+ x = |B+ x|2 = 0.
sodass B+ x der Nullvektor ist und B+ x = (A+ − λ ∗ 1)x = 0 gilt.
Für eine normale Matrix sind also die Eigenwerte von A+ die komplex konjugierten Eigenwerte
von A. Es seinen nun xi und x j zwei Eigenvektoren zu zwei unterschiedlichen Eigenwerten λi
und λ j . Dann gilt
und
Ax j = λ j x j .
Axi = λi xi
+
Wenn wir nun die zweite Gleichung von links mit xi multiplizieren, erhalten wir
xi
+
Ax j = λ j xi
+
x j.
Es gilt aber auch
xi
+
A = A+ xi
+
= λi∗ xi
+
= λi xi
+
.
Damit erhalten wir insgesamt
(λi − λ j ) xi
+
x j = 0.
Da wir λi 6= λ j vorausgesetzt haben, müssen die Eigenvektoren orthogonal sein.
Bemerkung:
Für eine hermitische Matrix (A+ = A) gilt λ = λ ∗ . Somit sind die Eigenwerte reel.
30
2.6.8 Basiswechsel und Ähnlichkeitstransformationen
Vektoren kann man als Komponenten bezüglich einer gegebenen Basis darstellen. Mit der Basis
(e1 , . . . , en ) sei der Vektor v durch


v1


v = v1 e1 + · · · + vn en ,
mit dem Spaltenvektor
v =  ... 
vn
gegeben.
Wir wollen nun untersuchen wie sich die Koordinaten ändern, wenn wir auf eine alternative
Basis übergehen. Dafür führen wir eine neue Basis (e0 1 , . . . , e0 n ) ein. Die Basisvektoren seien
durch
n
e0 j = ∑ Si j ei
i=1
miteinander verknüpft. Damit ergibt sich für den Vektor v:
n
n
n
n
n
n
j=1
j=1
i=1
i=1
j=1
∑ v0j e0j = ∑ v0j ∑ Si j ei = ∑ ∑ v0j Si j
v = ∑ vi ei =
i=1
Wir identifizieren also:
!
ei .
n
vi =
∑ Si j v0j .
j=1
Kompakter lässt sich schreiben:
v = S v0
bzw.
v0 = S−1 v
mit der Transformationsmartrix S, die den Basiswechsel beschreibt.
Wir können in ähnlicher Weise die Transformation des linearen Operators A beschreiben. Es
gelte y = Ax in der Basis (e1 , . . . , en ). In der Basis (e01 , . . . , e0n ) lautet die Transformaion y0 = A0 x0 .
Mit der Relation von oben erhalten wir
y = Sy0 = Ax = ASx0
⇒
Sy0 = ASx0
⇒
y0 = S−1 ASx0 = A0 x0 .
Damit ergibt sich:
A0 = S−1 AS.
Die obige Gleichung ist ein Beispiel für eine Ähnlichkeitstransformation. Solche Ähnlichkeitstransformationen sind sehr nützlich, da sie Rechnungen stark vereinfachen können.
31
Für Ähnlichkeitstransformationen ergeben sich die folgenden Eigenschaften:
(i) Falls A = 1, dann gilt A0 = 1, da:
A0 = S−1 1S = S−1 S = 1.
(ii) Es gilt: det (A) = det (A0 ), da:
det A0 = det S−1 AS = det S−1 · det (A) · det (S) = det (A) · det S−1 S = det (A) .
(iii) Das charakteristische Polynom und damit die Eigenwerte von A stimmen mit denen von
A0 überein:
det A0 − λ 1 = det S−1 AS − λ 1 = det S−1 (A − λ 1)S = det S−1 det (A − λ 1) det (S)
= det (A − λ 1) .
(iv) Die Spur der Matrix bleibt unverndert:
tr A0 = ∑ A0ii = ∑ S−1 i j A jk Ski = ∑ Ski S−1 i j A jk = ∑ δk j A jk = ∑ A j j = tr (A) .
i
i jk
i jk
j
jk
Bemerkung:
Von besonderer Bedeutung sind unitäre Transformationen, bei denen S eine unitäre Matrix ist.
Unitäre Transformationen führen Orthonormalbasen ineinander über:
0
0
ei+ e j =


!+ 
∗
+ 
+
∑ δki ek ∗ ∑ δr j er = ∑ δik∗ ∑ δr j e|{z}
k er  = ∑ δik δk j = S S i j = δi j
r
r
k
k
k
δkr
Für unitäre Transformationen gilt ferner:
(i) Falls A hermitisch (antihermitisch), dann ist auch A0 hermitisch (antihermitisch).
(ii) Falls A unitär ist (d.h. A+ = A−1 ), dann ist auch A unitär.
zu(i)
0
(A )+ = (S+ AS)+ = S+ A+ S = ±S+ AS = ±A
zu(ii)
0
0
0
+
(A )+ A = (S+ AS)+ (S+ AS) = S+ A+ |{z}
SS+ AS = S+ A
AS = 1
|{z}
1
1
2.6.9 Diagonalisierung von Matrizen
A sei die Darstellung eines linearen Operators bzgl. der Basis (e1 , . . . , en ). Nun betrachten wir
eine alternative Basis x j = ∑ni=1 Si j ei , wobei x j die Eigenvektoren des linearen Operators A sind,
d.h. es gilt:
Ax j = λ j x j .
In der neuen Basis gilt: A0 = S−1 AS. Das Matrixelement
Si j ist dann einfach die i-te Komponente
1
2
n
des j-ten Eigenvektors, sodass wir S = x x . . . x erhalten.
32
Daraus folgt:
A0i j = S−1 AS
ij
= ∑ S−1
ik
Akl Sl j = ∑ S−1
ik
Akl x j
l
= ∑ S−1
kl
kl
Die Matrix A0 lautet also:



A0 = 

kl
λ1
0
..
.
0
λ2
..
.
···
0
..
.
0
···
..
.
0
···
0
λn
ik
λ j xkj = ∑ λ j S−1
S
ik k j
= λ j δi j
k



.

Damit ist das „Rezept“ zur Diagonalisierung von Matrizen vervollständigt. Da die Matrix S invertierbar sein muss, müssen die n-Eigenvektoren linear unabhängig sein und eine Basis des
zugehörigen Vektorraums bilden.
Beispiel: Wir wollen nun die Matrix


1 0 3
A =  0 −2 0 
3 0 1
diagonalisieren, falls möglich.
1.Schritt: Bestimmung der Eigenwerte

1−λ

0
det(A − λ 1) = det
3
0
−2 − λ
0

3
0  = (1 − λ )2 (−2 − λ ) + 9(2 + λ ) = (4 − λ )(λ + 2)2
1−λ
Damit lauten die Eigenwerte: λ1 = 4 & λ2 = λ3 = −2
2.Schritt: Bestimmung der Eigenvektoren
Aus Ax = 4x ergibt sich der normierte Eigenvektor
 
1
1  
1
√
0
x =
2
1
Wir betrachten nun das LGS:
Ax = −2x
also
I x1 + 3x3 = −2x1
⇒
II −2x2 = −2x2
III 3x1 + x3 = −2x3 = −2x3
x3 = −x1
⇒
x3 = −x1


s
Damit erhalten wir den allgemeinen Eigenvektor x =  b .
−s
Offensichtlich ist x orthogonal zu x1 für beliebige s, b (wie erwartet, da A symmetrisch ist und
folglich normal).
33
Für die Diagonalisierung ist es günstig mit einem Satz orthonormaler EV zu arbeiten, so dass
wir


 
1
0
1
1
und
x3 = √  1 
x2 = √  0 
2
2
−1
0
festlegen.
3.Schritt: Diagonalisierung von A
Die Transformationsmatrix S hat die Spaltenvektoren xi , so dass


1 √0
1
1
S= √  0
2 0 
2
1 0 −1




 
1 √0
1
1 √0
1
1 0 3
4 0
0
1
⇒ S+ AS =  0
2 0   0 −2 0   0
2 0  =  0 −2 0 
2
3 0 1
0 0 −2
1 0 −1
1 0 −1
34
3 Differentialrechnung im Rn
(. . . ) was Essentielles. Hätte ich ein Mathematiklehrbuch, würde ich es lesen. Ein
Mathematiklehrbuch ist einfach, unverlogen, lieb und unbestechlich. Und so leicht
verständlich: Man muss nur fleißig sein, und schon versteht man alles (. . . )
Max Goldt - Die Radiotrinkerin
3.1 Funktionen mehrerer Variablen
Funktionen mehrerer Variablen können Flächen im Raum beschreiben. Wenn beispielsweise die
z-Koordinate Funktion der x- und y-Koordinate ist, d.h. z = f (x, y) gilt, und die Funktion eindeutig und reellwertig ist, beschreibt sie eine Fläche im dreidimensionalen Raum. (Beispiel: Die
Oberfläche eines Gebirges ohne Überhänge.)
Die hier vorgestellten Begriffe und Methoden sind allgemeiner gültig. Zur Veranschaulichung
ist es aber nützlich, sich der entsprechenden Begriffe zu bedienen.
Die partielle Ableitung ist die Ableitung der Funktion bei der man eine Variable festhält. Man
schreibt die partielle Ableitung in der Form
∂f
= ∂x f = fx
bzw.
∂x
Die Technik der partiellen Ableitung sei am Beispiel
∂f
= ∂y f = fy
∂y
f (x, y) = x3 y − exy
erläutert.
Dann ergibt sich
∂x f (x, y) = 3x2 y − yexy
(d.h. die y-Variable wird wie eine Konstante behandelt),
analog ergibt sich
∂y f (x, y) = x3 − xexy
Man kann natürlich auch höhere und gemischte Ableitungen berechnen:
∂ ∂f
= ∂xx f = 6xy − y2 exy
∂x ∂x
∂xy f = 3x2 − (1 + xy)exy = ∂yx f
usw.
In dem vorliegenden Beispiel kann man die Reihenfolge der partiellen Ableitungen vertauschen.
Dies gilt aber nur dann, wenn die beiden gemischten Ableitungen in dem betreffenden Punkt
stetig sind. Die Regeln lassen sich in analoger Weise für Funktionen mit mehreren Variablen
verallgemeinern.
35
3.2 Das totale Differential und die totale Ableitung
Beim totalen Differential betrachten wir die Änderung des Funktionswertes für simultane Änderungen von x und y.
∆ f = f (x + ∆x, y + ∆y) − f (x, y)
= f (x + ∆x, y + ∆y ) − f (x, y + ∆y ) + f (x, y + ∆y ) − f (x, y)
f (x + ∆x, y + ∆y) − f (x, y + ∆y )
f (x, y + ∆y) − f (x)
]∆x + [
]∆y
=[
∆x
∆y
≈∂x f (x, y)∆x + ∂y f (x, y)∆y
Für infinitesimale Änderungen wird die Formel exakt, also
d f = ∂x f dx + ∂y f dy
und für Funktionen mit mehreren Variablen ergibt sich analog
df =
∂f
∂f
∂f
dx1 +
dx2 + ... +
dxn
∂ x1
∂ x2
∂ xn
Beispiel: Das totale Differential der Funktion f (x, y) = y ∗ exp(x + y) lautet:
d f = ∂x f dx + ∂y f dy = y ∗ exp(x + y)dx + (y + 1) ∗ exp(x + y)dy
Die obige Formel galt nur für unabhängige Variablen. Wir betrachten aber nun den Fall, dass die
Variablen voneinander abhängen und nur eine Variable tatsächlich unabhängig ist, also
xi = xi (x1 )
mit i = 2, ..., n
Man kann dann in diesem Fall die xi durch x1 ersetzen und dann das totale Differential der
Funktion f = f (x1 ) berechnen. Alternativ kann man die totale Ableitung aus der Kettenregel
df
∂f
∂ f dx2
∂ f dxn
=
+
+ ... +
dx1 ∂ x1 ∂ x2 dx1
∂ xn dx1
bestimmen.
Beispiel: Bestimmen Sie die totale Ableitung von
f (x, y) = x2 + 3xy
∂f
= 2x + 3y
∂x
⇒
mit y = arcsin(x)
∂f
= 3x
∂y
dy
1
=√
dx
1 − x2
df
1
= 2x + 3y + 3x ∗ p
dx
(1 − x2 )
Direkte Methode: f (x) = x2 + 3x ∗ arcsin(x)
⇒
df
1
1
= 2x + 3 ∗ arcsin(x) + 3x ∗ √
= 2x + 3y + 3x ∗ √
2
dx
1−x
1 − x2
36
3.3 Exakte und inexakte Differentiale
Bei einigen Problemstellungen ist die Funktion f zu einem gegebenen Differential gesucht. Die
Bestimmung von f ist i.A. nicht trivial. Für das Beispiel d f = xdy + ydx kann man die Funktion
f (x, y) = x ∗ y + const. sofort angeben. Solche Differentiale nennt man exakt.
Schwieriger wird es für
xdy + 3ydx = (∂y f (x, y))dy + (∂x f (x, y))dx
Integration bezüglich x:
f (x, y) = 3xy + g(y)
Integration bezüglich y:
f (x, y) = xy + h(x)
Offensichtlich sind die beiden Resultate inkompatibel und das Differential nicht exakt. Eine notwendige und hinreichende Bedingung für exakte Differential ist die folgende:
Es sei
d f = A(x, y)dx + B(x, y)dy
Offensichtlich gilt:
∂f
∂f
=A &
=B
∂x
∂y
Wenn f(x,y) zweimal stetig differenzierbar in dem Punkt (x,y) ist, muss gelten
∂xy f = ∂yx f bzw. ∂x B = ∂y A
Im vorangegangenen Beispiel gilt:
∂x B = 1 und ∂y A = 3
woraus wie erwartet folgt, dass das Differential nicht exakt ist.
Für ein totales Differential in n-Variablen ergibt sich entsprechend:
n
d f = ∑ gi (x1 , ..., xn )dxi
i=1
Das Differential ist exakt, falls für alle Paare (i,j) gilt:
∂gj
∂ gi
=
∂xj
∂ xi
3.4 Rechenregeln für partielle Ableitungen
Für partielle Ableitungen kann man einige nützliche Identitäten herleiten, wenn man z = f (x, y)
als zu x & y gleichberechtigte Variable betrachtet. Dann gilt beispielsweise x = x(y, z) und y =
y(x, z).
dx = (
∂x
∂x
)z dy + ( )y dz
∂y
∂z
dy = (
∂y
∂y
)z dx + ( )x dz
∂x
∂z
und
37
Damit erhalten wir:
dx = (
∂x ∂y
∂x ∂y
∂x
)z ( )z dx + [( )z ( )x + ( )y ]dz
∂y ∂x
∂y ∂z
∂z
Für z = const. gilt dann dz = 0 und somit
(
∂x ∂y
)z ( )z = 1
∂y ∂x
(
∂x
∂y
)z = ( )−1
∂y
∂x z
sofern die partiellen Ableitungen nicht verschwinden. Für konstantes x (dx = 0) ergibt sich
(
⇒ (
∂x
∂x ∂y
)z ( )x + ( )y = 0
∂y ∂z
∂z
∂x ∂y ∂z
)z ( )x ( )y = −1 (zyklische Relation)
∂y ∂z ∂x
Kettenregel: Es sei f = f (x1 , x2 , ..., xn ) wobei xi = xi (u). Dann ergibt sich
n
df
∂ f dxi
=∑
du i=1 ∂ xi du
Beispiel: f (x, y) = xe−y
mit x(u) = 1 + αu, y = β u3
3
3
∂ f dx ∂ f dy
df
=
+
=e−β u ∗ α + x ∗ e−β u ∗ 3β u2
du
∂ x du ∂ y du
3
=(α + 3β u2 + 3αβ u3 )e−β u
3.5 Variablentransformation
Zur Lösung physikalischer Probleme kann es nützlich sein, Variablen einzuführen, die besonders
gut an die Symmetrie des physikalischen Problems angepasst sind.
Es sei nun
xi = xi (u1 , ..., un ) und f = f (x1 , ..., xn )
Für die Ableitung der Funktion nach u j gilt dann nach der Kettenregel:
n
∂f
∂ f ∂ xi
=∑
j = 1, ..., m
∂ u j i=1 ∂ xi ∂ u j
Für unabhängige Variablen {xi } und {u j } gilt dann m = n.
Beispiel: Ein wichtiges Beispiel sind ebene Polarkoordinaten
x = r ∗ cos(φ )
y = r ∗ sin(φ )
Aufgabe: Stellen Sie die Relation
∂2 f ∂2 f
+
mit f = f (x, y)
∂ x2 ∂ y2
38
als eine Relation für f (r, φ ) in den Koordinaten (r, φ ) dar.
Zunächst gilt:
x2 + y2 = r2 (cos2 φ + sin2 φ ) = r2 ⇒ r =
p
x 2 + y2
und
y
r ∗ sin φ
y
=
= tan φ ⇒ φ = arctan( )
x r ∗ cos φ
x
Wir erhalten damit:
∂r
x
x
∂r
=p
= = cos φ ,
= sin φ
∂x
r
∂y
x 2 + y2
−1
y
−y − sin φ
∂φ
=p
=
=
2
∂x
r
r
1 + y2 /x2 x
,
∂φ
cos φ
=
∂y
r
so dass
∂
∂
sin φ ∂
= cos φ
−
∂x
∂r
r ∂φ
&
∂
∂
cos φ ∂
= sin φ
+
∂y
∂r
r ∂φ
Mit den Ausdrücken für ∂x f und ∂y f ergibt sich nach einigen Umformungen
∂2 f 1 ∂ f
∂2 f ∂2 f
1 ∂2 f
+
=
+
+
∂ x2 ∂ y2
∂ r2 r ∂ r r2 ∂ φ 2
3.6 Taylor-Entwicklung
In höheren Dimensionen lautet die Taylorentwicklung
∞
f (x) =
1
∑ n! [(∆x ∗ ∇)n f (x)]x=x
0
n=0
mit ∆xi = xi − x0 und ∆x = (∆x1 , ..., ∆xn )T
f (x) = f (x1 , ..., xn ) und ∇ = (∂ x1 , ..., ∂ xn ) (Gradient)
Spezialfälle:
• n = 2:
∞
f (x, y) =
1
∂
∂
∑ n! [(∆x ∂ x + ∆y ∂ y )n f (x, y)]x ,y
0
0
n=0
• Entwicklung von f (x, y) bis zur Ordnung [ (∆x)2 bzw. (∆y)2 und (∆x∆y) ]
1 ∂2 f
∂2 f
∂2 f
1
∂
∂
[ 2 (∆x)2 + 2
∆x∆y + 2 (∆y)2 ] = (∆x + ∆y )2 f (x, y)
2! ∂ x
∂ x∂ y
∂y
2!
∂x
∂y
39
3.7 Stationäre Punkte von Funktionen mit mehreren Variablen
Die notwendige Bedingung für das Auftreten eines stationären Punktes ist das Verschwinden der
partiellen Ableitungen von f (x1 , ..., xn )
∂f
=0
∂ xi
für alle xi
Wenn wir nun die Art des stationären Punktes bestimmen wollen, können wir die Taylorentwicklung betrachten. In führender Ordnung gilt am stationären Punkt(∂xi f = 0)
∆ f = f (x) − f (x0 ) ≈
1
∂2 f
∆xi ∆x j
∑
2 i, j ∂ xi ∂ x j
Nun sei die Matrix M definiert durch:
Mi, j =
∂2 f
∂ xi ∂ x j
so dass
1
∆ f = ∆xT M∆x mit ∆xT = (∆x1 , ..., ∆xn )
2
Da die Matrix symmetrisch ist, hat sie reelle Eigenwerte λr und n orthogonale Eigenvektoren er ,
so dass für normierte Eigenvektoren er gilt:
Mer = λ er , eTr es = δrs
Die Eigenvektoren bilden eine Basis im Rn , so dass
∆x = ∑ αr er
r
und damit
1
1
∆ f = ∆xT M∆x = ∑ λr er
2
2 r
Ein Minimum liegt also vor, wenn alle Eigenwerte von M positiv sind, ein Maximum, wenn alle
Eigenwerte negativ sind.
Falls einige Eigenwerte positiv und einige negativ sind liegt ein Sattelpunkt vor.
Bem.: Sollten einige Eigenwerte Null sein und die übrigen alle positiv (bzw. negativ) sein, so
kann mit dieser Methode nicht entschieden werden, welche Art des stationären Punktes vorliegt.
Wir wollen nun die Bedingungen für eine Funktion f (x, y) explizit formulieren. Die Matrix M
lautet in diesem Fall
M=
fxx
fyx
fxy
fyy
Die Eigenwertgleichung lautet dann:
2
( fxx − λ )( fyy − λ ) − fxy
=0
40
⇒ 2λ1,2 = ( fxx + fyy ) ±
q
2
( fxx − fyy )2 + 4 fxy
Damit liegt ein Minimum vor, falls fxx , fyy > 0 und
q
2)
fxx + fyy > ( fxx + fyy )2 − 4( fxx fyy − fxy
bzw.
2
fxx fyy − fxy
>0
Analog für Maxima und Sattelpunkte.
3.8 Extrema mit Nebenbedingungen
Im vorangegangenen Kapitel haben wir uns mit der Charakterisierung von Extrema unabhängiger
Variablen beschäftigt. Häufig gibt es aber weitere Zwangsbedingungen, die einen Zusammenhang zwischen den Variablen herstellen. Beispiele für solche Fragestellungen sind: Finde das
Maximum einer Funktion f(x,y) auf einem Kreis mit Radius R, sodass x2 + y2 = R2 .
Eine Möglichkeit zur Lösung eines solchen Problems besteht natürlich darin, die Zwangsbedingungen dazu zu nutzen, die abhängigen Variablen zu ersetzen.
Einen direkteren Zugang bietet die Methode der Lagrange’schen Multiplikatoren. Dazu betrachten wir die Funktion f(x,y) deren Maximum wir unter der Zwangsbedingung g(x, y) = c bestimmen wollen. Für unabhängige Variablen muss für ein Maximum
df =
∂f
∂f
dx +
dy = 0
∂x
∂y
sein und damit fx = 0 = fy . Durch den Zusammenhang zwischen x und y sind dx & dy nicht
unabhängig, sodass aus der Stationarität nicht notwendigerweise fx = 0 = fy folgt.
Für die Zwangsbedingung folgt aber
dg =
∂g
∂g
dx + dy = 0
∂x
∂y
da g(x, y) = c = const. gilt. Damit erhalten wir
d( f + λ g) = (
∂f
∂g
∂f
∂g
+ λ )dx + (
+ λ )dy = 0
∂x
∂x
∂y
∂y
Wir fordern nun, dass in dieser Gleichung dx und dy unabhängig sind, so dass λ die Bedingungen
∂g
∂f
∂g
∂f
+λ
=0 &
+λ
=0
∂x
∂x
∂y
∂y
erfüllen muss. Die obigen Gleichungen legen zusammen mit der Zwangsbedingung g(x, y) = c
die Variablen x,y,c der stationären Punkte fest.
B̆eispiel: Bestimmen Sie das Maximum der Funktion f (x, y) = 1 + xy auf dem Einheitskreis!
Es gilt also offenbar g(x, y) = x2 + y2 = 1
⇒ (i) y + 2λ x = 0 & (ii) x + 2λ y = 0
41
(i)
⇒ x = −2λ y ⇒ y − 4λ 2 y = 0 ⇒ (1 − 4λ 2 )y = 0
⇒λ =±
1
& x = ∓y
2
1. Fall: y = x ⇒ x = ± √12 y = ± √12
2. Fall: y = −x ⇒ x = ∓ √12 y = ± √12
Die Maximalwerte werden für x = y = ± √12 erreicht, die übrigen stationären Punkte sind Minima.
Die Methode der Lagrange’schen Multiplikatoren kann man auf mehrere Variablen verallgemeinern: Wir suchen also Extrema der Funktion f (x1 , ..., xn ) mit den Nebenbedingungen
g1 (x1 , ..., xn ) = 0
.
.
.
gm (x1 , ..., xn ) = 0
(m < n)
Die Extrema ergeben sich also aus
∂F
∂ xi
= 0 (i = 1, ..., n) und den Nebenbedingungen, wobei
F(x1 , ...xn , λ1 , ..., λm ) = f (x1 , ..., xn ) + λ1 g1 (x1 , ..., xn ) + ... + λm gm (x1 , ..., xn )
Bem.: Die Wahl c1 = c2 = ... = cm = 0 stellt keine Einschränkung dar, da man die jeweiligen
Konstanten einfach auf beiden Seiten abziehen kann.
42
4 Integralrechnung im Rn
4.1 Zweidimensionale Integrale
Kurve C, die das Gebiet R begrenzt.
Wir betrachten das Integral einer Funktion über dem Gebiet R, das von einer geschlossenen
Kurve C begrenzt werde.
Wir unterteilen nun das Gebiet in N Teilstücke ∆R p mit Teilfläche ∆A p ; p = 1, 2, ..., N. Es sei
(x p , y p ) ein beliebiger Punkt in der Teilfläche ∆R p . Nun betrachten wir die Summe
N
S=
∑ f (x p , y p )∆A p
p=1
im Limes N → ∞.
Wenn der Wert eindeutig ist, dann ist der Grenzwert das zweidimensionale Integral
Z
Z Z
I=
f (x, y)dA =
R
f (x, y)dxdy
R
wobei dA für die infinitisimalen Flächenelemente ∆A p → 0 steht.
Eine Möglichkeit das Integral auszuwerten besteht darin, das Integral entlang horizontaler Streifen auszuwerten, also
Z y=d Z x=x2 (y)
I=
f (x, y)dx dy
x=x1 (y)
y=c
Die Werte x1 (y) und x2 (y) hängen vom jeweiligen Gebiet ab. Alternativ kann man das Integral
auch entlang vertikaler Streifen parallel zur y-Achse auswerten:
Z x=b Z y=y2 (x)
I=
f (x, y)dy dx
x=a
y=y1 (x)
Die Reihenfolge der Integration beeinflusst offenbar den Wert des Integrals nicht.
Bem.: Bei unserer Betrachtung haben wir vorausgesetzt, dass jede Linie parallel zur x- bzw. yAchse die Kurve C (auch: ∂ R =Rand von R) nur zweimal schneidet. Diese Voraussetzung kann
in der Regel durch Zerlegung des Integrationsgebiets erfüllt werden.
Beispiel: Berechnen Sie das Integral
Z Z
I=
x2 ydxdy
R
43
wobei R das Gebiet ist, das durch x = 0, y = 0 und y = 1 − x begrenzt wird.
Z x=1 Z 1−y
x2 ydy)dx
1 1 3 1 4 1 5 1
1
2
2
x (1 − x) dx = ( x − x + x ) =
2
2 3
2
5
60
0
(i)I =
=
(
0
Z y=1 Z x=y−1
(ii)I =
(
y=0
=
2
x ydx)dy =
Z y=1 3
x y x=1−y
[
x=0
Z 1
(1 − y)3 y
0
0
x=0
Z 1
1
3
y=0
dy =
3
]x=0 dy
Z 1
1 − 3y2 + 3y3 − y4
3
0
1 1 2
1 5 1
1
33 4
dy = ( y − y y − y ) =
3 2
4
5
60
0
Wir können also die wie erwartet die Reihenfolge der Integration vertauschen.
Bem.: Alternativ kann man die Notation
Z y2 (x)
Z b
I=
dy f (x, y) =
dx
y1 (x)
a
Z x2 (y)
Z d
dx f (x, y)
dy
x1 (y)
c
benutzen.
4.2 Dreifachintegrale
Die Integration lässt sich auch für höherdimensionale Integrale fortsetzen. Wir betrachten dazu
das dreidimensionale Gebiet R das wir wieder in N Teilgebiete ∆R p mit Volumen ∆Vp , p =
1, ..., N aufteilen. Es sei ferner (x p , y p , z p ) ein beliebiger Punkt in ∆R p .
Wir bilden analog zum zweidimensionalen Integral die Summe
N
S=
∑ f (x p , y p , z p )∆Vp
p=1
Im Limes N → ∞, ∆Vp → 0 ergibt sich dann das Integral
Z
I=
Z Z Z
f (x, y, z)dV =
f (x, y, z)dxdydz
R
R
falls S einen eindeutigen Wert annimmt.
Für praktische Rechnungen benutzen wir wieder die Form
Z y2 (x)
Z x2
I=
dx
x1
Z z2 (x,y)
dz f (x, y, z)
dy
y1 (x)
z1 (x,y)
Bem.: (i) Analog zum zweidimensionalen Integral kann man für konvexe Gebiete die Reihenfolge der Integration vertauschen.
(ii) Die Definition kann in einfacher Weise für höhere Dimensionen verallgemeinert werden.
44
4.3 Variablentransformation
4.3.1 Transformationen im R2
Variablentransformationen ermöglichen es häufig die Integration stark zu vereinfachen, weil sich
die Integralgrenzen und/oder der Integrand stark vereinfachen.
In zwei Dimensionen besteht die Aufgabe darin, dass wir die Koordinaten x,y durch u(x,y) und
v(x,y) ausdrücken und die Integralgrenzen sowie die infinitisimalen Flächenelemente dA = dxdy
anpassen. Wir setzen voraus, dass u,v differenzierbar sind in jedem Punkt des Gebietes R.
Wir müssen also die Fläche des durch die Eckpunkte K,L,M,N begrenzten Gebiets bestimmen.
Offensichtlich ist v = const. entlang des Linienelements KL. Dieses Linienelement hat eine x(y)Komponente parallel zu ∂∂ ux du( ∂∂ uy du). Analog gilt für KN, dass das Element nur Komponenten in
Richtung (∂ x/∂ v)dv und (∂ y/∂ v)dv hat. Die Fläche eines Parallelogramms ist gegeben durch
A = |a| |b| sin Φ = |a × b|
Da die beiden Vektoren in der (x,y)-Ebene liegen, hat das Kreuzprodukt nur eine von Null verschiedene Komponente, die z-Komponente. Insgesamt lautet also das Flächenelement
∂x ∂y
∂ y ∂ x ∂ x ∂ y ∂ y ∂ x dudv
dA = du dv − du dv = −
∂u ∂v
∂u ∂v
∂u ∂v ∂u ∂v
Mit der Jacobi-Matrix:
45
∂ (x, y) ∂ x ∂ y ∂ x ∂ y J=
≡
−
=
∂ (u, v) ∂ u ∂ v ∂ v ∂ u ∂y
∂u
∂y
∂v
∂x
∂u
∂x
∂v
ergibt sich für das Flächenelement
∂ (x, y) dudv
dxdy = ∂ (u, v) Insgesamt erhalten wir
Z Z
∂ (x, y) dudv
g(u, v) ∂ (u, v) R‘
Z Z
I=
f (x, y)dxdy =
R
wobei R’ das Gebiet R in den Koordinaten u,v beschreibt.
Beispiel: Berechne I =
RR
R (a +
p
x2 + y2 )dxdy auf der Kreisfläche x2 + y2 = a2 .
Für dieses Problem bieten sich ebene Polarkoordinaten an, mit
x = r cos φ
y = r sin φ
In Polarkoordinaten lautet das Integral
∂ (x, y) drdφ
(a + r) ∂ (u, v) R0
Z Z
I=
Die Jacobi-Determinante kann man leicht berechnen:
sin φ = r(cos2 φ + sin2 φ ) = r
r cos φ ∂ (x, y) cos φ
J=
=
−r
sin φ
∂ (u, v)
Damit ergibt sich für das Integral
Z 2π
Z Z
I=
R0
(a + r)rdrdφ =
Z a
dφ
0
0
Beispiel: Berechnung des Integrals I =
5πa3
1 2 1 3
dr(ar + r ) = 2π ar + r =
2
3
3
2
R ∞ −x2
dx
∞ e
2
Die Funktion e−x besitzt keine Stammfunktion. Zur Berechnung des bestimmten Integrals I
kann man aber folgenden Trick anwenden:
Wir berechnen das Integral I 2
I2 =
Z ∞
∞
2
e−x dx
Z ∞
2
e−y dy =
Z
e−(x
2 +y2 )
dxdy
R
∞
Dieses Integral vereinfacht sich offenbar in Polarkoordinaten, denn
ZZ
Z 2π
Z ∞
1 −r2 ∞
2
−r2
−r2
=π
I =
e r drdφ =
dφ
dr re = 2π − e
2
R0
0
0
0
√
⇒I= π
Bem.: Die Konvergenz des Integrals kann man zeigen, wenn man
46
2
a −x
bzw. wiederum I 2 (a) berechnet.
das endliche Integral: I(a) = −a
e
Das Integral über die innen liegende Kreisfläche stellt offenbar eine untere Schranke dar, das
über die äußere Kreisfläche eine obere. Wir erhalten
R
2
2
π(1 − e−a ) < I 2 (a) < π(1 − e−2a )
und damit
lim I 2 (a) = π
a→∞
4.3.2 Variablentransformation in Dreifachintegralen
Die Variablentranformationen in drei Dimensionen folgen dem gleichen Schema wie Transformationen in der Ebene. Das Volumenelement dVu,v,w hat für Variablen u(x,y,z), v(x,y,z) und
w(x,y,z) die Form
∂ (x, y, z) dudvdw
dVu,v,w = ∂ (u, v, w) mit der Jacobi-Determinante
∂ (x, y, z) J=
=
∂ (u, v, w) ∂x
∂u
∂x
∂v
∂x
∂w
∂y
∂u
∂y
∂v
∂y
∂w
∂z
∂u
∂z
∂v
∂z
∂w
wobei wir wieder die Invertierbarkeit der Funktionen u,v,w voraussetzen.
Die Transformationsregel für das Integral lautet dann
Z
I=
R
∂ (x, y, z) dudvdw
f (x, y, z)dxdydz =
g(u, v, w) ∂ (u, v, w) R0
Z
Für Kugelkoordinaten:
47
x = r sin θ cos φ
y = r sin θ cos φ
z = r cos θ
ergibt sich:
J = r2 sin θ , also dV = r2 sin θ drdθ dφ
Für Zylinderkoordinaten ergibt sich:
x = r cos φ , y = r sin φ , z = z
und damit
dV = rdrdφ dz
Allgemeine Eigenschaften von Jacobi-Determinanten:
Eine Transformation xi nach yi in n Dimensionen hat die Form
∂ (x1 , ..., xn ) dy1 ...dyn
dx1 dx2 ...dxn = ∂ (y1 , ..., yn ) wobei die n-dimensionale Determinante analog zum 2- bzw. 3-dimensionalen Fall bestimmt
wird.
Für Jacobi-Determinanten gelten die folgenden Rechenregeln:
∂ (x1 , ..., xn ) ∂ (x1 , ..., xn ) ∂ (y1 , ..., yn )
=
∂ (z1 , ..., zn ) ∂ (y1 , ..., yn ) ∂ (z1 , ..., zn )
sowie
∂ (x1 , ..., xn )
∂ (y1 , ..., yn ) −1
=
∂ (y1 , ..., yn )
∂ (x1 , ..., xn )
48
5 Vektoranalysis
5.1 Der Gradient
Für eine Funktion f : Ω → R (Ω sei ein Gebiet im Rn ) können wir das Differential an der Stelle
a ∈ Ω durch
d f (a) = ∂x1 f (a)dx1 + ... + ∂xn f (a)dxn
ausdrücken.
Eine alternative Schreibweise ergibt sich durch Einführung des Gradienten


∂x1 f (a)


.

∇ f (a) = 


.
∂xn f (a)
und des Vektors


dx1
 . 

dx = 
 . 
dxn
Damit ist das Differential in der Form
˙ = d f (a)
∇ f (a)dx
darstellbar, also als Skalarprodukt zwischen dem Gradienten und dem Vektor der Differentiale.
5.2 Raumkurven und Kurvenintegrale
Raumkurven α sind Abbildungen eines Intervalls I in den Rn , also


α1 (t)
 . 

α : I → Rn ,t → α(t) = 
 . 
αn (t)
Eine stetig differenzierbare Raumkurve nennt man regulär, wenn der Tangentenvektor α̇(t) an
keiner Stelle t ∈ I verschwindet.
Def.: Die Bildmenge α(I) heißt die Spur von I.
Beispiele:
(i) Die Archimedische Spirale
t→
t cost
t sint
ist eine reguläre Kurve (t>0)
49
(ii) Schraubenlinie (Wendelgang im Guggenheim Museum New York):


R cost
t →  R sint 
ht
(t ∈ R ). Die Schraubenlinie ist regulär für t ∈ R.
(iii) Die Zykloide
t − sint
1 − cost
1 − cost
sint
t→
(t ∈ R ), ist nicht regulär, da
α̇(t) =
=0
für t = 0, ±2π, ±4π, . . .
5.3 Länge und Bogenlänge
Definition: Die Länge L(C) eines Kurvenstücks ist definiert als das größte Element der in C
einbeschriebenen Sehnenpolygone.
Satz: Für eine stetig differenzierbare Parametrisierung der Kurve C: α : [a, b] → Rn gilt
Z b
L(C) = L(α) :=
kα̇(t)kdt
a
Dieser Satz erlaubt die praktische Berechnung von Längen von Raumkurven.
Beispiel: Für ebene Kurven α(t) = (t, y(t)) gilt:
˙ =
α(t)
1
ẏ(t)
q
kα̇(t)k = 1 + ẏ(t)2 .
→
und damit für Länge der Kurve
Lab (α) =
Z bq
1 + ẏ(t)2 dt.
a
50
5.4 Skalare Kurvenintegrale
Definition:
Das skalare Kurvenintegral bzw. Wegintegral von f über C wird durch
Z
Z b
Z
f ds =
C
f (x) ds :=
C
f (α(t)) kα̇(t)k dt
a
definiert, wobei ds = kα̇(t)k dt.
Beispiele:
Berechnen Sie die Masse und den Schwerpunkt eines kreisförmigen Drahtes mit Radius r und
homogener Dichte ρ. ρ ist eine „Längendichte“, hat also die Dimension kg
m.
Die Drahtschleife hat die Parametrisierung
q
cos(t)
α(t) = r
→
kα̇(t)k = sin2 (t) + cos2 (t) = r.
sin(t)
Z 2π
M=
Z
ρ r dt = 2πρr =
0
dm
C
Für den Schwerpunkt gilt:
S=
1
M
Z
I dm
→
Sx =
C
1
M
Z 2π
0
r cos(t) rρdt = 0
| {z }
=x(t)
und Analoges für Sy .
5.5 Vektorielle Kurvenintegrale
Definition:
Unter einem Vektorfeld auf dem Gebiet Ω ∈ Rn verstehen wir eine stetige Abbildung


v1 (x)


u : Ω → Rn ,
x → v(x) :  ...  .
vn (x)
Sind die Komponentenfunktionen v1 , . . . , vn zusätzlich σ -fach stetig differenzierbar (also
Cσ -Funktionen), so spricht man von einem Cσ -Vektorfeld.
Beispiele:
• Geschwindigkeitsvektoren von Strömungen
• Elektrische und magnetische Felder
• Gravitationsfeld
Definition:
Für ein Vektorfeld v auf Ω ∈ Rn und eine reguläre C1 Kurve α : [a, b] → Rn in Ω definieren wir
das vektorielle Kurven- oder Wegintegral durch
Z
α
v · dx :=
Z b
hv(α(t)), α̇(t)idt,
a
51
wobei wir mit h·, ·i das Skalarprodukt bezeichnen.
Beispiel: Ein Massenpunkt im Koordinatenursprung erzeugt das Gravitationsfeld (bis auf eine
Konstante)
 
x
x
1
 y .
U(x) = −
=
−
p
3
kxk3
x2 + y2 + z2
z
Wenn man einen weiteren Massenpunkt mit der Masse m = 1 entlang des Weges
α : [a, b] → Rn \{0} bewegt, so ist die dabei geleistete Arbeit gegeben durch:
−
Z
U · dx =
α
Z b
xẋ + yẏ + zż
a (x2 + y2 + z2 )3/2
dt,
wobei x = x(t) usw. gilt.
5.5.1 Verhalten bei Umparametrisierung:
Es sei C ein stetig differenzierbares Kurvenstück in Ω und α, β zwei Parametrisierungen. Es
gelte ferner α = β ◦ h. Dann gilt
(R
Z
falls ḣ > 0,
v dx
vdx = β R
α
− β v dx falls ḣ < 0.
Eine Orientierung einer Kurve C kann dadurch festgelegt werden, dass man eine Parametrisierung β als positiv orientiert definiert. Dann ist jede Parametrisierung α = β ◦ h mit h > 0 (h < 0)
positv (negativ) orientiert.
5.6 Konservative Vektorfelder und Potential
Definition:
R
Ein Vektorfeld v auf Ω ∈ Rn heißt konservativ oder exakt, wenn das Kurvenintegral γ v dx nur
von den Endpunkten abhängt, nicht aber vom Verlauf von γ.
Bemerkung:
Offensichtlich verschwinden Kurvenintegrale über geschlossene Kurven bei konservativen Kraftfeldern.
Satz:
Ein Vektorfeld v auf Ω ∈ Rn ist genau dann konservativ, wenn es eine C1 -Funktion U : Ω → R
gibt mit
v = ∇ U.
Wir nennen U eine Stammfunktion oder ein Potential des Vektorfeldes. Es gilt
Z
v · dx = U(x1 ) −U(x0 ),
γ
wobei mit x0 der Anfangs- und mit x1 der Endpunkt von γ bezeichnet wird.
Satz:
Ein C1 -Vektorfeld v auf Ω besitzt ein Potential, wenn es die Integrationsbedingungen
∂ vi
∂ vk
=
∂ xk
∂ xi
für i 6= k
52
erfüllt und wenn Ω ein einfaches Gebiet ist.
Bemerkung:
In einem einfachen Gebiet lässt sich jede geschlossene Kurve stetig auf einen Punkt zusammenziehen, ohne dabei Ω zu verlassen.
5.7 Weitere Vektoroperatoren
Definition: Divergenz
Für C1 -Vektorfelder v = (v1 , . . . , vn ) auf Ω ∈ Rn erklären wir die Divergenz durch
div v =
∂ v1
∂ vn
+···+
= ∇ · v.
∂ x1
∂ xn
Beispiel:

x 2 y2
v =  y2 z2 
x 2 z2

→
div V = 2(xy2 + yz2 + zx2 )
Definition: Der Laplace-Operator
U : Ω → R,
wobei U eine C2 -Funktion ist.
σU := ∂x2 U + ∂y2 U + ∂z2 U = div(∇ U) = (∇)2 U
Beispiel:
Es sei Φ = xy2 z3 . Damit ergibt sich
∆Φ = ∂x2 Φ + ∂y2 Φ + ∂z2 Φ = 2xz3 + 6xy2 z
Definition: Rotation
Die Rotation von C1 -Vektorfeldern v auf Ω ∈ R3 ist definiert durch


∂2 v3 − ∂3 v2
rot v =  ∂3 v1 − ∂1 v3  = ∇ × v.
∂1 v2 − ∂2 v1
Einige nützliche Rechenregeln:
(i) ∇ × ∇U = 0
(ii) ∇ · ∇ ×V = 0
(iii) ∇ · ( f ·V ) = (∇ f )V + f · ∇ ·V
(iv) ∇ × ∇ ×V = 0
(v) ∇(V ×W ) = (∇ ×V )W −V · (∇ ×W )
(vi) ∇ × ( fV ) = ∇ f ×V + f ∇ ×V
(vii) ∇ × (V ×W ) = (divV ) ·W + (divW ) ·V + divW − divV
53
5.8 Oberflächenintegrale
Charakterisierung von Flächenstücken im R3
Erinnerung:
Raumkurven sind Abbildungen eines Intervalls in den Rn :
Abbildung 6: Kurven im R3
Analog:
Flächenstücke im R3 sind Abbildungen zweidimensionaler Intervalle in den R3 :
Abbildung 7: Flächen im R3
Definition: Flächenparametrisierung
Als Flächenparametrisierung bezeichnen wir eine injektive Cr -Abbildung (r ≥ 1) auf einem
Gebiet U ∈ R2 , die durch
Φ : U → R3
gegeben ist. Es gilt also:


Φ1 (u)
u = (u1 , u2 ) → Φ(u) =  Φ2 (u) 
Φ3 (u)
wobei ∂1 Φ(u) und ∂2 Φ(u) an jeder Stelle u ∈ U linear unabhängig sind.




∂1 Φ(u) = 
∂ Φ1 (u)
∂ u1
∂ Φ2 (u)
∂ u1
∂ Φ3 (u)
∂ u1




 ; ∂2 Φ(u) = 
∂ Φ1 (u)
∂ u2
∂ Φ2 (u)
∂ u2
∂ Φ3 (u)
∂ u2



Die Vektoren ∂1 Φ(u) und ∂2 Φ(u) sind Tangentenvektoren der Koordinatenlinien an der Stelle u
(siehe Abb.).
Das von ∂1 Φ(u) und ∂2 Φ(u) aufgespannte Flächenelement hat offenbar nur dann eine von Null
verschiedene Fläche, wenn die beiden Vektoren linear unabhängig sind.
54
Beispiele für Flächen in R3 :
(i) Ebene:
(u1 , u2 ) 7→ a + u1 a1 + u2 a2
mit a1 × a2 6= 0
a, a1 , a2 ∈ R
(ii) Obere (untere) Halbkugel:

u1


u2

(u1 , u2 ) 7→ 

 + p
R2 − kuk2
(−)

kuk < R
(iii) Sphäre ohne Nullmeridian:


sin θ cos φ
(φ , θ ) 7→  sin θ sin φ 
cos θ
mit 0 < φ
Der Nullmeridian muss ausgenommen werden, damit die Injektivität der Abbildung gewährleistet ist.
Def.: Flächenstücke:
Eine Menge M ⊂ R3 heißt Cr -Flächenstück (mit r ≥ 1), wenn sie das Bild einer Cr -Flächenparametrisierung Φ : R2 ⊃ U → R3 mit stetiger Umkehrabbildung
Φ−1 : M → U ist. Jede solche Abb. heißt eine (zulässige) Parametrisierung für M.
Bemerkung:
Die Stetigkeit der Umkehrabbildung stellt die Orientierbarkeit sicher (Gegenbeispiel: Möbius-Band). Durch die Definition auf offenen Teilmengen stellen wir
sicher, dass es keine Probleme mit der Differenzierbarkeit am Rand gibt.
Der Flächeninhalt von Flächenstücken
Für eine Parametrisierung Φ : R2 ⊃ U → R3 definieren wir
gik :=< ∂i Φ, ∂k Φ >
sowie
für i, k = 2 ;
g
g
g = det(gik ) = 11 12
g21 g22
Wir betrachten nun das Flächenelement Φ(R) mit dem “kleinen” Rechteck R = [u1 , u1 + ∆u1 ] ×
[u2 , u2 + ∆u2 ] und definieren die Vektoren v1 = ∂1 Φ(u); v2 = ∂2 Φ(u).
Das Flächenelement kann durch das Parallelogramm Ψ(R) approximiert werden. Für den Flächeninhalt des Parallelogramms AΨ ergibt sich AΨ = k(∆u1 v1 ) × (∆u2 v2 )k.
Wir betrachten nun:
kv1 × v2 k2 = kv1 k2 kv2 k2 sin2 φ
= kv1 k2 kv2 k2 (1 − cos2 φ )
2
2
2
= kv1 k kv2 k − < v1 , v2 > = g(u)
und damit gilt:
55
AΨ = k(∆u1 v1 ) × (∆u2 v2 )k =
p
g(u)∆u1 ∆u2
Die Gesamtfläche A(Φ) kann näherungsweise durch die Summe von N Parallelogrammen mit
den Aufpunkten u1 , . . . , uN und den Seitenlängen ∆u1 und ∆u2 beschrieben werden:
N
A(Φ) '
q
∑ g(uk )∆u1 ∆u2
k=1
Für kleine ∆u1 , ∆u2 wird durch die obige Summe das Integral A(Φ) :=
ximiert.
R p
k
g(u) du1 du2 appro-
Beispiel: Sphäre mit Radius r um den Ursprung
Sr = {(x, y, z)|x2 + y2 + z2 = r2 }
Diese Fläche ist kein Flächenstück, da die Abb. Φ(x, y, z) nicht injektiv ist. Wenn man den Nullmeridian ausnimmt
Sr0 = Sr \ N mit N = {(r cos θ , 0, r sin θ )|0 ≤ θ ≤ π}
erhält man ein Flächenstück. Sr0 ist am leichtesten durch Kugelkoordinaten parametrisierbar.


r sin θ cos φ
Φ : U → R ; (φ , θ ) 7→  r sin θ sin φ 
r cos θ
mit U = {(φ , θ )|0 < φ < 2π ; 0 < θ < π}
Für die Tangentenvektoren ergibt sich


−r sin θ sin φ
∂φ Φ =  r sin θ cos φ 
0

;

r cos θ cos φ
∂θ Φ =  r cos θ sin φ 
−r sin θ
gφ φ =< ∂φ Φ; ∂φ Φ > = r2 sin2 θ sin2 φ + r2 sin2 θ cos2 φ
= r2 sin2 θ
gφ θ =< ∂φ Φ; ∂θ Φ > = −r2 sin θ sin φ cos θ cos φ + r2 sin θ cos φ cos θ sin φ
= 0 =< ∂θ Φ; ∂φ Φ >= gθ φ
gθ θ =< ∂θ Φ; ∂θ Φ > = r 2
gφ φ gθ φ r2 sin2 θ 0 =
g=
gφ θ gθ θ 0
r2 = r4 sin2 θ
Abbildung 8: Parallelogramm Ψ(R)
56
Für die Gesamtfläche ergibt sich dann mit A(Φ) :=
A(Φ) :=
R p
g(u) du1 du2 :
k
Z 2π Z π
Z p
g(φ , θ ) dφ dθ =
0
Sr
r2 sin θ dφ dθ = 4πr2
0
Oberflächenintegrale
Es sei M ⊂ R3 ein Flächenstück und f : M → R eine Funktion. Dann ist das skalare Oberflächenintegral von f über M durch
Z
Z
f dA =
M
Z
f (x) dA(x) :=
M
p
f (Φ(u)) g(u) du1 du2
U
definiert, falls das Integral konvergiert.
5.9 Das vektorielle Oberflächenintegral
Orientierte Flächenstücke
Der von den Tangentenvektoren ∂1 Φ(u), ∂2 Φ(u) einer Parametrisierung Φ aufgespannte Teilraum des R3 heißt Tangentialraum von M um Punkt x = Φ(u) ∈ M. Der Tangentialraum wird
mit Tx M bezeichnet.
Das Einheitsnormalenfeld n : M → R3 wird durch
u(x) ⊥ Tx M ,
ku(x)k = 1
für x ∈ M
festgelegt.
Satz:
Für ein orientiertes Flächenstück M gibt es genau ein Einheitsnormalenfeld n von
M mit der Eigenschaft
u(x) = ±
∂1 Φ × ∂2 Φ
(u) mit x = Φ(u)
k∂1 Φ × ∂2 Φk
Das Pluszeichen gilt für positive, das Minuszeichen für negative Parametrisierungen.
Das vektorielle Oberflächenintegral
Es sei M ein orientiertes Flächenstück und v : M → R3 ein auf M stetiges Vektorfeld. Dann ist
das vektorielle Oberflächenintegral definiert durch
Z
M
v · dA =
Z
M
v(u) · dA(u) := ±
Z
U
< v ◦ Φ, ∂1 Φ × ∂2 Φ > du1 du2
wobei Φ : R2 ⊃ U → R3 eine Parametrisierung von M ist und das Vorzeichen entsprechend der
Parametrisierung gewählt wird.
57
Beispiele für das gerichtete Oberflächenintegral

u1

u2
Beispiel: Es sei Φ die Abb. u = (u1 , u2 ) 7→  q

a2 − (u21 + u22 )


 (obere Hemisphäre) und v =

u1
 0 .
0
Z
v · dA =
M
Z
< v(u), ∂1 Φ × ∂2 Φ > du1 du2
U




1
0
mit ∂1 Φ =  0  , ∂2 Φ =  1 
u1
z
u2
z
∂1 Φ × ∂2 Φ
=
< v(u), ∂1 Φ × ∂2 Φ >
u21
q
du1 du2
U
a2 − (u21 + u22 )
=
u1 u2
, − , 1)
z
z
2
u1 /z
ZZ 2
2πa3
r cos2 Φ
√
r dr dφ =
3
a2 − r 2
0
(
Z
=
↑
Polarkoord.
U
Beispiel: Wir betrachten das Integral über der Menge M mit
M = (x, y, z)|x2 + y2 = 2z < 1
Die Fläche wird parametrisiert durch


Φ : (u1 , u2 ) 7→ 
(Rotationsparaboloid)

u1
u2
u21 +u22

;
n(0, 0, 0) = (0, 0, −1)
2
Das Vektorfeld ist gegeben durch:


x3
v(x, y, z) =  x2 y 
xyz

u31

u21 u2
v ◦ Φ(u) = 
u1 u2 2
2
2 (u1 + u2 )

Der unnormierte Normalenvektor ∂1 Φ × ∂2 Φ ergibt sich aus:






1
0
−u1
∂1 Φ =  0  ; ∂2 Φ =  1 
∂1 Φ × ∂2 Φ =  −u2 
u1
u2
1
Z
v · dA = −
M
Z h
−u41 − u21 u22 +
i
u1 u2 2
(u1 + u22 ) du1 du2
2
M
Z2πZ1
=
0 0
=
(r4 sin4 φ + r4 sin2 φ cos2 φ − r4 sin φ cos φ )r dr dθ
| {z } |
{z
} |
{z
}
3
= 20
π
1
= 20
π
π
5
58
=0
5.10 Der Integralsatz von Gauß
Bevor wir uns dem Gaußschen Satz zuwenden, diskutieren wir zunächst die anschauliche Interpretation der Divergenz eines Vektorfeldes.
Die Strömung einer Flüssigkeit kann durch das Vektorfeld
f (x) = ρ(x)v(x) = ρ(x)v(x)e(x)
beschrieben werden, wobei ρ(x) die Dichte und v(x) = v(x)e(x) die Geschwindigkeit des Fluids
bezeichnet.
Abbildung 9: Fluss durch die Fläche eines Quaders
Wir betrachten nun einen um den Punkt x zentrierten Quader mit den Kantenlängen dx, dy, dz.
Der Fluss durch die Fläche A ist dann einfach f · n dy dz = fy dy dz. (Eine besonders einfache
Situation ergibt sich für v = v · ex mit v = const. und ρ(x) = const. = ρ. Durch die Fläche A
wird dann innerhalb eines Zeitintervalls ∆t die Flüssigkeitsmenge ρv · n dy dz · ∆t = ρv∆t dy dz
transportiert.)
Abbildung 10: transportiertierte Flüssigkeitsmenge innerhalb ∆t
Der “Nettoabfluss” ergibt sich aus der Differenz zwischen Abfluss durch die Fläche A und Zufluss durch B. Insgesamt erhält man für den Nettoabfluss
dx
dx
f x + , y, z · ex − f x − , y, z · ex dy dz
2
2
dx
dx
∂ f1 (x)
= f1 x + , y, z − f1 x − , y, z dy dz =
dx dy dz
2
2
∂ x1 | {z }
= dV
Analoge Resultate erhält man für die übrigen Seiten des Quaders.
59
Nun beschreibt das gerichtete Oberflächenintegral
Z
v · n dA
∂Ω
über eine geschlossene Fläche ∂Ω den Nettodurchsatz durch das von ∂Ω umschlossene Volumen
Ω. Wie wir durch Betrachtung eine infinitesimalen Quaders plausibel gemacht haben, ist der
Durchfluss mit der Divergenz verknüpft.
∇ · v dV = ∑ dAi ni · v
i=1
wobei dAi den Inhalt der i-ten Seitenfläche und ui die zugehörige Flächennormale bezeichnet.
Der Fluss durch das Volumen Ω ist dann einfach die Summe der Flüsse durch die infinitesimalen
Volumina. Die inneren Flächen tragen offenbar nicht bei, so dass man insgesamt den Gaußschen
Satz erhält:
Satz: Ist Ω ⊂ R3 ein Gaußsches Gebiet und v ein C1 -Vektorfeld auf einer Umgebung von Ω (abgeschlossenes Gebiet, “Ω mit Rand”), so gilt
Z
Z
v · dA =
div v dV =
∂Ω
Ω
Z
v · n dA
∂Ω
wobei u die Flächennormale auf den Randseiten von Ω bezeichnet
Bemerkung:
Als ein Gaußsches Gebiet bezeichnet man ein beschränktes Gebiet Ω, dessen
Oberfläche aus endlich vielen Flächenstücken besteht, die einen Normalenvektor
besitzen. “Löcher” müssen geeignet berücksichtigt werden.
5.11 Der Integralsatz von Stokes
Im Rahmen der Schulmathematik und der bisherigen Vorlesung haben Sie bereits 2 Integralsätze
kennengelernt.
Dies ist zunächst der Hauptsatz der Differential- und Integralrechnung
Zb
f 0 (x) dx = f (b) − f (a)
a
und dann die Integration von Gradienten entlang von Kurvenstücken γ
Z
∇U(x) · dx = U(x1 ) −U(x0 )
γ
wobei x0 den Anfangs- und x1 den Endpunkt des Weges darstellt.
Hier betrachten wir den Integralsatz von Stokes, der einen Zusammenhang zwischen vektoriellen
Oberflächenintegral und einem Wegintegral über den Rand der Fläche herstellt.
60
Integralsatz für Rechtecke
Wir betrachten das offene Rechteck R = ]a, b[ × ]c, d[ in R2 , P1 und P2 seien in einer Umgebung
von R stetig differenzierbar.
Dann gilt
Z
Z
(∂1 P2 − ∂2 P1 ) dx1 dx2 =
R
P1 dx1 + P2 dx2
∂R
Der Integrationsweg lässt sich folgendermaßen veranschaulichen
Abbildung 11: Integrationsweg für das Rechteck R
Das Integral über den Rand ∂ R von R ist also die Summe der Wegintegrale über die σ k (mit
k = 1, 2, 3, 4).
Die Wege haben die einfache Parametrisierung
t
b
σ 1 : [a, b] 7→ R2 ; t 7→
; σ 2 : [c, d] 7→ R2 ; t 7→
c
t
2
σ 3 : [a, b] 7→ R ;
t 7→
a+b−t
d
;
2
σ 4 : [c, d] 7→ R ;
a
c+d −t
t 7→
Entsprechend gilt:
Zd
Z
∂1 P2 dx1 dx2
=
Zb

c
R

Zd
=
(HDI)
a

∂ P2
(x1 , x2 ) dx1  dx2
∂ x1
(P2 (b, x2 ) − P2 (a, x2 )) dx2 =
c
σ1
P2 dx2 +
σ2
Z
P2 dx2 +
σ3
Z
Z
P2 dx2
∂R
σ1
R
R
R
∂R
Analog erhalten wir: ∂2 P1 dx1 dx2 = −
P2 dx2
σ4
Z
P2 dx2 =
(da
P2 dx2
σ4
Z
P2 dx2 +
=
Z
P2 dx2 +
σ2
Z
Z
=
Z
P2 dx2 = 0 )
σ3
P1 dx1
Der Integralsatz von Stokes lässt sich auch für allgemeinere Flächen im R3 formulieren. Dazu
führen wir den Begriff des zweidimensionalen Pflasters ein:
61
Definition:
Ein zweidimensionales Pflaster in R3 ist ein orientiertes Flächenstück M, für das
es eine C2 -Abbildung
Φ : U 7→ R3 ,
(u1 , u2 ) 7→ Φ(u1 , u2 )
auf einer Umgebung U von [0, 1]2 gibt, mit den Eigenschaften
(a) Die Einschränkung von Φ auf ]0, 1[2 ist eine positive Flächenparametrisierung
von M
(b) Die k-te Seitenkurve von Φ (k = 1, 2, 3, 4), eingeschränkt auf ]0, 1[
φk := Φ ◦ σk :]0, 1[7→ R3
ist entweder konstant (entartet) oder injektiv und regulär.
(c) Für die Seiten, d.h. die Spuren φk (]0, 1[) gilt: Jede nicht-entartete Seite trifft
höchstens eine weitere nicht entartete. Trifft sich die j-te Seite mit der k-ten
für j 6= k,
φ j (]0, 1[) ∩ φ j (]0, 1[) 6= 0
so gibt es eine C2 -Parametertransformation
h :]0, 1[7→]0, 1[ mit φ j = φn ◦ h und h < 0,
d.h. die gemeinsame Spur wird entgegengesetzt durchlaufen.
Bemerkung:
Den Begriff des Pflasters kann man anschaulich leicht verstehen: Ein Pflaster
entsteht durch eine differenzierbare Deformation des Einheitsquadrats, wobei die
Randstücke verklebt sein können.
Für solche Flächen lässt sich der Satz von Stokes wie folgt formulieren:
Ist v ein C1 -Vektorfeld auf Ω ⊂ R3 und M ein Pflaster mit |M| ⊂ Ω so gilt
Z
(∇ × v) · dA =
M
Z
v · dx
∂M
Der Beweis basiert darauf, das Vektorfeld v durch eine Parametrisierung auf das
Einheitsquadrat abzubilden und anschließend den Stokesschen Satz für Rechtecke
anzuwenden.
62