Mathematik 1 - für Wirtschaftsinformatik
Werbung

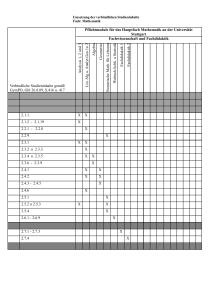
Mathematik 1 für Wirtschaftsinformatik Wintersemester 2012/13 Stefan Etschberger Hochschule Augsburg Mathematik 1 Stefan Etschberger Polarform komplexer Zahlen P ϕ 1 1. Grundlegende Bausteine 2. Grundlegende Werkzeuge 3. Aussagenlogik 4. Komplexe Zahlen Sinus, Kosinus über Reihen: 4.1. Einführung 4.2. Elementare Algebra cos ϕ = ∞ X n=0 2 2n (−1) n ϕ (2n)! ∞ X 2n+1 n ϕ sin ϕ = (−1) (2n + 1)! n=0 =1− 4 6 ϕ ϕ ϕ + − ... 2! 4! 6! ϕ3 ϕ5 ϕ7 =ϕ− + − ... 3! 5! 7! 4.3. Historie komplexer Zahlen 4.4. Geometrie 4.5. Anwendungen 5. Lineare Algebra 6. Lineare Programme Reihendarstellung der Exponentialfunktion: iϕ e = ∞ X (iϕ)n ϕ2 ϕ3 ϕ4 ϕ5 ϕ6 ϕ7 = 1 + iϕ − −i + +i − −i n! 2! 3! 4! 5! 6! 7! n=0 56 Gegeben: z1 = 1 + Gesucht: z1 · z2 √ 3 · i, z2 = 1 + i Mathematik 1 Stefan Etschberger Komplexe Funktionen visualisiert Gegeben: f:C→C mit f(z) = z4 + 1 Visualisiere Betrag von f(z) mittels Helligkeit (weiß entspricht 0, schwarz entspricht einer großen Zahl), und Winkel von f(z) durch Farben (z.B. rot: Winkel um 0, türkis: Winkel um π) 1. Grundlegende Bausteine 2. Grundlegende Werkzeuge 3. Aussagenlogik 4. Komplexe Zahlen 4.1. Einführung f(z) = z4 + 1 4.2. Elementare Algebra 4.3. Historie komplexer Zahlen 4.4. Geometrie 4.5. Anwendungen 5. Lineare Algebra 6. Lineare Programme 59 Mathematik 1 Stefan Etschberger Trigonometrie: Additionstheoreme Mittels eiϕ = cos ϕ + i sin ϕ gilt sin ϕ = eiϕ − e−iϕ 2i und cos ϕ = eiϕ + e−iϕ 2 1. Grundlegende Bausteine Damit leicht zu zeigen: Additionstheoreme, zum Beispiel: 2. Grundlegende Werkzeuge 3. Aussagenlogik 2 2 cos ϕ = cos 2ϕ + 1 cos(3ϑ) = 4 cos3 (ϑ) − 3 cos(ϑ) 4. Komplexe Zahlen 4.1. Einführung 4.2. Elementare Algebra 4.3. Historie komplexer Zahlen 4.4. Geometrie 4.5. Anwendungen 5. Lineare Algebra 6. Lineare Programme 60 Mathematik 1 Stefan Etschberger Netzwerke mit Wechselstrom In Wechselstromkreisen gilt für die Spannung u(t) bzw. den Strom j(t) in Abhängigkeit von der Zeit t cosinusförmiger Verlauf: u(t) = u0 · cos(ωt + α) und j(t) = j0 · cos(ωt + β) Betrachte u(t) und j(t) als Realteile komplexer Funktionen U(t) bzw. I(t), dann gilt: U(t) = u0 ei(ωt+α) und I(t) = j0 ei(ωt+β) 1. Grundlegende Bausteine 2. Grundlegende Werkzeuge 3. Aussagenlogik Praktisch bei linearen Elementen (Ohmscher Widerstand, Kapazität, Induktivität). Dann gilt Ohmsches Gesetz: U(t) = Z · I(t) 4. Komplexe Zahlen 4.1. Einführung 4.2. Elementare Algebra 4.3. Historie komplexer Zahlen 4.4. Geometrie 4.5. Anwendungen mit konstanten komplexen Widerständen Z gemäß: 5. Lineare Algebra 6. Lineare Programme Bezeichnung reelle Größe komplexer Widerstand Widerstand R Z=R Kapazität C Z= Induktivität L 1 i =− iωC ωC Z = iωL 61