3. Postkeynesianische Stabilisierungsmodelle 3.1.Warum ist eine

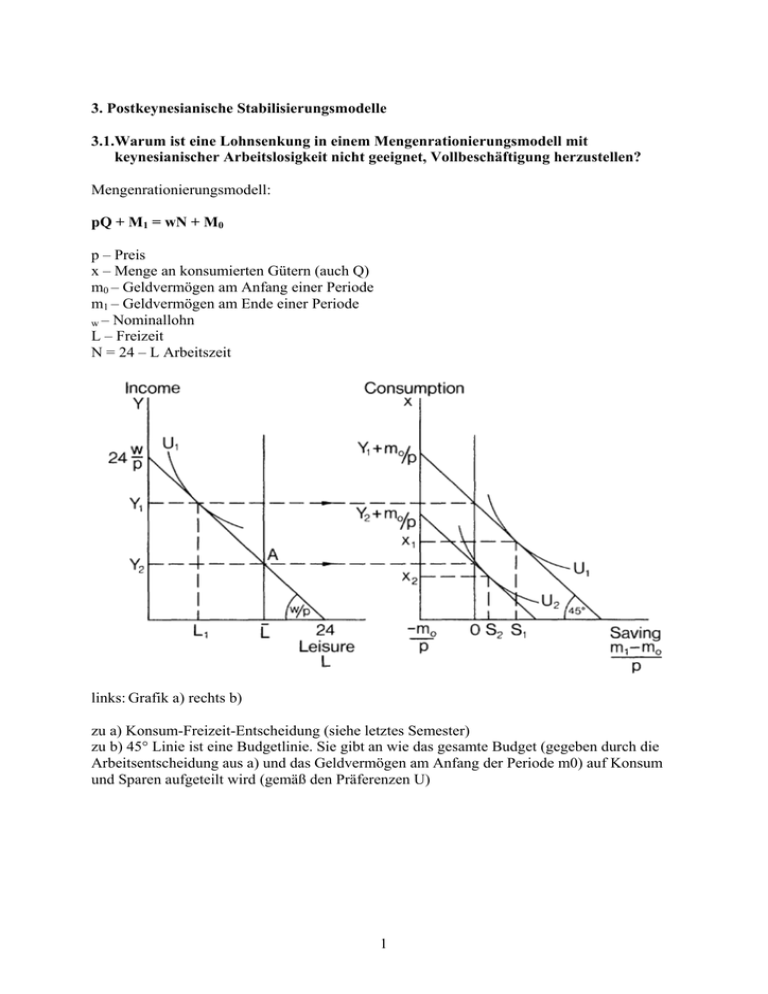
3. Postkeynesianische Stabilisierungsmodelle
3.1.Warum ist eine Lohnsenkung in einem Mengenrationierungsmodell mit
keynesianischer Arbeitslosigkeit nicht geeignet, Vollbeschäftigung herzustellen?
Mengenrationierungsmodell:
pQ + M1 = wN + M0
p – Preis
x – Menge an konsumierten Gütern (auch Q)
m0 – Geldvermögen am Anfang einer Periode
m1 – Geldvermögen am Ende einer Periode
w – Nominallohn
L – Freizeit
N = 24 – L Arbeitszeit
links: Grafik a) rechts b)
zu a) Konsum-Freizeit-Entscheidung (siehe letztes Semester)
zu b) 45° Linie ist eine Budgetlinie. Sie gibt an wie das gesamte Budget (gegeben durch die
Arbeitsentscheidung aus a) und das Geldvermögen am Anfang der Periode m0) auf Konsum
und Sparen aufgeteilt wird (gemäß den Präferenzen U)
1
zu c) Investitionen und Staatsausgaben werden zum Konsum dazu addiert, um die aggregierte
Nachfrage zu erhalten.
d)
zu d) Produktionsfunktion. Gewinnmax, wo Grenzprodukt der Arbeit gleich Reallohn
(Q1,N1)
Walras’sches Gleichgewicht
2
Variablen im Walras’schen Gleichgewicht sind mit WE subskribiert.
• In a) wird Anhand der Nutzenfunktion Uwe ein bestimmtes Konsumniveau YWe
erreicht, dies wird
• in b) zwischen konsumierten Gütereinheiten und Sparen aufgeteilt (SWE, XWE).
• In c) werden Investitionen und Staatsausgaben aufaddiert, so dass es zur aggregierten
Nachfrage DWE kommt.
• Es herrscht der Reallohn w/p, bei dem Vollbeschäftigung NWE herrscht.
• Æ alle Haushalte können die Arbeit anbieten, die sie wollen und die Güter
konsumieren, die sie wollen.
• Æ Alle Unternehmen können die Menge Arbeit beschäftigen, und die Menge Güter
produzieren, die ihrem Kalkül entspricht.
• Î alle Märkte sind im Gleichgewicht.
Kommt es zu einem höheren Reallohn w’/p
• wird nur die Menge NND beschäftigt,
• während zu dem höheren Reallohn die Menge NNS an Arbeit angeboten wird
• Æ Arbeitslosigkeit NNS-NND Æ Angebotsüberschuss am Arbeitsmarkt.
• Demgegenüber Nachfrageüberschuss am Gütermarkt.
Æ Der „Auktionator“ wird versuchen diese Ungleichgewichte zu beseitigen, indem er die
Löhne senkt.
Was aber, wenn es keinen „Auktionator“ gibt? Æ Fixe Preise Æ Entscheidungsvariable
ist nur die Menge.
3
Simulation:
c) die aggregierte Nachfrage fällt (I+G)
Æ effektive Nachfrage fällt auf D1,
Æ Output Q1,
Æ Beschäftigung N1.
Æ Über e) und a) führt dieses niedrigere Beschäftigungsniveau zu einem geringeren
Budget der Haushalte
Æ aggregierte Nachfrage nur noch D2
Æ Multiplikatoreffekte
Æ Neues Gleichgewicht indiziert mit K Æ Arbeitslosigkeit NWE-NK (Differenz
zwischen der Menge Arbeit, die zum herrschenden Reallohn angeboten wird und der
Menge die nachgefragt wird).
Wirkung einer Lohnsenkung in dieser Situation: (Preise sind fix)
Æ Kurve in a) wird flacher.
Æ In d) kommt es zu einer höheren Beschäftigung bei dem niedrigeren Reallohn.
Æ „Notionaler Output“ (in d)) und Arbeitsnachfrage würden steigen, aber die effektive
Nachfrage wirkt immer noch beschränkend (Kurve in c) unverändert).
Æ Gesamtoutput bleibt also unverändert.
Æ Aber: Löhne gesunken
Æ Budget der Haushalte verschiebt sich nach links
Æ Konsumnachfrage und Output sinken weiter.
Î Politikimplikation: m0 oder I+G erhöhen.
4