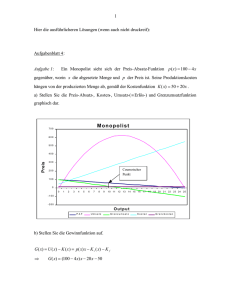
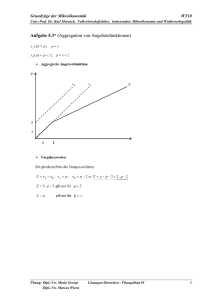
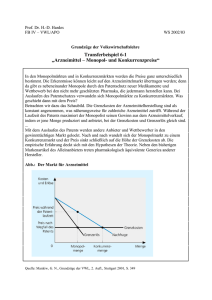
Kapitel 3.3
Werbung

Institut für Ökonomie und Recht der globalen Wirtschaft 1. Einführung/Motivation 2. Konsumtheorie 3. Produktionstheorie 4. Marktanalyse Produktionstheorie Technologische Bedingungen g g g Optimale Produktionsentscheidung Kostenfunktion und individuelles Angebot Literatur zu 3.3: Pindyck/Rubinfeld, 7.1‐7.4, 8.1‐8.5 (Hinweis: Anderer Aufbau in P/R darum Teile von ch.7 hier und Teile von ch. 8 auch für 3.2 relevant!) Varian, ch. 21 + 22 h © K. Morasch 2012 Institut für Ökonomie und Recht der globalen Wirtschaft Grundzüge der Mikroökonomik 132 3.1 Technologische Bedingungen 3.2 Optimale Produktionsentscheidung 3.3 Kostenfunktion und individuelles Angebot Kostenfunktion und individuelles Angebot Aufbau von Abschnitt 3.3: • Kostenkurven Durchschnittskosten (DK DVK) und Grenzkosten (GK) Durchschnittskosten (DK, DVK) und Grenzkosten (GK) • kurz‐ vs. langfristige Kosten g g p g g langfristig Anpassung der Betriebsgröße • optimale Angebotsmenge Preis = Grenzkosten • Angebotsfunktion Grenzkosten ab Minimum der DK bzw. DVK © K. Morasch 2012 Grundzüge der Mikroökonomik 133 3.1 Technologische Bedingungen 3.2 Optimale Produktionsentscheidung 3.3 Kostenfunktion und individuelles Angebot Institut für Ökonomie und Recht der globalen Wirtschaft Kostenfunktion: Gesamt‐, Durchschnitts‐ und Grenzkosten Idee: Kostenkonzepte graphisch in Abhängigkeit vom Outputniveau darstellen Gesamtkosten K (x) Kv ( x ) variable Kosten Durchschnitts‐ kosten DK( x ) Kf fixe Kosten K ( x ) Kv ( x ) K f DVK x ) DFK x) ( ( x x x durchschni ttliche durchschnittliche variable Kosten Grenzkosten GK( x ) © K. Morasch 2012 fixe Kosten d K ( x ) d Kv ( x ) d K f d Kv ( x ) dx dx dx dx Grundzüge der Mikroökonomik 134 3.1 Technologische Bedingungen 3.2 Optimale Produktionsentscheidung 3.3 Kostenfunktion und individuelles Angebot Institut für Ökonomie und Recht der globalen Wirtschaft Durchschnitts‐ und Grenzkosten – graphische Veranschaulichung DK GK GK DK DVK Kv x © K. Morasch 2012 Grundzüge der Mikroökonomik 135 Institut für Ökonomie und Recht der globalen Wirtschaft 3.1 Technologische Bedingungen 3.2 Optimale Produktionsentscheidung 3.3 Kostenfunktion und individuelles Angebot Zusammenhang zwischen Durchschnitts‐ und Grenzkostenkurven • Wenn DK fallend verläuft, dann muss gelten DK > GK. Grund: Damit DK fallen kann, müssen die Kosten eine zusätzliche Einheit geringer sein als die Durchschnittskosten der bereits produzierten Einheiten • Wenn DK ansteigend verläuft, dann muss gelten DK < GK. (Argumentation analog) • Im Minimum von DK sind die Stückkosten gleich den Grenzkosten. d DK( x ) d (K ( x ) x ) x dK dx K ! dK dK K 0 x K 2 dx dx x dx dx x • GK DK Die Argumentation Die Argumentation gilt analog für die DVK, da die Grenzkosten gleichermaßen gilt analog für die DVK da die Grenzkosten gleichermaßen die Änderung der Gesamtkosten und der variablen Kosten beschreiben. dDVK( x ) d (Kv ( x ) x ) x dKv dx Kv ! 0 dx dx x2 x © K. Morasch 2012 d Kv d Kv Kv Kv dx dx x d K Kv dx x GK DVK Grundzüge der Mikroökonomik Institut für Ökonomie und Recht der globalen Wirtschaft 136 3.1 Technologische Bedingungen 3.2 Optimale Produktionsentscheidung 3.3 Kostenfunktion und individuelles Angebot Verlauf der Stückkosten und durchschnittlichen variablen Kosten • Die Stückkostenkurve (DK) kann anfänglich fallend verlaufen. Dies ist durch die Existenz von Fixkosten und/oder durch fallende durchschnittliche variable Kosten ( durch durchschnittliche variable Kosten (DVK) bedingt. ) bedingt © K. Morasch 2012 • Die durchschnittlichen variablen Kosten können anfänglich fallen, weil der Output häufig mit zunehmendem Produktionsumfang weil der Output häufig mit zunehmendem Produktionsumfang effizienter produziert werden kann (z.B. wegen Spezialisierung). • ( g g p ) Die Existenz fixer Faktoren (z.B. begrenzte Managementkapazität) führt normalerweise ab einem gewissen Punkt zu einem Anstieg der durchschnittlichen variablen Kosten. Dominiert dieser Anstieg den Fi k Fixkostendegressionseffekt, so steigen auch die Stückkosten. d i ff k i h di S ü kk Grundzüge der Mikroökonomik 137 Institut für Ökonomie und Recht der globalen Wirtschaft 3.1 Technologische Bedingungen 3.2 Optimale Produktionsentscheidung 3.3 Kostenfunktion und individuelles Angebot Kurzfristige vs. langfristige Durchschnittskosten Erläuterung: l DK • kurzfristig abhängig von der Betriebsgröße g k: Kk ( x , k ( x1* )) KDK1 x Kk (x , k) KDK2 • langfristig wird k optimal angepasst Kk ( x , k ( x2* )) x Somit müssen die kurzfristigen Stü kk t Stückkosten mindestens so hoch i d t h h sein wie die langfristigen. Darstellung mit Isoquanten: g q Bewegung entlang des Output‐ Expansionspfades vs. horizontale Bewegung auf Höhe von q 2 Bewegung auf Höhe von . © K. Morasch 2012 Institut für Ökonomie und Recht der globalen Wirtschaft LDK x1* K x x x2* x Grundzüge der Mikroökonomik 138 3.1 Technologische Bedingungen 3.2 Optimale Produktionsentscheidung 3.3 Kostenfunktion und individuelles Angebot Optimale Angebotsmenge bei vollkommenem Wettbewerb • Ausgangspunkt: k Produzent nimmt den Marktpreis d d k p des Gutes als gegeben hin, d l b h d.h. als unabhängig von seinen eigenen Entscheidungen (Preisnehmer). • Annahme plausibel, wenn vollkommener Wettbewerb p , herrscht, d.h. , ‐ viele kleine Anbieter am Markt präsent sind und ‐ das Produkt homogen ist (d.h. alle Anbieter stellen ein identisches Produkt her). • Der einzelne Anbieter kann aus seiner Sicht „beliebig viel Der einzelne Anbieter kann aus seiner Sicht beliebig viel“ zum Marktpreis verkaufen. zum Marktpreis verkaufen Seine individuelle Nachfragkurve ist die horizontale Preislinie (unendlich elastisch), obwohl die Marktnachfrage fallend verläuft (geringere Elastizität). • Der Marktpreis stellt somit für den Anbieter auch den konstanten Grenzerlös dar, d.h. den zusätzlichen Erlös, den er durch Absatz einer weiteren Outputeinheit erzielt. • Dem stehen die Grenzkosten gegenüber, d.h. die zusätzlichen Kosten der weiteren Einheit. Dem stehen die gegenüber, d.h. die zusätzlichen Kosten der weiteren Einheit. • Solange der durch den Marktpreis gegebene Grenzerlös die Grenzkosten überschreitet, führt eine Ausweitung des Absatzes zu einer Erhöhung des Unternehmensgewinns. © K. Morasch 2012 Grundzüge der Mikroökonomik 139 Institut für Ökonomie und Recht der globalen Wirtschaft 3.1 Technologische Bedingungen 3.2 Optimale Produktionsentscheidung 3.3 Kostenfunktion und individuelles Angebot Optimale Angebotsmenge – graphische Analyse Aussage: DK, GK Die gewinnmaximale Angebotsmenge ergibt sich im Schnittpunkt zwischen p Preislinie und Grenzkostenkurve. Gewinn pro Stück GK DK DVK ZZu gegebenem b p ist it x1 gewinnmaximierend. Warum? Rückgang des Deckungsbeitrags sowohl bei Outputverringerung als auch bei Outputerhöhung als auch bei Outputerhöhung Beachte: Rechteck unter Preislinie ist Erlös, Fläche unter GK sind die Kv! © K. Morasch 2012 x1 Grundzüge der Mikroökonomik Institut für Ökonomie und Recht der globalen Wirtschaft x 140 3.1 Technologische Bedingungen 3.2 Optimale Produktionsentscheidung 3.3 Kostenfunktion und individuelles Angebot p = GK keine hinreichende Bedingung für Gewinnmaximum! DK, GK GK DK DVK Beachte: x2 ist kein Gewinnmaximum! p p = GK GK ist nur eine notwendige, it i t di keine hinreichende Bedingung für ein Gewinnmaximum! x2 © K. Morasch 2012 x1 Grundzüge der Mikroökonomik x 141 3.1 Technologische Bedingungen 3.2 Optimale Produktionsentscheidung 3.3 Kostenfunktion und individuelles Angebot Institut für Ökonomie und Recht der globalen Wirtschaft Optimale Angebotsmenge – analytische Lösung Produktion an einem Standort Produktion an zwei Standorten max px K ( x ) p K ( x ) x max p( x1 x 2 ) K 1 ( x1 ) K 2 ( x 2 ) x p K 1 ( x1 ), p K 2 ( x 2 ) K 1 ( x1 ) K 2 ( x 2 ) d.h. Verteilung der Gesamtmenge so, dass an beiden Standorten dieselben Grenzkosten vorliegen. © K. Morasch 2012 Grundzüge der Mikroökonomik 142 3.1 Technologische Bedingungen 3.2 Optimale Produktionsentscheidung 3.3 Kostenfunktion und individuelles Angebot Institut für Ökonomie und Recht der globalen Wirtschaft Individuelles Angebot ‐ Konzept bisher: • gewinnmaximale Produktionsmenge zu gegebenem Preis ( e s e e sc a t ege o o (Preisnehmerschaft wegen vollkommener Konkurrenz) e e o u e ) jetzt: • Angebotsfunktion des Produzenten (Marktpreis variieren, Anpassung der Produktionsmenge) • Grenzkostenfunktion als individuelle Angebotsfunktion. Beachte: © K. Morasch 2012 • Relevant ist lediglich der ansteigende Ast der Grenzkosten. • Kurzfristig müssen zumindest die DVK, langfristig die gesamten DK erlöst werden. Grundzüge der Mikroökonomik 143 Institut für Ökonomie und Recht der globalen Wirtschaft 3.1 Technologische Bedingungen 3.2 Optimale Produktionsentscheidung 3.3 Kostenfunktion und individuelles Angebot Individuelles Angebot – graphische Darstellung DK, GK GK DK DVK Grenzkostenfunktion als als inverse Angebotsfunktion p p GK ( x ) p x A( p) x © K. Morasch 2012 Grundzüge der Mikroökonomik 144