Skript - Mathe Online

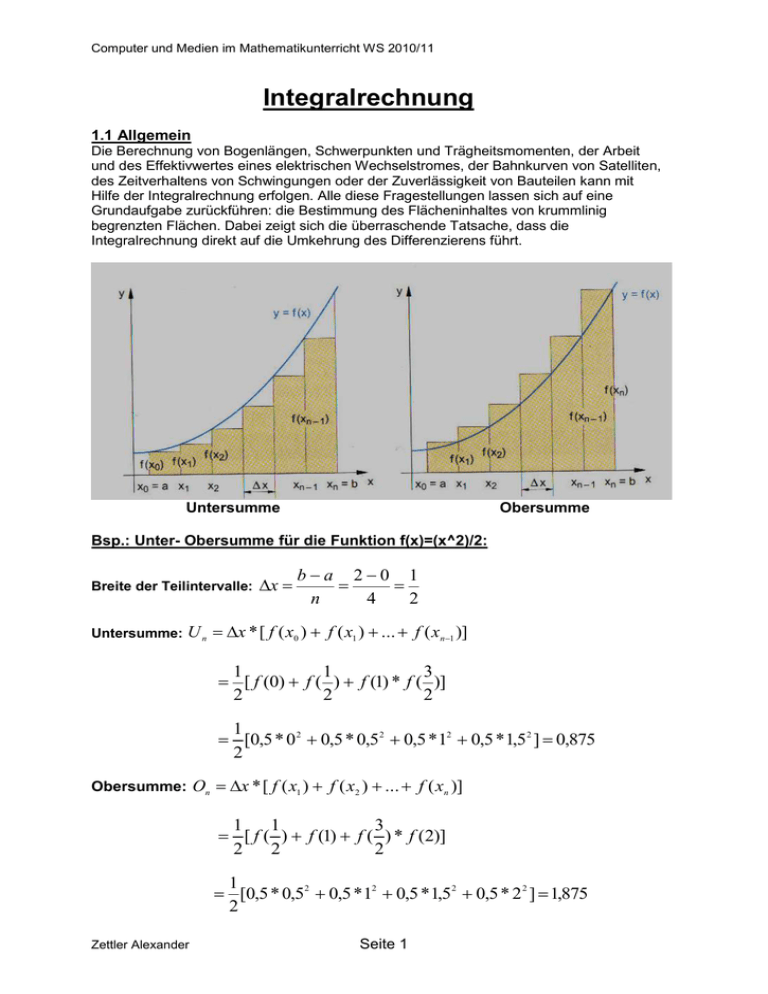
Computer und Medien im Mathematikunterricht WS 2010/11
Integralrechnung
1.1 Allgemein
Die Berechnung von Bogenlängen, Schwerpunkten und Trägheitsmomenten, der Arbeit
und des Effektivwertes eines elektrischen Wechselstromes, der Bahnkurven von Satelliten,
des Zeitverhaltens von Schwingungen oder der Zuverlässigkeit von Bauteilen kann mit
Hilfe der Integralrechnung erfolgen. Alle diese Fragestellungen lassen sich auf eine
Grundaufgabe zurückführen: die Bestimmung des Flächeninhaltes von krummlinig
begrenzten Flächen. Dabei zeigt sich die überraschende Tatsache, dass die
Integralrechnung direkt auf die Umkehrung des Differenzierens führt.
Untersumme
Obersumme
Bsp.: Unter- Obersumme für die Funktion f(x)=(x^2)/2:
Breite der Teilintervalle:
Untersumme:
x 
ba 20 1


n
4
2
U n  x * [ f ( x0 )  f ( x1 )  ...  f ( xn1 )]
1
1
3
 [ f (0)  f ( )  f (1) * f ( )]
2
2
2
1
 [0,5 * 0 2  0,5 * 0,52  0,5 * 12  0,5 * 1,52 ]  0,875
2
Obersumme: On  x * [ f ( x1 )  f ( x2 )  ...  f ( xn )]
1
1
3
 [ f ( )  f (1)  f ( ) * f (2)]
2
2
2
1
 [0,5 * 0,52  0,5 * 12  0,5 * 1,52  0,5 * 2 2 ]  1,875
2
Zettler Alexander
Seite 1
Computer und Medien im Mathematikunterricht WS 2010/11
1.2 Bestimmtes Integral
Es sei y = f(x) eine Funktion, die auf dem Intervall [a, b] definiert und beschränkt ist.
Man zerlegt nun das Intervall [a, b] in n gleich breite Teilintervalle und bildet für diese
Zerlegung die Obersumme O n und die Untersumme U n .
Existiert dann für n

als auch der Grenzwert
lim On
n 
sowohl der Grenzwert
lim U n
n 
der Folge der Untersumme
der Folge der Obersumme und stimmen diese Grenzwerte
überein, so heißt die Funktion y = f(x) integrierbar auf [a, b].
Der gemeinsame Grenzwert wird bestimmtes Integral von y = f(x) auf [a, b] genannt.
b
Man schreibt:
 f ( x)
d x  lim
U n ( nlim
On ).
n

a
Bezeichnungen: f(x)
x
a, b
[a, b]
………Integrand
………Integrationsvariable
………untere bzw. obere Integrationsgrenze
………Integrationsintervall
Anmerkung:



Integrierbar sind, was nicht weiter begründet wird, vor allem die stetigen Funktionen
und auch die stückweise stetigen Funktionen. Für die Integrierbarkeit einer Funktion
bestehen weniger strenge Forderungen als für die Differenzierbarkeit.
Geometrische Deutung: Das bestimmte Integral von y = f(x) auf [a , b] ist der
orientierte Flächeninhalt der fLäche zwischen dem Graphen von y = f(x) und der
x-Achse von x = a bis x = b.
Ist eine Funktion y = f(x) integrierbar, kann nach einer Zerlegung des
Integrationsintervalles in n Teilintervalle jeder Funktionswert in einem Teilintervall als
Höhe eines Rechtecks genommen werden: stets erhält man im Grenzfall n
∞
b
als Grenzwert
 f ( x) dx.
a

In der Formulierung als Grenzwert der Untersummen gilt:
b

a
n 1
f ( x) dx  lim
 f ( xi ) x .
n 
i 0
Daraus leitet sich historisch die Schreibung eines
bestimmten Integrals her. Das Integralzeichen


ist ein in die Länge gezogenes S;
es erinnert, dass das Integral der Grenzwert einer Summe ist.
Die Integrationsvariable kann beliebig bezeichnet werden:
b
b
b
a
a
a
 f ( x) dx   f (t ) dt   f (u )  ....


Das bestimmte Integral ist als Grenzwert einer Produktsumme definiert (woraus sich
die geometrische Deutung als Flächeninhalt ergibt). Viele physikalische Größen
werden als solche Grenzwerte und damit als Integrale definiert.
Das besprochene Integral, das so genannte RIEMANN – Integral, ist der einfachste,
aber für die Anwendung wichtigste Integralbegriff. Es gibt noch andere
Integrallbegriffe.
Zettler Alexander
Seite 2
Computer und Medien im Mathematikunterricht WS 2010/11
1.3 Stückweise Integration
Stückweise Integration nach Zerlegung des Integrationsintervall:
Für a < c < b gilt:
b
c
b
a
a
c
 f ( x) dx   f ( x) dx   f ( x) dx.
1.4 Bestimmtes Integral als Summe von orientierten Flächeninhalten

a
b
b
a
 f ( x) dx    f ( x) dx.
// Vertauschen der Integrationsgrenzen bewirkt
einen Vorzeichenwechsel.
a

 f ( x) dx  0
a
Zettler Alexander
Seite 3
Computer und Medien im Mathematikunterricht WS 2010/11
Im Überblick:
1. Es sei U n die Untersumme und O n die Obersumme einer Funktion y = f(x) für eine
Zerlegung des Intervalls [a , b] in n gleich breite Teilintervalle. Existieren dann die
Grenzwerte lim U n und lim On und stimmen sie überein, so heißt die Funktion
n
n
integrierbar. De gemeinsame Grenzwert wird bestimmtes Integral von y = f(x) auf
dem Intervall [a , b] genannt.
y = f(x) heißt Integrand, x Integrationsvariable, a und b sind die Integrationsgrenzen.
2. Geometrische Deutung: Das bestimmte Integral ist gleich dem (orientierten)
Flächeninhalt der Fläche zwischen dem Funktionsgraphen und der x-Achse.
3. Stetige oder stückweise stetige Funktionen sind integrierbar.
4. Stückweise Integration bei einer Zerlegung des Integrationsintervalles [a , b]:
a

c
b
a
a
c
 f ( x) dx   f ( x) dx   f ( x) dx.
Ist a < c < b, so gilt:
5. Vereinbarungen:
b
b
f ( x) dx    f ( x) dx
b
a
sowie
a
 f ( x) dx  0
a
1. 5 Hauptsatz der Differential- und Integralrechnung
1.5.1 Stammfunktion und unbestimmtes Integral
Die Integration ist die Umkehrung der Differentiation. F(x) ist die Stammfunktion von f(x),
wenn F’(x)=f(x). Außerdem besitzt eine Funktion unendlich viele Stammfunktionen.
Bsp.: Ermittle eine Stammfunktion von f(x)=x³+2x²+1
integrieren
f(x)= x³+2x²+1
f ( x) 
x4 x3

 xC
4
3
differenzieren
Die Menge aller Stammfunktionen von f(x) wird als unbestimmtes Integral der Funktion f(x)
bezeichnet.
Schreibweise:
f(x)
x
C
 f ( x)dx  F ( x)  C
 Integrand
 Integrationsvariable
 Integrationskonstante
Die Integrationskonstante darf bei einem unbestimmten Integral nicht weggelassen werden.
Gibt man C einen Wert, so bekommt man die zu dieser Konstante gehörige Stammfunktion.
Zettler Alexander
Seite 4
Computer und Medien im Mathematikunterricht WS 2010/11
Die Probe für die unbestimmte Integration lautet:
 f ( x)dx '  f ( x)
Bsp.: Ermittle das unbestimmte Integral.
6
2
3
 ( x  x  x )  dx 
4
x7 x3 3 3

 x C
7
3 4
1.5.2 Hauptsatz der Differential- und Integralrechnung
Wenn man eine stetige Funktion f(t) hat dann gilt:
x
a.) Die Funktion A( x) 
 f (t )dt
ist die Stammfunktion von f(t). A’(x)=F(x).
a
b.) Wenn F(x) eine beliebige Stammfunktion von f(t) ist dann gilt:
b
 f ( x)dx  F (b)  F (a)
a
Jede Flächenfunktion A(x) ist eine Stammfunktion und kann durch Integrieren ermittelt
werden.
Existiert keine Stammfunktion von f(x), (kommt bei stetigen Funktionen vor), oder wenn die
Stammfunktion nicht ermittelt werden kann verwendet man zur Berechnung des bestimmten
Integrals numerische Methoden.
Bsp.:
3
 x³ 
3
2(2 x²  3)dx  22 x²dx  23dx  22 x²  321dx  2   3  2  3  x2  C 
3
3
3
3
3
 3³ (2)³ 
 2 
 3  3  (2)  C
3 
3
 8
 2  9    15  C
3

35
70 45
25
 2   15  C 

C 
C
3
3
3
3
1.6 Grundintegrale
Man kann eine Integrationsaufgabe kaum direkt mit Hilfe der
Grundintegrale lösen, jedoch bilden sie einen guten Ausgangspunkt für das
praktische Rechnen. Weitere Grundintegrale finden sie auf der
Formelsammlung.
Zettler Alexander
Seite 5
Computer und Medien im Mathematikunterricht WS 2010/11
n
 x dx 
x n 1
C
n 1
 cosh xdx  sinh x  C
1
1
 xdx  ln x  C
 cos
ax
a
dx

C

ln a
 sin
 sin xdx   cos x  C

 cos xdx  sin x  C
1 x
2
x
1
x
2
x
e
dx   cot x  C
1
1 x2
1
 sinh xdx  cosh x  C
dx  tan x  C
x
2
dx  arcsin x  C
dx  arctan x  C
dx  e x  C
1.7 Integrationsmethoden
1.7.1 Faktor- und Summenregel
Faktorregel:
 a  f ( x)  dx  a   f ( x)  dx
// Ein konstanter Faktor a kann vor das Integral gesetzt
werden
Summenregel:
  f ( x)  g ( x) dx   f ( x)  dx   g ( x)  dx
// Eine Summe (Differenz) von Funktionen
kann auch gliedweise integriert werden.
Beispiel zur Faktor-und Summenregel:
6.13d) (Buch III.JG s.207)
x
2
1

2 
1
x
 dx 
1
x

 dx // Man erkennt wenn man im Zähler für x  x  x einsetzt
2
x
lässt sich der Ausdruck x kürzen.
 3

2

 1 3
1
1 x
1
1
x  dx    x  dx     C   x 2  C   x 3  C   x  x  C
3
2
2 
3
3
 3
 2

Alexander Zettler
1
2
Seite 6
Computer und Medien im Mathematikunterricht WS 2010/11
1.7.2 Integration durch Substitution
- Lineare Substitution
 f (a  x  b)  dx
allg.:
, es gilt u  a  x  b => u ( x)  u
Bsp 6.22a) (s.210)
 (3  2 x)
4
 dx
// Man nimmt den Ausdruck in der Klammer als u (x) an, bildet die
Ableitung u (x ) und drückt das Differential dx durch du aus.
u  u ( x)  3  2 x => u ( x)  2
du
du
u ( x) 
 dx 
dx
2
Somit ergibt sich:
4
u 
 1
du 1
1 u 5
1
5
   u 4  du     C    u 5  C   3  2 x   C
2 2
2 5
10
 10
- Multiplikation der Funktion f(x) mit ihrer Ableitung f'(x)
allg.:
 u ( x)  u ( x)  dx
Diese Methode wendet man an, wenn im Integral 2 Funktionen miteinander multipliziert
werden und eine der beiden Funktionen die Ableitung der anderen Funktion entspricht.
Bsp:
 sin( x)  cos( x)  dx
// Hier erkennt man sofort, dass sin(x) abgeleitet cos(x) ergibt.
Daher:
u ( x)  sin( x) , u ( x)  cos( x)
dx 
du
cos(x)
 u  cos( x) 
// Die Umformung auf dx erfolgt wie vorhin
du
u2
sin 2 ( x)
  u  du 
C 
C
cos( x)
2
2
Alexander Zettler
Seite 7
Computer und Medien im Mathematikunterricht WS 2010/11
- Zähler ist Ableitung des Nenners
u ( x)
 u( x)  dx
allg.:
Diese Methode ist vergleichbar mit dem vorherigem Integraltyp. Der einzige Unterschied
besteht darin indem 2 Funktionen einen Bruch bilden und der Zähler die Ableitung des
Nenners ist.
Bsp 6.35a) (s.211)
x
2
x
 dx
1
u ( x)  x 2  1 , u ( x)  2  x
u ( x) 
=>
x du
1
1
du
du
 dx 
dx
2x
1
1
 u  2 x  2   u  du  2  ln u  C  2  ln x
2
1  C
- Zusammengesetzte Funktion mal innere Ableitung
 f u( x) u ( x)  dx
allg.:
Bsp 6.36a) (s.211)
 xe
x2
 dx
// In diesem Beispiel erkennt man, wenn man den Ausdruck x² als innere
Funktion annimmt und entsprechend die Ableitung bildet würde sich durch die
Umformung auf dx die Variable x kürzen.
u ( x)  x 2 , u ( x)  2  x
du
du
u ( x) 
 dx 
dx
2x
2
du 1
1
ex
   e u  du   e u  C 
C
=>  x  e 
2x 2
2
2
u
1.7.3 Partielle Integration
allg.:
 u ( x)  v( x)  dx u ( x)  v( x)   u ( x)  v( x)  dx
Kurz :  u  v   dx  u  v   u   v  dx
Alexander Zettler
Seite 8
Computer und Medien im Mathematikunterricht WS 2010/11
Vorgangsweise:
Der Integrand f(x) des Integrals
 f ( x)  dx
wird in zwei Faktoren zerlegt: f(x)=u(x).v'(x)
Dabei sollte man bei der Zuordnung der beiden Faktoren folgende Richtlinie beachten:
-
Faktor u(x) wird so gewählt, dass das Differenzieren des Faktors einfacher wird
Faktor v'(x) wird so gewählt, dass das Integrieren nicht komplizierter wird
Bsp 6.45b) (s.214)
e
4 x
 sin( 4 x)  dx
u ( x)  sin( 4 x) , v( x)  e 4 x // Diese Faktoren wurden deshalb so gewählt, weil man
beim Differenzieren und Integrieren dieser Faktoren sich
leichter tut als umgekehrt.
u ( x)  4  cos( 4 x) , v( x)   v ( x)  dx 
e
=>

4 x
e 4 x
4
e 4 x
e 4 x
 sin( 4 x)  dx  sin( 4 x) 
 4  cos( 4 x) 
 dx
4 
4
e 4 x
 sin( 4 x)   e  4 x  cos( 4 x)  dx
4
Hier wurde der 4er gekürzt und das MinusZeichen wurde aus dem Integral
herausgehoben und wurde zum +
Das neu entstandene Integral kann wiederum mit der part. Integration gelöst werden.
u ( x)  cos( 4 x) , v( x)  e 4 x
u ( x)  4  sin( 4 x) , v( x) 
=>
4 x
 e  sin( 4 x)  dx 
e 4 x
4


e 4 x
e 4 x
e 4 x
 sin( 4 x)  cos(4 x) 
   4  sin( 4 x) 
 dx
4
4
4


=> 
 e 4 x

e 4 x
 sin( 4 x)  
 cos( 4 x)   sin( 4 x)  e 4 x  dx
4
 4

=> 
e 4 x
e 4 x
 sin( 4 x) 
 cos( 4 x)   sin( 4 x)  e 4 x  dx
4
4
Alexander Zettler
Seite 9
// Würde man den Integralausdruck
am Schluss weiter integrieren würde
man auf keine Lösung kommen da
der Intergrierprozess nie endet.
Daher bringt man diesen Ausdruck auf
die andere Seite
Computer und Medien im Mathematikunterricht WS 2010/11
2   e 4 x  sin( 4 x)  dx  
e 4 x
e 4 x
 sin( 4 x) 
 cos( 4 x) / 2
4
4
e 4 x
e 4 x
 sin( 4 x) 
 cos( 4 x)
8
8
e 4 x
4 x
e

sin(
4
x
)

dx


 sin( 4 x)  cos( 4 x)   C

8
4 x
 e  sin( 4 x)  dx  
Alexander Zettler
Seite 10
/ durch Herausheben ergibt sich
/ Lösung