Harmonische Schwingungen und komplexe Zahlen

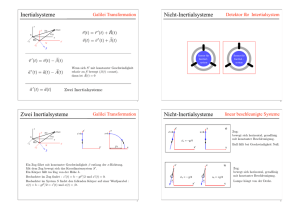
202
c Daniel Bättig
8 Harmonische Schwingungen und komplexe Zahlen ⃝
Heft 8
Tabelle 8.1 Ort eines Fahrzeugs, berechnet aus dem Ortsvektor s = s(t)
Harmonische Schwingungen und komplexe
Zahlen
Zeit (in s)
0,0 0,5 1,0 1,5 2,0 2,5 3,0
3,5
4,0
4,5
5,0
x-Position (in m) 0,0 0,479 0,841 0,997 0,909 0,598 0,141 -0,351 -0,757 -0,978 -0,959
y-Position (in m) 0,0 0,125 0,500 1,125 2,000 3,125 4,500 6,125 8,000 10,125 12,500
B
10
Zusammenfassung Wechselströme in elektrischen Netzwerken, Schwingungen von
Objekten und Spektroskopie von komplexen Molekülgruppen sind Phänomene, die
Ingenieurinnen und Ingenieure interessieren. Um die Phänomene zu beschreiben,
benötigt man mathematische Modelle: die Sinusschwingung – auch harmonische
Schwingung genannt – und komplexe Zahlen. In diesem Kapitel werden beide Konzepte vorgestellt.
8.1 Ableiten bei Vektoren, Weg- und Geschwindigkeitsvektor
Spaltenvektoren mit zwei oder drei Komponenten spielen in der Physik eine Rolle,
um Kräfte oder Geschwindigkeiten zu beschreiben. Solche Kräfte können von der
Zeit t abhängen, wie etwa die Kraft F gegeben durch
⎛
⎞
4 kN s−1 · t
F = F(t) = ⎝ 3 kN ⎠
2 kN s−2 · t 2
Man definiert die Ableitung dF/dt (oder Änderungsrate) eines solchen Vektors nach
t, indem man die Komponenten des Vektors einzeln ableitet. Beim gegebenem Vektor ist also
⎞
⎛
4 kN s−1
dF ⎝
=
0 kN s−1 ⎠
dt
4 kN s−2 · t
Die zweite Komponente von F ist konstant. Daher ist die zweite Komponente der
Ableitung von F nach t null.
Beispiel 8.1 (Weg und Geschwindigkeit in der Ebene und im Raum). Der Ort eines
Fahrzeugs, dass sich in der xy-Ebene oder in einem drei-dimensionalen Koordinatensystem bewegt, kann mit der Ortsvektor s = s(t) charakterisiert werden. Die
201
Abb. 8.1 Zurückgelegter
Weg s = s(t) eines Fahrzeugs: A ist Startpunkt, B ist
Endpunkt
4
0
v(2)
s(2)
A
−1
0
1
Spitze des Ortsvektors bezeichnet die Position des Fahrzeugs. Ist etwa
%
&
1 m · sint
s = s(t) =
für 0 s ≤ t ≤ 5 s
0,5 m s−2 · t 2
so ist der Startpunkt s(0 s) = (0 | 0) m und der Endpunkt s(5 s) = (−0,96 | 12,5) m.
Die Position des Fahrzeugs lässt mit einer Wertetabelle wie in Tab. 8.1 darstellen.
Man kann auch den zurückgelegten Weg (eine Kurve in der Ebene) visualisieren, indem man die Punkte aus der Wertetabelle darstellt und durch kleine Geradenstücke
verbindet. Am schnellsten geht dies mit Computerprogrammen wie MATLAB oder
Julia. Hier die Befehle mit MATLAB dazu, wenn man 10 000 Punkte als Wertetabelle wählt:
matlab> t = linspace(0,5,10000);
matlab> xPosition = sin(t); yPosition = 0.5*t.ˆ2;
matlab> plot(xPosition,yPosition)
Mit Julia lauten die Eingaben:
julia>
julia>
julia>
julia>
t = linspace(0,5,10000);
xPosition = sin(t); yPosition = 0.5*t.ˆ2;
using Gadfly;
plot(x=xPosition,y=yPosition,
Geom.line(preserve_order=true))
Mit einem Taschenrechner können solche Kurven mit ParametricPlot gezeichnet werden. Abbildung 8.1 zeigt den entstandenen Weg. Der Geschwindigkeitsvektor des Fahrzeugs zum Zeitpunkt t ist die Ableitung des Ortsvektors s = s(t):
%
&
ds
1 m · cost
=
v = v(t) =
1 m s−2 · t
dt
8.1 Ableiten bei Vektoren, Weg- und Geschwindigkeitsvektor
203
204
c Daniel Bättig
8 Harmonische Schwingungen und komplexe Zahlen ⃝
y
Dies ist ein ortsgebundener Vektor. Der Anfangspunkt des Vektor ist jeweils die
Spitze des Ortsvektors s = s(t). Abbildung 8.1 zeigt die Situation für den Zeitpunkt
t = 2 s. Der Geschwindigkeitsvektor liegt jeweils tangential an der Wegkurve. Die
Norm des Geschwindigkeitsvektors nennt man auch die Geschwindigkeit v = v(t).
Sie beträgt
'
v = v(t) = ||v(t)|| = (1 m · cos(t))2 + (1 m s−2 · t)2
Zum Zeitpunkt t = 2 s ist sie v = 2,043 m/s.
Die kinetische Energie Ekin eines Körpers mit Masse m und dem Geschwindigkeitsvektor c ist mit einem Skalarprodukt berechenbar. Man hat
A
s(0)
α (t)
ϕ
s(t)
x
0
Abb. 8.2 Drehbewegung eines Zeigers der Länge A mit
konstanter Winkelgeschwindigkeit ω : α (t) = ω · t + ϕ
y
−A
−A
0
A
A
1
Ekin = · m · v • v
2
Will man die Leistung dEkin /dt bestimmen, so muss man also ein Skalarprodukt
von Vektoren ableiten. Sind a und b zwei Spaltenvektoren mit zwei Komponenten
so ist
%%
& %
&&
d
d
d
a1 (t)
b (t)
• 1
= (a1 (t) · b1(t) + a2(t) · b2 (t))
(a • b) =
a2 (t)
b2 (t)
dt
dt
dt
Mit der Produktregel erhält man
d
(a • b) = a′1 (t) · b1 (t) + a1(t) · b′1(t) + a′2(t) · b2 (t) + a2(t) · b′2(t)
dt
Fasst man den ersten und dritten, sowie den zweiten und vierten Summanden zusammen erhält man:
Theorem 8.1 (Ableiten eines Skalarprodukts). Die Produktregel gilt auch beim
Ableiten eines Skalarprodukts:
d
da
db
(a • b) =
•b+a•
dt
dt
dt
Die Leistung dEkin /dt ist daher
(
)
d
1
dEkin 1
= · m · (v • v) = · m · v′ • v + v • v′ = m · v • v′ = m · v • a
dt
2
dt
2
Dabei ist a der Beschleunigungsvektor.
Der nächste Abschnitt befasst sich mit einem Punkt, der sich auf einem Kreis
bewegt.
t
t0
Abb. 8.3 Die y-Koordinate
des drehenden Zeigers: ein
Auf- und Ab, das eine harmonische Schwingung darstellt.
T
−A
8.2 Drehbewegung und harmonische Schwingung
Abbildung 8.2 zeigt im Gegenuhrzeigersinn und auf dem Einheitskreis drehenden
Punkt oder Zeiger. Der Zeiger hat Länge A. Zum Zeitpunkt t = 0 beträgt sein Winkel
zur x-Achse ϕ . Der Winkel α = α (t) zur x-Achse zum Zeitpunkt t beträgt
α = α (t) = ω · t + ϕ
In dieser Formel sind ω und ϕ Winkel in Bogenmaß, also dimensionslose Zahlen.
Die Formel besagt, dass sich der Zeiger mit einer konstanten Winkelgeschwindigkeit dα /dt = ω im Gegenuhrzeigersinn bewegt.
Die y-Koordinate y = y(t) des Endpunktes des Zeigers bewegt sich damit auf und
ab. Sie lautet mit der Definition (siehe Abb. 2.6) der Sinusfunktion:
y = y(t) = A · sin(ω · t + ϕ )
(8.1)
Abbildung 8.3 zeigt den Graph der Auslenkung y = y(t) in Funktion der Zeit
t ≥ 0. Man sagt, dass y = y(t) eine harmonische Schwingung ist. Eine harmonische
Schwingung ist charakterisiert durch die Gleichung (8.1) und damit durch die Amplitude A, durch die Kreisfrequenz ω und den Nullphasenwinkel ϕ . Die drei Größen
8.2 Drehbewegung und harmonische Schwingung
205
206
c Daniel Bättig
8 Harmonische Schwingungen und komplexe Zahlen ⃝
y
y
Z1 + Z2
Z2
0,5
x
t
Abb. 8.4 Zwei harmonische
Schwingungen
2·π
4·π
lassen sich sehr einfach aus dem Zeigerdiagramm bestimmen. Man kann sie auch
aus dem Graphen der Schwingung (siehe Abb. 8.3) über die Schwingungsdauer T
und den Punkt t0 bestimmen. Der Zeiger bewegt sich mit einer Winkelgeschwindigkeit von ω . Eine volle Umdrehung des Zeigers entspricht einem Winkel von 2 · π .
Also ist ω · T = 2 · π . Weiter ist der Zeitpunkt t0 in Abb. 8.3 so gelegt, der Zeiger in
diesem Moment auf der positiven x-Achse liegt. Also ist α = α (t) = ω · t + ϕ = 0
(oder ein Vielfaches von 2 · π ). Man erhält damit
T=
2π
,
ω
t0 = −
ϕ
ω
Den Kehrwert der Schwingungsdauer nennt man die Frequenz: f = 1/T . Zusammengefasst hat man:
Theorem 8.2. Eine harmonische Schwingung y(t) = A · sin(ω · t + ϕ ) lässt sich im
Zeigerdiagramm durch einen im mathematisch positiven Sinn mit der Winkelgeschwindigkeit ω rotierenden Zeiger der Länge A darstellen. Zum Zeitpunkt t = 0
befindet sich der Zeiger in einer Position, die durch den Nullphasenwinkel ϕ festgelegt ist.
Harmonische Schwingungen werden damit über einen Vektor Z – den Zeiger –
und die Zahl ω codiert. Ist ω < 0, so läuft der Zeiger im Uhrzeigersinn. Der Zeiger
zum Zeitpunkt t = 0 nennt man den Nullzeiger der harmonischen Schwingung.
Wenn verschiedene Kräfte aus ein schwingendes System wirken, werden die auftretenden Schwingungen überlagert. Abbildung 8.4 zeigt zwei harmonische Schwingungen y = y1 (t) (schwarze Linie) und y = y2 (t) (graue Linie) mit
y1 (t) = sin(t + π /18),
y2 (t) = 1,5 · sin(t + π /2)
Beide Schwingungen haben die gleich Kreisfrequenz 1 s−1 . Überlagert man die
beiden Schwingungen, erhält man y1 (t) + y2 (t). Um dies auszurechnen, ist es nicht
praktisch mit den obigen Schwingungsgleichungen zu arbeiten. Sinusfunktionen
können nämlich nur mühsam mit Hilfe von Additionstheoremen addiert werden.
Z1
Abb. 8.5 Die Nullzeiger
der beiden harmonischen
Schwingungen aus Abb. 8.4
und Addition der beiden
Nullzeiger
Einfacher ist es mit den zugehörigen Zeigern zu rechnen. Abbildung 8.5 zeigt die
beiden Nullzeiger Z1 und Z2 . Man hat
Z1 = [1, ∠ π /18],
Z2 = [1,5, ∠ π /2]
Man addiert nun die beiden Nullzeiger Z1 und Z2 . Die Auslenkung der Überlagerung zum Zeitpunkt t = 0 ist die y-Komponente von Z1 + Z2 . Dieses Verfahren
lässt sich für jeden Zeitpunkt t anwenden. Die beiden Zeiger drehen aber gleich
schnell. Daher dreht das Parallelogramm in Abb. 8.4 mit der gleichen Winkelgeschwindigkeit mit! Die Überlagerung der beiden harmonischen Schwingungen ist
deshalb wieder eine harmonische Schwingung mit Kreisfrequenz ω = 1 s−1 ! Der
Nullzeiger Z der Überlagerung ist
Z = Z1 + Z2 = [1, ∠ π /18] + [1,5, ∠ π /2] = [1,9418, ∠ 1,0389]
Dieser Zeiger hat eine Länge von 1,9418. Der Winkel zur x-Achse beträgt 1,0389.
Daher ist
y1 (t) + y2(t) = 1,9418 · sin(t + 1,0389)
eine harmonische Schwingung mit Amplitude 1,9418 und Nullphase 1,0389 (≈
59,5◦). Abbildung 8.6 zeigt das Resultat.
Die Konsequenz aus den Überlegungen am Zeigerdiagramm ist
Theorem 8.3. Die Überlagerung zweier harmonischen Schwingungen y1 (t) = A1 ·
sin(ω ·t + ϕ1 ) und y2 (t) = A2 ·sin(ω ·t + ϕ2 ) mit gleicher Kreisfrequenz ω ist wieder
eine harmonische Schwingung:
y1 (t) + y2(t) = A · sin(ω · t + ϕ )
Der Nullzeiger Z der Überlagerung lautet Z = Z1 + Z2 :
[A, ∠ ϕ ] = [A1 , ∠ ϕ1 ] + [A2, ∠ ϕ2 ]
8.3 Komplexe Zahlen
207
c Daniel Bättig
8 Harmonische Schwingungen und komplexe Zahlen ⃝
208
z
y
i = (0 | 1)
0,5
1 = (1 | 0)
x
t
Abb. 8.6 Addition (gestrichelte Linie) zweier harmonische Schwingungen
2·π
Abb. 8.8 Eine komplexe Zahl z mit Realteil
x und Imaginärteil y
4·π
Abb. 8.9 Die komplexen Zahlen i und 1
y
0,5
t
Abb. 8.7 Überlagerung zweier harmonischer Schwingungen y1 (t) = sint und
y2 (t) = sin(3t), die nicht die
gleiche Frequenz haben
2·π
4·π
Die Überlegungen am Zeigerdiagramm zeigen auch, dass die Überlagerung
zweier nicht gleich frequenter harmonischer Schwingungen (z.B. y1 (t) = sint und
y2 (t) = sin(3t)) in der Regel keine harmonische Schwingung mehr ist. Abbildung 8.7 zeigt dies ebenfalls.
Ein Punkt in der Ebene ist auch durch den Endpunkt eines Ortsvektors bestimmt.
Man visualisiert daher komplexe Zahlen durch solche Vektoren und nennt sie dann
Zeiger. Abbildung 8.8 zeigt eine komplexe Zahl dargestellt als Punkt. Komplexe
Zahlen liegen in der xy-Ebene, die man in diesem Zusammenhang die gaußsche
Zahlenebene nennt. Weiter nennt man x = ℜz = Re z den Realteil von z und y =
ℑz = Im z den Imaginärteil von z. So hat die Zahl z = (2 | − 4), den Realteil 2 und
den Imaginärteil −4. Zwei komplexe Zahlen nennt man gleich, wenn ihre Real- und
Imaginärteile gleich sind.
Den Punkt (0 | 1) bezeichnet man mit i. Diese komplexe Zahl heisst imaginäre
Einheit. Komplexe Zahlen der Form (x | 0) schreibt man kurz als x, also (x | 0) = x
(siehe Abb. 8.9).
Addiert werden zwei komplexe Zahlen, indem man die zugehörigen Ortsvektoren addiert. Man hat also
z1 + z2 = (x1 | y1 ) + (x2 | y2 ) = (x1 + x2 | y1 + y2 )
Die zweite wichtige Rechenart für komplexe Zahlen ist die Multiplikation. Sie wird
wie folgt definiert:
8.3 Komplexe Zahlen
In Bereichen der Technik sind reelle Zahlen nicht praktisch, um Phänomene aus
der Physik und Chemie zu beschreiben. Werden beispielsweise zwei gleichfrequente harmonische Schwingungen überlagert, so ist es schwierig Sinusfunktionen zu
addieren. Bei elektrischen Netzwerken möchte man das ohmsche Gesetz U = R · I
für den Gleichstrom auf Situationen übertragen, wo Wechselströme, Kondensatoren
und Spulen vorhanden sind. Mit komplexen Zahlen lassen sich solche Situationen
meistern. Komplexe Zahlen werden in diesem Abschnitt definiert und es wird gezeigt, wie man mit ihnen rechnet. Man definiert:
Definition 8.1. Eine komplexe Zahl z ist ein Punkt in der xy-Ebene, also ein geordnetes Paar (x | y) von reellen Zahlen.
Definition 8.2. Multipliziert man die imaginäre Einheit i mit sich selbst, entsteht
die Zahl −1:
i2 = i · i = (−1 | 0) · (0 | − 1) = (−1 | 0) = −1
Man multipliziert zwei komplexe Zahlen z1 und z2 , indem man die üblichen Rechneregeln aus den reellen Zahlen (Kommutativ-, Assoziativ- und Distributivgesetz)
beibehält und – wenn nötig – die obige Zusatzregel für die Multiplikation von i · i
benutzt.
Mit dieser Definition lässt sich beispielsweise die Zahl (0 | 4) als 4 · i schreiben.
Weiter ist
(3 | 4) = (3 | 0) + (0 | 4) = 3 + 4 · i
Man hat daher allgemein für eine komplexe Zahl z
8.3 Komplexe Zahlen
209
z = (x | y) = x + y · i
c Daniel Bättig
8 Harmonische Schwingungen und komplexe Zahlen ⃝
210
(8.2)
z
z
r
Man nennt die Schreibweise x + y · i die kartesische Darstellung einer komplexen
Zahl. Mit dieser Schreibweise sind der Real- und Imaginärteil der komplexen Zahl
schnell ablesbar und der Zeiger einfach visualisierbar.
ϕ
Beispiel 8.2 (Erste Rechenbeispiele). Man betrachtet die beiden komplexen Zahlen
z1 = (8 | 3) = 8 + 3 · i
und
z∗
z1 = (−4 | 2) = −4 + 2 · i
Die Definition der Addition und Multiplikation, besagt, dass die üblichen Rechenregeln zu reellen Zahlen gelten sollen. Also ist
Abb. 8.10 Komplexe Zahl z und konjugiert
komplexe Zahl z∗
Abb. 8.11 Komplexe Zahl z als Zeiger: Angabe von ϕ und r
z1 + z2 = (8 + 3 · i) + (−4 + 2 · i) = 4 + 5 · i
Die Summe ist also der Punkt (4 | 5). Weiter ist – man multipliziert mit dem Distributivgesetz aus –:
z1 · z2 = (8 + 3 · i) · (−4 + 2 · i) = −32 − 12 · i + 16 · i + 6 · i2 = −32 − 4 · i + 6 · i2
Mit der Rechenregel i2 = −1 erhält man
z1 · z2 = −32 + 4 · i − 6 = −38 + 4 · i
Dies ist der Punkt (−38 | 4). Schwieriger ist es, die Division z2 /z1 zu rechnen. Hier
hilft ein Trick mit geschicktem Erweitern des Bruchs:
−4 + 2 · i −4 + 2 · i 8 − 3 · i (−4 + 2 · i) · (8 − 3 · i)
=
·
=
8+3·i
8+3·i 8−3·i
64 − 9 · i2
Man multipliziert nun den Zähler aus. Im Nenner wird mit der Regel i2 = −1 zu
64 + 9 = 73. Man erhält:
−4 + 2 · i −26 + 28 · i −26 28
=
=
+
· i = −0,356 + 0,384 · i
8+3·i
73
73
73
Man nennt die Zahl z∗ , gegeben durch z∗ = x − y · i, die zu z = x + y · i konjugierte
Zahl (siehe Abb. 8.10). So ist also
(4 + 7 · i)∗ = 4 − 7 · i
Die Konsequenz dieser Rechnungen ist:
Theorem 8.4. In der Form z = x + y · i sind die Addition und die Multiplikation
dasselbe Rechnen wie mit reellen Zahlen mit der Zusatzregel i2 = −1.
Die kartesische Form erlaubt es, komplexe Zahlen schnell zu visualisieren, von
Hand zu addieren und subtrahieren und zu multiplizieren: !. Schwieriger ist es
von Hand zwei komplexe Zahlen in kartesischer Form zu dividieren. Hier muss der
Bruch geschickt mit der konjugierten Zahl des Nenners erweitert werden: ".
Mit MATLAB oder mit Julia kann man mit komplexen Zahlen rechnen. Der Realteil einer komplexen Zahl z bestimmt man mit real(z), den Imaginärteil mit
imag(z) und die komplex konjugierte Zahl mit dem Befehl conj(z). Mit MATLAB sieht dies so aus
matlab> z1 = 8 + 3i; z2 = -4 + 2i;
matlab> real(z1)
ans =
8
matlab> conj(z1)
ans =
8.0000 - 3.0000i
matlab> z1 + z2
ans =
4.0000 + 5.0000i
matlab> z1 * z2
ans =
-38.0000 + 4.0000i
matlab> z2 / z1
ans =
-0.3562 + 0.3836i
Mit Julia gibt man komplexe Zahl wie folgt ein
julia>
julia>
8
julia>
-38
z1 = 8 + 3im; z2 = -4 + 2im;
real(z1)
z1*z2
+ 4im
Eine oft benutzte Zahl ist 1/i. Man erhält mit der Gleichung i2 = −1:
1
= −i
i
8.3 Komplexe Zahlen
211
212
c Daniel Bättig
8 Harmonische Schwingungen und komplexe Zahlen ⃝
In der Technik, vor allem bei Anwendungen zu Schwingungen und elektrischen
Netzwerken, braucht man komplexen Zahlen um Zeiger zu modellieren. Zeiger sind
Orstvektoren in der xy-Ebene, eindeutig bestimmt durch ihre Länge und ihren Winkel zur x-Achse:
2 · ei·3·π /4
3 · ei·π /4
Definition 8.3. Ist z eine komplexe Zahl, dargestellt durch einen Zeiger, so nennt
man die Polarkoordinaten ϕ und r des Zeigers z das Argument und den Betrag von z.
Abbildung 8.11 zeigt die Situation. Den Betrag r von z – also der Abstand der Zahl
zum Nullpunkt – schreibt man wie bei einer reellen Zahl als |z|. Das Argument einer
komplexen Zahl notiert man oft mit arg(z). Mit MATLAB und mit Julia berechnet
man das Argument einer komplexen Zahl z mit angle(z) und den Betrag mit
abs(z). Mit MATLAB lässt sich ein Zeiger z mit
Es zeigt sich nun, dass sich zweite Faktor mit einer Exponentialfunktion ausdrücken
lässt! Nach Abschnitt 5.10 ist die Exponentialfunktion u(ϕ ) = exp(a · ϕ ) definiert
als die Funktion mit
du
= a · u(ϕ ) und u(0) = 1
dϕ
Betrachtet man g(ϕ ) = cos ϕ + i · sin ϕ , so ist g(0) = 1. Weiter ist
dg
(ϕ ) = − sin ϕ + i · cos ϕ = i · (cos ϕ + i · sin ϕ ) = i · g(ϕ )
du
Also muss g(ϕ ) eine Exponentialfunktion sein: g(ϕ ) = exp(i · ϕ ). Dies nennt man
die Euler-Formel
exp(i · ϕ ) = cos ϕ + i · sin ϕ
(8.3)
Zusammengefasst hat man:
Theorem 8.5. Ein Zeiger z mit Argument ϕ und Betrag r lässt sich schreiben als
z = r · exp(i · ϕ ) = r · ei·ϕ
Dies nennt man die Polarform oder Zeigerform einer komplexen Zahl.
Bei der Polarform einer komplexen Zahl sind das Argument und der Betrag der
Zahl schnell ablesbar und der Zeiger einfach visualisierbar. Die Polarform ist also
für Zeiger ebenso praktisch wie die kartesische Form für Punkte. Abbildung 8.12
zeigt mehrere Zeiger mit ihrer Zeigerform.
Beispiel 8.3 (Rechenbeispiele
mit der Polarform). Die Zahl 1 + i hat Argument π /4
√
und Abstand 2 von Nullpunkt. Dies lässt sich mit einer Skizze schnell verifizieren.
Daher ist
√
1*+,+ i = * 2 ·+,
ei·π /4-
Punktform
matlab> compass(z)
zeichnen. Ist z = x + y · i erhält man mit Hilfe des Betrags r und des Arguments ϕ
von z:
z = x + i · y = r cos ϕ + i · r sin ϕ = r · (cos ϕ + i · sin ϕ )
3 · e−i·π /2
Abb. 8.12 Mehrere komplexe
Zahlen, dargestellt als Zeiger
2 · ei·π /3
Zeigerform
Die komplexe Zahl
hat Betrag 2 und Argument π /3. Ihr Zeiger hat also
einen Winkel von 60◦ zur x-Achse und eine Länge von 2.
Die Zahl i (oder der Punkt (0 | 1)) hat einen Winkel von 90◦ zur x-Achse. Sie ist
eine Einheit vom Nullpunkt entfernt. Daher ist
i = 1 · ei·π /2 = ei·π /2
Dies ist die Zeigerform von i. Weiter ist e2π ·i = 1 und ei·π = −1.
In der Polarform lassen sich komplexe Zahl schnell multiplizieren, dividieren
und potenzieren. Ist
z1 = 2 · eiπ /4
und
z2 = 3 · e−iπ /6
so ist
z1 · z2 = 2 · eiπ /4 · 3 · e−iπ /6 = 6 · ei·(π /4−π /6) = 6 · ei·π /12
Analog ist
2
2eiπ /4
= · ei·(π /4+π /6) = 0,667 · ei·5π /12
3e−iπ /6 3
Die Zahl hat einen Winkel von 180◦/12 = 15◦ zur x-Achse. Ihr Abstand zum Nullpunkt beträgt 2/3.
Um (1 + i)16 von Hand zu rechnen, format man die Zahl 1 + i zuerst in Polarform
um. Man erhält
.√
/16
(1 + i)16 =
2 · ei·π /4
= 28 · ei·4π
Dies ist der Zeiger mit Winkel 4π zur x-Achse und Betrag 28 = 256. Damit ist
(1 + i)16 = 256.
Die obigen Rechnungen zeigen, dass die Polarform es ermöglicht, Zeiger schnell
zu visualisieren, von Hand zu multiplizieren, zu dividieren und zu multiplizieren.
Schwieriger ist es von Hand zwei Zeiger zu addieren.
8.4 Komplexe Zahlen: grafisch addieren und multiplizieren
y
213
y
z1 · z2
z1 + z2
z2
z2
ϕ2
x
ϕ1
c Daniel Bättig
8 Harmonische Schwingungen und komplexe Zahlen ⃝
8.5 Erste Anwendungen der komplexen Zahlen
In diesem Abschnitt wird dargestellt, dass komplexe Zahlen benutzt werden können,
um mit harmonischen Schwingungen zu rechnen und Nullstellen von Polynomen zu
nennen.
Eine harmonische Schwingung, gegeben durch die Gleichung
ϕ1 + ϕ2
z1
214
z1
x
y(t) = A · sin(ω · t + ϕ )
Abb. 8.13 Addition von Zeigern
(8.5)
ist durch einen Zeiger Z mit Länge A festgelegt. Der Zeiger dreht sich dabei mit
Winkelgeschwindigkeit ω (siehe Abb. 8.2 und zum Zeitpunkt t = 0 hat er einen
Winkel von ϕ zur x-Achse. Der Zeiger Z kann als komplexe Zahl y(t) aufgefasst
werden. In Zeigerform geschrieben hat man damit
Abb. 8.14 Multiplikation von Zeigern
Taschenrechner sind in der Lage mit komplexen Zahlen zu rechnen. Resultate
können – je nach Anwendungszweck – in kartesischer Form oder als Zeiger dargestellt werden.
y(t) = A · ei·(ω ·t+ϕ )
(8.6)
Man nennt dies auch die komplexe Darstellung einer harmonischen Schwingung.
Der Imaginärteil dieses Zeigers ist die eigentliche Schwingung y(t):
8.4 Komplexe Zahlen: grafisch addieren und multiplizieren
Auslenkung:
Komplexe Zahlen lassen sich in kartesischer Form und in Polarform gut rechnen.
Wie bei Vektoren kann man zudem die Grundrechenoperationen – hier die Addition
und die Multiplikation – auch grafisch durchführen.
Die Addition zweier komplexer Zahlen z1 und z2 entspricht der Addition von
Zeigern oder Ortsvektoren. Dies veranschaulicht Abb. 8.13. Die Multiplikation lässt
sich grafisch verstehen, wenn man die beiden komplexen Zahlen z1 und z2 in Zeigerform schreibt:
z1 = r1 · ei·ϕ1 ,
z2 = r2 · ei·ϕ2
Dann ist
z1 · z2 = r1 · r2 · ei·(ϕ1 +ϕ2 )
Die Beträge der beiden komplexen Zahlen werden daher multipliziert und die Argumente werden addiert. Dies lässt sich so schreiben:
| z1 · z2 |=| z1 | · | z2 |,
arg(z1 · z2 ) = arg(z1 ) + arg(z2 )
(8.4)
Abbildung 8.14 zeigt grafisch das entstandene Resultat. Eine Konsequenz aus der
Rechnung ist: Multipliziert man einen Zeiger z mit der imaginären Einheit i, so wird
der Zeiger z um 90◦ im Gegenuhrzeigersinn gedreht.
y(t) = ℑy(t)
Der Nullzeiger ist die Position des Zeigers zum Zeitpunkt t = 0:
Nullzeiger y(0) = A · ei·ϕ
Mit der komplexen Darstellung einer harmonischen Schwingung, einer Exponentialfunktion lässt sich besonders gut rechnen. Die Darstellung der Schwingung mit
Gleichung (8.5), einer Sinusfunktion, ist unpraktisch. Dies illustriert das folgende
Rechnung:
Sind y1 (t) und y2 (t) zwei harmonische Schwingungen mit der gleichen Kreisfrequenz ω , so lauten sie in komplexer Form:
y1 (t) = A1 · ei·(ω ·t+ϕ1 ) ,
y2 (t) = A2 · ei·(ω ·t+ϕ2 )
Die Überlagerung der beiden Schwingung lässt sich mit dieser Polarform berechnen:
.
/
y1 (t) + y2 (t) = A1 · ei·(ω ·t+ϕ1 ) + A2 · ei·(ω ·t+ϕ2 ) = A1 · ei·ϕ1 + A2 · ei·ϕ2 ·ei·ω ·t
*
+,
=z
Der Term in der Klammer ist eine Summe z von zwei Zeigern. Diese Summe z kann
man in Polarform schreiben:
z = A · ei·ϕ
Daraus folgt
y1 (t) + y2 (t) = A · ei·ϕ · ei·ω ·t = A · ei·(ω ·t+ϕ )
8.5 Erste Anwendungen der komplexen Zahlen
215
c Daniel Bättig
8 Harmonische Schwingungen und komplexe Zahlen ⃝
216
Entstanden ist wiederum eine harmonische Schwingung. Damit hat man das Folgende:
Theorem 8.6. Die Überlagerung zweier gleich frequenter harmonischer Schwingungen, gegeben durch y1 (t) = A1 · sin(w ·t + ϕ1 ) und y2 (t) = A2 · sin(w ·t + ϕ2 ), ist
wieder eine harmonische Schwingung:
y1 (t) + y2 (t) = A · sin(w · t + ϕ )
mit
1×
1×
1×
3×
1×
A · eiϕ = A1 · eiϕ1 + A2 · eiϕ2
1×
1×
Hier ein Beispiel dazu:
Beispiel 8.4 (Überlagerung zweier harmonischer Schwingungen). Die zwei Schwingungen y1 (t) = 3 · sin(t + 2) und y2 (t) = 10 · sin(t + 4) haben die gleiche Kreisfrequenz. Die Überlagerung ist der beiden Schwingungen ist daher auch harmonisch
mit Amplitude A und Phase ϕ . Diese lauten:
A · ei·ϕ = 3 · ei·2 + 10 · ei·4 = 9,16 · e−2,58·i
Abb. 8.15 Vier Nullstellen des Polynoms
p4 (x), alle einfach
4.0000 - 3.0000i
2.0000 + 0.0000i
-1.0000 + 0.0000i
Also ist y1 (t) + y2 (t) = 9,16 · sin(t − 2,58). In komplexer Form geschrieben, lautet
das Resultat 9,16 · ei·(t−2,58).
Mit Julia erhält man:
Polynome spielen in der Technik einer Rolle, um Punkte zu interpolieren (siehe
Abschnitt 5.5. Pole von rationale Funktionen – also Nullstellen von Polynomen –
spielen eine Rolle um zu analysieren, wie dynamische Systeme wie Luftseilbahnen,
Autos, Brücken oder elektrische Netze auf Einflüsse von außen (Luftbewegungen,
Erschütterungen) reagieren. Das Polynom p2 (x) = 1 + x2 lässt sich mit komplexen
Zahlen faktorisieren:
julia>
julia>
4.0 +
4.0 2.0 +
-1.0 +
(x − i) · (x + i) = x2 − i2 = 1 + x2
using Polynomials;
p4 = Poly([-50; -9; 31; -9; 1]); roots(p4)
3.0im
3.0im
0.0im
0.0im
Das Polynom hat also die vier Nullstellen 4 + 3 · i, 4 − 3 · i, 2 und −1 (siehe
Abb. 8.15). Man hat also
Es besitzt damit zwei komplexe Nullstellen: i und −i. Man kann allgemein zeigen,
dass ein Polynom p(z) vom Grad n
p(z) = a0 + a1 · z + a2 · z2 + · · · + an · zn
sich dank komplexen Zahlen in lineare Faktoren zerlegen lässt:
p(z) = an (z − z1 )(z − z2 ) · · · (z − zn )
Dabei sind z1 , z2 , . . . , zn die Nullstellen von p. Man nennt dies den Fundamentalsatz
der Algebra. Um die Nullstellen zu berechnen, verwendet man Programme. Mit
MATLAB oder mit Julia ist dies der Befehl roots():
Beispiel 8.5 (Komplexe Nullstellen). Gegeben ist das Polynom p4 (x) = −50 − 9x +
31x2 − 9x3 + x4 . Die Nullstellen, ermittelt mit MATLAB, lauten
matlab> p4 = [1; -9; 31; -9; -50];
ans =
4.0000 + 3.0000i
Abb. 8.16 Nullstellen des Polynoms p5 (x)
roots(p4)
p4 (x) = −50 − 9x+ 31x2 − 9x3 + x4 = (x− (4 + 3 ·i))·(x− (4 − 3 ·i))·(x− 2)·(x+ 1)
Man sagt, dass die vier Nullstellen alle einfach sind, da jeder Faktor nur einmal
erscheint. Die fünf Nullstellen des Polynoms p5 (x) = −16 + 40x − 44x2 + 26x3 −
8x4 + x5 sind:
matlab> p5
ans =
1.0000 +
1.0000 2.0000 +
2.0000 +
2.0000 -
= [1; -8; 26; -44; 40; -16]; roots(p5)
1.0000i
1.0000i
0.0000i
0.0000i
0.0000i
Die Nullstellen sind also 1 + i, 1 − i und die Zahl 2 (dreifach). Man hat deshalb:
p5 (x) = −16 + 40x − 44x2 + 26x3 − 8x4 + x5 = (x − (1 + i)) · (x − (1 − i)) · (x − 2)3
8.6 Ortskurven
217
218
c Daniel Bättig
8 Harmonische Schwingungen und komplexe Zahlen ⃝
Eingang: x(t)
ω = −0,8 s−1
System
ω = π /8
Antwort: y(t)
Abb. 8.17 Eine Radaufhängung mit einem
McPherson-Federbein (aus [1])
ω = 0,5 s−1
ω = π /2
Abb. 8.18 Schematische Darstellung von
Eingang und Antwort eines Systems
ω = 0,8 s−1
ω = 1 s−1
Die Nullstelle x = 2 ist dreifach. Abbildung 8.16 visualisiert die drei Nullstellen mit
ihrer Vielfachheit.
Beachten Sie aber – dies wurde schon in Theorem 5.1 erwähnt –, dass der Algorithmus roots() nummerisch instabil ist! Die berechneten Nullstellen können also
schlecht sein.
Abb. 8.19 Ortskurve ei·ω ·2 s mit Nullzeigern
Abb. 8.20 Ortskurve eines angeregten Pendels
Beispiel 8.6 (Eine einfache Ortskurve). Ein System habe die Ortskurve
Nullzeiger(ω ) = 1 · ei·ω ·2 s
8.6 Ortskurven
In der Mechanik und in der Elektrotechnik betrachtet man Systeme wie Luftseilbahnen, Fahrzeugfederungen und elektrische Schaltkreise (siehe Abb. 8.17). Sie werden
durch eine harmonische Schwingungen x = x(t) = sin(ω ·t) angeregt oder gestört“.
”
Das System bewegt sich: y = y(t). Man nennt die Störfunktion x(t) auch die Eingangsgröße des Systems und die Funktion y(t) auch das Antwortsignal oder die
Ausgangsgröße des Systems. Abbildung 8.18 zeigt die Situation schematisch.
Oft reagiert das angeregte System mit einer harmonischen Schwingung mit einer
Kreisfrequenz, die gleich der Anregungskreisfrequenz ω von x = x(t) ist. Es ist also
– in komplexer Form geschrieben –:
y = y(t) = A · e
i·(ω ·t+ϕ )
Die Amplitude A und die Phase ϕ der Schwingung – und damit der Nullzeiger
des Antwortsignals – hängen von der Anregungskreisfrequenz ω ab: A = A(ω ),
ϕ = ϕ (ω ). Für jedes ω erhält man somit einen Nullzeiger:
Nullzeiger(ω ) = A(ω ) · ei·ϕ (ω )
Verbindet man die Endpunkte der Zeiger erhält man eine Kurve in der Ebene.
Man spricht von einer Ortskurve. Der Graph der Ortskurve nennt man ein NyquistDiagramm. Es stellt also die Antwort eines Systems (den Nullzeiger) in Funktion
der angeregten Kreisfrequenz dar.
für angelegte Kreisfrequenzen 0 ≤ ω ≤ π . Das System reagiert also so, dass für jede
angelegte Kreisfrequenz ω , die Amplitude A = 1 bleibt. Die Phase gegenüber der
angelegten Schwingung hängt von ω ab und beträgt ω ·2 s. Stellt man die Nullzeiger
in Funktion von ω dar, durchlaufen sie einen Kreis mit Mittelpunkt (0 | 0) und Radius eins. Abbildung 8.19 zeigt die Ortskurve. Mit MATLAB kann man die Ortskurve
wie folgt grafisch darstellen:
matlab> omega = linspace(0, pi, 1000);
matlab> nullzeiger = exp(1i*omega*2);
matlab> plot(nullzeiger)
Mit Julia stellt man die Ortskurve wie folgt dar:
julia>
julia>
julia>
julia>
omega = linspace(0, pi, 1000);
nullzeiger = exp(1im*omega*2);
using Gadfly;
plot(x=real(nullzeiger),y=imag(nullzeiger),
Geom.line(preserve_order=true))
Beispiel 8.7 (Nyquist-Diagramm eines Pendels). Ein Pendel wird mit der harmonischen Schwingung x = x(t) = sin(ω · t) angeregt. Dabei kann ω eine positive oder
negative Zahl sein. Das Pendel reagiert mit einer Schwingung y = y(t) mit Kreisfrequenz ω . Der Nullzeiger dieser Schwingung laute
Nullzeiger(ω ) =
2
(i · ω )2 + 0,4 · i · ω + 1
8.6 Ortskurven
219
Der Nenner ist ein Polynom vom Grad zwei. Mit MATLAB lässt sich diese Ortskurve für −100 s−1 ≤ ω ≤ 100 s−1 darstellen:
matlab> omega = linspace(-100, 100, 10000);
matlab> nzeiger = 2./((1i*omega).ˆ2+0.4i*omega+1);
matlab> plot(nzeiger)
Abbildung 8.20 zeigt den Graph der Ortskurve. Der Punkt auf der Ortskurve, der am
weitesten vom Nullpunkt ist, zeigt die maximale erzeugbare Amplitude des Pendels
an. Mit MATLAB berechnet sich dies wie folgt:
matlab> [AmplitudeMax, index] = max(abs(nzeiger));
matlab> AmplitudeMax
AmplitudeMax =
5.1031
matlab> omega(index )
ans =
-0.9591
Die maximal erzeugbare Amplitude des Pendels lautet 5,10. Erzeugt wird sie bei
einer Kreisfrequenz von −0,9591 s−1 (und bei 0,9591 s−1 ).
220
c Daniel Bättig
8 Harmonische Schwingungen und komplexe Zahlen ⃝
Körper mit einer Horizontal- vH und Vertikalgeschwindigkeit vV von einem Punkt
mit Koordinaten (x0 | y0 ) so gilt für die Flugbahn, wenn man den Luftwiderstand
nicht berücksichtigt:
x(t) = x0 + vH · t,
1
y(t) = − · g · t 2 + vV · t + y0
2
(a) Zeichnen Sie die Flugbahn für verschiedene Abwurfgeschwindigkeiten, wenn
x0 = 0 m und y0 = 10 m.
(b) Berechnen Sie den Zeitpunkt t, zudem der Körper den Boden berührt, wenn
x0 = 0 m und y0 = 10 m ist.
(c) Berechnen Sie den Geschwindigkeitsvektor v = v(t) zum Zeitpunkt t.
(d) Wie lautet der Beschleunigungsvektor a = a(t)? Überrascht Sie das Resultat?
8.4. Bestimmen Sie bei den folgenden harmonischen Schwingungen Amplitude,
Kreisfrequenz, Nullphasenwinkel, Frequenz und Schwingungsdauer (Einheiten: Zeit
t in Sekunden, Auslenkungen in Zentimetern):
y1 (t) = 15 sin(8t)
y3 (t) = 3 sin(6π t + 2)
y2 (t) = 2 sin(8t − π /36)
y4 (t) = 12 cos(7t + π /3)
Zeichnen Sie die Nullzeiger der Schwingungen.
Aufgaben
8.1. Ein Fahrzeug in der xy-Ebene ist zum Zeitpunkt t mit 0 ≤ t ≤ 1 im Punkt P =
P(t) = (x(t) | y(t))
x(t) = t − t 2 ,
y(t) = t + t 2
(a) Skizzieren Sie die Fahrkurve von Hand mit Hilfe einer Wertetabelle.
(b) Zeichnen Sie die Fahrkurve mit MATLAB oder mit Julia.
(c) Berechnen Sie den Geschwindigkeitsvektor und den Beschleunigungsvektor.
Zeichnen Sie den Ortsvektor, den Geschwindigkeitsvektor und den Beschleunigungsvektor zum Zeitpunkt t = 0,5 in die Graphik der Fahrkurve.
8.2. Ein Fahrzeug fährt auf einer Kurve im Raum. Die Position P = P(t) = (x | y | z)
des Fahrzeugs zum Zeitpunkt t ist – für 0 ≤ t ≤ 11 – gegeben durch
x(t) = 2t cos(t),
y(t) = 2t sin(t),
z(t) = t 2
(a) Zeichnen Sie die Kurve mit MATLAB oder mit Julia.
(b) Berechnen Sie den Geschwindigkeitsvektor und den Beschleunigungsvektor des
Fahrzeugs.
(c) Bestimmen Sie die räumliche Steigung des Fahrzeugs zum Zeitpunkt t.
8.3. In einem kartesischen Koordinatensystem entspricht die x-Achse dem flachen
Boden und die y-Achse misst den vertikalen Abstand zum Boden. Wirft man einen
8.5. (a) Stellen Sie die beiden harmonischen Schwingungen f (t) = 2 sin(2t + π /2)
und g(t) = 3 sin(2t) grafisch dar. Zeichnen Sie auch ihre Nullzeiger.
(b) Berechnen Sie die Amplitude, die Frequenz und den Nullphasenwinkel der
Überlagerung f (t) + g(t). Zeichnen Sie die so entstandene Schwingung.
(c) Zwei gleich frequente Wechselspannungen U1 = 40 sin(314t + 0,1) und U2 =
70 cos(314t) (U1 bzw. U2 in Volt, t in Sekunden) werden überlagert. Welche Wechselspannung entsteht?
8.6. Gegeben sind die beiden harmonischen Schwingungen y1 (t) = 5 · sin(2t + 3)
und y2 (t) = 5,1 · sin(2t − 0,3). Wie lauten die Amplitude, die Phase und die Kreisfrequenz der Überlagerung y1 (t) + y2(t)?
8.7. Gegeben ist eine harmonische Schwingung f (t) = 7, /!2 · sin(4π t). Bestimmen
Sie die Amplitude und den Nullphasenwinkel einer gleich frequenten Schwingung
g(t) so, dass die Überlagerung f (t) + g(t) die Amplitude 22,5 und eine Phasenverschiebung von π /3 gegenüber der Schwingung f (t) aufweist.
8.8. Bestimmen Sie die Phasenverschiebung zwischen zwei gleich frequenten harmonischen Schwingungen gleicher Amplitude so, dass ihre Summe eine harmonische Schwingung derselben Amplitude ergibt. Wie gross sind dabei die Phasenverschiebungen zwischen der Summe und den beiden Teilschwingungen? (Tipp:
Arbeiten Sie mit dem Zeigerdiagramm. Sie müssen nichts rechnen!)
8.9. Abbildung 8.21 zeigt den Graphen einer harmonischen Schwingung y = y(t).
Die Funktionsgleichung von y = y(t) lautet
8.6 Ortskurven
221
222
c Daniel Bättig
8 Harmonische Schwingungen und komplexe Zahlen ⃝
y
y
2
1
t
Abb. 8.21 Eine harmonische Schwingung y = y(t)
(Zeiteinheit t in Sekunden,
Auslenkung y in cm)
x
−2
2
4
Abb. 8.22 Vier Punkte und
drei Zeiger
y(t) = A · sin(ω · t + ϕ )
Wie lauten A, ω und ϕ ? Zeichnen Sie zudem den Nullzeiger der Schwingung.
8.10. Von zwei gleich frequenten harmonischen Schwingungen y1 (t), y2 (t) und ihrer Summe z(t) = y1 (t) + y2(t) kennt man die folgenden Angaben:
Kreisfrequenz Amplitude Nullphasenwinkel
y1 (t)
2π
5
π /4
6
y2 (t)
2π
z(t)
2π
7
zwischen 0 und π
Berechnen Sie die fehlenden Nullphasenwinkel von y2 (t) und z(t). (Tipp: Machen
Sie eine Skizze mit Zeigern!)
8.11. Die Summe zweier gleich frequenter harmonischer Schwingungen y1 (t) und
y2 (t) hat Amplitude 10 cm und Schwingungsdauer 5 s. Der Nullphasenwinkel von
y1 beträgt π /6, der Nullphasenwinkel von y2 beträgt 3π /4 und die Amplituden von
y1 und y2 verhalten sich wie 2:1. Bestimmen Sie die Amplituden von y1 und y2 , und
berechnen Sie den Nullphasenwinkel von y1 + y2 .
8.12. Berechnen Sie von Hand und kontrollieren Sie mit einem Taschenrechner, mit
MATLAB oder mit Julia:
(1 + 2i) · (2 + 3i) [(4 − 5i) + (2 + 3i)]2 (4 − 5i) · (2 + i) i3
i4
i5
i6
Berechnen Sie die folgenden Brüche von Hand
17
4+i
1
1 − 2i
4 + 3i
3 − 4i
8.13. SchreibenSie die folgenden komplexen Zahlen in Zeigerform auf:
√
1−i
− 2 + 2i
5 + 5i
1 + 3i
Kontrollieren Sie die Resultate mit einem Taschenrechner, mit MATLAB oder mit
Julia.
−2
2
8.14. Es sei z = a + b · i. Geben Sie Formeln für z2 , z3 , z + z∗ , z − z∗ , z · z∗ und 1/z.
8.15. Zeichnen Sie die Zeiger 2 · e3π i , 7 · eiπ /4 und 2 · ei·7π /2 und bestimmen Sie
daraus ihre Real- und Imaginärteile.
8.16. (a) Zeichnen Sie die Zeiger eiπ , 2eiπ /4 und 2e−π i .
(b) Man überlagert zwei gleich frequente Wechselspannungen U1 = 50ei·(300t+1) und
U2 = 80ei·(300t+50) (t in Sekunden, Spannungen in Volt). Bestimmen Sie mit einem
Taschenrechner, mit MATLAB oder mit Julia die Frequenz, die Amplitude und den
Nullphasenwinkel der entstandenen Wechselspannung.
8.17. Bestimmen Sie mit einem Rechner alle komplexen Lösungen z der Gleichungen z2 + 0,1z + 100 = 0, z2 − 2z + 2 = 0 und z2 = −16. Stellen Sie die Lösungen
grafisch dar.
8.18. Berechnen Sie mit MATLAB oder mit Julia alle Nullstellen der Polynome
p1 (x) = x5 − 8x4 + 10x3 + 44x2 − 155x + 300
p2 (x) = x5 − 7x4 + 23x3 − 45x2 + 48x − 20
p3 (x) = x3 + 3x2 + 3x + 1
p4 (x) = x10 + 1
Zeichnen Sie die Nullstellen als Punkte in der komplexen Ebene und geben Sie ihre
Vielfachheiten an.
8.19. Abbildung 8.22 zeigt verschiedene Punkte und Zeiger. Wie lauten die Punkte
und Zeiger?
8.20. (a) Gegeben ist die Ortskurve
Nullzeiger(ω ) = 2ei·ω − i
Wenn ω alle reellen Zahlen durchläuft, so bewegt sich Nullzeiger(ω ) auf einer Kurve in der komplexen Ebene. Überlegen Sie sich, wie diese Kurve aussieht.
(b) Dieselbe Frage für
Literaturverzeichnis
223
Nullzeiger(ω ) =
5
(i · ω )2 + 0,1 · i · ω + 5
mit −20 ≤ ω ≤ 20. Dies ist schwieriger als Aufgabe (a). Erstellen Sie deshalb nur
einen MATLAB- oder Julia-Plot der Kurve! Finden Sie den Punkt auf der Ortskurve,
der am weitesten vom Nullpunkt entfernt ist.
8.21. Die Admittanz Y ( komplexer Leitwert“) eines Serieschwingkreises ist
”
1
Y=
1
R + iω L +
iω C
(a) Geben Sie eine Formel für den Betrag A von Y an.
(b) Es seien R, L und C fest, aber ω ≥ 0 variabel. Der obige Betrag A wird damit zu
einer Funktion von ω . Wie gross ist A in den Extremfällen ω = 0 und ω = ∞?
(c) Es sei L = 100 µH und C = 0,01µF. Erstellen Sie mit MATLAB oder mit Julia
den Graphen von A(ω ) in den drei Fällen R = 20 Ω, 60 Ω und 200 Ω. Für welchen
Wert von ω ist A(ω ) maximal?
Literaturverzeichnis
1. Tröster, F.: Steuerungs- und Regelungstechnik für Ingenieure. Oldenburg Wissenschaftsverlag GmbH (2005)