4. Paramagnetismus

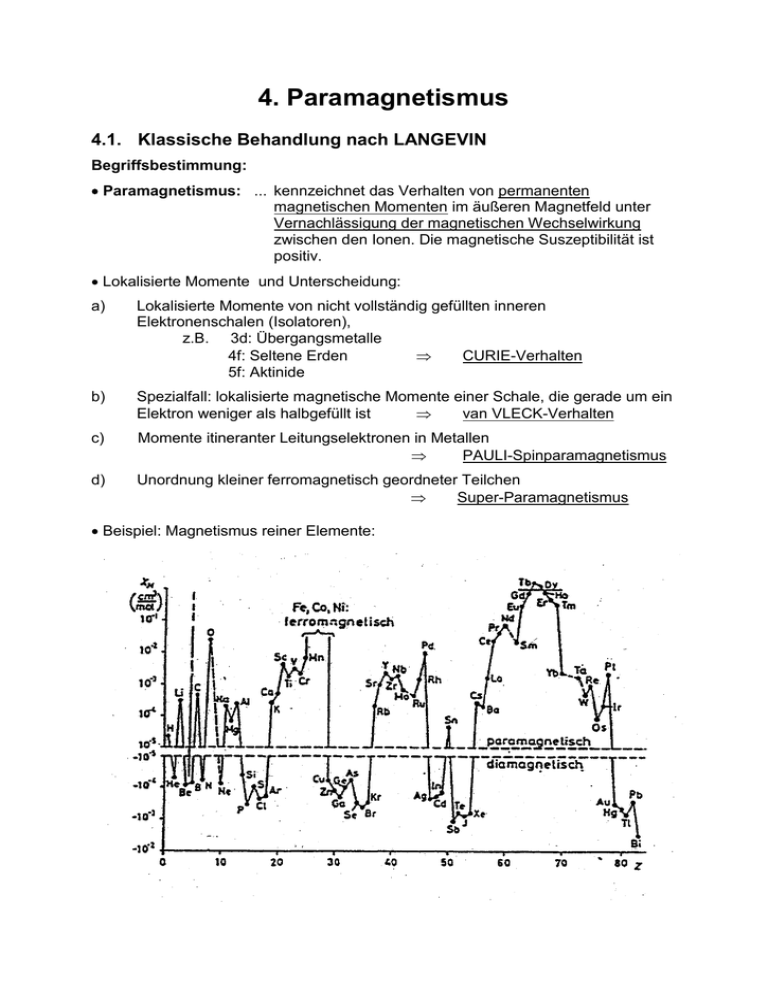
4. Paramagnetismus
4.1. Klassische Behandlung nach LANGEVIN
Begriffsbestimmung:
 Paramagnetismus: ... kennzeichnet das Verhalten von permanenten
magnetischen Momenten im äußeren Magnetfeld unter
Vernachlässigung der magnetischen Wechselwirkung
zwischen den Ionen. Die magnetische Suszeptibilität ist
positiv.
 Lokalisierte Momente und Unterscheidung:
a)
Lokalisierte Momente von nicht vollständig gefüllten inneren
Elektronenschalen (Isolatoren),
z.B. 3d: Übergangsmetalle
4f: Seltene Erden

CURIE-Verhalten
5f: Aktinide
b)
Spezialfall: lokalisierte magnetische Momente einer Schale, die gerade um ein
Elektron weniger als halbgefüllt ist

van VLECK-Verhalten
c)
Momente itineranter Leitungselektronen in Metallen

PAULI-Spinparamagnetismus
d)
Unordnung kleiner ferromagnetisch geordneter Teilchen

Super-Paramagnetismus
 Beispiel: Magnetismus reiner Elemente:
Thermodynamische Berechnung der Suszeptibilität:
Für den Fall einer nicht vollständig besetzten Elektronenschale folgt J  0 (Ausnahme
siehe 4.3). Der Grundzustand des Systems ist (2J+1)-fach entartet.
Bei Betrachtung der Energieverschiebung in Störungsrechnung entsprechend 3.3
verschwinden die beiden ersten Terme in
f i  B B z  L z  g S S z  f i 
Ei   B Bz  f i Lz  g S S z f i  
E i  E i´
i  i´
2

e 2 Bz2
8me
Z
fi
 (x
n 1
2
n
 y n2 f i
nicht.
Der erste Term ist jedoch selbst in starken Magnetfeldern viel größer (ca. Faktor
104.....106) als die beiden anderen, so dass nur dieser Beitrag in der nachfolgenden
Diskussion behandelt wird:
WIGNER-ECKART-Theorem:
Die Berechnung der (2J+1)-dimensionalen Matrix wird durch die Anwendung des
WIGNER-ECKART-Theorems (allg. Theorem der Tensor-Algebra) wesentlich
vereinfacht (Es wird eine „Faktorisierung“ beim Übergang zum Gesamtdrehimpuls
erreicht):
„Die Matrixelemente eines Vektoroperators im (2J+1)-dimensionalen Raum der
Eigenzustände der Operatoren
Ĵ 2 und Ĵ z für einen bestimmten Wert J sind
proportional zu den Matrixelementen des Operators
 Lˆ  g S Sˆ  g ( JLS )  Jˆ
Ĵ selbst.“
(g......LANDÉ-Faktor des Gesamtsystems, s.o.)
 Ei   B B z  g f i J z f i  ....
Statistische Betrachtung:
Außerdem ist zu beachten, dass wegen der Entartung des Grundzustandes ein
Gleichsetzen von Grundzustandsenergie und Freier Energie (vgl. 3.3) nicht
realisierbar ist.
Die Berechnung der Suszeptibilität ist deshalb über die Ableitung im Rahmen der
statistischen Mechanik vorzunehmen:
Betrachtet wird ein System mit n Energiezuständen Ei. Damit ist die
Zustandssumme
Z   exp(  Ei / kT )
i
Besetzungswahrscheinlichkeit:
wi ( Ei ) 
1
exp(  Ei / kT )
Z
2S+1 = 8
Zustände
Beispiel: Besetzungwahrscheinlichkeit für ein Spinsystem mit S = 7/2 (z.B. Gd 3+)
Die Magnetisierung ergibt sich dann zu
F
 ln Z
1 Z
 kT
 kT
B
B
Z B
E
1   1  E
M  kT   i exp(  Ei / kT )   wi i
Z  kT  i B
B
i
M 

Daraus kann der allgemeine Ausdruck für die Suszeptibilität ermittelt werden:
M
M
2F


  0
  0
H
B
B 2
2
Ei
 2 Ei
1 Z
1
1  Ei 
1
   0 [ 2
exp(  Ei / kT )  
exp(  Ei / kT )   
 ( ) exp(  Ei / kT )]

2
Z i B
Z i  B 
kT
Z B i B
2
 2 Ei
1 1  Ei
1
1 1

 Ei 
   0 [ 2
exp(  Ei / kT )   
exp ( Ei / kT ) 


 exp(  Ei / kT )]

2
Z i B
Z kT i  B 
Z kT  i B

2
Unter Nutzung des Ausdrucks für die Besetzungswahrscheinlichkeit heißt das:
2
E 
 2 Ei
1 
1
 E 
     wi i    wi

wi  i 

2
kT  i
B 
kT i
B
 B 
i
2
Als Ausdruck für die paramagnetische Suszeptibilität einer Schale mit J  0 erhält
man dann unter Verwendung des CURIE-Terms (1. Summand) der EnergieEigenwerte (s.o.)
 para   0 g  B
2
2
2
 1 
1

  f i J z f i wi  

 fi J z fi
kT i

 kT  i
2

wi  .

Diskussion:

Die beiden Summanden beschreiben das CURIE-Verhalten.  para  C / T (mit
C... Curie Konstante). Die mathematische Struktur dieser Terme
 ...2   ...2 entspricht dem Ausdruck für die spezifische Wärmekapazität
cV.
Die Betrachtung gilt unter der Voraussetzung kT >> gBB
2
2
Für H  0 kann der Term  ...  M  vernachlässigt werden, da eine




paramagnetische Substanz im Nullfeld keine Magnetisierung aufweist.
Für H >> 0 ist dieser Ausdruck jedoch in die Betrachtung einzubeziehenDie
Temperaturabhängigkeit ergibt sich zu T-1.
Die im allgemeinen komplexe Betrachtungsweise kann jedoch auch vereinfacht
dargestellt werden:
Klassische Näherung nach LANGEVIN
Es erfolgt eine Betrachtung von Ionen der Konzentration n mit magnetischen

Momenten m  , deren Richtung ohne Feld isotrop verteilt sind, d.h. M ( B  0)  0 :
- Der Anteil der Momente im Winkelbereich
2

0
0
 d  12 sin d  4
   ist 1 2 sin d mit
- Aus der BOLTZMANN-Statistik ergibt sich
B
die Wahrscheinlichkeit, dass ein Teilchen die
Energie
E  m  B cos
hat zu

mit x  m B
w  exp(  E / kT )  exp( m B cos / kT )  exp( x cos )
kT
(1)
- Die Momentkomponente in z-Richtung ist
mz  m cos
Die relative Ausrichtung der Momente zum Feld kann damit berechnet werden. Im
klassischen Fall sind alle Winkel  zugelassen. Mit (1) ergibt die Mittelung über die
Kugelobefläche
2
cos  
M ( B, T )

MS

 d  cos  exp( x cos ) sin d
0
0

0
0
(2)
 d  exp( x cos ) sin d
y  cos 
Substitution
2

dy   sin d
1
cos  
 2  y  exp( xy)dy
1
1
 2  exp( xy)dy

Z
N
(3)
1
exp( xy)
du
 v   exp( xy)
 1 und v 
x
dy
exp( xy)
Z   uv´dy  uv   vu´dy mit  1  vdy 
x2
Nun wird partiell integriert: u  y  u  
M
cos 

MS
1
x
e
x

 (1)e  x  1x (e x  e  x )
1 x x3

coth
x

   ....  L( x)
x
x)
1
x
3 45
(
e

e
x
Entwicklung coth x 
1 x
  O( x 3 )
x 3
L(x) bezeichnet man
als LANGEVIN-Funktion.
x=m*B/kBT
(4)
Diskussion:

Für x<<1 bzw. kleine B/T ergibt sich aus (4) für die Hochtemperatursuszeptibilität. Die Reihenentwicklung in (4) wird nach dem linearen Term
abgebrochen:
L( x)  cos 
x 1 m B
 
und mit (2)
3 3 kT
2
m B
m B nm B
M ( B, T )  M S
 nm

3kT
3kT
3kT
(5)
Die Hochtemperatursuszeptibilität ist damit
C 

M  0 nm 2 C


H
3kT
T
....CURIE-Gesetz
(6)
Die CURIE-Konstante ist proportional zu m*2. Damit kann das atomare
magnetische Moment unmittelbar aus dem Anstieg der Kurve 1/= f(T) ermittelt
werden.
4.2 Brillouin-Funktion
In Folge der Richtungsquantelung des Drehimpulses können sich nur 2J+1 diskrete
Werte einstellen.
Es ergeben sich die Enegieniveaus E mz   m z g J  B B und
mit der Definition x

g J  B JB m * B

kT
kT
J.... Quantenzahl des Drehimpulses entspr. HUNDscher Regeln
mz...Magnetquantenzahl mit -J  mz  +J
die Polarisation als Summe über die möglichen Einstellungen
J
cos  
M (H ,T )

MS

mz
J
Mz   J
J
exp( mJz x)
 exp(
Mz  -J
mz
J
x)

(2J  1)
x
 2J  1  1
coth 
x   coth
 B( x)
2J
2J
 2J  2J
B(x) entspricht der BRILLOUIN-Funktion. .......... B( x) J 
 L( x )
(7)
Diskussion:




Für x = 0, d.h. für den Fall B = 0 bzw. T   ist B(x) = 0. Damit ist also die
Magnetisierung des Paramagneten gleich Null. Es existiert keine spontane
Magnetisierung.
Für x   , d.h. für Fall B   bzw. T = 0 ist B(x) = 1. Das heißt, dass alle
Momente parallel zum Feld ausgerichtet sind („Sättigung“).
Es gilt B(x)= -B(-x). Beim Umpolen des Feldes dreht sich auch die
Magnetisierung um (trivial !).
Für x<<1 bzw. kleine B/T ergibt sich aus (7) durch Reihenentwicklung


J 1
(J  1) (J  1) 2  J 2 3
B( x)  cos 
x
x  ....
3J
90J 3
und mit m*=gBJ unter Vernachlässigung des kubischen Terms
(J  1) m B
B
2
M ( B, T )  M S  cos   ng B J 
 ng 2  B (J  1)J
3J kT
3kT
(8)
(9)
Somit ist die Hochtemperatursuszeptibilität
2
M n 0 g 2  B (J  1)J n 0 meff
C
C 



H
3kT
3kT
T
2
....CURIE-Gesetz
(10)
J=S=7/2
M/MS
J=5/2
J=3/2
=m*B/kT
Beispiel:
Als Beispiel soll wiederum ein Zweiniveau-Spinsystem mit J = S = ½ betrachtet
werden. Damit ergeben sich die Einstellmöglichkeiten für den Drehimpuls mS = 1/2.
Aus Gleichung (7) folgt dann
cos  
M ( B, T )

MS
1 / 2
1 / 2
exp(  x)  11 // 22 exp(  x)
x3
 tanh x  x 
 ....
exp(  x)  exp(  x)
3
Damit gilt
M ( B, T )  n
B2B
kT
Besetzungswahrscheinlichkeit
Beispiel 7:
n 
C
 0 B 
kT
T
2
und
Polarisation M/MS
Wie sehen für das betrachtete paramagnetische Zweiniveausystem
Magnetisierung, Energiedichte, spezifische Wärme und Entropie in
Abhängigkeit von der Temperatur bei konstantem Magnetfeld aus ?
4.3
van Vleck – Paramagnetismus
Einen speziellen Fall stellen Systeme dar, bei denen eine Elektronenschale genau
ein Elektron weniger als die entsprechende halb gefüllte Schale hat (z.B. Eu 3+).
Damit gilt J = 0 und der Grundzustand ist nicht entartet.
Bei Berechnung der Energieverschiebung des Grundzustandes in Störungsrechnung
(s.o.) verschwindet der lineare Term. Der Term zweiter Ordnung ist jedoch nicht
notwendigerweise gleich Null, weil der Einfluss (schwach besetzter) angeregter
Zustände berücksichtigt wird.
Damit ist die Verschiebung der Grundzustandsenergie im Magnetfeld
E f 

f  B B z  L z  g S S z  f ´
Ef  Ef´
f f´
2
e 2 Bz2

8me
Z
f
 (x
i 1
2
i
 yi2 f ´
und man erhält durch zweifache Ableitung die Suszeptibilität
 
0 2 F
B 2
  0 n
 2 E f
B 2

f Lz  g S S z f ´
  0 n 2 B2 
Ef´  Ef

f'

2
e2

6 me
Z

i 1
ri
2




Der erste Summand ist wegen Ef´ > Ef positiv und beschreibt den van VLECKParamagnetismus.
Beide Terme in (*) sind klein und temperaturunabhängig.
(*)